MECHANIKA TEORETYCZNA

Temat nr 5

Analiza statyczna układów tarcz sztywnych.

Obliczanie reakcji więzów.

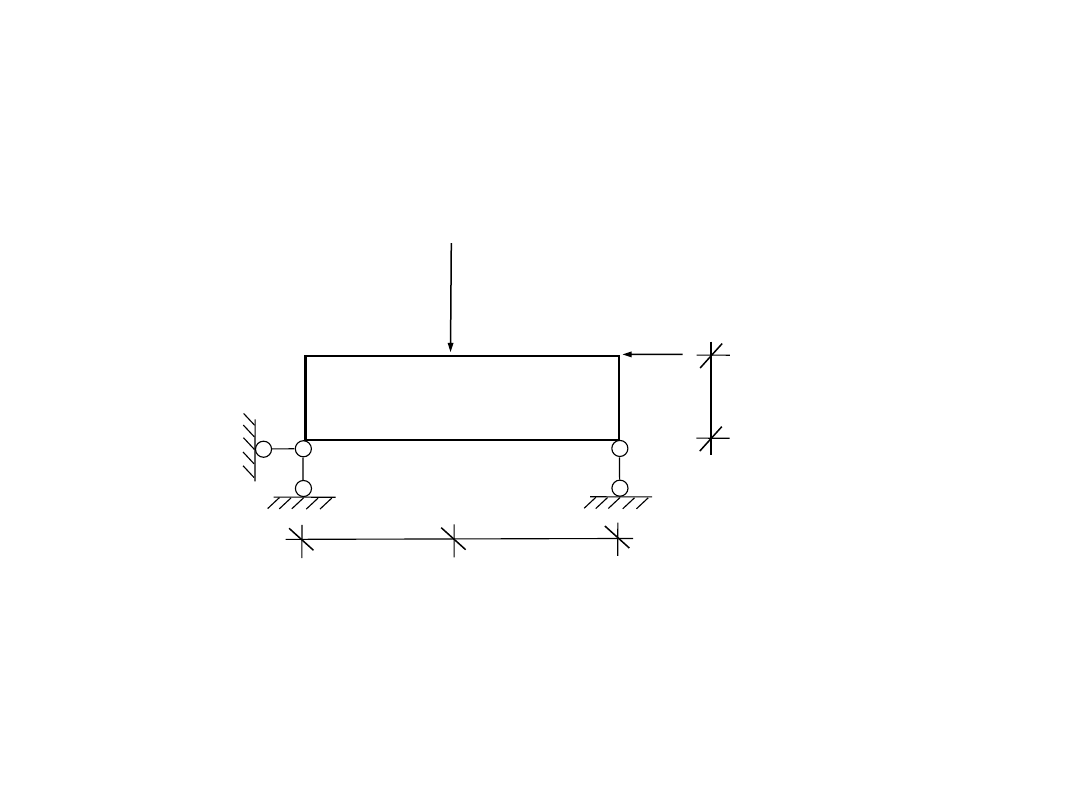
Zadanie 1: Przeprowadzić analizę geometryczną i statyczną
tarczy sztywnej.

P

1

= 12 kN

P

2

= 5 kN

2,0 m

4,0 m

4,0 m

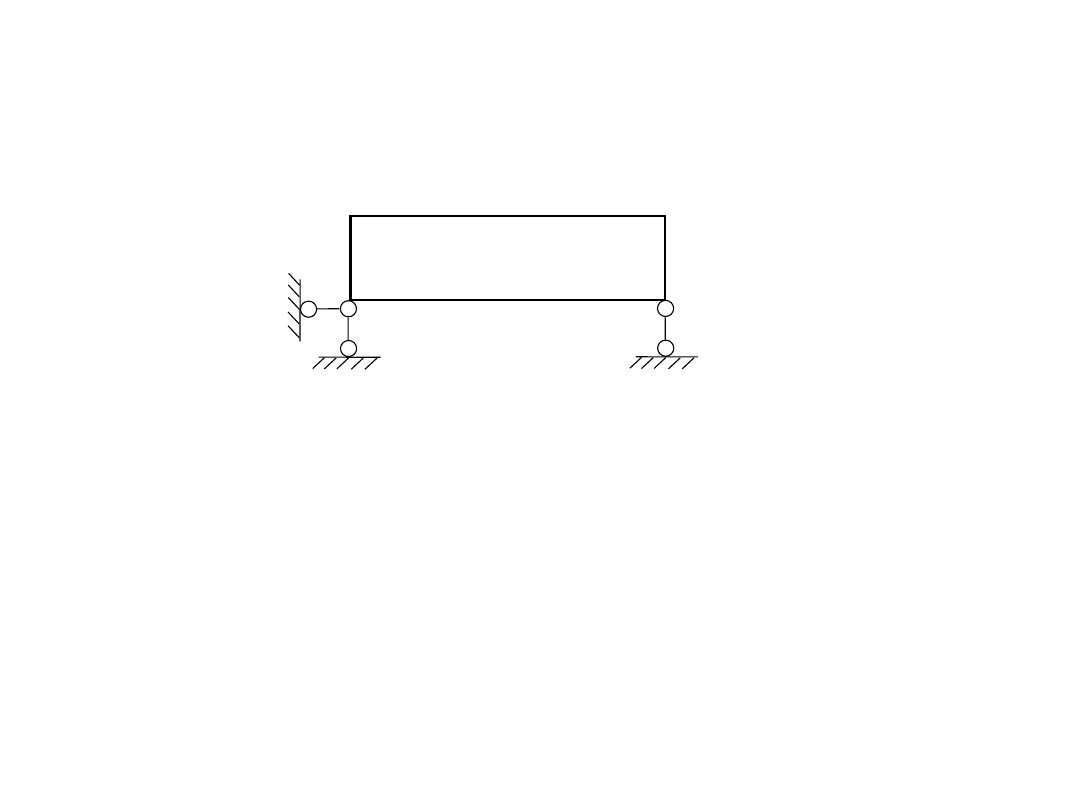
1) analiza geometrycznej niezmienności

1

2

3

I

warunek konieczny:

t = 1

p = 3

3t = p

warunek dostateczny:

kierunki trzech prętów nie
przecinają się w jednym punkcie

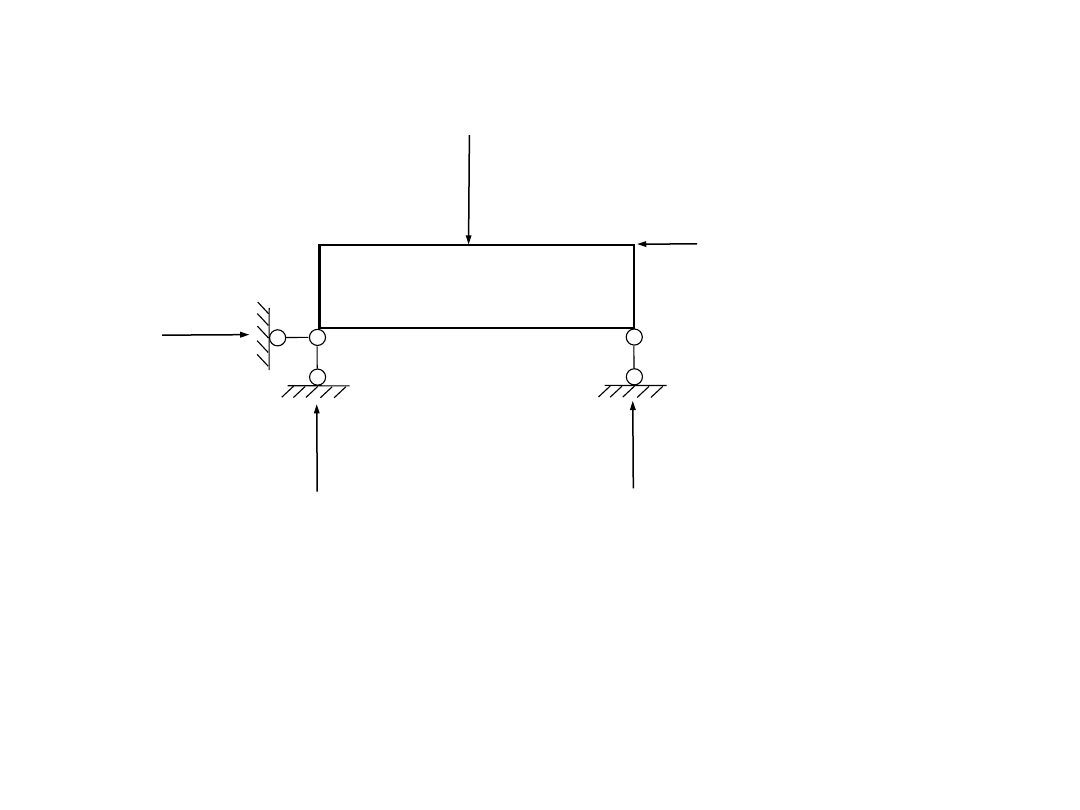
2) obliczenie reakcji więzów

P

1

= 12 kN

P

2

= 5 kN

R

1

R

2

R

3

Równania równowagi:

S

X = 0

S

Y = 0

S

M = 0

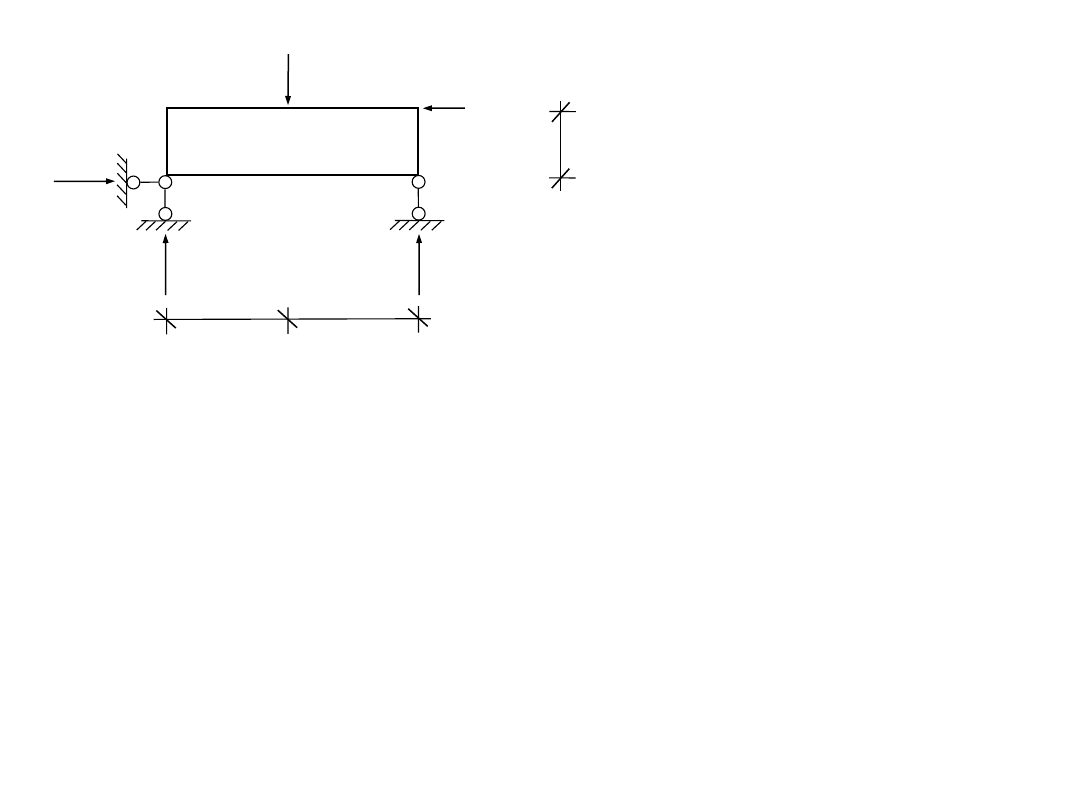
1º

S

X = 0

R

1

– 5 = 0

R

1

= 5 kN

2º

S

Y = 0

R

2

+ R

3

– 12 = 0

R

2

= 12 – R

3

3º

S

M

A

= 0

– 12·4 + 5·2 + R

3

·8

= 0

8·R

3

= 38

R

3

= 4,75 kN

z 2º R

2

= 12 – R

3

R

2

= 12 – 4,75

R

2

= 7,25 kN

P

1

= 12 kN

P

2

= 5 kN

R

1

R

3

R

2

A

B

2,0 m

4,0 m

4,0 m

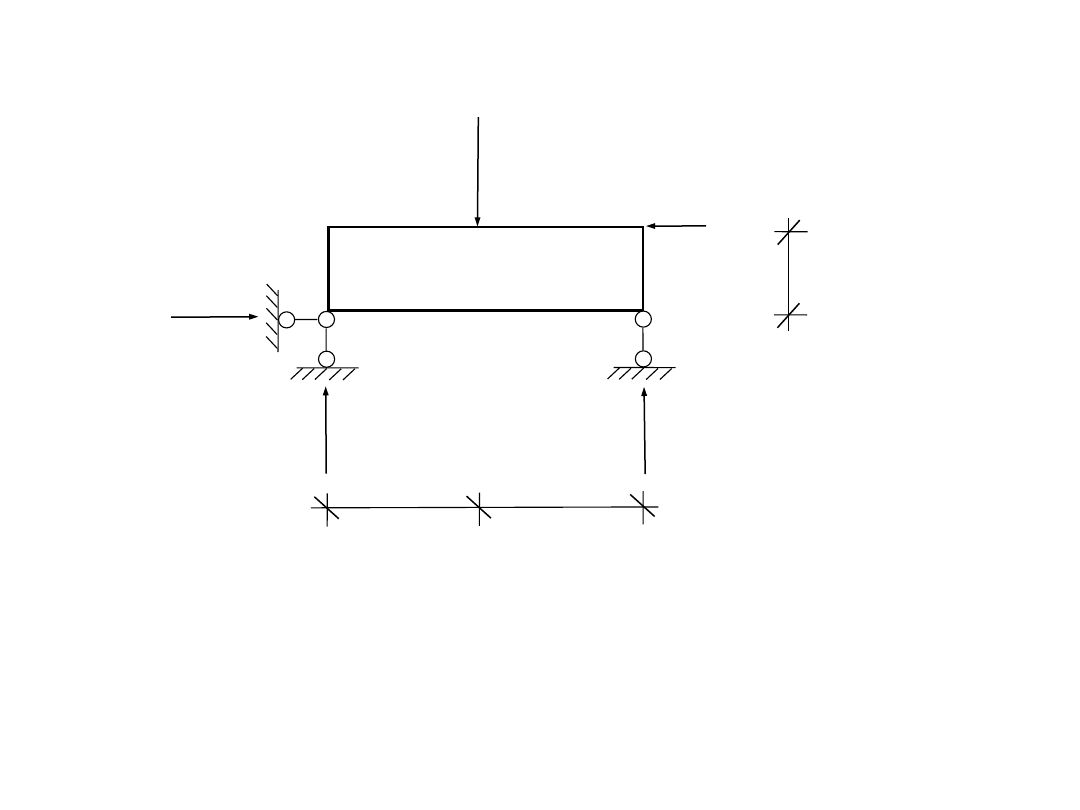
3) sprawdzenie reakcji

S

M

C

= 0

–12·4 + 5·2 + 4,75·8 = 0

0 = 0

L = P

P

1

= 12 kN

P

2

= 5 kN

R

1

= 5 kN

R

2

= 7,25 kN

R

3

= 4,75 kN

A

B

C

2,0 m

4,0 m

4,0 m

Zadanie 2: Przeprowadzić analizę geometryczną i statyczną
układu tarcz sztywnych.

P

1

= 10 kN

2,0 m

2,0 m

1,0 m

3,0 m

2,0 m

2,0 m

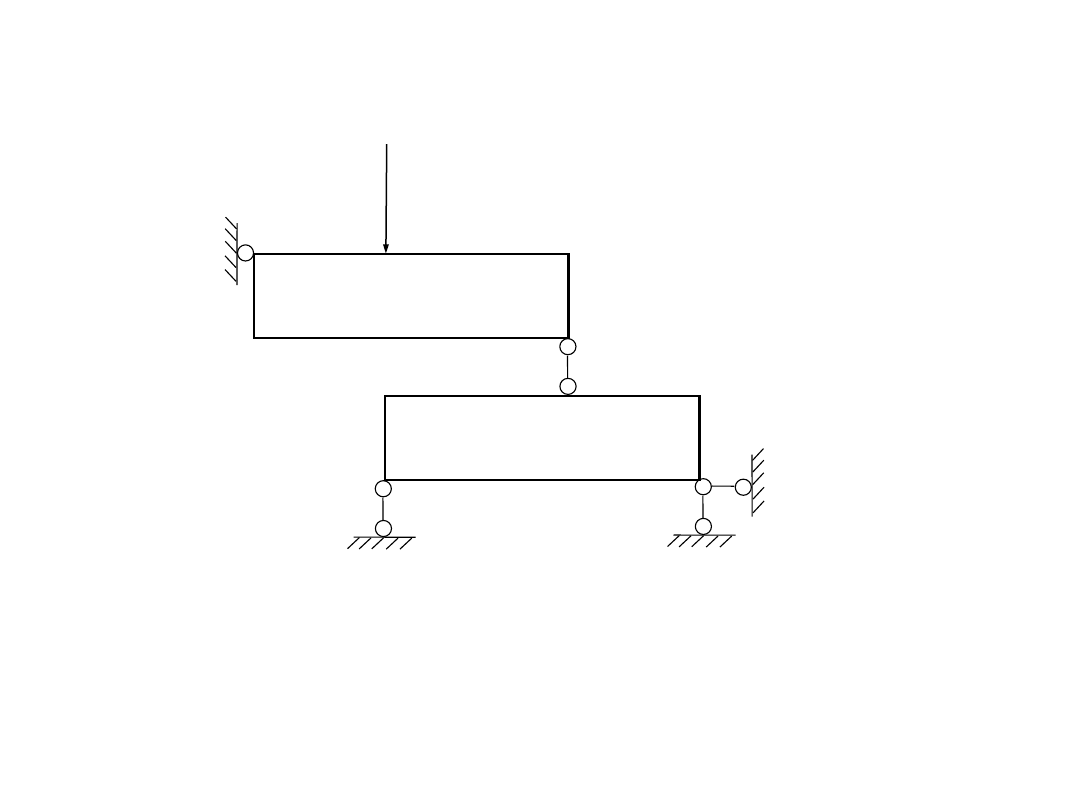
1) analiza geometrycznej niezmienności

warunek konieczny:

t = 2

p = 6

3t = p

warunek dostateczny:

1) tarcza II podparta trzema prętami

2) Tarcza I podparta przegubem i prętem

I

I I

(1,2)

P

1

= 10 kN

3

4

5

A

6

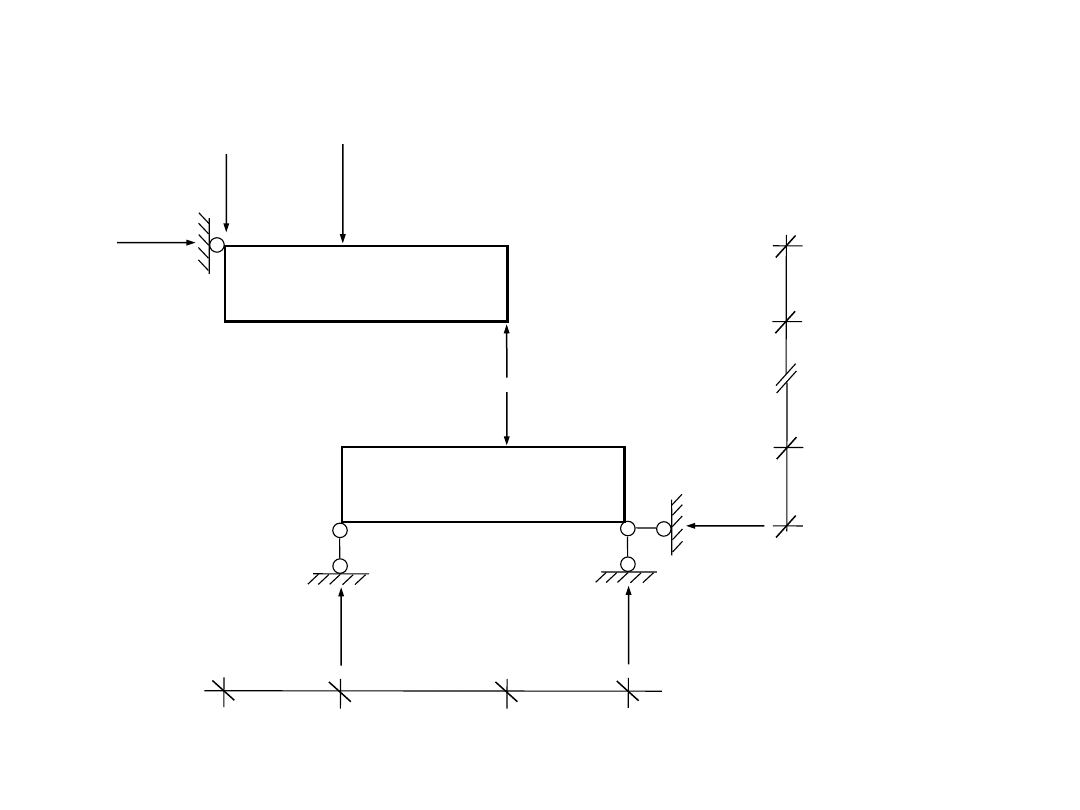
2) obliczenie reakcji więzów

I

R

3

P

1

= 10 kN

R

1

R

2

II

R

3

R

6

R

5

R

4

3,0 m

2,0 m

2,0 m

2,0 m

2,0 m

1,0 m

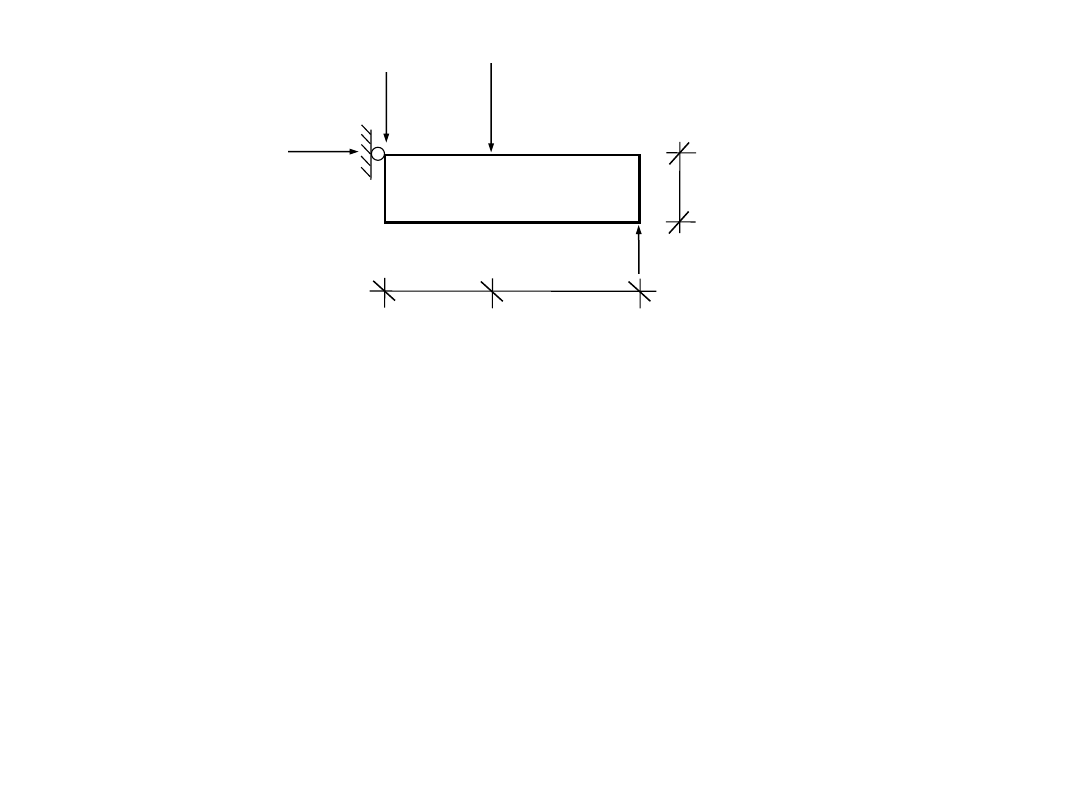
1º

S

X

I

= 0

R

2

= 0

2º

S

M

A

I

= 0

– 10·2 + R

3

·5 = 0

R

3

= 4kN

3º

S

Y

I

= 0

– R

1

– 10 + R

3

= 0

R

1

= – 6kN

sprawdzenie reakcji:

S

M

B

I

= 0 : R

1

·5

– R

2

·2 + 10·3 = 0

– 6·5

+ 10·3 = 0

L = P

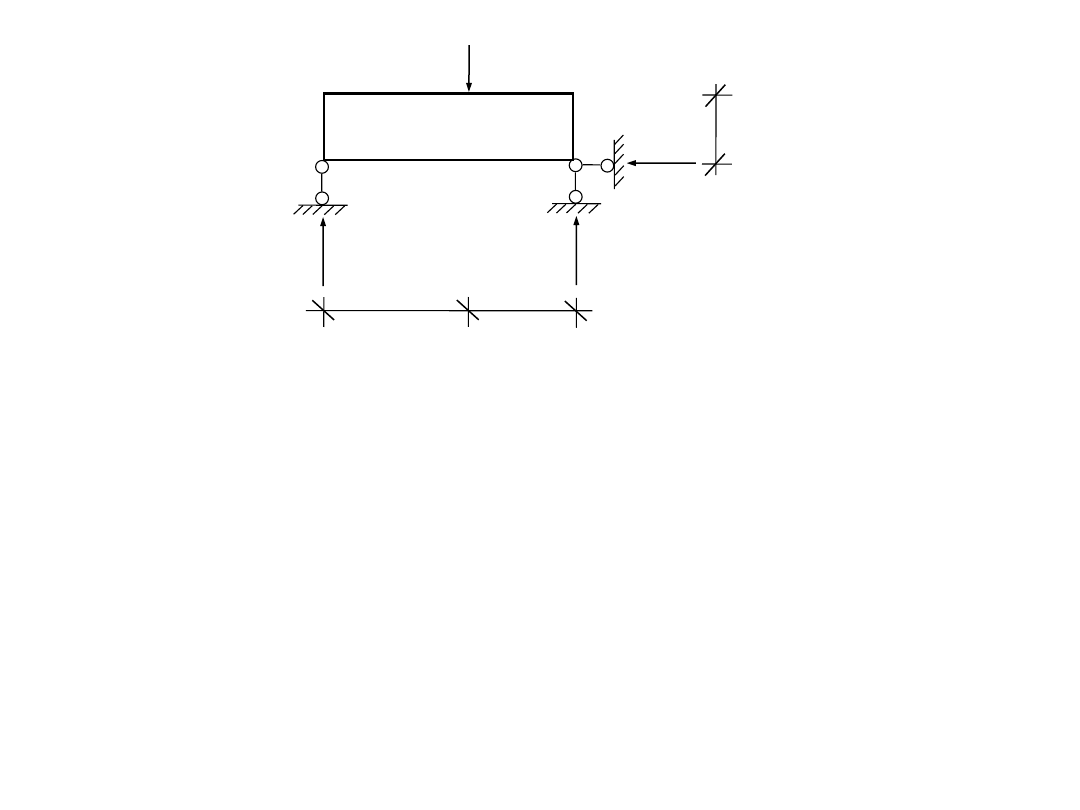
Tarcza I

R

3

I

P

1

= 10 kN

R

1

R

2

3,0 m

2,0 m

2,0 m

A

B

Tarcza II

1º

S

X

II

= 0

R

6

= 0

2º

S

M

C

II

= 0

– R

3

·3 + R

5

·5 = 0

R

5

= 2,4kN

3º

S

Y

II

= 0

R

4

+ R

5

– R

3

= 0

R

4

= R

3

– R

5

R

4

= 1,6kN

sprawdzenie reakcji:

S

M

D

I

= 0 : – R

4

·5 + R

3

·2 = 0

– 1,6·5

+ 4·2 = 0

L = P

R

5

II

R

3

= 4kN

R

6

R

4

C

D

2,0 m

3,0 m

2,0 m

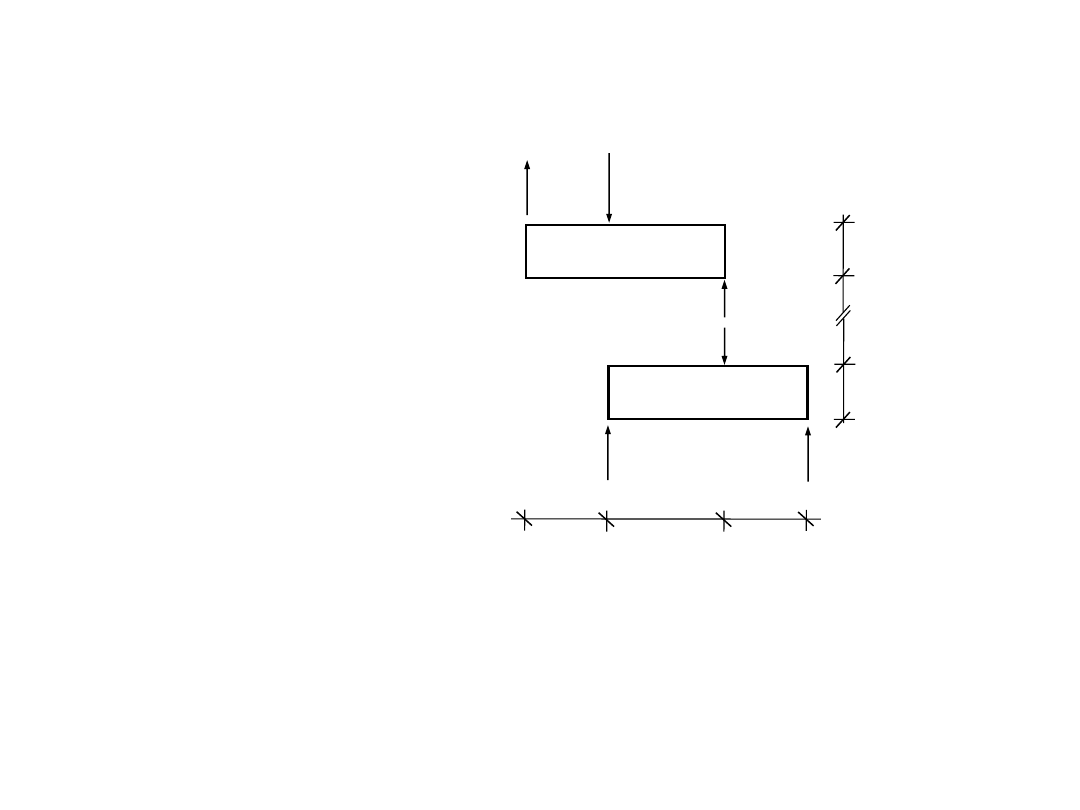
Rysunek zestawieniowy

10 kN

6 kN

I

4 kN

II

4 kN

2,4 kN

1,6 kN

3,0 m 2,0 m

2,0 m

2,0 m

2,0 m

1,0 m

sprawdzenie dla układu tarcz I+II:

S

Y

I+II

= 0 : – 10 + 6 + 2,4 + 1,6 = 0

L = P

3) sprawdzenie reakcji więzów

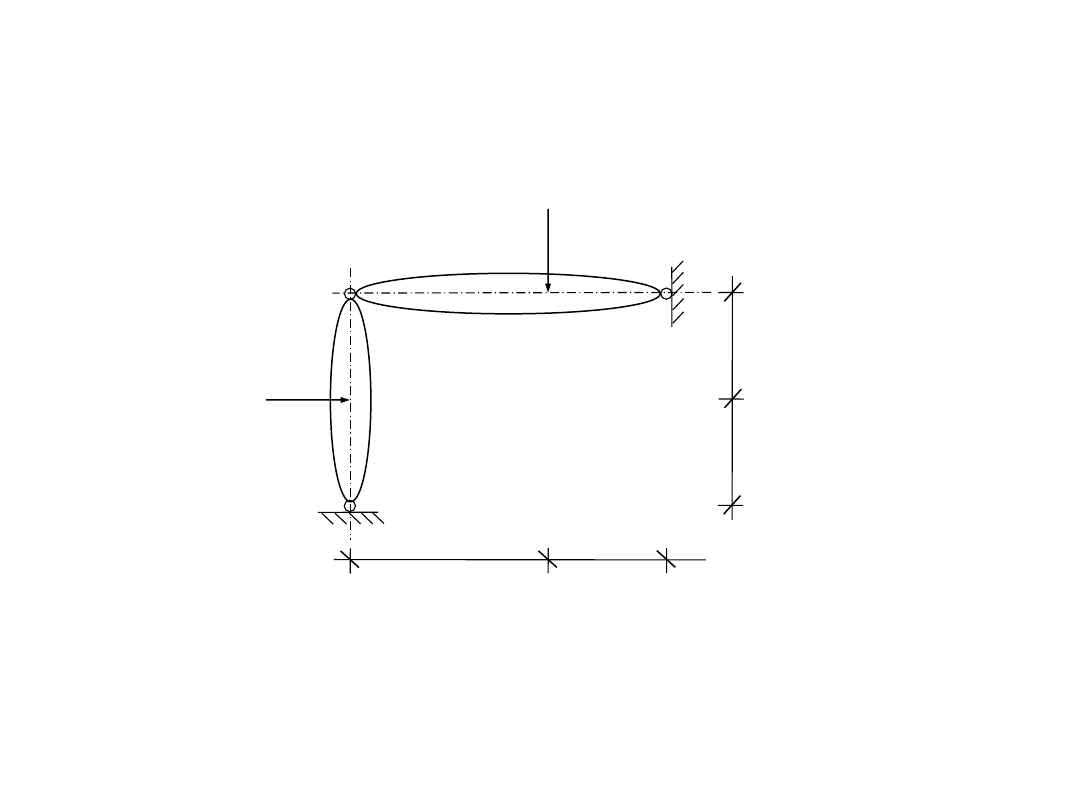
Zadanie 3: Przeprowadzić analizę geometryczną i statyczną
układu tarcz sztywnych.

P

1

= 10 kN

P

2

= 5 kN

4,0 m

2,0 m

2,0 m

2,0 m

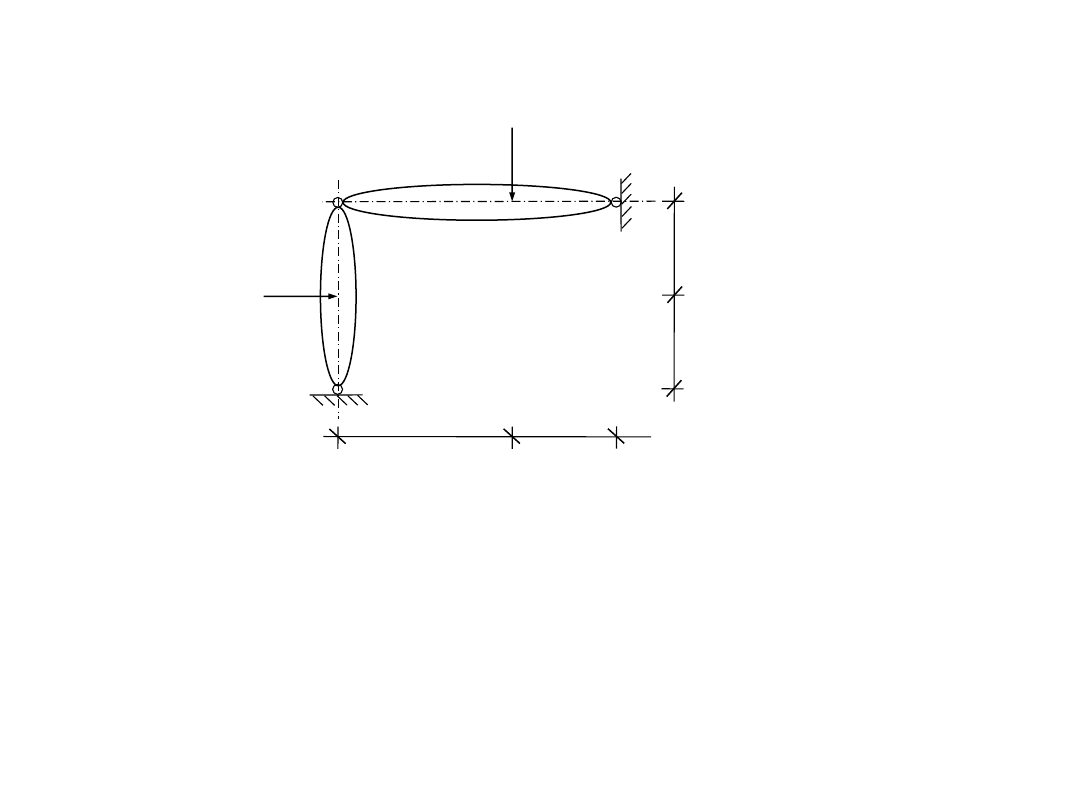
1) analiza geometrycznej niezmienności

warunek konieczny:

t = 2

p = 6

3t = p

A

B

C

(1,2)

(3,4)

(5,6)

warunek dostateczny:

1) układ trójprzegubowy

P

1

= 10 kN

P

2

= 5 kN

4,0 m

2,0 m

2,0 m

2,0 m

I

II

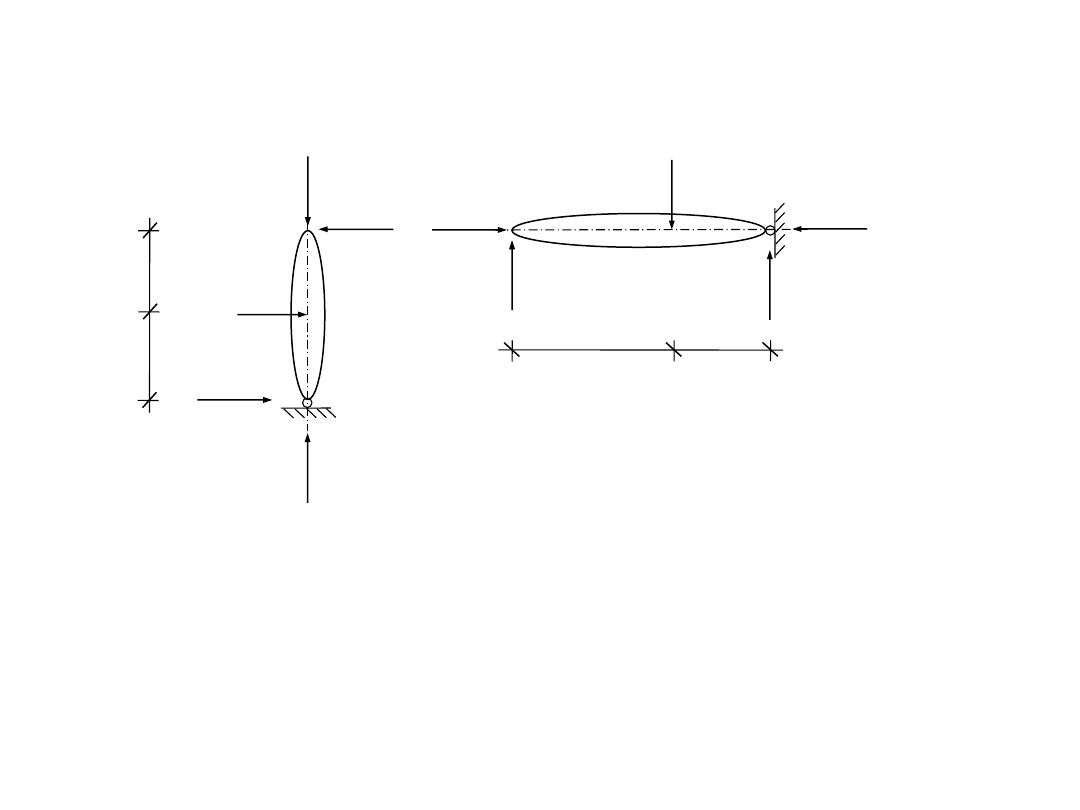
2) obliczenie reakcji więzów

2,0 m

2,0 m

P

2

= 5 kN

R

1

R

2

R

4

R

3

I

A

B

4,0 m

2,0 m

P

1

= 10 kN

R

4

R

3

R

5

R

6

II

B

C

1º

S

M

B

II

= 0

– 10·4 + R

5

·6 = 0

R

5

= 6,67kN

2º

S

M

A

I+II

= 0

– 5·2 – 10·4 + R

5

·6 + R

6

·4 = 0

R

6

= 2,5kN

3º

S

X

I+II

= 0

R

2

– R

6

+ 5 = 0

R

2

= – 2,5kN

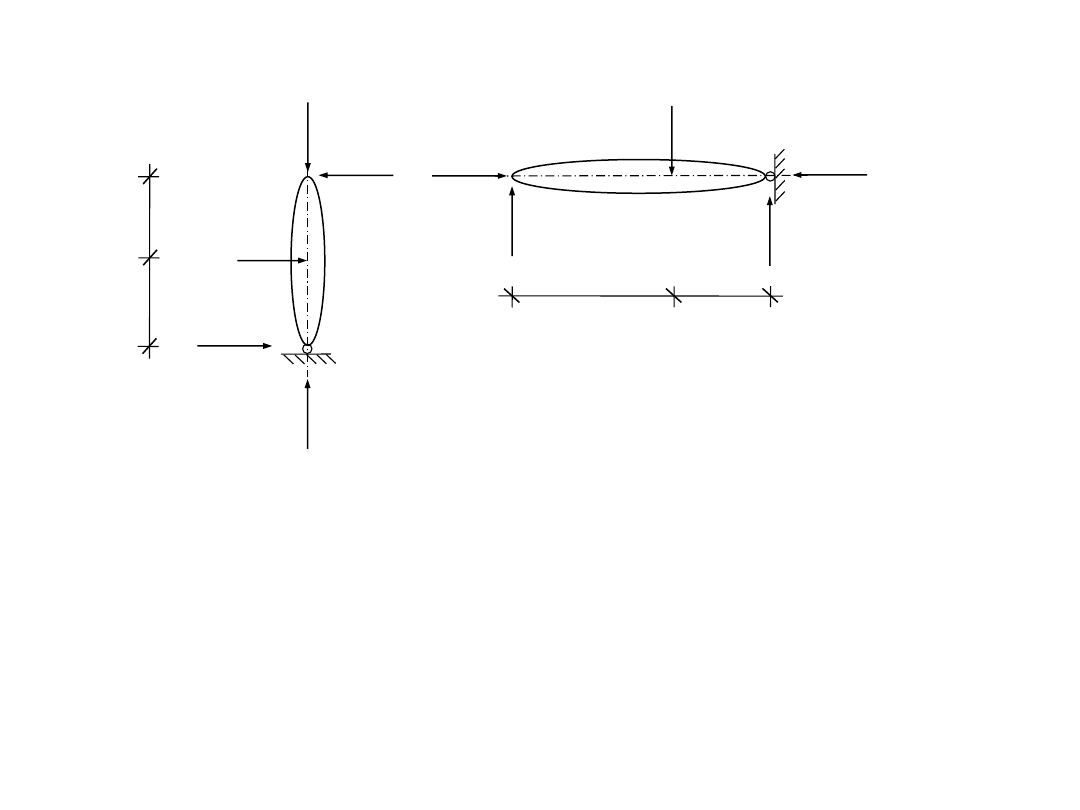
2,0 m

2,0 m

P

2

= 5 kN

R

1

R

2

R

4

R

3

I

A

B

4,0 m

2,0 m

P

1

= 10 kN

R

4

R

3

R

5

R

6

II

B

C

4º

S

Y

I+II

= 0

R

1

– 10 + R

5

= 0

R

1

= 10 – 6,67

R

1

= 3,33kN

5º

S

X

I

= 0

R

2

+

5

– R

4

= 0

R

4

= – 2,5 + 5

R

4

= 2,5kN

6º

S

Y

I

= 0

R

1

– R

3

= 0

R

3

= 3,33kN

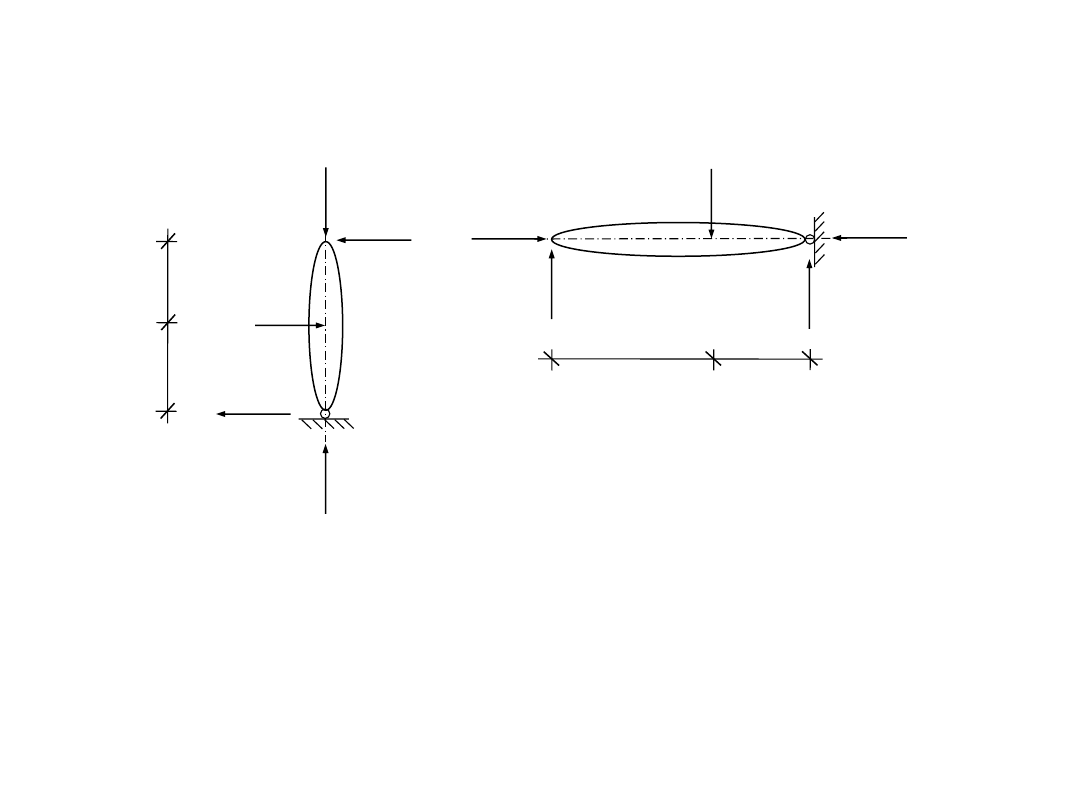
3) sprawdzenie reakcji więzów

Rysunek zestawieniowy

I

2,0 m

2,0 m

5 kN

3,33 kN

2,5 kN

2,5 kN

3,33 kN

A

B

4,0 m

2,0 m

10 kN

2,5 kN

3,33 kN

6,67 kN

2,5 kN

B

C

II

S

M

C

I+II

= 0

– 3,33·6 – 2,5·4 + 5·2 + 10·2 = 0

L=P

S

M

B

I

= 0

– 2,5 ·4 + 5·2 = 0

L=P

S

Y

II

= 0

3,33 + 6,67 – 10 = 0

L=P