
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-1
EKSTRAPOLACJA ITEROWANA RICHARDSONA
Do obliczenia pewnej wielkości stosuje się metodę numeryczną z
parametrem h. Wynikiem jej działania jest F(h). Wartością dokładną jest
F(0). Trudności obliczeniowe rosną, gdy h maleje.
Zakładamy, że znamy postać rozwinięcia (
....
p
p
p
3
2
1
<
<
)
....
h
a
h
a
h
a
a
)
h
(
F
p
p
p
3
2
1
3
2
1
0
+
+
+
=
F(0) ekstrapolujemy na podstawie kilku obliczonych wartości
F(h
0
), F(q
-1
h
0
), F(q
-2
h
0
), F(q
-3
h
0
)... q>1
Ekstrapolacja iterowana Richardsona pozwala na utworzenie ciągu
funkcji
),....
h
(
F
),
h
(
F
),
h
(
F
3
2
1
, którego n-ty wyraz ma rozwinięcie:
....
h
a
h
a
h
a
a
)
h
(
F
n
n
n
p
n
,
n
p
n
,
n
p
n
,
n
n
2
1
2
1
0
+
+
+
+
+
+
+
=
.

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-2
Sposób obliczeń: dana wartość początkowa h
0
i liczba q>1, stosuje się
wzór rekurencyjny:
....
,
,
n
,
A
)
h
(
F
...,
,
,
k
,
q
A
A
A
A
...
,
,
m
),
h
q
(
F
A
n
,
n
n
p
k
,
m
k
,
m
k
,
m
k
,
m
m
,
m
k
4
3
2
3
2
1
1
2
1
0
1
1
0
1
1
1
1
0
0
=
=
=
−
−
+
=
=
=
−
−
−
−
−
−
−
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-3
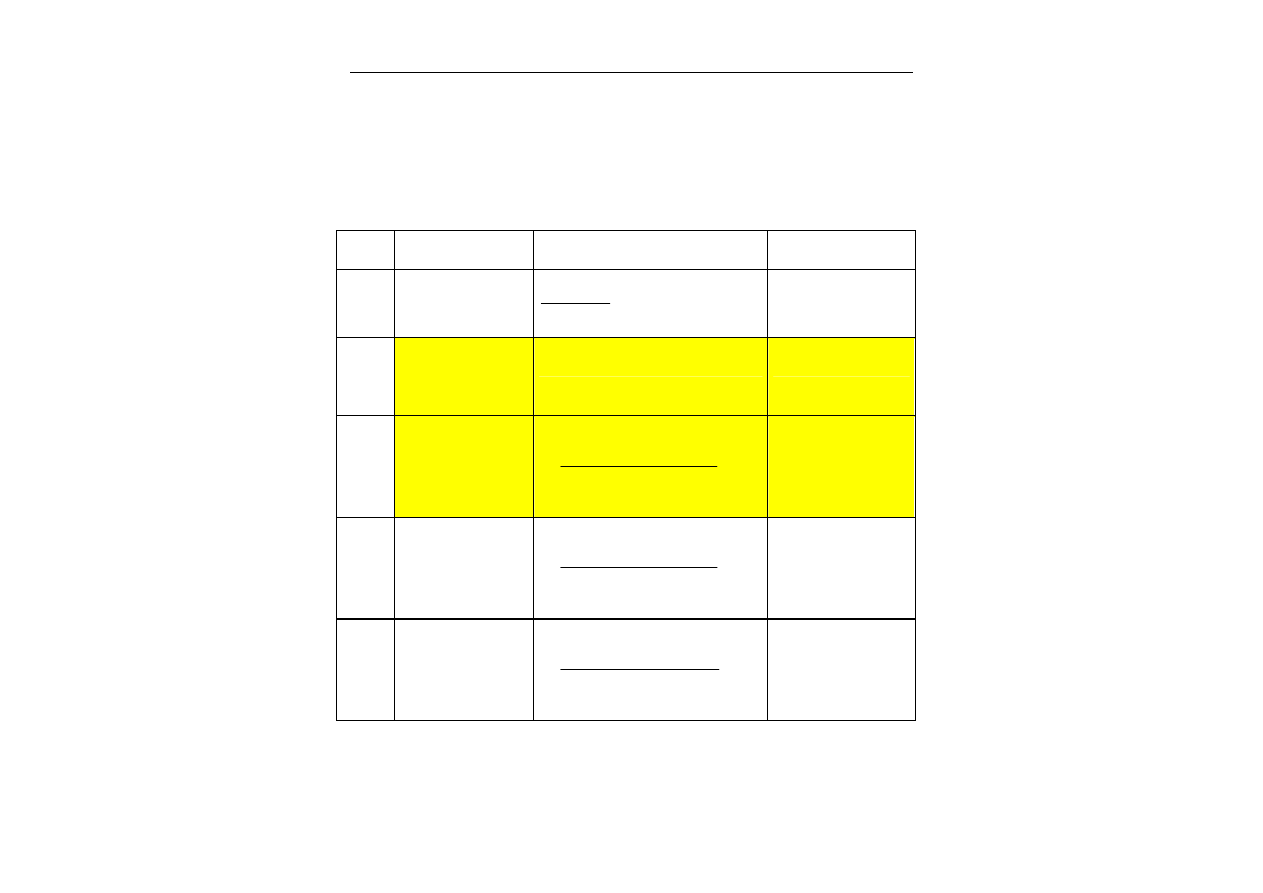
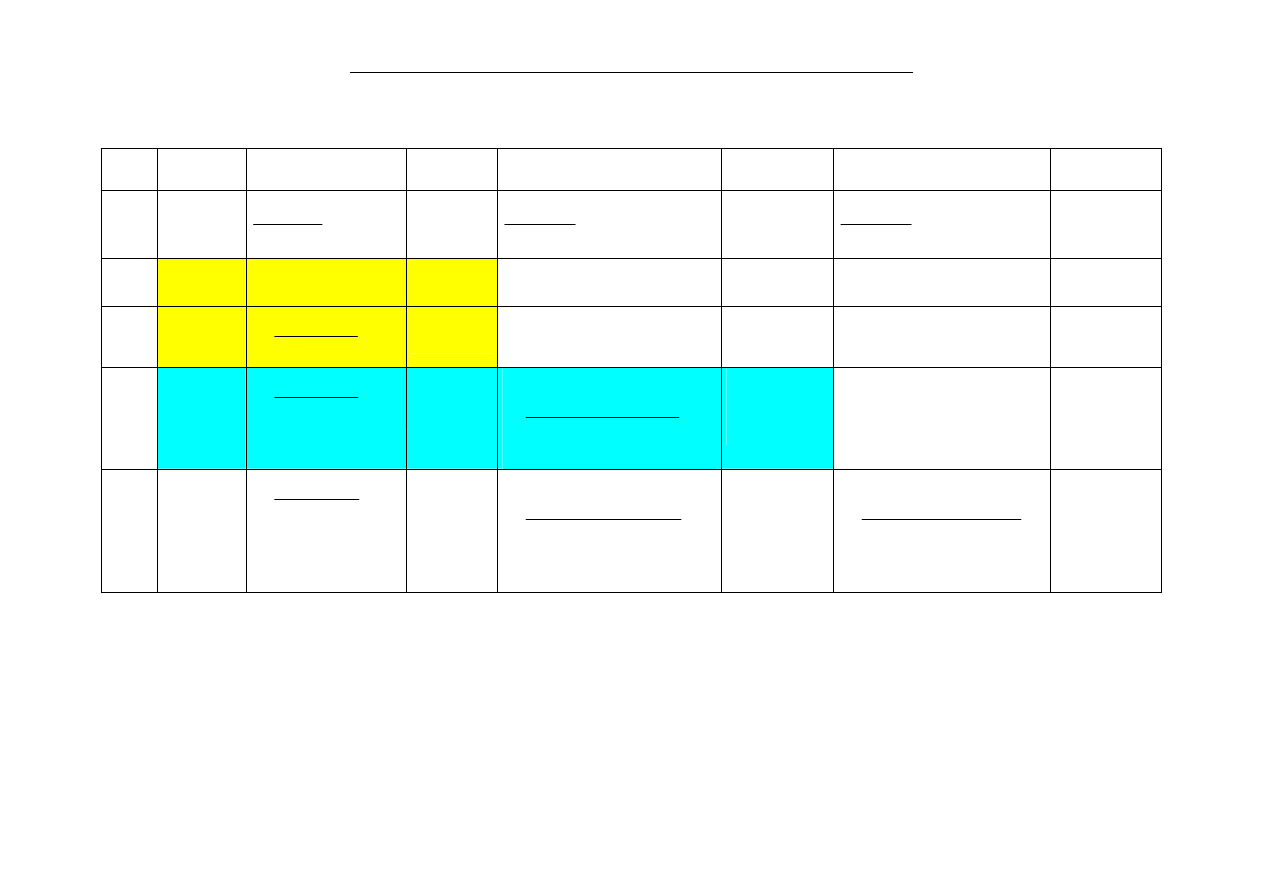
Schemat obliczeń:
1
1
1
−
−
−
−
=
Δ
k
,
m
k
,
m
A
A
k 0
1
m
1
1
−
Δ
p
q
0
)
h
(
F
A
,
0
0
0
=
1
)
h
q
(
F
A
,
0
1
0
1
−
=
+
1
1
0
0
0
1
−
−
p
,
,
q
A
A
=
)
h
(
F
A
,
0
2
1
1
=
2
)
h
q
(
F
A
,
0
2
0
2
−
=
+
1
1
0
1
0
2
−
−
p
,
,
q
A
A
=
)
h
q
(
F
A
,
0
1
2
1
2
−
=
3
)
h
q
(
F
A
,
0
3
0
3
−
=
+
1
1
0
2
0
3
−
−
p
,
,
q
A
A
=
)
h
q
(
F
A
,
0
2
2
1
3
−
=
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-4
k 0
1
2
3
m
1
1
−
Δ
p
q
1
2
−
Δ
p
q
1
3
−
Δ
p
q
0
A
F h
0 0
0
,
( )
=
1
A
F q h
1 0
1
0
,
(
)
=
−
+
A
A
q
p
1 0
0 0
1
1
,
,
−
−
=
A
F h
1 1
2
0
,
( )
=
2
A
F q h
2 0
2
0
,
(
)
=
−
+
A
A
q
p
2 0
1 0
1
1
,
,
−
−
=
A
F q h
2 1
2
1
0
,
(
)
=
−
+
1
2
1
1
1
2
−
−
p
,
,
q
A
A
=
)
h
(
F
A
,
0
2
2
2
=
3
A
F q h
3 0
3
0
,
(
)
=
−
+
A
A
q
p
3 0
2 0
1
1
,
,
−
−
=
A
F q h
3 1
2
2
0
,
(
)
=
−
+
1
2
1
2
1
3
−
−
p
,
,
q
A
A
=
)
h
q
(
F
A
,
0
1
3
2
3
−
=
+
1
3
2
2
2
3
−
−
p
,
,
q
A
A
=
)
h
(
F
A
,
0
4
3
3
=

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-5
Zastosowanie do różniczkowania numerycznego
L
+
+
+
+
=
+
)
x
(
f
!
h
)
x
(
'
'
f
!
h
)
x
(
'
hf
)
x
(
f
)
h
x
(
f
)
(
0
3
3
0
2
0
0
0
3
2
Różnica progresywna
L
+
+
+
=
−
+
=
)
x
(
f
!
h
)
x
(
'
'
f
!
h
)
x
(
'
f
h
)
x
(
f
)
h
x
(
f
)
h
(
D
)
(
P
0
3
2
0
0
0
0
3
2
...
,
p
,
p
,
p
3
2
1
3
2
1
=
=
=

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-6
Różnica centralna
L
L
L
+
+
+
=
=
⎭
⎬
⎫
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+
−
−
⎩
⎨
⎧
−
⎟
⎠
⎞
⎜
⎝
⎛
+
+
+
+
=
=
−
−
+
=
)
x
(
f
!
h
)
x
(
f
!
h
)
x
(
'
f
)
x
(
f
!
h
)
x
(
'
'
f
!
h
)
x
(
'
hf
)
x
(
f
)
x
(
f
!
h
)
x
(
'
'
f
!
h
)
x
(
'
hf
)
x
(
f
h
h
)
h
x
(
f
)
h
x
(
f
)
h
(
D
)
(
)
(
)
(
)
(
C
0
5
4
0
3
2
0
0
3
3
0
2
0
0
0
3
3
0
2
0
0
0
0
5
3
3
2
3
2
2
1
2
...
,
p
,
p
,
p
6
4
2
3
2
1
=
=
=
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-7
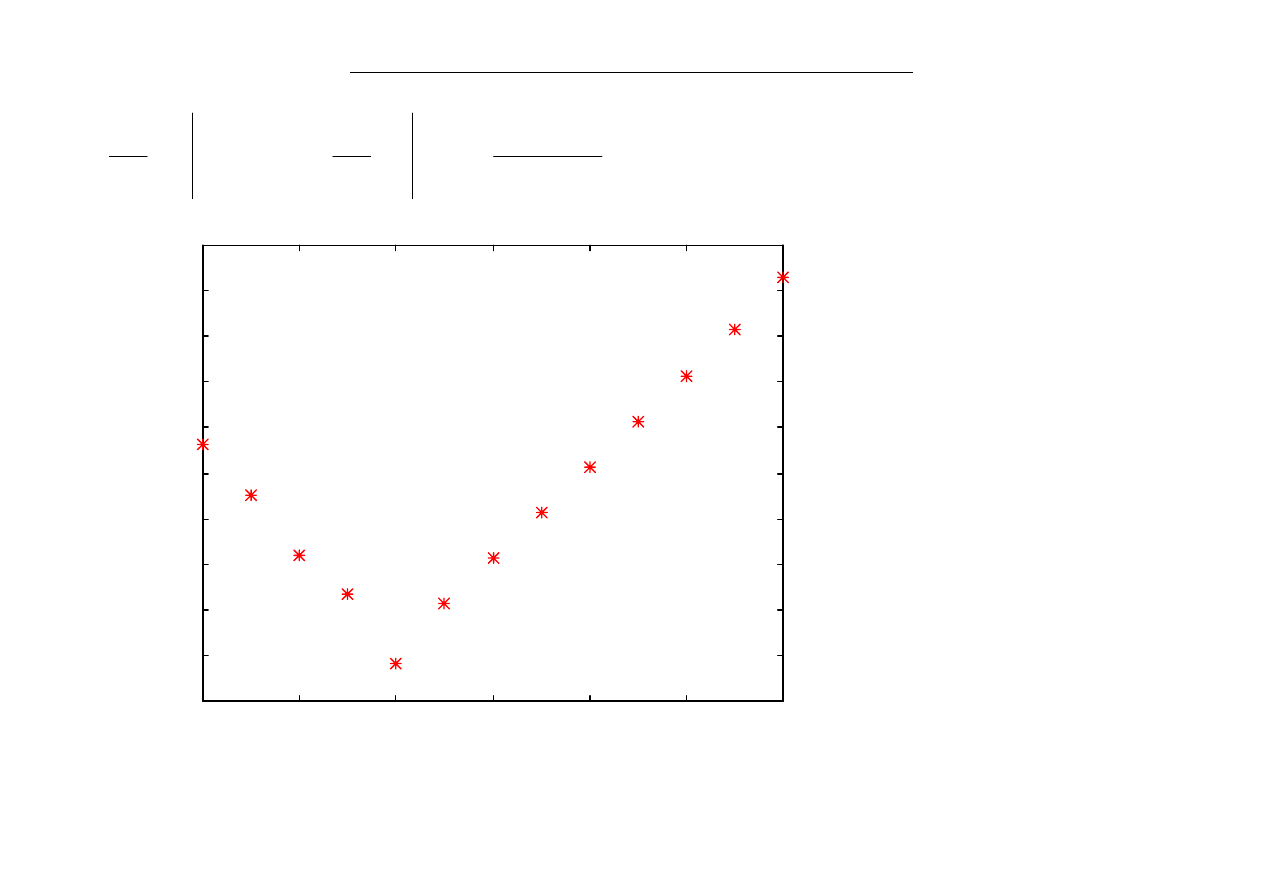
?
e
dx
d
x
x
=
=1
h
e
e
e
dx
d
h
x
x
−
≈
+
=
1
1
h=10
-n
-12
-10
-8
-6
-4
-2
0
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
n
lo
g10(
b
la
d)
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-8
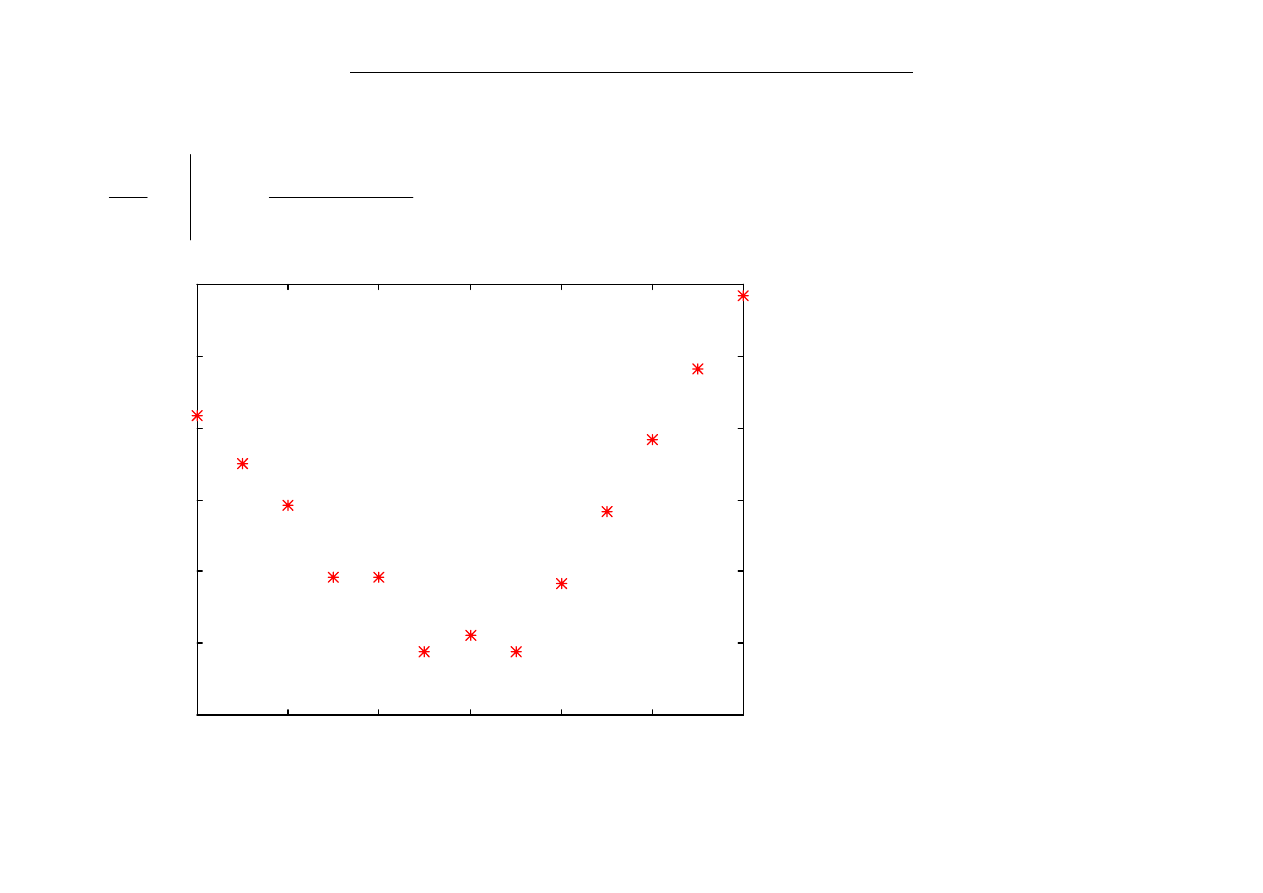
h
e
e
e
dx
d
h
h
x
x
2
1
1
1
−
+
=
−
≈
h=10
-n
-12
-10
-8
-6
-4
-2
0
-12
-10
-8
-6
-4
-2
0
n
log10(
b
la
d)

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
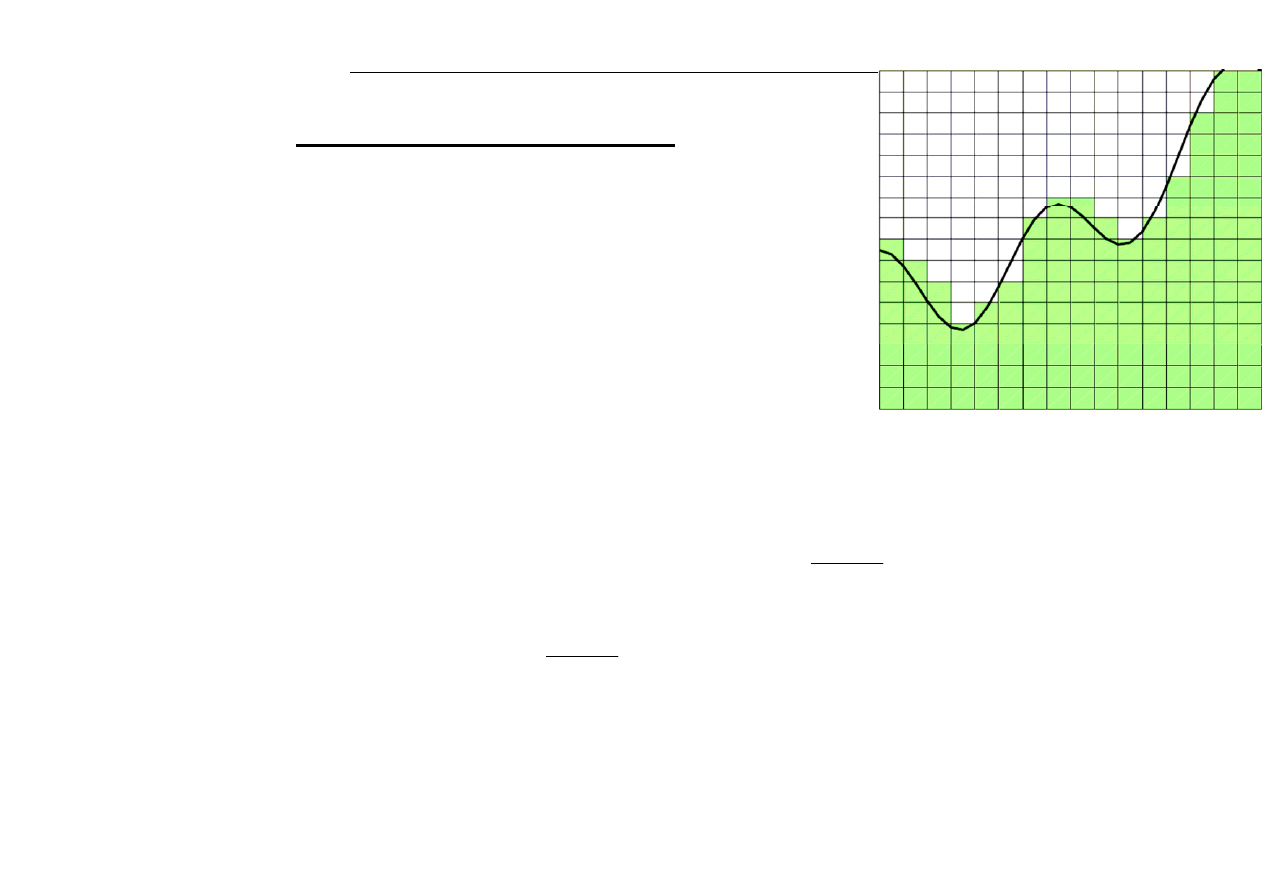
W3-9
Z Ekstrapolacji Richardsona
0.2
0.4
0.6
0.8
1
-14
-12
-10
-8
-6
-4
-2
h
log10(
bl
ad)
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-10
Całkowanie numeryczne
Kwadratura:
∫
∑
=
=
b
a
n
k
k
k
)
x
(
f
A
dx
)
x
(
f
0
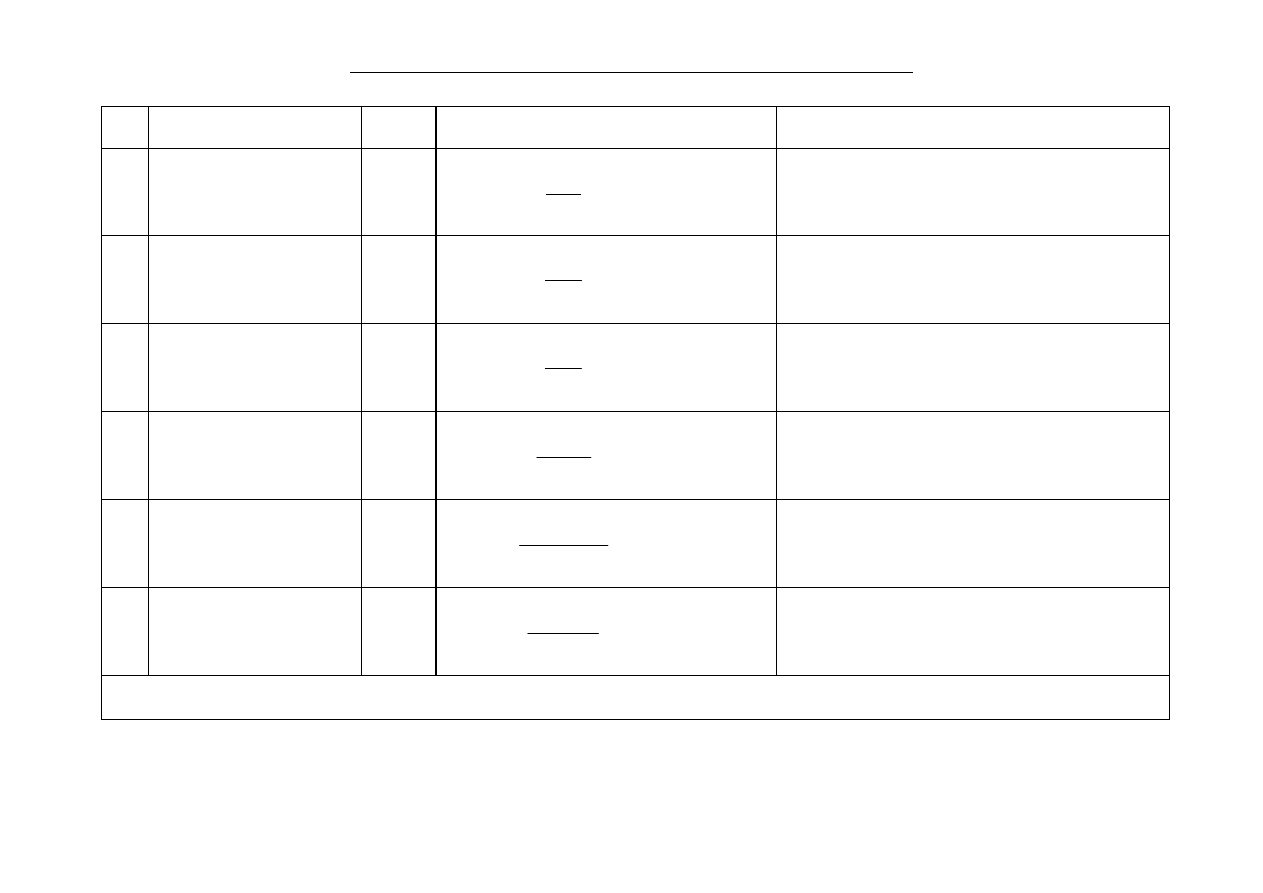
KWADRATURY NEWTONA-COTESA
uzyskane przez interpolację wielomianem z węzłami
równoodległymi
n
a
b
h
,
n
,...,
i
,
ih
a
x
i
−
=
=
+
=
0
)
x
(
P
)
x
(
f
f
,
f
ns
a
b
dx
)
x
(
P
dx
)
x
(
f
i
n
i
i
b
a
n
i
i
i
n
b
a
=
=
−
=
≈
∫
∑
∫
=0
σ
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-11
n
σ
i
ns
błąd nazwa
1 1 1
2
)
(
f
h
)
(
ξ
2
3
12
1
wzór trapezów
2 1 4 1
6
)
(
f
h
)
(
ξ
4
5
90
1
wzór Simpsona
3 1 3 3 1
8
)
(
f
h
)
(
ξ
4
5
80
3
wzór "trzech ósmych"
4 7 32 12 32
7
90
)
(
f
h
)
(
ξ
6
7
945
8
wzór Milne'a
5 19 75 50 50
75 19
288
)
(
f
h
)
(
ξ
6
7
12096
275
-
6 41 216 27 272
27 216 41
840
)
(
f
h
)
(
ξ
8
9
1400
9
wzór Weddle'a
h- długość przedziału,
ξ
- punkt pośredni

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-12
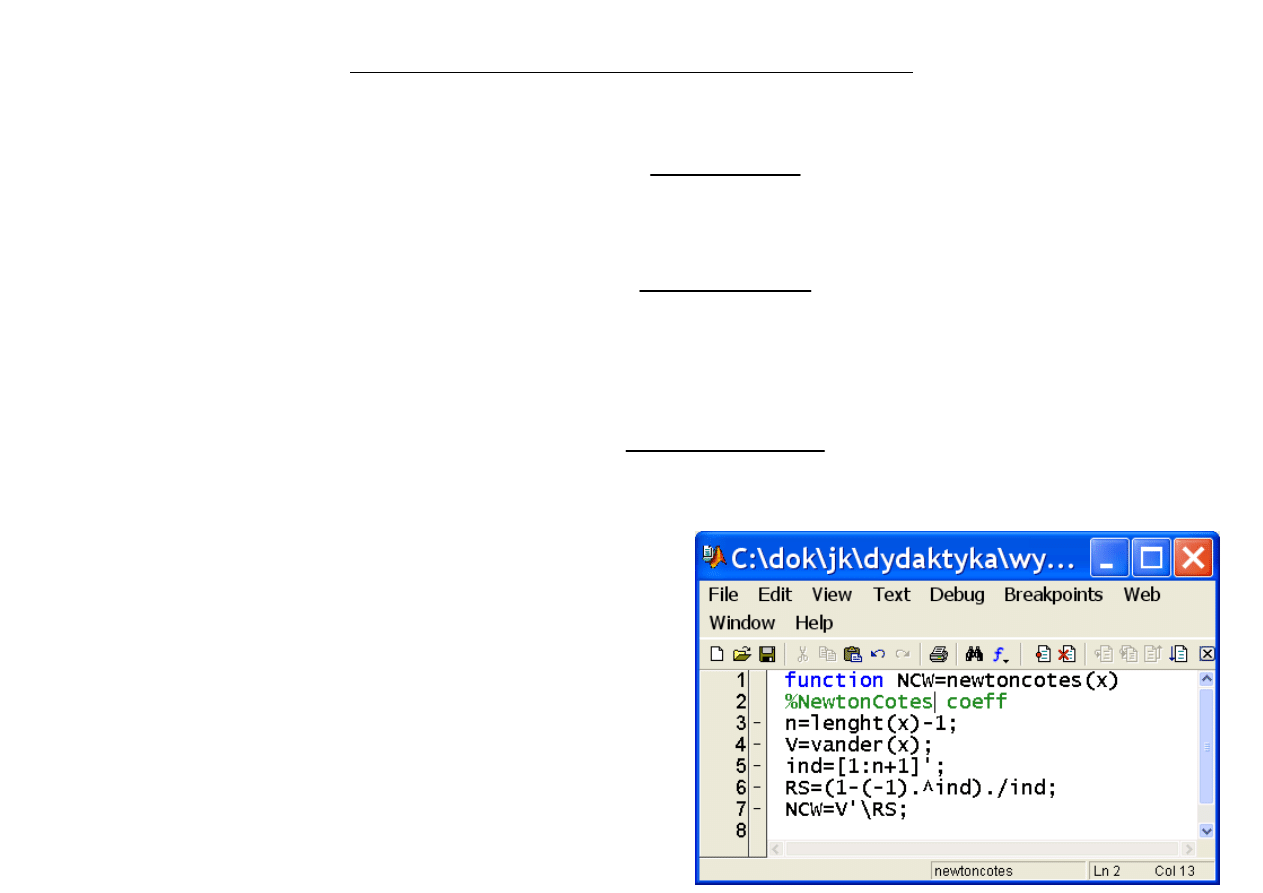
Obliczenie współczynników kwadratur Newtona-Cotesa:
Dane są węzły x
0
,x
1
,..,x
n
. Chcemy, by kwadratura całkowała dokładnie (na przedziale [–1
1])stałą:
1
1
1
1
1
1
1
1
1
0
0
0
1
1
0
0
0
)
(
x
dx
x
x
w
x
w
x
w
n
n
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
+
+
+
−
−
∫
L
oraz funkcje x, x
2
, …x
n
:
2
1
1
2
2
2
1
1
1
1
2
1
1
1
1
1
1
0
0
)
(
x
dx
x
x
w
x
w
x
w
n
n
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
+
+
+
−
−
∫
L
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
0
0
+
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
+
+
+
+
−
−
+
∫
n
)
(
n
x
dx
x
x
w
x
w
x
w
n
n
n
n
n
n
n
n
L
W postaci macierzowej:
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-13
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
−
−
−
−
−
−
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
1
1
1
2
1
1
1
1
1
1
2
1
0
1
0
1
1
1
1
1
0
0
0
1
0
0
n
)
(
)
(
)
(
w
w
w
x
x
x
x
x
x
x
x
x
n
n
n
n
n
n
n
M
M
L
M
M
M
M
K
L
transponowana macierz Vandermode’a

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-14
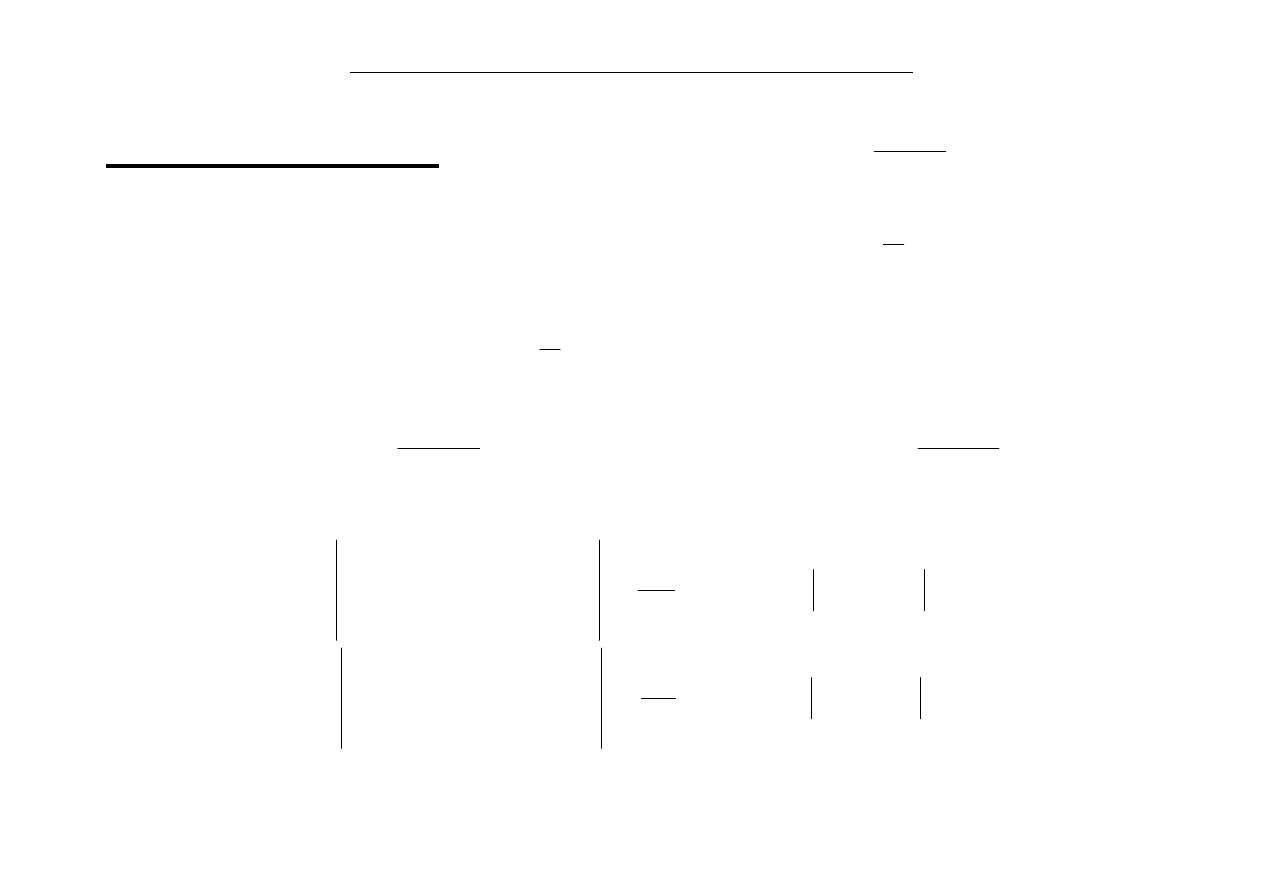
Kwadratura Newtona-Cotes’a o n+1 węzłach obliczy dokładnie całkę wielomianu
stopnia n. Można zmienić układ węzłów, tak by zwiększyć stopień wielomianu
całkowanego dokładnie przez kwadraturę korzystającą z n węzłów.
Kwadratury Gaussa pozwalaja na dokładne całkowanie wielomianów stopnia do
2n-1 przy n węzłach.
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-15
Kwadratury złożone
n
a
b
h
,
n
,...,
i
,
ih
a
x
i
−
=
=
+
=
0
Wzór prostokątów
)
h
(
R
)
h
x
(
f
h
dx
)
x
(
f
n
i
i
b
a
=
+
≈
∑
∫
−
=
1
0
2
Wzór trapezów
[
]
)
h
(
T
)
x
(
f
)
x
(
f
h
dx
)
x
(
f
n
i
i
i
b
a
=
+
≈
∑
∫
−
=
+
1
0
1
2
⎥⎦
⎤
⎢⎣
⎡
+
−
+
+
+
+
=
2
2
)
b
(
f
)
h
b
(
f
)
h
a
(
f
)
a
(
f
h
)
h
(
T
L
Oszacowanie błędu obcięcia:
(
)
)
(
'
'
f
h
a
b
)
h
(
R
dx
)
x
(
f
b
a
ξ
2
24
1
−
≤
−
∫
(
)
)
(
'
'
f
h
a
b
)
h
(
T
dx
)
x
(
f
b
a
ξ
2
12
1
−
≤
−
∫

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-16
L
+
+
+
+
=
∫
6
3
4
2
2
1
h
a
h
a
h
a
dx
)
x
(
f
)
h
(
T
b
a
Metoda Romberga=
=złożona kwadratura trapezów+ekstrapolacja Richardsona
q=2, p
i
=2i
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-17
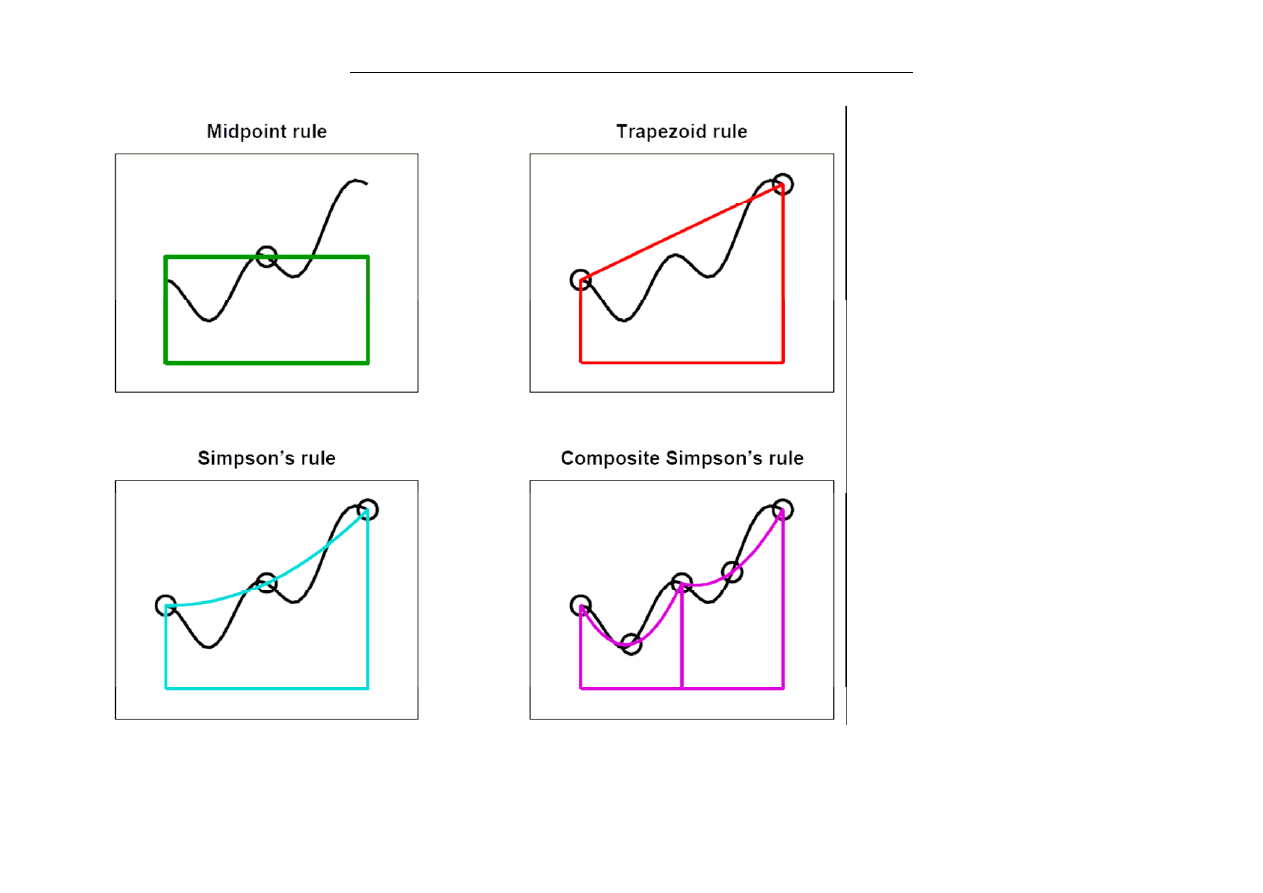
Kwadratury adaptacyjne
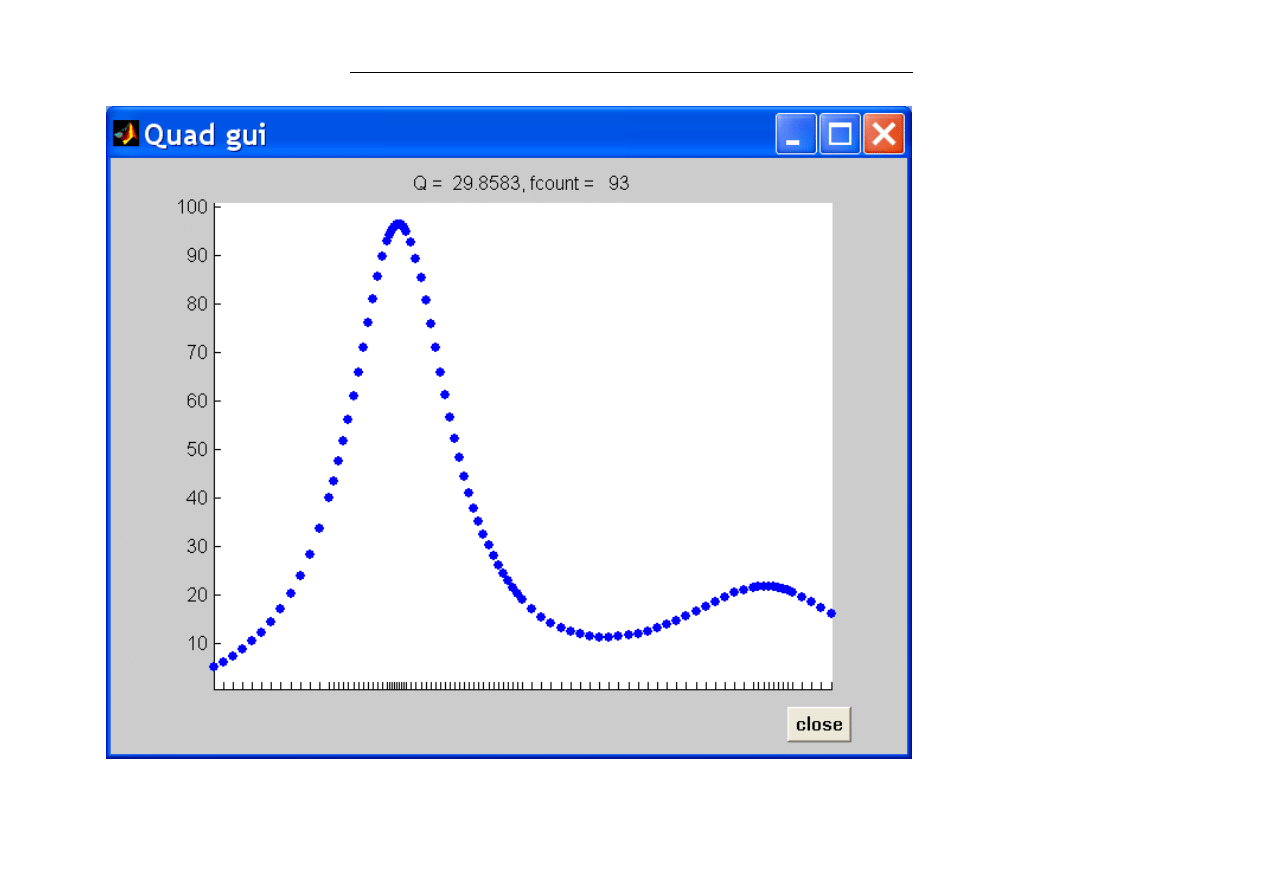
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 3
W3-18
Wyszukiwarka
Podobne podstrony:
metody w2 et
metody w1 et
MetodyOpt Biofiz 2013 w3 polaryzacja
Metody badań społecznych W3, Metody badań społecznych
Metody numeryczne w3
metody badawcze w socjologii w3
metody numeryczne i w3
metody numeryczne w3 (2)
metody numeryczne w3
Metody numeryczne w3
więcej podobnych podstron