Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Metody numeryczne (analiza numeryczna

)

- nauka zajmująca się rozwiązywaniem problemów matematycznych
metodami arytmetycznymi
- sztuka doboru spośród wielu możliwych procedur takiej, która jest
„najlepiej” dostosowana do rozwiązania danego zadania
Mathematics + Computer Science + Engineering = Scientific
Computing

Oszacowanie błędu numerycznego obliczenia

przy n+1

obliczeniach wartości f(x)

∫

b

a

dz

)

x

(

f

Metoda trapezów

2

1

3

12n

)

(

''

f

)

a

b

(

ξ

−

Metoda Simpsona

4

2

4

5

180 n

)

(

f

)

a

b

(

)

(

ξ

−

W1 - 1

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

1. Odpowiednie sformułowanie zadania
2. Metoda numeryczna + analiza błędu
3. Algorytm
4. Implementacja

1. Błąd danych wejściowych
2. Błąd zaokrągleń w czasie obliczeń
3. Błąd metody (obcięcia)
4. Błąd wnoszony przez uproszczenia modelu matematycznego
5. Błąd człowieka

a~

jest przybliżeniem wartości dokładnej a

a

Błąd bezwzględny:

a~

a

−

=

Δ

Błąd względny:

0

≠

−

=

Δ

=

a

,

a

a

a~

a

a

a

ε

a

)

(

a

a

a

a~

a

a

a

ε

ε

+

=

+

=

Δ

+

=

1

0

1

≠

−

=

−

=

Δ

=

a

,

a

a~

a

a

a~

a

a

a

ε

uogólnienie na wartości wektorowe

szacowanie modułów błędów

W1 - 2

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Przenoszenie się błędów w obliczeniach numerycznych

1. Analiza bezpośrednia krok po kroku – analiza przedziałowa:

4

4

.

y~

=

poprawnie zaokrąglona, więc

45

4

35

4

.

y

.

<

<

05

0.

y

<

Δ

0115

.

0

35

.

4

05

.

0

=

<

y

ε

0976

2.

y~

=

1095

2

0857

2

.

y

.

<

<

0119

0.

y

<

Δ

0057

0.

y

<

ε

3

10.

x~

=

poprawnie zaokrąglona, więc

35

10

25

10

.

x

.

<

<

05

0.

x

<

Δ

049

0

25

10

05

0

.

.

.

x

=

<

ε

.....................................................................

5175

.

2

)

~

~

ln(

~

=

+

=

y

x

z

5225

.

2

)

ln(

5125

.

2

<

+

<

y

x

005

.

0

<

Δ

z

0020

.

0

<

z

ε

W1 - 3

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

2. Wykorzystanie podstawowych wzorów:

a

)

(

a

a

a

a~

a

a

a

ε

ε

+

=

+

=

Δ

+

=

1

0

1

≠

−

=

−

=

Δ

=

a

,

a

a~

a

a

a~

a

a

a

ε

1

1

1

ε

,

x~

,

x

,

2

2

2

ε

,

x~

,

x

Iloczyn:

2

1

x

x

y

=

2

1

2

1

2

1

2

2

1

1

2

1

2

1

1

1

1

1

1

1

1

ε

ε

ε

ε

ε

ε

ε

+

≈

−

+

+

=

−

+

+

=

−

=

)

)(

(

x

x

)

(

x

)

(

x

x

x

x~

x~

y

więc

2

1

ε

ε

ε

+

<

y

Pierwiastek:

x

y

=

ε

ε

ε

ε

ε

ε

2

1

1

8

1

2

1

1

1

1

1

1

1

2

≈

−

+

−

+

=

−

+

=

−

+

=

−

=

.....

)

(

x

)

(

x

x

x~

y

więc

ε

ε

2

1

<

y

Iloraz:

2

1

x

x

y

=

2

1

2

2

1

2

1

2

2

1

2

1

1

2

1

2

1

1

1

1

1

1

1

1

1

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

−

≈

+

−

=

−

+

+

=

−

+

+

=

−

=

)

(

)

(

)

(

)

(

)

(

x

x

x

)

(

x

x~

x

x

x~

y

więc

2

1

ε

ε

ε

+

<

y

W1 - 4

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Suma:

2

1

x

x

y

±

=

2

1

2

2

2

1

1

1

2

1

2

2

1

1

2

1

2

1

1

1

1

1

x

x

x

x

x

x

x

x

)

(

x

)

(

x

x

x

x~

x~

y

±

±

±

=

−

±

+

±

+

=

−

±

±

=

ε

ε

ε

ε

ε

więc

2

2

1

2

1

2

1

1

ε

ε

ε

x

x

x

x

x

x

y

±

+

±

<

W1 - 5

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

3. Metoda przybliżona – metoda różniczki zupełnej

)

x

,...,

x

,

x

(

x

n

2

1

=

)

x~

,...,

x~

,

x~

(

x~

n

2

1

=

,

)

x

(

y

)

x~

(

y

y

−

=

Δ

)

x

(

y

i

x

n

i

i

y

)

x~

(

x

y

Δ

∂

∂

≈

Δ

∑

=1

i

x

n

i

i

y

)

x~

(

x

y

Δ

∂

∂

<

Δ

∑

=1

i

i

x

n

i

i

i

i

x

n

i

i

i

y

y

)

x~

(

x

y

y

x

x

)

x~

(

x

y

y

x

y

ε

ε

∑

∑

=

=

∂

∂

=

Δ

∂

∂

≈

Δ

=

1

1

i

x

n

i

i

i

y

)

x~

(

x

y

y

x

ε

ε

∑

=

∂

∂

<

1

metodą przybliżoną

0024

.

0

<

z

ε

W1 - 6

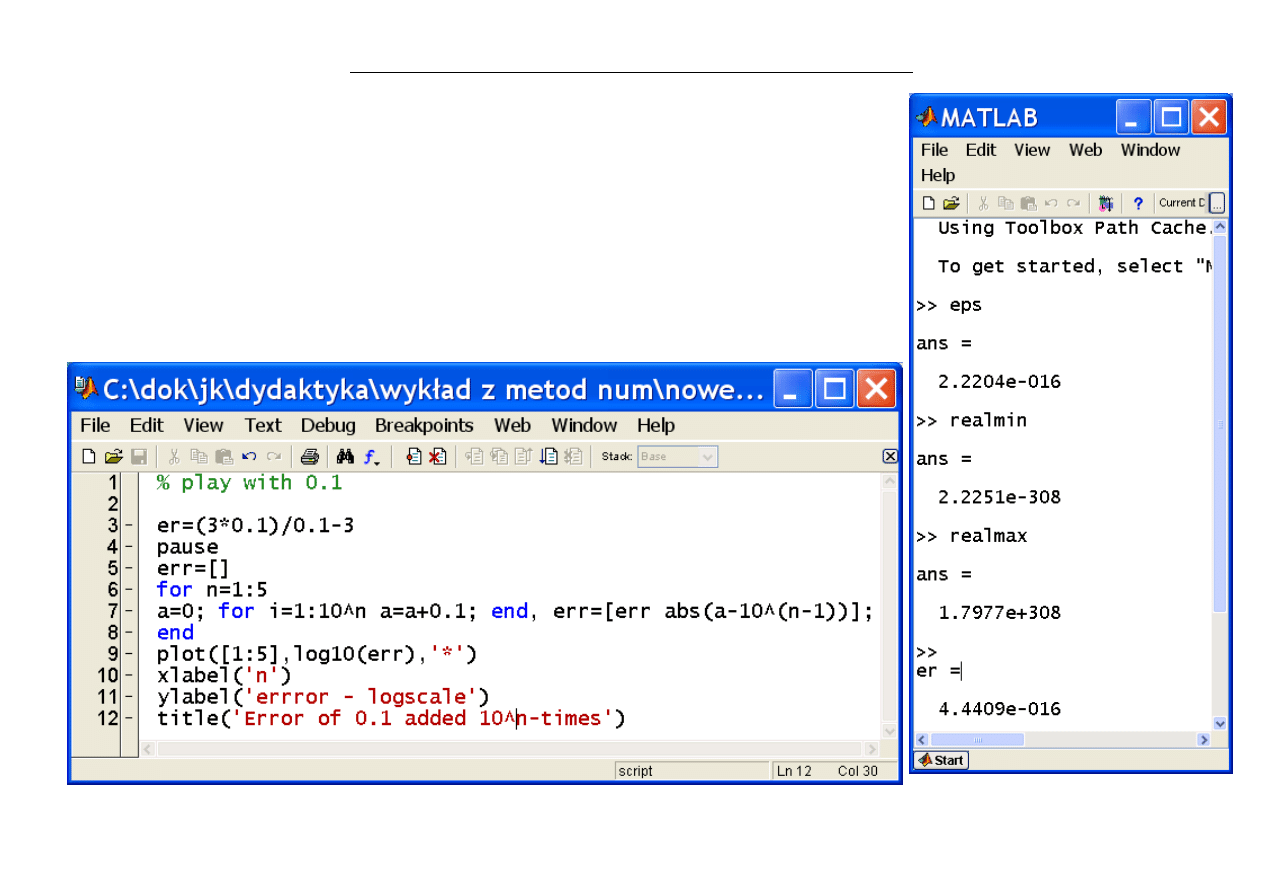
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Przykład 1: Błędy dodawania 0.1

W1 - 7

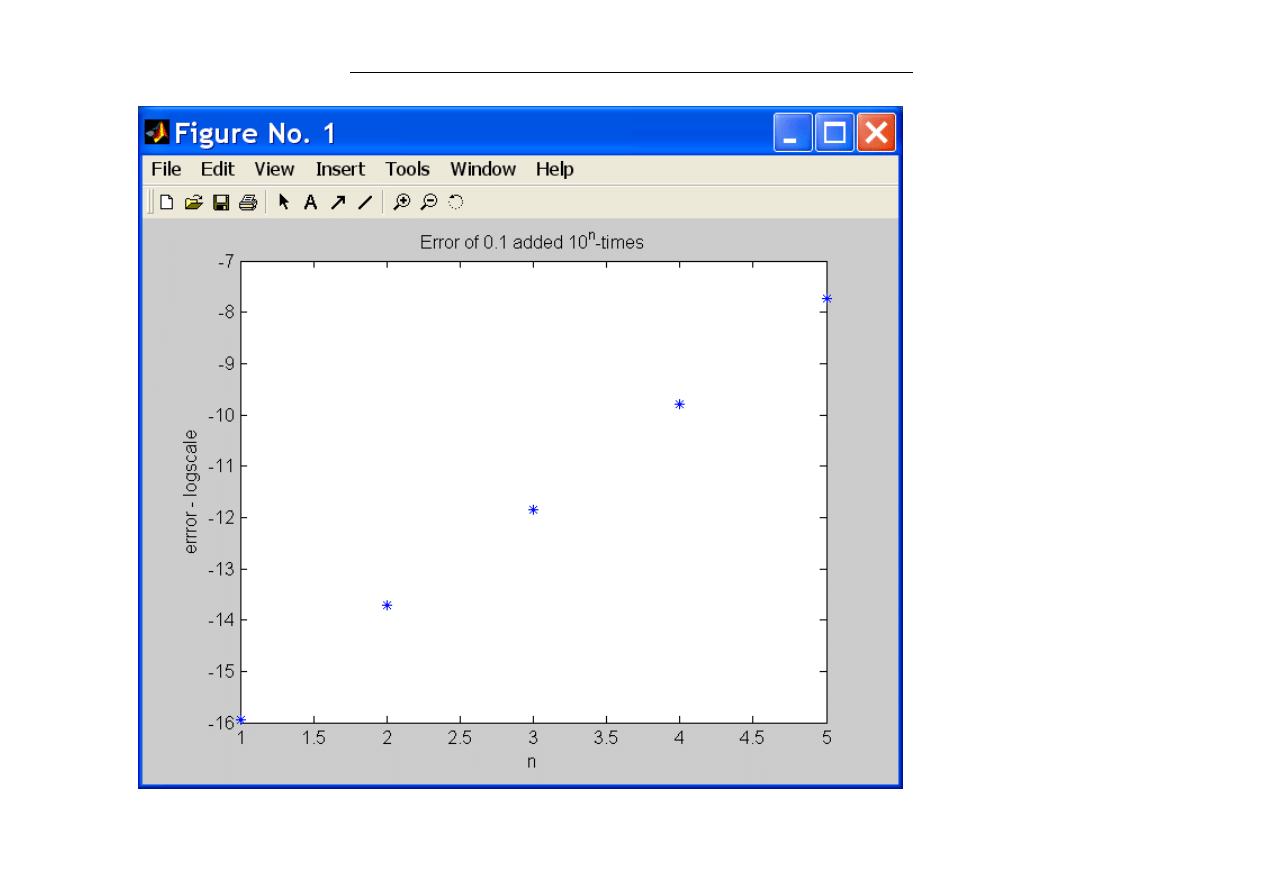
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

W1 - 8

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Przykład 2: Przenoszenie błędów

Zmierzono średnicę kuli z dokładnością do

05

0.

±

cm i otrzymano

7

.

3

~ =

d

cm. Użyto

przybliżonej wartości

14

.

3

~ =

π

Oszacuj względny i bezwzględny błąd obliczonej objętości kuli.

π

=3.14159265358979……,

3

6

1

d

V

π

=

3

~

~

6

1

~

d

V

π

=

=26.5084

05

.

0

≤

Δ

d

05

.

0

7

.

3

05

.

0

−

≤

d

ε

=0.0137

π

π

π

−

=

Δ

~

= - 0.00159265358979……

π

ε

=-5.0696e-004

0016

.

0

<

Δ

π

00051

.

0

<

π

ε

Analiza przedziałowa:

3

3

75

.

3

1416

.

3

6

65

.

3

14

.

3

6

⋅

<

<

⋅

V

1

1

25.4482<V<27.6117

{

}

4482

.

25

265084

,

5084

.

26

6117

.

27

max

−

−

<

Δ

V

=max{1.1033, 1.0602}=1.1033

4484

25

1033

1

.

.

V

<

ε

=0.0434

W1 - 9

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Metoda różniczki zupełnej:

,

i

x

n

i

i

i

y

x

x

y

y

x

ε

ε

∑

=

∂

∂

<

1

)

~

(

i

x

n

i

i

y

x

x

y

Δ

∂

∂

<

Δ

∑

=1

)

~

(

=8.4422,

14

.

3

7

.

3

2

14

.

3

7

.

3

2

1

=

=

=

=

=

∂

∂

π

π

π

d

d

d

d

V

=21.4933

7

.

3

3

7

.

3

6

1

=

=

=

∂

∂

d

d

d

V

π

05

0

4933

21

0016

0

4422

8

.

.

.

.

V

⋅

+

⋅

<

Δ

=1.0882

0137

.

0

4933

.

21

00051

.

0

4422

.

8

⋅

+

⋅

<

V

d

V

V

π

ε

0137

.

0

4933

.

21

0882

.

1

5084

.

26

75

.

3

00051

.

0

4422

.

8

0882

.

1

5084

.

26

1416

.

3

⋅

−

+

⋅

−

<

V

ε

=0.0440

Z definicji:

d

V

ε

π

3

ε

ε

+

<

=0.00051+3 0.0137=0.0416

V

V

V

V

ε

ε

−

≤

Δ

1

~

=

0416

.

0

1

5084

.

26

0416

.

0

−

⋅

=1.1506

W1 - 10

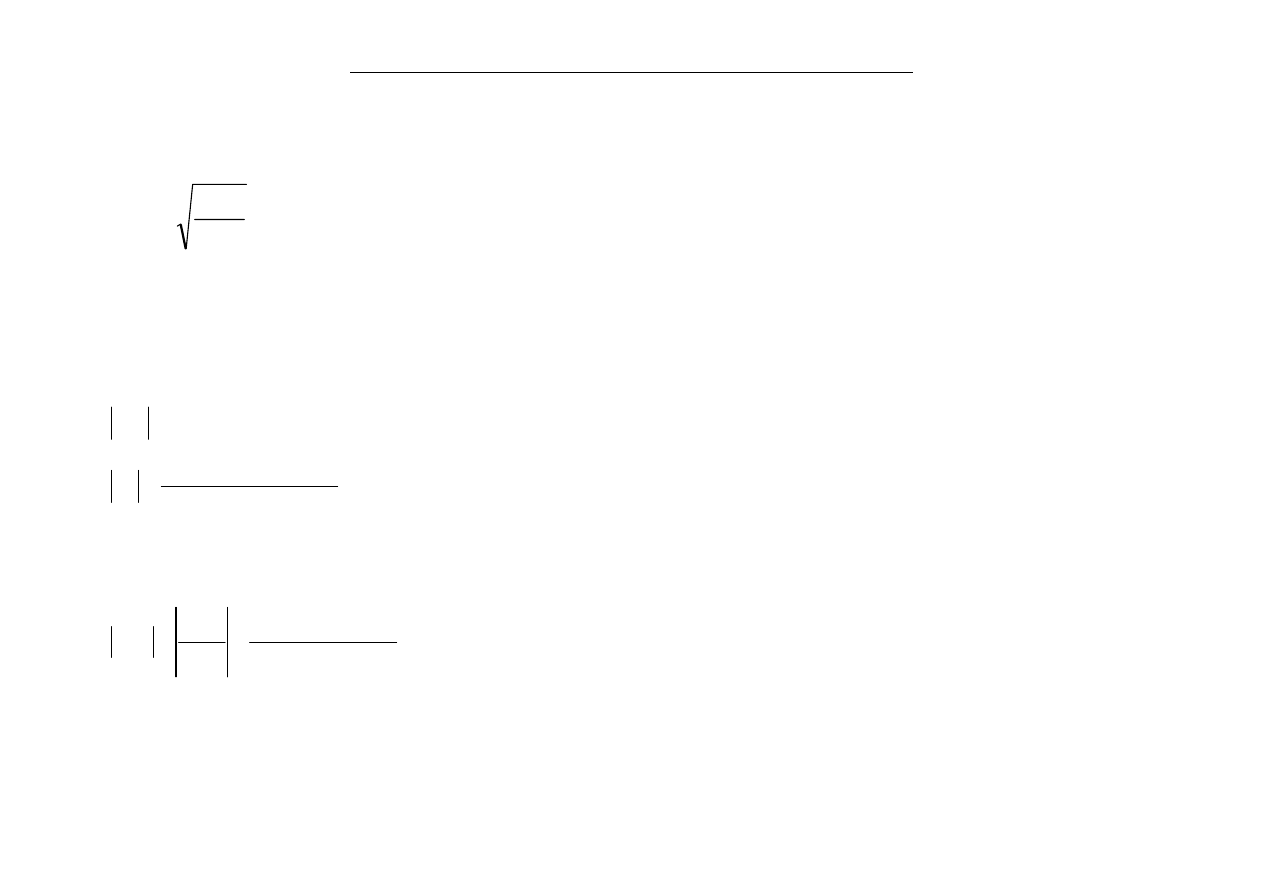
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Przykład 3: Przenoszenie błędów

Oszacuj błąd względny i bezwzględny y jeśli:

x~

= 1,00 (wszystkie cyfry są poprawne) i .

1

1

+

+

=

x

x

y

(1 jest liczbą dokładną)

wszystkie cyfry w

x~

= 1,00 są poprawne (

x~

= 1,00 otrzymano po zaokrągleniu do 2 cyfr

poprzecinku), czyli:

[

]

0050

.

0

..

00502513

.

0

10

*

00

,

5

00

,

1

10

*

00

,

5

10

*

00

,

5

10

*

00

,

5

00

,

1

,

10

*

00

,

5

00

,

1

3

3

3

3

3

=

=

−

<

≤

Δ

+

−

∈

−

−

−

−

−

x

x

x

ε

Sposoby rozwiązania mogą być różne, na przykład tak:
1.

x

x

Δ

=

Δ

+1

3

3

3

1

1

10

*

5

,

2

10

*

5

00

,

2

10

*

5

1

−

−

−

+

+

=

−

<

+

Δ

=

x

x

x

ε

W1 - 11

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

2.

(

)

1

1

2

1

+

+

+

<

x

x

x

x

ε

ε

ε

=

(

)

3

3

10

*

75

,

3

10

*

50

,

2

00

,

5

2

1

−

−

=

+

3

1

3

3

1

1

1

10

*

65

,

2

10

*

07

,

7

*

10

*

75

,

3

1

00

,

1

00

,

1

10

*

75

,

3

1

~

~

1

−

−

−

−

+

+

+

=

=

+

=

+

−

<

Δ

x

x

x

x

x

x

x

x

ε

ε

3. 1 jest dokładna

1

+

Δ

=

Δ

x

x

y

3

3

3

10

*

55

,

1

10

*

65

,

2

1

00

.

1

00

.

1

1

10

*

65

,

2

1

~

~

1

−

−

−

=

−

+

+

=

Δ

−

+

+

Δ

<

y

y

y

x

x

ε

W1 - 12

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 1

Przykład 4: Cyfry poprawne

Skróć liczby by zachować 3 cyfry poprawne:
(błąd bezwzględny musi być mniejszy od 0.5*10

-3

)

0,12395

± 5*10

-6

⇒ 0,124 ± 5,5*10

-5

(5,5*10

-5

<0.5*10

-3

– 3 cyfry poprawne)

0,12315

± 5*10

-6

⇒ 0,123 ± 1,55*10

-4

(1,55*10

-4

<0.5*10

-3

– 3 cyfry poprawne)

0,12350

± 5*10

-6

⇒ 0,124 ± 5,05*10

-4

(5,05*10

-4

> 5*10

-3

– 2 cyfry poprawne, więc musimy

pozostawić 0,1235)

Przykład 5: Utrata cyfr znaczących
Przekształć wyrażenia tak, by uniknąć utraty cyfr znaczących:
1)

1

1

2

−

+

x

= (niebezpieczeństwo błędu dla x bliskich 0):

1

1

2

−

+

x

=

(

)

=

+

+

+

+

−

+

1

1

1

1

1

1

2

2

2

x

x

x

=

+

+

−

+

1

1

1

1

2

2

x

x

1

1

2

2

+

+

x

x

2)

=

−

−

1

2

x

x

(niebezpieczeństwo błędu dla dużych x)

(

)

=

−

+

−

−

1

1

2

2

2

x

x

x

x

1

1

2

−

+ x

x

=

−

−

1

2

x

x

(

)

=

−

+

−

+

−

−

1

1

1

2

2

2

x

x

x

x

x

x

W1 - 13