
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Liniowe zadanie aproksymacji średniokwadratowej
funkcja przybliżana
)
x
(
f
,
siatka węzłów
)
x
(
f
f
,
m
,...,
i
,
x
i
i
i
=
= 0
dane: punkty węzłowe
m
,...,
i
)
f
,
x
(
i
i
0
=
współczynniki wagowe
m
,...,
i
w
i
0
0
=
>
funkcje
bazowe
n
,...,
i
)
x
(
i
0
=
ϕ
funkcja aproksymująca
∑
=
=
n
i
i
i
*
)
x
(
c
)
x
(
f
0
ϕ
szukane stałe takie by
i
c
min
w
)
f
)
x
(
f
(
i
i
i
*
m
i
→
−
∑
=
2
0
W2 - 1
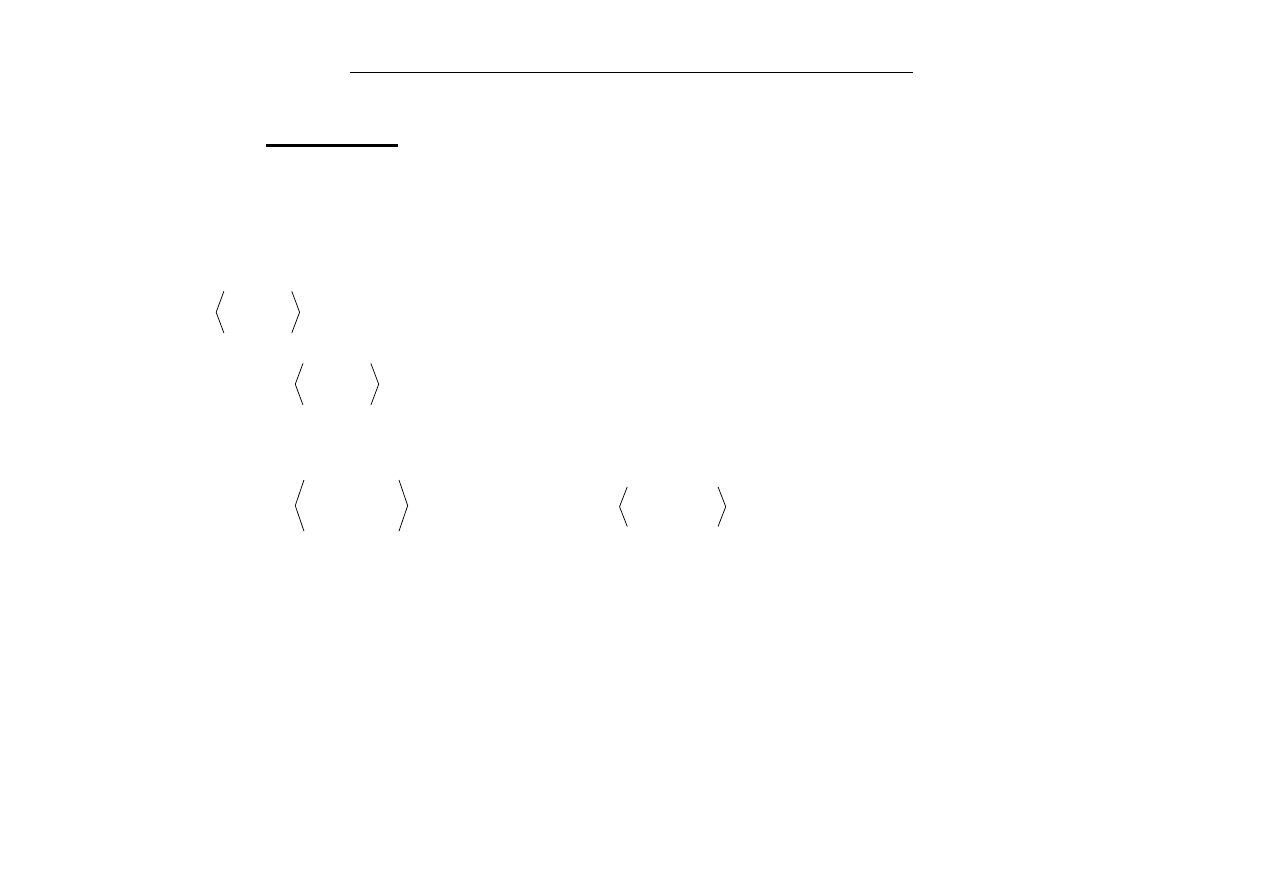
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Notacja:
dla dowolnych funkcji
),
(
g
),
(
f
⋅
⋅
przy danej siatce
węzłów i wsp. wagowych
i
i
m
i
i
w
)
x
(
g
)
x
(
f
:
g
,
f
∑
=
=
0
Jeżeli
0
=
g
,
f
to funkcje
),
(
g
),
(
f
⋅
⋅
nazywamy
ortogonalnymi.
Jeżeli
0
=
j
i
f
,
f
dla
j
i
≠
i
0
≠
i
i
f
,
f
to funkcje
,...
,
i
),
(
f
i
2
1
=
⋅
układem (rodziną) funkcji
ortogonalnych.
W2 - 2
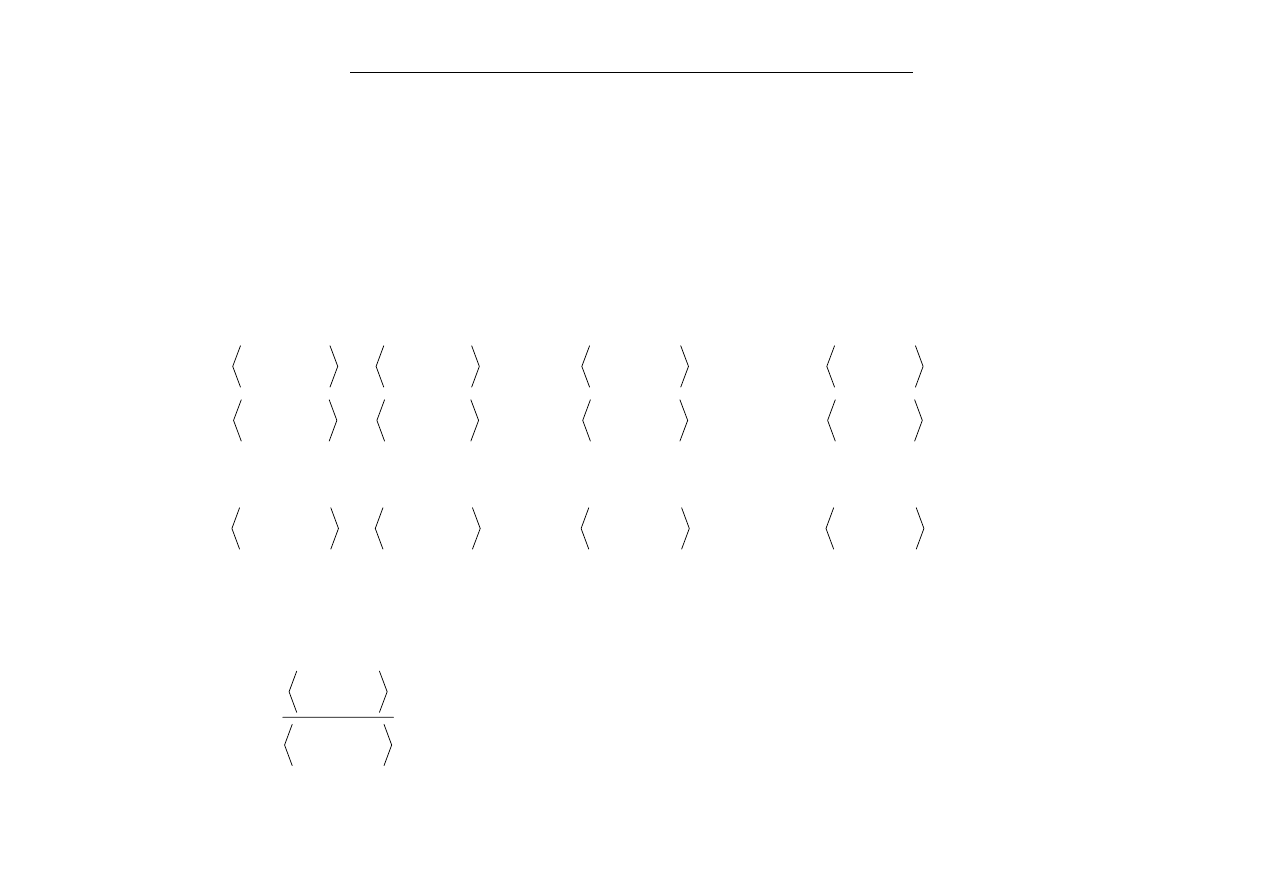
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Twierdzenie
Jeżeli funkcje bazowe są liniowo niezależne to liniowe
zadanie aproksymacji średniokwadratowej ma jedyne
rozwiązanie. Rozwiązanie to spełnia układ równań
normalnych;
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
n
n
n
n
n
n
n
n
f
f
f
c
c
c
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
,
,
,
,
,
,
,
,
,
,
,
,
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
0
L
M
L
L
L
L
L
L
L
Jeżeli funkcje bazowe są rodziną funkcji ortogonalnych to
rozwiązanie upraszcza się do:
n
,...,
i
,
,
,
f
c
i
i
i
i
0
=
=
ϕ
ϕ
ϕ
W2 - 3

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Przykład
n
,...,
i
,
x
)
x
(
i
i
0
=
=
ϕ
1
1
0
1
0
=
=
=
m
x
,
...
,
m
x
,
x
, m=10
m
,...,
i
,
w
i
0
1
=
=
n
el. max. mac. odwr.
1 0.9
2 12.5
3 375
4 9
874
5 252
828
6
8 771 904
7 3.9133e+008
n
el. max. mac. odwr.
8 1.9908e+010
9 1.4199e+012
10 2.4218e+014
W2 - 4

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Wielomiany Czebyszewa
,...
,
n
,
x
)
x
cos
arc
n
cos(
)
x
(
T
n
1
0
1
1
=
≤
≤
−
=
,...
,
n
)
x
(
T
)
x
(
xT
)
x
(
T
,
x
)
x
(
T
)
x
(
T
n
n
n
2
1
2
1
1
1
1
0
=
−
=
=
=
−
+
Współczynnik wiodący wielomianu
)
x
(
T
n
jest równy
2
n-1
dla n=1,2,.
)
x
(
T
)
(
)
x
(
T
n
n
n
1
−
=
−
Wielomian
)
x
(
T
n 1
+
ma n+1 zer
,....
,
n
,
n
,...,
,
k
,
)
n
(
)
k
(
cos
x
k
1
0
1
0
1
2
1
2
=
=
+
+
=
π
W2-5

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Układ wielomianów
)
x
(
T
),...,
x
(
T
),
x
(
T
n
1
0
jest
ortogonalny względem wag
1
=
i
w
i węzłów
i
x
, które są
zerami wielomianu
)
x
(
T
n 1
+
:
⎪
⎩
⎪
⎨
⎧
=
=
+
≠
=
+
≠
=
0
1
0
2
1
0
j
i
dla
n
j
i
dla
n
j
i
dla
T
,
T
j
i
W2-6
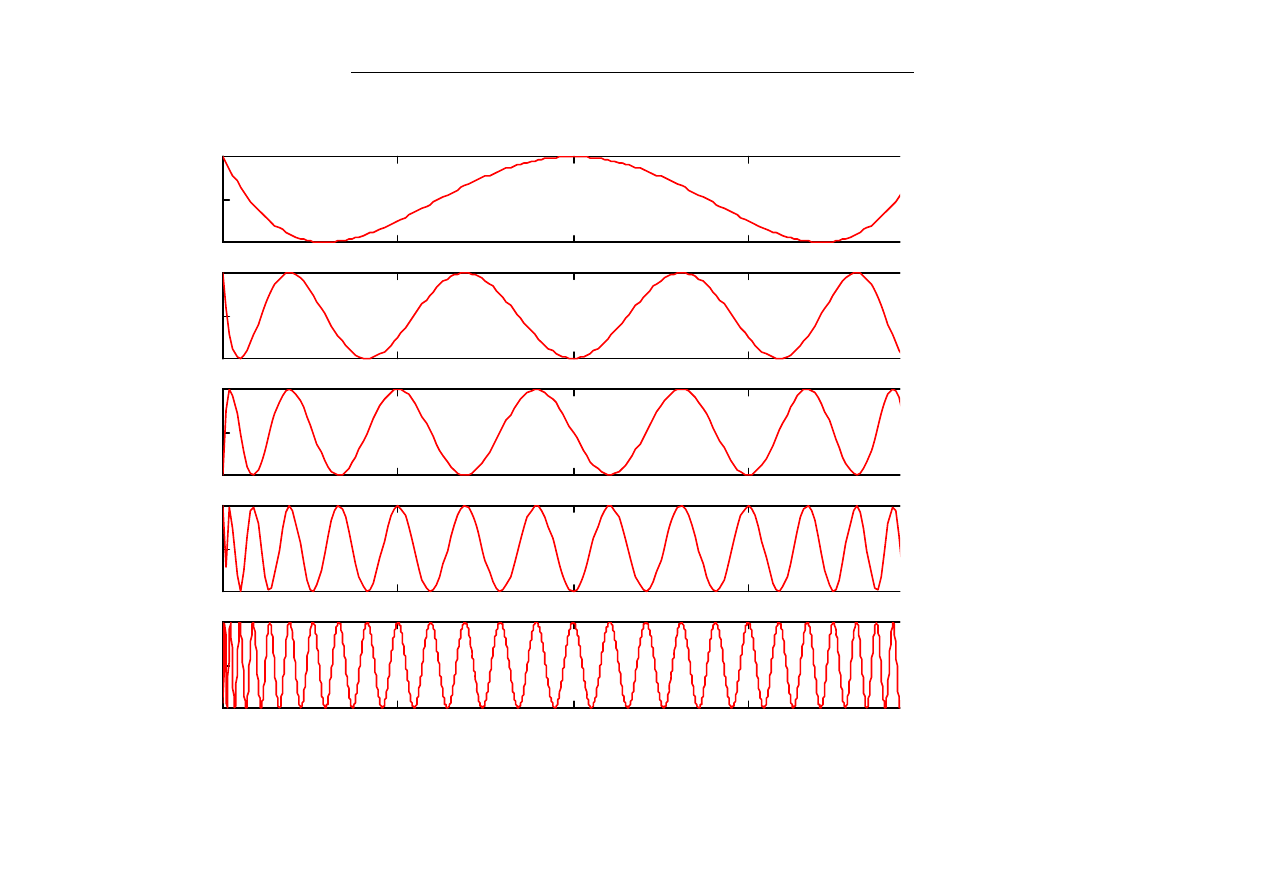
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
-1
-0.5
0
0.5
-1
0
1
T4
(x
)
-1
-0.5
0
0.5
-1
0
1
T
10(
x)
-1
-0.5
0
0.5
-1
0
1
-1
-0.5
0
0.5
-1
0
1
T3
0
(x
)
-1
-0.5
0
0.5
-1
0
1
T6
0
(x
)
W2-7

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Zadanie wielomianowej aproksymacji jednostajnej
funkcja przybliżana
)
x
(
f
,
siatka węzłów
)
x
(
f
f
,
m
,...,
i
,
x
i
i
i
=
= 0
dane: punkty węzłowe
m
,...,
i
)
f
,
x
(
i
i
0
=
funkcja aproksymująca
∑
=
=
n
i
i
i
*
x
a
)
x
(
f
0
ma być
wielomianem stopnia co najwyżej n
szukane stałe takie by
i
a
min
f
)
x
(
f
max
i
i
*
i
→
−
Tw. Weierstrassa
Jeżeli funkcja f(x) jest ciągła w skończonym przedziale
[ ]
b
,
a
, to dla każdego
0
>
ε
istnieje wielomian
)
x
(
P
n
stopnia n, taki że dla każdego
[ ]
b
,
a
x
∈
,
ε
<
−
)
x
(
P
)
x
(
f
n
W2-8

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Interpolacja
funkcja przybliżana
)
x
(
f
,
siatka węzłów
)
x
(
f
f
,
n
,...,
i
,
x
i
i
i
=
= 0
Dla dowolnych, różnych n+1 punktów węzłowych istnieje
dokładnie jeden wielomian interpolacyjny stopnia, co
najwyżej n taki, że
i
i
f
)
x
(
P
=
dla i=0,1,...,n
Wzór interpolacyjny Lagrange’a
∏
∑
≠
=
=
−
−
=
i
k
k
k
i
k
i
i
x
x
f
)
x
(
P
0
0
n
n
x
x
W2-9

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Współczynniki wielomianu interpolacyjnego
0
1
1
1
c
x
c
x
c
x
c
)
x
(
P
n
n
n
n
+
+
+
+
=
−
−
L
można obliczyć z:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
0
1
0
0
1
1
1
1
f
f
f
f
c
c
c
c
x
x
x
x
x
x
x
x
x
x
x
x
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
M
M
L
L
M
M
O
M
M
L
L
macierz
Vandermonde’a
,
jest nieosobliwa jeśli węzły x
i
są różne, ale źle uwarunkowana (trudno ją
odwrócić)
W2-10

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Jeśli wielomian P(x) ma współczynniki
to możemy obliczyć jego
wartości
)
x
(
P
),
x
(
P
),
x
(
P
w punktach
:
0
1
1
c
c
,
c
,
c
,
n
n
L
−
m
L
1
0
m
x
,
x
,
x
L
1
0
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
0
1
1
1
1
1
1
1
1
1
1
1
0
1
0
0
1
1
0
1
1
1
1
c
c
c
c
x
x
x
x
x
x
x
x
x
x
x
x
)
x
(
P
)
x
(
P
)
x
(
P
)
x
(
P
n
n
m
n
m
n
m
m
n
m
n
m
n
n
n
n
m
m
M
L
L
M
M
O
M
M
L
L
M
Schemat Hornera:
n=3
0
1
2
2
3
3
c
x
c
x
c
x
c
)
x
(
P
+
+
+
=
=
(
)
0
1
2
2
3
c
x
c
x
c
x
c
+
+
+
=
(
)
(
)
0
1
2
3
c
x
c
x
c
x
c
+
+
+
więc:
c
2
c
1
c
0
c
3
= a
3
a
3
x
a
2
x
a
1
x
a
2
=c
2
+a
3
x
a
1
=c
1
+a
2
x
P(x)=c
0
+a
1
x
W2-11
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Interpolacja przez rodzinę trójkątną
)
x
x
(
)
x
x
)(
x
x
(
)
x
(
)
x
x
)(
x
x
(
)
x
(
)
x
x
(
)
x
(
)
x
(
n
n
1
1
0
1
0
2
0
1
0
1
−
−
−
−
=
−
−
=
−
=
=
L
L
ϕ
ϕ
ϕ
ϕ
,
0
1
1
1
1
c
)
x
(
c
)
x
(
c
)
x
(
c
)
x
(
P
n
n
n
n
+
+
+
+
=
−
−
ϕ
ϕ
ϕ
L
0
0
0
0
0
f
c
c
)
x
(
P
f
=
⇒
=
=
0
1
0
1
1
0
0
1
1
1
1
x
x
c
f
c
c
)
x
x
(
c
)
x
(
P
f
−
−
=
⇒
+
−
=
=
L
=
⇒
+
−
+
−
−
=
=
2
0
0
2
1
1
2
0
2
2
2
2
c
c
)
x
x
(
c
)
x
x
)(
x
x
(
c
)
x
(
P
f
…………..
W2-12

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Rekurencyjne tworzenie wielomianów interpolacyjnych
Reszta wzoru interpolacyjnego:
Jeżeli funkcja
)
(
f
⋅
ma ciągłe pochodne do rzędu n+1 a
)
(
P
⋅
jest wielomianem interpolacyjnym stopnia n, to
)
x
x
(
)
(
f
)!
n
(
)
x
(
P
)
x
(
f
n
i
i
)
n
(
∏
=
+
−
+
=
−
0
1
1
1
ξ
gdzie
ξ
jest pewnym punktem z najmniejszego przedziału
domkniętego zawierającego
n
x
,...,
x
,
x
0
W2-13

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
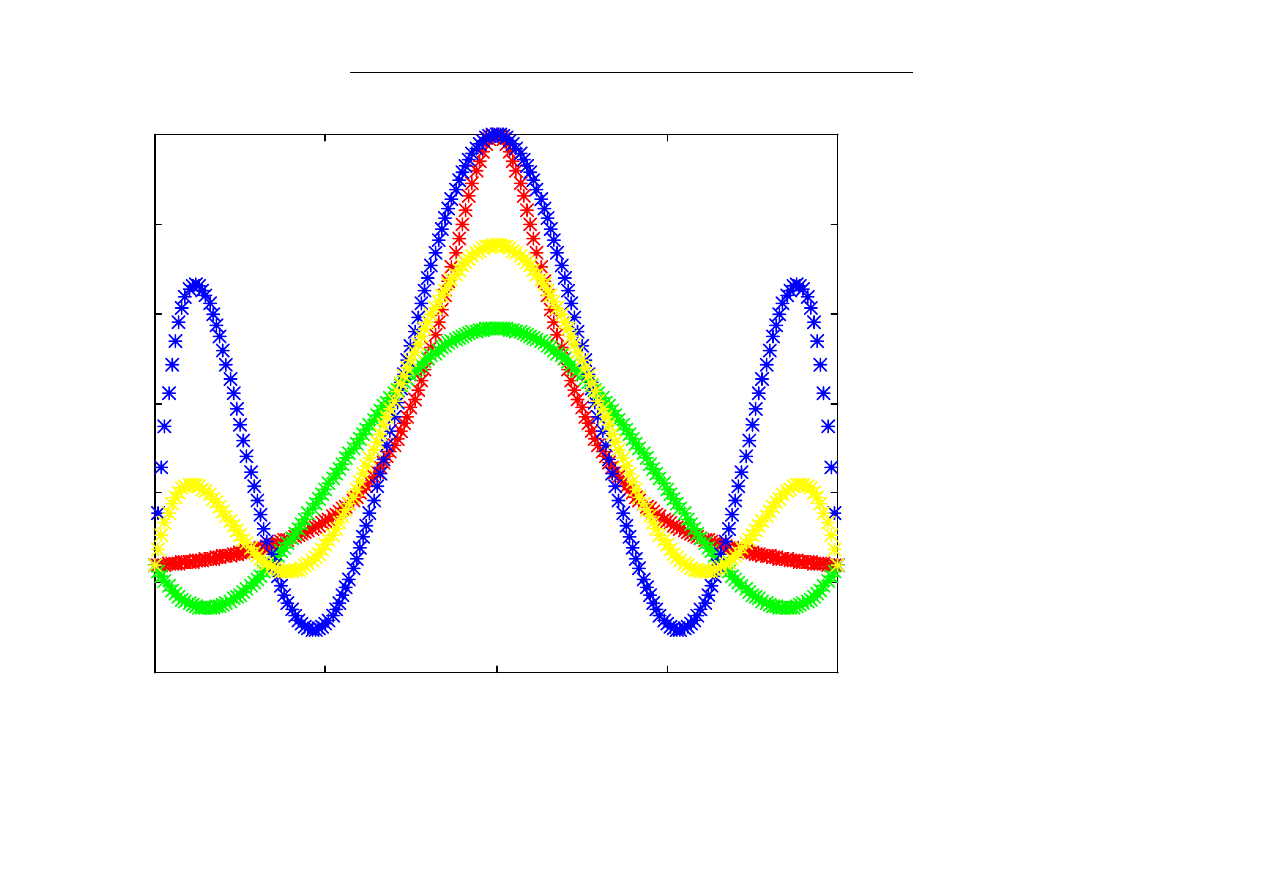
Przykład:
2
5
1
1
)
x
(
)
x
(
y
+
=
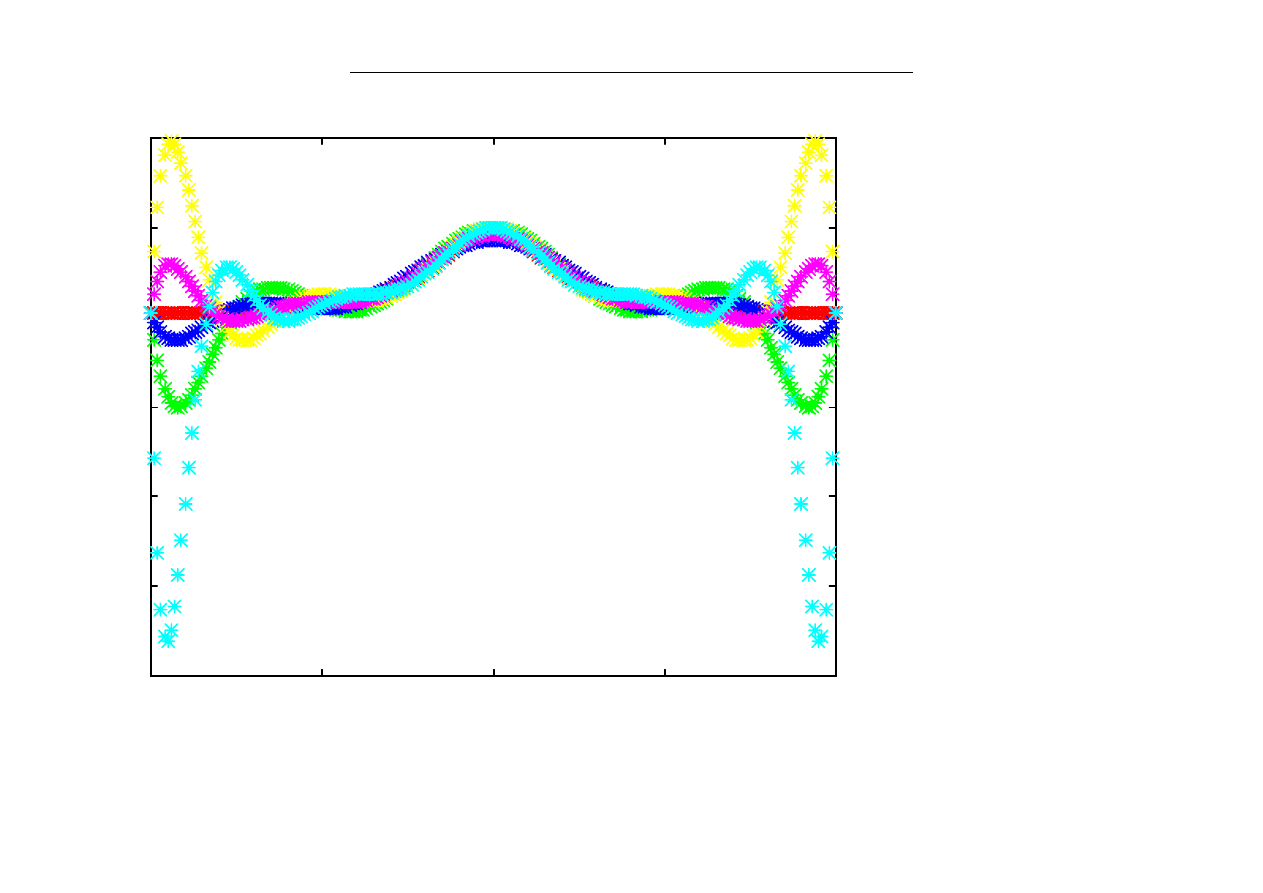
węzły równoodległe w [-1,1]
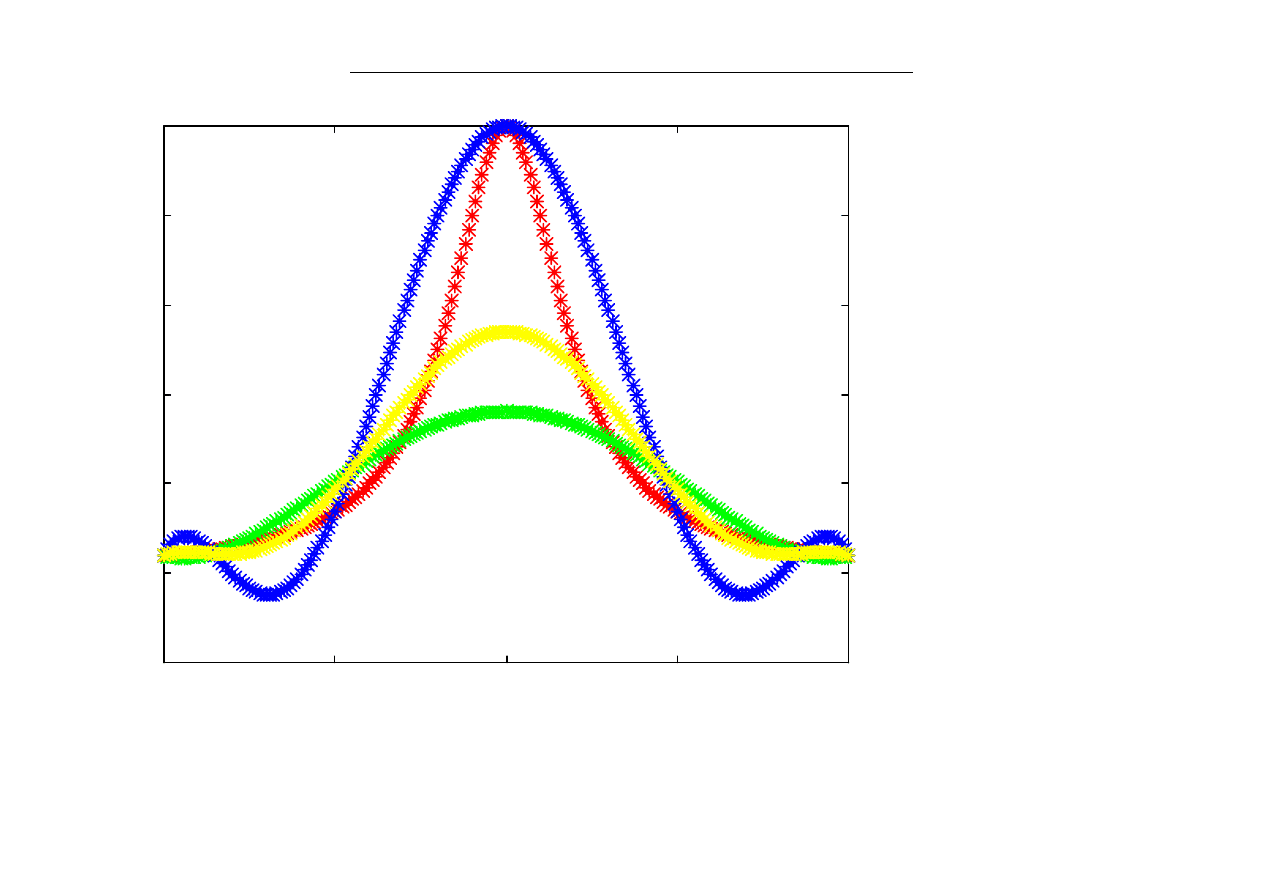
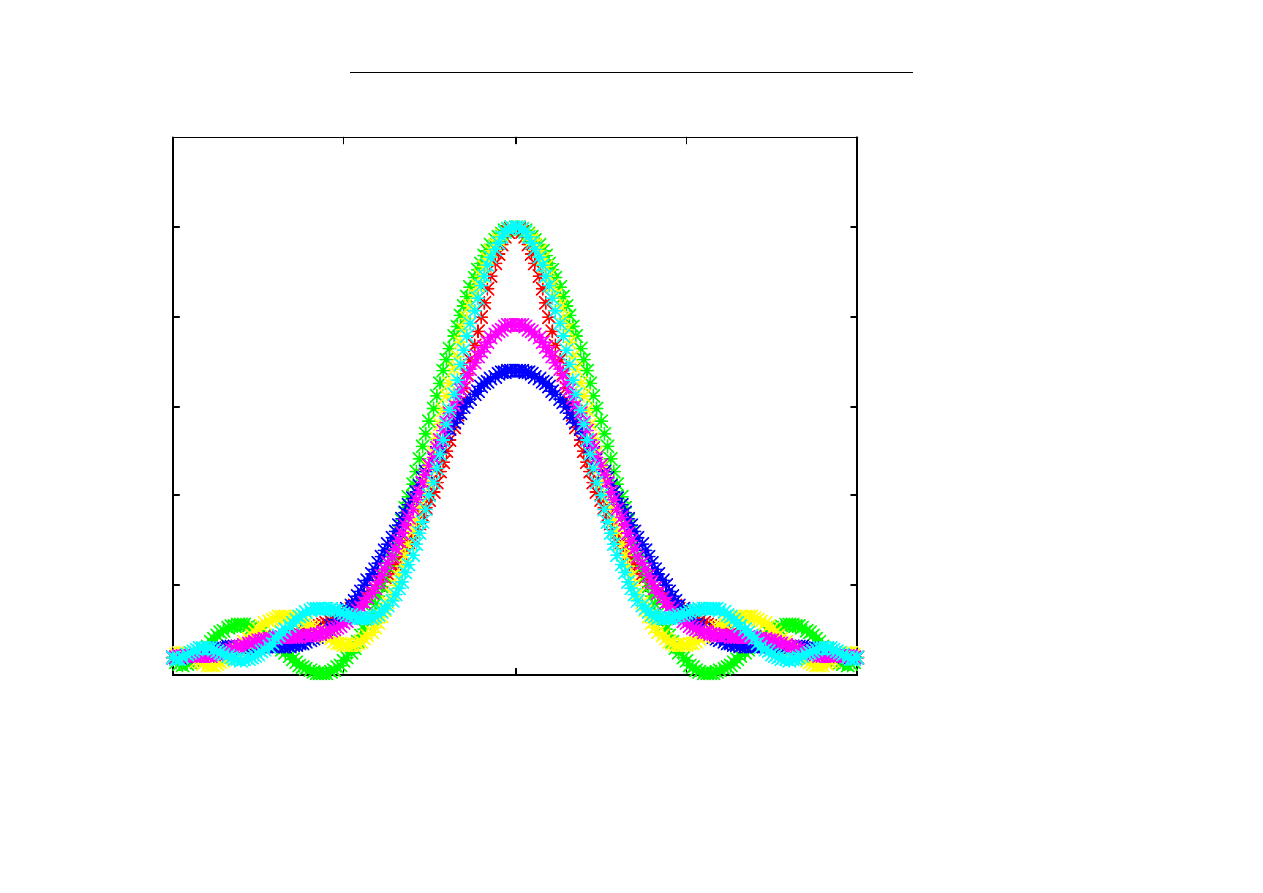
węzły Czebyszewa w [-1,1]
w=[];x=[];y=[];apr=[];
xx=-1:.01:1;yy=1./(1+(5*xx).^2);
for n=4:16
h=2/n;
for i=1:n+1
x(n,i)=-1+(i-1)*h;
end
y(n,1:n+1)=1./(1+(5*x(n,1:n+1)).^2);
w=polyfit(x(n,1:n+1),y(n,1:n+1),n);
apr(n,:)=polyval(w,xx);
end
w=[];x=[];y=[];apr=[];
xx=-1:.01:1;yy=1./(1+(5*xx).^2);
for n=4:16
for i=1:n+1
x(n,1:n+1)=-seqcheb(n+1,2);
end
y(n,1:n+1)=1./(1+(5*x(n,1:n+1)).^2);
w=polyfit(x(n,1:n+1),y(n,1:n+1),n);
apr(n,:)=polyval(w,xx);
end
W2-14
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
-1
-0.5
0
0.5
1
-0.2
0
0.2
0.4
0.6
0.8
1
n=5,6,7
W2-15
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
-1
-0.5
0
0.5
1
-4
-3
-2
-1
0
1
2
n=8,9,10,11,12
W2-16
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
-1
-0.5
0
0.5
1
-0.2
0
0.2
0.4
0.6
0.8
1
n=5,6,7
W2-17
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
-1
-0.5
0
0.5
1
0
0.2
0.4
0.6
0.8
1
1.2
n=8,9,10,11,12
W2-18

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
Interpolacja odcinkowa
Czemu budować wielomian interpolacyjny wysokiego stopnia na
całym przedziale?
Interpolacja odcinkowo liniowa
[
]
W przedziale
przyjmujemy
1
+
k
k
x
,
x
k
k
k
k
k
k
x
x
f
f
)
x
x
(
f
)
x
(
L
−
−
−
+
=
+
+
1
1
L(x) jest ciągłą funkcja w całej dziedzinie x, ale pierwsza pochodna L’(x), nie jest
ciągła.
W2-19
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
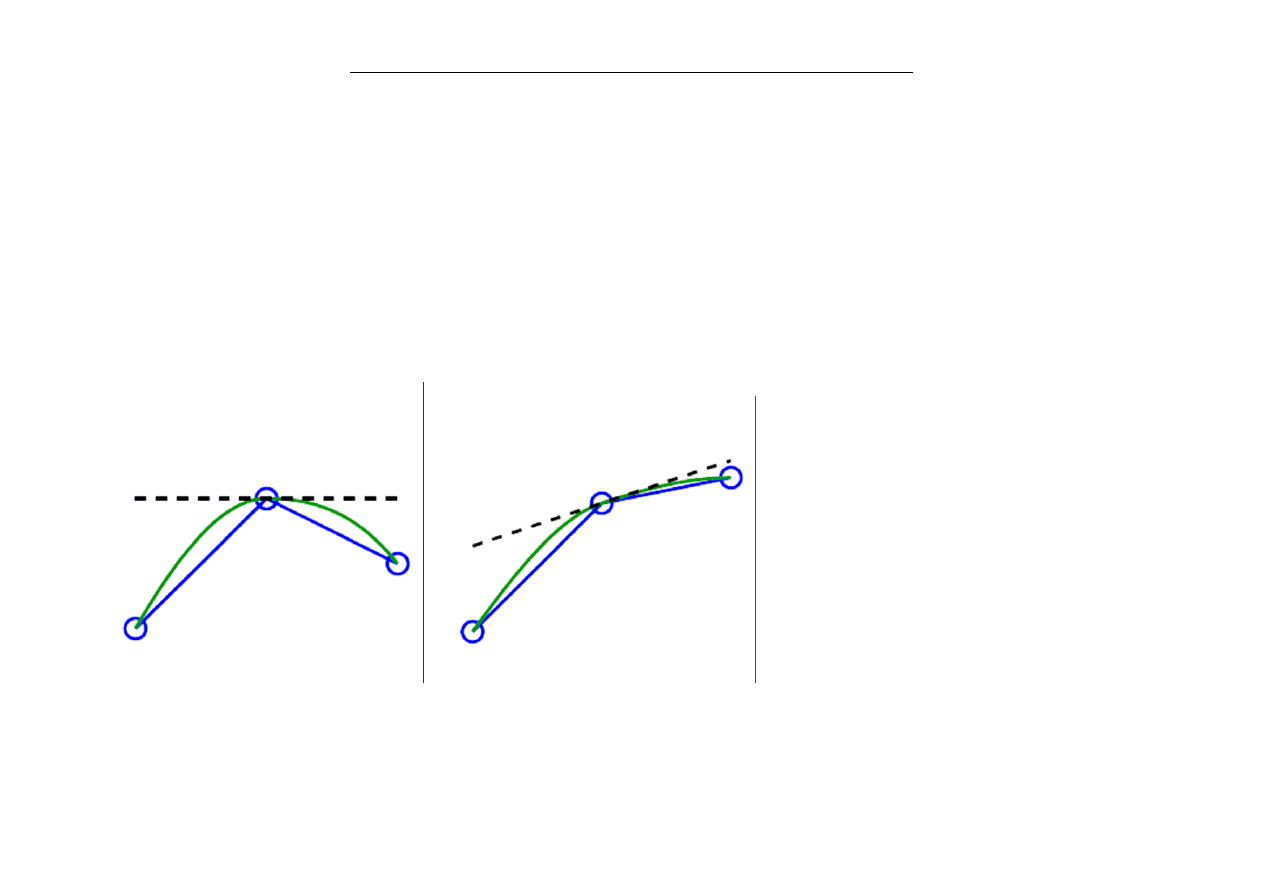
Odcinkowa interpolacja sześcienna Hermite’a
Interpolacja wielomianem stopnia 3, który spełnia 4 warunki: 2 nałożone na
wartosci funkcji i 2 na (nieznane) wartości pochodnej.
Jeśli znamy i wartości funkcji i jej pierwszej pochodnej w punktach węzłowych
interpolacja Hermite’a może odtworzyć te wartości. Jeśli nie znamy wartości
pochodnej (nachyleń funkcji) trzeba je w jakis sposób narzucić. Sposobymoga być
różne, na przykład w procedurach
Matlaba pchip i spline:
.
nachylenia
pchip
W2-20

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
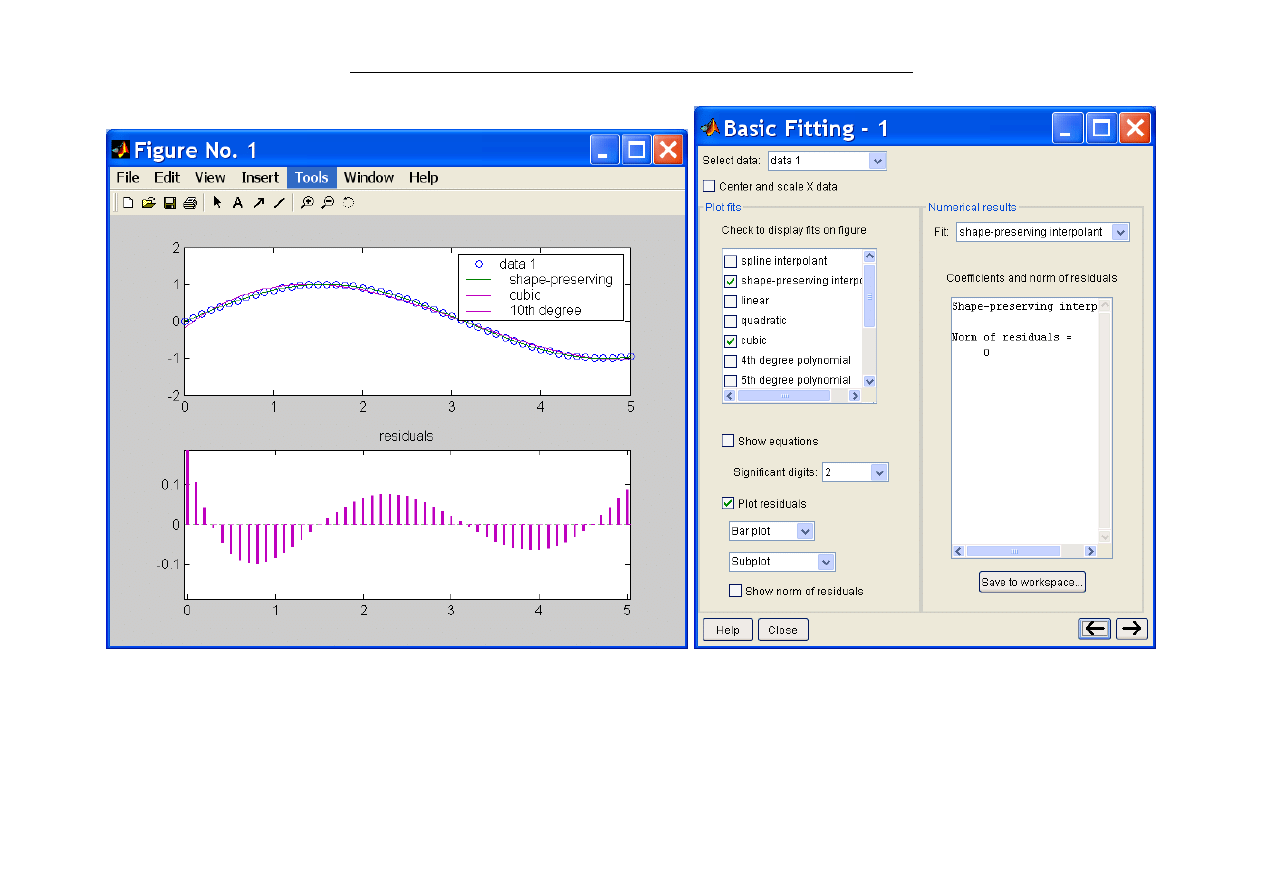
Interpolacja przez funkcje sklejane (splines) (sześcienne)
Interpolacja wielomianami stopnia 3 o ciagłej drugiej pochodnej.
Koncepcja funkcji sklejanych pojawia się także w problemach:
interpolacji i aproksymacji funkcji wielowymiarowych,
interpolacji wielomianami wyższego stopnia,
interpolacji z adaptacja węzłów.
W2-21
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 wykład 2
W2-22
Document Outline
Wyszukiwarka
Podobne podstrony:
metody w3 et
metody w1 et
Metody analizy?ektywności ekonomicznej inwestycji W2
metody numeryczne w2 (2)
Metody wykrywania zagrozenia przedsiebiorstwa upadkiem w2
Metody T[1],w1,w2
Metody numeryczne w2
Metody oceny, W2 Ryzyko, Email Template
więcej podobnych podstron