Metody numeryczne

dr Jan Smykla

Teoria błędów

• Definicje i pojęcia związane z

błędami

• Podstawowe źródła błędów
• Metody obliczania błędów
• Błędy działań arytmetycznych na

liczbach przybliżonych

• Problem odwrotny teorii błędów

Definicje i pojęcia związane z

błędami

Teoria błędów

Często znak błędu nie jest znany. Wówczas stosuje
się pojęcie błędu bezwzględnego  =  

a

Liczbą przybliżoną nazywa się liczbę różniącą
się nieznacznie od dokładnej liczby A i zastępującą ją
w obliczeniach.

a

Błędem liczby nazywamy różnicę  = A -

a

a

a

Gdy < A ( > A), to liczba jest wartością
przybliżoną z niedomiarem (nadmiarem) liczby A.

a

a

a

Aby otrzymać dokładną liczbę A, należy do
przybliżonej liczby dodać błąd tej liczby, tj. A = +


a

a

a

Wyróżniamy tu dwa przypadki:

•liczba A jest znana (wtedy  oblicza się ze wzoru

(1.1)

•liczba A jest nieznana (wtedy zamiast nieznanego
błędu , który praktycznie trudno jest wyznaczyć,

wprowadza się oszacowanie z góry, tzw. kres
górny błędu bezwzględnego)

Błędem bezwzględnym  liczby przybliżonej

nazywa się wartość bezwzględną różnicy pomiędzy
liczbą dokładną A i liczbą przybliżoną

= A - 

(1.1)

a

a

a

Kresem górnym błędu bezwzględnego 

liczby przybliżonej nazywa się każdą liczbę nie
mniejszą od błędu bezwzględnego tej liczby

 = A -  

(1.2)

a

a

a

a

Błąd bezwzględny (albo jego kres) nie
charakteryzuje dokładności pomiarów czy obliczeń.
Wprowadza się więc pojęcie błędu względnego.

Wynika stąd, że liczba A zawarta jest w granicach

A -   A  A + 

(1.3)

czyli A - 

jest przybliżeniem z niedomiarem, zaś A

+ 

przybliżeniem liczby A z nadmiarem

a

a

a

a

(1.4
)

Błędem względnym  liczby przybliżonej

nazywa się stosunek błędu bezwzględnego  tej

liczby do wartości bezwzględnej liczby dokładnej A
(A  0)

A







a

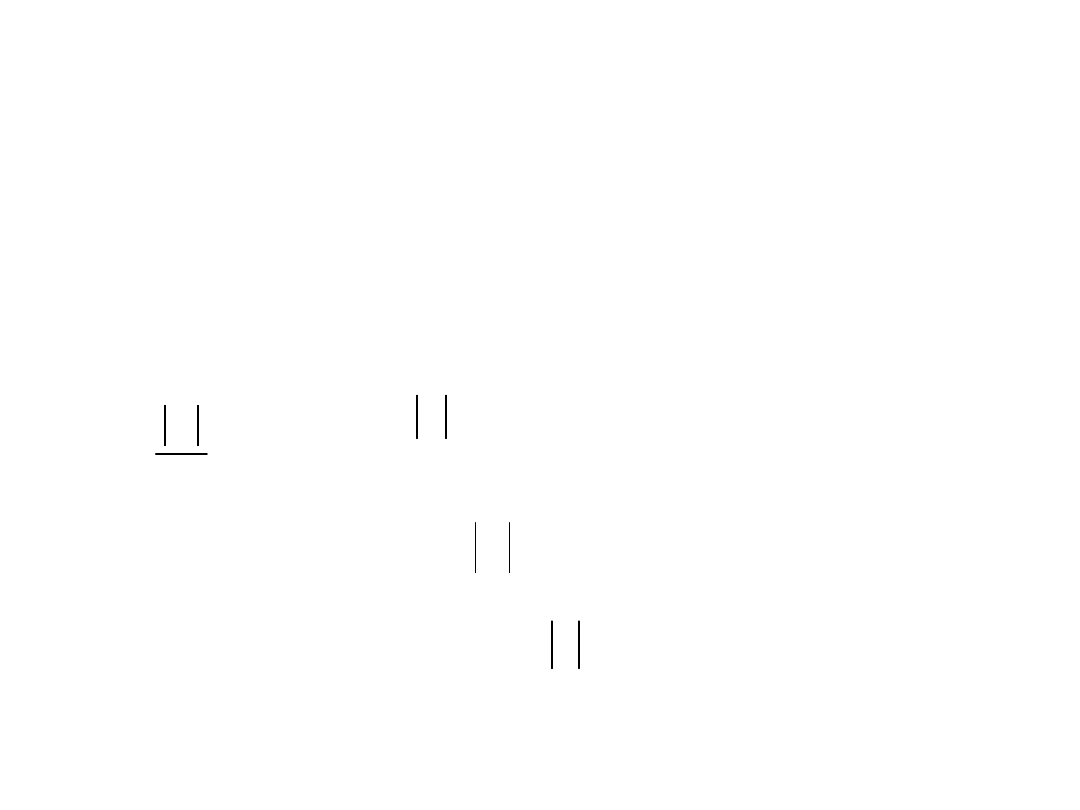
Podobnie jak dla błędu bezwzględnego, definiuje się
kres górny błędu względnego

Kresem górnym błędu względnego 

liczby

przybliżonej a nazywa się każdą liczbę nie mniejszą
od błędu względnego tej liczby

  

(1.5)

tj. , czyli

Zatem za kres górny błędu bezwzględnego można
przyjąć



A



a



(1.6)

a

A







a

a

A







a

a

W praktyce A  , więc .
Znając 

otrzymujemy przedział, w którym

zawarta jest liczba dokładna A = (1± 

)

a

a

a







a

a

a

a

Podstawowe źródła błędów

Wszystkie zagadnienia rozwiązywane metodami
numerycznymi są obarczone na ogół pewnymi
błędami. Błędy te można podzielić na pięć grup:

1. Błędy metody

2. Błędy zaokrąglenia

3. Błędy obcięcia

4. Błędy początkowe

5. Błędy działań arytmetycznych na liczbach

przybliżonych

Błędy metody

Błędy te są związane z samym sformułowaniem
zagadnienia matematycznego. Sformułowania
matematyczne rzadko opisują realne zjawiska.
Zazwyczaj dają ich bardziej lub mniej
wyidealizowane modele. Często zmuszenie
jesteśmy do przyjęcia pewnych warunków
upraszczających. Na przykład w zagadnieniach
mechaniki przyjmuje się, że pręt wahadła ma masę
zerową. Błędy metody musimy uwzględnić w
końcowym wyniku, tzn. musimy je oszacować.

Rozpatrzmy funkcję , która w punkcie x

0

posiada

wszystkie pochodne aż do rzędu n włącznie. Dla
funkcji można utworzyć wielomian W

n

(x)

następującej postaci:

)

(x

f

)

(x

f













n

n

n

x

x

n

x

f

x

x

x

f

x

x

x

f

x

f

x

W

0

0

)

(

2

0

0

)

2

(

0

0

)

1

(

0

!

)

(

...

!

2

)

(

!

1

)

(

)

(

)

(

















(1.7)

Wielomian W

n

(x) tworzy (n+1) pierwszych

składników rozwinięcia funkcji w szereg
Taylora. Interesuje nas błąd przybliżenia

)

(x

f

)

(

)

(

)

(

x

W

x

f

x

r

n

n





(1.8)

Jest sprawą oczywistą, że r

n

(x) maleje ze wzrostem

indeksu n. Różnicę r

n

(x) o postaci

nazywamy resztą Peano. Wzór Peano ma liczne
zastosowania, ale odnoszą się one do samego
punktu x

0

lub do punktów dostatecznie bliskich

punktowi x

0

.





n

n

x

x

n

x

r

0

!

)

(







(1.9)

Istnieją jeszcze inne postacie szeregu Taylora, np.
reszta Lagrange’a wyrażona następującym wzorem:





1

0

)

1

(

)!

1

(

)

(

)

(











n

n

n

x

x

n

c

f

x

r

(1.10)

Przy założeniu, ze funkcja f(x) jest (n+1)-krotnie
różniczkowalna. Tak zwany punkt pośredni c spełnia
jeden z warunków:

x

0

< c < x lub x < c <x

0

.

Resztę w tej postaci można dokładnie oszacować
dla różnych wartości x.

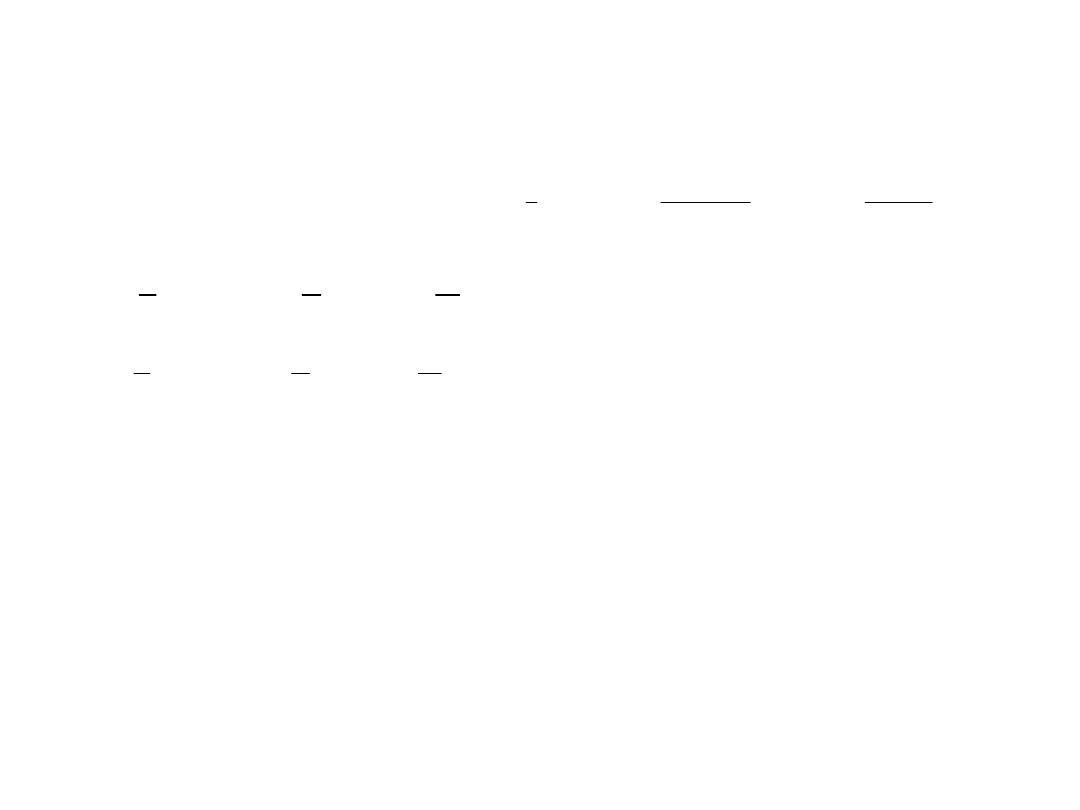
Błędy obcięcia

Błędy obcięcia powstają podczas obliczeń na wskutek
zmniejszania liczby działań. Postępujemy tak na ogół
przy obliczaniu sum nieskończonych (szeregów-
). Chcąc np. obliczyć
wartość funkcji e

x

zastępujemy go
sumą skończoną

o odpowiednio dobranej

wartości n.

n

n

i

i

x

x

n

x

x

x

i

e

!

1

...

2

1

1

!

1

2

0

















...

!

1

...

2

1

1

!

1

2

0





















n

i

i

x

x

n

x

x

x

i

e

 



































0

2

1

1

2

1

0

!

)

2

(

)

1

(

cos

,

!

)

1

2

(

1

sin

,

!

1

i

i

i

i

i

i

i

i

x

i

x

x

i

x

x

x

i

e

Innym przykładem będzie obliczanie wartości funkcji
określonych jako granice ciągów nieskończonych. Na
ogół powstaje konieczność zakończenia obliczeń na
pewnym wyrazie ciągu. Przerwanie takie powoduje
powstanie błędu obcięcia. Jeżeli np. obliczamy wartość
całki oznaczonej jako granicę sum przybliżających
całkę o coraz to gęstszym podziale, to przyjęcie jednej
z tych sum jako wartości bliskiej całce oznacza
wprowadzenie błędu obcięcia. Również zastąpienie
wartości pochodnej jej ilorazem różnicowym powoduje
powstanie błędu obcięcia.

Odmianą błędu obcięcia jest błąd urwania
(schopping), polegający na odrzuceniu cyfr
rozwinięcia binarnego wykraczających poza przyjętą
liczbę bitów na mantysę. Może on powstać przy
zapisywaniu liczby w postaci binarnej
zmiennopozycyjnej. Jeżeli na mantysę przeznaczymy t
bitów, to kres błędu względnego wyniesie 2

-t+1

.

Efektem błędu urwania może być błąd zaokrąglenia.

Błędy zaokrąglenia

Zaokrągleniem liczby nazywamy odrzucenie w niej
wszystkich cyfr poczynając od pewnego miejsca.
Powstaje przy tym błąd zaokrąglenia, który należy
dodawać do początkowego błędu bezwzględnego
liczby.

Przy zaokrąglaniu liczb obowiązują pewne zasady:

•jeśli pierwsza z odrzuconych cyfr jest mniejsza od
5, to pozostałych cyfr dziesiętnych nie zmienia się,

•jeśli pierwsza z odrzuconych cyfr jest większa od
5, to do ostatniej pozostawionej cyfry dodaje się 1,

•jeśli pierwsza z odrzuconych cyfr jest równa 5, a
wśród odrzuconych cyfr są liczby różne od zera, to
ostatnią pozostałą cyfrę zwiększa się o 1,

•jeśli pierwsza z odrzuconych cyfr jest równa 5, a
pozostałe odrzucone cyfry są zerami, to do
ostatniej pozostawionej cyfry dodaje się 1, gdy jest
ona nieparzysta, a pozostawia się ją bez zmian, gdy
jest ona parzysta (jest to reguła cyfry parzystej).

Błędy początkowe

Błędy te występują w związku z obecnością we

wzorach matematycznych parametrów liczbowych,
których wartości można określić jedynie w
przybliżeniu. Należą do nich np. wszystkie stałe
fizyczne oraz błędy danych początkowych. Błędy tego
typu mogą występować również wtedy, gdy ułamek
dziesiętny przekształca się do postaci używanej w
komputerze.

Błędy działań arytmetycznych na

liczbach przybliżonych

Ta grupa błędów jest związana z wykonywaniem

działań arytmetycznych na liczbach przybliżonych.
Jest rzeczą oczywistą, że przy wykonywaniu działań
na liczbach przybliżonych przenosimy do wyników
obliczeń błędy danych początkowych. W tym sensie
błędy działań są nie do usunięcia.

Metody obliczania błędów

Metoda różniczki zupełnej

Podstawowe zadanie teorii błędów można
sformułować następująco:

Wyznaczyć błąd danej funkcji, gdy dane są błędy
wszystkich jej argumentów.

Niech będzie dana funkcja różniczkowalna y = f(x

1

,

x

2

,..., x

n

). Oznaczmy przez |x

i

| (i = 1,2,...,n) błędy

bezwzględne argumentów tej funkcji. Wtedy błąd
bezwzględny tej funkcji można zapisać w postaci:

|y| = | f(x

1

+ x

1

, x

2

+ x

2

,..., x

n +

x

n

) - f(x

1

, x

2

,...,

x

n

)|. (1.11)

W praktyce |x

i

| są wielkościami małymi, których

kwadratów i wyższych potęg można nie brać pod
uwagę. Można zatem przyjąć





























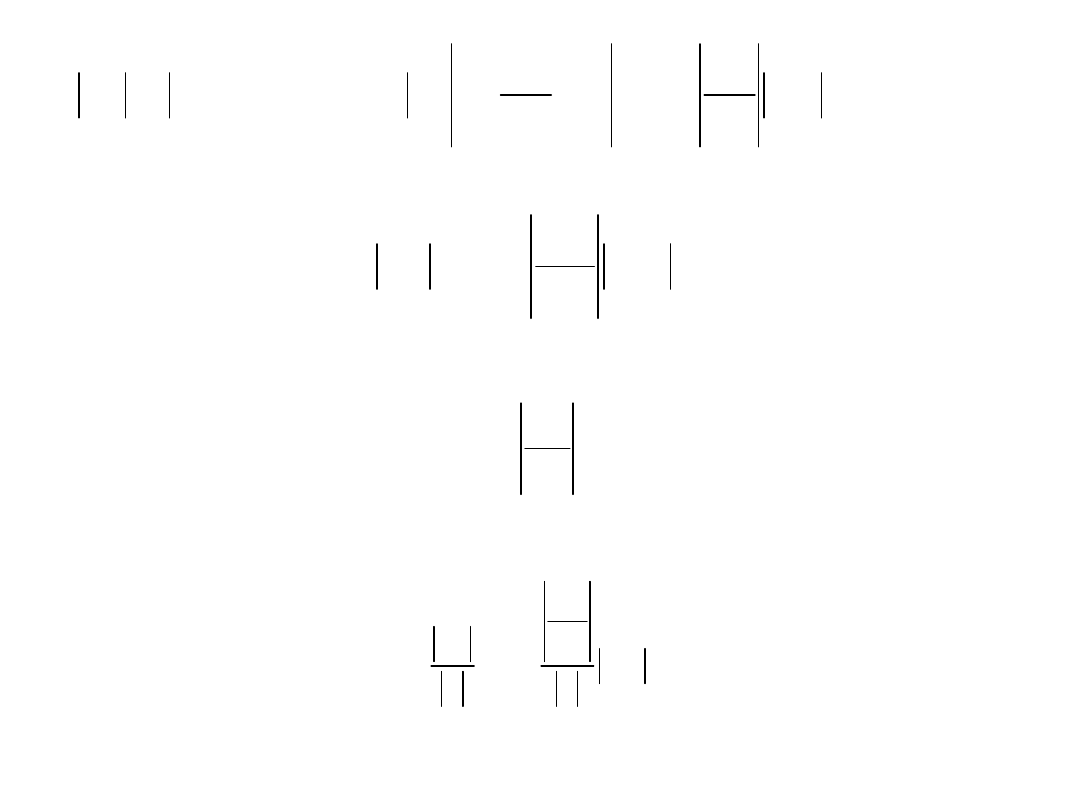
n

i

i

i

n

i

i

i

n

x

x

f

x

x

f

x

x

x

df

y

1

1

2

1

)

,...,

,

(

(1.11)

a
więc















n

i

i

i

x

x

f

y

1

(1.12)

Stąd dla kresów górnych można zapisać
następującą zależność















n

i

i

i

x

x

f

y

1

(1.14
)

Błąd względny rozpatrywanej funkcji wyrazi się
wzorem

















n

i

i

i

x

y

x

f

y

y

y

1



(1.15
)

przy założeniu,
że

.

0

)

,...,

,

(

2

1



n

x

x

x

f

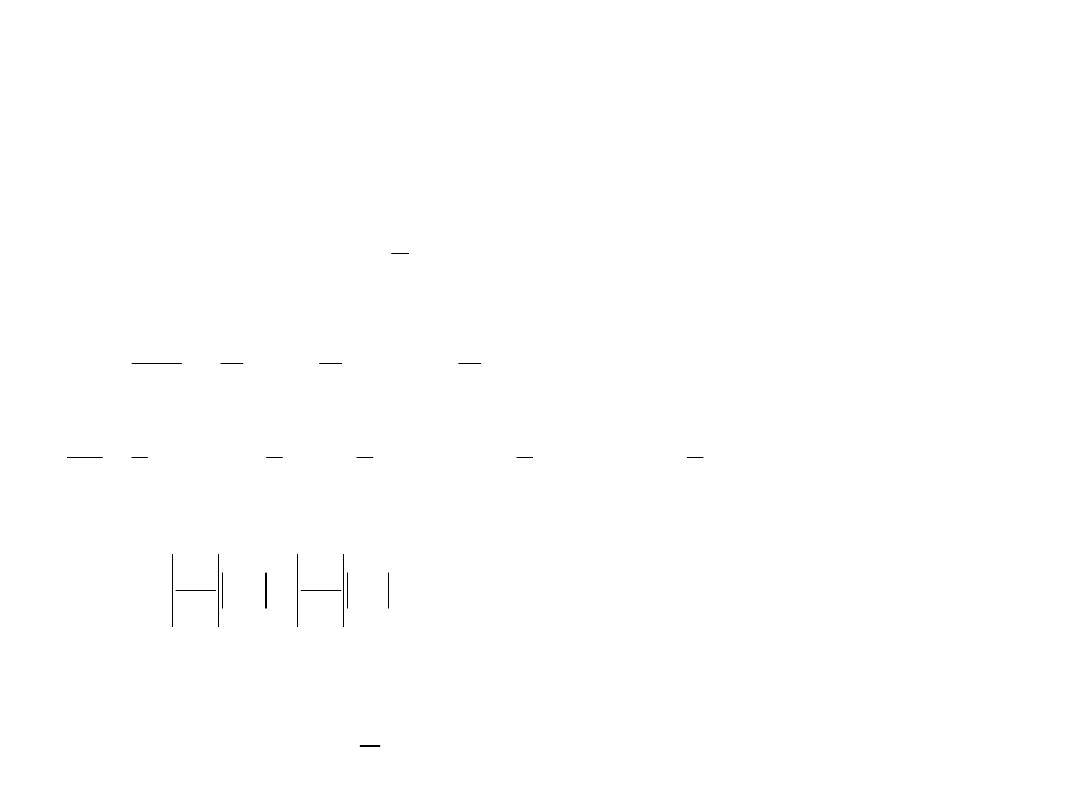
Przykład

Znaleźć kres górny błędu bezwzględnego objętości
kuli, jeśli średnica kuli wynosi d = 3,7cm ± 0,05cm; 

= 3,14 ± 0,0016

Rozwiązanie

Objętość kuli wynosi V = . Traktując



oraz d

jako wielkości zmienne, obliczamy pochodne
cząstkowe

3

6

1

d



44

,

8

)

6

(

4421

,

8

653

,

50

6

1

7

,

3

6

1

6

1

3

3



















d

V



21,49

21,4933

42,9866

2

1

69

,

13

14

,

3

2

1

7

,

3

14

,

3

2

1

2

1

3

6

1

2

2

2

































d

d

d

V





Korzystając ze wzoru (1.14)
otrzymamy:

.

09

,

1

05

,

0

49

,

21

0016

,

0

44

,

8

3

cm

d

d

V

V

V

































Zatem ostatecznie otrzymujemy

3

3

3

09

,

1

51

,

26

6

1

cm

cm

d

V

V













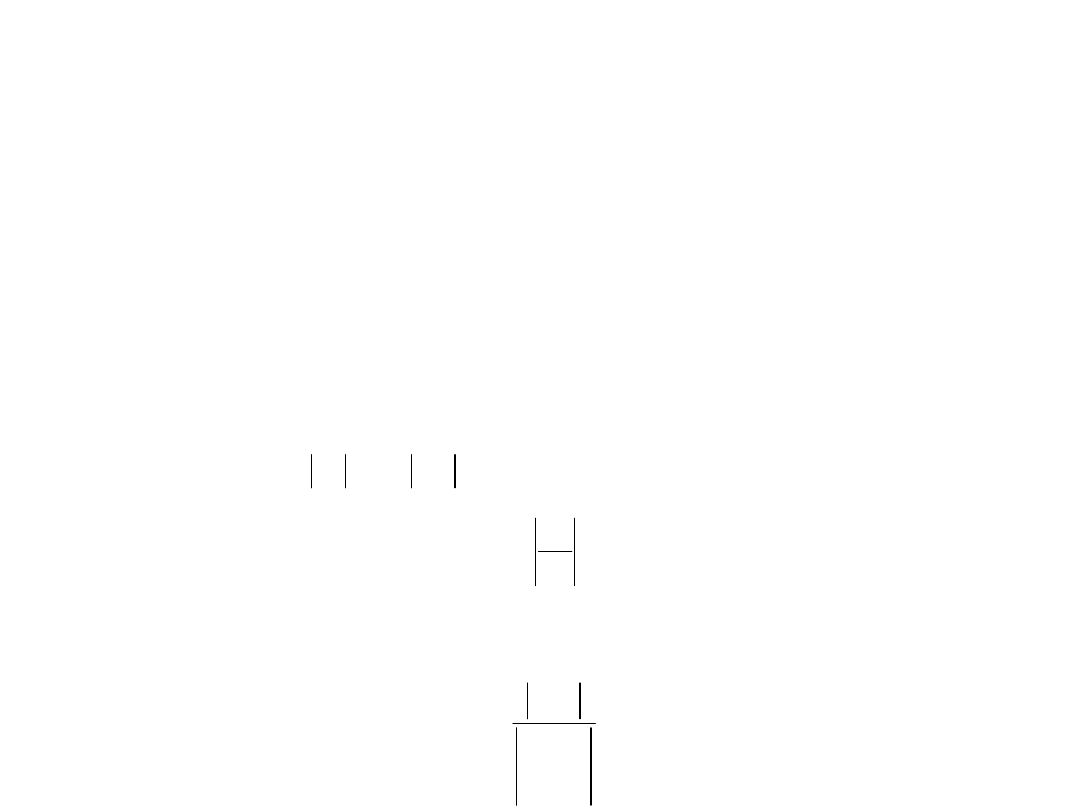
Błędy działań arytmetycznych na liczbach
przybliżonych

Błąd sumy

Niech będą danymi liczbami
przybliżonymi. Rozpatrzmy ich sumę algebraiczną

n

x

x

x

,...,

,

2

1

n

n

i

i

x

x

x

x

y















...

2

1

1

Korzystając ze wzoru (1.13) zapiszemy
następującą zależność na błąd bezwzględny sumy
liczb przybliżonych

,

1











n

i

i

x

y

(1.23)

ponieważ dla każdego i=1,2,...n

.

1







i

x

y

Dla błędu względnego sumy algebraicznej liczb
przybliżonych prawdziwa jest zależność













n

i

n

i

i

i

y

x

x

1

1



(1.24)

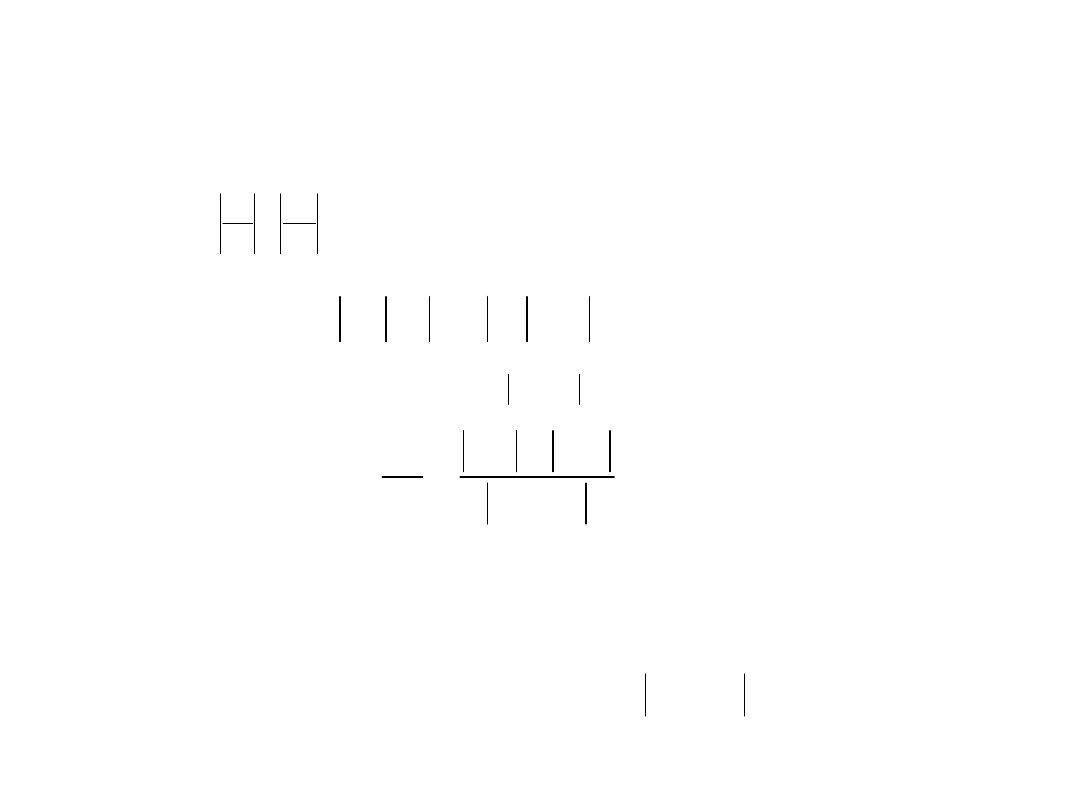
Błąd różnicy

Rozważmy różnicę dwóch liczb przybliżonych

2

1

x

x

y





(1.25)

Ponieważ , więc zgodnie z (1.13) błąd
bezwzględny różnicy tych liczb wyrazi się wzorem

1

2

1













x

y

x

y

.

2

1

x

x

y











(1.26)

2

1

2

1

x

x

x

x

y

y

y

















(1.27)

Zatem błąd względny różnicy jest równy

2

1

x

x 

W przypadku odejmowania liczb przybliżonych
należy zwrócić uwagę na mogącą wystąpić tzw.
stratę dokładności. Jeżeli liczby przybliżone x

1

i x

2

różnią się nieznacznie i są obarczone małymi
błędami bezwzględnymi, to ich różnica
jest mała. Ze wzoru (1.27) wynika, że błąd
względny różnicy będzie znaczny.

2

1

x

x 

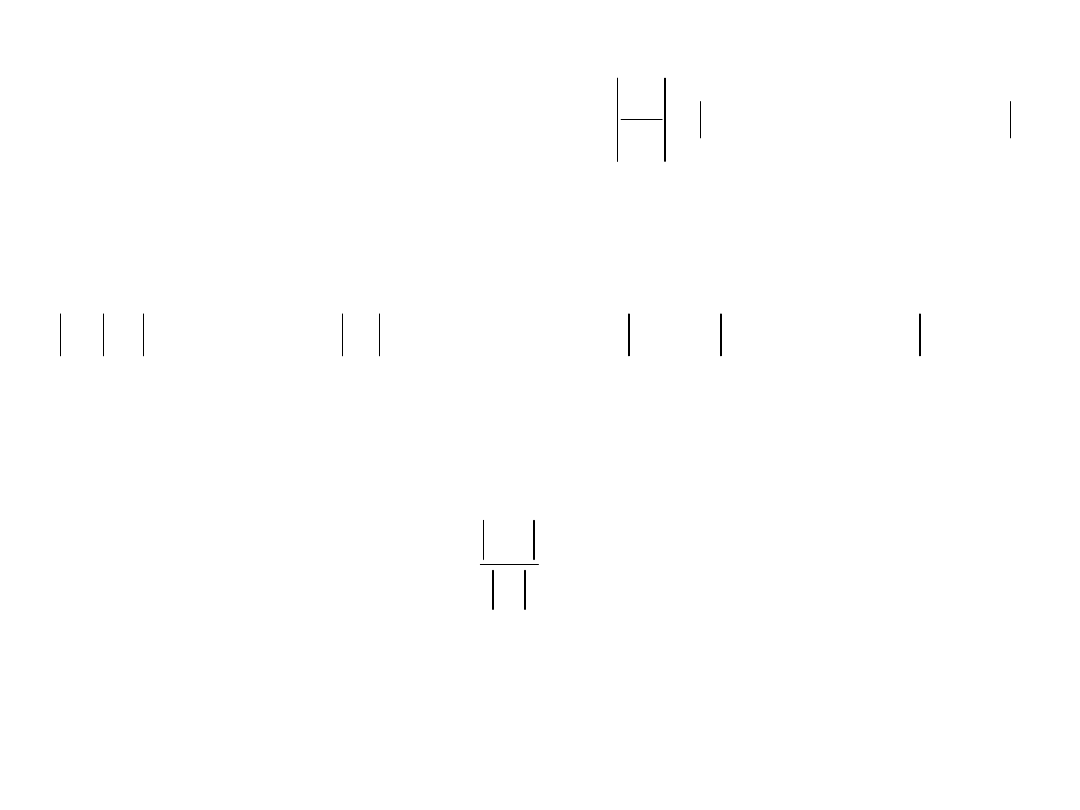
Błąd iloczynu

Niech . Wówczas

n

x

x

x

y









...

2

1

n

i

i

i

x

x

x

x

x

x

y























...

...

1

1

2

1

Korzystając ze wzoru (1.13) otrzymamy następującą
zależność na błąd bezwzględny iloczynu liczb
przybliżonych

n

n

n

x

x

x

x

x

x

x

x

x

x

y





































...

...

...

...

2

1

3

2

1

2

1

(1.28
)

Błąd względny iloczynu n liczb przybliżonych
różnych od zera nie przewyższa sumy błędów
względnych tych liczb. A zatem















n

i

i

n

i

i

i

y

x

x

x

1

1





(1.29)

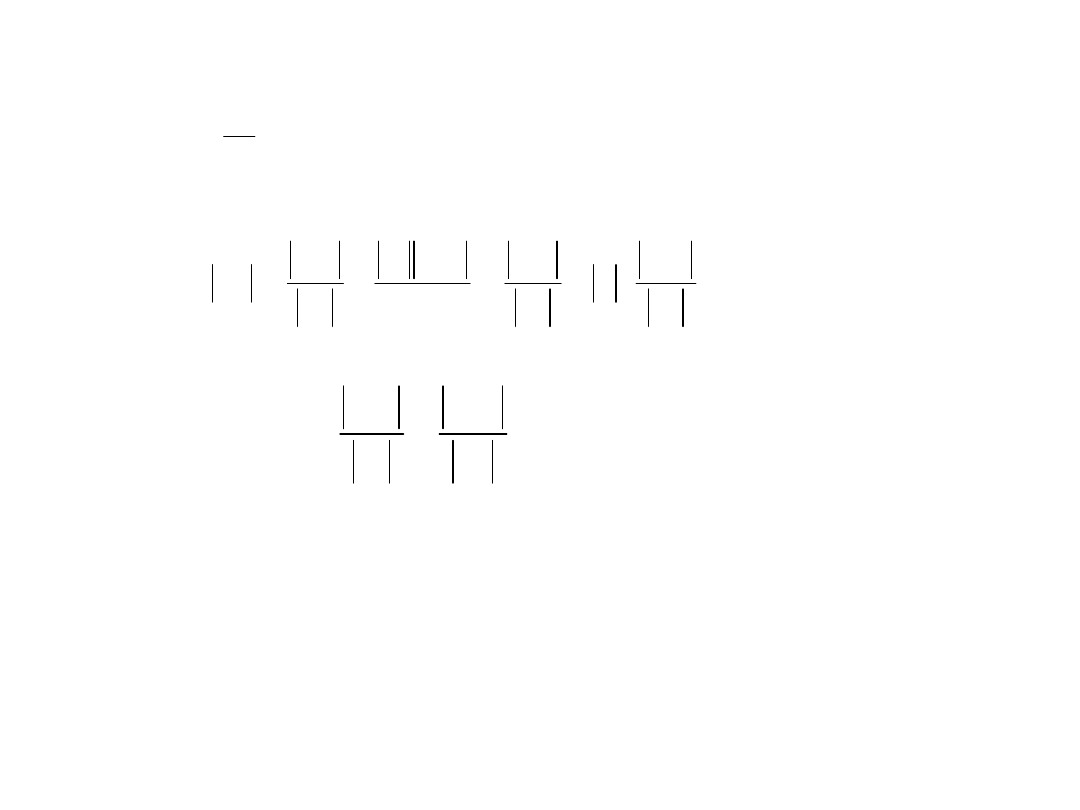
Błąd ilorazu

Jeżeli , to wzory na błąd względny i
bezwzględny ilorazu tych liczb są następujące

2

1

x

x

y 

2

2

2

1

2

2

2

1

2

1

x

x

y

x

x

x

x

x

x

x

y





















(1.30)

2

1

2

2

1

1

x

x

x

x

x

x

y



















(1.31)

Problem odwrotny teorii błędów

W praktyce ważny jest również problem odwrotny
do problemu omówionego przy przedstawieniu
różniczki zupełnej. Można go sformułować
następująco:

Jakie mogą być błędy bezwzględne argumentów
funkcji, aby błąd bezwzględny funkcji nie
przekraczał zadanej wartości.

Dla uproszczenia rozważań zakładamy, że wszystkie
pochodne cząstkowe (i=1,2,...,n) wpływają
jednakowo na powstanie

ogólnego błędu bezwzględnego funkcji
.

Jest to tzw. zasada równego wpływu. Zakładając, że
składniki sumy we wzorze (1.14) są równe, czyli

i

x

f





)

,...,

,

(

2

1

n

x

x

x

f

y 

n

n

x

x

f

x

x

f

x

x

f

x

x

f









































...

1

1

2

2

1

1

(1.36)

Otrzymujemy

(1.37)

Z powyższych zależności otrzymujemy następujący
wzór:

(i = 1,2,...,n).
(1.38)

i

i

i

n

i

i

x

x

f

n

x

x

f

y

























1

i

i

x

f

n

y

x











Przykład

Promień podstawy walca wynosi r  2cm, a wysokość

walca h  3cm. Z jaką dokładnością bezwzględną

należy określić r oraz h, żeby objętość walca V obliczyć
z dokładnością do 0,1cm

3

?

Dan

e:



V



0,1cm

3

r  2

cm
h  3

cm
 

3,14
V  r

2

h

Szukan

e:



r



h





Rozwiązanie

Dla powyższych danych otrzymujemy w
przybliżeniu:

Ponieważ n=3, to na podstawie wzoru (1.38)
otrzymamy

3

2

2

2

2

0

,

12

6

,

12

7

,

37

2

cm

h

r

v

cm

r

h

V

cm

rh

r

V































003

,

0

12

3

1

,

0

003

,

0

6

,

12

3

1

,

0

001

,

0

7

,

37

3

1

,

0



























h

r