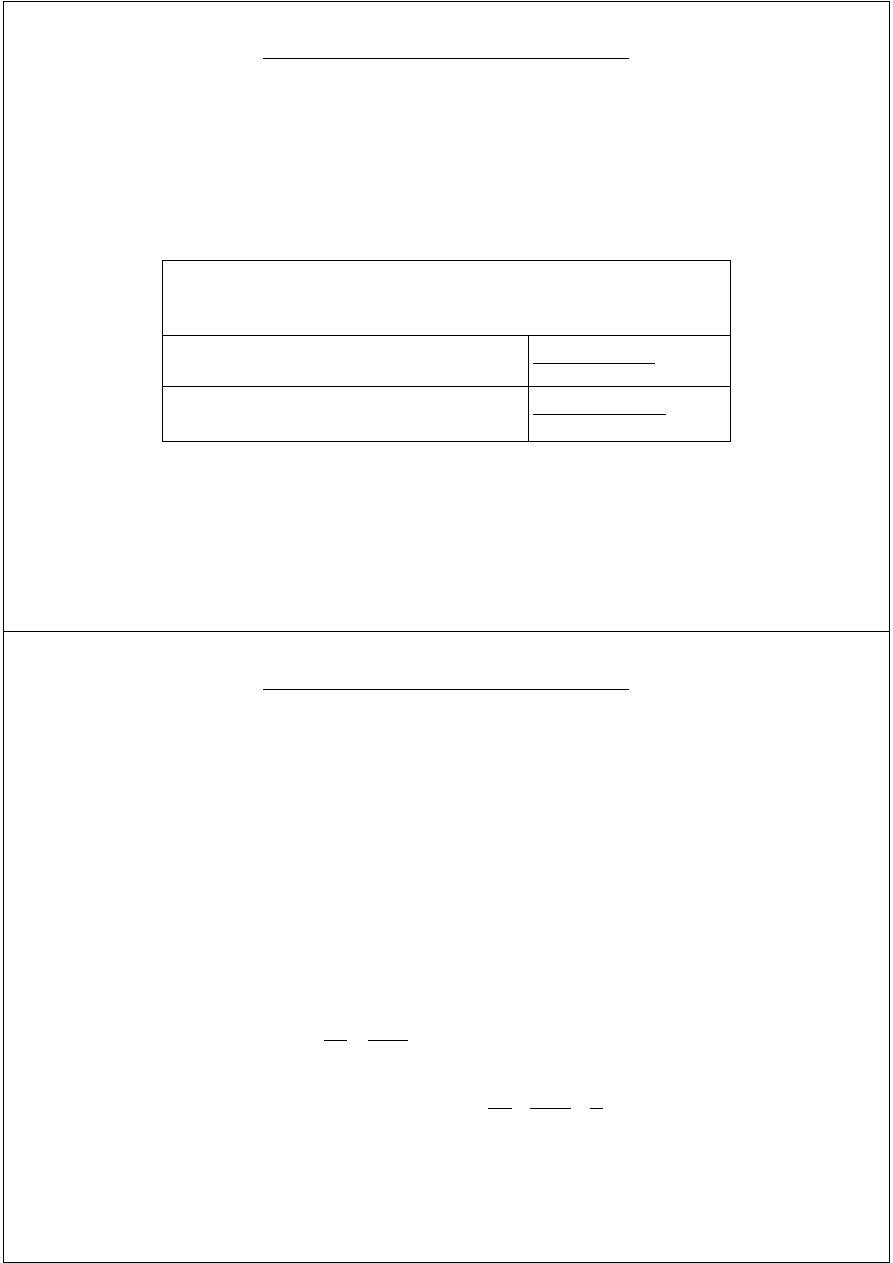
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 1

W1 - 1

b

a

dz

)

x

(

f

Metody numeryczne (analiza numeryczna

)

- nauka zajmująca się rozwiązywaniem problemów matematycznych
metodami arytmetycznymi
- sztuka doboru spośród wielu możliwych procedur takiej, która jest
„najlepiej” dostosowana do rozwiązania danego zadania

Oszacowanie błędu numerycznego obliczenia

∫

przy n+1

obliczeniach wartości f(x)

Metoda trapezów

2

3

12n

(

''

f

)

a

−

1

)

ξ

b

(

Metoda Simpsona

4

4

5

180 n

f

)

a

)

(

−

2

)

(

ξ

b

(

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 1

W1 - 2

a

1. Odpowiednie sformułowanie zadania
2. Metoda numeryczna + analiza błędu
3. Algorytm
4. Implementacja

1. Błąd danych wejściowych
2. Błąd zaokrągleń w czasie obliczeń
3. Błąd metody (obcięcia)
4. Błąd wnoszony przez uproszczenia modelu matematycznego
5. Błąd człowieka

Błąd względny:

uogólnienie na wartości wektorowe

~ jest przybliżeniem wartości dokładnej a

Błąd bezwzględny:

∆

a

a~

a

−

=

0

≠

−

=

∆

=

a

,

a

a

a~

a

a

a

ε

a

)

(

a

a

a

a~

a

a

a

ε

ε

+

=

+

=

∆

+

=

1

0

1

≠

−

=

−

=

∆

=

a

,

a

a~

a

a

a~

a

a

a

ε

szacowanie modułów błędów

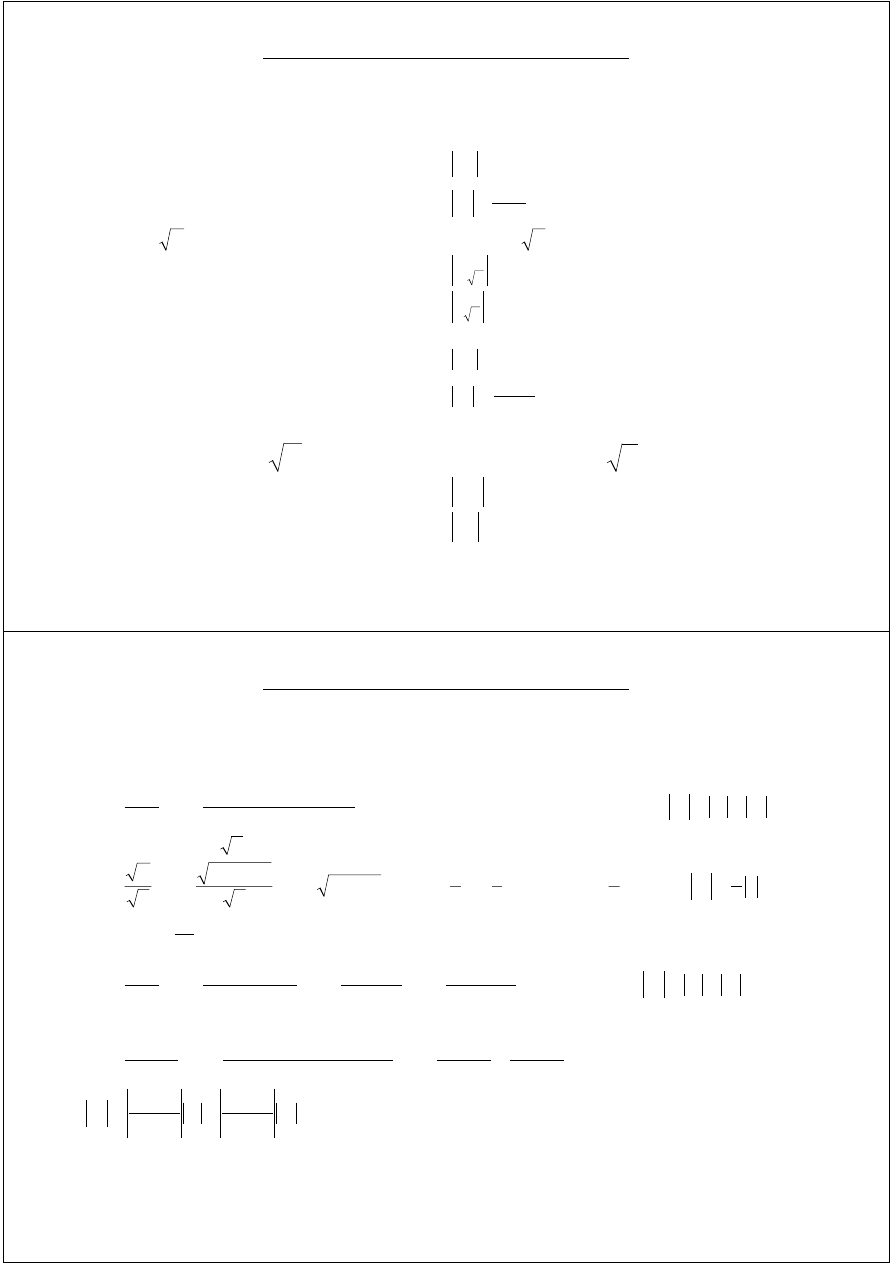
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 1

W1 - 3

4

4

.

y

Przenoszenie się błędów w obliczeniach numerycznych

1. Analiza bezpośrednia krok po kroku:

~ =

45

4

35

4

.

y

.

poprawnie zaokrąglona, więc

<

<

05

0.

y

<

∆

0115

.

0

35

.

4

05

.

0

=

<

y

ε

0976

2.

y~

=

2

1095

2

0857

.

y

.

<

<

0119

0.

y

<

∆

0057

0.

y

<

ε

3

10.

x~

=

35

10

25

10

.

x

.

poprawnie zaokrąglona, więc

<

<

05

0.

x

<

∆

049

0

25

10

05

0

.

.

.

x

=

<

ε

.....................................................................

5175

.

2

)

~

~

ln(

~

=

+

=

y

x

z

5225

.

2

)

<

2

1

ε

+

ε

ε

<

y

ε

2

1

<

ε

y

2

ε

2

1

x

x

y

±

=

1

ε

ε

+

<

y

ln(

5125

.

2

+

<

y

x

005

.

0

<

∆

z

0020

.

0

<

z

ε

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 1

2

1

ε

ε

+

≈

1

W1 - 4

1

1

1

ε

ε

ε

ε

ε

ε

2

1

8

1

2

1

1

1

1

1

1

1

2

≈

−

+

−

+

=

−

+

=

−

+

=

−

=

.....

)

(

x

)

(

x

x

x

2. Wykorzystanie podstawowych wzorów

ε

,

x~

,

x

2

2

2

,

ε

,

x~

,

x

2

1

x

x

y

=

Iloczyn:

2

1

2

1

2

2

1

1

2

1

2

1

1

1

1

1

1

1

ε

ε

1

−

)

ε

ε

ε

+

+

=

−

+

+

=

−

=

)(

(

x

x

)

(

x

)

(

x

x

x

x~

x~

y

więc

Pierwiastek:

x

y

=

~

y

więc

Iloraz:

2

1

x

x

y

=

2

1

2

2

1

2

1

2

2

1

2

1

1

2

1

2

1

1

1

1

1

1

1

1

1

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

−

≈

+

−

=

−

+

+

=

−

+

+

=

−

=

)

(

)

(

)

(

)

(

)

(

x

x

x

)

(

x

x~

x

x

x~

y

więc

Suma:

2

1

2

2

2

1

1

2

1

2

2

1

1

2

1

2

1

1

1

1

1

x

x

x

x

x

x

x

x

)

(

x

)

(

x

x

x

x

1

±

~

x~

y

±

±

=

−

±

+

±

+

=

−

±

±

=

ε

ε

ε

ε

ε

więc

2

2

1

2

1

2

1

1

ε

ε

ε

x

x

x

x

x

x

y

±

+

±

<

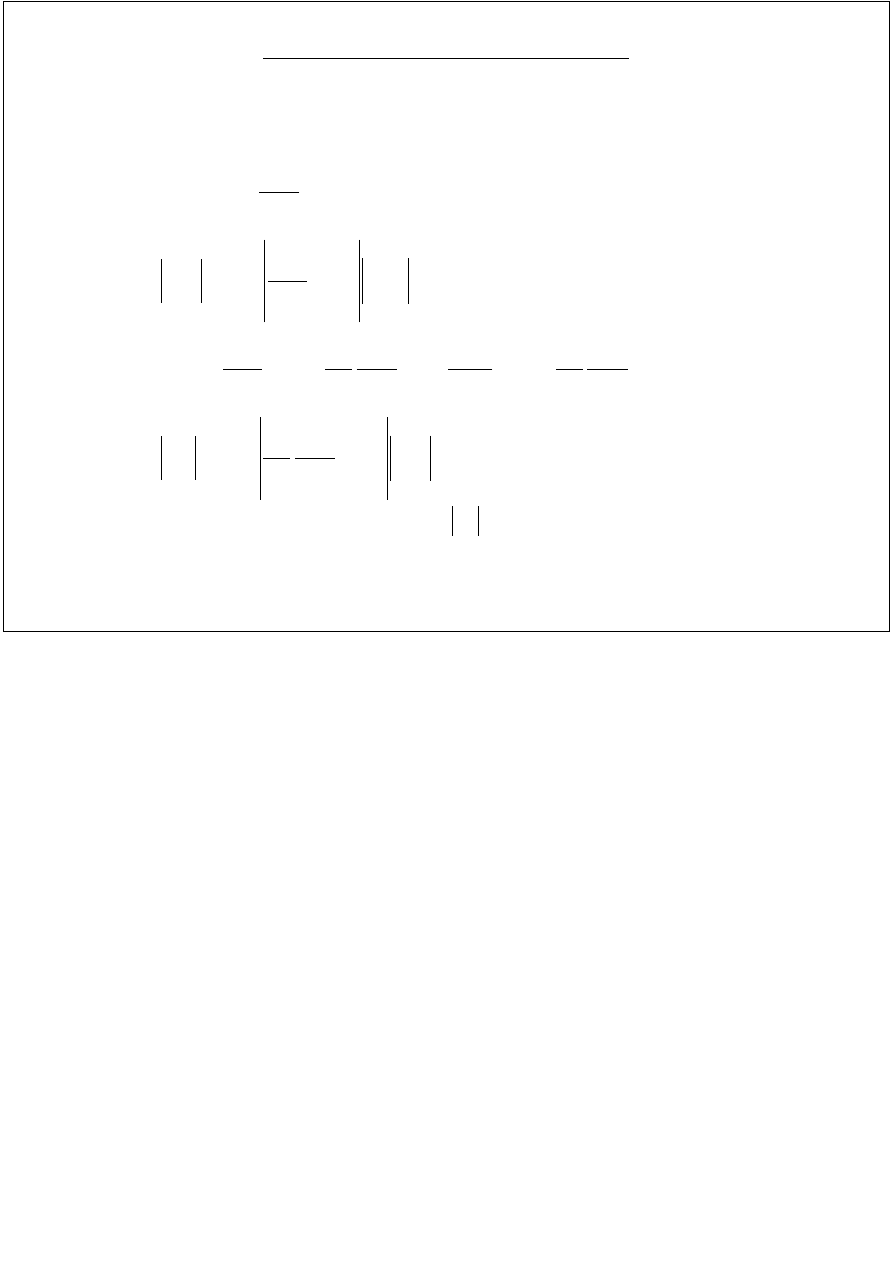
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 1

W1 - 5

3. Metoda przybliżona

)

x

,...,

x

,

x

(

x

n

2

1

=

,

)

x~

,...,

x~

,

x~

(

x~

n

2

1

=

)

x

(

y

)

x

(

y

)

x~

(

y

y

−

=

∆

i

x

n

i

i

y

)

x~

(

x

y

∆

∂

∂

≈

∆

∑

=1

i

x

n

i

i

y

)

x~

(

x

y

∆

∂

∂

<

∆

∑

=1

)

x~

(

i

i

x

n

i

i

i

x

n

i

i

i

y

y

x

y

y

x

x

)

x~

(

x

y

y

x

y

ε

ε

∑

∑

=

=

∂

∂

=

∆

∂

∂

≈

∆

=

1

1

i

(

y

ε

i

x

n

i

)

x~

ε

∑

=

<

i

x

y

y

x

∂

∂

1

i

<

z

ε

metodą przybliżoną

0024

.

0