
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-1
Interpolacja
funkcja przybliżana
)
x
(
f
,
siatka węzłów
)
x
(
f
f
,
n
,...,
i
,
x
i
i
i
=
= 0
Dla dowolnych, różnych n+1 punktów węzłowych istnieje
dokładnie jeden wielomian interpolacyjny stopnia, co
najwyżej n taki, że
i
i
f
)
x
(
P
=
dla i=0,1,...,n
Wzór interpolacyjny Lagrange’a
∏
∑
≠
=
=
−
−
=
n
i
k
k
k
i
k
n
i
i
x
x
x
x
f
)
x
(
P
0
0
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-2
Interpolacja przez rodzinę trójkątną
Rekurencyjne tworzenie wielomianów interpolacyjnych
Niech
)
(
,...,
1
,
0
x
k
i
i
i
P
będzie wielomianem stopnia nie
większego od k, spełniającym równania węzłów
k
i
,...,
i
,
i
1
0
:
k
j
j
i
f
j
i
x
k
i
i
i
P
,...,
0
)
(
,...,
1
,
0
=
=
Wtedy zachodzi wzór rekurencyjny
n
i
i
f
x
i
P
,...,
0
)
(
=
=
0
)
(
1
,...,
1
,
0
)
0
(
)
(
,...,
2
,
1
)
0
(
)
(
,...,
1
,
0
i
x
k
i
x
x
k
i
i
i
P
k
i
x
x
x
k
i
i
i
P
i
x
x
x
k
i
i
i
P
−
−
−
−
−
=
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-3
Metoda
Aitken’a
0
x
0
0
f
)
x
(
P
=
1
x
1
1
f
)
x
(
P
=
)
x
(
P
,1
0
2
x
2
2
f
)
x
(
P
=
)
x
(
P
,2
0
)
x
(
P
,
, 2
1
0
3
x
3
3
f
)
x
(
P
=
)
x
(
P
,3
0
)
x
(
P
,
, 3
1
0
)
x
(
P
,
,
,
3
2
1
0
4
x
4
4
f
)
x
(
P
=
)
x
(
P
,4
0
)
x
(
P
,
, 4
1
0
)
x
(
P
,
,
,
4
2
1
0
)
x
(
P
,
,
,
,
4
3
2
1
0
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-4
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
i
i
i
i
i
i
i
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
P
y
x
x
x
m
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
P
y
x
x
x
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
x
x
P
x
P
y
x
x
x
x
x
x
P
x
x
x
P
x
x
x
P
x
P
y
x
x
x
x
P
y
x
x
x
x
P
x
P
x
P
x
P
x
P
y
x
x
x
i
−
−
−
=
−
−
−
=
−
−
−
=
−
−
−
=
=
−
−
−
−
=
−
−
−
=
−
−
−
=
=
−
−
−
−
=
−
−
−
=
=
−
−
−
−
=
=
−
=
−
=
−
−
−
−
−
1
,
2
,
,
1
,
0
1
,
,
1
,
0
1
,
,
1
,
0
2
,
1
,
0
2
,
1
,
0
2
,
2
,
1
,
0
1
,
0
1
,
0
1
,
1
,
0
0
0
0
,
0
3
2
3
,
1
,
0
3
2
,
1
,
0
2
3
,
2
,
1
,
0
3
1
3
,
0
3
1
,
0
1
3
,
1
,
0
3
0
3
3
0
0
3
,
0
3
3
3
3
2
1
2
,
0
2
1
,
0
1
2
,
1
,
0
2
0
2
2
0
0
2
,
0
2
2
2
2
1
0
1
1
0
0
1
,
0
1
1
1
1
0
0
0
0
,
,
1
,
0
,
2
,
1
,
0
,
1
,
0
,
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
3
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
)
(
)
(
)
(
)
(
1
)
(
0
)
(
)
(
)
(
)
(
)
(
K
K
K
K
K
O
M
M
M
M
M
M
M
K

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-5
Reszta wzoru interpolacyjnego:
Jeżeli funkcja
)
(
f
⋅
ma ciągłe pochodne do rzędu n+1 a
)
(
P
⋅
jest wielomianem interpolacyjnym stopnia n, to
)
x
x
(
)
(
f
)!
n
(
)
x
(
P
)
x
(
f
n
i
i
)
n
(
∏
=
+
−
+
=
−
0
1
1
1
ξ
gdzie
ξ
jest pewnym punktem z najmniejszego przedziału
domkniętego zawierającego
n
x
,...,
x
,
x
0
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-6
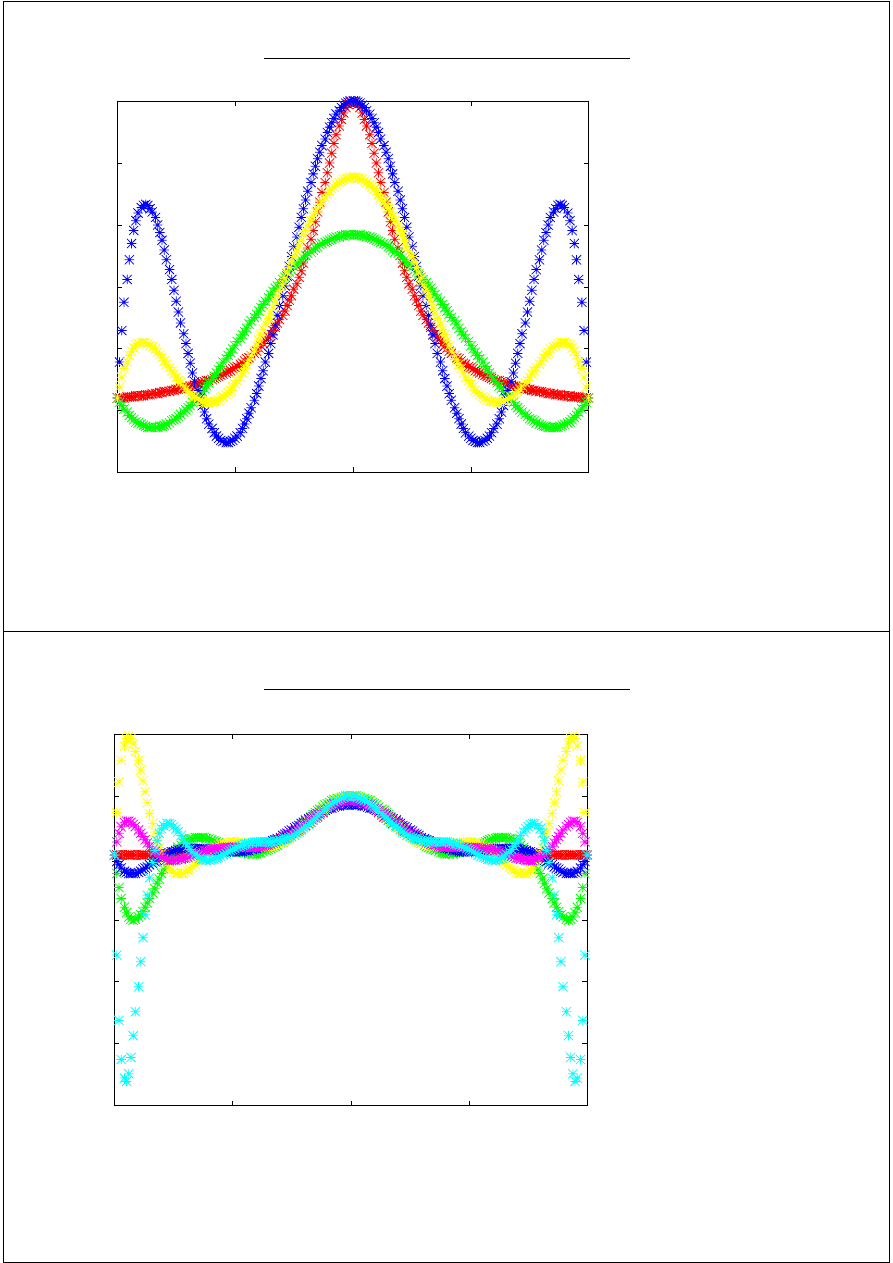
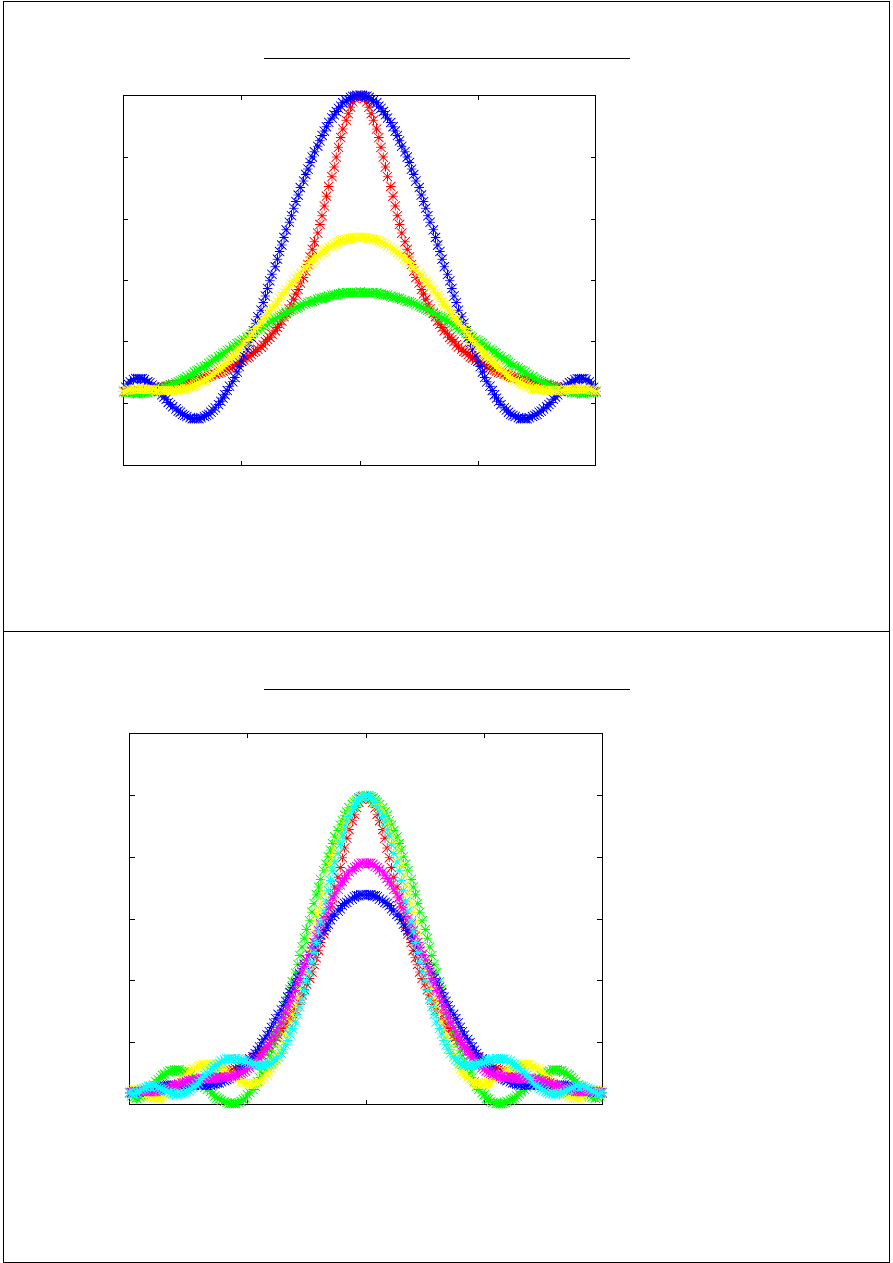
Przykład:
2
5
1
1
)
x
(
)
x
(
y
+
=
węzły równoodległe w [-1,1]
węzły Czebyszewa w [-1,1]
w=[];x=[];y=[];apr=[];
xx=-1:.01:1;yy=1./(1+(5*xx).^2);
for n=4:16
h=2/n;
for i=1:n+1
x(n,i)=-1+(i-1)*h;
end
y(n,1:n+1)=1./(1+(5*x(n,1:n+1)).^2);
w=polyfit(x(n,1:n+1),y(n,1:n+1),n);
apr(n,:)=polyval(w,xx);
end
w=[];x=[];y=[];apr=[];
xx=-1:.01:1;yy=1./(1+(5*xx).^2);
for n=4:16
for i=1:n+1
x(n,1:n+1)=-seqcheb(n+1,2);
end
y(n,1:n+1)=1./(1+(5*x(n,1:n+1)).^2);
w=polyfit(x(n,1:n+1),y(n,1:n+1),n);
apr(n,:)=polyval(w,xx);
end
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-7
-1
-0.5
0
0.5
1
-0.2
0
0.2
0.4
0.6
0.8
1
n=5,6,7
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-8
-1
-0.5
0
0.5
1
-4
-3
-2
-1
0
1
2
n=8,9,10,11,12
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-9
-1
-0.5
0
0.5
1
-0.2
0
0.2
0.4
0.6
0.8
1
n=5,6,7
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 3
W3-10
-1
-0.5
0
0.5
1
0
0.2
0.4
0.6
0.8
1
1.2
n=8,9,10,11,12
Wyszukiwarka
Podobne podstrony:
metody numeryczne i w3
metody numeryczne w3 (2)
metody numeryczne w3
Metody numeryczne w3
Metody numeryczne w6
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
MN energetyka zadania od wykładowcy 09-05-14, STARE, Metody Numeryczne, Część wykładowa Sem IV
METODA BAIRSTOWA, Politechnika, Lab. Metody numeryczne
testMNłatwy0708, WI ZUT studia, Metody numeryczne, Metody Numeryczne - Ćwiczenia
Metody numeryczne Metoda węzłowa
Metody numeryczne, wstep
metody numeryczne w4
Metody numeryczne PDF, MN macierze 01 1
Metody numeryczne w11
metody numeryczne i w9
więcej podobnych podstron