(1) Stan fizyczny obiektu w dowolnej chwili czasu t jest opisany przez funkcję falową

Ψ

(x,t).

(6)

Funkcja

Ψ

(x,t) jest rozwiązaniem równania Schrodingera zależnego od czasu.

Główne postulaty fizyki kwantowej

Pozostałe postulaty fizyki kwantowej

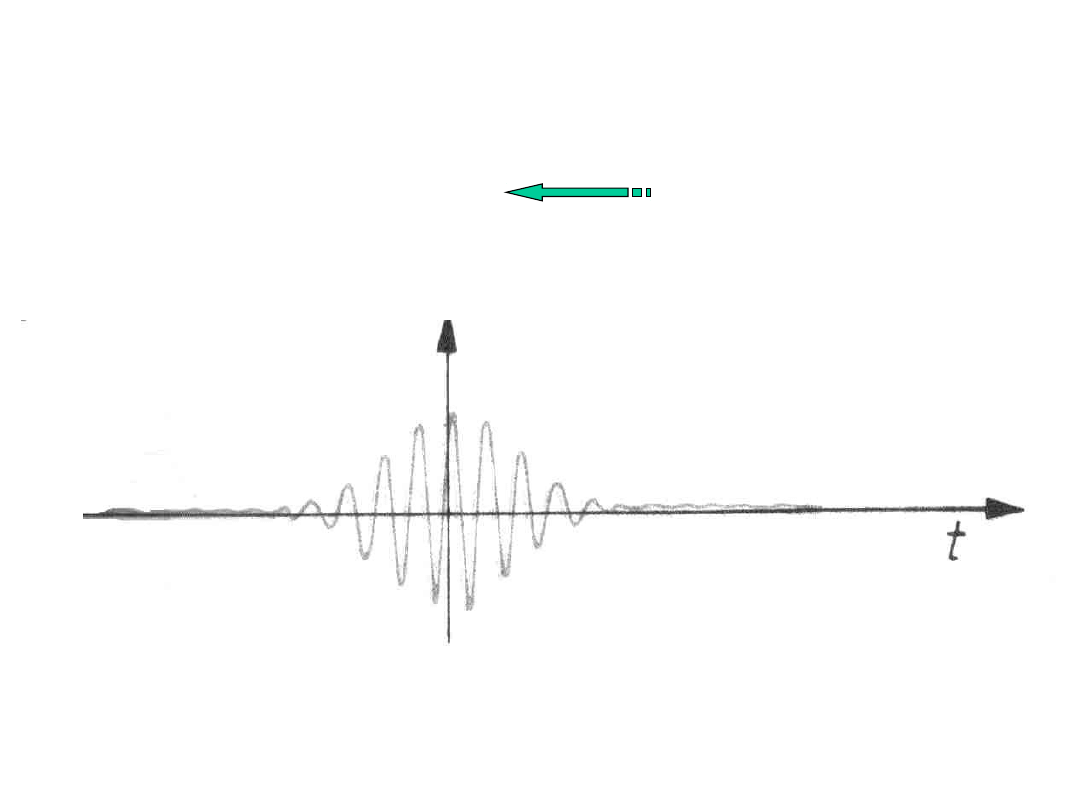
Czy można pogodzić lokalizację obiektu z jego własnościami falowymi?

Fala płaska jest zupełnie zdelokalizowana.

Czy istnieją bardziej „zlokalizowane fale”?

Ψ  x ,t =Ae

i  kx−ωt 

Fala płaska

Sumując wiele fal płaskich o bliskich częstościach otrzymamy tzw. paczkę falową, która wykazuje już pewną

lokalizację w przestrzeni.

 

x ,t =



o

− 

∫

Ae

i kx− t 

d 



0



Suma nieskończonej ilości fal sinusoidalnych będzie

wtedy dana funkcją:



(x,t)

x

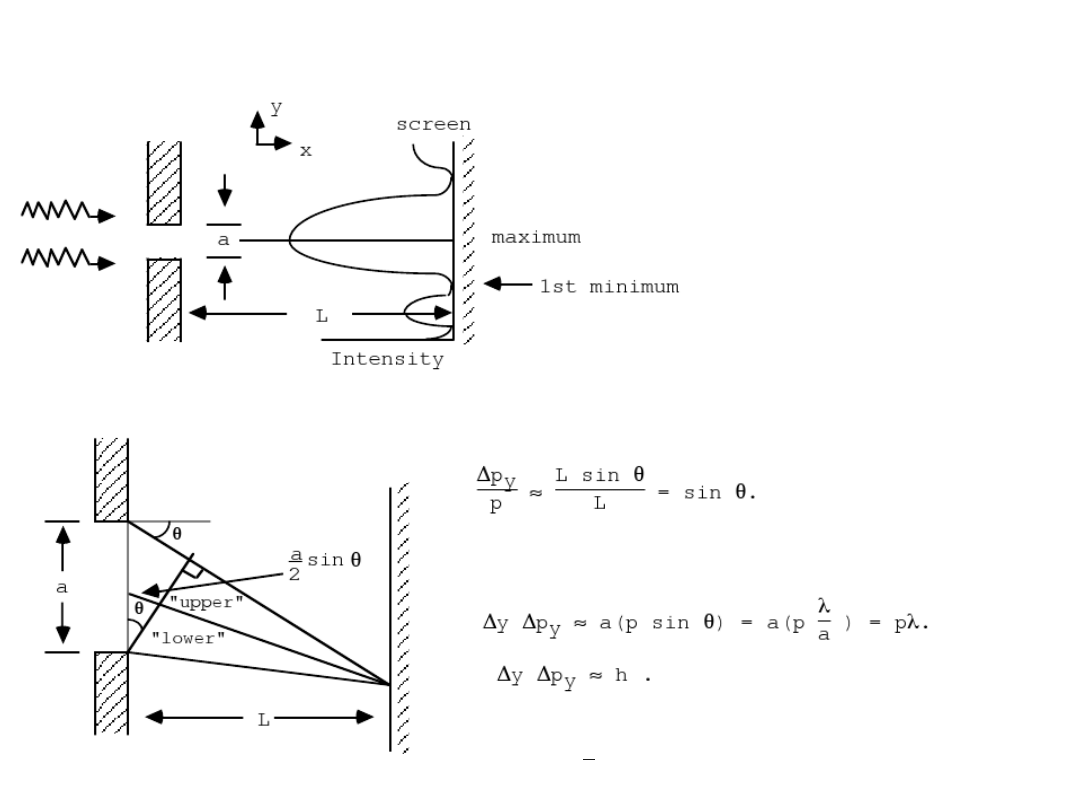
The uncertainty principle (konsekwencja opisu falowego)

Obraz dyfrakcyjny na pojedyńczej szczelinie.

Zdecydowana większość energii fali jest

zlokalizowana w obszarze zerowego maksimum.

Dla cząstek oznacza to, że większość cząstek uderzyła

w ekran w obszarze zerowego maksimum.

Aby cząstka uderzyła w ekran w obrębie maksimum

zerowego rzędu, jej składowa prostopadła pędu musi

spełniać poniższą relację:



y  p

y



ℏ
2

Dla pierwszego minimum mamy zależność:

a sin =1⋅

Ostatecznie, po dokładniejszej analizie otrzymujemy:

Położenie cząstki w tym eksperymencie jest wyznaczone z

dokładnością równą szerokości szczeliny

Czy wszystkie wielkości fizyczne można wyznaczyć z dowolną dokładnością?

paczka falowa porusza się

nie

z prędkością fazową:

u=

/k

lecz z prędkością grupową: v

g

=d

/dk

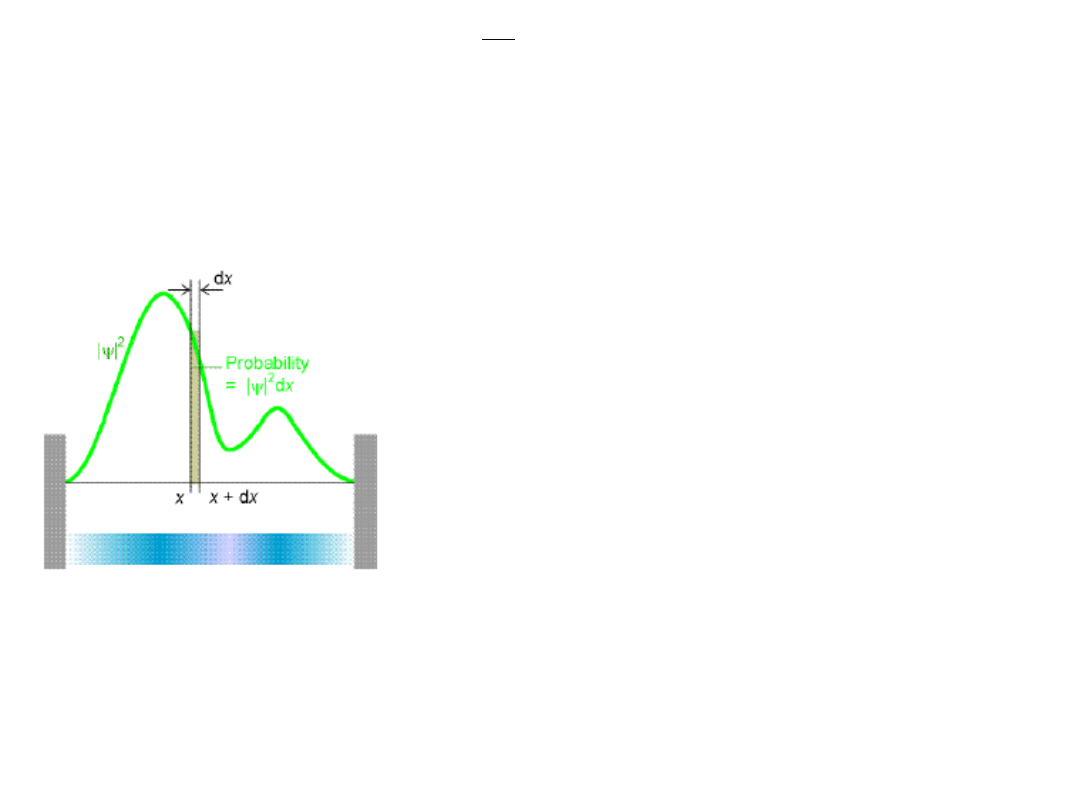
Interpretacja funkcji falowej

Max Born: interpretacja funkcji falowej a
położenie cząstki

Ψ

(x,t)

|

2

dx

opisuje prawdopodobieństwo

znalezienia cząstki w przedziale <x, x+dx>

w chwili t.

∫

−∞

∞

∣

x ∣

2

dx=1

Prawdopodobieństwo znalezienia cząstki w całym obszarze.

(6)

Funkcja

Ψ

(x,t) jest rozwiązaniem równania Schrodingera zależnego od czasu.

H Ψ r ,t =i ℏ

∂

Ψ r ,t 

∂

t

Dlaczego równanie Schrodingera a nie zwykłe równanie falowe?

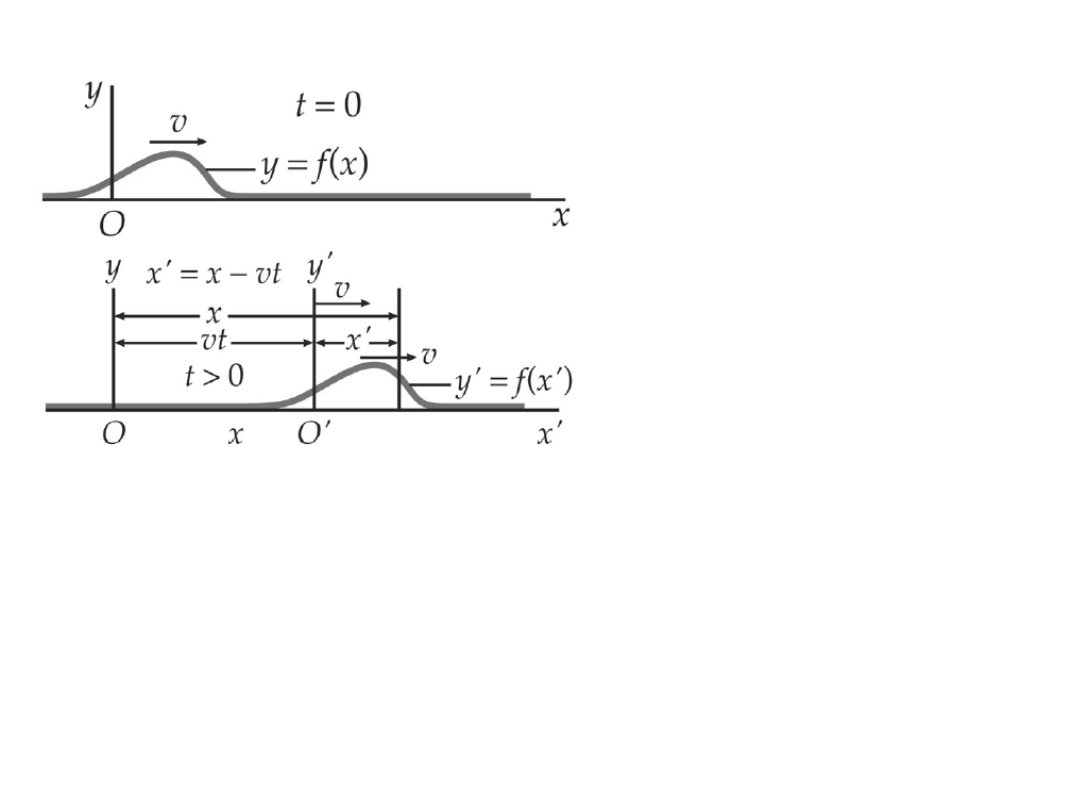
Równanie falowe

Zaburzenie przemieszcza się z punktu O do O' bez zmiany

kształtu.

dla t=0 f(x,t) = f(x)
dla dowolnej chwili t, f(x,t)=f(x-vt)

gdyby zaburzenie poruszało się w przeciwnym kierunku
mielibyśmy f(x,t)=f(x+vt)

Ogólnie: Ψ r ,t =Ψ r±vt − funkcja falowa

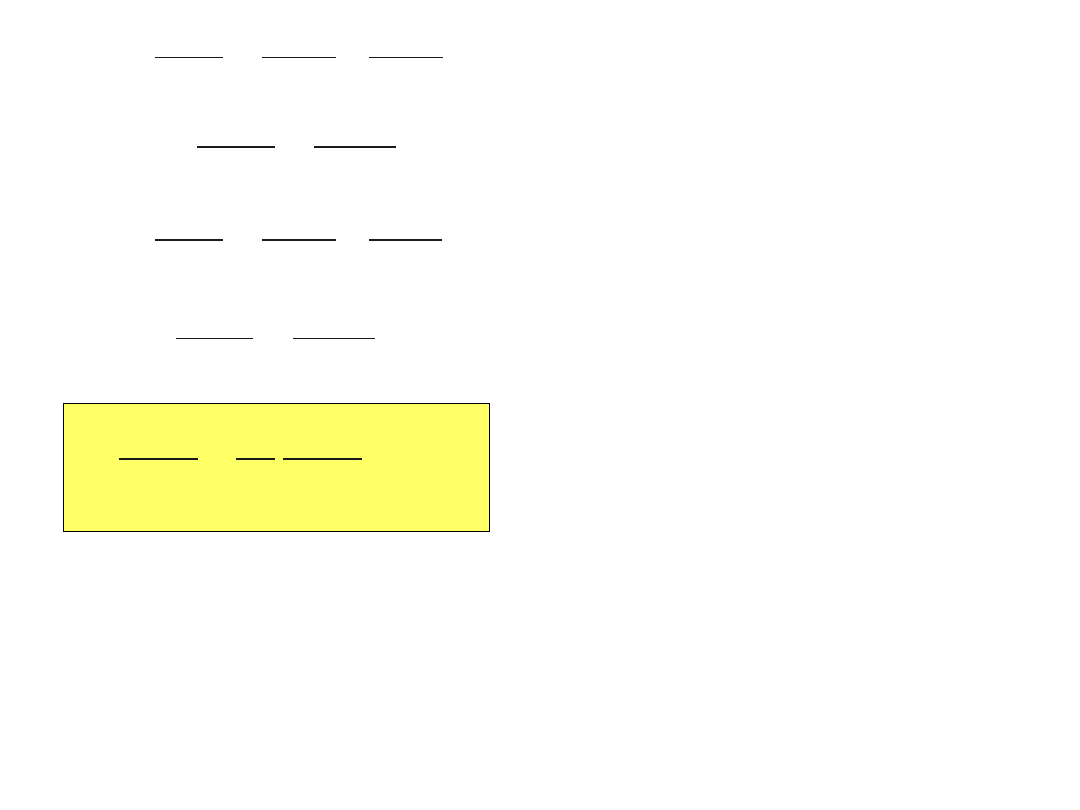
Równanie

falowe:

∂ 

∂

x

=

∂ 

∂

x ' 

⋅

∂

x ' 

∂

x



∂

2



∂

x

2



=

∂

2



 ∂

x '

2





∂ 

∂

t

=

∂ 

∂

x ' 

⋅

∂

x ' 

∂

t



∂

2



∂

t

2



=

∂

2



 ∂

x '

2



⋅

v

2



∂

2



∂

x

2

−

1

v

2

∂

2



∂

t

2

=

0

Równanie falowe

Klasyczna Funkcja Hamiltona

Funkcja całkowitej enegii, gdzie energia kinetyczna jest wyrażona
przy pomocy pędu

Nazywana jest funkcją hamiltona lub hamiltonianem układu

Ta funkcja hamiltona układu jest zasadnicza dla transformacji z
fizyki klasycznej do kwantowej.

Joseph-Louis Lagrange

Leonhard Euler

Sir William Rowan Hamilton (1805-1865)

Twórcy mechaniki
klasycznej

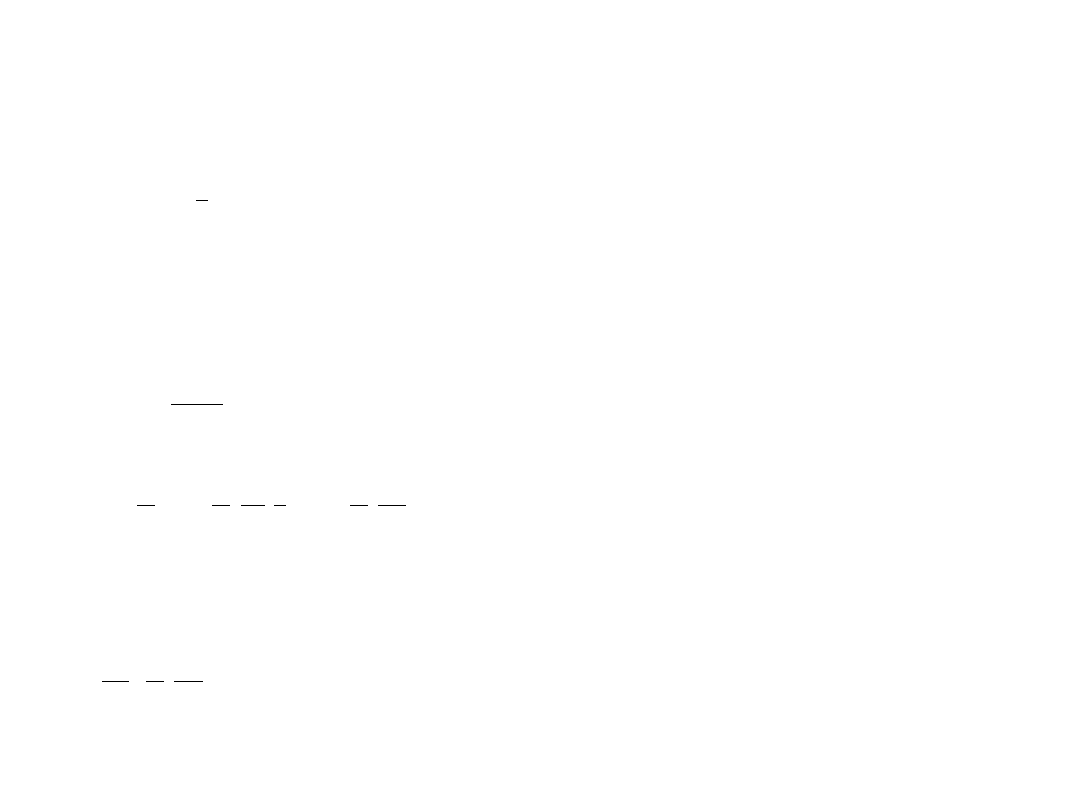
Metoda funkcji Lagrange`a (

tylko dla sił potencjalnych

)

E=K V

K=

1

2

mv

2

Energia kinetyczna

V =V  x 

Energia potencjalna

Dla sił potecjalnych:

F

x

=−

∂

V  x 

∂

x

=

ma

x

=

m ¨x

m ¨x=

d

dt



m ˙x =

d

dt

 ∂

∂ ˙

x



1
2

m ˙x

2

=

d

dt



∂

K

∂ ˙

x



Stąd otrzymujemy:

−

∂

V

∂

x

=

d

dt



∂

K

∂ ˙x



Ponieważ

K=K  ˙x ⇒

∂

K

∂

x

=

0

V =V  x ⇒−

∂

V

∂ ˙x

=

0

Stąd otrzymujemy:

∂

K−V 

∂

x

=

d

dt



∂

K −V 

∂ ˙x



lub

d

dt



∂

L

∂ ˙x

−

∂

L

∂

x

=

0

Gdzie L jest funkcją Lagrange'a

zdefiniowaną jako

L=K−V

Równanie Lagrange'a lub Eulera-

Lagrange'a

Współrzędne uogólnione: q

i

, p

i

˙

q

i

=

f  ˙x

1

, ˙x

2

,⋯, ˙x

l



Przykład oscylatora harmonicznego

L=

m ˙x

2

2

−

kx

2

2

Z równania Lagrange'a mamy

m x−−kx=0

lub

m x=−kx

q

i

=

f  x

1

,x

2

,⋯, x

l



L= L q

i

, ˙q

i



d

dt



∂

L

∂ ˙q

i

−

∂

L

∂

q

i

=

0

Równanie Eulera-Lagrange'a we współrzędnych

uogólnionych (kanonicznych)

Startujemy z funkcji Lagrange'a zależnej od

współrzędnych uogólnionych i prędkości

uogólnionych

L=L q

i

, ˙q

i



Funkcja Hamiltona. Równania Hamiltona.

Definiujemy pęd uogólniony

(kanoniczny)

p

i

=

∂

L

∂ ˙q

i

H=H q

i

, ˙p

i



Definiujemy funkcję współrzędnych i

pędu

H  q

i

, ˙p

i

=

p

i

˙

q

i

−

L  ˙q

i

, q

i



Gdzie za prędkości uogólnione należy podstawić z zależności:

˙

q

i

=

∂

H

∂

p

i

Wtedy równania Eulera-Lagrange'a można zapisać w postaci:

d

dt



∂

L

∂ ˙q

i

−

∂

L

∂

q

i

=

d

dt



p

i

−

∂

L

∂

q

i

=

0

∂

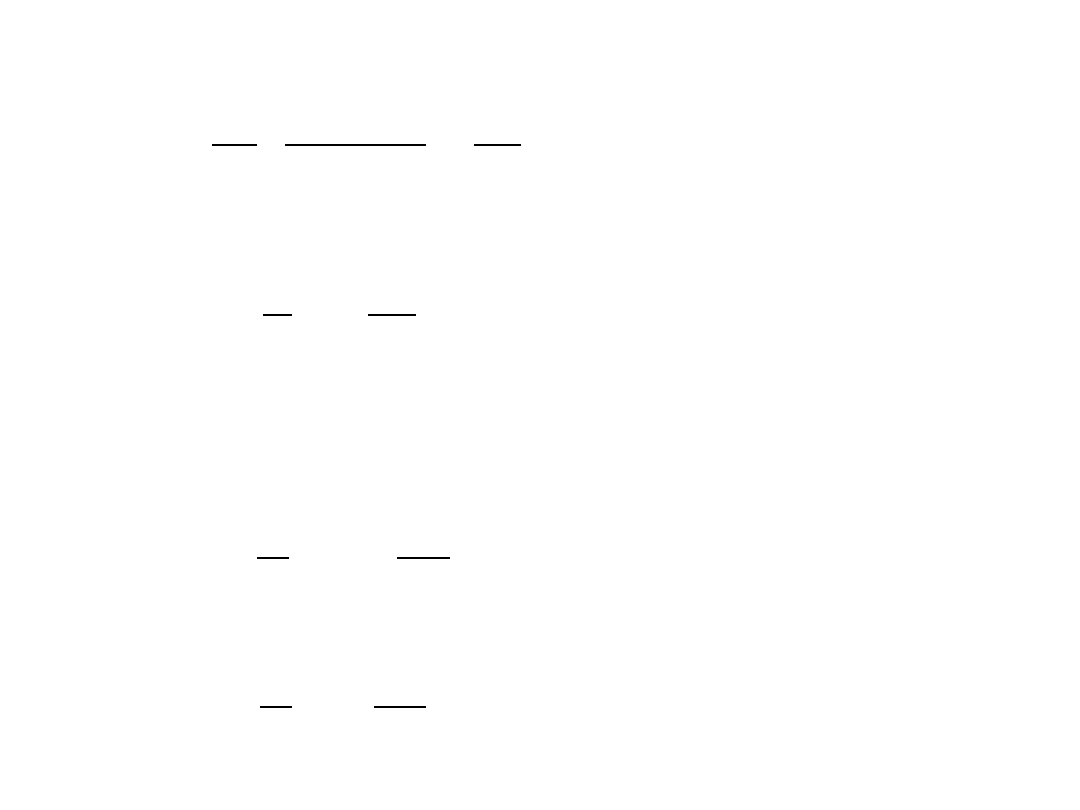
L

∂

q

i

=

∂

p

i

˙

q

i

−

H 

∂

q

i

=−

∂

H

∂

q

i

Ponieważ

d

dt



p

i



∂

H

∂

q

i

=

0

to

Ostatecznie otrzymujemy dwa równania:

d

dt



q

i

=

∂

H

∂

p

i

d

dt



p

i

=−

∂

H

∂

q

i

Są to tzw. Równania Hamiltona

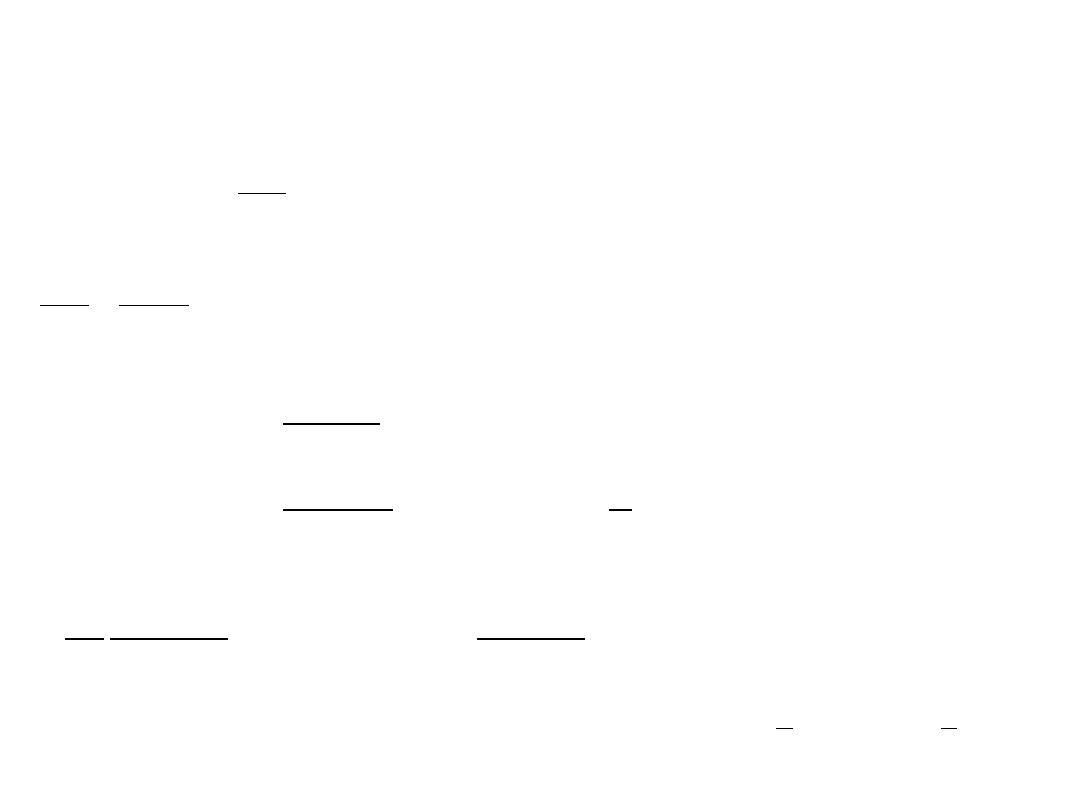
Energia całkowita cząstki ( często nazywana funkcją Hamiltona ) poruszającej się wzdłuż osi x

E=

p

x

2

2m



V  x , t 

gdzie V(x,t) – energia potencjalna cząstki

p

x

2

2m

=

ℏ

2

k

2

2m

E=ℏ ω

Jeżeli rozważymy najprostszą falę płaską:

Ψ  x ,t =Ae

i  kx−ωt 

∂

2

Ψ  x ,t 

∂

x

2

=−

k

2

Ψ  x ,t 

∂

Ψ  x , t 

∂

t

=−

iωΨ x ,t =−i

E
ℏ

Ψ  x ,t 

−

ℏ

2

2m

∂

2

Ψ  x , t 

∂

x

2



V  x , t  Ψ  x , t =i ℏ

∂

Ψ  x , t 

∂

t

Równanie Schrodingera
zależne od czasu

V  x , t =V  x  ⇒

Jeżeli

Ψ  x , t =Ae

ikx

e

−

i

E
ℏ

t

=

Φ  x  e

−

i

E

ℏ

t

Uzasadnienie postaci równania Schrodingera

[

−

ℏ

2

2m

∂

2

∂

x

2



V  x

]

Φ  x =EΦ x 

Równanie Schrodingera niezależne od czau

∫

−∞

∞

∣

Φ  x ∣

2

dx=1

Funkcja

Φ

(x) jest klasy C

1

, tzn. ciągłą wraz z 1-szą pochodną

(warunek konieczny istnienia drugiej pochodnej)

Równanie Schrodingera zależne i niezależne od czasu można prosto uogólnic do 3 wymiarów.