Zadania do projektu 2

1. Masy i współrzędne czterech punktów materialnych są następujące:
m

1

 = 5 kg 

x

1 

= y

1

 = 0 cm

m

2

 = 3 kg 

x

2

 = y

2

 = 8 cm

m

3

 = 2 kg 

x

3

 = 3 cm; y

3 

= 0 cm

m

4

 = 6 kg 

x

4

 = - 2 cm; y

4

 = -6 cm

Proszę znaleźć współrzędne środka masy tej grupy punktów materialnych. 

2. Kulka ołowiana o masie m

1

 = 500 g, która porusza się z prędkością v

1

 = 10 m/s, 

zderza się z nieruchomą kulką woskową o masie m

2

 = 200g, następnie obie kulki 

poruszają się razem. Jaka jest energia kinetyczna kulek po zderzeniu?

3. Cztery jednakowe ciała o równych masach m = 20 g leżą na prostej w pewnych 

odstępach od siebie. W skrajne ciało uderza takie samo ciało, które porusza się z 
prędkością v

0

 = 10 m/s wzdłuż prostej, na której rozłożone są ciała. Jaka jest energia 

kinetyczna układu ciał, jeśli zderzenie jest niesprężyste.

4. Pręt o długości L = 1 m i o ciężarze P = 15 N jednym końcem jest przymocowany 

na zawiasie do sufitu. pręt jest utrzymywany w położeniu odchylonym za pomocą 
sznura pionowego przywiązanego do swobodnego końca pręta. Jakie jest naprężenie 
T  sznura,   jeśli   środek   ciężkości   pręta   znajduje   się   w   odległości  s   =   0.4   m  od 
zawiasu.

5. Pręt jednorodny z przymocowanym na jednym z jego końców ciężarem o masie m 

znajduje się w równowadze w położeniu poziomym, jeśli jest podparty w odległości 
1/5 swojej długości od ciężaru. Ile wynosi masa pręta M?

6. Jaka siła grawitacyjna działa na kosmonautę o masie 60 kg znajdującego się  na 

orbicie  o promieniu dwukrotnie większym od promienia Ziemi? 

7. Jeśli siła przyciągania między dwoma kulami wzrosła 16 razy to jak zmieniła się 

odległość między nimi? 

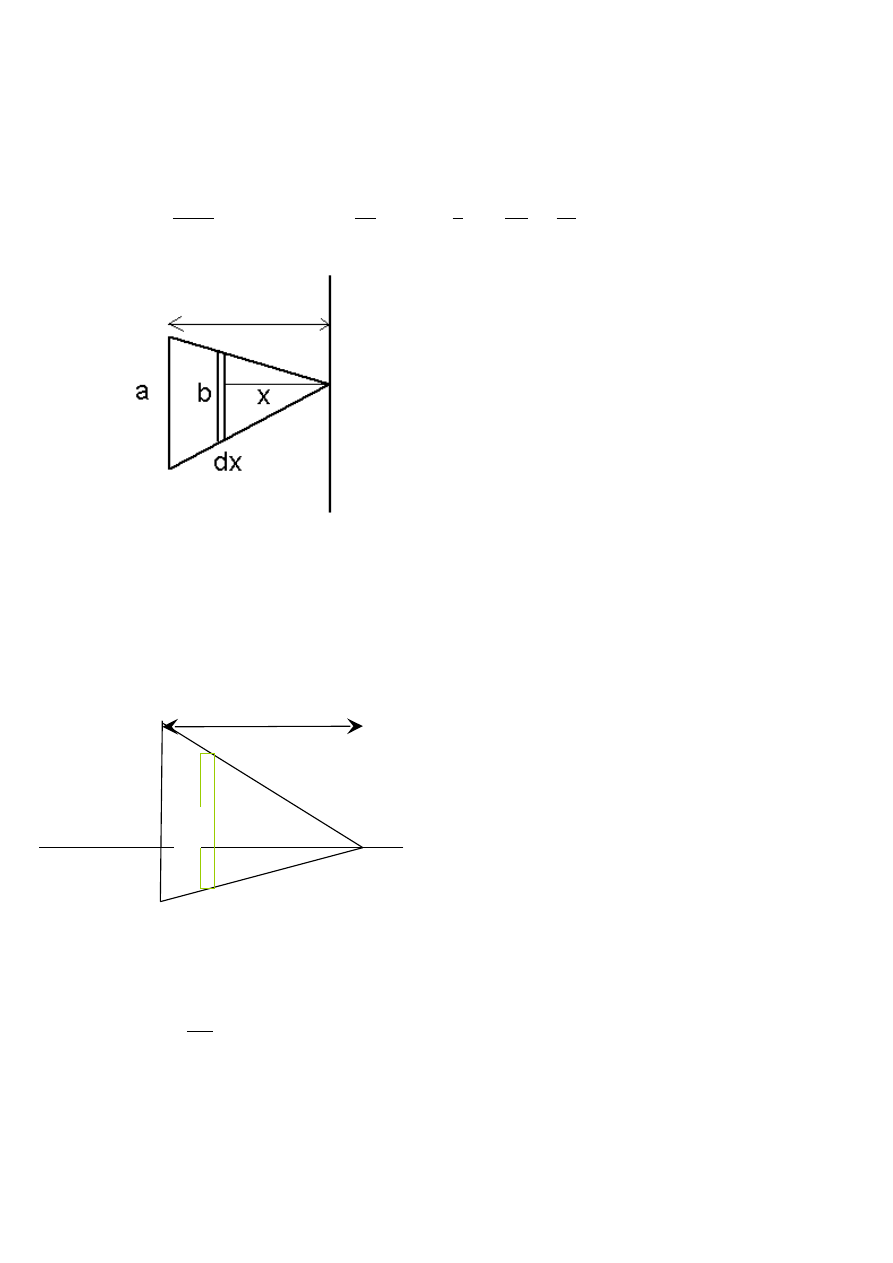
8. Jaki jest moment bezwładności trójkąta o podstawie a i wysokości h oraz gęstości 

powierzchniowej 

σ

:

a). względem podstawy jako osi
b). względem osi przechodzącej przez wierzchołek A równolegle do podstawy a.

Dzielimy trójkąt na paski i rozpatrujemy dowolny pasek o długości b i grubości dx odległy od 
podstawy trójkąta o x.

Masa 

dm = 

σ

ds = 

σ

bdx

Dla trójkąta obowiązuje nastpująca zależność:

 b/a =(h-x)/h stąd b = a(h-x)/h

dm = 

σ

(a(h-x)/h)dx 

Moment bezwładności trójkąta: I = 

3

4

3

3

2

0

2

2

12

1

)

4

3

1

(

)

(

ah

h

x

x

a

dx

h

x

x

a

dx

x

h

x

h

a

I

dm

x

I

h

m

σ

σ

σ

σ

=

−

=

−

=

−

=

=

∫

∫

∫

b) 
Odległość paska od osi obrotu wynosi x.
Z rysunku: b/a = x/h
b = ax/h

Masa 

dm = 

σ

ds = 

σ

bdx = 

σ

(ax/h)dx

Moment bezwładności:

∫

∫

=

=

h

m

dx

x

h

a

I

dm

x

I

0

3

2

σ

9. Jaką minimalną pracę należy wykonać, aby blok o masie M i o kształcie sześcianu 

(długość krawędzi a) przewrócić na drugi bok?

a

b

dx

h-x

h

x

oś

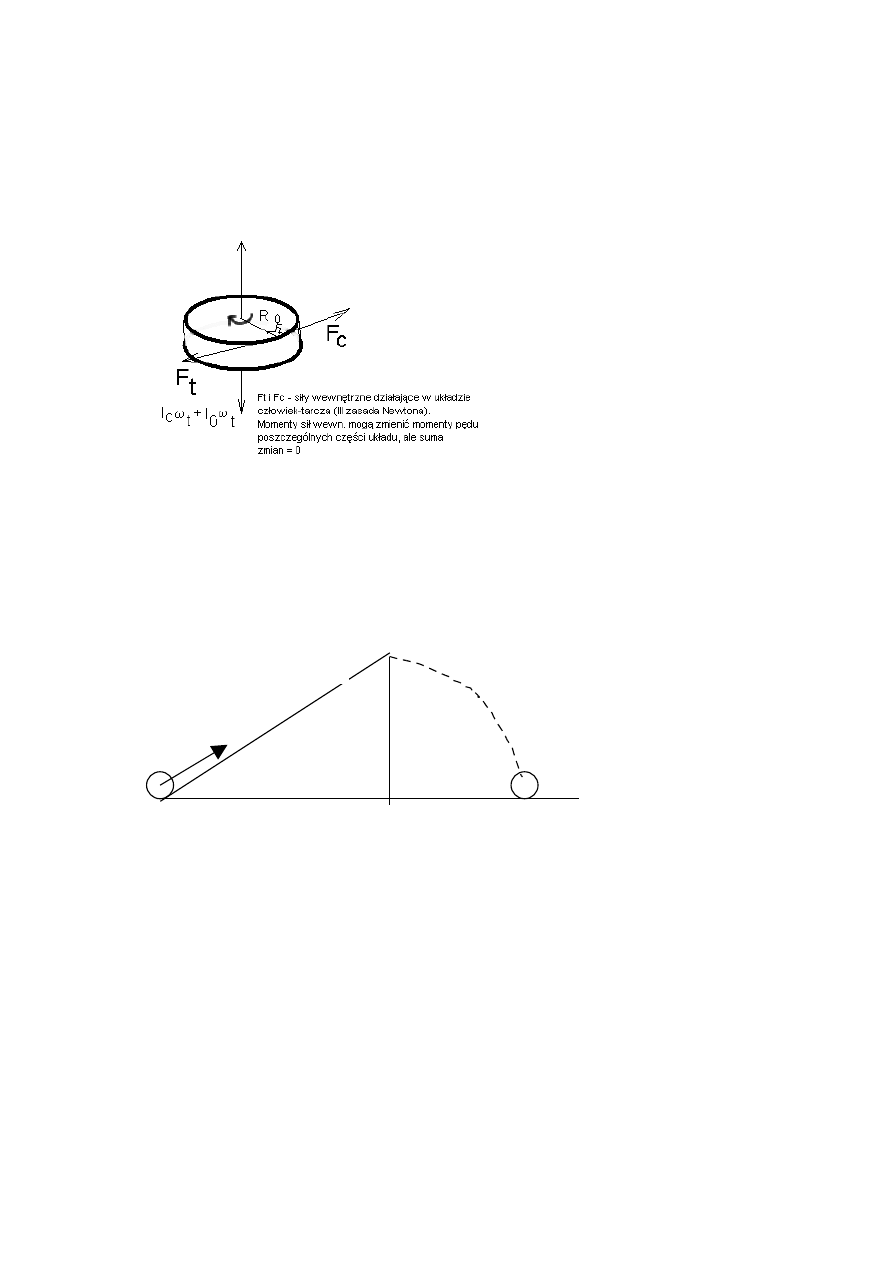
10. Na brzegu poziomo ustawionej tarczy o momencie bezwładności I (względem osi 

pionowej przechodzącej przez środek tarczy) i promieniu R znajduje się człowiek o 
masie m. Obliczyć prędkość kątową tarczy 

ω

, gdy człowiek zacznie się poruszać 

wzdłuż jej brzegu z prędkością v względem niej.

11. Obliczyć moment bezwładności cienkiego krążka o promieniu R = 10 cm i masie m 

= 200 g, jeżeli wiruje on wokół osi stycznej do krawędzi krążka.

12. Na równię o wysokości h wtacza się walec z prędkością v

0

. Z jaką prędkością v

1 

spadnie walec po osiągnięciu końca równi, jeśli toczy się po równi bez poślizgu? 
Moment bezwładności walca I=mR

2

/2, R – to promień walca, a m – masa walca.

Gdy   nie   występuje   poślizg,   siły   tarcia   nie   wykonują   pracy,   więc   obowiązuje   zasada  
zachowania energii.

13. Ciężka szpula z nawiniętą nicią, do której przyłożono siłę F leży na płaszczyźnie 

poziomej. W którą stronę i z jakim przyspieszeniem liniowym będzie poruszać się 
szpula w zależności od kąta między kierunkiem działania siły a płaszczyzną. Masa 
szpuli m, zewnętrzny i wewnętrzny promień odpowiednio R i r, moment 
bezwładności względem osi przechodzącej przez środek I

o

.

v

0

B

A

C

h

Proszę zacząć od sformułowania równania ruchu postępowego i równania ruchu obrotowego 
względem osi przechodzącej przez środek masy.

T

a

R

r

F

α