Zadania do projektu 3
1. Z jakim przyspieszeniem a i w jakim kierunku powinna poruszać się kabina windy,
aby znajdujące się w niej wahadło sekundowe (jest to okres drgań T
0
dla
nieruchomego wahadła) w czasie t=2.5 min wykonało N=100 wahań?
2. Sześcian wykonuje małe wahania w płaszczyźnie poziomej, poruszając się bez tarcia
po wewnętrznej powierzchni kuli. Jaki jest okres wahań sześcianu, jeśli kula opuszcza
się w dół z przyspieszeniem a=g/3. Promień R kuli = 0.2 m i jest znacznie większy od
długości krawędzi sześcianu.
3. Fala o częstotliwości f = 500 Hz biegnie z szybkością v = 340 m/s. Z jaką różnicą faz
drgają punkty odległe o l = 0.15 cm?
4. Zegar z wahadłem sekundowym (T
0
=1 s) na powierzchni Ziemi idzie dokładnie. Jakie
będzie opóźnienie zegara, jeśli zostanie on umieszczony na wysokości h=200 m?
5. Wyznaczyć częstotliwość n drgań akustycznych w stali, jeżeli odległość między
najbliższymi punktami fali akustycznej różniącymi się w fazie o
π
/2 jest równa l=1.54
m. Prędkość fali w stali v=5000 m/s.
6. Przy górnym otworze naczynia cylindrycznego, do którego ruchem jednostajnym
wlewa się woda, umieszczono kamerton. Dźwięk kamertonu wzmacnia się, gdy
odległości od otworu do powierzchni wynoszą h
1
=0.25 m i h
2
=0.75 m. Jaka jest
częstotliwość drgań kamertonu. Prędkość dźwięku v=340 m/s.
7. Poziom natężenia dźwięku wywoływanego przez jadący samochód w odległości l
1
=
50 m wynosi 50 dB. Jaki będzie poziom natężenia dźwięku w odległości l
2
= 100 m?
8. Do kalorymetru zawierającego lód o masie m
l
i temperaturze t
l
=0˚C została
wpuszczona para o temperaturze t
p
=100˚C. Ile wody będzie w kalorymetrze, gdy stopi
się lód? Dane są ciepło skraplania pary wodnej c
s
i ciepło topnienia lodu c
t
.
9. Etanol o gęstości
ρ
=791 kg/m
3
przepływa jednostajnie przez poziomą rurę, której pole
przekroju poprzecznego zmniejsza się od wartości S
1
= 1.2x10
-3
m
2
do wartości
S
2
=S
1
/2. Różnica ciśnień w wąskim i szerokim końcu rury wynosi 4120 Pa. Jaki jest
strumień objętościowy etanolu?
Wskazówka: Przepływ jest jednostajny, więc należy zastosować równanie Bernoulliego.
10. Proszę przedstawić na wykresach p-V, p-T i V-T przemianę izotermiczną dla jednego
kilomola gazu o temperaturze T=T
1
i T=3T
1
.
11. W cylindrze pod tłokiem znajduje się powietrze. Tłok ma kształt pokazany na
rysunku:
Ciężar tłoka P = 60 N, powierzchnia przekroju cylindra wynosi S
0
= 20 cm
2
. Ciśnienie
atmosferyczne: p
o
= 10
5
N/m
2
= 760 mmHg.
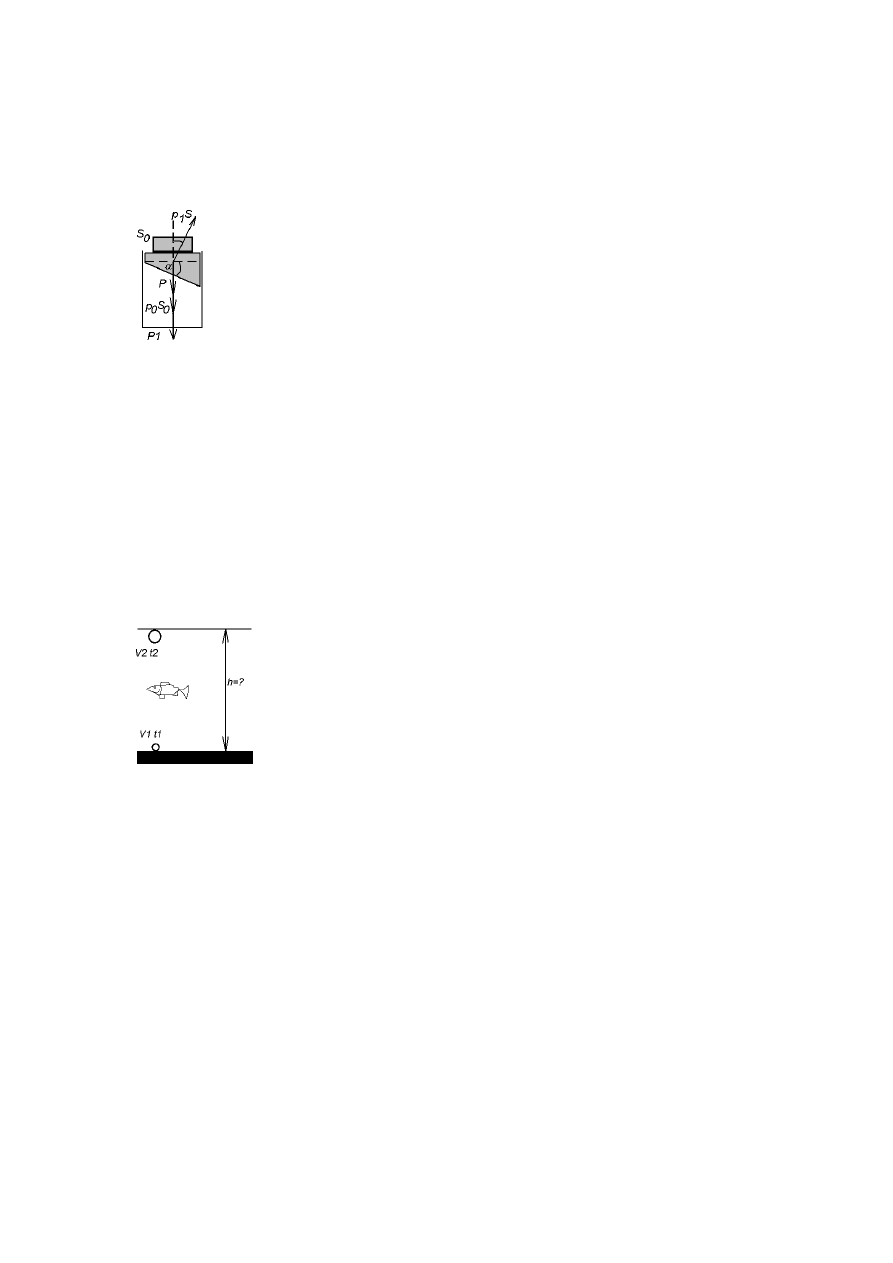
Jaki ciężar P
1
należy położyć na tłok, aby oby objętość powietrza w cylindrze
zmniejszyła się dwukrotnie? Nie uwzględniamy tarcia i przyjmujemy stałą
temperaturę.
Odp. 260 N
Wskazówka: Obliczcie ciśnienie p1 wewnątrz cylindra bez ciężaru na tłoku, a
następnie zapiszcie analogiczne równanie, gdy leży ciężar. Skorzystajcie z prawa Boyle'a
i Mariotta.
12. Objętość pęcherzyka metanu powiększa się 3-krotnie przy wypływaniu z dna jeziora
na powierzchnię. Temperatura wody na dnie wynosi t
1
= 7
o
C, a na powierzchni t
2
=
17
o
C. Oblicz głębokość jeziora. Założenia: metan traktujemy jako gaz doskonały,
Ciśnienie atmosferyczne p
o
= 10
5
N/m
2
. Gęstość wody
ρ
= 10
3
kg/m
3
.
Wskazówka: Zapiszcie równania gazu dla dna i dla powierzchni. Ciśnienie przy
powierzchni będzie równe atmosferycznemu. Na dnie ciśnienie jest wyższe o ciśnienie
słupa wody.
13. Jaka całkowita zmiana entropii w wyniku zmieszania m
1
= 300 g azotu (
µ
1
=28 g/mol)
oraz m
2
=200g CO
2
(
µ
2
=44 g/mol). Temperatury i ciśnienia gazów przed zmieszaniem
były jednakowe. Proces mieszania zachodzi w układzie izolowanym cieplnie przy
stałej objętości. Stała gazowa R = 8.31 J/(mol K).
Wskazówka; Zmiana entropii będzie sumą zmian entropii dla każdego z gazów;
skorzystajcie z I zasady termodynamiki (energia wewnętrzna układu nie zmieni się).
14. Manometr gazowy w pomieszczeniu o temperaturze t
1
= 17
o
C wskazuje ciśnienie p =
2.4x10
5
N/m
2
. Na ulicy wskazanie manometru zmniejsza się o
∆
p = 4x10
4
N/m
2
. Jaka
jest temperatura na ulicy, jeśli ciśnienie atmosferyczne jest równe p
0
= 10
5
N/m
2
?
15. Naczynie cylindryczne o długości L = 85 cm jest rozdzielone na dwie części tłokiem
ruchomym. Przy jakim położeniu tłoka ciśnienie w obu częściach cylindra będzie
jednakowe, jeśli jedna część jest wypełniona tlenem, a druga taką samą masą wodoru?
Temperatura w obu częściach jest taka sama. Masa cząsteczkowa tlenu wynosi
µ
O2
=
32g/mol;
µ
H2
= 2g/mol.
Odp. x = 5 cm
16. Naczynie o kształcie sześcianu zawiera N = 10
-6
kmol gazu doskonałego. Znaleźć
ciśnienie gazu, jeśli masa cząsteczki jest równa m
0
= 3x10
-23
g, a średnia prędkość
ruchu termicznego wynosi v = 500 m/s. Zderzenia ze ściankami są zderzeniami
doskonale sprężystymi.
Wskazówka: wyznaczcie zmianę pędu molekuły; po czasie t wszystkie molekuły z
prostopadłościanu o objetości V zderzą się ze ścianką, o ile poruszają się w kierunku
niej. Liczba tych molekuł wynosi n, a liczba molekuł w jednostce objętości to n
o.
Obliczcie popęd siły dla wszystkich cząstek i wyliczcie ciśnienie.