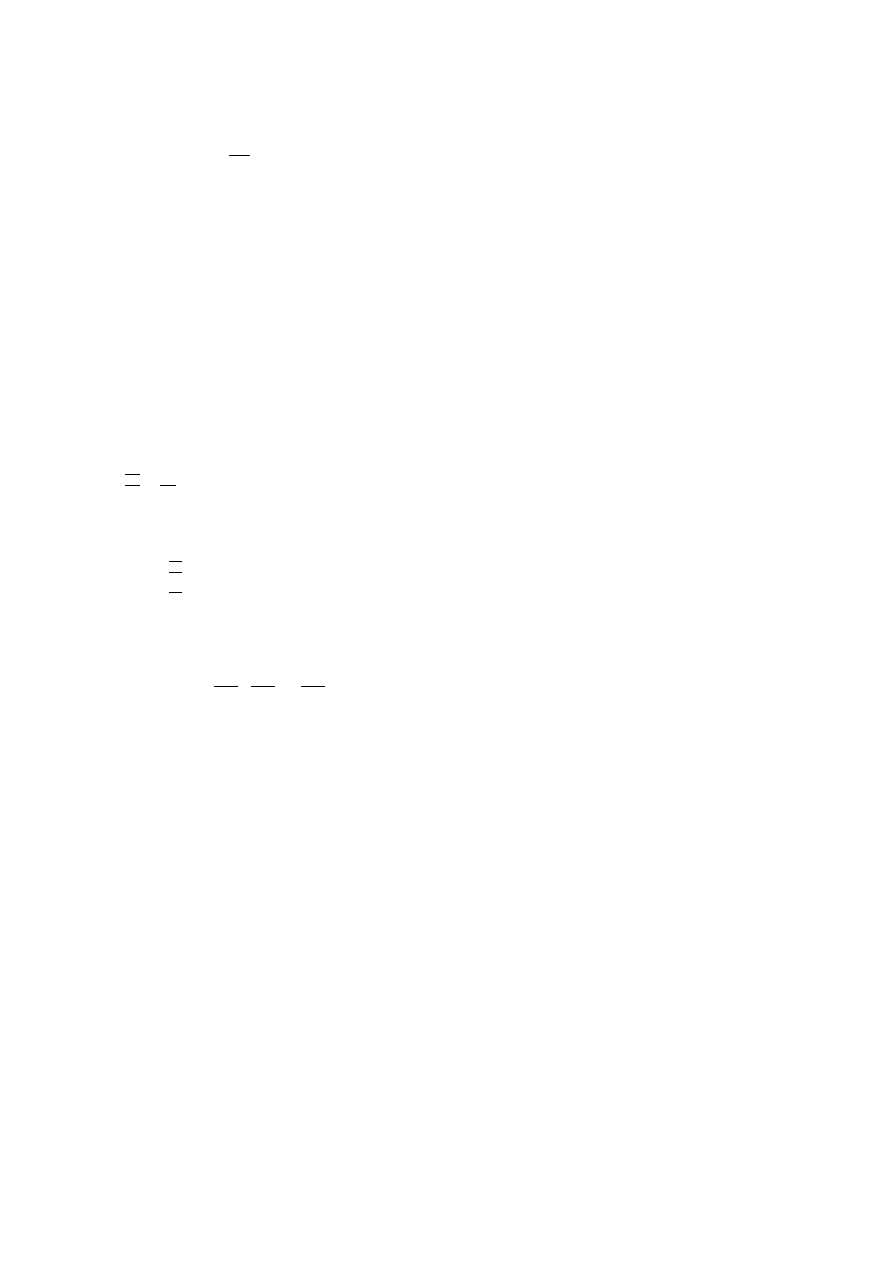
Iloczyn skalarny:
Funkcja jest iloczyne skalarnym w danej przestrzeni jeżeli spełnione sa następujące warunki:
1)
<x,x> ≥0 , <x,x>=0↔ x=0
2)
<x,y>=<y,x> V x,y є v
3)
<ax+by,z>=a<x,z>+b<y,z>
Norma wektora i jej własności:
Norma wektora vєV dana jest wzsorem ||v||=
Własnośc normy: ||v||=0↔v=0 , ||v||≥0, ||α*v||=||α||*||v||
Tożsamośc równoległoboku:
Dowód
Nierównośc Schwarza :
|<u,v>
|≤||u||*||v||
Dowod:
Własnośc trójkata:
||u+v||≤||u||+||v||
Dowód:
Wektory ortogonalne:
Mówimy że wektory
,
przestrzeni euklidesowej są ortogonalne jeżeli spełniają warunki: <
Twierdzenie pitagorasa dla przestrzeni euklidesowej:
Wektory
Dowód:
Dla dowolnych wektorów
Układy ortogonalne:
Zbiór wektorów przestrzeni euklidesowej nazywamy ortogonalnym wtedy i tylko wtedy gdy każde dwa wektory z tego
zboru sa ortogonalne. Każdy ortogonalny układ niezerowych wektorów przestrzeni euklidesowej jest liniowo niezależny.
Układ ortogonalny:
Zb
iór wektorów przestrzeni euklidesowej nazywamy układem ortogonalnym gdy jest to układ ortogonalny złożony z
unormowanych wektorów.
Algorytm ortogonalizacji Grama Schmita:
Mamy u1,u2…,un
v1=u1
v2=u2-
v3=u3-
22. WSPÓŁRZĘDNE WEKTORA W BAZIE:
Mamy zbiory wektorów v
1
, v
2
, … , v
n
oraz wektor u.
ORTONORMALNEJ:
α
1
=<u,v
1
>
α
2
=<u,v
2
>
.
α
n
=<u,v
n
>
ORTOGONALNEJ:
α
1
=
α
2
=
.
α
n
=
23. MACIERZ ORTOGONALNA I JEJ WŁASNOŚCI:
Macierz A jest ortogonalna A*A
T
=I i A
T
*A=I A
-1
=A
T
Własności:
A
-1
=A
T
Iloczyn macierzy ortogonalnych jest macierzą ortogonalną
25. RZUT ORTOGONALNY NA PODPRZESTRZEŃ – TW. O JEDNOZNACZNOŚCI
Niech E
0
będzie skończenie wymiarową podprzestrzenią przestrzeni euklidesowej E oraz niech {
będzie
bazą ortonormalną podprzestrzeni E
0.
Wtedy dla dowolnego wektora
εE . Istnieje jednoznacznie wyznaczony rzut
tego wektora na podprzestrzeń E
0
. Rzut ten jest określony wzorem:
Uwaga: Dla bazy ortogonalnej {
podprzestrzeni E
0
powyższy wzór przyjmuje postać:
27. WZÓR MACIERZY NA RZUT ORTOGONALNY:
*
MACIERZ RZUTU:
*
28. METODA NAJMNIEJSZYCH KWADRATÓW I „NAJLEPSZE ROZWIĄZANIE” SPRZECZNEGO UKŁADU
RÓWNAŃ:
30. MACIERZ SYMETRYCZNA I JEJ WARTOŚCI WŁASNE:
Macierz symetryczna
– wtedy, gdy na przekątnej znajdują się dowolne liczby, a pozostałe są względem tej przekątnej
symetryczne: A=
Własności:
Dla macierzy symetrycznych S, T i liczb(skalarów) a, b macierz aS+bT jest symetryczna
Dla dowolnej macierzy A macierze A+
oraz A
są symetryczne
31. ORTOGONALNA DIAGONALIZACJA MACIERZY SYMETRYCZNEJ:
Macierz rzeczywista jest ortogonalnie diagonalizowalna jest symetryczna.
Macierz A jest ortogonalnie diagonalizowalna, gdy istnieje macierz ortogonalna P oraz macierz diagonalna D, taka że:
35. TW. SYLVESTERA:
Macierz symetryczna
zadaje formę kwadratową:
a)
Dodatnio określona
b)
Ujemnie określoną
c)
Dodatnio póło kreśloną
detA=0
d)
Ujemnie póło kreśloną
detA=0
e)
W pozostałych przypadkach nieokreślon
Tw. Cayleya Hamiltona:
Kazda macierz kwadratowa spelnia swoje rownanie charakterystyczne:
Dowod:
Niech
Oznaczamy B=A-
i macierz dopełnienia B0
Wtedy detB=
Zatem:
B*
Z drugiej strony wyrazy amcierzey B0 sa wielomianami stopnia n-1 od zmiennej
Zatem możemy zapisać:
Stad:
B*(B0)
(A
Możemy porównać współrzędne ostatniego wielomianu z wielomianem wyzej i dostajemy:
AB0=a0I AB1-B0=a1I AB2-
B1=a2I….. A
-
=
Obliczamy:
Odwzorowanie liniowe: def. φ: V W jest odwzorowaniem liniowym wtedy i tylko wtedy gdy: (a)
,
V
φ(
+
)=φ(
+φ(
) (b)
V α k φ(α
) =αφ(
Twierdzenie o jednoznaczności odwzorowania liniowego. Niech
będzie bazą (uporządkoway układ wektorów) w przestrzeni V,
, wówczas istnieje dokładnie jedno
odwzorowanie liniowe φ:V W takie, że φ(
)=
i=1,2,...,n. Dowód. Weźmy dowolny wektor v V. Wtedy v zapisuje się
jednoznacznie w postaci v=
*
+...+
*
. Zadaje odwzorowanie: φ(v)=
φ(
)+
φ(
. Sprawdzam, że φ jest liniowe oraz
φ(
)=
. Weźmy v=
*
+...+
*
, u=
*
+...+
*
, wtedy: v+u=(
+
)
+...+(
+
)
, φ(v+u)=(
+
)
+...+(
+
)
,
v)+ (u)=
*
+...
*
+
+...+
= (
+
)
+...+(
+
)
. Tw. o postaci jądra i obrazu odwzorowania liniowego: Niech
L:U V będzie przekształceniem liniowym. Wtedy: (1) zbiór KerL(jądro) jest podprzestrzenią liniową przestrzeni U. (2) Zbiór
ImL(obraz) jest podprzestrzenią liniową przestrzeni V. Dowód: (1) oczywiście KerL V oraz KerL . Niech
,
KerL i
,
R.
Wówczas L(
)=L(
=
. Zatem L(
+
)=
L(
)+
L(
)=
*
+
*
= . To oznacza, że
+
KerL. (2) ImL V oraz
ImL . Niech
,
ImL i
,
R. Wtedy istnieją wektory
,
U takie, że L(
)=
i L(
)=
. Korzystając z liniowości
przekształcenia L otrzymamy: L(
+
)=
L(
)+
L(
)=
+
. Wektor
+
jest obrazem wektora
+
U
w przekształceniu L, czyli:
+
ImL. Twierdzenie o wymiarach jądra i obrazu. (dim-wymiar) Niech V,W będą skooczenie
wymiarowymi przestrzeniami liniowymi oraz niech :V W, będzie przekształceniem liniowym. Wtedy:
dim(Ker )+dim(Im )=dimV. Odwzorowanie liniowe nie podwyższa wymiarów tzn. dim (Im ) dimV. Dowód: Oznaczmy: dimV=n,
dim(Ker )=k (1) Niech 0<k<n. Niech
,...,
będzie bazą Ker V. Uzupełniamy
,...,
,
,
,...,
– baza V.
,...,
/ Ker . Wystarczy pokazad, że wektory (
), (
stanowią bazę Im . Sprawdzam liniową niezależnośd: niech
(
)+...+
(
)=Θ stąd: (
+...+
)= Θ tzn:
+...+
Ker . Stąd:
K
+...+
=
+...+
,
+...+
-...-
= Θ
,...,
są bazą=>
=
=...=
=...=
=0. Sprawdzam, że
(
),..., (m) generują Im . Weźmy w Im tzn: w= (v),gdzie v V, v=
+...+
w= (
+...+
)=
(
)+
(
)+...+
(
)+
(
)+...+
(
) (2) k=0<n =>Ker ={Θ} Zaczynam dowód:
...,
-
baza V,dalej tak samo jak w (1). (3) k=n tzn. Ker =V=> v V (v)=Θ, dim(Im )=0, dim Ker + 0 = dim V. Twierdzenie o zmianie
macierzy przekształcenia przy zmianie baz. Niech L:U V będzie przekształceniem liniowym oraz neich A będzie macierzą tego
przekształcenia w bazie Bu={
,...,
} przestrzeni U oraz w bazie Bv={
,...,
} przestrzeni V. Wtedy macierz A’ przekształcenia
liniowego L w bazie B’u={
’,...,
’} przestrzeni U oraz w bazie B’v={
’,...,
’} przestrzeni V ma postad: A’=
AP, gdzie P oznacza
macierz przejścia z bazy Bu do bazy B’u, a Q macierz przejścia z bazy Bv do bazy B’v. Uwaga: Jeżeli L jest przekształceniem liniowym
przestrzeni V w siebie, to zależnośd między macierzą A tego przekształcenia w bazie Bu={
,...,
} i macierzą A’ przekształcenia w
bazie B’u={
’,...,
’} ma postad: A’=
AP, gdzie P oznacza macierz przejścia z bazy Bu do bazy B’u. Działania na
przekształceniach. (1) Niech
i
:U->V będą przekształceniami liniowymi. Sumą przekształceo
i
nazywamy przekształcenie
(
+
):U->V określone wzorem (
+
)(
)=
(
)+
(
) dla
U (2) Niech L:U->V będzie przekształceniem liniowym oraz niech
α R. Iloczynem liczby α i przekształcenia L nazywamy przekształcenie (αL):U->V określone wzorem: (αL)(
)=α(L(
)) dla
U. (3)
Niech L:U->V oraz K:V->W będą przekształceniami liniowymi. Złożeniem przekształceo L i K nazywamy przekształcenie (K L):U->W
określone wzorem: (K L)(
)=K(L(
)) dla
U (4) Niech przekształcenie liniowe L:U->V będzie różnowartościowe oraz niech ImL=V.
Przekształceniem odwrotnym do przekształcenia L nazywamy przekształcenie (
):V->U określone wzorem: (
)( )=
=L(
)
dla
U oraz V
8. Warunki odwracalności odwzorowania liniowego Niech L:U->V będzie
przekształceniem liniowym przestrzeni skooczenie wymiarowych tego samego wymiaru. Ponad to A niech będzie macierzą
przekształcenia L w ustalonych bazach przestrzeni U i V. Wówczas następujące warunki są równoważne:
1. przekształcenie L jest odwracalne (bijekcją);
2. przekształcenie L jest różnowartościowe (monomorfizm);
3. Ker L={0};
4. Im L=V;
5. rzA=dimV
6. detA≠0
Równoważnośd tych warunków wynika z ciągu implikacji: 1=>2=>3=>4=>5=>6=>1
Dowód:
1=>2Równoważnośd przekształcenia L wynika z def. Odwracalności przekształcenia.
2=>3Załóżmy, że przekształcenie L jest różnowartościowe. Wówczas dla dowolnych dwóch wektorów u
1
, u
2
ϵU z warunku u
1
≠u
2
wynika, że L(u
1
) ≠L(u
2
). Jeżeli zatem u≠0, to L(u) ≠0. Wektor 0 jest zatem jedynym wektorem, którego obraz jest wektorem
zerowym w przestrzeni V. Stąd Ker L={0}.
3=>4 Załóżmy, że Ker L={0}. Ze wzoru dim Ker L + dim Im L=dim U wynika, ze dim Im L= dim U. Ale dim U=dimV, więc dim Im L =dim
V. Zbiór Im L jest podprzestrzenią liniową przestrzeni V, przy czym wymiary obu przestrzeni są równe. Stąd wynika, że Im L=V. 4=>5
Załóżmy, że Im L=V. Z (*) wynika, że rzA=dim Im L, zatem rzeczywiście rz A= dim V. 5=>6
Załóżmy, że rzA=dimV=n. Macierz A jest macierzą kwadratową stopnia n, więc det A≠0.
6=>1 Załóżmy, że det A≠0. Stąd wynika, że rzA=dimV. Ale rzA=dim Im L, więc Im L= V. Załóżmy teraz, że L(u
1
)=L(u
2
). Wówczas L(u
1
-
u
2
)= L(u
1
)- L(u
2
)=0. Stąd wynika, że AX=0, gdzie X jest kolumnowym wektorem współrzędnych wektora u
1
-u
2
=0, czyli u
1
=u
2
.
Przekształcenie L jest zatem różnowartościowe, jego obrazem jest cała przestrzeo V. To oznacza, ze L jest odwracalne.
9. Związek działao na odwzorowaniach z działaniami na macierzach
1. Niech przekształcenie liniowe L
1
,L
2
:U->V mają w ustalonych bazach przestrzeni U i V odpowiednio macierze przekształceo A
L1
i
A
L2
. Wtedy macierz A
L1+L2
sumy L
1
+L
2
tych przekształceo ma w tych samych bazach przestrzeni U i V postad: A
L1+L2
= A
L1
+ A
L2
2. Niech przekształcenie liniowe L:U->V ma w ustalonych bazach przestrzeni U i V macierz przekształcenia A
L
oraz niech αϵR. Wtedy
macierz A
αL
iloczynu liczby α i przekształcenia L ma w tych samych bazach przestrzeniu U i V postad: A
αL
=αA
L
3. Niech przekształcenia liniowe L: U->V oraz K: V->W mają w ustalonych bazach przestrzeni U, V i W odpowiednio macierze A
L
i A
K
.
Wtedy macierz A
K○L
złożenia K○L tych przekształceo ma w tych samych bazach przestrzeni U,V i W postad: A
K○L
=A
K
*AL.
4. Niech przekształcenie liniowe L: U->V ma przekształcenie odwrotne L
-1
:V->U. Ponadto niech A
L
i A
L
-1
oznaczają odpowiednio
macierze przekształceo L i L
-1
w ustalonych bazach przestrzeni U i V. Wtedy: A
L
-1
=(A
L
)
-1
10. Wartości i wektory własne odwzorowania liniowego i macierzy
Niech A będzie macierzą przekształcenia liniowego L: V->V w bazie B={v
1
,v
2
…,v
n
} przestrzeni liniowej V ( rzeczywistej i zespolonej).
Wówczas:
1. λ jest wartością włąsną przekształcenia L , gdy: det(A- λI)=0
2. wektor v jest wektorem własnym przekształcenia L odpowiadającym wartości własnej λ , gdy jego współrzędne {x
1
,x
2
,….,x
n
} w
bazie B są niezerowym rozwiązaniem układu równao:(A – λI)
11. Twierdzenie o liniowej niezależności wektorów własnych
Wektory własne odpowiadające różnym wartościom własnym przekształcenia liniowego są liniowo niezależne.
DOWÓD:
Załóżmy nie wprost, że wektory v
1
,v
2
….,v
n
są liniowo zależne. Niech 1≤L≤k oznacza największą liczbę, dla której wektory v
1
,v
2
….,v
n
są liniowo niezależne. Z założenia 1≤L≤k z określenia liczby l wynika, że wektory v
1
,v
2
,…v
L
,v
L+1
są liniowo zależne. Oznacza to
istnienie liczb α
1
,α
2
,…,α
L
,α
L+1
, nie wszystkich równych zeru i takich, że: α
1
v
1
+α
2
v
2
+….+ α
L
v
L
+ α
L+1
v
L+1
=0
Po nałożeniu na obie strony tej równości przekształcenia L i i wykorzystaniu def. Wektora własnego otrzymujemy zależnośd:
L(α
1
v
1
+α
2
v
2
+….+ α
L
v
L
+ α
L+1
v
L+1
)= α
1
L(v
1
)+α
2
L(v
2
)+….+ α
L
L(v
L
)+ α
L+1
L(v
L+1
)= α
1
λ
1
v
1
+α
2
λ
2
v
2
+….+ α
L
λ
L
v
L
+ α
L+1
λ
L+1
v
L+1
=L(0)=0
Z drugiej strony:
λ
L+1
(α
1
v
1
+α
2
v
2
+….+ α
L
v
L
+ α
L+1
v
L+1
)= λ
L+1
*0=0
Zatem:
α
1
(λ
1
-λ
L+1
)v
1
+ α
2
(λ
2
-λ
L+1
)v
2
+…+ α
L
(λ
L
-λ
L+1
)v
L
=(α
1
λ
1
v
1
+ α
2
λ
2
v
2
+…+ α
L
λ
L
v
L
)- (α
1
λ
L+1
v
1
+ α
2
λ
L+1
v
2
+…+ α
L
λ
L+1
v
L
)= -α
L+1
λ
L+1
v
L+1
+ α
L+ 1
λ
L+1
v
L+1
=0
Z liniowej niezależności wektorów v
1
,v
2
….,v
L
wynika, że:
α
1
(λ
1
-λ
L+1
)=0, α
2
(λ
1
-λ
L+1
)=0, …., α
L
(λ
L
-λ
L+1
)=0
Ale wartości własne λ
1
,λ
2
,…,λ
k
są parami różne, więc α
1
=0, α
2
=0, …., α
L
=0
Równośd definiująca liczby α
1
,α
2
,…,α
L
,α
L+1
wygląda następująco:
0*v
1
+0*v
2
+…+0*v
L
+α
L+1
v
L+1
= α
L+1
v
L+1
=0
Ale v
L+1
≠0, więc α
L+1
=0. Otrzymaliśmy sprzecznośd z liniową zależnością wektorów v
1
,v
2
,…v
L
,v
L+1
. Stąd wniosek, że wektory v
1
,v
2
,…v
k
są liniowo niezależne.
12. Krotnośd algebraiczna wartości własnej
Krotnością algebraiczną wartości własnej λ nazywamy jej wielokrotnośd, jako pierwiastka wielomianu charakterystycznego
(oznaczenie K
a
(λ)).
Krotnośd geometryczna wartości własnej
Krotnością geometryczną wartości własnej λ nazywamy dimV
λ
(oznaczenie K
g
(λ))
13. Twierdzenie o warunkach diagonalizowalności macierzy
Niech A będzie macierzą rzeczywistą (zespoloną) stopnia n. Wówczas następujące warunki są równoważne:
1. macierz A jest diagonalizowalna
2. wektory własne macierzy A tworzą bazę przestrzeni R
n
(C
n
)
3. A=PBP
-1
, gdzie B jest macierzą diagonalną, której główną przekątną tworzą kolejne wartości własne macierzy A, zaś
odpowiadające im wektory własne tworzą kolejne kolumny macierzy P.
14. Wielomian charakterystyczny macierzy
Niech A będzie macierzą rzeczywistą (zespoloną). Wielomianem charakterystycznym macierzy A nazywamy wielomian rzeczywisty
( zespolony) określony wzorem: W
A
(λ)=det(A-λI)