•

Fala: definicja, równanie falowe, przykłady fal

Każde rozprzestrzeniające się zaburzenie (drgania, odkształcenia,...) nazywamy falą. Z falą
poprzeczną mamy do czynienia wtedy, kiedy drgania zachodzą w kierunku prostopadłym do fali. Z
falą podłużną – gdy zachodzą w kierunku równoległym.
Równanie fali:

gdzie Ψ – to funkcja opisująca wychylenie (w zależności od położenia i od czasu), a v to prędkość
rozchodzenia się fali, r – położenie i oczywiście t – czas. Rozwiązaniem równania jest funkcja
(dowolna) argumentu u takiego, że: u=x±vt.
Przykłady fal: -fala harmoniczna (gdy poszczególne cząstki ośrodka drgają ruchem harmonicznym
z częstotliwością kątową niezależną od czasu i położenia)
-fala płaska (gdy wielkości opisujące ruch ośrodka zależą tylko od czasu i jednej ze współrzędnych
kartezjańskich [np. x])
-fala kulista (gdy wielkości opisujące falę zależą tylko od czasu i odległości od pewnego punktu w
przestrzeni nazywanego centrum(środkiem) fali)

•

Światło jako fala elektromagnetyczna

Fala elektromagnetyczna jest to rozchodzące się w przestrzeni zmienne pole elektromagnetyczne.
Są to fale poprzeczne – wektory natężenia pola elektrycznego E i magnetycznego H są wzajemnie
prostopadłe i leżą w płaszczyźnie, która jest prostopadła do kierunku rozchodzenia się fali.
Równania Maxwella podają zależność między E i H.

Oznaczenia: D – indukcja pola elektrycznego, B – indukcja pola magnetycznego, ρ – gęstość
objętościowa ładunków elektrycznych. Kropki oznaczają pochodną po czasie.
Współczesna nauka, zgodnie z dualizmem korpuskularno-falowym postrzega światło jednocześnie
jako strumień cząstek (fotonów) i falę elektromagnetyczną. Naturę falową światła potwierdzają
zjawiska takie jak dyfrakcja, interferencja i polaryzacja światła.

•

Widmo promieniowania elektromagnetycznego

Jest to podział fal elektromagnetycznych ze względu na częstotliwość lub długość. Obejmuje:
- fale radiowe (częstotliwości rzędu kHz i MHz, długości fali rzędu kilometrów i metrów)
- mikrofale (częstotliwości rzędu GHz, długości fali rzędu centymetrów i milimetrów)
- podczerwień (częstotliwość : 10

11

-10

14

Hz, długości od milimetra do mikrometra)

- światło widzialne (długości fal: 400

÷

800 nm)

- ultrafiolet [nadfiolet] (długości fal: 10

÷4

00 nm)

- promieniowanie rentgenowskie (długości fal: 0,005

÷1

0 nm)

- promieniowanie gamma (długości fal poniżej 10

-12

m)

•

Wektor Poyntinga

Ilość energii przechodzącej przez jednostkę powierzchni prostopadłej do kierunku
rozprzestrzeniania się energii na jednostkę czasu określa wektor Poyntinga (wektor chwilowej
gęstości strumienia energii). Zapisujemy go jako iloczyn wektorowy:

2

2

2

2

2

1

t

v

r

∂

Ψ

∂

=

∂

Ψ

∂

0

0

=

=

=

+

=

−

B

div

D

div

B

E

rot

E

D

H

rot















ρ

σ

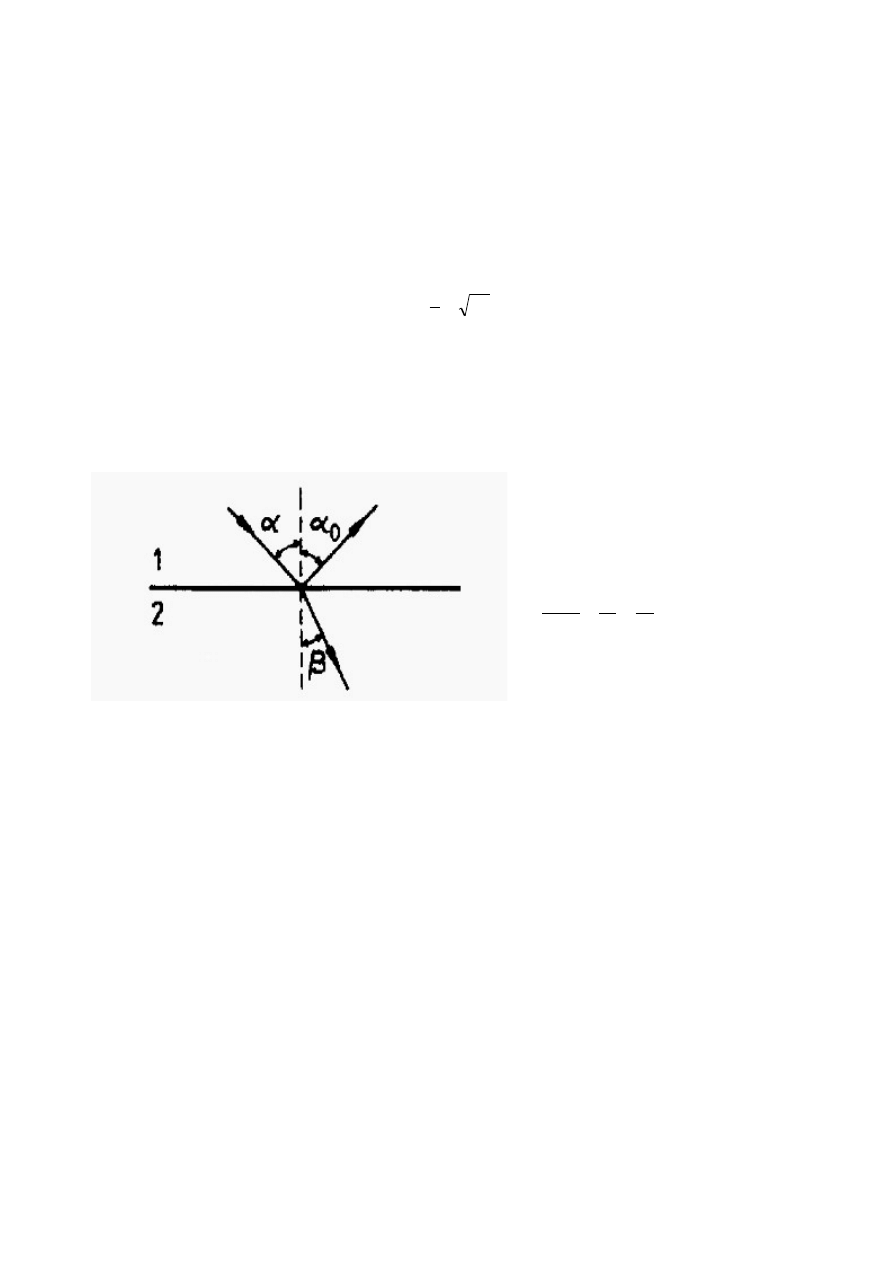
S – wektor Poyntinga E – natężenie pola elektrycznego, H – natężenie pola magnetycznego.
Dzięki temu wektorowi możemy określić szybkość przepływu energii przez jednostkową
powierzchnię fali elektromagnetycznej.

•

Współczynnik załamania. Dyspersja.

Stosunek prędkości światła w próżni (c) do prędkości fazowej światła w ośrodku v:

gdzie ε i μ to względne przenikalności ośrodka, odpowiednio elektryczna i magnetyczna.
Dyspersja – zależność prędkości fazowej fal od częstotliwości, długości fali albo wektora
falowego.Ośrodki, w których zachodzi to zjawisko nazywa się ośrodkami dyspersyjnymi. Dyspersja
fal elektromagnetycznych nie występuje jedynie w próżni.

•

Prawa Sneliusa.

Prawa Sneliusa dotyczą odbicia i załamania światła.

1. Promienie: padający, odbity i
załamany leżą w jednej płaszczyźnie.
2. Kąt padania jest równy kątowi odbicia
3. Między kątem załamania a kątem
padania zachodzi związek:

gdzie α – kąt padania, β – kąt załamania,
n

1

i n

2

– bezwzględne współczynniki

załamania, n

21

– względny współczynnik

załamania ośrodka w którym rozchodzi się fala załamana, w stosunku do ośrodka, w którym
rozchodzi się fala padająca.

•

Zasada Fermata.

Opisuje rozchodzenie się (propagację) fal i mówi, że fala porusza się między dwoma punktami po
takiej drodze, na której pokonanie zużywa ekstremalną ilość czasu (zazwyczaj jest to najmniejsza
ilość czasu, ale w szczególnych przypadkach może być na odwrót).
Dla światła jest to zasada minimum drogi optycznej. Można z niej wyprowadzić wszystkie
podstawowe prawa optyki geometrzycznej. Z zasady Fermata wynika prawo prostoliniowego
rozchodzenia się światła w ośrodku ciągłym.

•

Zasada Huyghensa i Huyghensa-Fresnela.

Zasada Huyghensa – każdy punkt ośrodka, do którego dociera fala staje się środkiem nowej fali
kulistej. Zasada ta pozwala wyjaśnić prawa odbicia i załamania światła, jednak nie wystarcza do
wyjeśnienia zjawisk dyfrakcji.
Zasada Huyghensa-Fresnela - Nowe czoło fali odtwarza się w wyniku nakładania się fal
cząstkowych pochodzących z sąsiadujących ze sobą punktów ośrodka..
Zasady Huyghensa i Fermata są równoważne (choć zasada Huyghensa podkreśla falową naturę
światła)

•

Dualizm cząsteczkowo-falowy: zjawiska, świadczące o falowej albo o cząsteczkowej
naturze światła.

H

E

S







×

=

ε µ

=

≡

v

c

n

21

1

2

2

1

sin

sin

n

n

n

v

v

≡

=

=

β

α

Współczesna optyka postrzega światło jako strumień cząstek (fotonów) i jednocześnie falę
elektromagnetyczną. Istnieją zjawiska z udziałem światła, które potwierdzają naturę falową światła,
jak również takie, które potwierdzają naturę korpuskularną światła.

Zjawiska potwierdzające naturę falową światła

Zjawiska potwierdzające naturę korpuskularną
światła

-interferecja (spójne nakładanie się fal)
-dyfrakcja (ugięcie się fali)
-polaryzacja (fala spolaryzowana oscyluje tylko
w jednym kierunku, niespolaryzowana – w
wielu)

-zjawisko fotoelektryczne wewnętrzne
-zjawisko fotoelektryczne zewnętrzne
(z.f. polega na przekazywaniu przez fotony
swojej energii elektronom ośrodka)
-zjawisko Comptona (zmiana częstotliwości lub
długości fal fotonów rozpraszanych na
elektronach lub nukleonach)

•

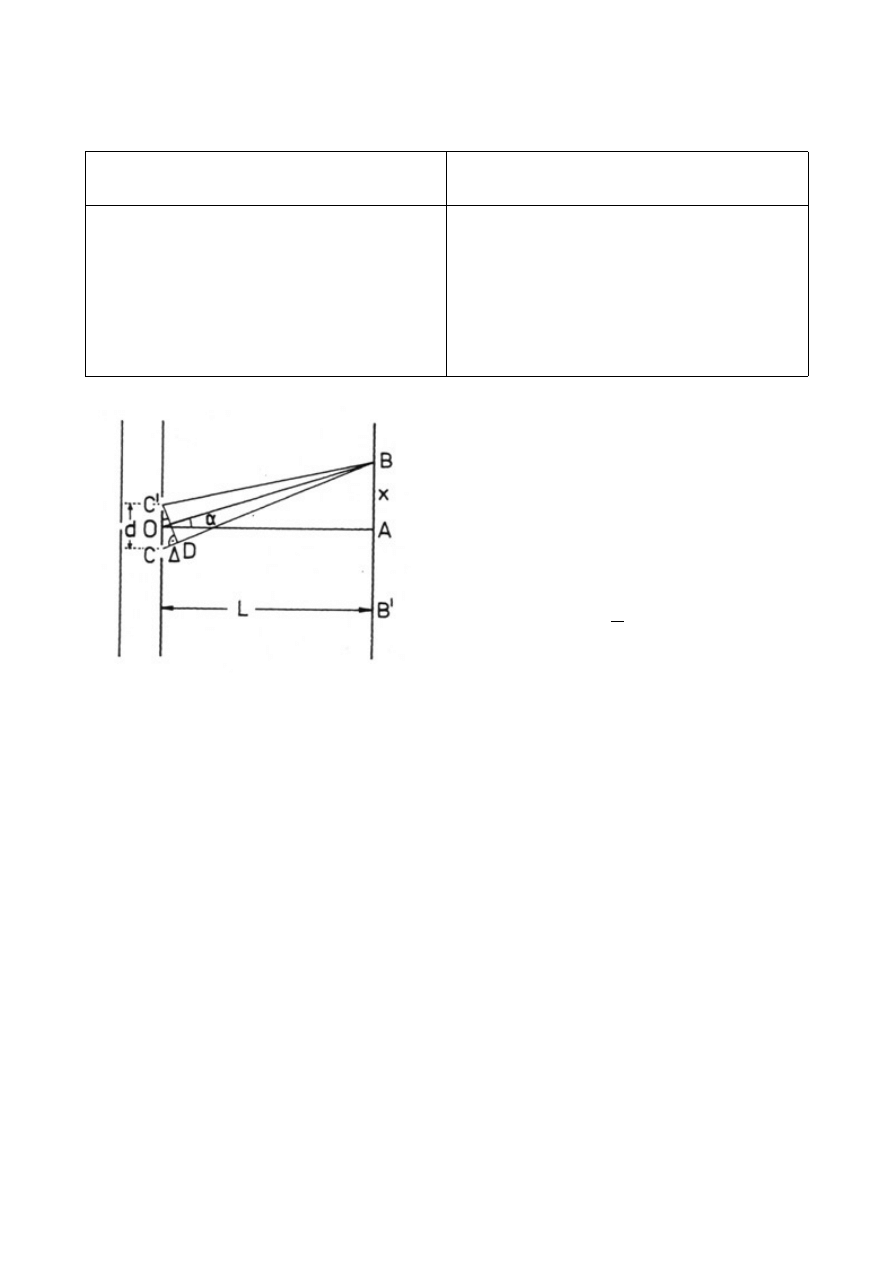
Doświadczenie Younga: opis, wnioski.

Doświadczenie polegało na przepuszczeniu światła
spójnego (np. przepuszczonego przez pojedyńczą
szczelinę) przez dwie blisko położone szczeliny. W
wyniku interferencji na ekranie powstają ciemne i
jasne prążki w miejscach wzmocnienia i wygaszenia.
Doświadczenie to potwierdziło falową naturę światła.
Przeprowadzenie doświadczenia Younga może pomóc
w oszacowaniu długości fali:

•

Interferencja: definicja, warunki konieczne, pojęcia podstawowe (np. droga i czas
koherencji).

Fale spójne są to fale o stałej różnicy faz lub drgające zgodnie w fazie. W wyniku nakładania się fal
spójnych następuje zwiększenie lub zmniejszenie amplitudy wypadkowej, zjawisko to nazywamy
interferencją (nakładanie się fal w ogólności nazywamy superpozycją). Nakładanie się fal
niespójnych prowadzi tylko do zwiększenia się natężenia światła; w tym przypadku nie obserwuje
się interferencję.
„Odpowiednikiem” emitowanego fotonu w opisie falowym światła jest paczka falowa (ograniczony
w czasie i przestrzeni zbiór fali sinusoidalnych). Aby 2 paczki mogły interferować muszą na siebie
trafić. Istnieje pewna charakterystyczna różnica dróg ΔL

0

między dwiema paczkami, żeby mogły

one jeszcze ze sobą interferować. Nazywamy ją drogą (długością) koherencji. Różnica czasu
między paczkami to czas koherencji Δt

0

= ΔL

0

/ c

Czas koherencji jest powiązany z Δf (szerokością widma, czyli zakresem częstości) wzorem:

Jednym z warunków koniecznych spójności jest więc wysoka monochromatyczność światła (jak
najmniejsza szerokość widma).

•

Dyfrakcja.

Jest to ugięcie fali na przesłonie o wymiarach tego samego rzędu co długość fali. Najprostszym
przykładem jest dyfrakcja na pojedyńczej szczelinie. Zgodnie z zasadą Huygensa każdy punkt

d

L

x

≈

λ

1

2

0

≈

∆

∆

t

f

π

szczeliny o szerokości d, jest nowym źródłem fali. Między źródłami zachodzi interferencja, co
powoduje wzmacnianie i osłabianie światła rozchodzącego się w różnych kierunkach.

•

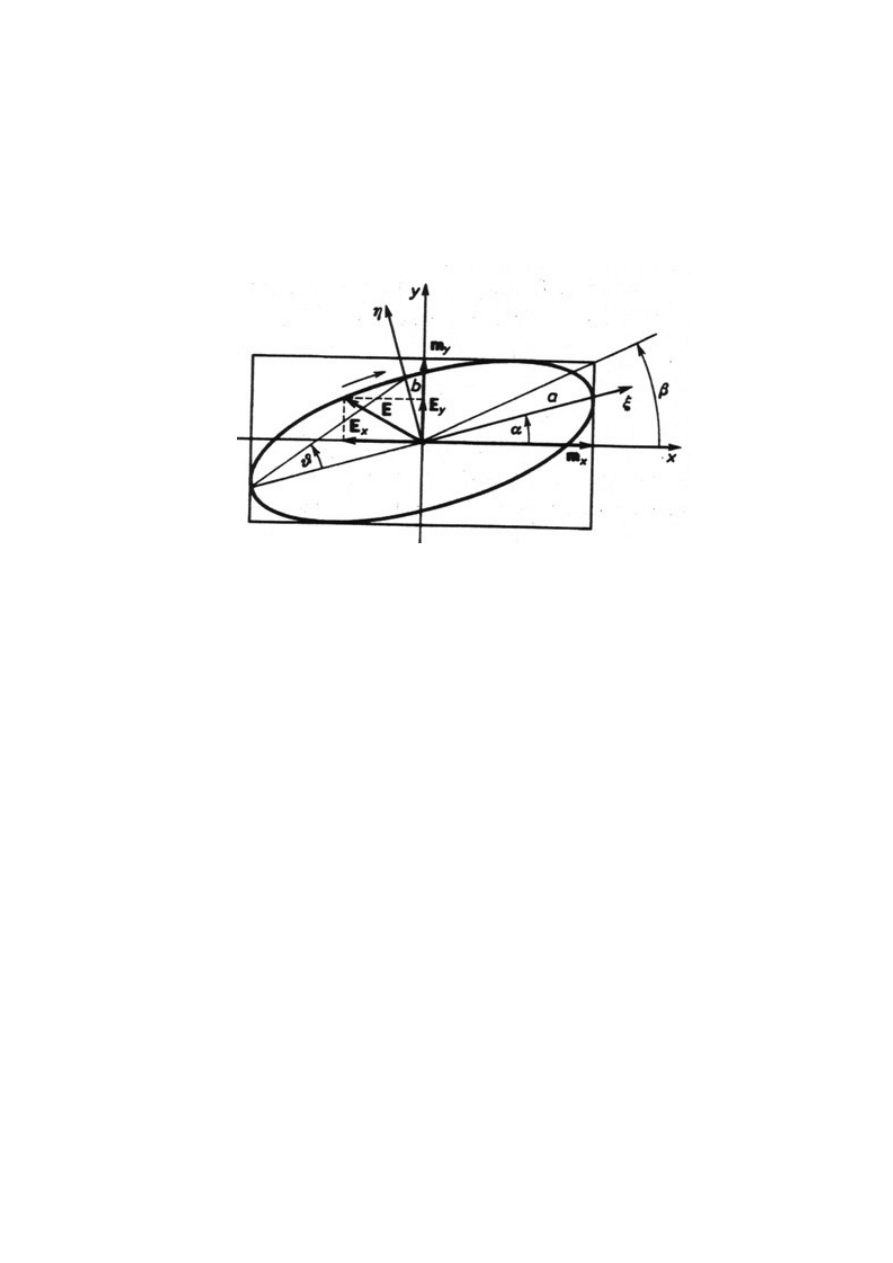
Polaryzacja światła: definicja, metody opisu, sposoby polaryzacji światła.

Światłem niespolaryzowanym lub naturalnym nazywa się światło, w którym występują fale
elektromagnetyczne (poprzeczne) o wektorach H i E skierowanych we wszystkich możliwych
kierunkach. Światło spolaryzowane, w przeciwieństwie do niespolaryzowanego, oscyluje tylko w
jednym kierunku. Polaryzację można opisać parametrami elipsy, która odpowiada końcowi wektora
natężenia pola elektrycznego E:

-kąt przekątnej β – przekątna prostokąta wyznaczonego przez amplitudy m

x

i m

y

.

-kąt azymutu α – między dużą osią elipsy stanu polaryzacji a osią x
-skrętność – fala powyżej jest prawoskrętna (zg. z ruchem wsk. zegara)
-eliptyczność – iloraz małej i dużej osi elipsy e=b/a
-kąt eliptyczności – tg tego kąta jest równy eliptyczności
Płaszczyzna drgań – płaszczyzna drgań wektora E. Płaszczyzna polaryzacji – płaszczyzna drgań
wektora H.
Metody polaryzacji:
-selektywne pochłanianie (polaroidy)
-załamanie, odbicie [przy kącie padania równym kątowi Brewstera, czyli takiemu kątowi, którego
tangens jest równy n (współczynnikowi załamania)] światło odbite jest całkowicie spolaryzowane.

•

Zwierciadła (definicja, podział, podstawowe wielkości charakteryzujące).

Zwierciadła są to powierzchnie, które niemal całkowicie odbijają padające na nie światło.
Zwierciadło płaskie to odbijająca płaska powierzchnia (np. powierzchnia metalu, szkła).
Zwierciadło płaskie daje obraz pozorny, położony symetrycznie do przedmiotu względem
zwierciadła.
Zastosowania zwierciadeł płaskich:
-

zmiana kierunku promieni świetlnych (biegu wiązki) - np. peryskopy;

-

pomiar małych kątów (np. galwanometr, waga skręceń);

-

pomiar kątów w urządzeniach typu sekstans, teodolit

Ponadto - zwierciadła zakrzywione – kuliste (wklęsłe i wypukłe) i eliptyczne, hiperboliczne,
paraboliczne.
Zwierciadło kuliste – podstawowe wartości charakteryzujące – promień krzywizny R, odległość
ogniskowa f = R/2 (dla zwierciadła wypukłego przyjmuje wartość ujemną), powiększenie liniowe w

•

Soczewki (definicja, podział, podstawowe wielkości charakteryzujące).

Soczewką nazywamy przezroczystą bryłę ograniczoną ograniczoną powierzchniami kulistymi

(najczęsciej), walcowymi lub parabolicznymi.
Wyróżniamy soczewki skupiające i rozpraszające.
Wzór soczewkowy:

s – odległość od soczewki do przedmiotu, s' – odległość od soczewki do obrazu przedmiotu
f' – odległość od soczewki do ogniska obrazowego, R – promienie krzywizn soczewki
Oś optyczna – prosta przechodząca przez środki krzywizn soczewki.
Zdolność zbierająca – odwrotność f' wyrażona w dioptriach.
Wzór Newtona (zz')=(f')

2

POWIĘKSZENIE SOCZEWKI:

Powiększenie poprzeczne:

Powiększenie podłużne:

Powiększenie wizualne:

•

Pryzmat (definicja, podstawowe wielkości charakteryzujące).

Pryzmat to bryła przezroczysta, której 2 płaszczyzny ograniczające tworzą kąt γ, nazywany kątem
łamiącym pryzmatu. Zastosowania pryzmatów:
-

pomiar współczynnika załamania na goniometrach (spektrometrach);

-

odchylanie biegu wiązki w przyrządach optycznych (jak zwierciadła);

-

rozszczepienie wiązki światła białego na widmo.

δ

min

to kąt minimalnego odchylenia.

•

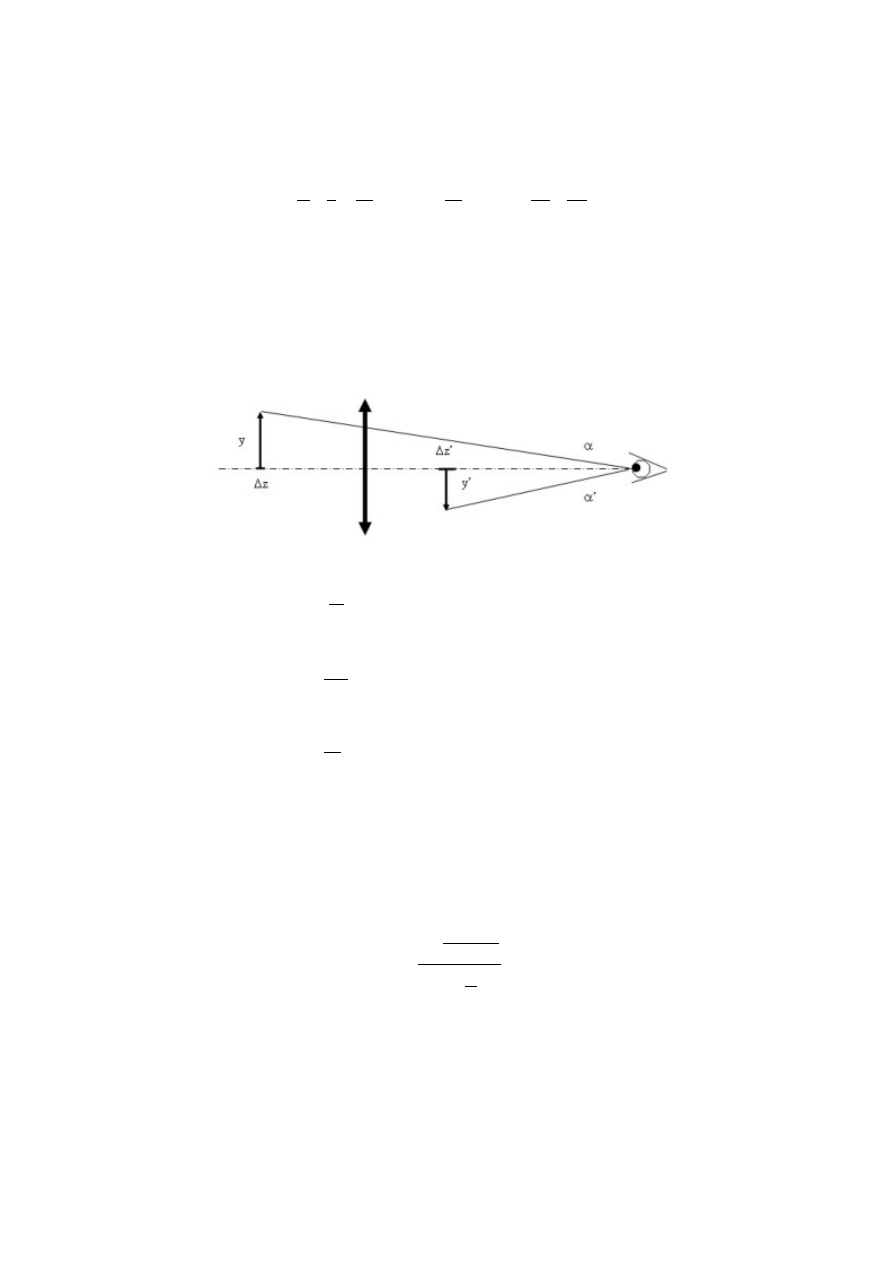
Lupa (odległość dobrego widzenia!).

Lupa – najprostszy przyrząd, dający obraz pozorny, powiększony, prosty – pojedyncza soczewka
zbierająca (skupiająca).
Powiększenie kątowe lupy:

(

)









−

−

=

=

−

2

1

1

1

1

'

1

'

1

1

'

1

R

R

n

f

f

s

s

2

sin

2

sin

min

γ

δ

γ +

=

n

y

y

p

'

=

z

z

∆

∆

=

'

β

α

α

'

=

w

Odległość dobrego widzenia: odległość dla której oko ludzkie widzi ostry obraz o maksymalnym
powiększeniu, ale nie musi się akomodować do widzenia w innej odległości niż wynika z
naturalnego ustawienia mięśni oka.

•

Mikroskop (do czego służy, budowa, schemat)

Mikroskop to przyrząd do obserwacji przedmiotów małych, znajdujących się blisko obserwatora.
Składa się ze skupiającego obiektywu o krótkiej ogniskowej, który daje rzeczywisty, powiększony i
odwrócony obraz przedmiotu i okularu, również skupiającego, który pełni rolę lupy, przez która
oglądamy obraz dawany przez obiektyw.

Powiększenie mikroskopu:

gdzie l – długość tubusa.

•

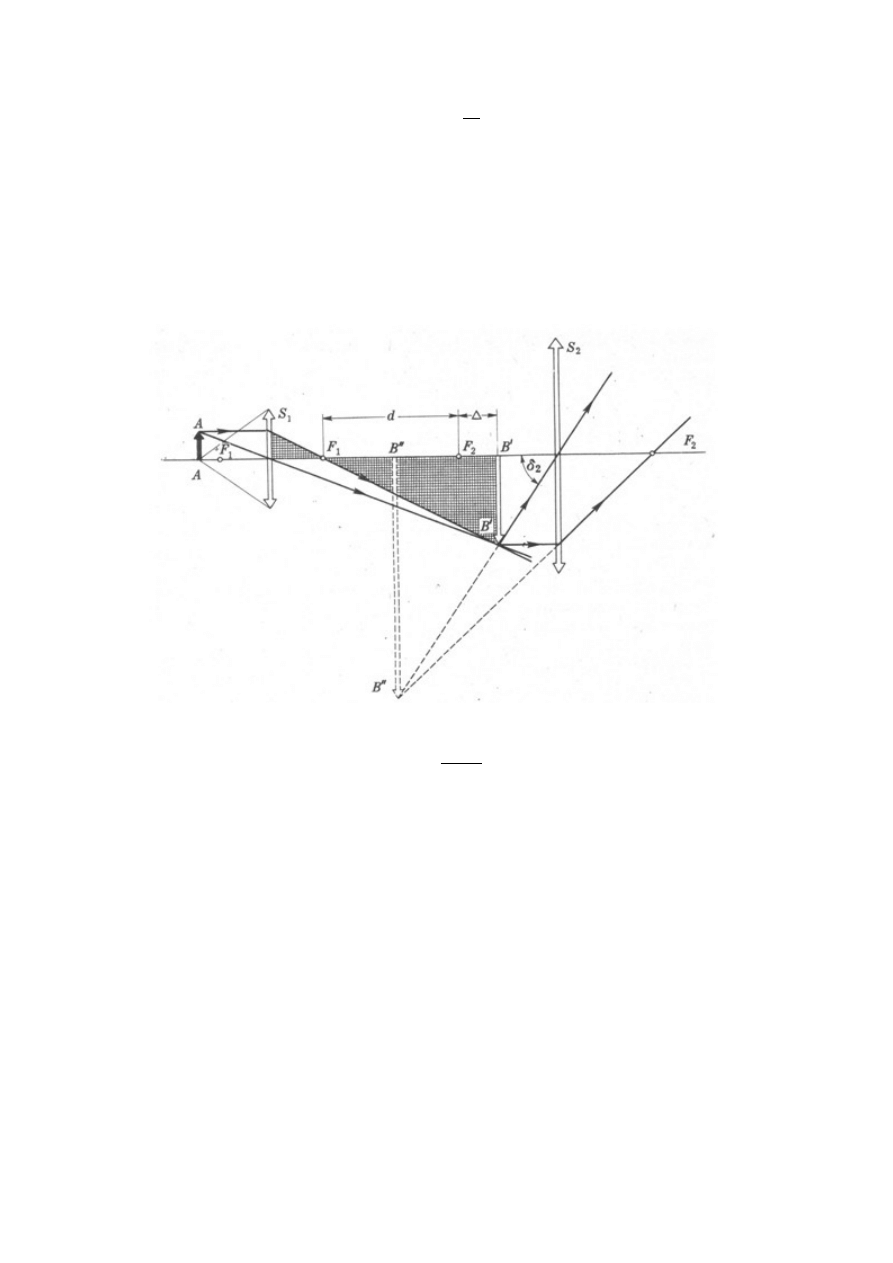
Luneta (do czego służy, budowa, schemat, typy lunet).

Luneta to przyrząd, służący do obserwacji przedmiotów odległych, ale dużych – luneta tworzy
obraz tego przedmiotu pomniejszony, ale w bliższej odległości od oka. Składa się z obiektywu i
okularu.
Układ lunety jest układem teleskopowym – bezogniskowym (ognisko obrazowe obiektywu
pokrywa się (niemal) a ogniskiem przedmiotowym okularu.
Typy lunet:
-astronomiczne refraktory (Keplera) – dwa układy soczewkowe, zbierające;
-astronomiczne reflektory – układy zwierciadlane;
-ziemskie (nieodwracające) – z dodatkową soczewką pomocniczą, odwracającą obraz (też:
lornetki);
-ziemskie (holenderskie) Galileusza – z okularem rozpraszającym
Luneta astronomiczna:
Dwa układy skupiające:
-obiektyw – układ o dużej ogniskowej i dużej średnicy (jego obudowa jest zwykle przesłoną

'

'

1

f

s

w

+

=

'

'

2

1

f

f

l

D

w

⋅

=

aperturową i zarazem źrenicą wejściową);
-okular – układ o małej ogniskowej i mniejszej średnicy (źrenica wyjściowa tworzy się zwykle
nieco za okularem i jest średnicy źrenicy oka).

Powiększenie lunety w=f

1

'/f

2

'

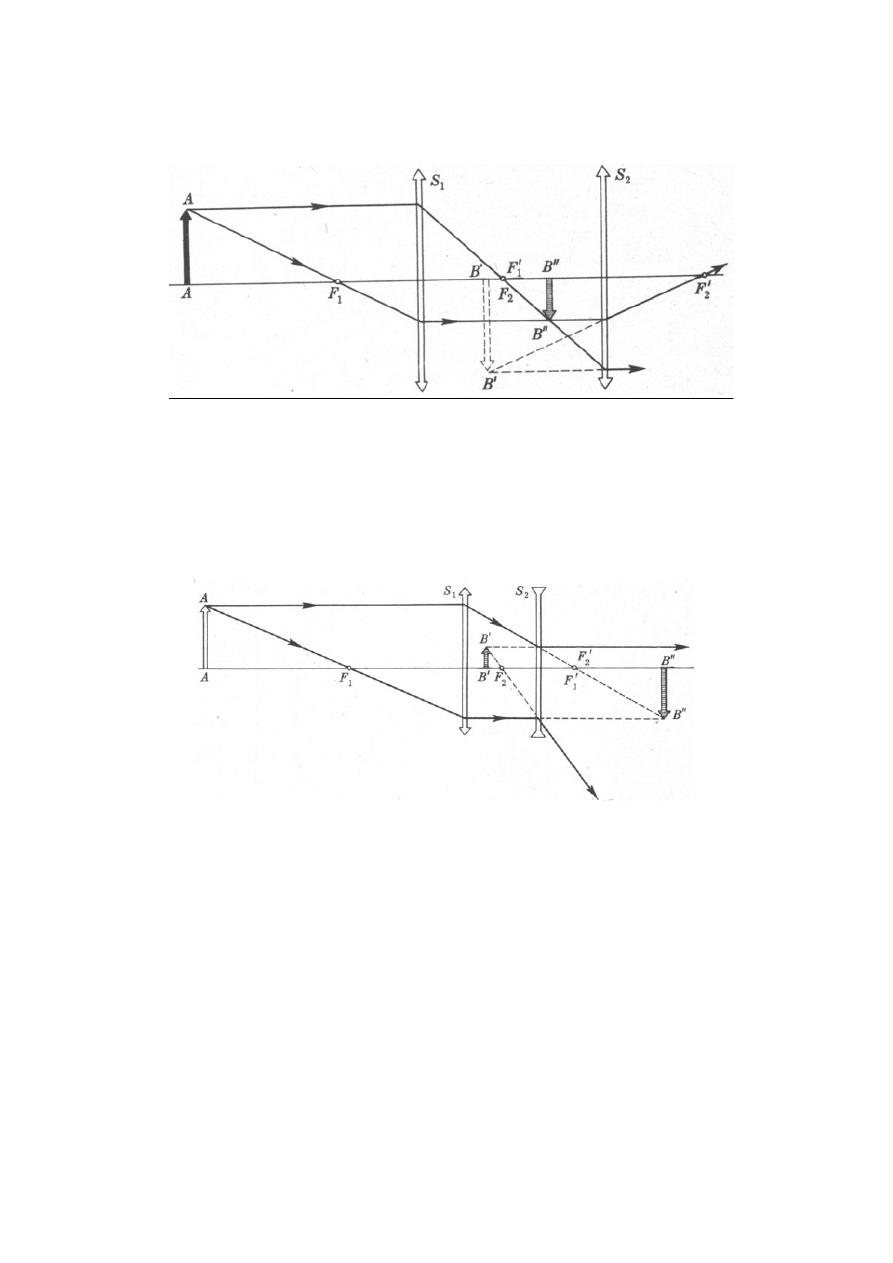
Luneta ziemska typu Galileusza:
Dwa układy:
-

skupiający obiektyw (jak w astronomicznej);

-

rozpraszający okular (dzięki temu obraz jest urojony, ale nie odwrócony).

Lunety ziemskie mają zwykle dużo mniejsze powiększenia, co wynika z wad odwzorowania
trudniejszych do skompensowania w przypadku układów rozpraszających.

•

Zdolność rozdzielcza: oka, przyrządu.

W każdym układzie optycznym obraz przedmiotu otrzymuje się za pomocą wiązki promieni o
rozmiarach poprzecznych ograniczonych wielkością źrenicy wejściowej i w związku z tym w
każdym układzie zachodzą zjawiska dyfrakcji. Zdolność rozdzielcza układu to zdolność układu do
rozróżniania punktów przedmiotu. Mierzymy ją odległością, między rozróżnianymi punktami bądź
kątem, pod którym widoczny jest obraz. Również zdolność rozdzielcza oka ludzkiego jest
ograniczona – przez budowę siatkówki i zjawiska dyfakcji na źrenicy.

•

Przesłony w układzie optycznym: źrenice, luki.

Przesłony to elementy układu optycznego, które ograniczają i formują wiązkę światła,
przechodzącego przez układ:
-ograniczają wady związane z odległością promienia od osi (astygmatyzm, częściowo koma);
-wprowadzają wady związane z kątem wiązki z osią optyczną (astygmatyzm, krzywizna pola) i
ograniczeniami dyfrakcyjnymi.

• Promień aperturowy – promień, który wychodzi z osiowego punktu przedmiotu.
• Promień polowy – promień, który wychodzi ze skrajnego (najdalszego od osi) punktu przedmiotu.
• Przesłona aperturowa – to ta przesłona fizyczna, która najbardziej ogranicza pęk promieni
aperturowych.
• Przesłona polowa – to ta przesłona fizyczna, która najbardziej ogranicza pęk promieni polowych.
• Obrazy przesłon w przestrzeni przedmiotowej i obrazowej to:
-źrenice (obrazy przesłony aperturowej);
-luki (obrazy przesłony polowej);
Apertura numeryczna – miara zdolności rozdzielczej – zależy od maksymalnego kąta rozwarcia
promieni trafiających do obiektywu i od współczynnika załamania światła. A=n sin α

•

Aberracje przyrządów optycznych (podział, krótkie definicje).

Wady odwzorowania przez układy optyczne powstające przy używaniu szerokich wiązek światła
boądż przy używaniu światła niemonochromatycznego nazywają się aberracjami.
Aberracja geometryczna – skutek użycia zbyt szerokiej wiązki światła.
Aberracja chromatyczne-skutek użycia światła niemonochromatycznego.
Używanie szerokich wiązek światła powoduje powstawanie aberracji sferycznej i komy.
Aberracja sferyczna powoduje, że obrazem punktu na osi optycznej nie jest punkt lecz koło (koło
rozproszenia)
Koma - brak symetrii wiązki względem osi układu – gdy punktowy przedmiot leży poza osią
optyczną, to w zależności od kąta wiązki z osią i odległością środka wiązki od osi optycznej, obraz
punktu pozaosiowego wygląda jak jasny krążek o coraz większej średnicy z rozszerzającym się
ogonem – kometa
Astygmatyzm - wiąże się z odkształceniem powierzchni falowej po przejściu przez soczewkę –
skośna wiązka, padająca nawet na środek soczewki, po przejściu przez nią wykaże dwa
„przewężenia” w różnej odległości od soczewki – dwa „ogniska”
Krzywizna pola – skutek działania przesłon w układzie, wprowadzających ograniczenia
dyfrakcyjne.

•

Promieniowanie cieplne: rozkład Plancka, prawo Kirchhofa, Stefana-Boltzmanna,
Wiena.

Promieniowanie cieplne - promieniowanie elektromagnetyczne, które powstaje w wyniku
chaotycznego, cieplnego ruchu cząsteczek ciała i odbywa się kosztem energii tego ruchu.
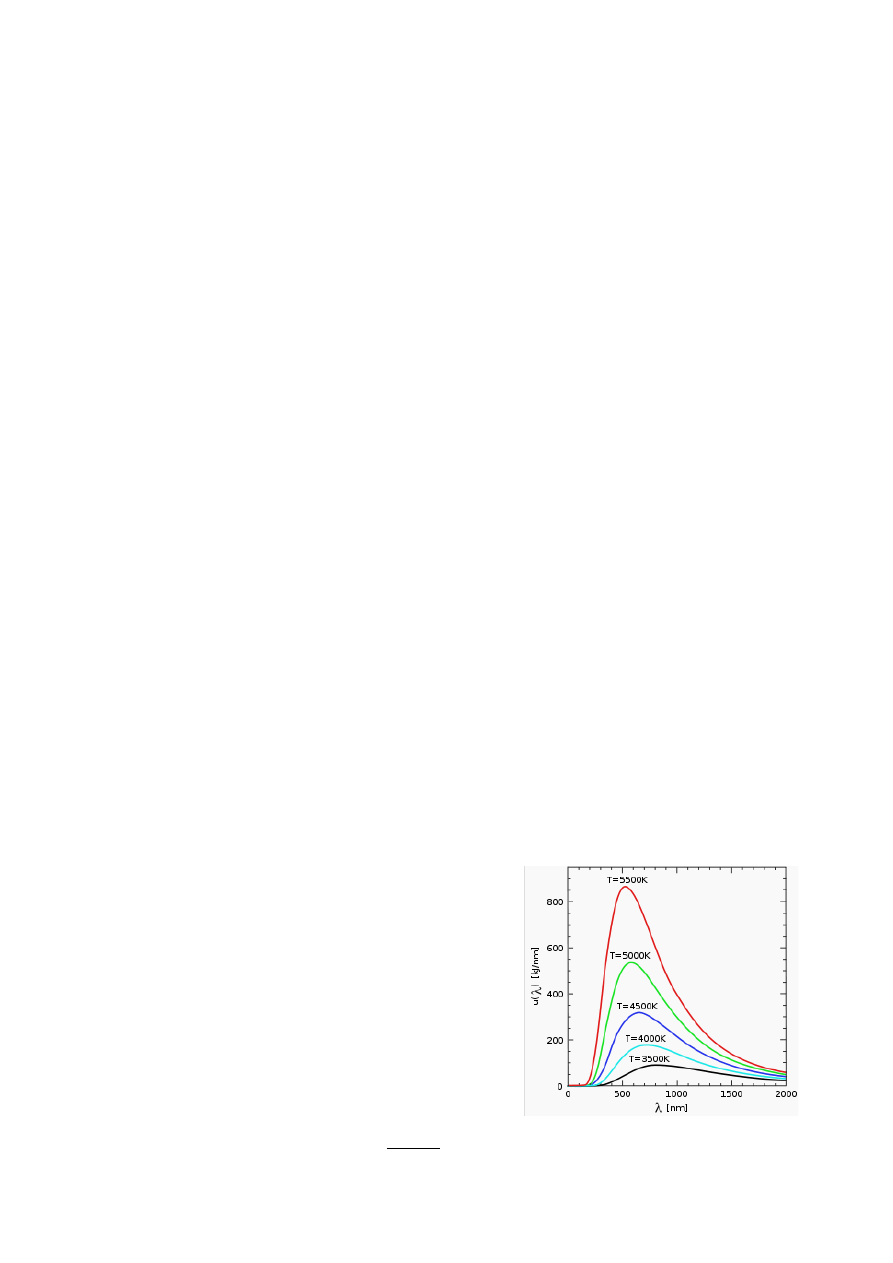
Rozkład Plancka dotyczy promieniowania ciała doskonale czarnego.
Ciało doskonale czarne – pojęcie stosowane w fizyce dla określenia ciała pochłaniającego
całkowicie padające na nie promieniowanie
elektromagnetyczne
Zdolność emisyjna ciała E(ν,T) - E(ν,T)d ν to ilość energii
promieniowania wysyłanej w postaci promieniowania EM o
częstotliwości νν +d ν przez jednostkową powierzchnię
ciała o temperaturze T w jednostce czasu. Rozkład Plancka
zależności zdolności emisyjnej od długości fali dla różnych
temperatur.
Wnioskiem z rozkładu Plancka jest prawo Wiena.
Prawo Kirchhoffa:
Stosunek zdolności emisyjnej do zdolności absorpcyjnej jest
dla każdej powierzchni funkcją częstotliwości i temperatury

( )

( ) ( )

T

T

A

T

E

,

,

,

ν

ε

ν

ν

=

Prawo Stefana-Boltzmanna:
Całkowita zdolność emisyjna ciała doskonale czarnego, obliczona jako całka ze zdolności emisyjnej
po wszystkich częstościach, jest proporcjonalna do czwartej potęgi temperatury
Prawo przesunięć Wiena:
Maksimum energii w widmie promieniowania ciała doskonale czarnego występuje dla długości fali
λ

max

, dla której: λ

max

T=const.

•

Zjawisko fotoelektryczne zewnętrzne (definicja, wzór Einsteina) i wewnętrzne.

Zjawisko fotoelektryczne odkryto podczas doświadczenia Hertza, gdy zaobserwowano, że światło
padające na katodę wywołuje przepływ prądu elektrycznego.
Zaobserwowano wówczas fakty przeczące falowej naturze światła (nie zaobserwowano progu
natężenia światła, od którego miało się zaczynać zjawisko, energia elektronów nie zależała od
natężenia światła ale zależała od częstotliwości)
Idea Einsteina – światło traktujemy jako strumień fotonów – cząstek o skwantowanej energii E=hν.
Każdy foton może być zaabsorbowany przez jeden elektron.
Bilans energetyczny pochłaniania fotonu opisuje wzór Einsteina:

W

0

– praca wyjścia (energia potrzebna do oderwania elektronu od powierzchni metalu), E

K

– energia

kinetyczna.
Zewnętrzne zjawisko fotoelektryczne zachodzi gdy w wyniku pochłaniania elektronów następuje
emisja elektronów.
Wewnętrzne zjawisko fotoelektryczne – przejście fotoelektronu z pasma walencyjnego do pasma
przewodnictwa.

•

Zjawisko Comptona.

W 1923 roku Arthur Compton przeprowadził doświadczenie, które potwierdziło pogląd, że przy
udziale fotonów przekazywane są zarówno pęd, jak i energia. W jego eksperymencie wiązka
promieniowania rentgenowskiego była rozpraszana na folii metalowej, a w promieniowaniu
rozproszonym pojawia się promieniowanie o większej długości fali niż to padające. (Dzieje się tak
ponieważ przy zderzeniu się fotonu rentgenowskiego z elektronem, kierunek fotonu się zmieni
(zostanie rozproszony), zaś elektron zostanie odrzucony – uzyska energię kinetyczną, którą uzyska
od fotonu. Energia rozproszonego fotonu jest mniejsza, a zatem częstotliwość mniejsza, zaś długość
fali większa). Wg fizyki klasycznej długość fali rozproszonego promieniowania nie powinna się
zmienić. Doświadczenie to potwierdziło pogląd, że przy udziale fotonów oprócz energii
przekazywany jest też pęd.
Pęd fotonu:

•

Hipoteza de Broglie`a.

Francuski uczony de Broglie zauważył, że elektrony wykazują podobne do fotonów właściwości
interferencyjne i zasugerował, że zależności

są prawdziwe dla wszystkich cząstek (nie tylko dla fotonów). Wykorzystać je możemy do
przypisania cząstce o pędzie p pewnej długości fali – długości fali de Broglie'a. Opis falowy może
wykorzystywany do opisu niewielkich obiektów – np. elektronów (elektron można traktować jako
falę materii i może on interferować sam ze sobą). Kot natomiast nie jest falą materii i nie może
interferować sam ze sobą – co za ulga dla kotów!

K

E

W

h

+

=

0

ν

λ

ν

h

c

h

p

=

=

ν

λ

h

E

h

p

=

=

Każdą cząstkę można opisać za pomocą amplitudy prawdopodobieństwa:

Prawdopodobieństwo znalezienia cząstki w chwili t w punkcie (x,y,z) jest proporcjonalne do

natężenia

(

)

2

,

,

,

t

z

y

x

ψ

.Jest to tzw. funkcja falowa, ponieważ jej właściwości matematyczne są

takie same, jak właściwości fali. Funkcja falowa nie ma bezpośredniego znaczenia fizycznego. Nie
można jej nawet zmierzyć.

•

Równanie Schrödingera (pojęcie funkcji falowej, wzór [stacjonarne!], do czego służy?)

Funkcje falowe spełniają równanie Schrödingera. Jest to podstawowe równanie mechaniki
kwantowej, opisujące ruch mikrocząstek. Jest to odpowiednik równań ruchu z mechaniki
klasycznej.
Równanie Schrödingera dla ruchu jednowymiarowego, niezależne od czasu. (E – całkowita energia
mechaniczna, U(x) -energia potencjalna.

Za pomocą równania Schrödingera możemy znaleźć funkcję falową dla poruszającej się cząstki
.-Warunki brzegowe: dla dużych wartości |x| prawdopodobieństwo znalezienia cząstki równe jest
zero;
-Tylko pewne wartości energii En i odpowiadające im funkcje n spełniają te warunki – nazywamy
je wartościami własnymi i funkcjami własnymi.

•

Zasada nieoznaczoności Heisenberga (funkcja falowa!).

Konsekwencją dualizmu korpuskularno-falowego jest zasada nieoznaczoności zaproponowana
przez Heisenberga. Stwierdza ona, że położeniu i pędowi cząstki nie można równocześnie przypisać
wartości pomiarowych z nieograniczoną dokładnością. Jeżeli cząstka jest zlokalizowana w
przestrzeni z odchyleniem standartowym Δx to nie posiada określonego pędu, lecz pewien rozkład
pędów o szerokości Δp. Matematycznie zasadę zapisujemy:

•

Model atomu wodoru Bohra: założenia (wcześniejsze Rutheforda plus dodane przez
Bohra), wnioski.

Rutherford przeprowadził doświadczenie, w którym bombardował metalową folię cząstkami alfa i
badał w jaki sposó przechodziły one przez folię (większość przechodziła nie zmieniając kierunku,
część odbiła się od folii). Doprowadziło to do stworzenia przez niego koncepcji budowy atomu:
-materia skupiona w jądrze o niewielkich (w porównaniu z wymiarami atomu) rozmiarach,
dodatnio naładowanym
-niewielkie elektrony o ładunkach ujemnych krążą wokół jądra po ściśle określonych orbitach.
Bohr założył dodatkowo, że:
-moment pędu opisujący ruch elektronów jest skwantowany

-podczas zmiany orbity, któej towarzyszy zmiana energii elektronu, atom emituje foton, którego
energia równa jest:

Z postulatu Bohra wynika że promienie orbit oraz energie elektronów na poszczególnych orbitach
są również skwantowane (można otrzymać wzór na promień n-tej orbity i energię elektronu na tej
powłoce – wzory te nie sprawdzają się dla atomów wieloelektronowych).
Dla atomu wodoru mamy E

n

=-13,6(1/n

2

) eV.

(

)

t

z

y

x

,

,

,

ψ

( )

( )

[

]

( )

x

x

U

E

m

dx

x

d

ψ

ψ

−

−

=

2

2

2

2



2



≥

∆

∆

p

x



n

L

=

•

Zasada Pauliego. Co to jest spin? (wypadałoby zacząć od liczb kwantowych...)

W. Pauli podał w 1925 r zasadę: na jednej orbicie mogą znajdować się nie więcej niż dwa elektrony,
opisane tą samą falą stojącą (funkcją falową).
Stan elektronu opisywany był wówczas przez 3 liczby kwantowe: główną n, poboczną l i
magnetyczną m.
Dla poszczególnych wartości liczby głównej istniały poszczególne ilości kombinacji:
n=1 – tylko 1 kombinacja – l=0 i m=0 [czyli wg zasady Pauliego 2 elektrony]
n=2 – 4 kombinacje – l=0,1 i m=-1,0,1 [8 elektronów]
n=3 – 9 kombinacji czyli 18 elektronów
Nieco później odkryto wewnętrzny moment pędu elektronu (niezwiązany z ruchem po orbicie) –
tzw. spin. Może on przyjmować wartości: ħ/2 i - ħ/2
Doszła zatem do opisu funkcji falowej elektronu jeszcze jedna (spinowa) liczba kwantowa.

•

Rodzaje wiązań cząsteczkowych (krótki opis w języku funkcji falowych).

Między cząsteczkami kryształu ciała stałego mogą istnieć trzy rodzaje wiązań:

- jonowe (mechanizm analogiczny jak w przypadku tworzenia cząsteczki związku

chemicznego);

- kowalencyjne (jak wyżej); przykład: diament (węgiel!);
- metaliczne – specjalny rodzaj wiązań, charakterystyczny dla metali – czyli pierwiastków, które

posiadają słabo związane z resztą struktury atomu tzw. elektrony walencyjne (na najwyższej
powłoce); funkcje falowe takich elektronów są bardzo rozciągłe („rozmyte”
prawdopodobieństwo) a fakt, że elektron taki znajdzie się dość blisko sąsiedniego rdzenia
atomowego powoduje jeszcze większe „rozciągnięcie” funkcji falowej. Prowadzi to do
„rozprzestrzeniania” się funkcji falowej na cały kryształ – taki elektron jest właściwie
niezwiązany z żadnym konkretnym rdzeniem atomowym i może być traktowany jako
swobodny (elektron przewodnictwa).

•

Model pasmowy półprzewodnika.

W kryształach o wiązaniach kowalencyjnych (german, krzem) odległość wzajemna studni
atomowych jest taka, że powstałe pasma energetyczne elektronów walencyjnych nie nakładają się
na siebie. Między zapełnionym pasmem zawierającym elektrony walencyjne (elektrony ostatniej
powłoki) a następnym, wyższym, niezapełnionym pasmem, istnieje przerwa energetyczna (mniejsza
niż 2eV). Aby taki kryształ przewodził prąd elektryczny, w tym wyższym, niezapełnionym paśmie
energetycznym musi znajdować się „nieco” elektronów. W temperaturze pokojowej jest ich tam
naprawdę niewiele... Dlatego pierwiastki takie nazywamy półprzewodnikami.