ANALIZA SCHEMATÓW BLOKOWYCH
OPIS UKŁADÓW ZA POMOCĄ ZMIENNYCH STANU
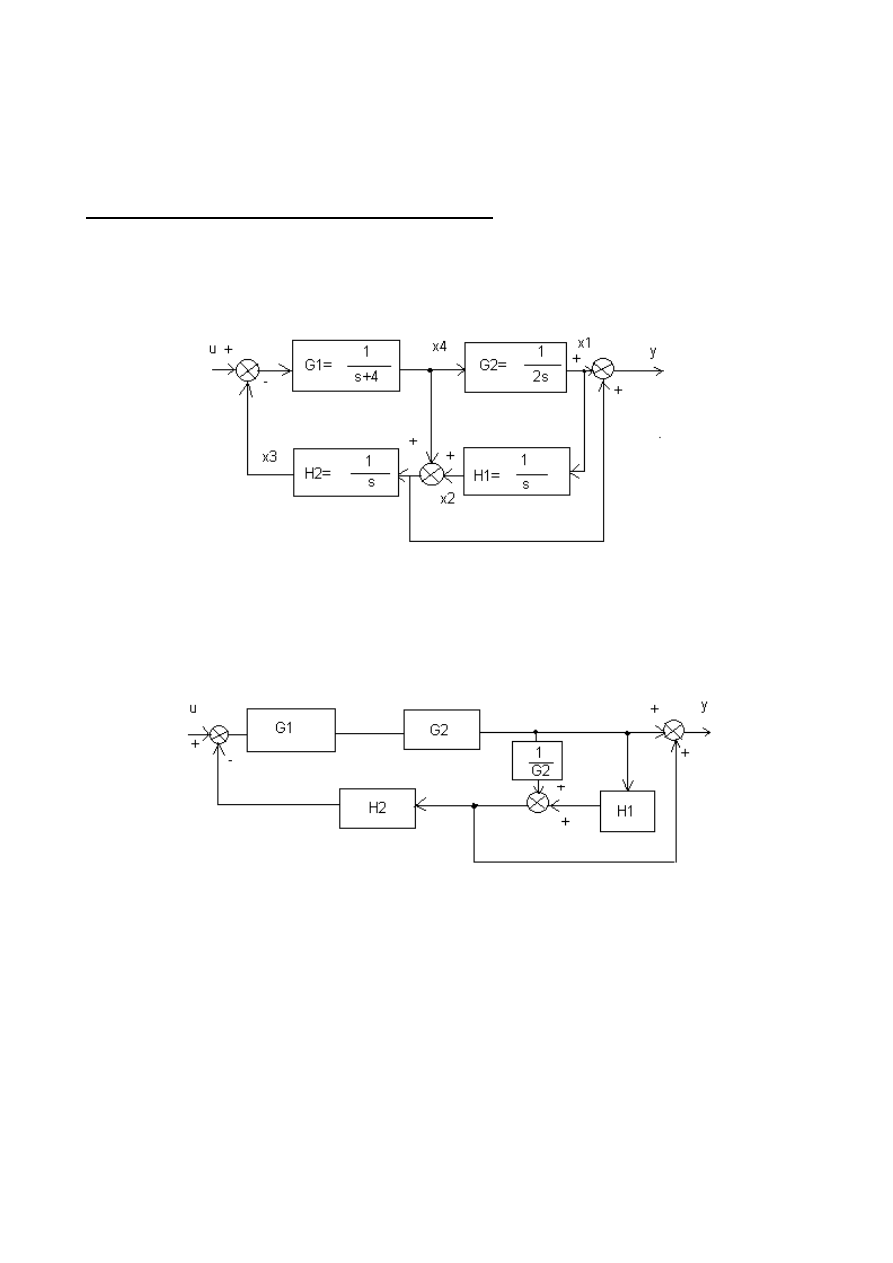
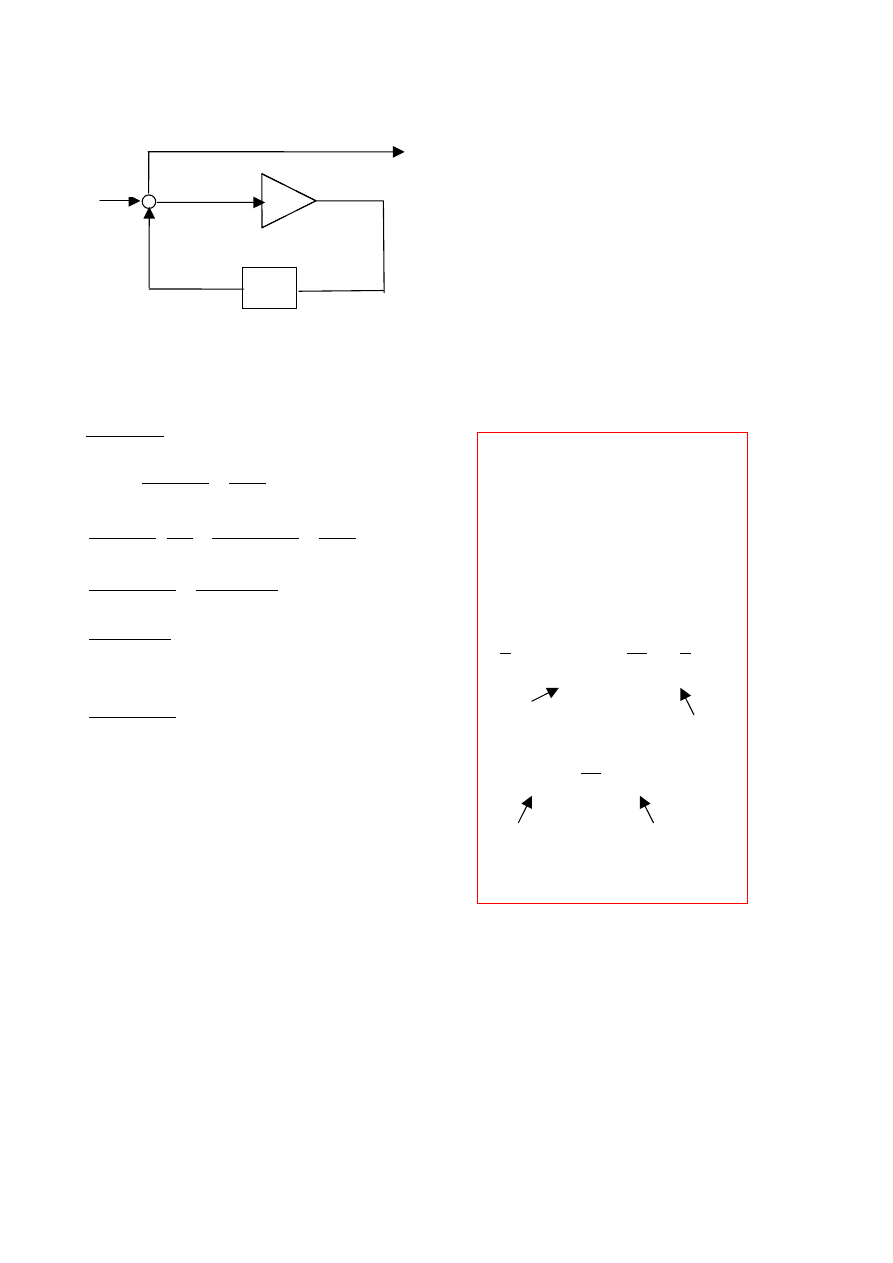
Zadanie 1 (Zmienne stanów i schematy blokowe układów)
Problem:
Wyznaczyć transmitancję od u do y układu:
Rozwiązanie:
1) Przesuwamy węzeł za blok G2:
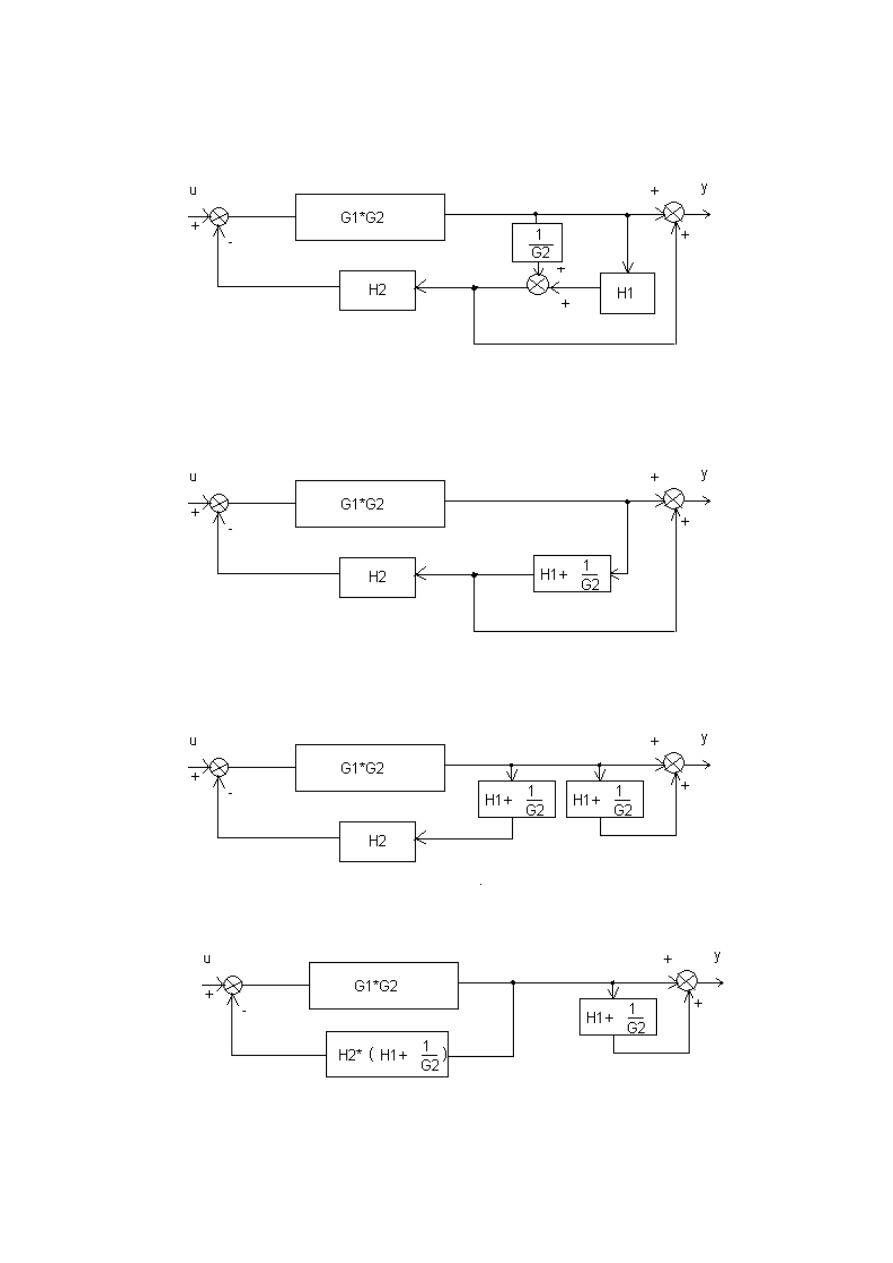
2) Łączymy szeregowo G1 i G2 :
3) Łączymy równolegle H1 i 1/G2:
4) Przesuwamy węzeł przed blok H1+1/G2:
5) Łączymy szeregowo H2 i H1 + 1/G2:
6) Upraszczamy połączenie równoległe po prawej stronie:
7) Upraszczamy sprzężenie zwrotne:
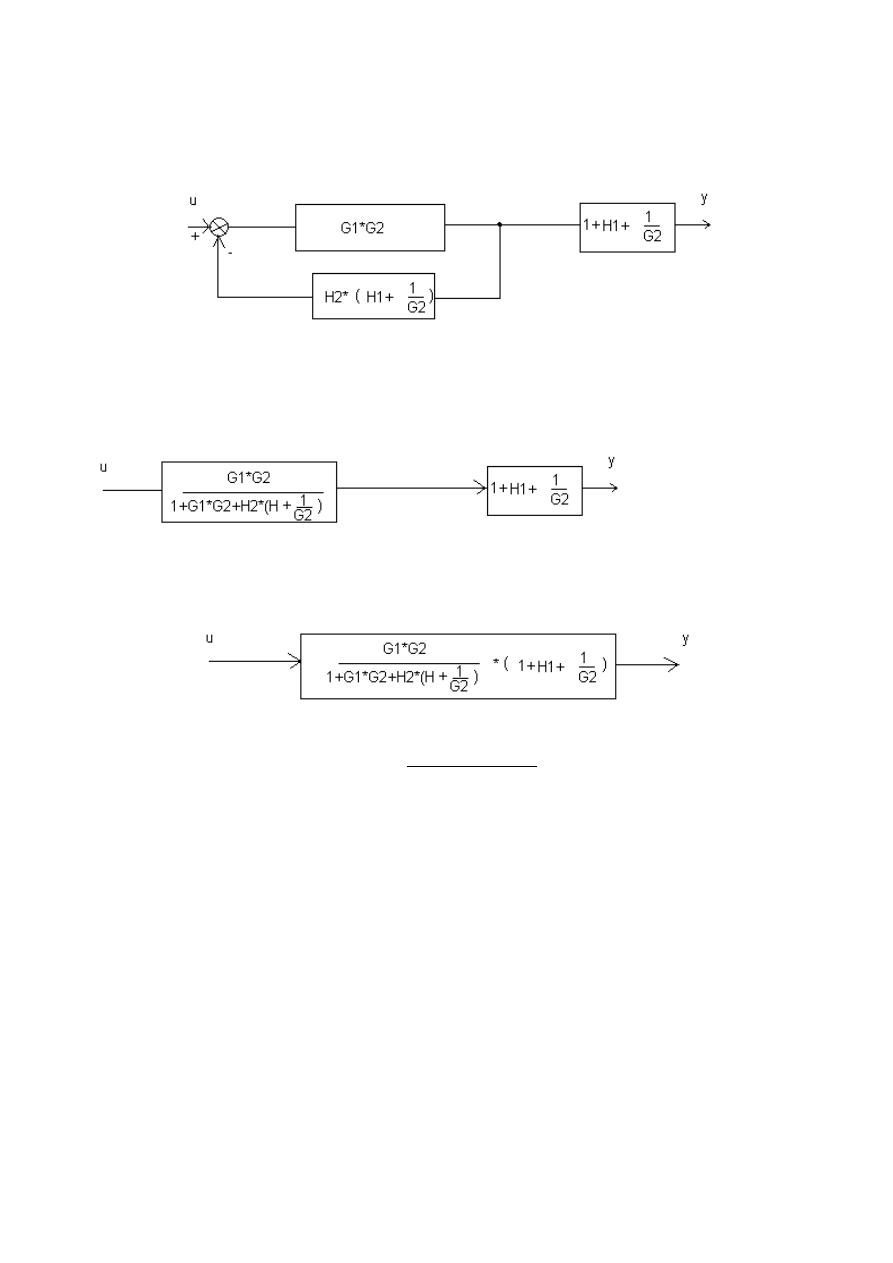
8) Łączymy szeregowo pozostałe dwa układy:
Po podstawieniu poszczególnych transmitancji do wzoru otrzymamy transmitancje wypadkową:
1
2
3
2
1
2
)
(
2
3
4
2
+
+
+
+
+
=
s
s
s
s
s
s
G
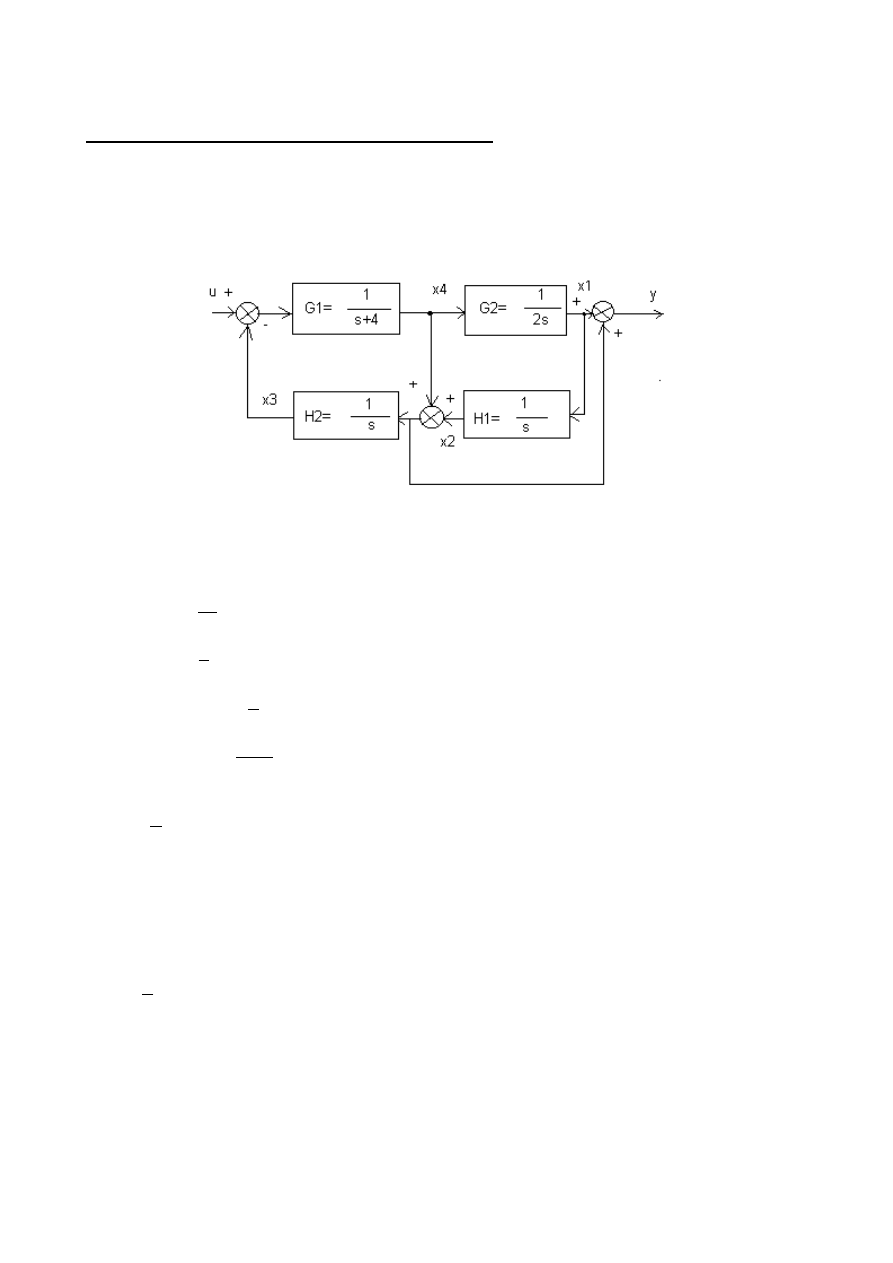
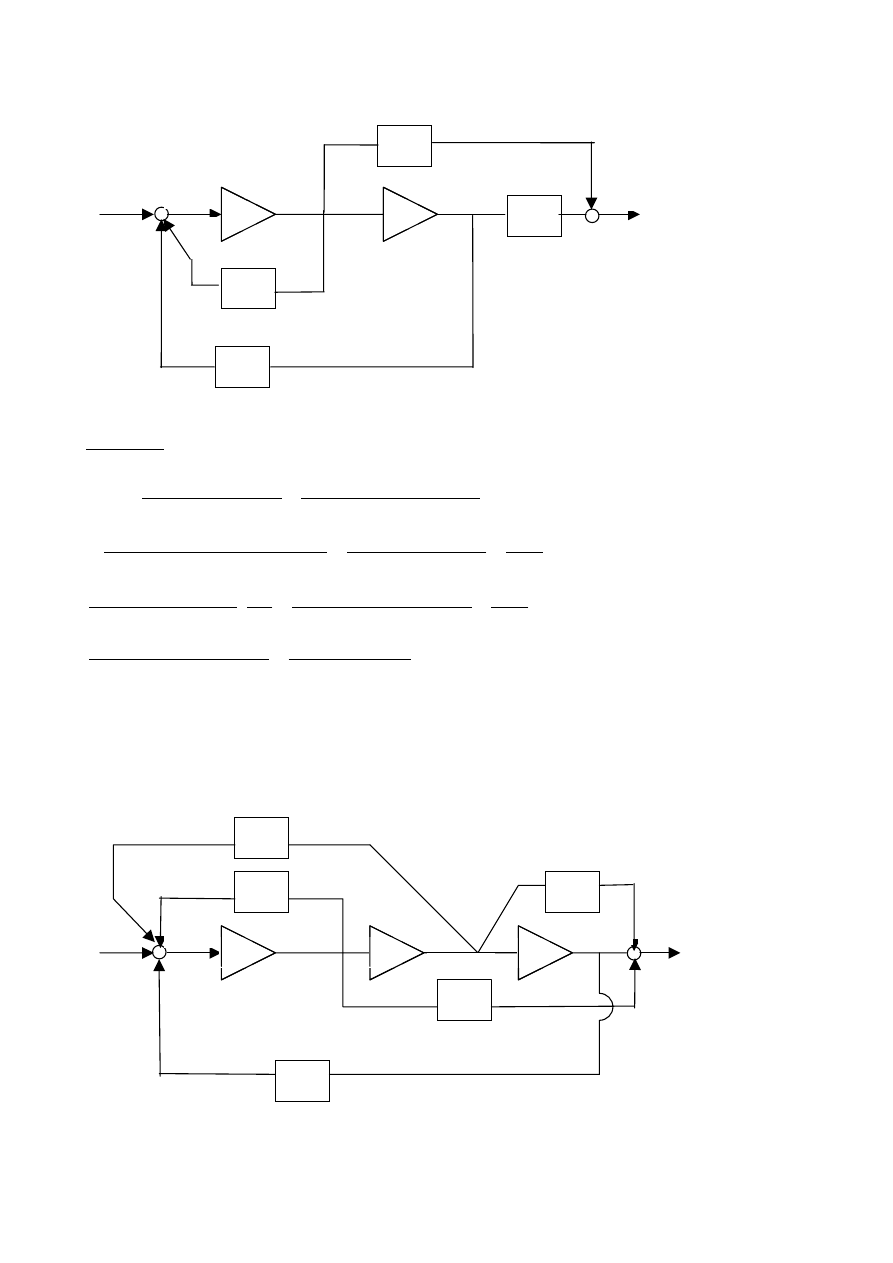
Zadanie 2 (Zmienne stanów i schematy blokowe układów)
Problem:
Napisać równanie stanu i równania wyjścia dla zmiennych stanu z rysunku:
Rozwiązanie:
−
⋅
+
=
−
⋅
=
+
⋅
=
+
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
)
(
4
1
)
(
)
(
1
)
(
1
2
1
3
3
1
4
4
2
4
2
2
3
1
1
1
2
4
4
2
1
x
u
s
x
u
G
x
x
x
s
x
x
H
x
x
s
x
H
x
x
s
x
G
x
(1)
+
⋅
−
−
=
⋅
⇒
−
=
⋅
+
⋅
+
=
⋅
=
⋅
⋅
=
⋅
u
x
x
x
s
x
u
x
x
s
x
x
x
s
x
x
s
x
x
s
4
3
4
3
4
4
4
2
3
1
2
4
1
4
4
2
1
(2)
)
(
)
(
4
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
)
(
4
3
4
4
2
3
1
2
4
1
t
u
t
x
t
x
t
x
t
x
t
x
t
x
t
x
t
x
t
x
t
x
+
⋅
−
−
=
+
=
=
⋅
=
(3)

Równanie stanu:
=
4
3
2
1
x
x
x
x
&
&
&
&
*
4
1
0
0
1
0
1
0
0
0
0
1
2
1
0
0
0
4
4
4 3
4
4
4 2
1
A
−
−
+
4
3
2
1
x
x
x
x
{
u
B
*
1
0
0
0
(4)
Równanie wyjścia:
4
2
1
x
x
x
u
D
x
C
y
+
+
=
⋅
+
⋅
=
(5)
[
]
⋅
=
4
3
2
1
1
0
1
1
x
x
x
x
y
(6)
Przykłady przekształcania transmitancji na zmienne stanu
Metoda bezpośrednia
Przykład 1
Równanie zmiennych stanu
[ ] [ ] [ ] [
[ ] [ ] [ ] [ ] [ ]
u
x
y
u
x
x
y
u
x
x
u
x
x
⋅
+
⋅
−
=
+
−
=
=
⋅
+
⋅
−
=
+
−
=
•
•
•
1
1
1
1
1
1
1
1
]
)
(
1
)
(
)
(
)
(
1
)
(
1
1
)
(
)
(
)
(
1
1
)
(
)
(
)
(
)
(
1
)
(
1
1
)
(
)
(
)
(
1
1
1
1
1
1
1
)
(
s
E
s
s
U
s
E
s
E
s
s
E
s
s
E
s
U
s
E
s
s
U
s
E
s
Y
s
E
s
Y
s
s
U
s
U
s
Y
s
s
s
s
s
s
s
s
G
⋅
−
=
⋅
+
=
+
⋅
=
=
+
=
=
=
+
=
+
=
⋅
+
+
=
Mnożąc licznik i mianownik transmitancji przez s
-n
otrzymamy
n
n
n
n
n
n
s
a
s
a
s
a
s
b
s
b
s
b
s
U
s
Y
s
G
−
−
−
−
−
−
−
−
+
+
+
+
+
+
+
=
=
0
1
1
1
1
0
1
1
1
1
...
1
...
)
(
)
(
)
(
prz
y czym Y(s) i U(s) są odpowiednio transformatą
Laplace’a odpowiedzi i wymuszenia.
W zależności mamy:
)
(
)
...
(
)
(
0
1
1
1
1
s
E
s
b
s
b
s
b
s
Y
n
n
n
−
−
−
−
+
+
+
=
przy czym
n
n
n
s
a
s
a
s
a
s
U
s
E
−
−
−
−
+
+
+
+
=
0
1
1
1
1
...
1
)
(
)
(
Zależność możemy również zapisać w postaci:
)
(
)
...
(
)
(
)
(
0
1
1
1
1
s
E
s
a
s
a
s
a
s
U
s
E
n
n
n
−
−
−
−
+
+
+
−
=
•
x
x
1
E(s) s
-1
E(s)
U(s)
Y(s)
-1
∫
Przykład 2
[
]
[
]
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
2
)
(
)
(
)
(
)
(
1
)
(
)
(
)
(
1
)
(
)
(
3
)
(
2
3
2
)
(
)
(
)
(
3
2
)
(
)
(
3
2
)
(
1
)
(
)
(
)
(
1
3
2
1
3
2
)
(
)
(
1
3
2
)
(
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
⋅
−
⋅
−
=
+
+
⋅
=
⇒
=
+
+
⋅
⋅
+
⋅
⋅
=
+
⋅
=
=
+
=
+
=
+
+
=
+
+
+
=
⋅
+
+
+
=
+
+
+
=
s
s
E
s
s
E
s
U
s
E
s
s
s
E
s
U
s
E
s
s
s
U
s
s
E
s
s
E
s
s
s
E
s
Y
s
E
s
s
s
Y
s
E
s
s
s
Y
s
s
s
U
s
U
s
Y
s
s
s
s
s
s
s
s
s
s
U
s
Y
s
s
s
s
G
D
C
Równanie zmiennych stanu –
W następnych przykładach nie
będzie one wyprowadzone.
[ ]
[
]
[ ] [ ]
u
x
x
y
u
x
x
x
x
x
x
u
x
x
x
x
x
y
x
x
⋅
+
⋅
=
⋅
+
⋅
−
−
=
+
=
+
−
−
=
=
+
=
=
•
•
•
•
0
2
3
1
0
1
1
1
0
2
3
3
2
2
1
2
1
2
1
2
1
1
2
2
B
A
2
E(s) s
-1
E(s) s
-2
E(s)
U(s)
Y(s)
∫
∫
2
•
x
1
•
x
3
-1
-1
Przykład 3
[
]
[
]
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
3
2
3
2
3
2
2
2
3
2
2
2
2
)
(
60
)
(
47
)
(
12
)
(
)
(
60
47
12
1
)
(
)
(
5
4
)
(
)
(
)
(
5
4
)
(
60
47
12
1
)
(
)
(
)
(
60
47
12
1
5
4
60
47
12
1
5
4
)
(
)
(
60
47
12
1
5
4
60
35
5
12
7
1
5
4
)
5
)(
12
4
3
(
1
5
4
)
5
)(
4
)(
3
(
1
5
4
)
(
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
⋅
⋅
−
⋅
⋅
−
⋅
⋅
−
=
+
+
+
⋅
=
+
+
⋅
=
=
+
+
=
+
+
+
=
+
+
+
+
+
=
⋅
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
+
+
=
=
+
+
+
+
+
+
=
+
+
+
+
+
=
s
s
E
s
s
E
s
s
E
s
U
s
E
s
s
s
s
E
s
U
s
s
s
s
E
s
Y
s
E
s
s
s
s
Y
s
s
s
s
U
s
U
s
Y
s
s
s
s
s
s
s
s
s
s
s
s
s
s
U
s
Y
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
s
G
-47
5
-12
-60
4
U(s)
E(s)
E(s) s
-1
E(s) s
-2
E(s) s
-3
∫
∫
∫
Y(s)
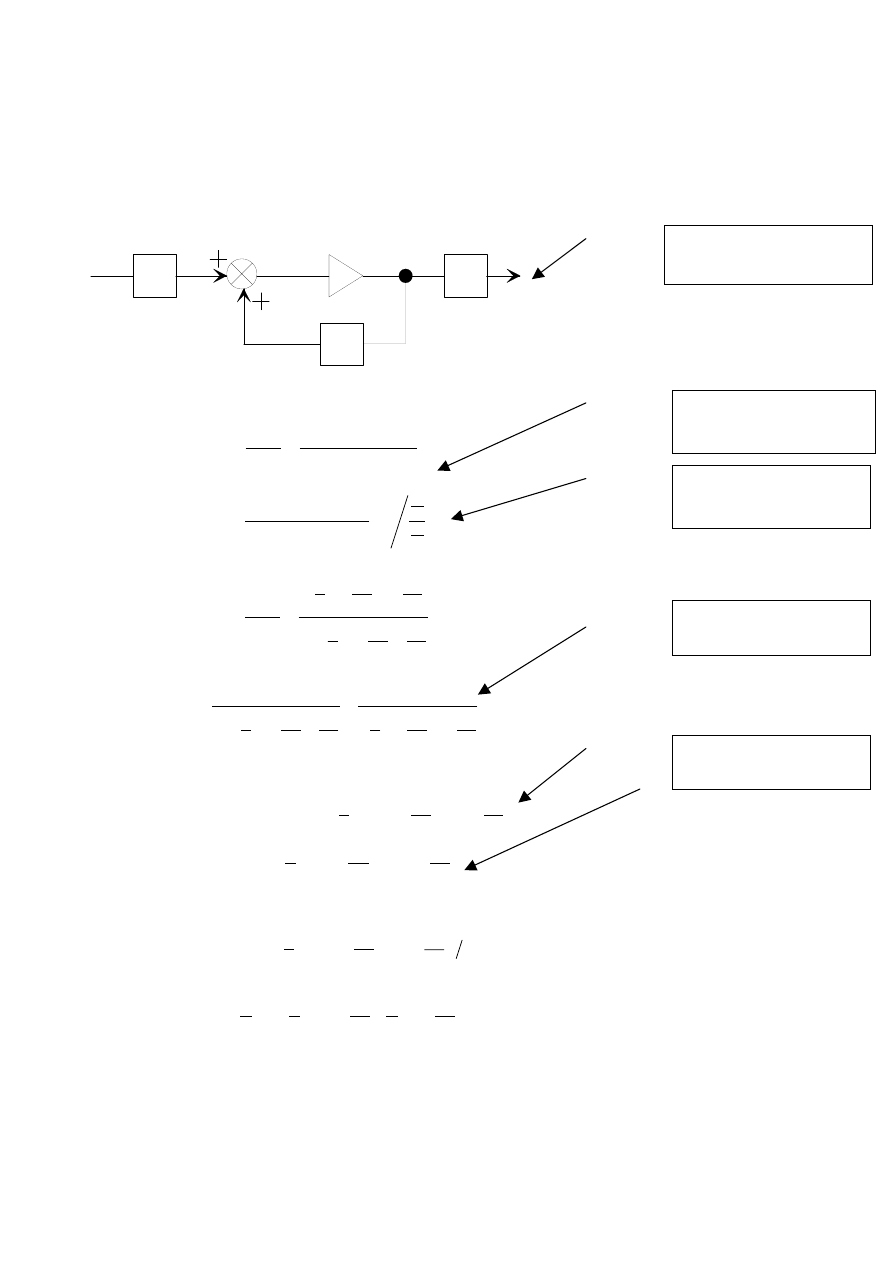
Przykład 4
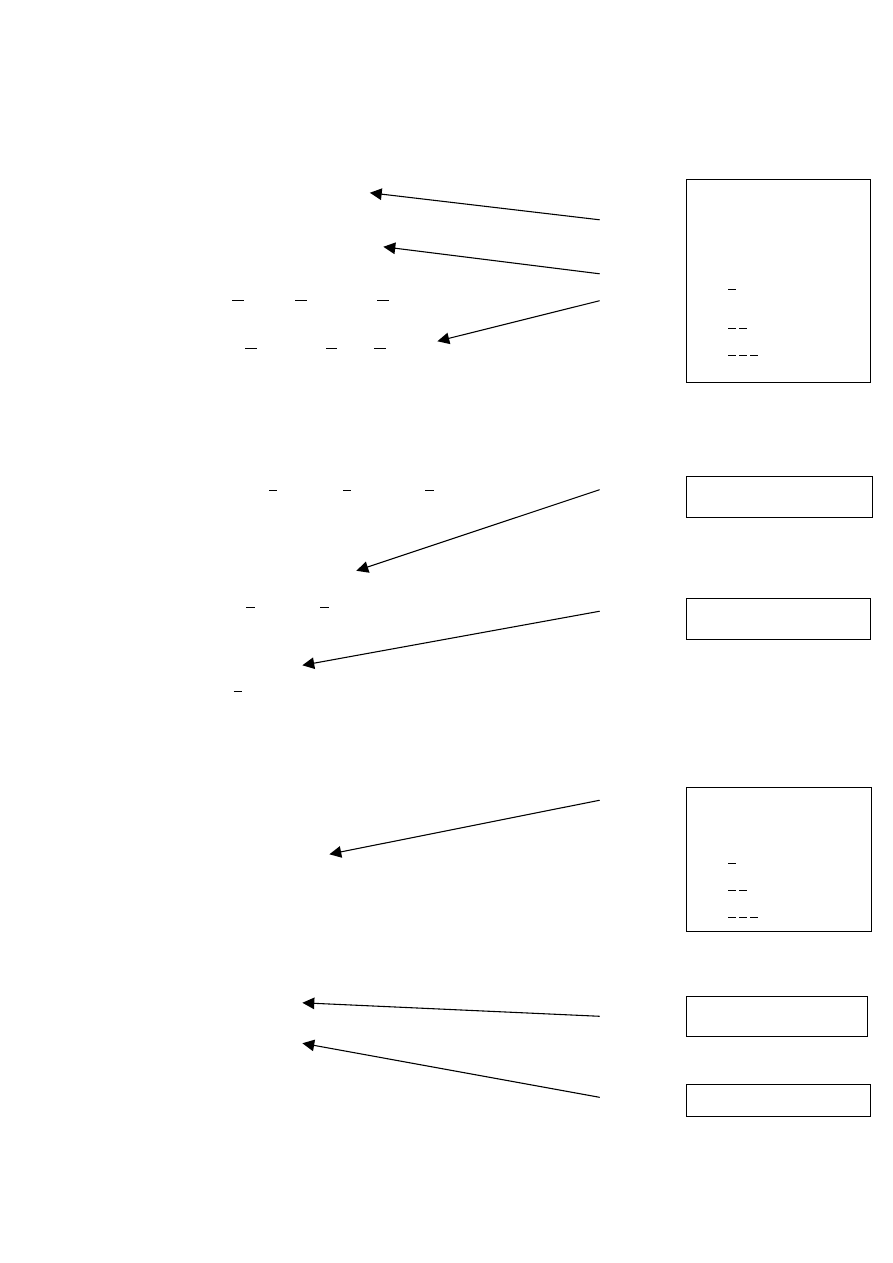
Problem:
Układ jednowymiarowy o schemacie ogólnym przedstawionym na rysunku 1., o transmitancji G(s) opisać
równaniami stanu i równaniami wyjścia. Narysować schemat blokowy wynikający z obliczeń zmiennych
stanów.
Schemat układu jednowymiarowego
o wejściach r=1 , wyjściach m=1 i
o n=3 równaniach stanu
•
x
x
∫
t )
y(t)
u(t)
A
B
C
Rys.1Schemat ogólny układu
Transmitancja G(s) to stosunek
transmitancji sygnału wyjściowego
Y(s) do transmitancji sygnału
sterującego U(s).
Rozwiązanie:
( )
( )
( )
1
2
2
2
1
3
2
3
2
+
+
+
+
+
=
=
s
s
s
s
s
s
U
s
Y
s
G
(1)
Mnożymy licznik i mianownik
transmitancji G(s) przez
odwrotność najwyższej potęgi w
mianowniku
( )
3
3
1
1
2
3
2
1
2
2
2
1
3
s
s
s
s
s
s
s
s
G
+
+
+
+
+
=
(2)
( )
( )
( )
3
2
3
2
1
1
2
1
2
1
2
1
1
1
3
s
s
s
s
s
s
s
U
s
Y
s
G
+
+
+
+
+
=
=
(3)
Wprowadzamy zmienną E(s) i
przekształcając równanie (3)
otrzymujemy poniższą zależność
( )
( )
( )
3
2
3
2
1
2
1
1
1
3
1
1
2
1
2
s
s
s
s
Y
s
s
s
s
U
s
E
+
+
=
+
+
+
=
(4)
Równania (5) i (6) otrzymujemy
przez wymnożenie stronami
równania (4)
( )
( )
( )
( )
( )
3
2
1
1
2
1
2
s
s
E
s
s
E
s
s
E
s
E
s
U
+
+
+
=
(5)
( )
( )
( )
( )
3
2
1
2
1
1
3
s
s
E
s
s
E
s
s
E
s
Y
+
+
=
(6)
Przekształcając równanie (5) otrzymujemy:
( )
( ) ( )
( )
( )
2
:
1
1
2
1
2
3
2
s
s
E
s
s
E
s
s
E
s
U
s
E
−
−
−
=
(7)
( )
( )
( )
( )
( )
3
2
1
2
1
1
1
2
1
s
s
E
s
s
E
s
s
E
s
U
s
E
−
−
−
=
(8)
Na podstawie równania (8) wyznaczamy równania stanu w postaci wektorowej:
2
1
1x
x
=
•
(9)
3
2
1x
x
=
•
(10)
•
x
E
W równaniach (9),(10),(11)
występują poniższe
podstawienia:
( )
3
=
s
( )
3
2
1
x
x
s
E
s
=
=
•
( )
2
1
1
1
x
x
s
E
s
s
=
=
•
( )
1
1
1
1
x
s
E
s
s
s
=
( )
1
2
3
3
2
1
2
1
2
1
x
x
x
s
U
x
−
−
−
=
•
( )
s
U
x
x
x
x
2
1
2
1
2
1
3
2
1
3
+
−
−
−
=
•
(11)
Równanie stanu w postaci wektorowo-macierzowej:
( )
s
U
x
x
x
x
x
x
⋅
+
⋅
−
−
−
=
•
•
•
2
1
3
2
1
2
1
2
1
3
2
1
0
0
1
1
0
0
0
1
0
(12)
Macierz stanu o wymiarach
n x n (13)
−
−
−
=
2
1
2
1
1
1
0
0
0
1
0
A
(13)
=
2
1
0
0
B
(14)
Macierz sterowania o
wymiarach n x r (14)
Równanie stanu w uproszczonej postaci:
( )
( )
( )
t
Bu
t
Ax
t
x
+
=
•
(15)
Równanie wyjścia (16)
powstało po podstawieniu do
równania (6) następujących
wyrażeń:
( )
3
1
x
s
E
s
=
( )
2
1
1
x
s
E
s
s
=
( )
1
1
1
1
x
s
E
s
s
s
=
Równanie wyjścia powstało po przekształceniu równania (6):
3
2
1
3
2
x
x
x
y
+
+
=
(16)
Równanie wyjścia w postaci macierzowej:
[
]
( )
s
U
x
x
x
y
⋅
+
⋅
=
0
3
1
2
3
2
1
(17)
[
]
3
1
2
=
C
(18)
0
=
D
(19)
Macierz wyjścia o wymiarach
m x n
Równanie wyjścia w uproszczonej postaci:
y(t)=Cx(t) (20)
Stała macierz transformacji o
wymiarach m x r
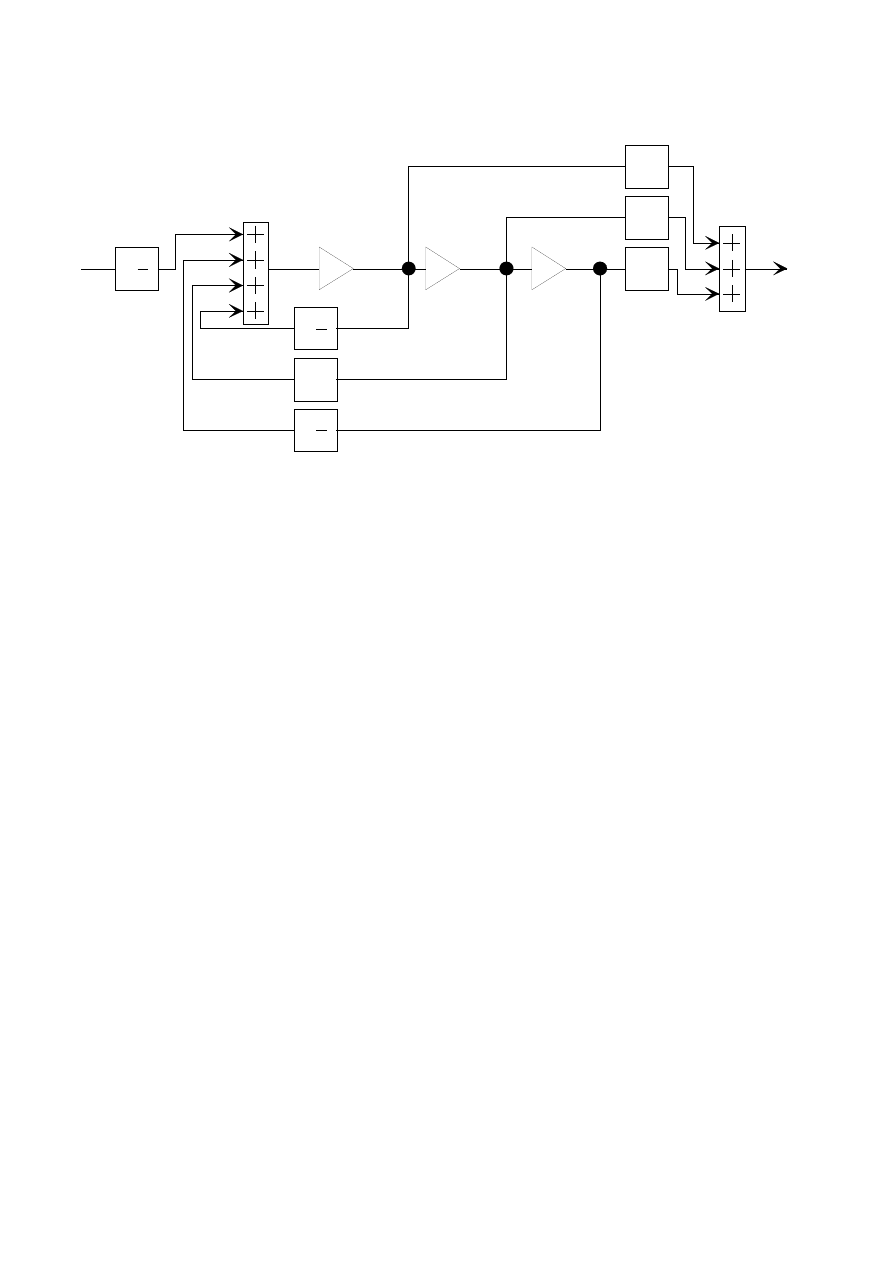
ys.2 Schemat blokowy układu regulacji spełniający równania stanu i wyjścia dla transmitancji G(s).
u(t)
y(t)
∫
∫
∫
1
x
1
2
•
= x
x
2
3
•
= x
x
3
•
x
2
1
−
2
1
−
2
1
−
2
−
2
1
3
R
Wyszukiwarka
Podobne podstrony:
Pomoc do nauki na mieszanki v1 0 1
[LAB5]Tutorial do kartkówki
BEP wieloasortymentowa produkcja rozwiązanie szczególne pomoc do zadania domowego formuły
pomoc do projektu
Marynata do kartkówki z grilla
Pomoc do testu
pomoc do referatu
Pomoc do cw 3
PYTANIA DO KARTKÓWKI NR 5, 2013
Lekarska pomoc do samobójstwa
pomoc do egz
pomoc do stozkowych
Pomoc do MATLABA
pomoc do pracy łukasza, Studia, Doktryny pedagogiczne
zakładam firme mapa myśli - pomoc do filmu, Psychologia, OHP
Pytania do kartkowki stropodachy, Politechnika Krakowska, V Semestr 2, Budownictwo ogólne, Kartkowka
analityczna teoria do 3 kartkowki
POMOC DO OBSERWACJI NIEBA W SIERPNIU, NAUKA, geografia, Geografia(1)
Pomoc do arkuszy kalkulacyjnych v1
więcej podobnych podstron