Opracowała: mgr inż. M.Rutkowska

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z podstawowymi własnościami sygnałów

modulowanych częstotliwościowo (FM) i fazowo (PM) oraz wyznaczenie parametrów
modulacji.

2. Wprowadzenie teoretyczne

Modulacja polega na uzmiennianiu parametrów standardowego przebiegu zwanego
przebiegiem nośnym lub falą nośną przez sygnał modulujący. Sygnał otrzymany w wyniku
operacji modulacji nazywa się sygnałem zmodulowanym.
W systemach modulacji kąta amplituda sygnału zmodulowanego jest stała w czasie, a zmia-
nom zależnym od sygnału modulującego ulega tylko kąt. W zależności od sposobu
uzmienniania kąta φ(t) w takt zmian sygnału modulującego rozróżniamy dwa podstawowe
rodzaje modulacji kątowej: modulację fazy (PM) i modulację częstotliwości (FM).

Modulacja fazy jest rodzajem modulacji kątowej, w której sygnał modulujący bezpośrednio

oddziałuje na fazę sygnału nośnego.
Niech

)

(t

u

n

oznacza sygnał nośny

u

n



t =U

n

cos 

n

t

n



,

(2.1)

gdzie

n

U - amplituda,

n

ω

- pulsacja,

n

ϕ

- faza sygnału nośnego.

Przez

)

(t

u

m

oznaczmy sygnał modulujący

u

m



t =U

m

cos

m

t

m

 ,

(2.2)

gdzie

m

U - amplituda,

m

ω

- pulsacja,

m

ϕ

- faza sygnału modulującego.

Sygnał zmodulowany fazowo ma postać:

u

n



t =U

n

cos[

n

t

n



k U

m

cos

m

t

m

]

,

(2.3)

gdzie k jest współczynnikiem proporcjonalności.
Podstawiając

∆ Ψ

=

⋅

m

U

k

otrzymuje się

u

n



t =U

n

cos[

n

t

n

 

cos

m

t

m

]

,

(2.4)

gdzie

 =

k U

m

(2.5)

nosi nazwę dewiacji fazy.

1

PODSTAWY TEORII SYGNAŁÓW I SYSTEMÓW

Laboratorium

ZFTiZF

Temat: Modulacja kąta

Ćwiczenie 7

Wykonawcy:

Ocena

Uwagi:

1. Dewiacja fazy jest amplitudą zmian fazy chwilowej sygnału zmodulowanego.
2. Dewiacja fazy jest wprost proporcjonalna do amplitudy sygnału modulującego.
3. Dewiacja fazy określa głębokość modulacji fazy.

Pulsację (częstotliwość) chwilową można wyrazić jako szybkość zmian fazy chwilowej



t=

d t

dt

(2.6)

zatem

t=

n



k

d u

m

dt

.

(2.7)

Ponieważ

u

m



t =U

m

cos

m

t

m



(2.8)

pulsacja (częstotliwość) chwilowa sygnału zmodulowanego fazowo wyraża się zależnością

t=

n



k

d

dt

U

m

cos

m

t

m



(2.9)

skąd



t=

n

−

k U

m



m

sin 

m

t

m

=

=

n

−  

m

sin 

m

t

m



(2.10)

Modulacji fazy towarzyszy zmiana pulsacji (częstotliwości) sygnału zmodulowanego.

Sygnał zmodulowany częstotliwościowo wyraża się wzorem:

u

n



t =U

n

cos[

n

t

n



sin 

m

t

m

]

,

(2.11)

gdzie

=

k U

m



m

(2.12)

nosi nazwę dewiacji częstotliwości.

Ogólnie zjawisko modulacji kątowej można opisać wzorem:

u

n



t =U

n

cos[

n

t

n



x sin

m

t] ,

(2.13)

gdzie

x=k U

m

= 

oraz =

m





2

dla modulacji fazowej,

x=

k U

m



m

=

oraz =

m

dla modulacji częstotliwościowej.

W procesie modulacji rozróżniamy dwa przypadki: modulację wąskopasmową i szerokopas-
mową.

Modulacja wąskopasmowa x <<1.
Sygnał zmodulowany można zapisać jako:

u

n



t =U

n

cos[

n

tx sin

m

t]=

=

U

n

[

cos

n

t cos x sin 

m

t −sin 

n

t sin x sin 

m

t ]

(2.14)

2

Ponieważ x<<1, to cos[ xsin

m

t]≈1 oraz sin  x sin 

m

t≈ x sin 

m

t  , zatem

u

n



t=U

n

cos[

n

t−x sin 

m

t sin

n

t]=

=

U

n

cos 

n

t

x

2

U

n

cos

n



m



t−

x

2

U

n

cos

n

−

m



t

(2.15)

gdzie

U

n

cos

n

t - sygnał nośny,

x

2

U

n

cos

n



m



t - górna wstęga boczna,

x

2

U

n

cos 

n

−

m



t - dolna wstęga boczna.

Modulacja szerokopasmowa x>>1
Dla x>>1 liczba par składowych bocznych jest znaczna. Do rozwinięcia wyrażenia

u

n



t =U

n

cos[

n

tx sin

m

t]

(2.16)

w szereg stosuje się funkcje Bessela.

Do obliczania szerokości widma służy wzór:

B=2F1x



x 

(2.17)

gdzie F =



m

2 

.

3

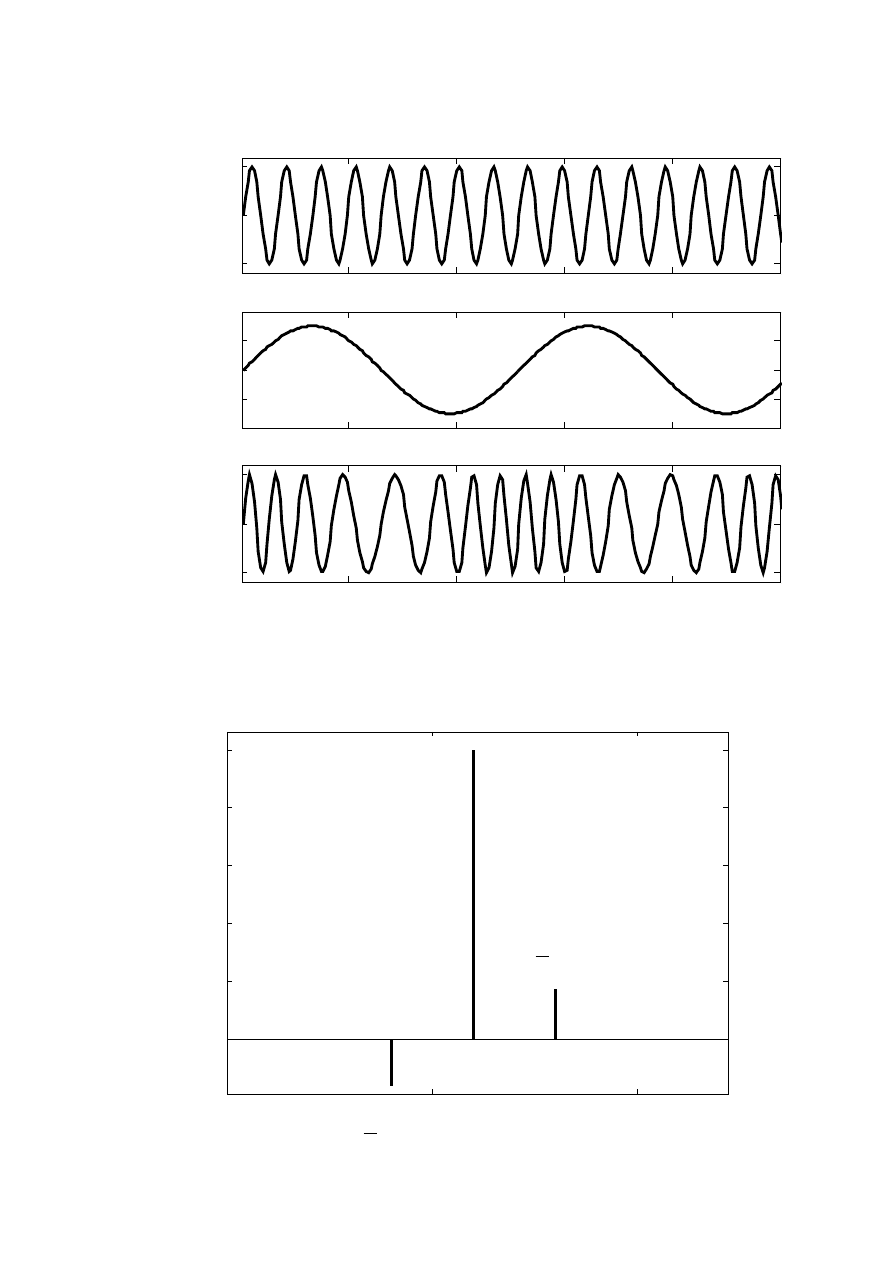
Przykład modulacji

a)

b)

c)

Rys.1. Modulacja fazy: a) sygnał nośny, b)sygnał modulujący, c) sygnał zmodulowany

o

xU

2

1

o

U

o

xU

2

1

n

ω

m

n

ω

−

ω

m

n

ω

+

ω

Rys.2. Widmo sygnału zmodulowanego sygnałem harmonicznym x<<1

4

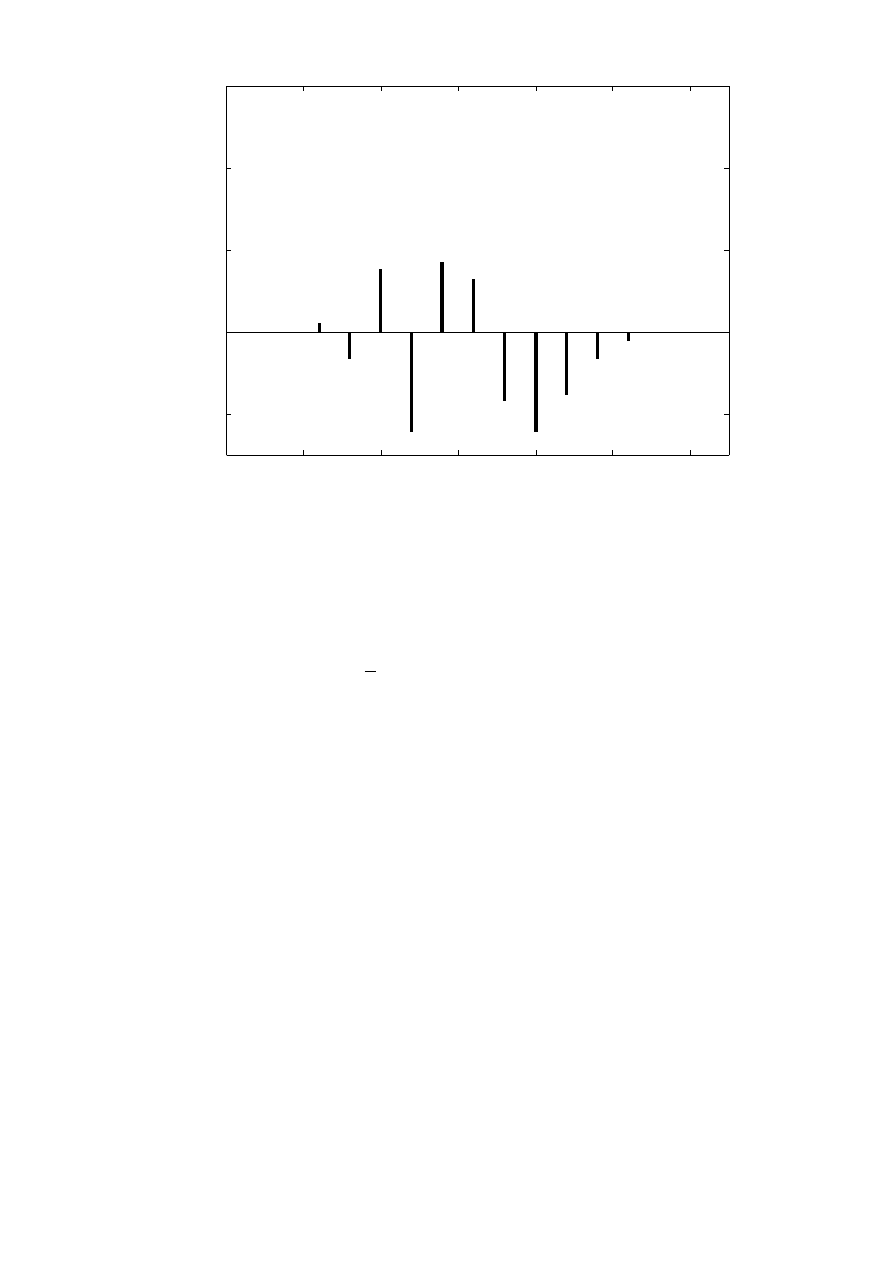
n

ω

o

U

Rys.3. Widmo sygnału zmodulowanego sygnałem harmonicznym x=2

3. Program ćwiczenia

- wygenerować ciąg próbek wartości chwilowych sygnału nośnego
- wygenerować ciąg próbek wartości chwilowych sygnału modulującego
- przeprowadzić modulację sygnałów
- określić parametry modulacji
- zaobserwować jak rozłożone są prążki w widmie sygnału zmodulowanego

- obliczyć (ze wzoru

n

U

x

W

⋅

=

2

1

) wysokości prążków dla k<<1 i porównać z wartością

odczytaną z widma.

4. Sprawozdanie z ćwiczenia

Sprawozdanie powinno zawierać obliczone wartości dewiacji fazy i częstotliwości dla sygnału
modulowanego FM i PM oraz porównanie w przypadku k<<1 wartości prążków obliczonych ze
wzoru i odczytanych z widma.

Sprawozdanie powinno zawierać także odpowiedzi na pytania:
- Jaki wpływ na ilość prążków w widmie ma współczynnik k?
- Dla jakich częstotliwości pojawiają się prążki w widmie zmodulowanym?
- Jaki wpływ na proces modulacji ma wartość amplitudy sygnału modulującego?

5

Tabela 1. Wyniki pomiarów

Lp.

k

Sygnał nośny

Sygnał modulujący

Sygn. zmod.

FM

Sygn. zmod.

PM

U

n

[V] f

n

[Hz]

ϕ

0

[

0

] U

m

[V] f

m

[Hz]

ϕ

0

[

0

] x[

0

] W1 W2 x[

0

] W1 W2

1

0,1

1

5

0

0,5

1

0

2

0,2

1

5

0

0,5

1

0

3

0,5

1

5

0

0,5

1

0

4

0,8

1

5

0

0,5

1

0

5

0,1

1

5

0

3

1

0

6

0,2

1

5

0

3

1

0

7

0,5

1

5

0

3

1

0

8

0,9

1

5

0

3

1

0

9

1

1

10

0

3

1

0

10

2

2

5

0

1

2

0

-

-

-

-

11

5

3

3

0

1

2

0

-

-

-

-

12 10

3

7

20

2

2

0

-

-

-

-

13 20

3

7

45

2

2

0

-

-

-

-

14 30

3

7

90

2

2

0

-

-

-

-

15

1

15

5

0

1

1

0

-

-

-

-

16

2

15

5

0

1

2

0

-

-

-

-

17

5

15

5

0

1

3

0

-

-

-

-

18

7

15

5

0

1

4

0

-

-

-

-

19

9

15

5

0

1

5

0

-

-

-

-

20 10

15

5

0

1

8

0

-

-

-

-

21

1

1

25

0

1

2

0

-

-

-

-

22

1

1

25

0

1

3

0

-

-

-

-

23

1

1

25

0

1

4

0

-

-

-

-

24

2

1

25

0

1

2

0

-

-

-

-

25

2

1

25

0

1

3

0

-

-

-

-

Oznaczenia: U

n

– amplituda sygnału nośnego, f

n

– częstotliwość sygnału nośnego,

ϕ

0

– faza

sygnału nośnego, U

m

– amplituda sygnału modulującego, f

m

– częstotliwość sygnału

modulującego, k – współczynnik modulacji, x – dewiacja, W1 - obliczona wartość amplitudy,
W2 – odczytana wartość amplitudy.

6