1

RUCH DRGAJĄCY

RUCH HARMONICZNY

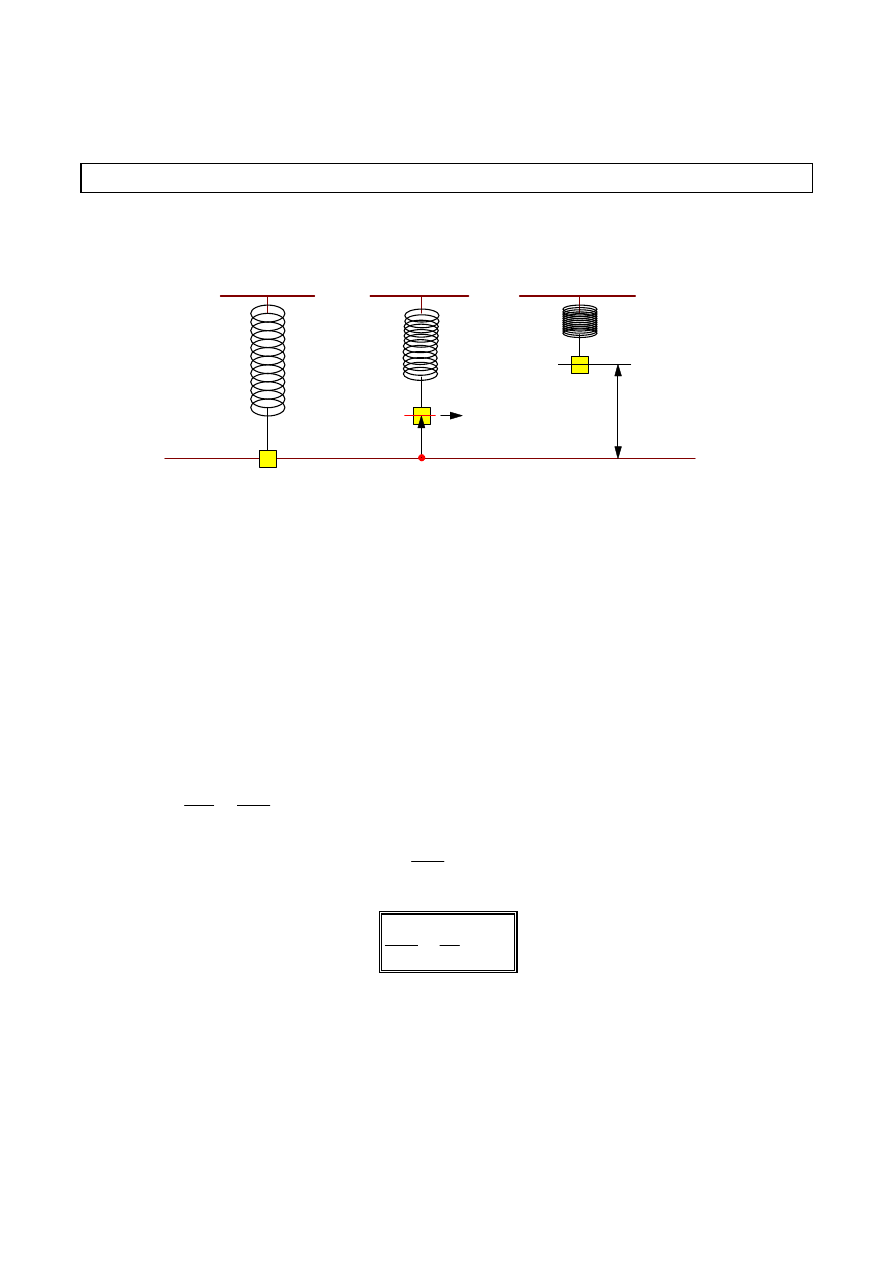
Ruchem harmonicznym , zwanym także ruchem drgającym prostym , nazywamy taki
ruch drgający , w którym wychylenie jest wprost proporcjonalne do działającej siły.

Wychylenie

X

r

jest wektorem zaczepionym w pozycji równowagi i wskazującym

położenie ciała drgającego.

Amplituda wyraża wartość maksymalnego wychylenia (A).

Zgodnie z definicją , w ruchu harmonicznym musi zachodzić związek:

X

k

F

r

r

−−−−

====

Znak „-” informuje , że wektory

F

r

i

x

r

mają zawsze przeciwne zwroty . Korzystając z

drugiej zasady dynamiki otrzymujemy:

ma

kX

==== −−−−

a

dV

dt

d x

dt

====

====

2

2

Przyśpieszenie jest drugą pochodną położenia po czasie.

m

d x

dt

kX

2

2

==== −−−−

d x

dt

k

m

X

2

2

0

++++

====

- różniczkowe równanie ruchu

Rozwiązaniem powyższego równania jest każda funkcja

x(t)

, która je spełnia . Aby

określić ogólny kształt takiej funkcji , kierujemy się następującymi przesłankami:

1. Wychylenie w ruchu harmonicznym zmienia się okresowo , a zatem poszukiwana
funkcja musi być okresowa.

2.Maksymalna wartość funkcji

x(t)

musi być równa

A

.

X

A

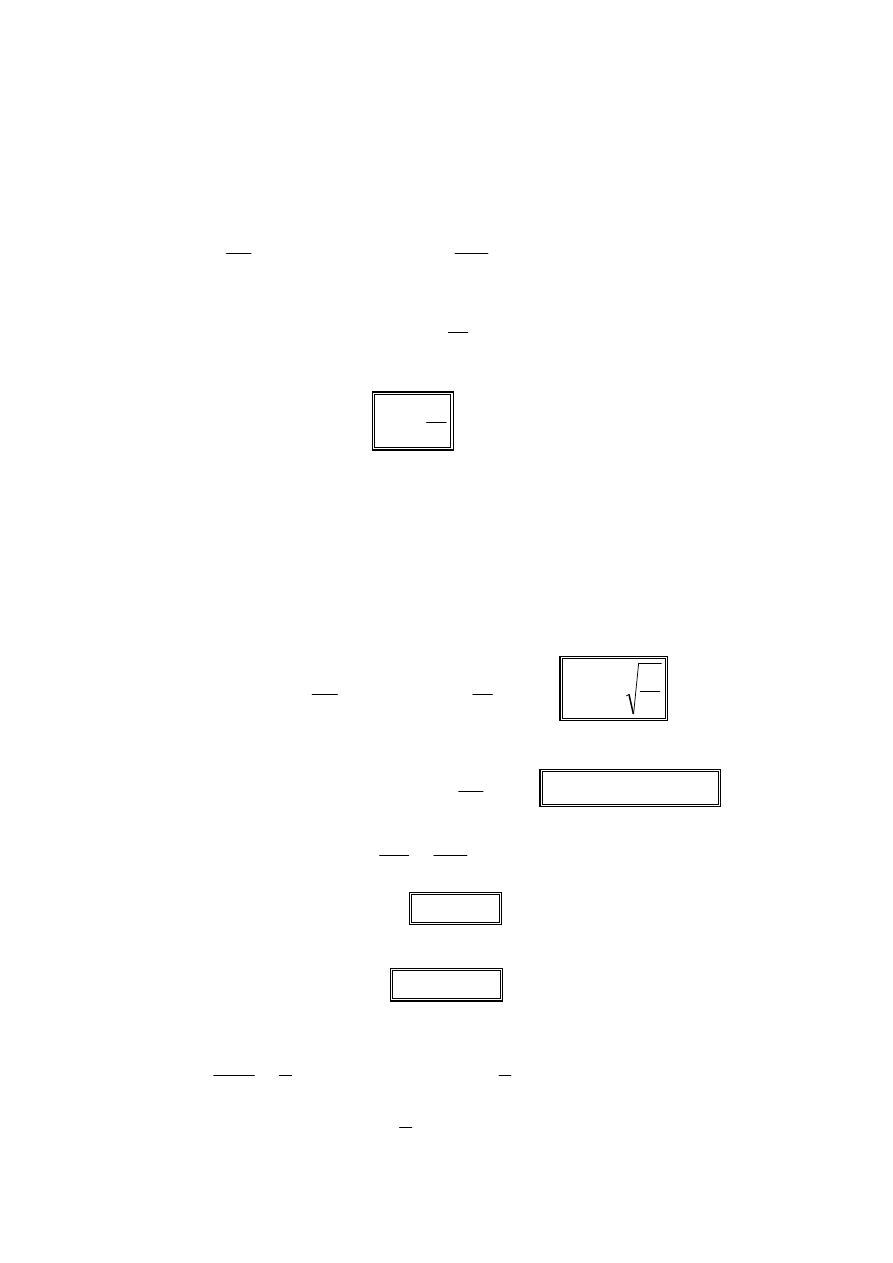
2

3.Ruch może się rozpocząć z każdej pozycji , a zatem

x(o

) nie musi być równe zeru.

Wszystkie powyższe warunki spełnia funkcja:

X=A sin(

ω

ω

ω

ω

t +

ϕ)

ϕ)

ϕ)

ϕ)

Ustalamy w jakim związku powinny być stałe :

ω

ω

ω

ω

, k

i

m

.

dx

dt

A

t

====

++++

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

cos(

)

d x

dt

A

t

2

2

2

==== −−−−

++++

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

sin(

)

−−−−

++++

++++

++++

====

A

t

k

m

A

t

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ϕϕϕϕ

2

0

sin(

)

sin(

)

ω

ω

ω

ω

2

====

k

m

Ustalamy okres (T) funkcji x(t).

x (t + T ) = x(t)

((((

))))

[[[[

]]]]

((((

))))

A

t

T

A

t

sin

sin

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ϕϕϕϕ

++++

++++

====

++++

ω

ω

ω

ω

t +

ω

ω

ω

ω

T +

ϕ

ϕ

ϕ

ϕ

=

ω

ω

ω

ω

t +

ϕ

ϕ

ϕ

ϕ

+ 2

ππππ

T

====

2

ππππ

ω

ω

ω

ω

;

ω

ω

ω

ω

2

====

k

m

T

m

k

====

2

ππππ

Prędkość w ruchu harmonicznym:

V

dx

dt

====

((((

))))

V

A

t

====

++++

ω

ω

ω

ω

ω

ω

ω

ω ϕϕϕϕ

cos

Przyspieszenie :

((((

))))

a

dV

dt

d x

dt

A

t

====

====

==== −−−−

++++

2

2

2

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

sin

a

x

==== −−−−ω

ω

ω

ω

2

Siła :

F

m

x

==== −−−− ω

ω

ω

ω

2

Energia kinetyczna:

((((

))))

((((

))))

[[[[

]]]]

E

mv

mA

t

mA

t

k

====

====

++++

====

−−−−

++++

2

2

2

2

2

2

2

2

1

2

1

2

1

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

cos

sin

((((

))))

E

m

A

x

k

====

−−−−

1

2

2

2

2

ω

ω

ω

ω

3

Energia całkowita :

E

E

k

====

.max

E

mA

====

1

2

2

2

ω

ω

ω

ω

Energia potencjalna :

E

E

E

p

k

==== −−−−

E

m

x

p

====

1

2

2

2

ω

ω

ω

ω

Wszystkie wielkości charakteryzujące ruch harmoniczny są funkcjami czasu.

Kąt, który określa chwilową wartość każdej z tych wielkości nazywamy fazą.

ω

ω

ω

ω

t +

ϕ

ϕ

ϕ

ϕ

- faza ruchu

t = 0

⇒

⇒

⇒

⇒

ω

ω

ω

ω

t +

ϕ

ϕ

ϕ

ϕ = ϕ ϕ

= ϕ ϕ

= ϕ ϕ

= ϕ ϕ

- faza początkowa

ZWI

Ą

ZEK RUCHU HARMONICZNEGO Z RUCHEM PO OKR

Ę

GU

Jeśli punkt materialny porusza się ruchem jednostajnym po okręgu, to rzut
prostokątny tego punktu na kierunek jednej ze średnic porusza się ruchem
drgającym. Można wykazać, że jest to ruch harmoniczny.

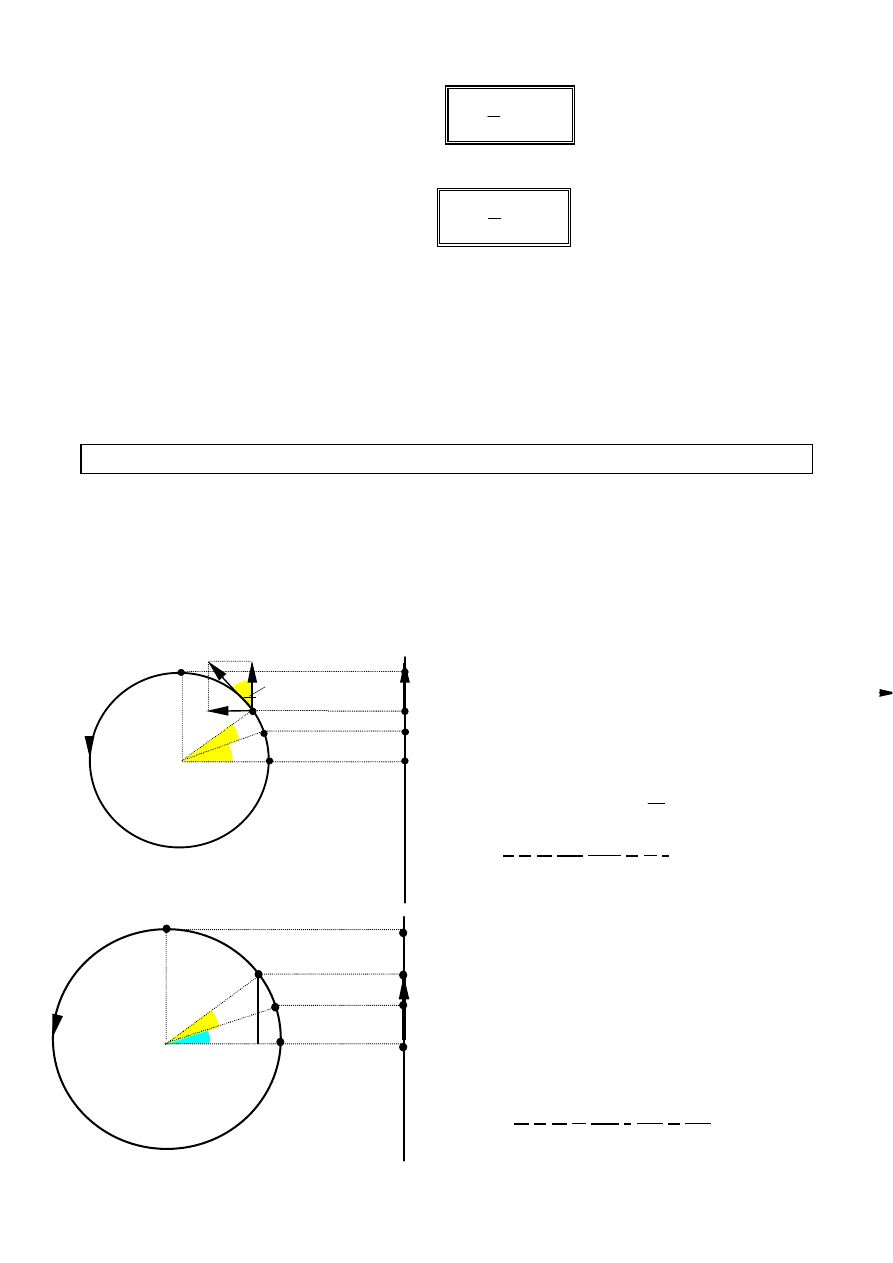
Podobnie można określić prędkość w ruchu

harmonicznym. Jeśli punkt porusza się po
okręgu ze stałą prędkością kątową

ω

ω

ω

ω,

to jego

rzut ma prędkość

V

r

, równą składowej

prędkości punktu, skierowanej w kierunku

X

r

.

V = A

ω

ω

ω

ω

cos (

α+ϕ)

α+ϕ)

α+ϕ)

α+ϕ)

V = A

ω

ω

ω

ω

cos (

ω

ω

ω

ω

t +

ϕ )

ϕ )

ϕ )

ϕ )

Punkt poruszający się ruchem jednostajnym

położenie maksymalnego wychylenia

(x = A)

położenie chwilowe

x(t)

położenie początkowe

x(o)

położenie równowagi

x = 0

x = A sin(

α + ϕ )

α + ϕ )

α + ϕ )

α + ϕ )

ω

ω

ω

ω αααα

αααα ω

ω

ω

ω

====

⇒

⇒

⇒

⇒

====

t

t

x = A sin (

ω

ω

ω

ω

t +

ϕϕϕϕ

)

V

r

V

r

α+ϕ

α+ϕ

α+ϕ

α+ϕ

ϕϕϕϕ

αααα

ω

ω

ω

ω

A

A

X

r

αααα ϕϕϕϕ

X

A

A

4

po okręgu doznaje przyspieszenia dośrodkowego:

a

A

r

==== ω

ω

ω

ω

2

Jego rzut ma przyspieszenie równe składowej równoległej do

r

X

.

((((

))))

a

A

====

++++

ω

ω

ω

ω

αααα ϕϕϕϕ

2

sin

((((

))))

a

A

t

====

++++

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

2

sin

Uwzględniając przeciwne zwroty

a

r

i

X

r

otrzymujemy:

a

A

t

==== −−−−

++++

ω

ω

ω

ω

ω

ω

ω

ω

ϕϕϕϕ

2

sin(

)

a

X

==== −−−−ω

ω

ω

ω

2

F

ma

F

m

x

====

⇒

⇒

⇒

⇒

==== ω

ω

ω

ω

2

WAHADŁO MATEMATYCZNE

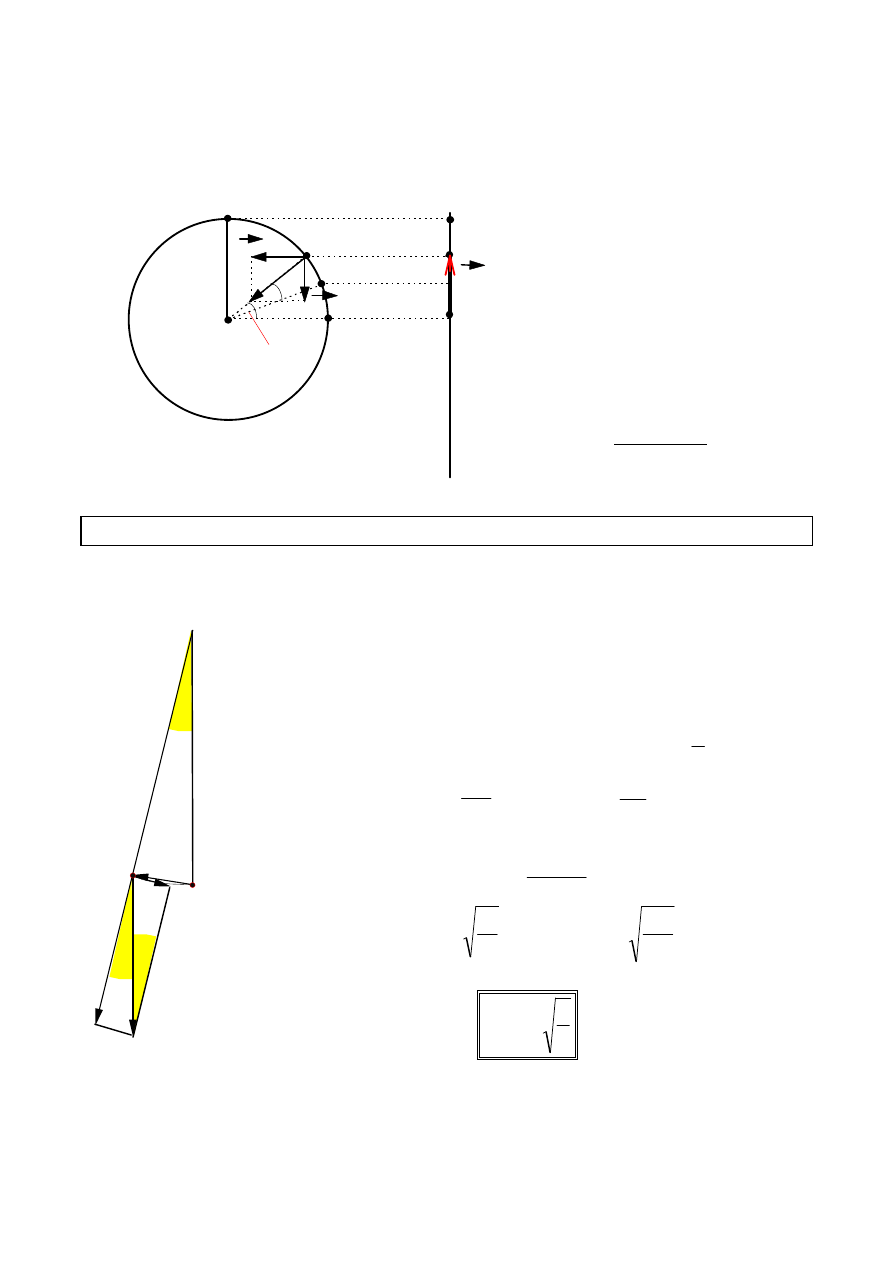
Wahadłem matematycznym nazywamy punktową masę zawieszoną na nieskończenie
cienkiej, nieważkiej i nierozciągliwej nici. Na wahadło wychylone z położenia

równowagi działa siła ciężkości mg . Jedna składowa siły
ciężkości powoduje naciąg nici , a druga składowa (F) - ruch
wahadła. Jeśli wychylenie wahadła jest nieznaczne w stosunku do
długości nici, to ruch wahadła można uważać za ruch drgający.

F = m g sin

αααα

αααα

αααα

≈≈≈≈

⇒

⇒

⇒

⇒

====

O

x

l

sin

F

mg

l

x

====













−−−−

====

x

l

mg

F

r

r

Ruch wahadła jest zatem ruchem harmonicznym.

k

m g

l

====

T

m

K

====

2

ππππ

T

ml

mg

====

2

ππππ

T

l

g

====

2

ππππ

Jeśli wahadło porusza się pod wpływem innych sił, przy czym wypadkowa sił
naciągających nić wahadła w pozycji równowagi wynosi

F

N

, to stosując

a

x

a

α+ϕ

X

r

F

r

αααα

l

l

mg

5

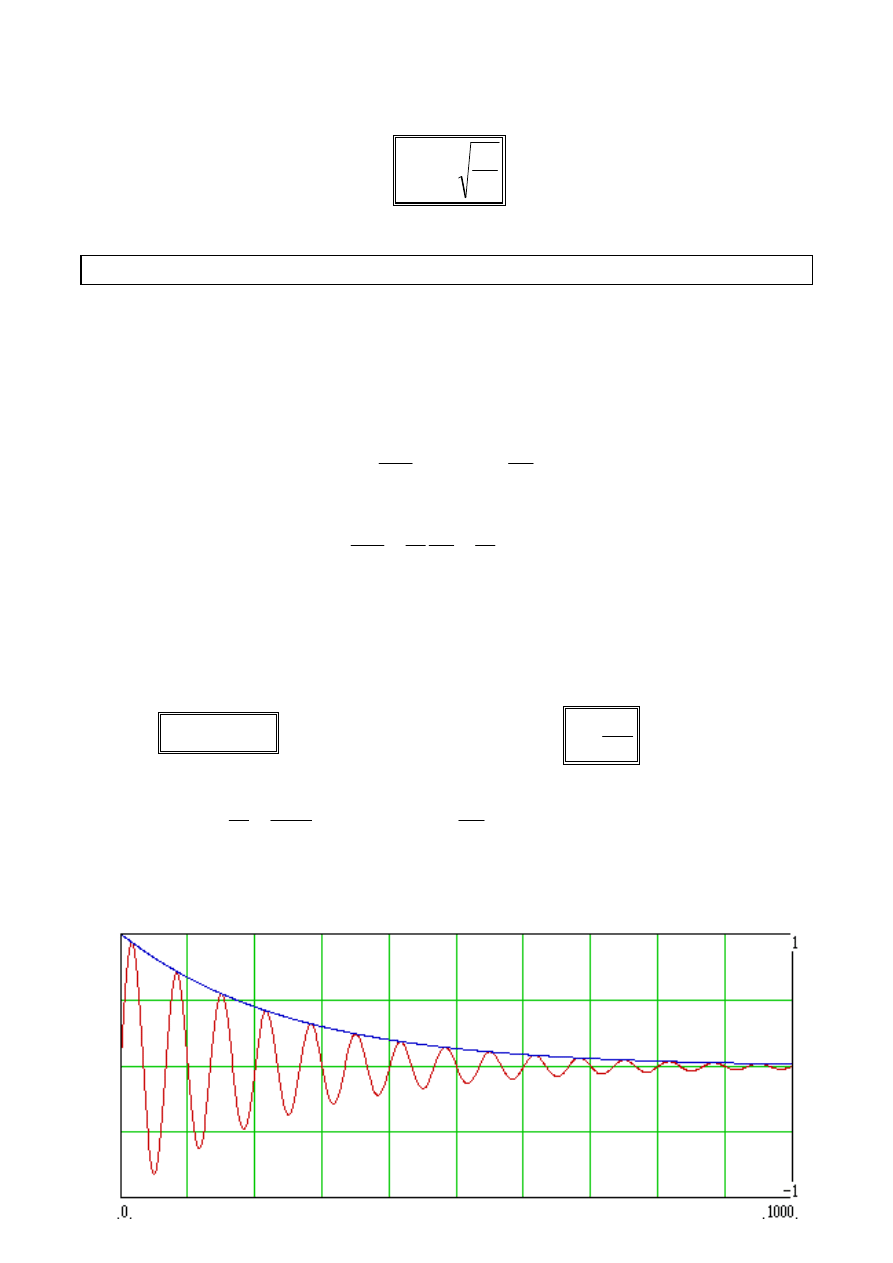
analogiczne rozumowanie, można wykazać, że okres wahań takiego wahadła wyraża
się wzorem:

T

ml

F

N

====

2

ππππ

DRGANIA TŁUMIONE

Drgania tłumione mają miejsce wtedy, gdy na ciało drgające ruchem harmonicznym
działa siła oporów ruchu wprost proporcjonalna do prędkości ciała.

F

kx

hV

==== −−−−

−−−−

m

d x

dt

kx

h

dx

dt

2

2

==== −−−−

−−−−

d x

dt

h

m

dx

dt

k

m

X

O

2

2

++++

++++

====

równanie ruchu

Można wykazać, że rozwiązaniem tego równania jest funkcja :

X = A sin (

ω

ω

ω

ω

t +

ϕ )

ϕ )

ϕ )

ϕ )

gdzie:

A

A e

t

====

−−−−

0

ββββ

−

amplituda drgań tłumionych,

ββββ ====

h

m

2

- stała tłumienia

ω

ω

ω

ω

2

2

2

4

====

−−−−

k

m

h

m

T

====

2

ππππ

ω

ω

ω

ω

- okres drgań tłumionych

Kształt funkcji

X = A sin (

ω

ω

ω

ω

t +

ϕ)

ϕ)

ϕ)

ϕ)

przedstawia poniższy wykres .

A

A e

t

====

−−−−

0

ββββ

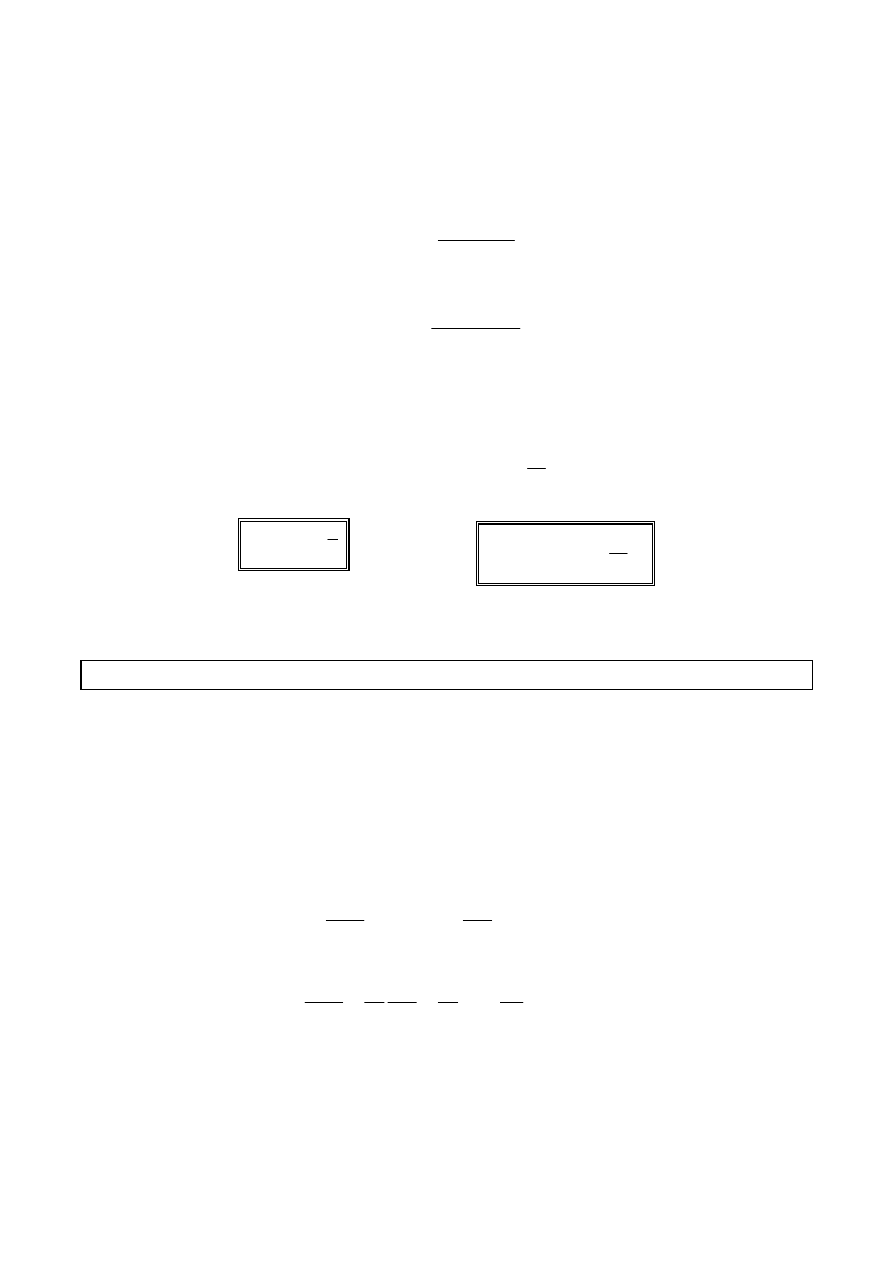
6

Szybkość zanikania drgań można określić podając stałą tłumienia lub tzw.
logarytmiczny dekrement tłumienia. Jest to logarytm naturalny ze stosunku amplitud
wziętych w odstępie okresu.

(((( ))))

((((

))))

Λ

Λ

Λ

Λ ====

++++

ln

A t

A t

T

Λ

Λ

Λ

Λ ====

−−−−

−−−−

++++

ln

(

)

A e

A e

t

t T

0

0

ββββ

ββββ

Λ

Λ

Λ

Λ ====

ln e

T

ββββ

Λ = βΤ

Λ = βΤ

Λ = βΤ

Λ = βΤ

⇒

⇒

⇒

⇒

ββββ ==== Λ

Λ

Λ

Λ

T

A

A e

T

t

====

−−−−

0

Λ

Λ

Λ

Λ

lub

A

A

T

t

====

−−−−











0

exp

Λ

Λ

Λ

Λ

DRGANIA WYMUSZONE

Drgania wymuszone mają miejsce wtedy, gdy na ciało drgające ruchem
harmonicznym działa siła wymuszająca określona równaniem :

F

w

= F

o

cos

ω

ω

ω

ω

t

F = - kX - h V + F

0

cos

ω

ω

ω

ω

t

m

d X

dt

kX

h

dX

dt

F

t

2

2

0

==== −−−−

−−−−

++++

cos

ω

ω

ω

ω

d X

dt

h

m

dX

dt

k

m

X

F

m

t

2

2

0

++++

++++

====

cos

ω

ω

ω

ω

- równanie ruchu

Można wykazać, że rozwiązaniem powyższego równania jest funkcja :

X = A sin (

ω

ω

ω

ω

t +

ϕϕϕϕ

)

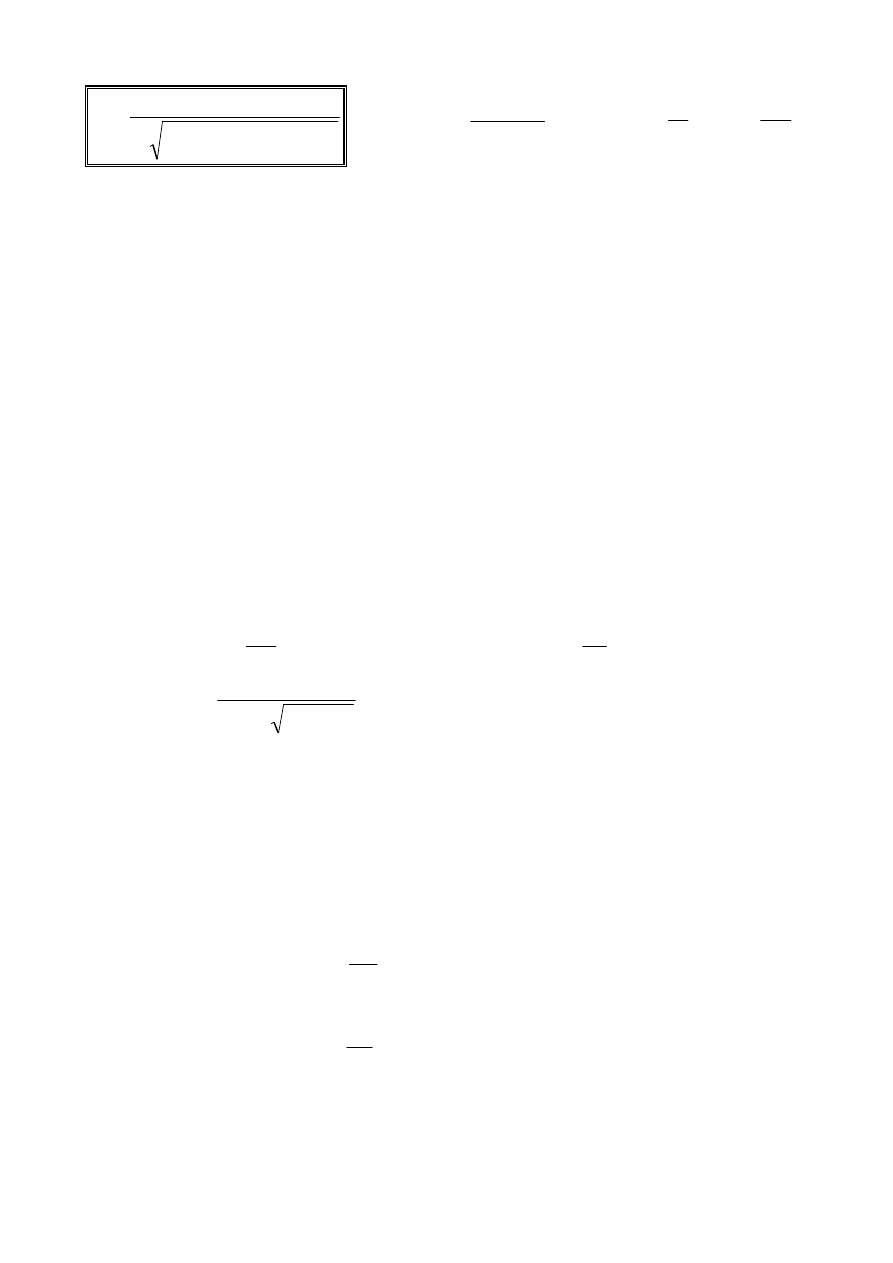
7

((((

))))

A

F

m

====

−−−−

++++

0

0

2

2

2

2

2

4

ω

ω

ω

ω

ω

ω

ω

ω

ββββ ω

ω

ω

ω

;

ctg

ϕϕϕϕ

βω

βω

βω

βω

ω

ω

ω

ω

ω

ω

ω

ω

====

−−−−

2

0

2

2

;

ω

ω

ω

ω

0

2

====

k

m

;

ββββ ====

h

m

2

Amplituda drgań wymuszonych jest maksymalna wtedy, gdy wyrażenie zawarte pod
pierwiastkiem przyjmuje wartość minimalną.

((((

))))

Y

====

−−−−

++++

ω

ω

ω

ω

ω

ω

ω

ω

ββββ ω

ω

ω

ω

0

2

2

2

2

2

4

ω

ω

ω

ω

2222

=

=

=

=

z

(((( ))))

Y z

z

z

z

====

−−−−

++++

++++

ω

ω

ω

ω

ω

ω

ω

ω

ββββ

0

4

0

2

2

2

2

4

(((( ))))

((((

))))

Y z

z

z

====

−−−−

−−−−

++++

2

0

2

2

0

4

2

2

ω

ω

ω

ω

ββββ

ω

ω

ω

ω

((((

))))

∆∆∆∆ ====

−−−−

++++

−−−−

4

4

4

4

0

4

2

0

2

4

0

4

ω

ω

ω

ω

ββββ ω

ω

ω

ω

ββββ

ω

ω

ω

ω

∆ = 16 β

∆ = 16 β

∆ = 16 β

∆ = 16 β

2222

(β

(β

(β

(β

2222

− ω

− ω

− ω

− ω

0000

2222

) ) ) )

((((

))))

Y

a

min

====

−−−− ====

−−−−

∆∆∆∆

4

4

2

0

2

2

ββββ ω

ω

ω

ω

ββββ

Z

b

a

min

==== −−−−

====

−−−−

2

2

0

2

2

ω

ω

ω

ω

ββββ

A

F

m

max

====

⋅⋅⋅⋅

−−−−

0

0

2

2

2

ββββ ω

ω

ω

ω

ββββ

ω

ω

ω

ω

2222

min

=

ω

ω

ω

ω

0000

2222

− 2 β

− 2 β

− 2 β

− 2 β

2

2

2

2

Amplituda drgań wymuszonych jest zatem maksymalna wtedy, gdy spełniony jest
warunek :

ω

ω

ω

ω

2

2

2

2

= ω

= ω

= ω

= ω

0000

2222

− 2 β

− 2 β

− 2 β

− 2 β

2

2

2

2

Przypadek taki nazywamy rezonansem. Jeśli stała tłumienia jest bliska zeru, to
amplituda drgań wymuszonych zmierza wtedy do nieskończoności.

T

0

0

2

==== ππππ

ω

ω

ω

ω

- okres drgań własnych

T

====

2

ππππ

ω

ω

ω

ω

- okres drgań wymuszonych

Jeśli stała tłumienia jest bliska zeru, to warunkiem rezonansu jest równość okresów
drgań własnych i siły wymuszającej .

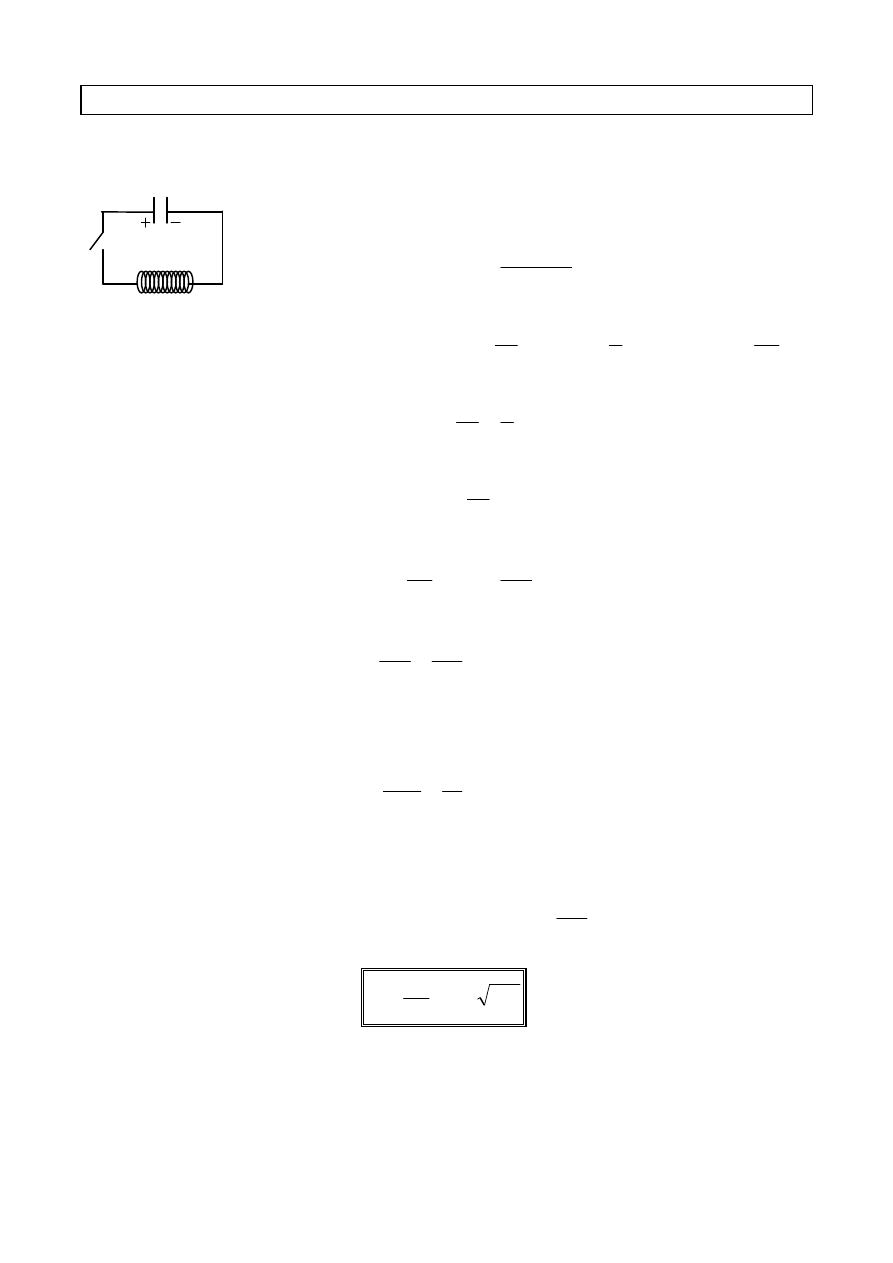
8

DRGANIA ELEKTRYCZNE

Rozważamy obwód LC zawierający naładowany kondensator .Zamknięcie obwodu

wywoła przepływ prądu. Prąd jest wywołany sumą napięć, których
ź

ródłem jest zwojnica i kondensator .

I

U

U

R

l

c

====

++++

IR = U

l

+ U

c

; U

L

dI

dt

l

==== −−−−

; U

q

c

c

====

; I

dq

dt

==== −−−−

R

O

L

dI

dt

q

c

O

≈≈≈≈

⇒

⇒

⇒

⇒

−−−−

++++ ====

q

LC

dI

dt

====

I

dq

dt

LC

d I

dt

==== −−−−

==== −−−−

2

2

d I

dt

LC

I

O

2

2

1

++++

====

Równanie opisujące prąd w takim obwodzie jest analogiczne do równania ruchu
harmonicznego :

d X

dt

k

m

X

O

2

2

++++

====

Natężenie prądu płynącego w obwodzie LC, po zamknięciu tego obwodu
przedstawia funkcja :

((((

))))

I

I

t

====

++++

0

sin

ω

ω

ω

ω

ϕϕϕϕ

;

ω

ω

ω

ω

2

1

====

LC

Okresem tej funkcji jest : T

LC

====

====

2

2

ππππ

ω

ω

ω

ω

ππππ

U

c

U

L