1

Programowanie dynamiczne

Programowanie dynamiczne

jest jedną z

technik

matematycznych,

którą

można

zastosować

do

rozwiązywania

takich

problemów jak:

 zagadnienie dyliżansu,
 zagadnienie finansowania inwestycji,
 optymalizacja

zapasów,

alokacja

zasobów,

 wymiana majątku trwałego itd.

Zagadnienie dyliżansu - poszukiwanie

optymalnej drogi w sieci

Podział całej trasy na etapy, a następnie

sekwencyjne rozwiązywanie, aż do znalezienia
rozwiązania optymalnego. Stosuje się tu tzw.

zasadę optymalności Bellmana

, w myśl

której "

Polityka optymalna ma tę własność,

że niezależnie od początkowego stanu i
początkowej decyzji pozostałe decyzje muszą
stanowić politykę optymalną ze względu na
stan wynikający z pierwszej decyzji

."

2

Oznacza to, iż optymalne rozwiązanie

zagadnienia

z

zakresu

programowania

dynamicznego, ma tę własność, że optymalne
rozwiązanie

dla

k-tego

etapu

jest

równocześnie rozwiązaniem optymalnym dla
etapów k+1, k+2, …N. Tak więc optymalne
rozwiązanie dla etapu pierwszego stanowi
optymalne rozwiązanie dla całego problemu.

Problem rozwiązuje się rozpoczynając

od poszukiwania rozwiązania dla ostatniego
etapu N, a następnie cofając się poszukuje się
rozwiązania dla etapu N-1. Uzyskane w ten
sposób rozwiązanie dla etapów N-1 oraz N
jest optymalne bez względu na to, w jaki
sposób osiągnięto etap N-1. Powtarzając w
powyższy sposób etap po etapie dochodzimy
do rozwiązania optymalnego dla pierwszego
etapu, a więc i dla całego problemu.

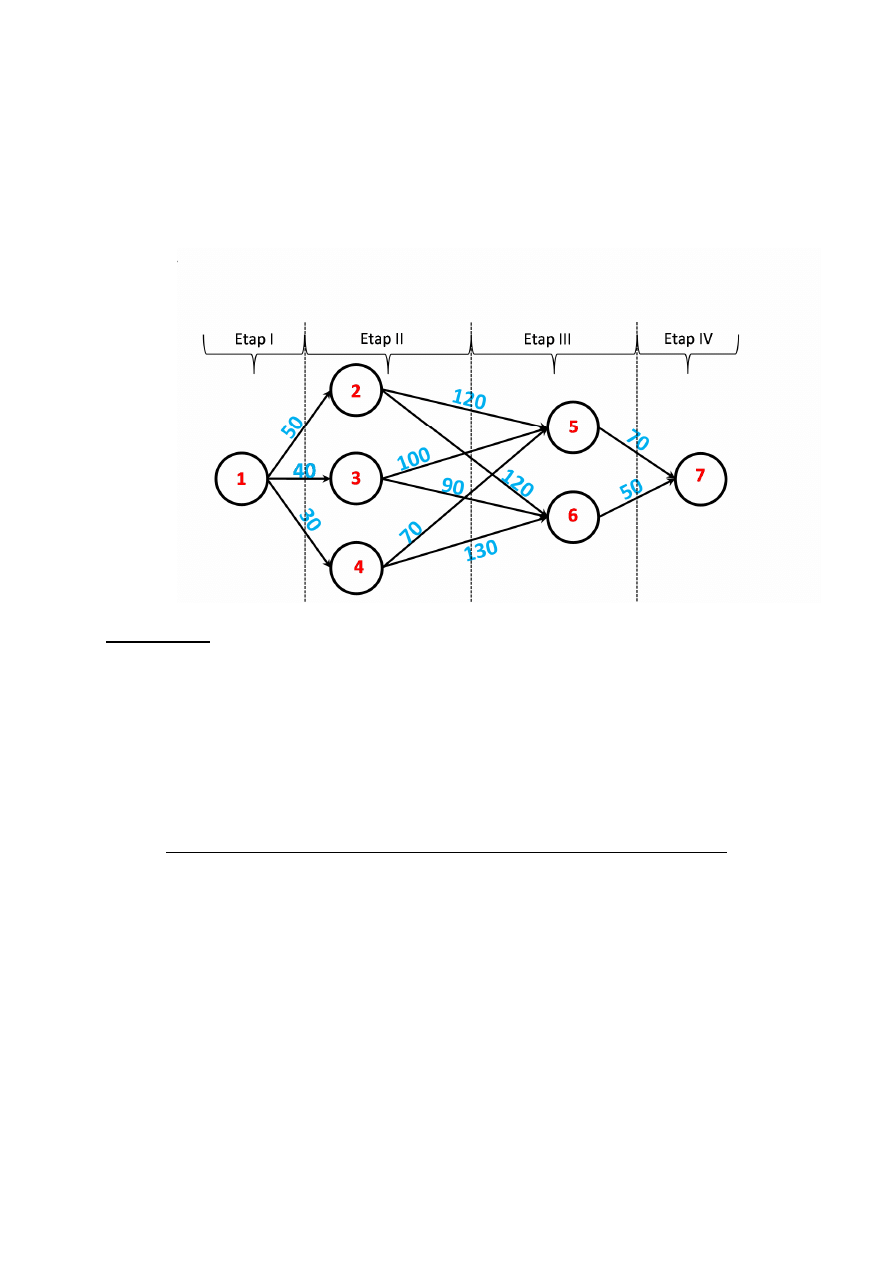
Przykład:

Kowalscy jadą samochodem na urlop nad

morze. Cała trasa została podzielona na kilka
etapów. Odległości między poszczególnymi
miastami, przez które można przejechać jadąc

3

od miejsca zamieszkania 1 do miejsca pobytu
nad morzem 7 są przedstawione poniżej.
Znaleźć najkrótszą trasę przejazdu z miejsca 1
do 7.








Krok I:

Załóżmy, że Kowalscy dotarli do etapu III. W
tej sytuacji odległość od celu wynosi:

od miasta 5:

d

5,7

=

70

km

od miasta 6:

d

6,7

=

50

km

w zależności od tego, w którym z miast w
etapie III zatrzymano się.

4

Krok II:

Cofamy się o jeden etap.

Odległość miast w

etapie II od celu (miasta 7) wynosi:

od miasta 2:

d

2,5

+ d

5,7

= d

2,5,7

120 +

70

= 190 km

d

2,6

+ d

6,7

= d

2,6,7

120 +

50

=

170

km

od miasta 3:

d

3,5

+ d

5,7

= d

3,5,7

100 +

70

= 170 km

d

3,6

+ d

6,7

= d

3,6,7

90 +

50

=

140

km

od miasta 4:

d

4,5

+ d

5,7

= d

4,5,7

70 +

70

=

140

km

d

4,5

+ d

6,7

= d

4,6,7

130 +

50

= 180 km

5

Tak więc: z miasta 2 do 7 należy wybrać

drogę d

2,6,7

=170 km; z miasta 3 do 7 drogę

d

3,6,7

=140 km; z miasta 4 do 7 drogę

d

4,5,7

=140 km.

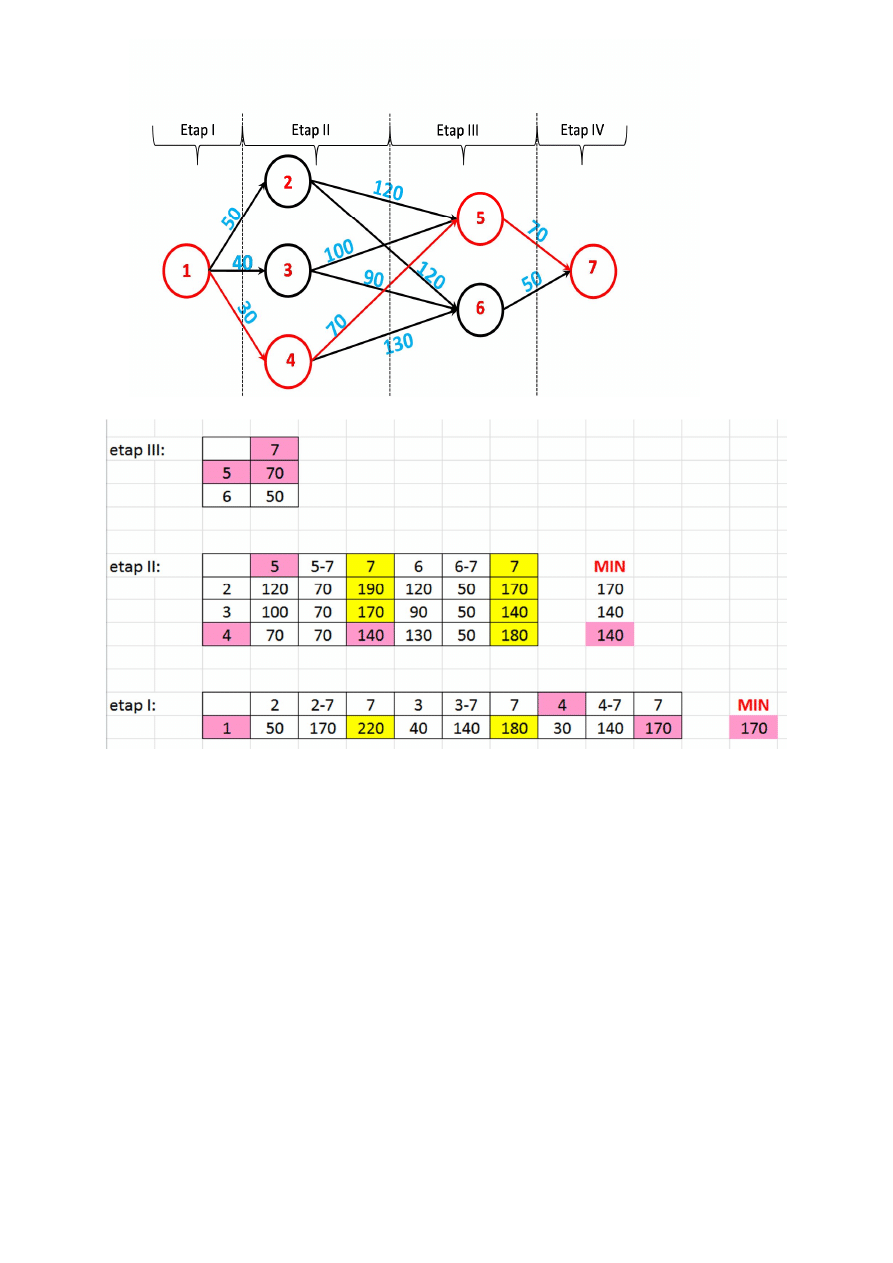
Krok III:

Cofamy się o jeden etap.

Odległość miast w

etapie I od celu wynosi:

od miasta 1:

d

1,2

+ d

2,6,7

= d

1,2,6,7

50 +

170

= 220 km

d

1,3

+ d

3,5,7

= d

1,3,5,7

40 +

140

= 180 km

d

1,4

+ d

4,5,7

= d

1,4,5,7

30 +

140

=

170

km

Z miasta 1 do 7 należy wybrać drogę

d

1,4,5,7

=170 km

.

6

Załóżmy, że pomyliśmy drogi i wyruszając

z miasta 1 zamiast do 4 pojechaliśmy do 3.
Jak należy zaplanować dalszą trasę?

od miasta 3:

d

3,5

+ d

5,7

= d

3,5,7

100 +

70

= 170 km

d

3,6

+ d

6,7

= d

3,6,7

90 +

50

=

140

km

7

Wybieramy drogę

d

3,6,7

liczącą

140

km.

Zagadnienie finansowania inwestycji

Przykład:

Janusz Owsianko parający się produkcją

płatków

śniadaniowych,

postanowił

zainwestować w nową linię technologiczną.
Zamierza w tym celu wziąć kredyt w
wysokości 5 mln zł. Miał do wyboru trzy linie
umownie nazwane A, B i C. Każda z tych linii
daje jednakowe zyski w przeliczeniu na 1 t
płatków. Miesięczne zdolności produkcyjne w
zależności od linii są następujące:

Zdolności

produkcyjne

(w setkach t)

Nakłady (w mln zł)

0

1

2

3

4

5

A

0

1

2

2

3

5

B

0

4

4

5

5

6

C

0

4

5

5

7

9

Jak

należy

rozlokować

nakłady,

aby

zoptymalizować

zdolności

produkcyjne

zakładu?

8

Krok I:

Załóżmy, że jedynym rozwiązaniem jest

zakup linii produkcyjnej C; biorąc pod uwagę
miesięczną zdolność produkcyjną:

Zdolności

produkcyjne

(w setkach t)

Nakłady (w mln zł)

0

1

2

3

4

5

C

0

4

5

5

7

9

należy całą kwotę kredytu, a zatem 5 mln zł
przeznaczyć na zakup tej linii, co da zdolność
produkcyjną na poziomie

9

setek ton.

Krok II:

Załóżmy teraz, że dostępne są dwie linie

produkcyjne C i B i całą kwotę dzielimy
między te linie:

(1)

Dzielimy

5 mln

:

C(5) + B(0) = 9 + 0 = 9
C(4) + B(1) = 7 + 4 =

11

MAX

C(3) + B(2) = 6 + 4 = 10
C(2) + B(3) = 5 + 5 = 10
C(1) + B(4) = 4 + 5 = 9
C(0) + B(5) = 0 + 6 = 6

9

(2)

Dzielimy

4 mln

:

C(4) + B(0) = 7 + 0 = 7
C(3) + B(1) = 5 + 4 =

9

MAX

C(2) + B(2) = 5 + 4 =

9

MAX

C(1) + B(3) = 4 + 5 =

9

MAX

C(0) + B(4) = 0 + 5 = 6

(3)

Dzielimy

3 mln

:

C(3) + B(0) = 5 + 0 = 5
C(2) + B(1) = 5 + 4 =

9

MAX

C(1) + B(2) = 4 + 4 = 8
C(0) + B(3) = 0 + 5 = 5

(4)

Dzielimy

2 mln

:

C(2) + B(0) = 5 + 0 = 5
C(1) + B(1) = 4 + 4 =

8

MAX

C(0) + B(2) = 0 + 4 = 4

(5)

Dzielimy

1 mln

:

C(1) + B(0) = 4 + 0 =

4

MAX

C(0) + B(1) = 0 + 4 =

4

MAX

10

Krok III:

Rozpatrzymy wszystkie możliwe kombinacje
podziału kwoty kredytu

5 mln

na linie C+B

dołączając teraz nakłady na linię A:

Linia

0

1

2

3

4

5

C+B

0

4

8

9

9

11

A

0

1

2

2

3

5

Istnieje 6 wariantów podziału kwoty 5 mln
kredytu pomiędzy linie C+B oraz A, które dają
następujący podział zdolności produkcyjnych:

(C+B)(0) + A(5) = 0 + 5 = 5
(C+B)(1) + A(4) = 4 + 3 = 7
(C+B)(2) + A(3) = 8 + 2 = 10
(C+B)(3) + A(2) = 9 + 2 =

11

MAX

(C+B)(4) + A(1) = 9 + 1 = 10
(C+B)(5) + A(0) = 11 + 0 =

11

MAX

Janusz Owsianko powinien zainwestować:



3 mln

w linie C i B oraz

2 mln

w linię A;

kwotę 3 mln przeznaczoną na linie C i B

11

dzielimy:

2 mln

na C i

1 mln

na B, co

wynika z

kroku II (3)

, czyli ostatecznie:

2 mln

w C i

1 mln

w B,

2 mln

w linię A

,

 bądź: całą kwotę

5 mln

w linie C i B, a

konkretnie

4 mln w C i 1 mln w B

, co

wynika

kroku II (1)

.

W obydwu wariantach dostanie maksymalne
zdolności wytwórcze na poziomie

11

setek t

płatków śniadaniowych w skali miesiąca.

Rozwiązanie w EXCEL:

Dynamiczne.xlsx,

arkusz: Janusz Owsianko

Zastosowanie winqsb:

File

New Problem

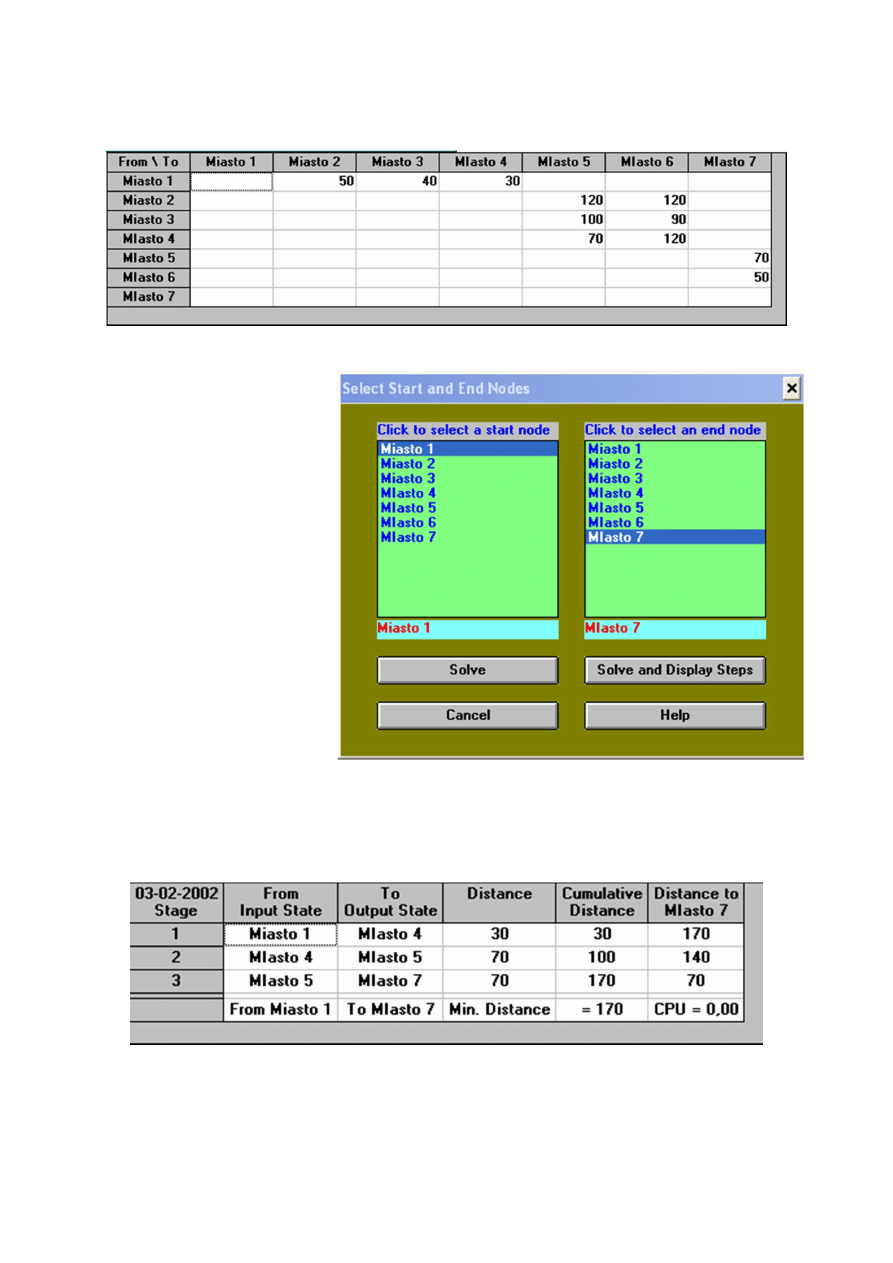
12

Solve and

Analyse

Solve the

Problem

Solve

13

Solve and Display Steps

Przez pomyłkę

pojechaliśmy do

miasta 3:

Results

Perform What

if Analysis

po naciśnięciu

OK:

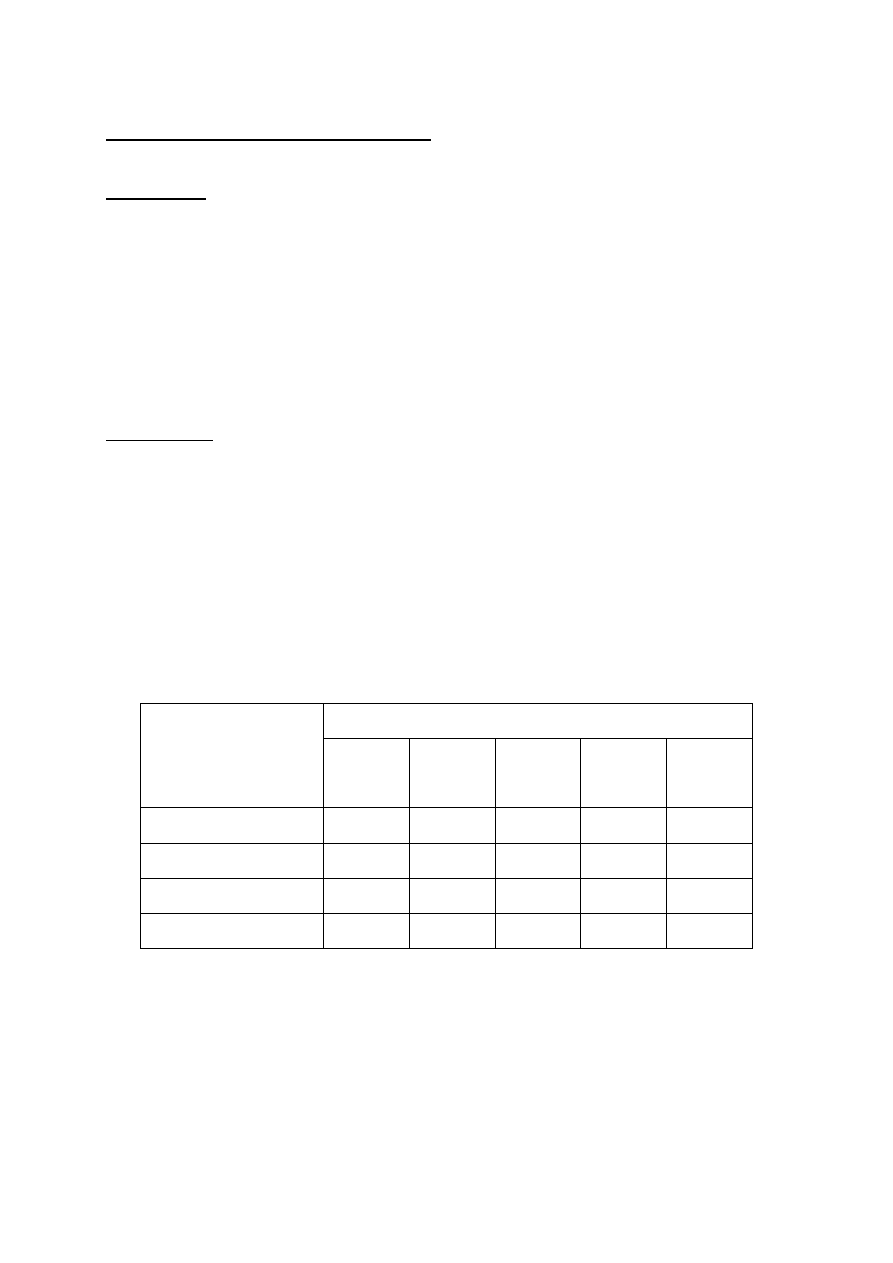
14

Zadania do rozwiązania:

Zad. 1. Kowalscy bardzo nie chcieli wracać do
domu z wczasów, a że pogoda była piękna
postanowili pojechać z miasta 7 do 1 najdłuższą
trasą. Jaka to trasa i ile liczy km?

Rozwiązanie: Trasa: 7-5-2-1; odległość 240 km.

Zad. 2.

Inwestor rozpoczynający pewne zadanie

inwestycyjne,

realizowane

za

pomocą

czterech

programów inwestycyjnych, które umownie nazwiemy
I, II, III i IV musi podjąć decyzję bazując wyłącznie na
kosztach jednostkowych (w tys. zł) wiążących się z
każdym z programów. Koszty te przedstawia poniższe
zestawienie.

Koszty

jednostkowe

(w tys. zł)

Nakłady (w mln)

0

1

2

3

4

I

100

85

75

60

50

II

100

70

62

52

40

III

100

90

80

70

60

IV

100

90

80

80

45

Jakie należy ponieść nakłady inwestycyjne na

poszczególne

programy

kierując

się

kryterium

minimalizacji kosztów jednostkowych?

Rozwiązanie: 4 mln zł na inwestycję IV; minimalny
koszt jednostkowy 45 tys. zł.