Kurs przygotowawczy do egzaminu maturalnego

Poziom podstawowy 2010

ZAJĘCIA NR 3

Zadanie 1
Przedstaw poniższe wyrażenia w postaci potęgi o podstawie a:

a)

( )

=

⋅

a

a

a

a

6

4

7

2

:

b)

(

)

(

)

=

⋅

⋅

2

3

5

3

2

7

a

a

a

a

c)

( ) ( )

( )

=

⋅

2

3

6

5

2

4

3

: a

a

a

a

d)

(

) ( )

(

)

=

⋅

⋅

⋅

3

2

3

5

2

3

4

3

a

a

a

a

a

Zadanie 2
Oblicz:

a)

=

⋅

75

3

g)

=

⋅

3

27

m)

=

⋅

18

8

b)

=

⋅

24

6

h)

=

⋅

5

45

n)

=

⋅

20

5

c)

=

5

:

320

i)

=

3

:

147

o)

=

17

:

68

d)

=

3

:

243

j)

=

5

,

0

:

5

,

12

p)

=

64

:

324

e)

=

9

:

144

k)

=

16

:

36

q)

=

49

:

196

f)

=

⋅

3

3

6

36

l)

=

3

27

17

4

r)

=

3

8

:

125

Zadanie 3
Usuń niewymierność z mianownika:

a)

3

2

5

b)

2

7

3

c)

3

2

3

−

d)

1

2

4

−

e)

1

3

6

+

f)

1

5

8

+

g)

7

3

7

2

1

−

−

h)

2

5

6

−

i)

3

7

12

−

j)

2

7

7

2

3

−

−

Zadanie 4
Uprość wyrażenia (wskazówka: usuń niewymierność z mianownika):

a)

=

+

2

2

2

2

b)

=

+

+

1

3

2

7

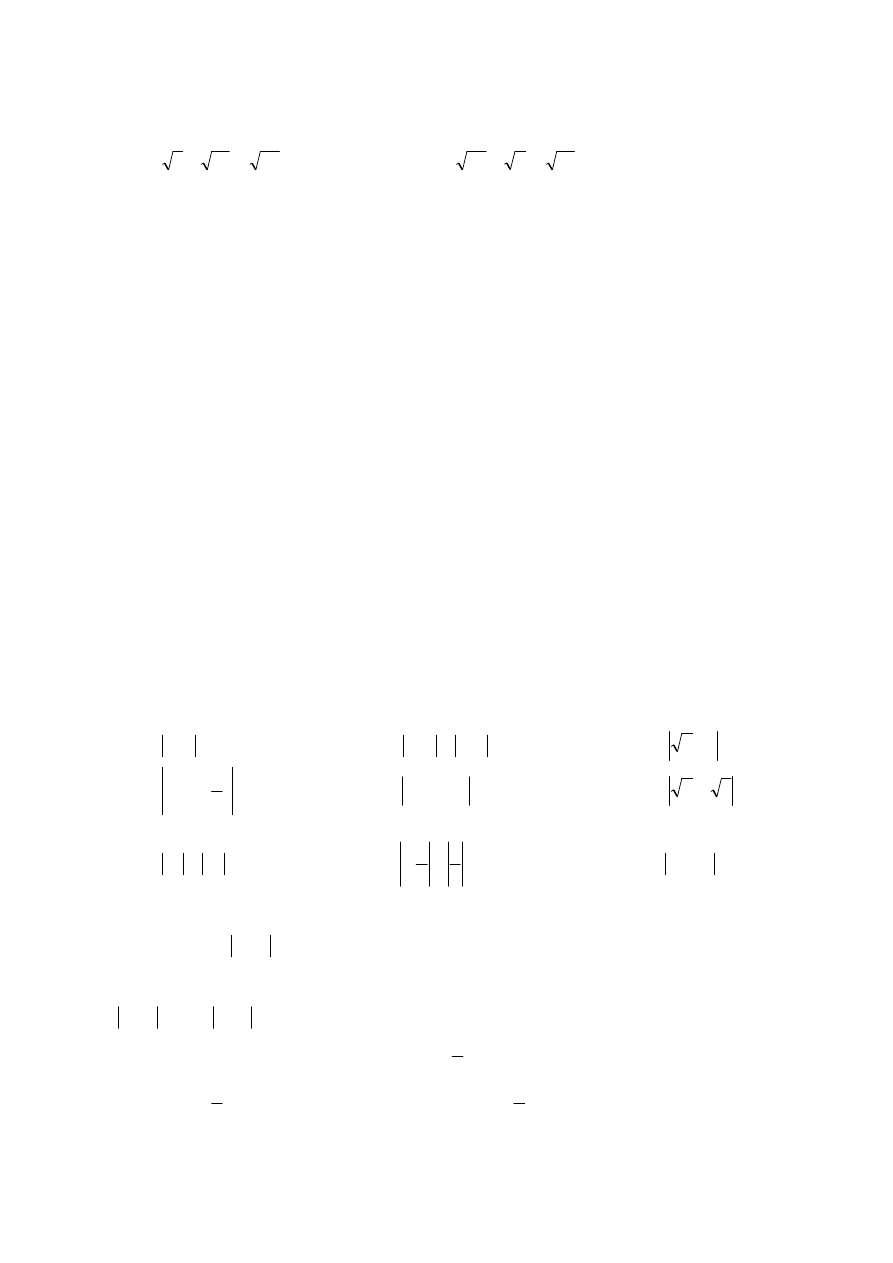
Zadanie 5
Wykaż prawdziwość równości:

a)

50

18

8

=

+

b)

3

3

3

16

2

54

=

−

Zadanie 6
Każdą z liczb wypisanych poniżej zapisz w postaci potęgi liczby 2 (jak w przykładzie):

a)

1

2

2

=

e) 32 =

b)

=

4

f) 64 =

c)

8 =

g) 128 =

d)

16 =

h) 256 =

Zadanie 7

a)

W jednym z mórz jest około

2

10

05

,

2

⋅

gatunków ryb. Zapisz liczbę gatunków bez

użycia notacji wykładniczej.

b)

Merkury znajduje się w odległości 57 900 000 km od Słońca. Zapisz tę odległość w

notacji wykładniczej.

c)

Polskę zamieszkuje około

7

10

9

,

3

⋅

ludzi. Ile milionów ludzi mieszka w Polsce?

(Wskazówka: Najpierw zapisz bez użycia notacji wykładniczej)

Zadanie 8
Zaznacz na osi liczbowej zbiór tych liczb x, których odległości od liczby 2 są:

a)

równe 3,

d) większe od 4,

b)

mniejsze od 1,

e) nie mniejsze niż 2.

c)

mniejsze lub równe 3,

Zadanie 9
Oblicz:

a)

=

−

14

d)

=

−

−

−

14

21

g)

=

−

1

2

b)

=













−

−

2

1

2

e)

( )

=

−

−

1

5

0

h)

=

−

3

2

c)

=

−

−

1

45

f)

=

−

−

5

1

5

2

i)

=

−

7

2

π

Zadanie 10
Oblicz wartość

4

2

2

−

+

x

dla:

Przykład: a) x = 0 [oznacza to, że w miejsce x wstawiamy 0, czyli:]

0

4

2

2

4

2

0

2

4

2

2

=

−

⋅

=

−

+

=

−

+

x

b)

2

−

=

x

d)

2

1

3

−

=

x

c)

6

1

2

−

=

x

e)

4

1

10

−

=

x

Zadanie 11
Zaznacz na osi liczbowej zbiór tych liczb x, które spełniają warunki:

a)

7

=

x

b)

4

−

=

x

c)

2

3

≤

+

x

d)

5

1

>

−

x

Zadanie 12
Rozwiąż równania:

a)

3

=

y

b)

5

−

=

−

y

c)

13

4

=

+

x

d)

8

6

=

−

x

e)

14

6

=

+

y

f)

18

2

=

x

Zadanie 13
Rozwiąż nierówność:

a)

5

<

a

b)

7

≥

x

c)

1

>

x

d)

7

5

>

−

x

e)

1

2

≥

+

x

f)

2

1

<

+

y