Uniwersytet Jana
Kochanowskiego w Kielcach

Bezrobocie wśród kobiet i mężczyzn w województwie małopolskim w
latach 2010 – 2014.

Oświadczam, że niniejsza praca została wykonana samodzielnie:

2015

Prezentacja danych statystycznych

Problematyka, która zajmiemy się w niniejszym projekcie, dotyczy osób (kobiet i mężczyzn)
pozostających

bez

pracy

w

latach

2010-

2014

w

województwie

małopolskim.

Dane są zaczerpnięte z Głównego Urzędu Statystycznego.
Zbiorowość statystyczna obejmuje 120 danych. Została ona podzielona na dwa zbiory. Za kryterium
podziału przyjmujemy podział ze względu na płeć. Zbiory są równoliczne i obejmują 60 kobiet i 60
mężczyzn będących bez pracy. Zbiorowość jest wielowymiarowa.
Jednostkę statystyczną będziemy charakteryzować za pomocą dwóch własności. Jednostką
statystyczną jest zatem liczba kobiet i mężczyzn pozostająca bez pracy w województwie małopolskim
w latach 2010 – 2014.
Podczas analizy danych posłużymy się dwoma cechami statystycznymi: cechą ilościową oraz cechą
jakościową. Cechą ilościową będzie tu liczba bezrobotnych, natomiast cechą jakościową płeć. Cechą
statystyczną zatem jest liczba bezrobotnych kobiet i mężczyzn w poszczególnych miesiącach w latach
2010 – 2014.
Do opracowania i analizy danych został wykorzystany program R oraz arkusz kalkulacyjny Microsoft
Excel.

R

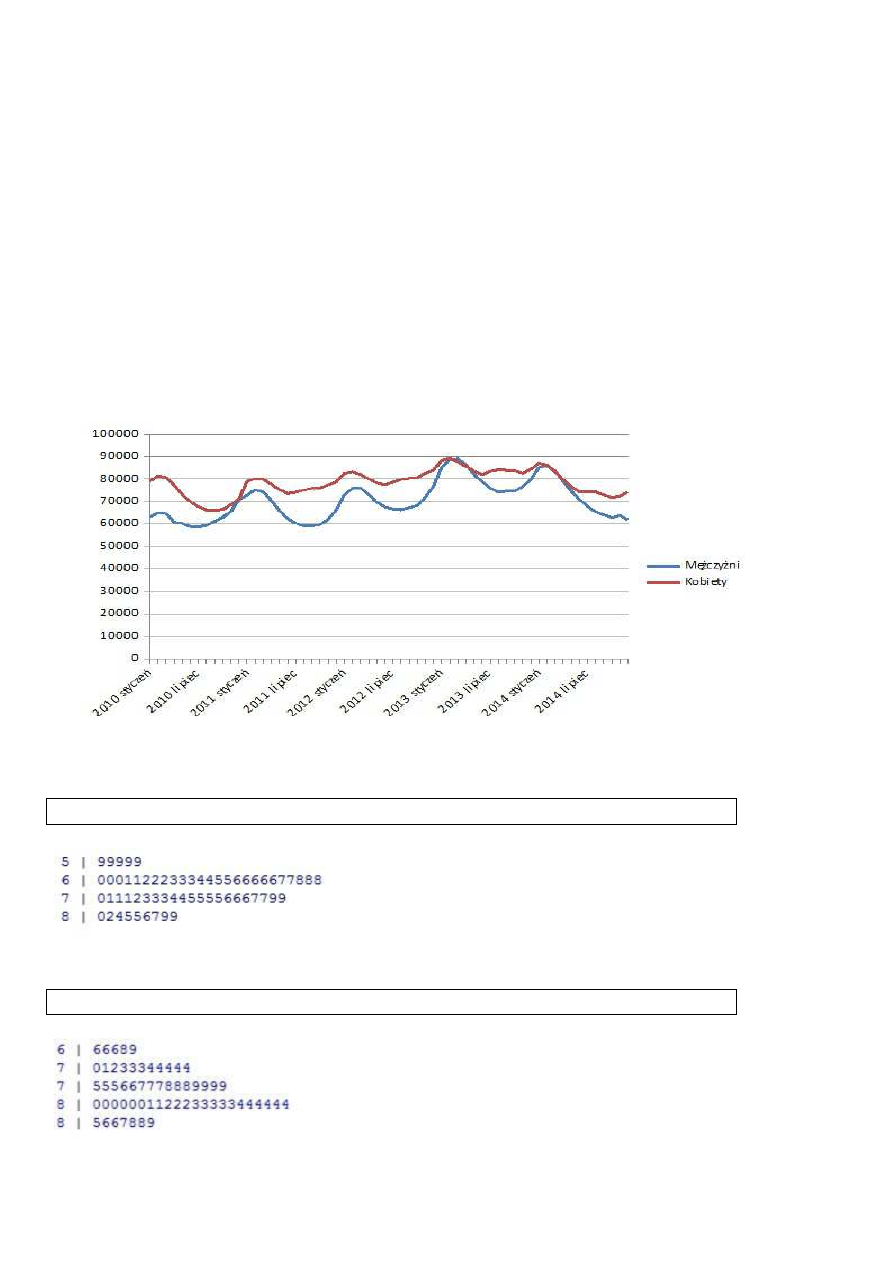
ysunek 1. Graficzna prezentacja danych. Źródło: obliczenia własne.

stem(M, scale=0.5)

R

ysunek 2. Wykres łodyga i liście dla bezrobotnych mężczyzn. Źródło: obliczenia własne.

stem(K, scale=0.5)

R

ysunek 3.Wykres łodyga i liście dla bezrobotnych kobiet. Źródło: obliczenia własne.

R

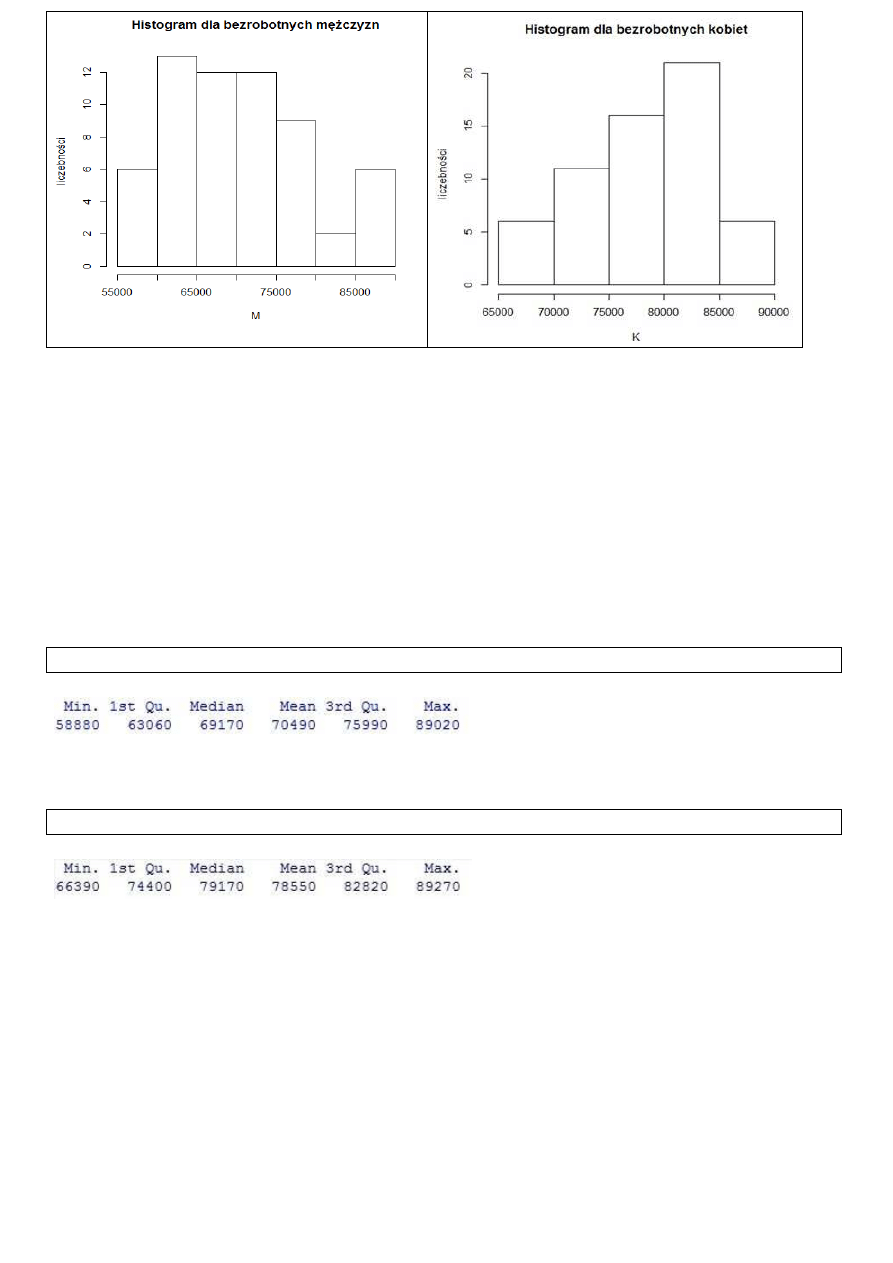
ysunek 4. Histogramy przedstawiający liczbę bezrobotnych mężczyzn po lewej oraz liczbę bezrobotnych kobiet po prawej .

Źródło: obliczenia własne.

Miary położenia
Do miar położenia zaliczymy: wartość minimalną i maksymalną, średnią z próby, medianę kwartyle
oraz mode (dominantę).
W programie R za pomocą funkcji

summary obliczymy podstawowe miary położenie dla

analizowanych danych. Graficznym odpowiednikiem funkcji summary jest wykres pudełkowy, który
zostanie przedstawiony poniżej.

Funkcja summary przedstawiają miary położenia danych z próby, dotyczących liczby mężczyzn
będących bez pracy.

summary(M)

Funkcja summary przedstawiają miary położenia danych z próby, dotyczących liczby kobiet będących
bez pracy.

summary(K)

R

ysunek 5. Wykresy pudełkowe przedstawiające miary położenia danych z próby, dotyczących liczby kobiet i mężczyzn

będących bez pracy.

Na podstawie analizy wykresu pudełkowego, można stwierdzić, że w grupie mężczyzn jest większe
rozproszenie

liczby

osób

bezrobotnych

w

poszczególnych

miesiącach

w

latach

2010 – 2014. Badane grupy charakteryzują się brakiem wartości odstających. Zauważamy, że
minimalna ilość bezrobotnych jest dużo niższa wśród mężczyzn niż wśród kobiet. Maksymalna liczba
osób bezrobotnych wśród kobiet i mężczyzn jest zaś porównywalna.

1. Wartość minimalna i maksymalna.
Zbadamy najmniejszą i największą liczbę bezrobotnych wśród kobiet i mężczyzn w latach
2010 – 2014.
Najmniej mężczyzn pozostających bez pracy było w lipcu 2010 roku. Liczba bezrobotnych mężczyzn
była równa 58880. Z kolei największe bezrobocie wśród mężczyzn odnotowuje się
w marcu 2013 roku, w którym to ilość bezrobotnych mężczyzn wzrosła do 89020 osób.
Wśród kobiet najmniejsze bezrobocie można odnotować w sierpniu 2010 roku. Bez pracy
pozostawało wówczas 66390 kobiet. Najwięcej kobiet nie pracowało w lutym 2013 roku, tj. 89270
kobiet.
Zauważamy, że bezrobocie wśród kobiet w województwie małopolskim w latach 2010 – 2014 jest
wyższe niż wśród mężczyzn. Zarówno minimalna, jak i maksymalna ilość bezrobotnych wśród kobiet
przewyższ liczbę bezrobotnych mężczyzn.
2. Średnia z próby
Zbadamy wokół jakiej wartości centralnej grupują się pomiary dotyczące ilości kobiet i mężczyzn
pozostających bez pracy.
Z powyższego wynika, że średnio 70490 mężczyzn pozostawało bez pracy w latach 2010 – 2014.
Wśród kobiet w latach 2010 – 2014 przeciętnie nie pracowało 78550 osób w wieku produkcyjnym.
Z powyższej analizy wynika, że średnio więcej kobiet pozostaje bez pracy niż mężczyzn.

3. Mediana
Mediana to środkowa wartość pomiarowa. Wyznaczymy ją dla poszczególnych jednostek
statystycznych.
Z powyższych rozważań wynika, że co najmniej połowa bezrobotnych mężczyzn była nie większa niż
69166 osób i jednocześnie co najmniej połowa była nie mniejsza niż 69166 osób.
W badanym okresie co najmniej połowa liczby kobiet pozostających bez pracy była nie większa niż
79171 osób i jednocześnie co najmniej połowa była nie mniejsza niż 79171 osób.
W badanym okresie środkowa wartość pomiarowa jest dużo niższa u mężczyzn, aniżeli u kobiet.

4. Kwartyle
W badanym okresie co najmniej 25 % liczby bezrobotnych mężczyzn było nie więcej niż 58880 osób i
jednocześnie co najmniej 75 % liczby mężczyzn bez pracy było nie mniej niż 58880 osób.
Co najmniej 75% liczby mężczyzn będących bez pracy jest nie więcej niż 75990 osób i równocześnie
co najmniej 25% liczba bezrobotnych w badanej grupie jest nie mniejsza niż 75990 osób.
Co najmniej 25 % liczby kobiet nie posiadających zatrudnienia było nie więcej niż 66390 osób i
jednocześnie co najmniej 75 % liczby kobiet bez pracy było nie mniej niż 66390 osób.
Co najmniej 75% liczby kobiet pozostających bez pracy jest nie więcej niż 82820 osób i równocześnie
co najmniej 25% jest nie mniej niż 82820 osób.
Zauważamy, że w badanych okresach liczba kobiet pozostających bez pracy przewyższa liczbę
mężczyzn bez zatrudnienia. Stwierdzamy że w województwie małopolskim w latach 2010 – 2014
liczba bezrobotnych kobiet była sporo większa niż liczba bezrobotnych mężczyzn.

5. Moda (Dominanta)
modalna(M)
[1] 73240
modalna(K)
[1] 82671

Najczęściej występującą wartością w próbie mężczyzn jest wartość 73240. Oznacza to, że w latach
2010 – 2014 najczęściej odnotowywano właśnie taką liczbę mężczyzn pozostających bez
zatrudnienia.
Wśród kobiet wartością dominującą jest wartość 82671. Zatem w badanym okresie najczęściej
odnotowywano taką liczbę kobiet będących bez pracy.
Zarówno wśród mężczyzn, jak i kobiet występuje jedna wartość dominująca. Mamy zatem do
czynienia z rozkładem jednomodalnym.
3. Miary rozproszenia
Miary rozproszenia to kolejna podstawowa grupa służąca do opisu danych z próby. Miary
rozproszenia wykorzystywane są do określenia rozkładu wartości zmiennej wokół wartości
centralnej np. średniej. Do miar rozproszenia zaliczamy takie statystyki jak: wariancję, odchylenie
standardowe, rozstęp z próby, współczynnik zmienności i odchylenie ćwiartkowe.

1. Wariancja z próby
Wariancja informuje nas o tym jak bardzo wartości analizowanego przez nas zbioru rozrzucone są
wokół średniej. Interpretacja wariancji jest następująca: im wyższa wartość wariancji, tym większe
rozproszenie wyników.
Wariancja w grupie bezrobotnych mężczyzn wynosi 72371191. Wśród grupy kobiet nie mających
zatrudnienia wariancja jest równa 3247504. Porównując wartości w obu analizowanych grupach
stwierdzamy jednoznacznie, że wartość wariancji jest zdecydowanie większa w grupie mężczyzn.
Oznacza to, że ta analizowana grupa wykazuje większe rozproszenie danych, tzn. większą
różnorodność dotyczącą liczby mężczyzn bez pracy w poszczególnych miesiącach w analizowanym
okresie.
2. Odchylenie standardowe z próby
Odchylenie standardowe to jedna z miar dzięki której możemy zbiór naszych danych
scharakteryzować pod kątem zróżnicowania wyników wokół centralnego punktu rozkładu.
Odchylenie standardowe informuje nas jak bardzo wartości jakieś zmiennej są rozrzucone wokół
średniej. Wysokie wartości odchylenia standardowego świadczą o dużym rozproszeniu wyników
wokół średniej.
Średnie bezrobocie wśród mężczyzn wynosi 70490 osób na miesiąc. Odchylenie standardowe
wykazuje, że bezrobocie wśród analizowanej grupy różni się od średniej liczby bezrobotnych o 8507
osób.
Średnia liczba bezrobotnych kobiet w analizowanym okresie jest równa 78550 osób/ miesiąc.
Odchylenie standardowe pokazuje, że bezrobocie wśród kobiet odchyla się od wartości średniej o

±

¿

5698 osób.
Zauważamy, że większe odchylenie standardowe wykazuje grupa bezrobotnych mężczyzn. Oznacza
to, że dane (ilość bezrobotnych mężczyzn) są bardziej rozproszone.
3. Rozstęp z próby
Rozstęp to różnica między największą i najmniejszą wartością występującą w analizowanym zbiorze
danych (X

max

– X

min

).

Wśród mężczyzn będących bez zatrudnienia rozstęp jest równy 30134. Jest to liczba, która wyraża
różnicę między największą a najmniejszą liczbą mężczyzn bez zatrudnienia w poszczególnych
miesiącach w latach 2010 – 2014.
U kobiet rozstęp jest równy wartości 22883. Wyraża to różnicę między największą a najmniejszą
liczbą bezrobotnych kobiet w danym okresie.
Z przeanalizowanych danych wynika, że większa wartość rozstępu jest populacji męskiej niż żeńskiej.
Oznacza to, że im większa wartość rozstępu tym większe rozproszenie wokół średniej. Możemy
stwierdzić, że wśród mężczyzn było małe i duże bezrobocie, gdyż rozstęp jest tutaj większy.
Natomiast wśród kobiet liczba bezrobotnych była zbliżona do średniej.
4. Współczynnik zmienności
Współczynnik zmienności jest ilorazem zmienności danej cechy – odchylenia standardowego i
średniej wartości tej cechy. Najczęściej wyrażany w procentach. Współczynnik zmienności jest bardzo
przydatny, kiedy chcemy porównać zróżnicowanie jakieś cechy z dwóch różnych zbiorów.
Współczynnik zmienności wśród bezrobotnych mężczyzn jest równy 12%. U kobiet będących bez
pracy współczynnik wykazuje wartość 7%. Zarówno odchylenia standardowe, jaki wartości średniej
w obu grupach różnią się znacząco. Mimo wszystko obie grupy wykazują małą zmienność.
5. Odchylenie ćwiartkowe
Odchylenie ćwiartkowe opiera się na medianie i kwartylach, a nie na średniej. Odchylenie ćwiartkowe
jest połową różnicy pomiędzy trzecim i pierwszym kwartylem. Z tego też faktu, odchylenie
ćwiartkowe oblicza zmienność jedynie połowy zebranych wyników, pomiędzy pierwszym i trzecim

kwartylem, czyli pomiędzy 25% i 75% wyników uszeregowanych od najniższej od najwyższej
wartości.
Odchylenie ćwiartkowe dla grupy mężczyzn bez zatrudnienia wynosi 6462. Oznacza to, że przeciętne
odchylenie 50% środkowych jednostek odchyla się o tą wartość od mediany. W grupie kobiet
odchylenie ćwiartkowe jest niższe i wynosi 4210. Stwierdzamy, że przeciętne odchylenie 50%
środkowych jednostek wśród kobiet bez pracy odchyla się o tą wartość od mediany.
6. Rozstęp międzykwartlowy
Rozstęp międzykwartylowy podaje długość odcinka, na którym leży 50% środkowych wartości w
uporządkowanej niemalejąco próbie.
W grupie mężczyzn rozstęp międzykwartlowy jest równy 12925, natomiast w grupie kobiet 8419.
4. Miary kształtu rozkładu
Miary kształtu rozkładu to jedna z trzech grup statystyk opisowych. Za pomocą miar kształtu
rozkładu, czyli skośności i kurtozy, jesteśmy w stanie opisać kształt rozkładu analizowanych przez
nas zmiennych, cech.

Skośność
Skośność to statystyka określająca asymetrię rozkładu analizowanej zmiennej, jedna z dwóch (obok
kurtozy) miar kształtu rozkładu. Skośność informuje nas o tym jak wyniki danej zmiennej kształtują
się wokół średniej. Współczynnik skośności dla rozkładu normalnego przyjmuje wartość „0” – brak
asymetrii rozkładu, rozkład jest idealnie symetryczny. Współczynnik skośności powyżej „0” świadczy,
że rozkład jest prawoskośny (dodatnioskośny), a wyniki poniżej „0” mówią nam, że mamy do
czynienia z rozkładem lewoskośnym (ujemnoskośnym)
Zauważamy, że w grupie mężczyzn bez pracy współczynnik skośności o wartości 0.4838432 jest
większy od 0 (0.4838432 > 0). Mamy zatem do czynienia z rozkładem prawoskośnym. Wyraźnie
widać, że w grupie mężczyzn występuje więcej wartości niskich niż wysokich.
U kobiet wartość współczynnika skośności jest ujemna (- 0.3407176 < 0). Oznacza to, że mamy do
czynienia z rozkładem lewoskośnym. W związku czym w grupie kobiet występuje więcej wartości
wysokich aniżeli niskich.
Kurtoza
Kurtoza to miara zagęszczenia (koncentracji) wyników wokół wartości centralnej. Kurtoza w
rozkładzie normalnym przyjmuje wartość „0”. Jeśli wartość tej statystyki jest większa od zera
wówczas mamy do czynienia z rozkładem leptokurtycznym (wysmukłym). Jeśli kurtoza jest mniejsza
od

zera

nasz

rozkład

jest

rozkładem

platykurtycznym

(spłaszczonym).

Kurtoza dostarcza nam informacji jak dużo uzyskanych przez nas wyników jest zbliżonych do
średniej.
W analizowanej grupie mężczyzn współczynnik kurtozy jest ujemny (- 0.8002988). Mamy zatem do
czynienia z rozkładem spłaszczonym . Podobnie jest w grupie kobiet. Współczynnik kurtozy jest
mniejszy od 0 i wynosi (– 0.5820252). Oznacza to, że w obu analizowanych grupach jest dużo
wyników (liczebność osób bezrobotnych) przyjmujących wartości skrajne.

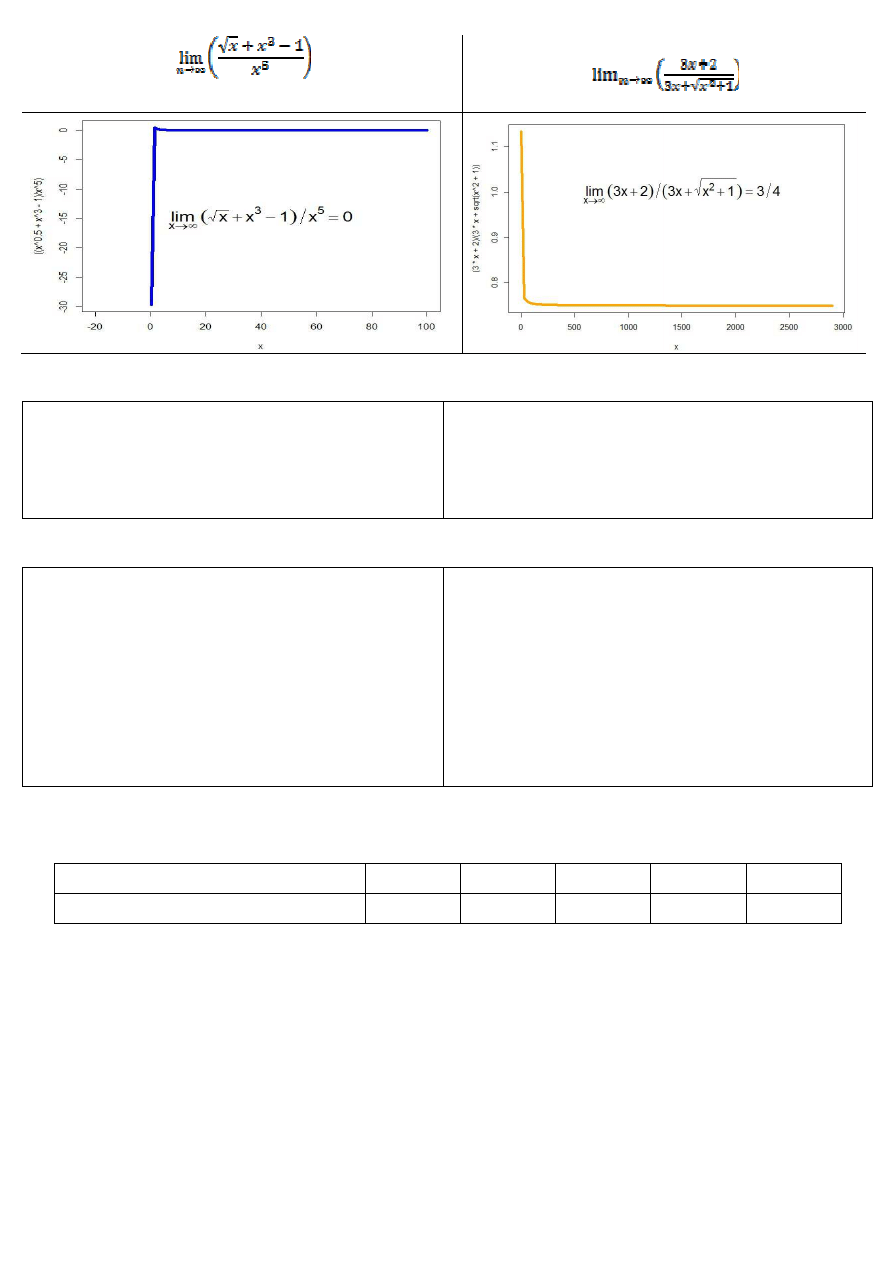
Graficzna prezentacja funkcji w programie R

Rysunek 6. Graficzna prezentacja granicy funkcji w programie R

curve(((x^.5+x^3-1)/x^5), from = -20, to = 100, col="blue" ,

lwd=5)

text(x=40,y=-15,labels=expression(lim((sqrt(x)+x^3-

1)/x^5,x%->%infinity)==0),cex=1.75)

curve((3*x+2)/(3*x+sqrt(x^2+1)), from = 1, to = 2900,

col = "orange", lwd=5)

text(x=1500, y=1, labels = expression(lim((3*x+2) / (3*x+

sqrt(x^2+1)), x%->% infinity )==3/4),cex=1.75)

Funkcje obliczające nasze granice przy użyciu pakietu R.

x=1
while(x<=100){
y=(x^.5+x^3-1)/(x^5)
x=x+0.1}
y

# Zatem nasza granica w plus nieskończoności dąży
do 0.

x=1
while(x<=100){
y=(3*x+2)/(3*x+sqrt(x^2+1))
x=x+0.1}
y

# Zatem nasza granica w plus nieskończoności zbiega
do 0.75

Przedział ufności

Obserwując liczbę awarii w sieci wodno-kanalizacyjnej w ciągu 100 dni w pewnym rejonie miasta otrzymano dane:

Dzienna liczba awarii

0

1

2

3

4

Liczba dni

15

33

25

16

10

Na poziomie ufności 1 - α =0,9 oszacować metodą przedziałową średnią dzienną liczbę awarii w losowo wybranym
dniu.

Elementem populacji generalnej jest dowolny dzień który był, jest , będzie. Cechą dla elementu populacji generalnej
jest liczba awarii sieci wodno-kanalizacyjnej w przeciągu dnia w pewnym rejonie miasta.
Z modeli na przedziały ufności dla średniej mamy, że założenia modelu spełnione są w modelu III, w którym cecha
może mieć dowolny rozkład i wielkość próby powinna być duża ( n>30).
Z treści zadania wynika, że mamy dużą próbę - n=100>30 przedstawioną za pomocą szeregu rozdzielczego. Więc
korzystamy z modelu na przedział ufności dla średniej, w którym cecha może mieć dowolny rozkład i wielkość próby
powinna być duża(n>30).

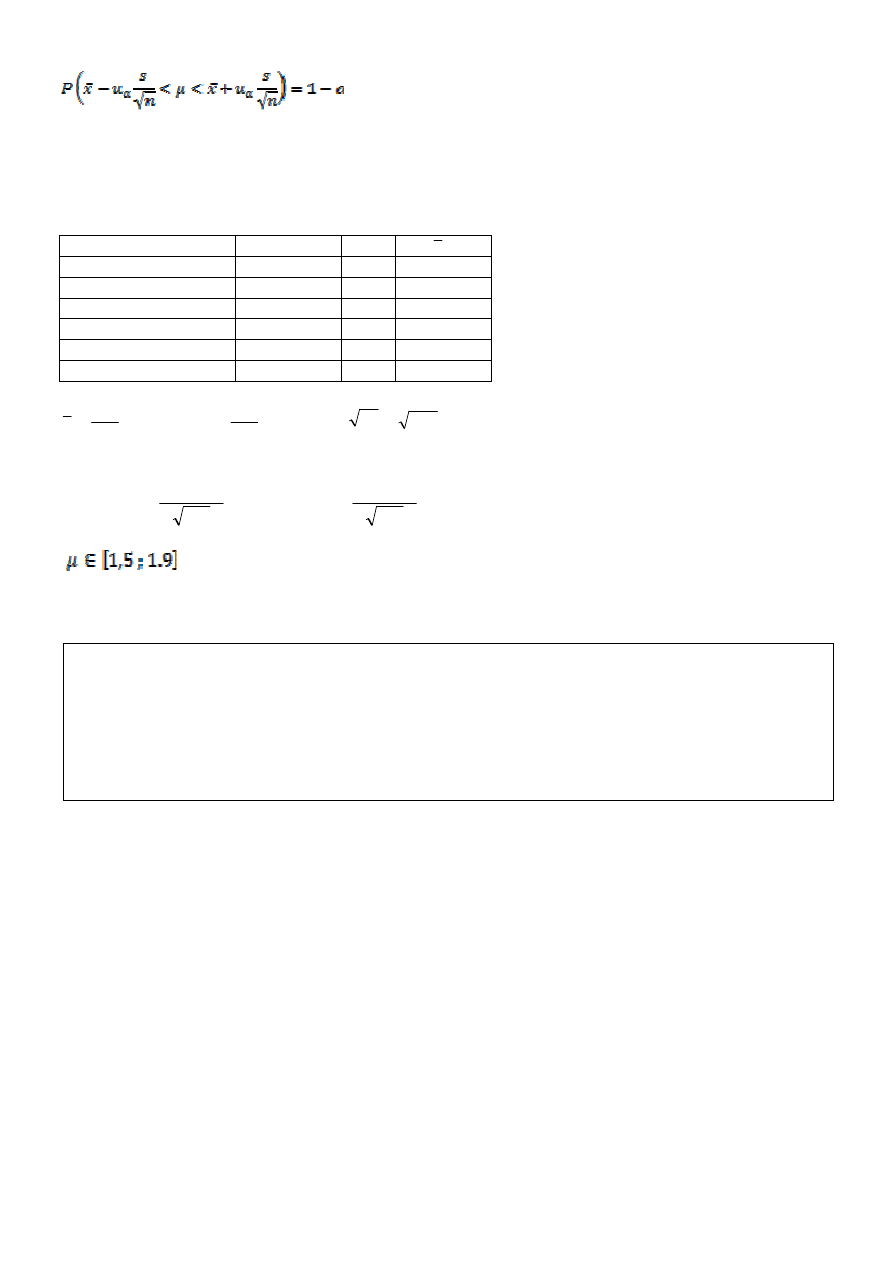
Zatem korzystamy z poniższego wzoru na przedział ufności

Cecha w populacji jest typu skokowego i przyjmuje tylko wartości całkowite. Wartości cech są środkami
przedziałów klasowych.

1

,

0

9

,

0

1

=

⇒

=

−

α

α

Dzienna liczba awarii: x

i

Liczba dni: n

i

x

i

* n

i

(x

i

-

x

)

2

* n

i

0

15

0

43,86

1

33

33

16,63

2

25

50

2.10

3

16

48

26,63

4

10

40

52,44

SUMA:

100

171

141.66

71

,

1

100

171

=

=

x

41

,

1

100

141

2

=

=

s

187434

,

1

41

,

1

2

=

=

=

s

s

Wyznaczamy przedział ufności

100

187434

,

1

645

,

1

71

,

1

100

187434

,

1

645

,

1

71

,

1

+

≤

≤

−

µ

- przedział pokrywa z prawdopodobieństwem

9

,

0

1

=

− α

teoretyczną średnią liczbę awarii w

przeciągu dnia w sieci wodno- kanalizacyjnej w pewnym rejonie miasta.

przedził_ufnosci=function(x,alpha) {
x1=mean(x)-qnorm(1-(alpha/2))*sd(x)/sqrt(length(x))
x2=mean(x)+qnorm(1-(alpha/2))*sd(x)/sqrt(length(x))
paste(c('('),c(x1=x1),c(';'),c(x2=x2),c(')'))
}

przedził_ufnosci(c(rep(0, times=15),rep(1,times=33), rep(2,times=25), rep(3,times=16), rep(4,times=10)) , 0.1)

Praca (projekt) zawiera:
1-skrypt z kodem R
2- pliki .txt z danymi
4-tabele (dwie pomocnicze z kodami)
9-rysunków (trzy bez numeracji)
7- ramek z kodami