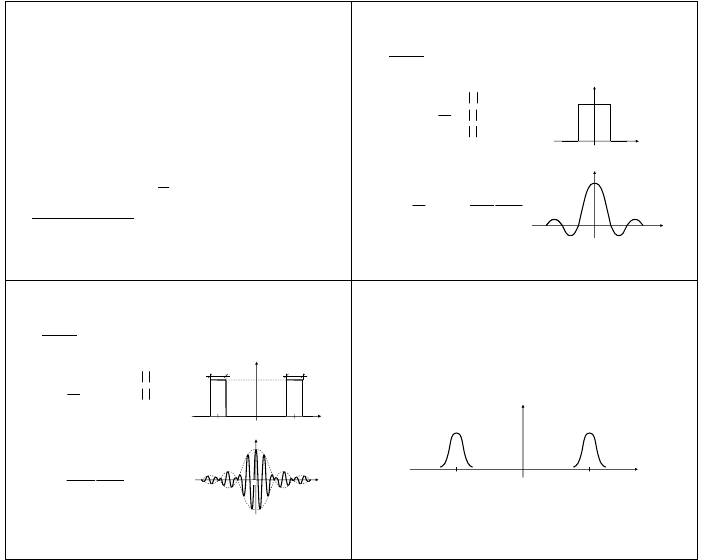
6. Przekształcenie Hilberta, sygnał analityczny.doc, 1/21
SYGNAŁY WĄSKOPASMOWE
1
Sygnały o ograniczonej szerokości widma
• reprezentację sygnału za pomocą sygnału analitycznego można wprowadzić dla szerokiej
klasy sygnałów, jest ona jednak szczególnie użyteczna w odniesieniu do sygnałów
wąskopasmowych
• sygnały, których widma są różne od zera jedynie w pewnym przedziale o skończonej
długości, nazywamy sygnałami o ograniczonej szerokości widma
• jeżeli
Γ jest skończonym przedziałem pulsacji, wówczas widmo sygnału o ograniczonej
szerokości można zapisać w postaci
( )
Γ
∈
ω
≠
ω
dla
0
X
( )
Γ
∉
ω
=
ω
dla
0
X
• ogólny model matematyczny sygnału o ograniczonej szerokości widma
( )
( )
∫
Γ
ω
ω
ω
π
=
d
e
X
t
x
t
j
2
1
1
opracowano na podstawie [1-5], wersja z dnia 02.10.2014
materiał nie jest pełnym i ścisłym pod względem formalnym opracowaniem poszczególnych tematów, stanowi
jedynie szkielet, wokół którego budowany jest wykład
6. Przekształcenie Hilberta, sygnał analityczny.doc, 2/21
SYGNAŁY WĄSKOPASMOWE (cd)
Przykład 1
idealny sygnał dolnopasmowy (o widmie rzeczywistym)
( )
ω
>
ω
ω
=
ω
ω
<
ω
=
ω
m
m
m
X
X
X
dla
dla
dla
0
2
0
0
czasowa postać sygnału
( )
t
t
X
d
e
X
t
x
m
m
m
t
j
m
m
ω
ω
π
ω
=
ω
π
=
∫
ω
ω
−
ω
sin
2
0
0
0
-π/ω
m
π/ω
m
-2π/ω
m
X
0
ω
m
/π
2π/ω
m
x(t)
t
0
X
0
-ω
m
ω
m
ω
X(ω)
6. Przekształcenie Hilberta, sygnał analityczny.doc, 3/21
SYGNAŁY WĄSKOPASMOWE (cd)
Przykład 2
idealny sygnał środkowopasmowy (o widmie rzeczywistym)
( )
ω
ω
∆
+
ω
=
ω
=
ω
∆
−
ω
ω
∆
+
ω
<
ω
<
ω
∆
−
ω
=
ω
0
2
0
0
0
0
0
0
h
pozostalyc
dla
dla
dla
X
X
X
czasowa postać sygnału
( )
t
t
t
X
t
x
0
0
cos
sin
2
ω
ω
∆
ω
∆
π
ω
∆
=
x(t)
t
0
0
-ω
0
X
0
2∆ω
2∆ω
ω
X(ω)
ω
0
6. Przekształcenie Hilberta, sygnał analityczny.doc, 4/21
SYGNAŁY WĄSKOPASMOWE (cd)
Sygnały wąskopasmowe
• sygnał wąskopasmowy jest szczególną klasą sygnałów o ograniczonej szerokości widma
• sygnał wąskopasmowy – sygnał o widmie skupionym w przedziale pulsacji o szerokości
ω
∆
, w otoczeniu wartości środkowych
0
ω
±
, przy czym
1
/
0
<<
ω
ω
∆
,
0
0
≠
ω
0
ω
- pulsacja podstawowa sygnału
0
-ω
0
ω
0
ω
|X(ω)|
6. Przekształcenie Hilberta, sygnał analityczny.doc, 5/21
SYGNAŁ ANALITYCZNY
• ważnym zagadnieniem w analizie sygnałów, zwłaszcza sygnałów modulowanych, jest
zagadnienie reprezentacji sygnału za pomocą drgania uogólnionego
• koncepcja drgania uogólnionego opiera się na pojęciu sygnału analitycznego
• sygnał rzeczywisty o znanym widmie
( )
ω
X
można przedstawić jednoznacznie jako
sumę dwóch sygnałów, z których każdy zawiera w swoim widmie tylko dodatnie lub
ujemne pulsacje, zatem
( )
( )
( )
( )
∫
∫
∫
∞
ω
∞
−
ω
∞
∞
−
ω
ω
ω
π
+
ω
ω
π
=
ω
ω
π
=
0
0
2
1
2
1
2
1
d
e
X
d
e
X
d
e
X
t
x
t
j
t
j
t
j
funkcja
( )
( )
∫
∞
ω
ω
ω
π
=
0
1
d
e
X
t
z
t
j
x
nazywa się sygnałem analitycznym stowarzyszonym z sygnałem rzeczywistym
( )
t
x
• można wykazać, że pierwsza z całek równa jest
( )
( )
t
z
d
e
X
x
t
j
*
0
1
=
ω
ω
π
∫
∞
−
ω
6. Przekształcenie Hilberta, sygnał analityczny.doc, 6/21
SYGNAŁ ANALITYCZNY (cd)
• skąd wynika związek między sygnałami
( )
t
x
i
( )
t
z
x
( )
( )
( )
[
]
( )
[
]
t
z
t
z
t
z
t
x
x
x
x
Re
2
1
*
=
+
=
• część urojona sygnału analitycznego
( )
( )
[
]
t
z
t
x
x
Im
ˆ
=
nazywa się sygnałem skojarzonym z sygnałem
( )
t
x
• zatem sygnałem analitycznym sygnału
( )
t
x
, nazywanym również postacią analityczną
sygnału
( )
t
x
, jest sygnał zespolony postaci
( )
( )
( )
t
x
j
t
x
t
z
x
ˆ
+
=
6. Przekształcenie Hilberta, sygnał analityczny.doc, 7/21
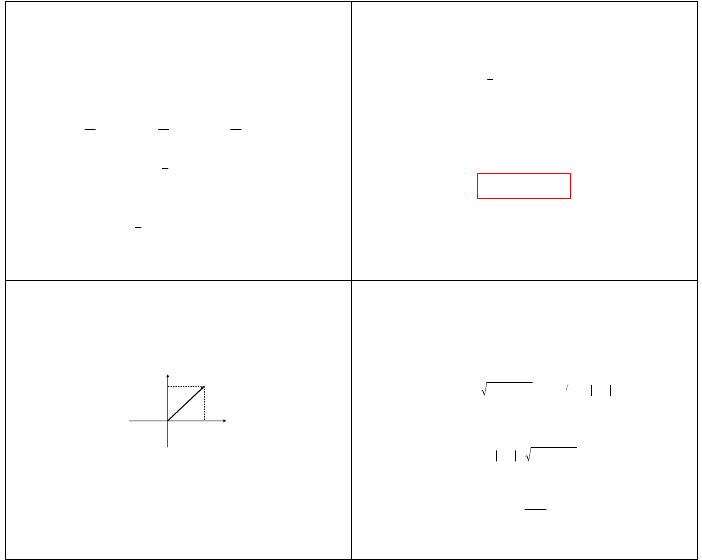
SYGNAŁ ANALITYCZNY (cd)
• sygnał analityczny można przedstawić na płaszczyźnie zmiennej zespolonej jako wektor,
którego moduł i kąt zmieniają się w czasie; rzutem sygnału analitycznego na oś
rzeczywistą w chwili
t
jest wartość sygnału
( )
t
x
w tej chwili
0
xˆ
z
x
x
Im
Re
6. Przekształcenie Hilberta, sygnał analityczny.doc, 8/21
SYGNAŁ ANALITYCZNY (cd)
Amplituda, pulsacja i faza chwilowe sygnału analitycznego
• pojęcie sygnału analitycznego umożliwia uogólnienie na sygnały nieharmoniczne pojęcia
amplitudy, pulsacji i fazy sygnału harmonicznego
• wykładnicza postać sygnału analitycznego
( ) ( )
( )
( )
( )
( ) ( )
[
]
( )
( )
t
z
j
x
t
x
t
x
j
x
x
e
t
z
e
t
x
t
x
t
x
j
t
x
t
z
arg
ˆ
arctg
2
2
ˆ
ˆ
=
+
=
+
=
ostatecznie
( )
( )
( )
t
j
x
e
t
X
t
z
ψ
=
• amplituda chwilowa (obwiednia rzeczywista)
( )
t
X
sygnału rzeczywistego
( )
t
x
(moduł jego sygnału analitycznego)
( )
( )
( )
( )
t
x
t
x
t
z
t
X
x
2
2
ˆ
+
=
=
• pulsacja chwilowa
( )
t
ω
sygnału rzeczywistego
( )
t
x
(pochodna argumentu jego
sygnału analitycznego)
( )
( )
t
t
t
d
d ψ
=
ω

6. Przekształcenie Hilberta, sygnał analityczny.doc, 9/21
SYGNAŁ ANALITYCZNY (cd)
• pojęcie fazy może być również uogólnione na sygnały nieharmoniczne, nie jest to jednak
uogólnienie jednoznaczne; pojęcie fazy chwilowej określa się względem arbitralnie
przyjętej pulsacji
0
ω
• fazą chwilową sygnału rzeczywistego
( )
t
x
, określoną względem pulsacji
0
ω
,
nazywamy funkcję
( )
t
ϕ
, taką że
( )
( )
t
t
t
ϕ
+
ω
=
ψ
0
(wybór wartości
0
ω
jest w zasadzie dowolny, jednak przykładowo dla sygnałów
wąskopasmowych przyjmuje się zwykle pulsację środkową ich widma prawostronnego,
wówczas obwiednia chwilowa
( )
t
X
i faza chwilowa
( )
t
ϕ
sygnału wąskopasmowego
zmieniają się w czasie wolno w porównaniu ze zmianami wartości chwilowej tego sygnału)
6. Przekształcenie Hilberta, sygnał analityczny.doc, 10/21
SYGNAŁ ANALITYCZNY (cd)
przykład
Wyznaczyć amplitudę chwilową, pulsację chwilową oraz fazę chwilową sygnału
harmonicznego
( )
(
)
0
0
cos
ϕ
+
ω
=
t
U
t
x
.
rozwiązanie
można wykazać, że sygnał
( )
t
xˆ
, skojarzony z sygnałem rzeczywistym
( )
(
)
0
0
cos
ϕ
+
ω
=
t
U
t
x
przyjmie postać
( )
(
)
0
0
sin
ˆ
ϕ
+
ω
=
t
U
t
x
zatem postać analityczna sygnału
( )
t
x
( )
( )
( )
(
)
(
)
(
)
( )
t
j
t
j
x
Ue
Ue
t
jU
t
U
t
x
j
t
x
t
z
ψ
ϕ
+
ω
=
=
ϕ
+
ω
+
ϕ
+
ω
=
+
=
0
0
0
0
0
0
sin
cos
ˆ
amplituda chwilowa
( )
( )
U
t
z
t
X
x
=
=
pulsacja chwilowa
( )
( )
(
)
0
0
0
d
d
d
d
ω
=
ϕ
+
ω
=
ψ
=
ω
t
t
t
t
t
faza chwilowa względem pulsacji
0
ω
( )
( )
⇒
ϕ
+
ω
=
ψ
t
t
t
0
( )
( )
0
0
0
0
ϕ
=
ϕ
⇒
ϕ
+
ω
=
ϕ
+
ω
t
t
t
t
6. Przekształcenie Hilberta, sygnał analityczny.doc, 11/21
SYGNAŁ ANALITYCZNY (cd)
Drganie uogólnione
• pojęcie sygnału analitycznego umożliwia wprowadzenie użytecznej w analizie sygnałów
wąskopasmowych reprezentacji sygnałów nieharmonicznych
• dla ustalonej pulsacji
0
ω
sygnał rzeczywisty
( )
t
x
można przedstawić
( )
( )
[
]
( )
( )
[
]
( )
( )
[
]
[
]
t
t
j
t
j
x
e
t
X
e
t
X
t
z
t
x
ϕ
+
ω
ψ
=
=
=
0
Re
Re
Re
ostatecznie
( )
( )
( )
[
]
t
t
t
X
t
x
ϕ
+
ω
=
0
cos
przedstawienie to nosi nazwę drgania uogólnionego
zatem jeśli
0
ω
jest częstotliwością środkową sygnału wąskopasmowego
( )
t
x
to sygnał
taki można traktować jako sygnał oscylacyjny o pulsacji chwilowej oscylującej wokół
pulsacji
0
ω
o zmiennej w czasie amplitudzie
( )
t
X
i fazie chwilowej
( )
t
ϕ
, inaczej
sygnał wąskopasmowy stanowi złożone drganie powstałe jako efekt jednoczesnej
modulacji amplitudy, pulsacji i fazy sygnału harmonicznego o pulsacji
0
ω
• podobnie
( )
( )
[
]
( )
( )
[
]
( )
( )
[
]
t
t
t
X
e
t
X
t
z
t
x
t
j
x
ϕ
+
ω
=
=
=
ψ
0
sin
Im
Im
ˆ
6. Przekształcenie Hilberta, sygnał analityczny.doc, 12/21
SYGNAŁ ANALITYCZNY (cd)
• wykorzystując tożsamość trygonometryczną drganie uogólnione można przedstawić
( )
( )
( )
[
]
( )
( )
( )
( )
( )
( )
t
t
x
t
t
x
t
t
t
X
t
t
t
X
t
t
t
X
t
x
Q
I
0
0
0
0
0
sin
cos
sin
sin
cos
cos
cos
ω
−
ω
=
=
ω
ϕ
−
ω
ϕ
=
ϕ
+
ω
=
podobnie
( )
( )
( )
[
]
( )
( )
( )
( )
( )
( )
t
t
x
t
t
x
t
t
t
X
t
t
t
X
t
t
t
X
t
x
Q
I
0
0
0
0
0
cos
sin
cos
sin
sin
cos
sin
ˆ
ω
+
ω
=
=
ω
ϕ
+
ω
ϕ
=
ϕ
+
ω
=
składowe
( )
( )
( )
t
t
X
t
x
I
ϕ
=
cos
( )
( )
( )
t
t
X
t
x
Q
ϕ
=
sin
nazywane są odpowiednio składową synfazową i składową kwadraturową i stanowią
sygnały wolnozmienne w porównaniu z sygnałem
( )
t
x
6. Przekształcenie Hilberta, sygnał analityczny.doc, 13/21
SYGNAŁ ANALITYCZNY (cd)
• drganie uogólnione można przedstawić również w postaci
( )
( )
( )
[
]
[
]
( )
( )
[
]
( )
[
]
t
j
t
j
t
j
t
t
j
e
t
X
e
e
t
X
e
t
X
t
x
0
0
0
~
Re
Re
Re
ω
ω
ϕ
ϕ
+
ω
=
=
=
• funkcję
( )
( )
( )
t
j
e
t
X
t
X
ϕ
=
~
nazywamy obwiednią zespoloną sygnału
( )
t
x
• przykładowy sygnał harmonicznego
( )
(
)
0
0
cos
ϕ
+
ω
=
t
U
t
x
, o analitycznej postaci
( )
(
)
0
0
ϕ
+
ω
=
t
j
x
Ue
t
z
można przedstawić
( )
( )
[
]
(
)
[
] [
] [
]
t
j
t
j
j
t
j
x
e
X
e
Ue
Ue
t
z
t
x
0
0
0
0
0
~
Re
Re
Re
Re
ω
ω
ϕ
ϕ
+
ω
=
=
=
=
gdzie
0
~
ϕ
=
j
Ue
X
jest amplitudą zespoloną sygnału harmonicznego, zatem obwiednia zespolona
( )
t
X
~
jest
uogólnieniem pojęcia amplitudy zespolonej na sygnały nieharmoniczne
6. Przekształcenie Hilberta, sygnał analityczny.doc, 14/21
SYGNAŁ ANALITYCZNY (cd)
• obwiednię zespoloną można przedstawić w postaci
( )
( )
( )
( )
( )
( )
( )
( )
( )
t
jx
t
x
t
t
jX
t
t
X
e
t
X
t
X
Q
I
t
j
+
=
ϕ
+
ϕ
=
=
ϕ
sin
cos
~
skąd otrzymujemy wyrażenia na obwiednię rzeczywistą
( )
( )
( )
( )
( )
( )
t
x
t
x
t
x
t
x
t
X
t
X
Q
I
2
2
2
2
ˆ
~
+
=
+
=
=
Widmo sygnału analitycznego
• jeżeli sygnał analityczny
( )
t
z
x
posiada widmo
( )
ω
x
Z
, wówczas
( )
( )
∫
∞
∞
−
ω
ω
ω
π
=
d
e
Z
t
z
t
j
x
x
2
1
ponieważ
( )
( )
∫
∞
ω
ω
ω
π
=
0
1
d
e
X
t
z
t
j
x
zatem
( )
( )
<
ω
>
ω
ω
=
ω
0
0
0
2X
Z
x
6. Przekształcenie Hilberta, sygnał analityczny.doc, 15/21
SYGNAŁ ANALITYCZNY (cd)
z liniowości przekształcenia Fouriera wynika
( )
( )
( )
ω
+
ω
=
ω
X
j
X
Z
x
ˆ
gdzie
( )
ω
Xˆ
- widmo sygnału skojarzonego
( )
t
xˆ
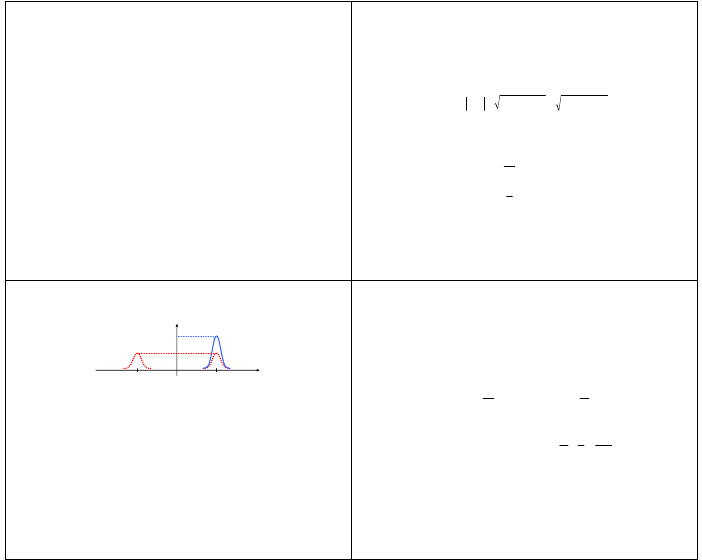
zatem
( )
( )
<
ω
>
ω
ω
=
ω
0
0
0
2X
Z
x
wtedy i tylko wtedy, gdy
( )
ω
X
i
( )
ω
Xˆ
będą związane zależnością
( )
( )
( )
<
ω
ω
>
ω
ω
−
=
ω
0
0
ˆ
jX
jX
X
inaczej
( )
( ) ( )
0
,
sgn
ˆ
≠
ω
ω
ω
−
=
ω
dla
X
j
X
-
ω
0
ω
0
|X(ω)|, |Z
x
(ω)
|
2X
0
X
0
0
ω
|X(ω)|
|Z
x
(ω)
|
6. Przekształcenie Hilberta, sygnał analityczny.doc, 16/21
PRZEKSZTAŁCENIE HILBERTA
• ponieważ widmo sygnału skojarzonego
( )
t
xˆ
jest iloczynem widm sygnału
( )
t
x
i funkcji
( )
ω
− sgn
j
, to sygnał ten jest splotem funkcji
( )
t
x
z pewną funkcją
( )
t
f
, która jest
odwrotną transformatą Fouriera funkcji
( )
ω
− sgn
j
można wykazać, że dla
0
≠
ω
( )
( )
[
]
t
d
e
j
t
f
t
j
π
=
ω
ω
−
π
=
∫
∞
∞
−
ω
1
sgn
2
1
czyli
( )
( ) ( )
( ) ( )
( )
( )
∫
∞
∞
−
τ
τ
−
τ
π
=
π
∗
=
∗
=
∗
=
d
t
x
t
t
x
t
f
t
x
t
x
t
f
t
x
1
1
ˆ
6. Przekształcenie Hilberta, sygnał analityczny.doc, 17/21
PRZEKSZTAŁCENIE HILBERTA (cd)
• można również wyrazić sygnał
( )
t
x
poprzez sygnał
( )
t
xˆ
z wyrażenia
( )
( ) ( )
0
,
sgn
ˆ
≠
ω
ω
ω
−
=
ω
dla
X
j
X
wynika
( )
( ) ( )
0
,
ˆ
sgn
≠
ω
ω
ω
=
ω
dla
X
j
X
zatem
( )
( ) ( )
( ) ( )
( )
( )
∫
∞
∞
−
τ
−
τ
τ
π
=
π
∗
−
=
∗
−
=
∗
−
=
d
t
x
t
t
x
t
f
t
x
t
x
t
f
t
x
ˆ
1
1
ˆ
ˆ
ˆ
wyrażenia
( )
( )
∫
∞
∞
−
τ
τ
−
τ
π
=
d
t
x
t
x
1
ˆ
( )
( )
∫
∞
∞
−
τ
−
τ
τ
π
=
d
t
x
t
x
ˆ
1
stanowią proste i odwrotne przekształcenie Hilberta
6. Przekształcenie Hilberta, sygnał analityczny.doc, 18/21
PRZEKSZTAŁCENIE HILBERTA (cd)
• inny zapis
( )
( )
[ ]
t
x
H
t
x
=
ˆ
( )
( )
[ ]
t
x
H
t
x
ˆ
1
−
=
• sygnał analityczny
( )
( )
( )
( )
( )
[ ]
t
x
jH
t
x
t
x
j
t
x
t
z
x
+
=
+
=
ˆ
• ponieważ
( )
( )
t
t
x
t
x
π
∗
=
1
ˆ
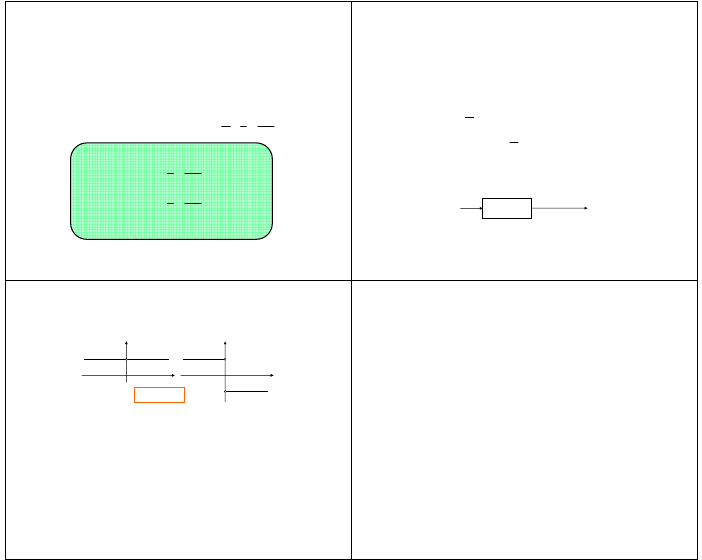
zatem sygnał
( )
t
xˆ
można traktować jako odpowiedź na
sygnał
( )
t
x
filtru o odpowiedzi
( )
t
t
h
π
=
1
oraz transmitancji częstotliwościowej
( )
( )
0
,
sgn
≠
ω
ω
−
=
ω
dla
j
j
H
X(ω)=X(ω) H( jω)
^
X(ω)
x(t)=x(t)∗h(t)
^
x(t)
filtr
kwadraturowy
6. Przekształcenie Hilberta, sygnał analityczny.doc, 19/21
PRZEKSZTAŁCENIE HILBERTA (cd)
filtr kwadraturowy realizuje przesunięcie fazy wszystkich składowych o kąt
°
− 90
w zakresie pulsacji dodatnich i
°
90
w zakresie pulsacji ujemnych, bez zmiany ich
amplitud (filtr ten nazywany jest również filtrem Hilberta)
Właściwości przekształcenia Hilberta
- liniowość
( )
( )
[
]
( )
[
]
( )
[
]
t
x
H
a
t
x
H
a
t
x
a
t
x
a
H
2
2
1
1
2
2
1
1
+
=
+
- transformata Hilberta funkcji parzystej (nieparzystej) jest funkcją nieparzystą (parzystą)
-π/2
arg H( jω)
1
0
ω
|H( jω)|
π/2
0
ω
H( jω)=-jsgn(ω)
6. Przekształcenie Hilberta, sygnał analityczny.doc, 20/21
PRZEKSZTAŁCENIE HILBERTA (cd)
- transformata transformaty
( )
[ ]
{
}
( )
t
x
t
x
H
H
−
=
- ortogonalność
( )
( )
[ ]
(
)
0
,
=
t
x
H
t
x
- identyczność funkcji autokorelacji
( ) (
)
(
)
( )
[ ]
(
)
[
]
(
)
τ
−
=
τ
−
t
x
H
t
x
H
t
x
t
x
,
,
- równość iloczynów skalarnych
( ) ( )
(
)
( )
[
]
( )
[
]
(
)
t
x
H
t
x
H
t
x
t
x
2
1
2
1
,
,
=
- równość energii (lub mocy średniej)
( ) ( )
(
)
( )
[ ]
( )
[ ]
(
)
t
x
H
t
x
H
t
x
t
x
,
,
=
- twierdzenie o splocie
( )
( )
( )
[
]
( )
( )
( )
[
]
t
x
H
t
x
t
x
t
x
H
t
x
t
x
2
1
2
1
2
1
∗
=
∗
↔
∗
( )
( )
( )
[
]
( )
[
]
t
x
H
t
x
H
t
x
t
x
2
1
2
1
∗
−
=
∗

6. Przekształcenie Hilberta, sygnał analityczny.doc, 21/21
BIBLIOGRAFIA
1. Szabatin J.: Podstawy teorii sygnałów. Wydawnictwa Komunikacji i Łączności,
Warszawa, 1982.
2. Szabatin J.: Przetwarzanie sygnałów. Materiały dydaktyczne Politechniki Warszawskiej,
2003,
www.ise.pw.pl/~szabatin
.
3. Baskakow S.I.: Sygnały i układy radiotechniczne. Wydawnictwo Naukowe PWN,
Warszawa, 1991.
4. Gonorowskij I.S.: Radiotechniczeskije cepi i signały. Sowietskoje Radio, Mockva, 1977.
5. Pasko M., Walczak J.: Teoria sygnałów. Wydawnictwo Politechniki Śląskiej,
Gliwice, 1999.
Wyszukiwarka
Podobne podstrony:
3 psyg,st www odblokowany
1 psyg,st www odblokowany
2 psyg,st www odblokowany
4 psyg,st www odblokowany
9 psyg,st www odblokowany
11 psyg,st www odblokowany
7 psyg,st www odblokowany
10 psyg,st www odblokowany
3 psyg,st www odblokowany
1 psyg,st www odblokowany
więcej podobnych podstron