7. Konwersja AC i CA.doc, 1/20
PRZETWORNIK ANALOGOWO-CYFROWY
1
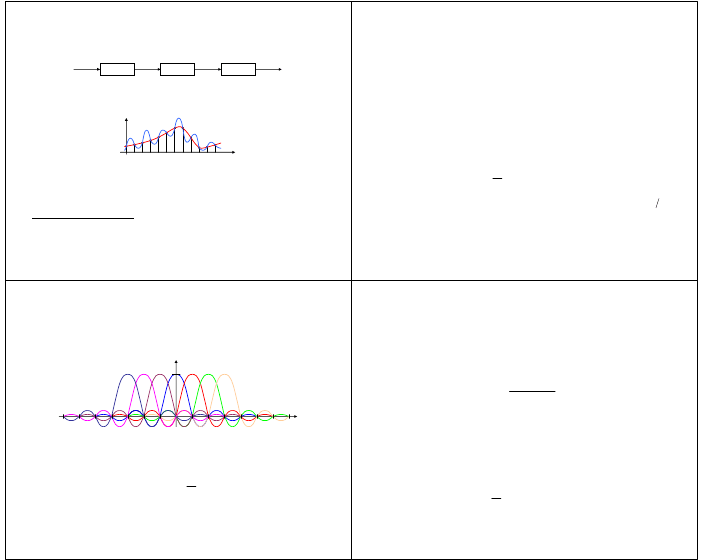
• schemat funkcjonalny układu przetwornika analogowo-cyfrowego
• operacja próbkowania dostarcza informacji o wartości chwilowej sygnału w momentach
próbkowania
• w ogólnym przypadku znajomość próbek sygnału nie wystarcza do odtworzenia postaci
analogowej sygnału
• odtworzenie z pełną dokładnością sygnału analogowego z próbek wymaga spełnienia
pewnych warunków ograniczających dotyczących struktury widmowej sygnału oraz
częstotliwości próbkowania
próbkowaniu bez strat poddawane mogą być jedynie sygnały
należące do klasy sygnałów o ograniczonej szerokości widma
1
opracowano na podstawie [1-3], wersja z dnia 02.10.2014
materiał nie jest pełnym i ścisłym pod względem formalnym opracowaniem poszczególnych tematów, stanowi
jedynie szkielet, wokół którego budowany jest wykład
0
t
x(t)
x(nT
s
)
x(nT
s
)
sygnał
dyskretny
sygnał
analogowy
Próbkowanie
Kwantowanie
Kodowanie
x(nT
s
)
sygnał
cyfrowy
sygnał
binarny
x(t)
~
x(nT
s
)
7. Konwersja AC i CA.doc, 2/20
ROZWINIĘCIE SYGNAŁÓW
W SZEREG KOTIELNIKOWA-SHANNONA
• dowolny sygnał
( )
t
x
, można rozwinąć w uogólniony szereg Fouriera postaci
( )
( )
∑
∞
=
=
0
i
i
i
t
u
a
t
x
gdzie:
( )
t
u
i
- wybrany układ funkcji ortogonalnych (funkcje bazowe)
i
a
- współczynniki rozwinięcia
• można wykazać, że zbiór funkcji próbkujących
Sa
( )
{
}
(
)
...
,
2
,
1
,
0
,
Sa
±
±
=
−
π
=
i
iT
t
T
t
u
s
s
i
tworzy w przestrzeni sygnałów o ograniczonej energii i ograniczonym do
s
m
T
π
=
ω
paśmie układ ortogonalny zupełny w przedziale
(
)
∞
∞
− ,
7. Konwersja AC i CA.doc, 3/20
ROZWINIĘCIE SYGNAŁÓW
W SZEREG KOTIELNIKOWA-SHANNONA (cd)
• graficzne przedstawienie kilku funkcji ze zbioru funkcji próbkujących
Sa
• zatem dowolny sygnał
( )
t
x
można rozwinąć w przedziale
(
)
∞
∞
− ,
w szereg względem
funkcji próbkujących
Sa
(szereg Kotielnikowa-Shannona) postaci
( )
(
)
∑
∞
−∞
=
−
π
=
i
s
s
i
iT
t
T
a
t
x
Sa
i=3
i=0
1
u
i
(t)
t
0
T
s
=1/(2f
m
)
T
s
2T
s
3T
s
4T
s
5T
s
6T
s
7
T
s
-T
s
-2T
s
-3T
s
-4T
s
-
5T
s
-6T
s
-7
T
s
i=1
i=2
i=-1
i=-2
i=-3
7. Konwersja AC i CA.doc, 4/20
ROZWINIĘCIE SYGNAŁÓW
W SZEREG KOTIELNIKOWA-SHANNONA (cd)
• współczynniki rozwinięcia uogólnionego szeregu Fouriera dla układu ortogonalnych
funkcji próbkujących
Sa
wyznacza się z następujących wzorów
( ) ( )
( )
∫
∫
∞
∞
−
∞
∞
−
=
dt
t
u
dt
t
u
t
x
a
i
i
i
2
• można wykazać, że współczynniki rozwinięcia
i
a
równe są wartościom (próbkom)
sygnału
( )
t
x
w chwilach
s
iT
( )
s
i
iT
x
a =
• zatem
( )
( )
(
)
( )
(
)
∑
∑
∞
−∞
=
∞
−∞
=
−
ω
=
−
π
=
i
s
m
s
i
s
s
s
iT
t
iT
x
iT
t
T
iT
x
t
x
Sa
Sa
7. Konwersja AC i CA.doc, 5/20
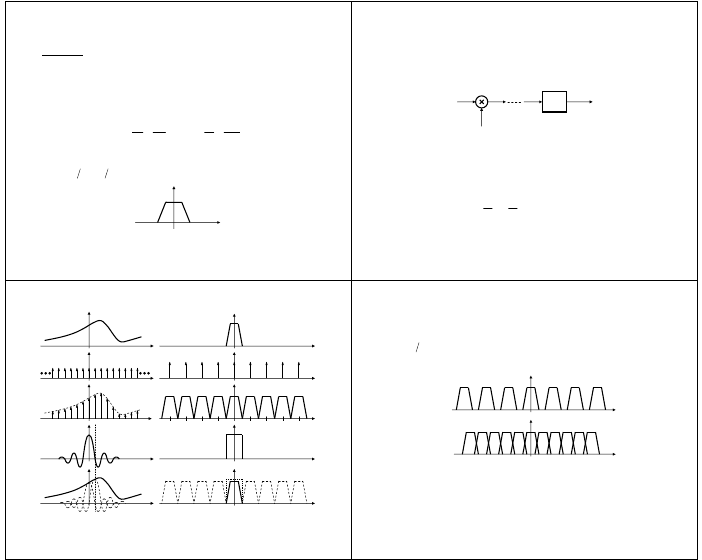
TWIERDZENIE O PRÓBKOWANIU
• twierdzenie:
Jeżeli sygnał
( )
t
x
jest sygnałem o widmie skończonym, określonym w paśmie
podstawowym w przedziale pulsacji
m
m
ω
≤
ω
≤
ω
−
lub częstotliwości
m
m
f
f
f
≤
≤
−
, gdzie stałe
0
>
ω
m
oraz
0
>
m
f
są najwyższymi niezerowymi
składowymi w pulsacji i w częstotliwości sygnału
( )
t
x
, wówczas sygnał
( )
t
x
jest równoważny zbiorowi swoich próbek odległych o stały przedział (okres)
m
s
s
T
ω
π
≤
ω
π
=
2
lub
m
s
s
f
f
T
2
1
1 ≤
=
inaczej
m
s
ω
≥
ω
2
lub
m
s
f
f
2
≥
m
m
sg
f
T
2
1
=
ω
π
=
- graniczny okres próbkowania, okres Nyquista
0
-ω
m
|X(ω)|
ω
m
ω
|X( f )|
f
-f
m
f
m
7. Konwersja AC i CA.doc, 6/20
TWIERDZENIE O PRÓBKOWANIU (cd)
• twierdzenie o próbkowaniu stanowi teoretyczną podstawę operacji przekształcania
sygnału ciągłego w równoważny mu sygnał dyskretny a następnie cyfrowy
• operację próbkowania możemy zdefiniować jako efekt mnożenia sygnału próbkowanego
przez dystrybucję grzebieniową
• sygnał analogowy
( )
t
x
o ograniczonej energii lub ograniczonej mocy średniej poddajemy
operacji pobierania jego wartości równomiernie w odstępach czasu
s
T
; otrzymany zbiór
próbek
( )
t
x
s
reprezentować będziemy ciągiem impulsów Diraca położonych w punktach
s
nT
i o wagach równych wartości sygnału
( )
s
nT
x
w tych punktach
( )
( )
( ) (
)
∑
∞
−∞
=
−
δ
=
ΙΙΙ
=
n
s
s
s
s
s
nT
t
nT
x
T
t
T
t
x
t
x
1
i nazywać sygnałem spróbkowanym, przyporządkowanym sygnałowi
( )
t
x
x
s
(t)
z(t)=x(t)
x(t)
h(t)
H( j
ω)
y(t)=1/T
s
III(t/T
s
)
H( j
ω)=Π(ω/ω
s
)
h(t)=1/T
s
Sa
[(ω
s
t)/2)
]
7. Konwersja AC i CA.doc, 7/20
0
ω
m
0
0 ω
m
H( jω)
X
s
(ω)
-ω
m
x
s
(t)
z(t)
h(t)
Y(ω)
0
x(t)
0
-ω
m
0
ω
s
T
s
0
T
s
0
0
ω
s
=2ω
m
1
ω
m
y(t)
0
-ω
m
t
X(ω)
Z(ω)
T
s
=π/ω
m
ω
*
*
x
x
ω
ω
ω
ω
t
t
t
t
7. Konwersja AC i CA.doc, 8/20
TWIERDZENIE O PRÓBKOWANIU (cd)
• w przypadku, gdy przedział próbkowania odbiega od jego wartości granicznej
m
sg
T
ω
π
=
, wówczas, w zależności od relacji
sg
s
T
T >
oraz
sg
s
T
T <
widmo
sygnału spróbkowanego przyjmie postać jak na rysunku
przypadek, w którym
sg
s
T
T >
wywołuje efekt nakładania się sąsiednich kopii widma
zwany aliasingiem
ω
X
s
(ω)
T
s
< T
sg
ω
X
s
(ω)
T
s
> T
sg
0
0
7. Konwersja AC i CA.doc, 9/20
TWIERDZENIE O PRÓBKOWANIU (cd)
Widmo sygnału spróbkowanego idealnie
• operacja próbkowania idealnego przebiega w układzie modulatora iloczynowego
• sygnał spróbkowany
( )
( ) ( )
t
y
t
x
t
x
s
=
• jego widmo
( )
( ) ( )
[
]
( ) ( )
[
]
ω
∗
ω
π
=
=
ω
Y
X
t
y
t
x
X
s
2
1
F
• po przekształceniach można wykazać, że
( )
(
)
∑
∞
−∞
=
ω
−
ω
=
ω
n
s
s
s
n
X
T
X
1
x
s
(t)
x(t)
y(t)=1/T
s
III(t/T
s
)
7. Konwersja AC i CA.doc, 10/20
KWANTOWANIE
• kwantowanie jest operacją przetwarzania sygnału dyskretnego w czasie i ciągłego
w wartościach w sygnał dyskretny w czasie i dyskretny w wartościach
• istota kwantowania sprowadza się do podziału zakresu zmian przetwarzanej wielkości na
skończoną liczbę
M
przedziałów kwantyzacji i określeniu (przybliżeniu) chwilowych
wartości próbek liczbą tych przedziałów
• na ogół przedziały kwantowania, nazywane kwantem lub krokiem kwantowania, mają
stałą szerokość, oznaczaną przez
q
• liczba przedziałów kwantowania najczęściej jest naturalną potęgą liczby 2
• z formalnego punktu widzenia operację kwantowania można opisać wyrażeniem
( )
( )
[
]
s
s
nT
x
Q
nT
x
=
~
gdzie
Q
jest operatorem przekształcenia - funkcją przyporządkowującą próbce
( )
s
nT
x
jej wartość skwantowaną
( )
s
nT
x
~
7. Konwersja AC i CA.doc, 11/20
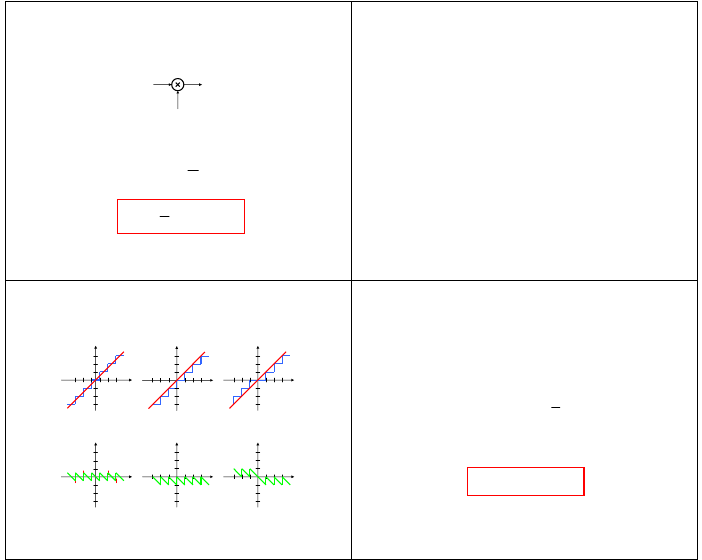
KWANTOWANIE (cd)
• w zależności od sposobu cyfrowej reprezentacji liczb ujemnych stosowane są najczęściej
trzy podstawowe sposoby kwantowania
• błąd kwantyzacji
( )
( ) ( )
s
s
s
nT
x
nT
x
nT
−
=
ε
~
-3q
-2q
3q
q
x
ε
2q
-q
q 2q 3q
-2q
-3q
-q
0
-3q
-2q
3q
q
x
ε
2q
-q
q 2q 3q
-2q
-3q
0
0
-3q/2
3q/2
5q/2
-3q
-2q
3q
q
x
ε
2q
-q
-5q/2
-q
0
-q
-2q
-3q
2q
q
-3q
-2q
3q
q
x
~
x
2q
3q
obcinanie
0
-q
-2q
-3q
2q
q
-3q
-2q
3q
q
x
~
x
2q
-q
3q
obcinanie
0
-q
-q/2
-3q/2
q/2
3q/2
5q/2
-3q
-2q
3q
q
x
~
x
2q
-5q/2
zaokrąglanie
7. Konwersja AC i CA.doc, 12/20
KWANTOWANIE (cd)
• błąd kwantyzacji
( )
( ) ( )
s
s
s
nT
x
nT
x
nT
−
=
ε
~
błąd kwantyzacji ma charakter losowy i nazywany jest szumem kwantowania, do jego
analizy używa się metod probabilistycznych
• miarą zniekształceń spowodowanych kwantowaniem jest parametr jest stosunek sygnał-
szum kwantowania
[ ]
N
S
SQNR
log
10
=
dB
S
- moc przetwarzanego sygnału na wejściu przetwornika
N
- moc szumu kwantowania
• można wykazać (Dodatek 1), że
[ ]
76
,
1
02
,
6
+
⋅
≅
b
SQNR
dB
7. Konwersja AC i CA.doc, 13/20
ODTWARZANIE SYGNAŁU Z PRÓBEK
• sposób odtwarzania sygnału analogowego z ciągu próbek pobranych z okresem
s
T
teoretycznie określa postać szeregu Kotielnikowa-Shannona (dla
m
s
ω
=
ω
2
)
( )
( )
(
)
( )
(
)
∑
∑
∞
−∞
=
∞
−∞
=
−
ω
=
−
π
=
i
s
m
s
i
s
s
s
iT
t
iT
x
iT
t
T
iT
x
t
x
Sa
Sa
znajomość wartości funkcji
Sa
pozwala numerycznie wyznaczyć wartość sygnału
( )
t
x
w dowolnej chwili czasu pomiędzy próbkami
ze względu na potrzebę nieskończonej liczby sumowań metoda nie ma znaczenia
praktycznego
• w praktyce operacja odtwarzania sygnału z próbek realizowana jest w sposób układowy
(przetwornik C/A plus filtr dolnoprzepustowy, lub w systemach impulsowych - filtr
dolnoprzepustowy)
• najprostszą metodą jest metoda schodkowa (ekstrapolacja zerowego rzędu) ale jest
obarczona stosunkowo dużym błędem, zależnym od okresu próbkowania
• mniejszym błędem (bardziej złożone układowo) obarczone są metody ekstrapolacji
pierwszego lub wyższych rzędów
7. Konwersja AC i CA.doc, 14/20
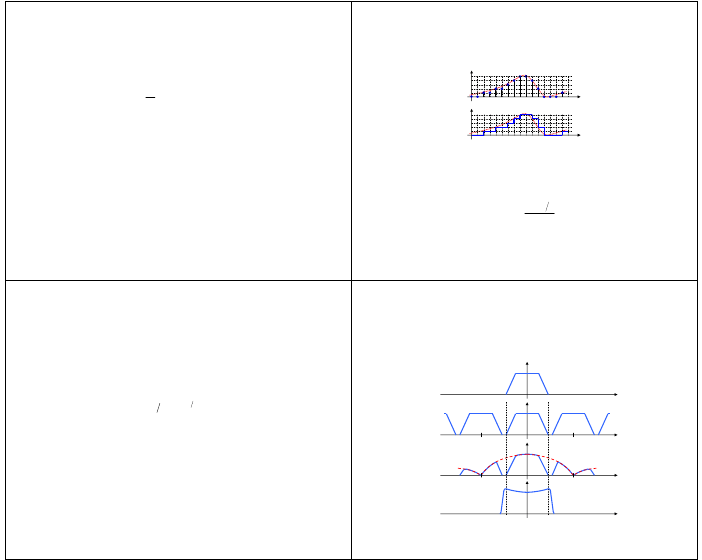
ODTWARZANIE SYGNAŁU Z PRÓBEK (cd)
• metoda schodkowa odtwarzania sygnału z próbek
• błąd odtwarzania metodą schodkową pociąga zniekształcenia widma sygnału
sygnał schodkowy
( )
t
x
~
stanowi sumę przesuniętych o
s
nT
impulsów prostokątnych
( )
t
p
o czasie trwania
s
T
i amplitudach równych wartościom kolejnych próbek sygnału
( )
s
nT
x
~
, zatem oznaczając
( )
−
Π
=
s
s
T
T
t
t
p
2
0
0
t
~
x(nT
s
)
t
~
x(t)
T
s
T
s
7. Konwersja AC i CA.doc, 15/20
ODTWARZANIE SYGNAŁU Z PRÓBEK (cd)
otrzymamy wyrażenie na sygnał schodkowy
( )
( ) (
)
∑
∞
−∞
=
−
=
n
s
s
nT
t
p
nT
x
t
x
~
widmo tego sygnału określone jest wyrażeniem
( )
(
)
(
)
∑
∞
−∞
=
ω
−
ω
−
ω
ω
=
ω
n
s
T
j
s
n
X
e
T
Sa
X
s
2
2
~
7. Konwersja AC i CA.doc, 16/20
ODTWARZANIE SYGNAŁU Z PRÓBEK (cd)
z wyrażenia wynika, że widmo amplitudowe sygnału schodkowego jest zniekształcone obwiednią
funkcji typu
Sa
, wielkość zniekształceń można zmniejszyć stosując większą częstotliwość
próbkowania (krótsze schodki) lub stosując specjalny dolnoprzepustowy filtr korekcyjny (filtr
wygładzający) o charakterystyce
( )
ω
j
H
H
( jω)
Sa(ωT
s
/2)
-ω
s
ω
X(ω)
~
X (ω)
X
s
(ω)
ω
m
-ω
m
ω
s
ω
m
-ω
m
ω
s
-ω
s
0
0
0
0
ω
ω
ω
7. Konwersja AC i CA.doc, 17/20
Dodatek 1
Wyprowadzenie wyrażenia na SQNR
• miarą zniekształceń spowodowanych kwantowaniem jest parametr jest stosunek sygnał-
szum kwantowania
[ ]
N
S
SQNR
log
10
=
dB
S
- moc przetwarzanego sygnału na wejściu przetwornika
N
- moc szumu kwantowania
dla bipolarnego przetwornika
b
-bitowego o zakresie przetwarzania
m
m
X
X ,
−
wartość kwantu wynosi
b
m
X
q
2
2
=
czyli
2
2
b
m
q
X
=
a średnią miarę mocy sygnału wejściowego
S
stanowi moc wzorcowego sygnału
harmonicznego o amplitudzie
m
X
8
2
2
2
2
2
2
2
b
m
m
q
X
X
S
=
=
=
7. Konwersja AC i CA.doc, 18/20
Wyprowadzenie wyrażenia na SQNR (cd)
wartość błędu kwantyzacji, w zależności od przyjętej techniki kwantyzacji może
przyjmować wartości z przedziału
2
,
2 q
q
−
,
0
,
q
−
lub
q
,
0
dla przykładu rozpatrzymy technikę kwantowania z zaokrągleniem, dla którego
2
,
2 q
q
−
∈
ε
, każda wartość błędu kwantyzacji z tego zakresu jest jednakowo
prawdopodobna, zatem posiada w powyższym przedziale rozkład równomierny
wartość mocy sygnału błędu (szumu kwantowania) (na obciążeniu jednostkowym) równa
jest jego wartości średniokwadratowej (dla sygnału o zerowej wartości średniej równa jest
jego wariancji)
[ ]
( )
12
1
2
2
2
2
2
2
2
q
d
q
d
p
E
N
q
q
=
ε
ε
=
ε
ε
ε
=
σ
=
ε
=
∫
∫
−
∞
∞
−
ε
ε
0
p (ε)
1
q
q/2
-q/2
7. Konwersja AC i CA.doc, 19/20
Wyprowadzenie wyrażenia na SQNR (cd)
zatem
[ ]
(
)
76
,
1
02
,
6
2
3
log
10
12
8
2
log
10
log
10
1
2
2
2
2
dB
+
⋅
≅
⋅
=
=
=
−
b
q
q
N
S
SQNR
b
b
[ ]
76
,
1
02
,
6
+
⋅
≅
b
SQNR
dB
7. Konwersja AC i CA.doc, 20/20
BIBLIOGRAFIA
1. Szabatin J.: Podstawy teorii sygnałów. WKŁ, Warszawa, 2003.
2. Szabatin J.: Przetwarzanie sygnałów. Materiały dydaktyczne Politechniki Warszawskiej,
2003,
www.ise.pw.pl/~szabatin
.
3. Gregg W.D.: Podstawy telekomunikacji analogowej i cyfrowej. WNT, Warszawa, 1983