
Rachunek prawdopodobieństwa
Wg Marka Fisza rachunek prawdopodobieństwa jest działem matematyki służącym do
wykrywania i badania prawidłowości w zakresie zdarzeń losowych.
Doświadczenie losowe
Doświadczenie losowe to takie, którego wyniku nie jesteśmy w stanie przewidzieć,
mimo sprecyzowania warunków, w jakich jest ono przeprowadzone.
Jest to realizacja (rzeczywista lub hipotetyczna) zespołu warunków z określonym
z góry zbiorem wyników.
Wyniki ω doświadczenia losowego są zdarzeniami elementarnymi, a ich zbiór
tworzy przestrzeń zdarzeń elementarnych Ω , przy czym zbiór ten może być skończony,
przeliczalny lub nieprzeliczalny.
Własności zdarzeń elementarnych :
a) jedno ze zdarzeń elementarnych na pewno wystąpi,
b) zajście jednego zdarzenia elementarnego wyklucza inne zdarzenie w tym samym doświadczeniu.
c) dane zdarzenie elementarne może zajść lub nie.
Przestrzeń zdarzeń elementarnych i σ-ciało. Zdarzenia losowe.
Każdy podzbiór w przypadku przestrzeni Ω skończonej lub przeliczalnej jest zdarzeniem losowym.
W przypadku przestrzeni nieprzeliczalnej wróżnia sie pewną klasę Z podzbiorów,
określaną jako
σ
-ciało i tylko elementy tej klasy nazywa się zdarzeniami losowymi.
Przeliczalnie addytywnym σ-ciałem zdarzeń przestrzeni zdarzeń elementarnych nazywa się
klasę Z jej podzbiorów spełniajacych następujące warunki:
a)
cała przestrzeń zdarzeń elementarnych na leży do tej klasy: Ω Є Z ,
b) dopełnienie A' ( czyli Ω\A) dowolnego zbioru A należącego do klasy Z jest elementem
tej klasy A Є Z => A' Є Z (warunek komplementatywności),
c)
suma co najwyżej przeliczalnej liczby zbiorów należących do klasy Z również należy
do tej klasy A
1
Є Z, ..., A
n
Є Z, ... => A
1
U
...
U
A
n
U
...) Є Z (warunek
przeliczalnej addytywności).
Aksjomatyczna definicja prawdopodobieństwa
Jeżeli Ω jest przestrzenią zdarzeń elementarnych, a L jej zbiorem zdarzeń losowych, to
prawdopodobieństwem jest funkcja P przyporządkowująca każdemu zdarzeniu A Є L liczbę
P(A ) spełniając następujące warunki:
a)
P(A ) ≥ 0, dla każdego zdarzenia A Є L ,
b) P(Ω) =1, (warunek unormowania),
c)
jeżeli A
1
, A
2
… są zdarzeniami losowymi parami rozłącznymi, to
P(A
1
∪ A
2
∪…) = P(A
1
) + P(A
2
)+... . (warunek przeliczalnej addytywności).
Prawdopodobieństwo P zdarzenia losowego jest funkcją P: σ→R , odwzorowującą σ -ciało
w zbiór liczb rzeczywistych.
Jeżeli zbiór zdarzeń elementarnych jest skończony i zawiera N elementów, to liczba wszystkich
możliwych jego podzbiorów (zdarzeń) łącznie ze zdarzeniem pewnym i niemożliwym wynosi 2
N
.
Zdarzeniem pewnym jest cała przestrzeń zdarzeń elementarnych, natomiast zdarzeniem
niemożliwym - podzbiór pusty ( 0 ) zbioru , czyli nie zawierający żadnego elementu.
a)
prawdopodobieństwo zdarzenia niemożliwego równa się zeru:
P(0) = 0,

b) prawdopodobieństwo zdarzenia jest nie większe od jedności
P(A ) ≤ 1,
c)
jeśli zdarzenie A pociąga zdarzenie B , to
P(A ) ≤ P(B ),
d) jeśli zdarzenie A pociąga zdarzenie B , to
P(B \A )=P(B )-P(A ),
e) jeżeli zdarzenia A
i
są rozłączne parami, to
f)
prawdopodobieństwo alternatywy dwóch dowolnych zdarzeń jest równe sumie
prawdopodobieństw tych zdarzeń pomniejszonej o prawdopodobieństwo ich
koniunkcji
P(A
U
B ) = P(A ) + P(B ) - P(AB ),
g)
prawdopodobieństwo alternatywy trzech dowolnych zdarzeń (czyli zajścia co najmniej
jednego z tych zdarzeń) jest równe:
P(A
U
B
U
C) = P(A ) + P(B ) + P(C) - P(AB ) - P(AC ) - P(BC ) + P(ABC ),
h) prawdopodobieństwo iloczynu zdarzeń niezależnych:
P(A
ÇB)=P(A)P(B).
Działania na zdarzeniach
Koniunkcją (iloczynem) dwóch zdarzeń A,B ЄZ nazywamy zdarzenie A
∩
B lub AB , składające się
z tych wszystkich zdarzeń elementarnych, które należą zarówno do zdarzenia A jak i zdarzenia B .
Koniunkcją dowolnej liczby zdarzeń jest więc zdarzenie polegające na zajściu wszystkich tych
zdarzeń.
Alternatywą (sumą) zdarzeń A, B Є Z nazywamy zdarzenie A
U
B , składające się ze zdarzeń ele-
mentarnych ω , które należą co najmniej do jednego ze zdarzeń A, B . Alternatywa dowolnej liczby
zdarzeń jest to zdarzenie polegające na zajściu co najmniej jednego z tych zdarzeń.
Różnicą A\B lub A - B zdarzeń A, B jest zdarzenie składające się z tych zdarzeń elementarnych ω ,
które należą do zdarzenia A , lecz nie należą do zdarzenia B . Różnica A \B zdarzeń A , B jest to
więc zdarzenie polegające na zajściu zdarzenia A i nie zajściu zdarzenia B .
zdarzeń.
Zdarzenie A pociąga zdarzenie B , tj. A
B , jeżeli każde zdarzenie elementarne ω
należące do zdarzenia A również należy do zdarzenia B . Zdarzenie A pociąga zdarzenie
B wtedy, gdy z zajścia zdarzenia A wynika zajście zdarzenia B .
Prawa de Morgana
(AB )' = A '
U
B' ;
(A
U
B )' = A'B' .
Przestrzeń probabilistyczna
Przestrzenią probabilistyczną nazywamy uporządkowaną trójkę (Ω, L, P) [lub (Ω,
σ
, P)].
Przestrzeń probabilistyczna danego doświadczenia losowego stanowi jego matematyczny opis.
Rzucając 2 razy monetą otrzymać możemy OO , OR , RO oraz RR .
więc przestrzeń zdarzeń elementarnych złożona jest z 4 elementów, a stąd utworzyć można
z nich 2
4
= 16 podzbiorów - elementów σ-ciała. Będą to:
-zbiory jednoelementowe: 4! / [1! (4-1)!] = 24 / 6 = 4:A
1
=OO A
2
= OR A
3
= RO A
4
= RR ,
-zbiory dwuelementowe: 4! / [2! (4-2)!] = 24 / 4 = 6:
A
5
=OO, OR A
6
=OO, RO A
7
=OO, RR A
8
=OR, RO A
9
=OR, RR A
10
=RO, RR ,
- zbiory trzyelementowe - 4! / [3! (4-3)!] = 24 / 6 = 4:
A
11
=OO, OR, RO , A
12
=OO, OR, RR , A
13
=OO, RO, RR , A
14
=OR, RO, RR ,
- dwa zbiory niewłaściwe - zbiór pusty i czteroelementowy:A
15
=Ø , A
16
=OO, OR, RO, RR .
Prawdopodobieństwa P przestrzeni probabilistycznej, przy założeniu, że zdarzenia
P(A
1
U
...
U
A
n
) = P(A
1
) +...+ P(A
n
),
B
A
Ì
Ì
jednoelementowe są jednakowo prawdopodobne:
P (A
1
) = ... = P (A
4
) = 1 / 4;
P (A
5
) = ... = P (A
10
) = 1 / 2;
P (A
11
) = ... = P (A
14
) = 3 / 4;
Przykłady działań na prawdopodobieństwach zdarzeń
Przykład 1.
Urządzenie A w komputerze tworzą bloki b
i
. Określić
prawdopodobieństwo jego bezawaryjnej pracy P(A ) w czasie t, wiedząc że bloki ulegają
uszkodzeniu niezależnie od siebie z jednakowym prawdopobieństwem p= P(A
i
) =
.
P(A ) = P(A
1
A
2
A
3
) = P(A
1
)P(A
2
)P(A
3
) = p
3
.
P(A) =
P(A ) = P(A
1
) + P(A
2
) - P(A
1
)P(A
2
) = 2p - p
2
= p(2-p),
P(A) =
P(A ) =
P(A
1
)+ P(A
2
)+ P(A
3
)- P(A
1
)P(A
2
)-P(A
1
)P(A
3
)-P(A
2
)P(A
3
)+P(A
1
)P(A
2
)(A
3
)=
= 3p + p
3
- 3p
2
,
P(A) =
P (A ) =
P(A
1
) [ P(A
2
) + P(A
3
) - P(A
2
)P(A
3
)] = p[2p- p
2
]
P(A) =
Przykład 2
P(A) = 0,6
P(B) = 0,7
P(A
U
B) = 0,8
A
B
A
U
B
Obliczyć:
P(B' )
P(B' ) =
1 - P(B)
=
1
-
=
Obliczyć:
P(A'B'
U
AB' )
Opis zadania:
A'
B'
->
A'B'
A
B'
->
AB'
A'B'
U
AB'
Rozw. P(A'B'
U
AB' ) = P[(A
U
B )' ]+ P(A ) - P(AB ) = [1- P(A
U
B) ]+P(A )-P(A )- P(B )+ P(A
U
B ) =
= 1 - P(B) =
1 -
=
0,3
1. Krok
3. Krok
(A
U
B )'
+
A
-
AB
1
-
B
1 - B
Dane:
P(A ) = 0,6
P(B )
P(A
U
B ) = 0,8
P(A ∩ B ) =
0,5
Obliczyć:
P(B' ) =
1 - P(B ) = 1 - [P(A
U
B ) - P(A ) + P(AB )];
0,7
A)
B)
D)
0,343
0,910
0,973
0,637
C)
P (A
15
) = P (Ø ) = 0;
P (A
16
) = P (Ω ) = 1.
0,7
=
0,3
0,7
P(A
U
B ) = P(A ) + P(B ) - P(AB );
P(B ) = P(A
U
B ) - P(A ) + P(AB );
P(B' ) = 1 - P(A
U
B ) + P(A ) - P(AB )= 1,0 -
0,8 + 0,6 -
0,5 = 0,3
Obliczyć:
P(A'B'
U
AB' )
P(A'B'
U
AB' )= P[(A
U
B )' ] + P(A )- P(AB ) = [1- P(A
U
B )] + P(A ) - P(AB )=
=
1
-
0,8 + 0,6 -
0,5 = 0,3
Przykład 3.
Dane: P(A ) = 0,6
P(B ) = 0,7
P(A U B) = 0,8
b) P(AB )=P(A )+P(B ) - P(A
U
B )=
0,6 + 0,7 - 0,8 =
e) P(A'B )= P(B ) - P(AB ) = 0,7 -
0,5 = 0,2
f)
P(AB' )=P(A )- P(AB )=
0,6 -
0,5 = 0,1
g)
P(A'
U
B )= P(A' )+ P(AB ) = 0,4 + 0,5 = 0,9
P( A'
U
B ) = P(A' ) + P(B ) - P(A' B ) =0,4 + 0,7 -
0,2 =
0,9
h) P(A
U
B') = P(B')+ P(AB) = 0,3 + 0,5 =
0,8
c) P[(AB )' ] = P(A' )+ P(B' )- P(A'B') =[1-P(A )]+[1- P(B )] - P[(A
U
B )'] =
= 0,4 + 0,3 - [1 - P( A
U
B )] = 0,4 + 0,3 - 0,2 =
0,5
P[(AB )' ] = 1- P(AB ) =
1
-
0,5 =
0,5
P[(AB )' ] = P( A'
U
B' )
d) P( A'B' )=P[( A
U
B )' ] = 1 - P(A
U
B ) =
1
-
0,8 =
P(A'B' ) =
P(A ')+P(B ')-P(A '
U
B ') = 0,4 + 0,3 -
= 0,2
0,5
####
0,5
-
0,4
B
0,6 =
a)
A
P(A' ) = 1- P(A ) = 1

P(A'B'
U
AB' )= P(A' ) + P(B' ) - P(A'
U
B' ) + P(A ) - P(AB ) =
= 1- P(A ) + 1 - P(B ) - P[(AB )'] + P(A ) - P(AB ) =
= 2 - P(A ) - P(B ) - [1 - P(AB )] + P(A ) - P(AB ) =
= 2 - P(A ) - P(B ) - 1 + P(AB ) + P(A ) - P(AB 1 - P(B ) =
= 1 - P(AB ) + P(A ) - P(A
U
B ), a więc jak wyżej.
Definicje prawdopodobieństwa
1
1. Klasyczna - Laplace 1812.
Gdy wszystkie zdarzenia elementarne są jednakowo możliwe, to prawdopodobieństwo zda-
rzenia losowego A jest równe ilorazowi liczby zdarzeń elementarnych sprzyjających temu
zdarzeniu i liczby wszystkich zdarzeń elementarnych: P(A) = k / n .
2. Definicja statystyczna, częstościowa, frekwencyjna.
Prawdopodobieństwem zdarzenia A nazywamy granicę częstości tego zdarzenia, gdy liczba
doświadczeń n rośnie nieograniczenie, tj.
3. Aksjomatyczna definicja Kołmogorowa podna została poprzednio.
Prawdopodobieństwo warunkowe i niezależność zdarzeń
Zdarzenia A i B są niezależne, gdy:
P(A
∩
B ) = P(A )P(B ).
Przykład 1. W magazynie są dobre i wadliwe karty graficzne pochodzące od dwóch
producentów. Niech kolejne symbole oznaczają:
A - karta dobra,
à - karta wadliwa,
B
1
- karta 1. producenta,
B
2
- karta 2. producenta,
a - karta dobra 1. producenta,
b - karta wadliwa 1. producenta,
c - karta dobra 2. producenta,
d - karta wadliwa 2. producenta.
A
Ã
A
Ã
B
1
a
b
a + b
B
1
9
1
10
B
2
c
d
c + d
B
2
36
4
40
a + c
b + d
a + b+ c + d = n
45
5
50
Prawdopodobieństwa warunkowe
a
a + b
i analogicznie
c
c + d ,
a
a + c ,
c
a + c
i
P(A|B ) =
P( A
∩
B )
P(B )
.
P(A ∩ B
1
)
P(B
1
)
=
P(Ã |B
2
)=
a / n
(a + b ) / n
P(A|B
2
) =
=
P(A|B
1
) =
P(A ∩ B
1
)
P (A )
=
P (Ã ∩ B
1
)
P (Ã )
P(Ã |B
1
)=
P (Ã ∩ B
1
)
.
P (B
1
)
P (Ã ∩ B
2
)
=
P (B
2
)
, a także
oraz
P(B
1
|Ã )=
=
P(B
1
|A ) =
P (A )
P(A ∩ B
2
)
P (B
2
)
P(B
2
|A ) =
P(A ∩ B
2
)
P(B
2
|Ã )=
P (Ã ∩ B
2
)
P (Ã )
i
P A
n
n
n
a
( )
lim
.
=
®¥
.
j
i
¹
Ustalmy prawdopodobieństwo, że losowo wybrana karta:
A
Ã
2
- jest dobra, gdy: a1) pochodzi od 1. producenta,
B
1
9
1
10
a2) pochodzi od 2. producenta,
B
2
36
4
40
- wiedząc, że jest dobra: b1) pochodzi od producenta 1.,
45
5
50
b2) pochodzi od producenta 2.:
a1)
P(A|B
1
) =
9
10
=
0,900
a2)
P(A|B
2
) =
36
40
=
0,900
b1)
P(B
1
| A ) =
9
45
=
0,200
P(B
1
) =
10
50
=
0,200
b2)
P(B
2
| A ) =
36
45
=
0,800
P(B
2
) =
40
50
=
0,800
Prawdopodobieństwa iloczynu zdarzeń
P(A ∩ B
1
)=
*
=
*
=
=
0,900
*
0,200
=
0,200
*
0,900
=
0,180
P(A ∩ B
1
)=
*
=
0,900
*
0,200
=
0,180
*
=
*
=
=
0,900
*
0,800
=
0,800
*
0,900
=
0,720
*
=
0,900
*
0,800 =
0,720
Przykład 2.
A
Ã
A
Ã
B
1
a
b
a + b
B
1
9
2
11
B
2
c
d
c + d
B
2
36
4
40
a + c b + d a + b+ c + d = n
45
6
51
Prawdopodobieństwa warunkowe
a
a + b
i analogicznie
c
a
c + d ,
a + c ,
c
.
a + c
Ustalmy prawdopodobieństwo, że losowo wybrana karta
- jest dobra, gdy a1) pochodzi od 1. producenta, a2) pochodzi od 2. producenta,
- wiedząc, że jest dobra b1) pochodzi od producenta 1. i b2) pochodzi od producenta 2.:
ad. a1) P(A|B
1
) =
9
11
=
0,818
P(A|B
2
) =
36
40
=
0,900
P(A ) =
45
/
51
=
0,882
b1)
P(B
1
|A ) =
9
45
=
0,200
P(B
1
) =
11
51
=
0,216
b2)
P(B
2
|A ) =
36
45
=
0,800
P(B
2
) =
40
51
=
0,784
=
0,900
=
/
50
P(A|B
2
) =
P(A ∩ B
2
)
P(B
2
| A ) =
P(A ∩ B
2
)
P(B
2
)
P(A|B
1
) =
P(A ∩ B
1
)
=
P(B
1
)
P(B
1
| A )
P(A ∩ B
2
)=
P(A )
P(B
2
)
P(A )=
45
P(A )
P(B
1
)
P(A|B
1
)
=
P(A )
P(A ∩ B
2
)=
P(A|B
2
)
P(B
2
)
P(B
2
| A )
P(A )
P(B
1
)
(a + b ) / n
a / n
P(A ∩ B
1
)
=
P(A )
=
P(B
1
| A) =
P(A )
/
/
/
/
/
/
/
/
/
/
/
/

Prawdopodobieństwa iloczynu zdarzeń
3
P(A ∩ B
1
)=
*
=
*
=
=
0,818
*
0,216
=
0,200
*
0,882
=
0,176
P(A ∩ B
1
)=
*
=
0,882
*
0,216
=
0,190
*
=
*
=
=
0,900
*
0,784
=
0,800
*
0,882
=
0,706
*
=
0,882
*
0,784 =
0,692
Zadanie
W ogólnej liczbie sprzedanych programów służących do analizy finansowej
40
%
pochodziło z firmy X (zdarzenie A ,
P(A )= 0,4
),
a
60
% z firmy Y (zdarzenie B ,
P(B )= 0,6 ).
50
% programów posiadało możliwość graficznej prezentacji wyników
analizy ( zdarzenie C , P(C )
=
0,5
),
przy czym zdolność tę miało
35
%
programów producenta X (P(C |A ) =
0,35 ).
A.
Wyznaczyć P(A | C )
P(A|C ) =
/
P(C )
=
P(C|A ) *
P(A )
=
0,35
*
0,4
=
0,14
P(A|C ) =
0,14
/
0,5
=
0,28
B.
Wyznaczyć P(B | C )
P(B|C ) =
/
P(C )
P(C )
=
+
=
0,5
=
0,5
-
0,14
=
0,36
P(B|C ) =
0,36
/
0,5
=
0,72
C.
Wyznaczyć P(C
|
B )
P(C|B ) =
/
P(B )
=
0,36
/
0,6
=
0,6
P(A )
P(B
2
| A )
P(A )
P(B ∩ C )
P(B ∩ C )
P(B ∩ C )
P(A ∩ C )
P(A ∩ C )
P(B ∩ C )
P(A ∩ C )
P(A|B
1
)
P(B
1
)
P(B
1
| A )
P(A|B
2
)
P(B
2
)
P(A ∩ B
2
)=
P(A )
P(B
2
)
P(A )
P(B
1
)
P(A ∩ B
2
)=

Prawdopodobieństwo całkowite
4
Jest stosowane w przypadku obliczania prawdopodobieństwa, gdy na określone zdarzenie ma
wpływ większa liczba zdarzeń losowych.
Załóżmy, że zdarzenie A może wystąpić, gdy zajdzie jedno z wykluczających się zdarzeń
E
1
, E
2
, ...,E
n ,
tworzących układ zdarzeń zupełnych, określonych na tej samej przestrzeni
probabilistycznej .
Zdarzenia E
i
spełniają więc warunki:
a)
, dla
oraz
b)
.
Niech będą znane prawdopodobieństwa tych zdarzeń P(E
1
), P(E
2
),...,P(E
n
) oraz prawdopo-
podobieństwa warunkowe zdarzenia A , jako równe P(A |E
1
), P(A |E
2
),...,P(A |E
n
).
W takim przypadku prawdopodobieństwo całkowite (zupełne) obliczymy:
P(A ) = P(A |E
1
) P(E
1
) + P(A |E
2
) P(E
2
) + ...+ P(A |E
n
) P(E
n
) =
.
Jeżeli więc A oznacza skutek, który może być wywołany jedną z rozłącznych przyczyn
E
1
, E
2
, ...,E
n ,
i któraś z tych przyczyn na pewno wystąpi, to prawdopodobieństwo
wystąpienia skutku A można określić jeszcze przed przeprowadzeniem eksperymentu (a priori).
Zadanie.
Przedsiębiorstwo otrzymuje ten sam detal od trzech dostawców. Pierwszy z nich
dostarcza
20
%,
drugi
30
%,
a trzeci 50
% detali, czyli prawdopodo-
bieństwa są równe odpowiednio P(E
1
) =
0,2
, P(E
2
) =
0,3 oraz
P(E
3
) =
0,5 .
Niektóre detale wykazują wady (zdarzenie A ), których prawdopodobieństwa wystąpienia u
dostawców są różne i wynoszą odpowiednio
P(A|E
1
) =
0,02 , P(A|E
2
) = 0,04 i
P(A|E
3
) =
0,03 .
Należy z góry określić prawdopodobieństwo wystąpienia detali wadliwych.
P(A )= 0,2
*
0,02
+
0,3
*
0,04
+
0,5
*
0,03
=
0,031 .
P(E
i
) 0,1
0,2
0,3
0,4
n
500
P(A|E
i
)
0,08
0,06
0,04
0,02
P(A |E
i
) P(E
i
) 0,008 0,012 0,012 0,008
P(A ) 0,040
(E
i
)
50
100
150
200
n
500,0
(A∩E
i
)
4
6
6
4
(A )
20,0
å
=
n
1
i
i
i
E
E
|
A
)
P(
)
P(
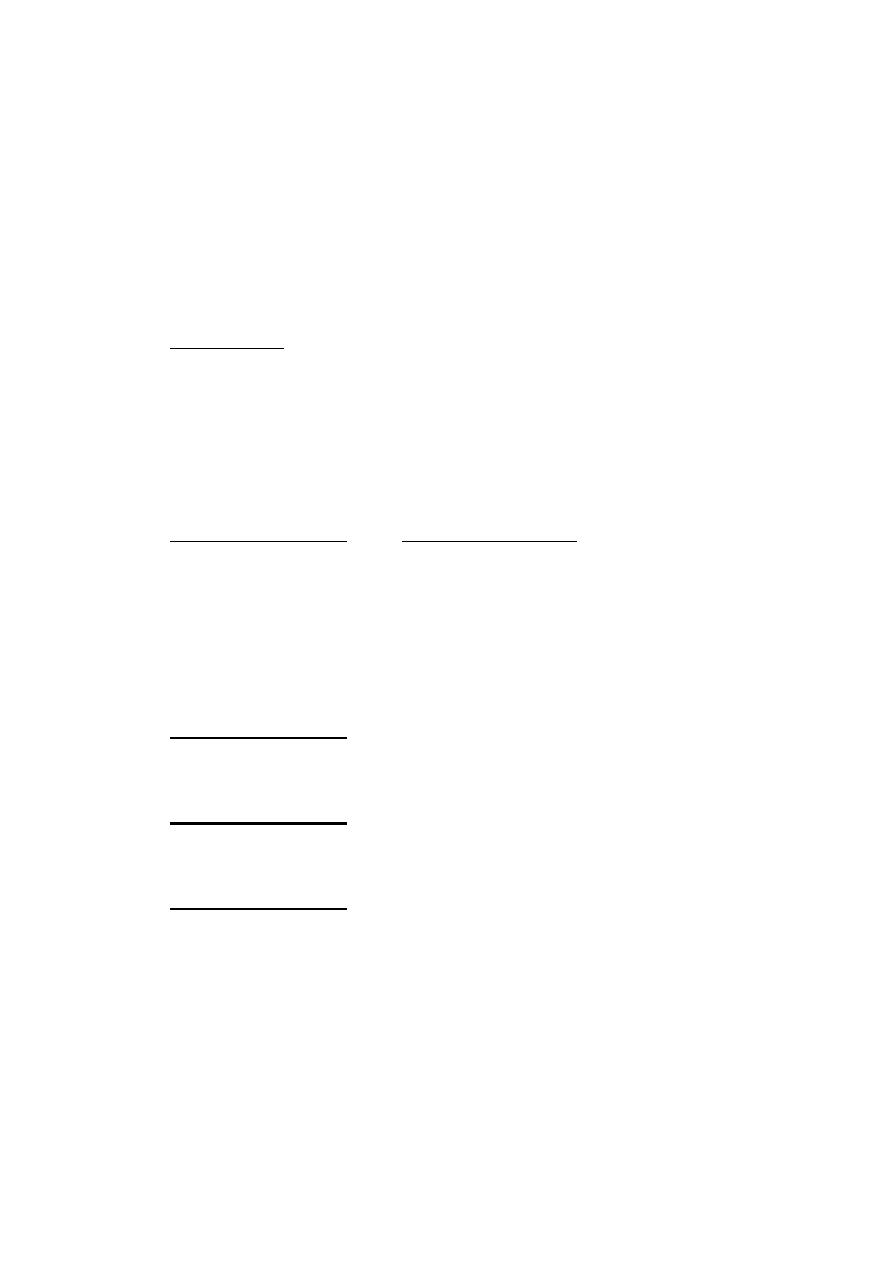
Wzór Bayesa
5
Załóżmy, że wykonano doświadczenie, w wyniku którego zaszło zdarzenie A . Zdarzenie to
może wystąpić tylko wówczas, gdy zajdzie jedno z wyłączających się zdarzeń
E
1
, E
2
,...,E
n ,
tworzących układ zupełny. Ponieważ nie wiemy, które z tych zdarzeń zajdzie, więc nazywamy
je hipotezami. Po zajściu zdarzenia A określić można, która z przyczyn
E
1
, E
2
,...,E
n ,
je wywołała, ustalając prawdopodobieństwa warunkowe
P (E
1
| A ).
Wiedząc, że
oraz
P(E
i
∩ A ) = P(A|E
i
) * P(E
i
) =
P(E
i
| A ) * P(A ),
otrzymamy:
Zadanie. Wykorzystując informacje podane w poprzednim zadaniu należy określić prawdo-
podobieństwa a posteriori, że losowo wybrany detal pochodzi od danego dostawcy.
Znając ustalone poprzednio prawdopodobieństwo całkowite można obliczyć kolejno:
0,02
*
0,2
0,031
0,04
*
0,3
0,031
0,03
*
0,5
0,031
,
,
=
0,38710
P(E
i
| A ) =
=
0,48387
P(E
i
| A ) =
P(A ∩ E
i
)
P(A )
P(E
i
| A ) =
P(A|E
i
) P(E
i
)
P(A )
P(A|E
i
) P(E
i
)
.
P(E
i
| A ) =
=
0,12903
=
P(E
i
| A ) =
.
å
=
n
1
i
i
E
A
)
)P(
E
|
P(
i
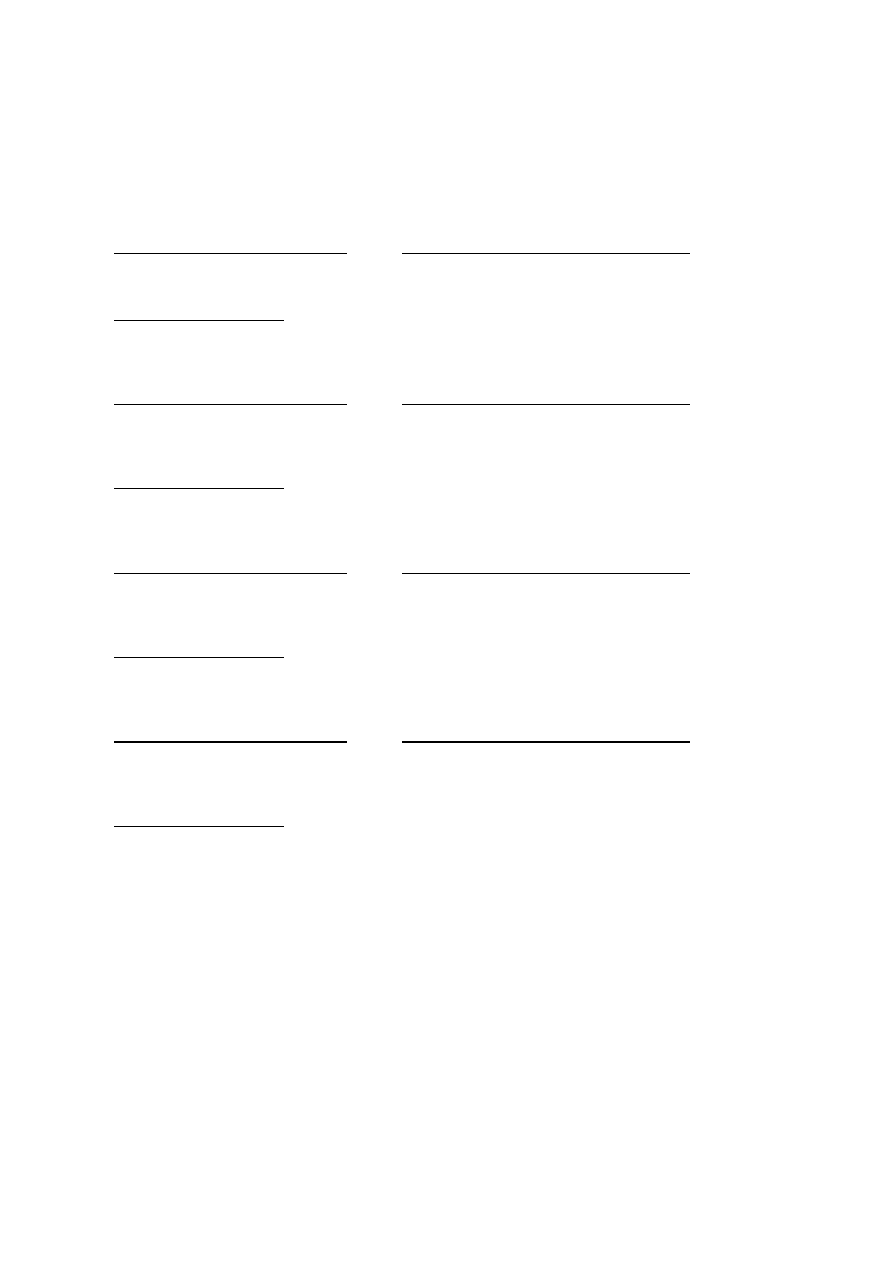
Zadanie.
6
Wiedząc, że moduły pamięci pochodzą od producenta A z prawdopodobieństwem P( A ) =
=
0,8 przy czym w dostawach od producenta A znajdowało się
60
% modułów
dobrych P(D | A ) = 0,6 , a u producenta B odsetek ten wynosił
70
% P(D |B ) =
0,7 ,
ustalić prawdopodobieństwa:
0,6
*
0,8
P(D |A )P(A ) P(D |B )P(B )
0,6
0,8
+
0,7
0,2
0,48
0,48
+
0,14
0,7
*
0,2
P(D |B )P(B ) P(D |A)P(A )
0,7
0,2
+
0,6
0,8
0,14
0,14
+
0,48
0,4
*
0,8
P(W |A )P(A ) P(W |B )P(B
0,4
0,8
+
0,3
0,2
0,32
0,32
+
0,06
0,3
*
0,2
P(W |B )P(B ) P(W |A )P(A )
0,3
0,2
+
0,4
0,8
0,06
0,06
+
0,32
P(A |D ) =
=
P(D | A )P(A )
=
=
=
0,7742
P(B |D ) =
P(D |B )P(B )
=
=
=
=
0,1579
P(B |W ) =
P(W |B )P(B )
=
=
0,2258
P(A |W ) =
P(W |A )P(A )
=
=
=
=
=
0,8421
=
+
+
+
+
+
+
*
*
*
*
*
*
*
*
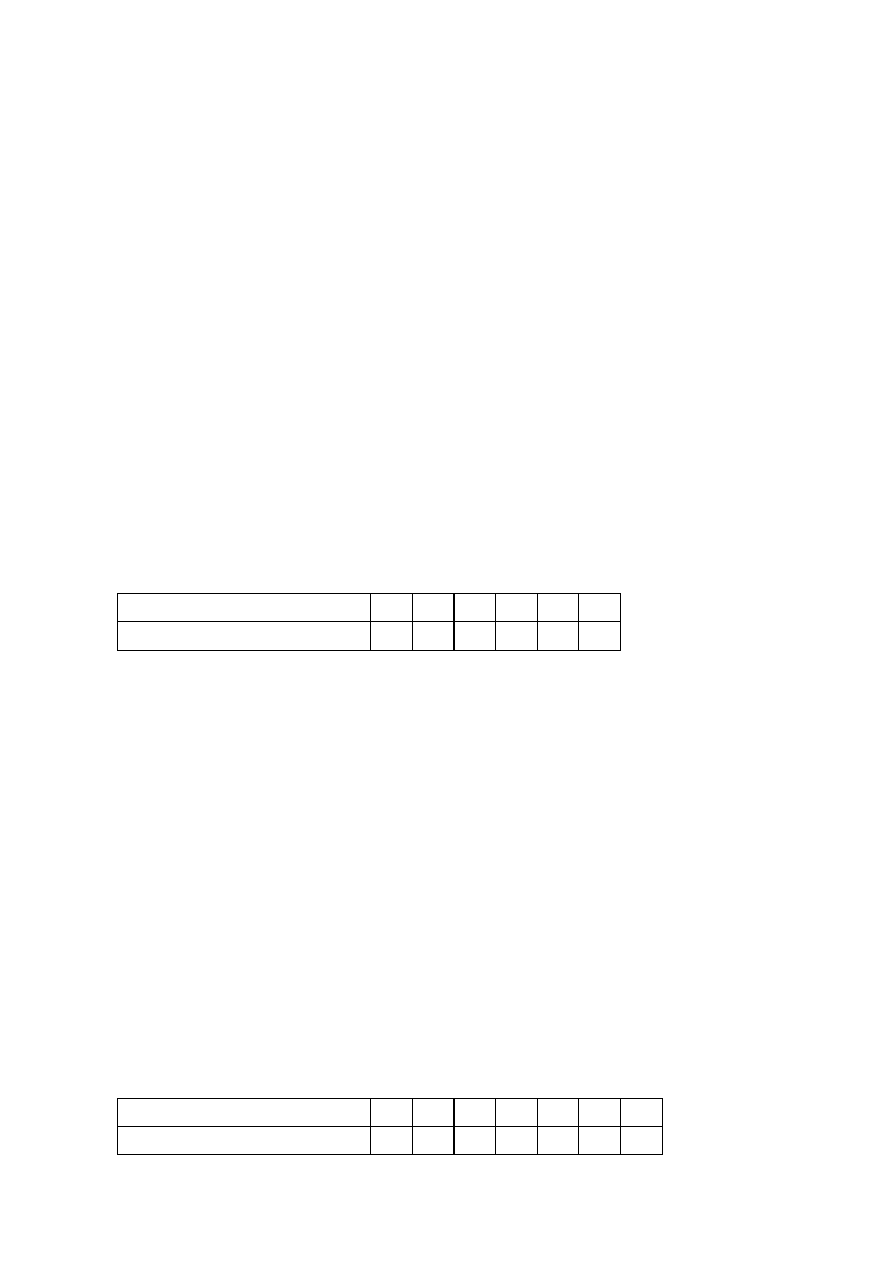
Rozkłady zmiennych losowych
Zmienna losowa skokowa. Przykład - jednokrotny rzut kostką.
Zbiór zdarzeń elementarnych Ω = {(1 oczko), (2 oczka), (3 oczka), (4 oczka),
(5 oczek) oraz (6 oczek)}.
Na tym zbiorze zdarzeń elementarnych określamy zmienną losową X:
X (1 oczko) = 1,
X (2 oczka) = 2,
X (3 oczka) = 3,
X (4 oczka) = 4,
X (5 oczek) = 5,
X (6 oczek) = 6.
Zakładając jednakowe prawdopodobieństwo każdewgo z wyników, rozkład
zmiennej losowej X jest następujący:
P (X =1) = P (1 oczko) = 1/6,
P (X =2) = P (2 oczka) = 1/6,
P (X =3) = P (3 oczka) = 1/6,
P (X =4) = P (4 oczka) = 1/6,
P (X =5) = P (5 oczek) = 1/6,
P(X=6) = P(6 oczek) = 1/6.
Funkcja prawdopodobieństwa zmiennej losowej skokowej:
Rozkład liczby uzyskanych oczek
Wartość zmiennej x
i
1
2
3
4
5
6
Prawdopodobieństwo p
i
1/6 1/6 1/6 1/6 1/6 1/6
Dystrybuanta zmiennej losowej skokowej:
.
Dystrybuanta zmiennej losowej X
x
1
2
3
4
5
6
> 6
F (x )
0
1/6 2/6 3/6 4/6 5/6
1
1
å
<
=
x
i
x
i
.
p
)
x
(
F
ï
ï
ï
ï
ï
ï
ï
ï
ï
î
ï
ï
ï
ï
ï
ï
ï
ï
ï
í
ì
>
£
<
£
<
£
<
£
<
£
<
£
=
6
x
dla
1
6
x
5
dla
6
/
5
5
x
4
dla
6
/
4
4
x
3
dla
6
/
3
3
x
2
dla
6
/
2
2
x
1
dla
6
/
1
1
x
dla
0
)
x
(
F
å
=
=
=
=
=
n
1
i
i
i
i
.
1
p
,
n
,...,
2
,
1
i
,
p
)
x
X
(
P
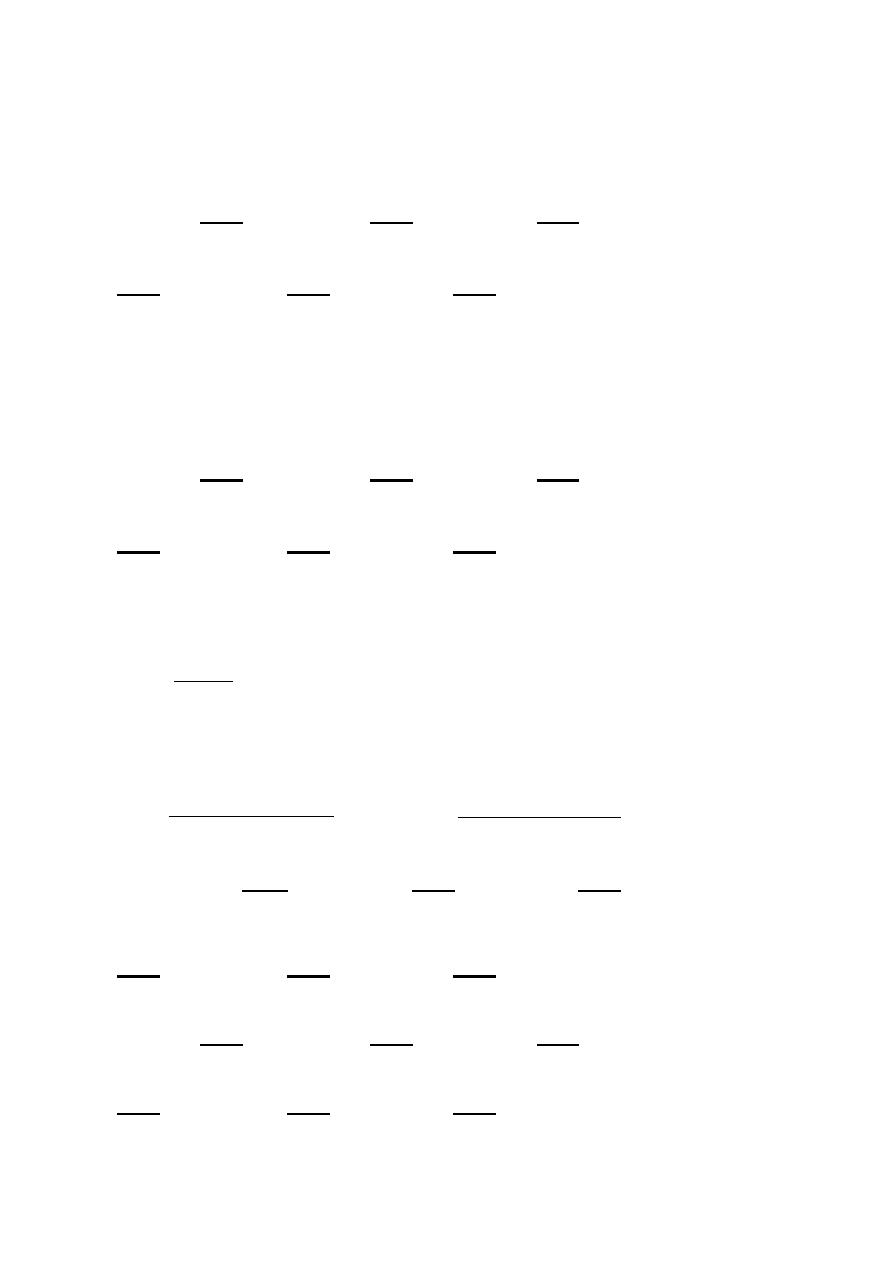
Wartość oczekiwana zmiennej losowej X
1
1
1
6
6
6
1
1
1
6
6
6
Wariancja zmiennej losowej X
1
1
1
6
6
6
1
1
1
6
6
6
Współczynnik zmienności
=
/
3,5 =
Współczynnik asymetrii i kurtoza
1
1
1
6
6
6
1
1
1
6
6
6
1
1
1
6
6
6
1
1
1
6
6
6
2
Zmienna losowa skokowa. Przykład - jednokrotny rzut kostką - gra.
3,5 )
4
+
( 6 - 3,5 )
4 =
1,73
3,5 )
4
+
( 3 - 3,5 )
4
+
+
( 4 - 3,5 )
4
+
( 5 -
( 6 - 3,5 )
3
= 0
K =
0,12
( 1- 3,5 )
4
+
( 2 -
( 3 - 3,5 )
3
+
+
( 4 - 3,5 )
3
+
( 5 - 3,5 )
3
+
1,71
0,488
0,20
( 1- 3,5 )
3
+
( 2 - 3,5 )
3
+
3,5 )
2
+
( 6 - 3,5 )
2
=
2,92
3,5 )
2
+
( 3 - 3,5 )
2
+
+
( 4 - 3,5 )
2
+
( 5 -
+
*
6
=
3,5
V(X) =
( 1- 3,5 )
2
+
( 2 -
+
*
3
+
+
*
4
+
*
5
E(X) =
*
1
+
*
2
å
=
=
n
1
i
i
i
x
p
)
X
(
E
å
=
-
=
n
1
i
2
i
i
))
X
(
E
x
(
p
)
X
(
V
)
X
(
E
V
s
s
=
3
n
1
i
3
i
i
))
X
(
E
x
(
p
A
s
s
å
=
-
=
=
s
A
[
]
[
]
4
n
1
i
4
i
i
))
X
(
E
x
(
p
K
s
å
=
-
=

Zbiór zdarzeń elementarnych Ω = {(1 oczko), (2 oczka), (3 oczka), (4 oczka),
(5 oczek) oraz (6 oczek)}.
Na tym zbiorze zdarzeń elementarnych określamy zmienną losową X :
X (1 oczko) = -10,
X (2 oczka) = -10,
X (3 oczka) = 10,
X (4 oczka) = -10,
X (5 oczek) = -10,
X (6 oczek) = 10.
Funkcja rozkładu (prawdopodobieństwa) zmiennej losowej skokowej:
P (X =10) = 1 / 3,
P (X =-10) = 2 / 3.
Dystrybuanta zmiennej losowej skokowej:
Wartość oczekiwana zmiennej losowej:
2
1
3
3
Wariancja:
2
1
3
3
Odchylenie standardowe:
Współczynnik asymetrii:
2
1
3
3
Kurtoza:
K =
2
1
3
3
3
Zmienna losowa ciągła. Przykład.
-3,3 ))
4
=
1,50
0,71
0,000127
(
-10 - ( -3,3 ))
4
+
(
10 - (
))
3
+
(
10 - ( -3,3 ))
3
=
- ( -3,3 ))
2
=
88,89
9,43
0,00119
(
-10 - ( -3,3
=
-3,33
V(X) =
(
-10 - ( -3,3 ))
2
+
(
10
E(X) =
*
-10
+
*
10
ï
ï
ï
î
ï
ï
ï
í
ì
>
£
<
-
-
£
=
10
x
dla
1
10
x
10
dla
3
/
2
10
x
dla
0
)
x
(
F
å
=
=
n
1
i
i
i
x
p
)
X
(
E
å
=
-
=
n
1
i
2
i
i
))
X
(
E
x
(
p
)
X
(
V
3
n
1
i
3
i
i
))
X
(
E
x
(
p
A
s
s
å
=
-
=
[
4
n
1
i
4
i
i
))
X
(
E
x
(
p
K
s
å
=
-
=
[
=
s
A
]
]

Dana jest funkcja:
.
Ażeby funkcja ta była gęstością zmiennej losowej X, muszą być spełnione
warunki:
1.
oraz
2.
.
A. Warunek 1. jest spełniony, ponieważ f(x) dla x < 0 równa jest zeru.
B. Wartość f(x) dla argumentów z przedziału (0, 1] jest dodatnia. Zachodzić
musi warunek:
,
ponieważ w przedziale (-∞, 0] oraz w przedziale [1, ∞) funkcja gęstości jest
równa zeru.
Mamy więc:
Dystrybuantę zmiennej losowej ciągłej definiujemy:
.
Dystrybuantę badanej zmiennej wyrazić więc można :
lub
.
4
Obliczmy prawdopodobieństwa: P (X =0,7), P (0<X <0,2), P (X <0,6), P (X >0,7).
ï
ï
ï
î
ï
ï
ï
í
ì
>
£
<
£
=
1
x
dla
0
1
x
0
dla
x
2
0
x
dla
0
)
x
(
f
0
)
x
(
f
³
ò
¥
¥
-
= 1
dx
)
x
(
f
ò
=
1
0
1
xdx
2
ò
ò
=
÷
ø
ö
ç
è
æ -
=
=
=
1
0
1
0
2
1
0
2
1
2
0
1
2
x
2
xdx
2
xdx
2
ò
¥
-
=
<
=
1
dx
)
x
(
f
)
x
X
(
P
)
x
(
F
ï
ï
ï
ï
î
ïï
ï
ï
í
ì
>
£
<
£
=
1
x
dla
0
1
x
0
dla
x
0
x
dla
0
)
x
(
F
2
0
7
,
0
7
,
0
x
xdx
2
)
7
,
0
X
(
P
7
,
0
7
,
0
2
=
=
=
=
ò
2
x
0
2
x
0
x
2
x
2
xdx
2
)
x
X
(
P
)
x
(
F
=
=
=
<
=
ò
a)
P (X =0,7)=0,
,
b)
lub
P (0<X <0,2) = F (0,2)-F (0)=0,04-0=0,04,
c)
lub P (X <0,6) = F (0,6) = 0,36,
d)
lub
Charakterystyki liczbowe rozkładu
a)
,
b)
lub
=
2 / 36
=
,
Me :
x
2
=1 / 2 , a stąd
Me =
=
.
Mo nie istnieje.
5
0,236
1 / 2
0,707
04
,
0
0
2
,
0
x
xdx
2
)
2
,
0
X
0
(
P
2
,
0
0
2
=
=
=
<
<
ò
0
7
,
0
7
,
0
x
xdx
2
)
7
,
0
X
(
P
7
,
0
7
,
0
2
=
=
=
=
ò
36
,
0
0
36
,
0
0
0
6
,
0
x
0
xdx
2
xdx
2
0
)
6
,
0
X
(
P
0
6
,
0
0
2
=
-
+
=
+
=
+
×
=
<
ò
ò
¥
-
.
51
,
0
49
,
0
1
)
7
,
0
(
F
1
)
7
,
0
X
(
P
1
)
7
,
0
X
(
P
)
7
,
0
X
(
P
1
)
7
,
0
X
(
P
1
)
7
,
0
X
(
p
=
-
=
-
=
<
-
=
=
=
+
<
-
=
£
-
=
>
51
,
0
49
,
0
1
7
,
0
1
x
xdx
2
)
7
,
0
X
(
P
1
7
,
0
2
=
-
=
=
=
>
ò
ò
¥
¥
-
=
dx
)
x
(
xf
)
X
(
E
ò
¥
¥
-
-
=
dx
)
x
(
f
)]
x
(
E
x
[
)
X
(
V
2
ò
¥
¥
-
-
=
2
2
)]
x
(
E
[
dx
)
x
(
f
x
)
X
(
V
.
36
2
9
4
4
2
9
4
0
1
4
x
2
3
2
dx
x
2
3
2
dx
x
2
x
)
X
(
V
4
2
1
0
3
1
0
2
2
=
-
=
-
=
÷
ø
ö
ç
è
æ
-
=
÷
ø
ö
ç
è
æ
-
×
=
ò
ò
s
3
2
)
0
(
2
0
0
1
3
x
2
0
dx
0
dx
x
2
dx
0
dx
)
x
(
f
x
)
X
(
E
3
1
1
0
1
3
2
0
=
-
=
+
+
=
+
+
=
=
ò
ò
ò
ò
¥
¥
-
¥
¥
-

Rozkład zero-jedynkowy
Funkcja rozkładu:
P (X =1) = p
oraz
P (X =0) = q,
przy p + q = 1.
Dystrybuanta
Wartość oczekiwana:
Wariancja:
Przykład - rzuty monetą.
Przyporządkujmy 1 wyrzuceniu orła, a wyrzuceniu reszki 0. Zakładając, że p = 0,5, zmienna
losowa X ma rozkład:
P (X =1) = 0,5
oraz
P (X =0) = 0,5 .
Charakterystyki liczbowe rozkładu
E (X ) =
1
*
0,5
+
0
*
0,5
=
0,5 ,
V (X ) =
0,5
*
0,5
=
0,25 ,
=
0,25
=
0,50 .
ï
ï
ï
ï
î
ïï
ï
ï
í
ì
>
£
<
£
=
1
x
dla
1
1
x
0
dla
q
0
x
dla
0
)
x
(
F
.
pq
)
p
1
(
p
p
p
p
q
0
p
1
)
X
(
V
2
2
2
2
=
-
=
-
=
-
×
+
×
=
s
,
p
q
0
p
1
)
X
(
E
=
×
+
×
=
Rozkład równomierny zmiennej skokowej
Dotyczy przypadku, gdy prawdopodobieństwo uzyskania wszystkich wyników
doświadczenia jest jednakowe. Przy skończonej liczbie wyników prawdopodobieństwo to
opisuje funkcja rozkładu:
1
n
i - numer realizacji,
n - liczba możliwych realizacji zmiennej losowej.
Charakterystyki liczbowe rozkładu
1
1
n
n
n
½
Σ
i
[x
i
- E(X )]
3
{{
Σ
i
}
½
}
3
n
Σ
i
[x
i
- E(X )]
4
{
Σ
i
}
2
Przykład
6 modułów programu zawiera po
1
,
2
,
3 ,
4 ,
5
6
błędów.
Wylosowanie któregokolwiek z modułów jest jadnakowo prawdopodobne:
P(X = x
i
) =
1 /
6
.
Znaleźć charakterystyki liczbowe tego rozkładu.
1
21
n
6
x
i
1
2
3
4
5
6
suma
1
n
n
½
Σ
i
[x
i
- E(X )]
3
*
0
3
{{
Σ
i
[x
i
-E(X )]
2
}
½
}
3
{(
17,5 )
½
}
3
n
Σ
i
[x
i
- E(X )]
4
6
*
{
Σ
i
}
2
17,5
2
P(X = x
i
) =
,
gdzie:
x
i
- i -ta realizacja zmiennej losowej X ,
Wartość oczekiwana:
Σ
i
x
i
Wariancja
Σ
i
[x
i
- E(X )]
2
Współczynnik asymetrii
[x
i
-E(X )]
2
Kurtoza
[x
i
-E(X )]
2
Wartość oczekiwana:
Σ
i
x
i
=
=
3,5
x
i
- E(X )
[x
i
- E(X )]
2
[x
i
- E(X )]
3
[x
i
- E(X )]
4
-2,5
6,25
-15,625
39,0625
-1,5
2,25
-3,375
5,0625
-0,5
0,25
-0,125
0,0625
0,5
0,25
0,125
0,0625
1,5
2,25
3,375
5,0625
2,5
6,25
15,625
39,0625
0
17,5
0
88,375
Σ
i
[x
i
- E(X )]
2
=
17,5
=
2,92
6
=
2,449
=
0,0
=
0
73,208
=
88,375
=
1,731
[x
i
-E(X )]
2
Przykład
6 modułów programu zawiera po
1
,
2
,
4 ,
6 ,
8
9
błędów.
Wylosowanie któregokolwiek z modułów jest jadnakowo prawdopodobne:
P(X = x
i
) =
1 /
6
.
Znaleźć charakterystyki liczbowe tego rozkładu.
1
30
n
6
x
i
1
2
4
6
8
9
suma
1
n
n
½
Σ
i
[x
i
- E(X )]
3
*
0
3
{{
Σ
i
[x
i
-E(X )]
2
}
½
}
3
{(
52,0 )
½
}
3
n
Σ
i
[x
i
- E(X )]
4
6
*
{
Σ
i
}
2
52,0
2
Wartość oczekiwana:
Σ
i
x
i
=
=
5
x
i
- E(X )
[x
i
- E(X )]
2
[x
i
- E(X )]
3
[x
i
- E(X )]
4
-4
16
-64
256
-3
9
-27
81
-1
1
-1
1
1
1
1
1
3
9
27
81
6
4
16
64
256
0
52
0
676
0,0
=
0
374,977
Σ
i
[x
i
- E(X )]
2
=
52
=
8,67
=
676
=
1,500
[x
i
-E(X )]
2
=
2,449
=
s
ss
Rozkład dwumianowy (binomialny, Bernoulliego, B (n, p ))
Funkcja rozkładu:
,
gdzie: k = 0,1,2,..,n oraz p + q = 1.
Dystrybuanta:
Wartość oczekiwana: E (X ) = np .
Wariancja:
V (X ) = npq.
Zmienna o tym rozkładzie opisuje doświadczenie polegające na przeprowadzeniu n (n > 1 )
niezależnych eksperymentów, wynikiem których mogą być tylko sukces lub porażka:
- prawdopodobieństwo wystąpienia sukcesu jest takie samo w kolejnych eksperymentach,
przy czym p + q =1,
- eksperymenty są niezależne.
Rozkład dwumianowy przy p = q jest symetryczny, przy p < q jest prawostronny, a przy
p > q - lewostronnie asymetryczny.
Przypadek dla n = 3 przy rzutach monetą. Sukcesem jest wyrzucenie orła.
Zbiór zdarzeń elementarnych Ω =
=
{(R,R,R), (R,R,O), (R,O,R), (O,R,R), (R,O,O), (O,R,O), (O,O,R), (O,O,O)}.
X
0
1
1
1
2
2
2
3
P ( A
i
)
q
3
q
2
p
q
2
p
q
2
p
p
2
q
p
2
q
p
2
q
p
3
Rozkład prawdopodobieństwa zmiennej losowej X :
Wartość zmiennej x
i
Prawdopodobieństwo p
i
np. dla p =
0,2
q = 0,8
Prawdopodobieństwo p
i
Prawdopodobieństwo otrzymania k sukcesów w określonej kolejności jest równe
p
k
q
n-k
.
Z kolei k sukcesów w dowolnej kolejności można otrzymać na tyle sposobów, ile jest
kombinacji k -elementowych z n elementów. Tak więc zdarzenie X =k jest sumą zdarzeń,
z których każde ma prawdopodobieństwo równe
p
k
q
n-k
.
Stąd mamy
dla k = 0,1,2,... .
3
p
3
1,000
Suma
( p + q )
3
= 1
0,008
3q
2
p
1
2
3p
2
q
0,512
0,384
0,096
0
q
3
å
<
-
÷÷
ø
ö
çç
è
æ
=
x
k
k
n
k
.
q
p
k
n
)
x
(
F
÷÷
ø
ö
çç
è
æ
k
n
k
n
k
q
p
k
n
)
k
X
(
P
)
k
,
p
,
n
(
B
-
÷÷ø
ö
ççè
æ
=
=
=
k
n
k
q
p
k
n
)
k
X
(
P
)
p
,
n
(
B
-
÷÷ø
ö
ççè
æ
=
=
=
Przykład - pięciokrotny rzut monetą.
Zmienną losową X jest liczba wyrzuconych orłów, czyli sukcesów. Prawdopodobieństwo
pojawienia się orła w każdym rzucie jest stałe i równe 1/2, a wyniki rzutów nie mają wpływu
na siebie.
Prawdopodobieństwa poszczególnych realizacji zmiennej losowej są równe:
5
1
0
1
5
1
0
2
2
32
5
1
1
1
4
1
1
1
2
2
2
16
5
1
2
1
3
1
1
2
2
2
4
8
5
1
3
1
2
1
1
3
2
2
8
4
5
1
4
1
1
1
1
4
2
2
16
2
5
1
5
1
0
1
5
2
2
32
Dystrybuanta
0
1
2
3
4
5
> 5
1
6
16
26
31
32
32
32
32
32
E (X ) =
5
* 0,5 = 2,5 ,
V (X ) =
5
* 0,5 * 0,5 =
,
=
=
.
Obliczmy prawdopodobieństwa: P (X<2 ), P (X>=4 ), P (2<=X <=4).
a)
P (X<2 ) = P (X =0) + P (X =1) = F (2) = 1
/
32
+
5
/
32
=
6
/
32 ,
b) P (X >=4 ) = P (X =4) + P (X =5) =1- P (X <4) = 1- F (4)
= 6
/
32 ,
c)
P (2<=X<=4 ) = P (X =2) + P (X =3) + P (X =4) = F (5) - F (2) = 25
/
32 .
=
1
32
1
1,25
P (X =5)=
=
1
*
1,25
1,12
*
5
32
P (X =4)=
=
5
*
*
=
*
=
10
32
P (X =3)=
=
10
*
*
=
10
32
P (X =2)=
=
10
*
*
=
5
32
P (X =1)=
=
5
*
=
1
32
P (X =0)=
=
0
1
F (x )
x
1
*
1
*
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
s
k
n
k
q
p
k
)
k
X
(
P
)
k
,
p
,
n
(
B
-
÷÷ø
ççè
=
=
=

Rozkład Poissona
Zmienna losowa X przyjmująca wartości 0, 1, 2, .... z prawdopodobieństwem
, k = 0, 1, 2, ... posiada rozkład Poissona.
Dystrybuanta:
.
Wartość oczekiwana: E (X ) = m.
Wariancja:
V (X ) = m.
Rozkładem tym można przybliżać rozkład dwumianowy, gdy spełnione są warunki:
- co najmniej 20 niezależnych doświadczeń,
- stały iloczyn np równy m ,
- wartość parametru m < 0,2.
Przykład
Zaobserwowano, że w ciągu miesiąca zdrzają się
3 awarie serwera.
Ustalić prawopobieństwa dla przypadków:
- awaria nie wystąpi, a więc k = 0 ,
- nastąpią 4 awarie, a więc k =
4 ,
- liczba awarii nie przekroczy
2 ,
3
0
-3
0 !
3
4
-3
4 !
c)
P (X =0) + P (X =1) + P (X =2) =
3
0
-3
0 !
3
1
-3
1 !
3
2
-3
2 !
=
Suma =
b)
e
0,050
a)
P (X =
0
) =
P (X =
4
) =
,
e
=
0,168
,
=
0,050
] +
P (X =
0
) =
e
=
= [
+ [
+ [
=
) =
P (X =
2
) =
e
=
] =
P (X =
1
0,423
0,149
0,224
] +
e
m
k
e
!
k
m
)
k
X
(
P
-
=
=
å
<
-
=
x
k
m
k
e
!
k
m
)
x
(
F
m
k
e
!
k
m
)
k
X
(
P
-
=
=

Rozkład geometryczny
Zmienna losowa X przyjmująca wartości 1, 2, .... z prawdopodobieństwem
k = 1,2,3, ...,
gdzie: p - prawdopodobieństwo sukcesu, q = 1 - p - prawdopodobieństwo porażki,
k - liczba doświadczeń do pojawienia się pierwszego sukcesu.
Dystrybuanta:
.
Wartość oczekiwana: E (X ) = 1 / p .
Wariancja:
V (X ) = q / p
2
.
Zakłada się tu niezależność doświadczeń i stałe prawdopodobieństwo sukcesu w każdym
doświadczeniu.
Przykład
Programista wykona swoje tygodniowe zadanie z prawdopodobieństwem 0,8 , a wykonaw-
stwo prac w poszczególnych tygodniach jest niezależne.
Zmienna losowa X , którą jest liczbą tygodni oczekiwania na osiągnięcie sukcesu (wykonanie
zadania) ma rozkład:
P (X =1) =
P (X =2) =
P (X =3) =
P (X =4) =
P (X =5) =
Ustalić prawdopodobieństwo, że programista wykona zaplanowaną pracę nie później niż w
2 tygodniu.
P (X <=2) = P (X =1) + P (X =2) = P (X <3) = F (3) =
.
Wartość oczekiwana: E (X ) =
1
/
0,8 =
.
Wariancja:
V (X ) = 0,2
/
=
.
0,80000
0,16000
0,03200
0,64
0,3125
0,00640
0,00128
0,960
1,25
,
pq
)
k
X
(
P
1
k
-
=
=
å
<
-
=
x
k
1
k
pq
)
x
(
F
Rozkład hipergeometryczny
Jest to zmienna losowa X o rozkładzie:
, k =0,1,..., min (R , n ),
gdzie: N - liczebność populacji, R - liczba jednostek z wyróżnioną cechą, n - liczebność
próby, k - liczba sukcesów.
Wartość oczekiwana: E (X ) = n R / N .
Wariancja:
V (X ) = npq (1-n/N ) / (1-1/N ),
gdzie: p = R /N , q = (N - R ) / N .
Przykład
Informatycy wyposażyli pomieszczenie w 4 komputery z posiadanych 10 , wiedząc że
3 spośród wszystkich posiadają po dwa procesory.
Rozkład zmiennej X , która może przyjmować wartości 0, 1, 2, 3 i parametrach N =
10 ,
R = 3 oraz n = 4 :
3
10
-
3
0
4
-
0
1
*
35
10
210
4
3
10
-
3
1
4
-
1
3
*
35
10
210
4
3
10
-
3
2
4
-
2
3
*
21
10
210
4
3
10
-
3
3
4
-
3
1
*
7
10
210
4
Ustalmy prawdopodobieństwo, że wśród wstawionych do pomieszczenia 4 komputerów,
co najmniej
2 z nich posiadają dwa procesory.
P (X >=2 ) = P (X =2) + P (X =3) =
+
=
.
Wartość oczekiwana: E (X )
=
4
*
3
/
10
=
.
3
10
-
3
1 -
4
/
10
10
10
( 1 - 1
/
10 )
=
0,1667
) =
=
=
0,5000
=
P (X =
0
) =
=
P (X =
1
P (X =
2
1,20
) =
=
=
0,3000
*
*
=
0,0333
0,3000
0,0333
Wariancja:
V (X )
=
4
*
P (X =
3
) =
,
.
,
,
.
=
0,560
0,3333
÷÷
ø
ö
çç
è
æ
÷÷
ø
ö
çç
è
æ
-
-
÷÷
ø
ö
çç
è
æ
=
=
n
N
)
k
n
R
N
k
R
)
k
X
(
P
( )(
)
( )
( )(
)
( )
( )(
)
( )
( )(
)
( )
Estymacja
I
1.
Przedzia
ł ufności dla średniej arytmetycznej
A. Za
łożenia:
a) populacja o rozk
ładzie normalnym
N (m ,
Ϭ ),
b) próba o liczebno
ści:
10
.
Suma
ŚredniaOdch. stand.
L.p.
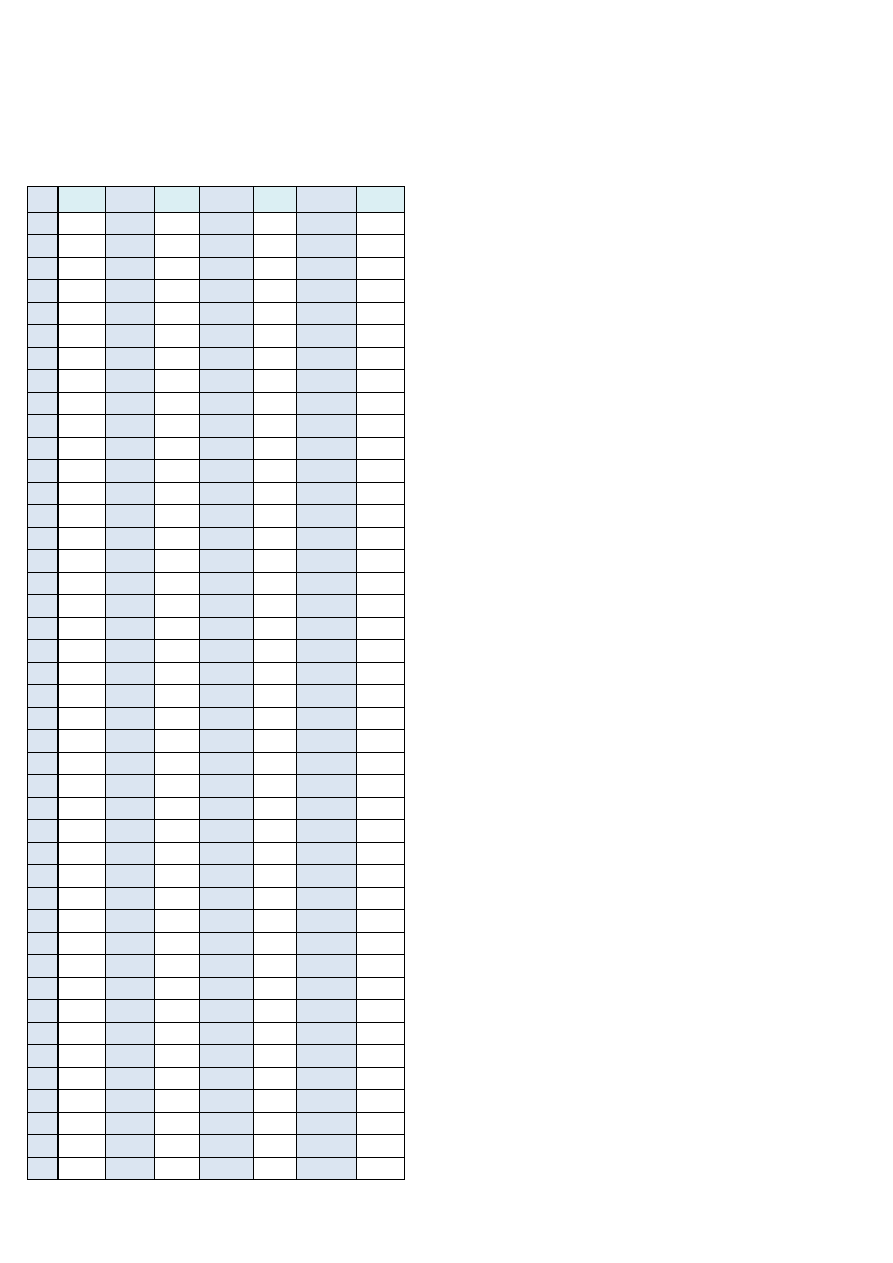
L.p.
1
2
3
4
5
6
7
8
9
10
X
102
112
116
120
124
130
131
134
138
143
1250,0
125
-23
-13
-9
-5
-1
5
6
9
13
18
0
529
169
81
25
1
25
36
81
169
324
1440,0
144
12,0
B.
Średni błąd średniej arytmetycznej przy braku informacji o odchyleniu standardowym w populacji i mało licznej próbie
12
9
Przedzia
ł ufności dla średniej z populacji
C. Przedzia
ły ufności dla podanej próby:
t
α = 0,05, v = 9
=
2,262
;
t
α = 0,01, v = 9
=
3,250
przy b
łędzie alfa = 0,05
P { 125
-
4
*
2,262
< μ <
125
+
4
*
2,2622 } = 1 - 0,05
P { 125
-
9,049
< μ <
125
+
9,049 } = 1 - 0,05
P { 115,95
< μ <
134
} = 1 - 0,05
=
0,95
przy b
łędzie alfa = 0,01
P { 125
-
4
*
3,25
< μ <
125
+
4
*
3,250
} = 1 - 0,05
P { 125
-
13,0
< μ <
125
+
13,0
} = 1 - 0,05
P
{ 112
< μ <
138
} = 1 - 0,05
2.
Przedzia
ł ufności dla wskaźnika struktury
II
=
=
4
)
(
x
x
n
1
i
i
-
å
=
2
1
)
(
x
x
n
i
i
-
å
=
1
-
=
n
S
x
s
{
}
a
s
m
s
a
a
-
=
×
+
<
<
×
-
-
=
-
=
1
1
,
1
,
x
n
v
x
n
v
t
x
t
x
P
Liczebno
ść próby n : 400
jednostki wadliwe m = 80
80
400
u
0,05
=
1,96
u
0,01
=
2,58
a) przy prawdopodobie
ństwie popełnienia pomyłki = 0,05
0,200
*
0,800
0,200
*
0,800
400
400
P (
0,200
-
1,96
*
0,02
< p < 0,200
+
1,96
*
0,02
) = 1 - 0,05
P (
0,161 < p <
0,2392 ) = 1 - 0,05
b) przy prawdopodobie
ństwie popełnienia pomyłki = 0,01
0,200
0,800
0,200
*
0,800
400
P (
0,200
-
2,58
*
0,02 < p < 0,200
+
2,58
*
0,02
)
= 1 -
0,01
P (
0,148 < p <
0,2516
)
= 1 - 0,01
Weryfikacja hipotez statystycznych
III
)
= 1 -
P (
0,05
0,01
P (
wska
źnik struktury m / n = w =
=
)
= 1 -
2,58
< p <
1,96
0,200
0,200
1,96
0,200
0,200
2,58
0,200
400
< p <
a
a
a
-
=
÷
÷
ø
ö
ç
ç
è
æ
-
+
<
<
-
-
1
)
1
(
)
1
(
n
w
w
u
w
p
n
w
w
u
w
P
-
-
×
+
+
1. Test dla wartości średniej populacji
Suma
ŚredniaOdch. stand.
L.p.
L.p.
1
2
3
4
5
6
7
8
9
10
X
96
98
104
102
102
101
104
100
97
96
1000,0
100
-4
-2
4
2
2
1
4
0
-3
-4
0
16
4
16
4
4
1
16
0
9
16
86,0
8,6
2,9
B.
Średni błąd średniej arytmetycznej przy braku informacji o odchyleniu standardowym w populacji i mało licznej próbie
2,9326
9
Korzystając z poprzednich danych ustalić, czy podana próba może pochodzić z populacji o
średniej równej:
.
Hipotezy statystyczne
1.
Hipotezy zerowe
Hipotezy alternatywne
a)
H
0
:
μ
-
μ
0
= 0
H
1
:
μ
-
μ
0
⧧ 0
b)
H
0
:
μ
-
μ
0
> 0
H
1
:
μ
-
μ
0
≤ 0
c)
H
0
:
μ
-
μ
0
< 0
H
1
:
μ
-
μ
0
≥ 0
2.
Ustalenie poziomu istotno
ści
α
3.
Statystyka testu u,
hipotezy : wg a)
100,0
-
102,9
0,98
t
α = 0,05, v = 9
=
2,262
;
t
α = 0,01, v = 9
=
3,250
2. Weryfikacja istotno
ści różnicy między wskaźnikiem struktury a ustaloną jego wartością
IV
Hipotezy statystyczne
=
-2,96
=
=
0,98
102,9
=
)
(
x
x
n
1
i
i
-
å
=
2
1
)
(
x
x
n
i
i
-
å
=
1
-
=
n
S
x
s
x
o
x
t
s
m
0
-
=

1.
Hipotezy zerowe
Hipotezy alternatywne
a)
H
0
: p = p
0
H
1
: p
⧧ p
0
,
b)
H
0
: p > p
0
H
1
: p
≤ p
0
,
c)
H
0
: p < p
0
H
1
: p
≥ p
0
.
2.
Ustalenie poziomu istotno
ści
α
3.
Statystyka testu u
,
m
,
(m - liczebno
ść jednostek wyróżnionych)
n
(n - liczebno
ść próby)
Za
łożenia:
Za
łożenia:
p
0
= 0,05
p
0
= 0,073
n = 400
n = 400
α =
0,05
α =
0,05
u
0,05
= 1,96
u
0,05
= 1,96
w = 0,10
w = 0,10
Hipotezy : wg a)
Hipotezy : wg a)
0,10
-
0,05
0,10
-
0,073
0,05
*
0,95
0,073
*
0,927
400
400
u
α = 0,1
:
1,645
;
u
α = 0,05
:
1,960 ;
u
α = 0,02
:
2,326 ;
u
α = 0,01
:
2,576 .
4,59
2,08
w =
=
u =
u =
=
n
p
p
p
w
u
)
1
(
0
0
0
-
-
=
- Estymacja
Badanie przedzia
łu ufności dla wskaźnika struktury:
Lp.
x
i
Lp.
x
i
Lp.
x
i
Lp.
x
i
1
1
56
1
111
0
166
1
2
0
57
1
112
0
167
1
3
1
58
1
113
1
168
1
4
1
59
0
114
1
169
0
5
0
60
0
115
1
170
0
6
0
61
0
116
0
171
1
7
0
62
1
117
1
172
0
8
1
63
1
118
0
173
1
9
0
64
1
119
0
174
0
10
1
65
0
120
0
175
1
11
0
66
0
121
0
176
0
12
1
67
0
122
0
177
1
13
0
68
0
123
1
178
0
14
1
69
0
124
0
179
1
15
0
70
1
125
0
180
0
16
1
71
0
126
1
181
0
17
0
72
0
127
0
182
1
18
1
73
0
128
0
183
0
19
0
74
0
129
0
184
0
20
1
75
1
130
1
185
0
21
1
76
0
131
1
186
0
22
0
77
1
132
1
187
0
23
0
78
0
133
0
188
0
24
0
79
1
134
1
189
0
25
1
80
0
135
0
190
0
26
0
81
1
136
1
191
1
27
0
82
0
137
1
192
1
28
0
83
1
138
1
193
1
29
0
84
0
139
1
194
1
30
0
85
0
140
1
195
1
31
1
86
0
141
0
196
1
32
1
87
1
142
0
197
0
33
1
88
1
143
0
198
0
34
0
89
1
144
0
199
0
35
0
90
0
145
1
200
0
36
0
91
0
146
0
201
1
37
1
92
0
147
1
202
0
38
1
93
1
148
1
203
1
39
0
94
1
149
1
204
1
40
0
95
1
150
0
205
0
41
0
96
0
151
0
206
0
42
1
97
0
152
0
207
0
43
1
98
1
153
0
208
1
6. Analiza zjawiska IV przy u
życiu metod statystyki indukcyjnej
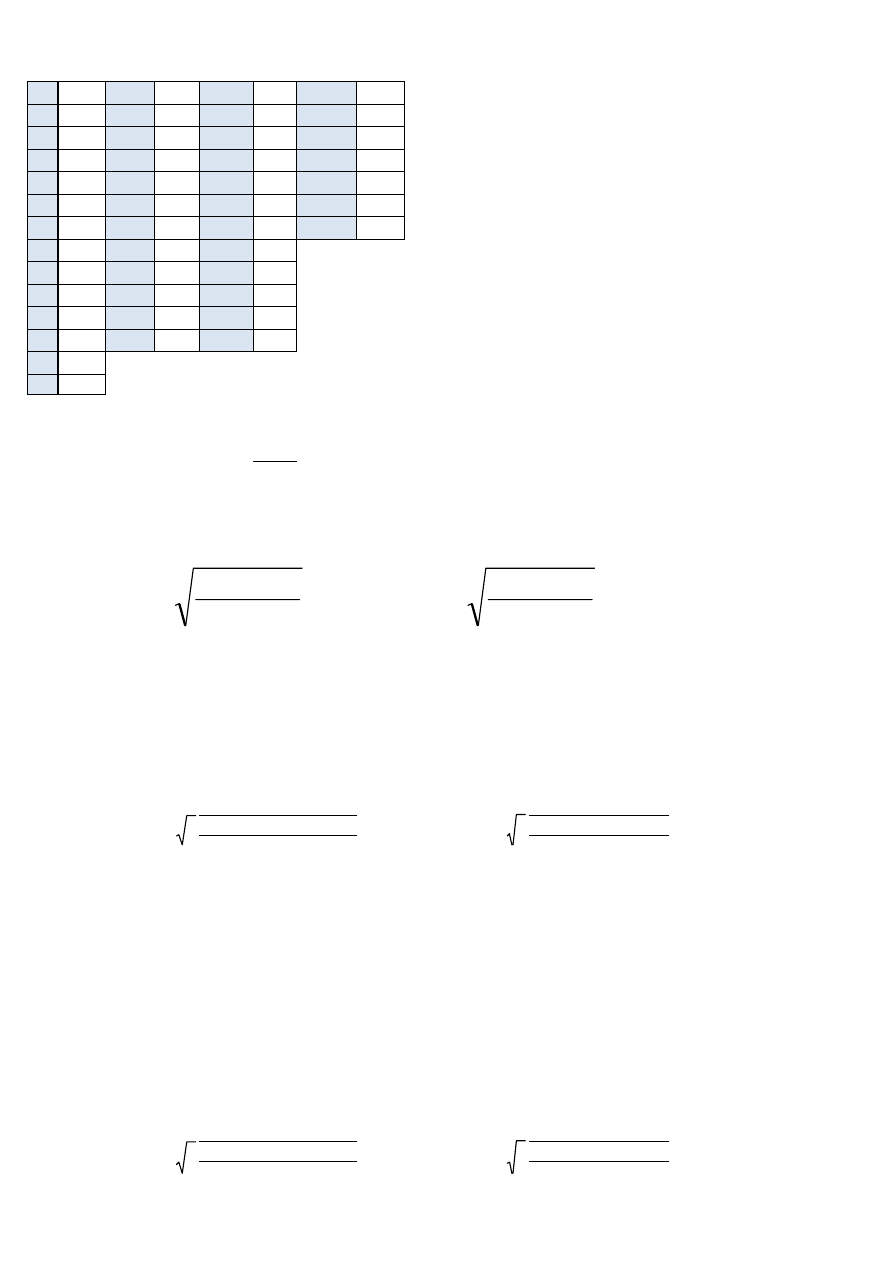
44
1
99
1
154
1
209
0
45
0
100
0
155
1
210
1
46
1
101
1
156
1
211
0
47
0
102
1
157
1
212
1
48
0
103
1
158
1
213
0
49
1
104
1
159
0
214
1
50
1
105
0
160
0
215
1
51
0
106
1
161
0
52
0
107
0
162
1
53
0
108
1
163
0
54
0
109
0
164
1
55
0
110
1
165
1
n
215
m
100
(m - jednostki wadliwe)
(n - liczebność próby)
m
n
a)
u
0,05
=
1,96
b)
u
0,01
=
2,58
p - wskaźnik struktury
n - liczebność prób
m - liczebność wybranej grupy z próby
U
α
- kwantyle odczytane z tablic rozkładu normalnego
a) przy prawdopodobieństwie popełnienia pomyłki = 0,05
0,465
*
0,535
0,465
*
0,535
215
215
P ( 0,465
-
1,96
*
0,03 < p < 0,465
+
1,96
*
0,034 ) = 1 - 0,05
P ( 0,398 < p < 0,532 ) = 0,95
b) przy prawdopodobieństwie popełnienia pomyłki = 0,01
0,465
*
0,535
0,465
*
0,535
215
215
) = 1 - 0,05
w =
=
P ( 0,465
1,96
2,58
) = 1 - 0,01
0,465
Wskaźnik struktury
Przedzia
ł od 39,8% do 53,2% obejmuje swym zasięgiem nieznaną nam wartość wskaźnika
struktury wadliwych modu
łów programów populacji wszystkich modułów z ufnością 0,95 i
prawdopodobie
ństwem popełnienia pomyłki 0,05.
P ( 0,465
2,58
< p < 0,465
< p < 0,465
1,96
a
a
a
-
=
÷÷
ø
ö
çç
è
æ
-
+
<
<
-
-
1
)
1
(
)
1
(
n
w
w
u
w
p
n
w
w
u
w
P
-
+
-
+

P ( 0,465
-
2,58
*
0,03 < p < 0,465
+
2,58
*
0,034 ) = 1 - 0,01
P ( 0,377 < p < 0,553 ) = 0,99
Przedzia
ł od 37,7% do 55,3% obejmuje swym zasięgiem nieznaną nam wartość wskaźnika
struktury wadliwych modu
łów programów populacji wszystkich modułów z ufnością 0,99 i
prawdopodobie
ństwem popełnienia pomyłki 0,01.
- Weryfikacja
n
215
(m - jednostki wadliwe)
m
100
(n - liczebność próby)
m
n
1.
Hipotezy zerowe
Hipotezy alternatywne
a)
H
0
: p = p
0
H
1
: p
⧧ p
0
p
0
testowany wskaźnik struktury
2.
Ustalenie poziomu istotności
α
α=0,05
3.
Statystyka testu u
m
(m - liczebność jednostek wyróżnionych)
n
(n - liczebność próby)
Założenia:
p
0
= 0,05
n = 215
α =
0,05
u
0,05
= 1,96
w = 0,465
Hipotezy : wg a)
0,465
-
0,05
0,05
*
0,95
215
Wnioski:
Do populacji
Obliczona statystyka testu u przekroczy
ła krytyczną wartość statystyki testu u przy
poziomie
α= 0,05 (także przy 0,01), co oznacza że założoną na wstępie hipotezę zerową należy
odrzucić.
Nasza grupa o wska
źniku struktury w=0,465 niepochodzi z populacji o wskaźniku struktury
p
0
, lecz pochodzi z populacji o wska
źniku struktury p różnym od p
0
, czyli ró
żnica między
wska
źnikiem struktury w populacji z której pochodzi próba p a wskaźnikiem struktury p
0
jest ró
żna od 0.
6. Analiza zjawiska V przy u
życiu metod statystyki indukcyjnej
Wskaźnik struktury
w =
=
0,465
w =
u =
=
27,93
n
p
p
p
w
u
)
1
(
0
0
0
-
-
=

Do próby
Ró
żnicę między wskaźnikiem struktury w a próby α wskaźnikiem z struktury p0 uznamy za
statystycznie istotn
ą (równocześnie silnie istotną) ponieważ obliczona statystyka testu u
przekroczy
ła wartość krytyczną statystyki testu u tak przy poziomie istotności u=0,05 i
0,01.
Wyszukiwarka
Podobne podstrony:
OiSS całość nowe 2011 materiały(1)
OiSS całość nowe 2011 materiały(1)
Grzymała Moszczyńska psychologia religii wybrane zagadnienia całość(NOWE)
Grzymała Moszczyńska religia a kultura całość(NOWE)
Jeffmar Flickan i Ijugnen całość(NOWE)
Całość wykłady, chomikowane nowe, ekonomia
socjologia calosc[1], chomikowane nowe, socjologia
Nowe ff bella calosc
Gente podr 2 (nowe wyd ) całość
zajcia 3 nowe
style nowe
Rozrˇd Šwiczenia nowe
pytania nowe komplet
I Nowe Zjawiska
więcej podobnych podstron