–1–

Laboratorium Mechaniki Technicznej

Wyznaczanie współczynnika restytucji

przy prostym, środkowym uderzeniu

opracował:
dr

inż. Marek Romanowicz

Białystok 2006

-2-

1. Cel

ćwiczenia

Celem ćwiczenia jest doświadczalne wyznaczenie współczynnika restytucji w przypadku

uderzenia prostego, środkowego dla par różnych materiałów.

2. Wiadomości teoretyczne

W celu wyprowadzenia wzoru na współczynnik restytucji – k w przypadku uderzenia

prostego, środkowego rozpatrzmy na początek zagadnienie uderzenia dwóch kul, pokazane na
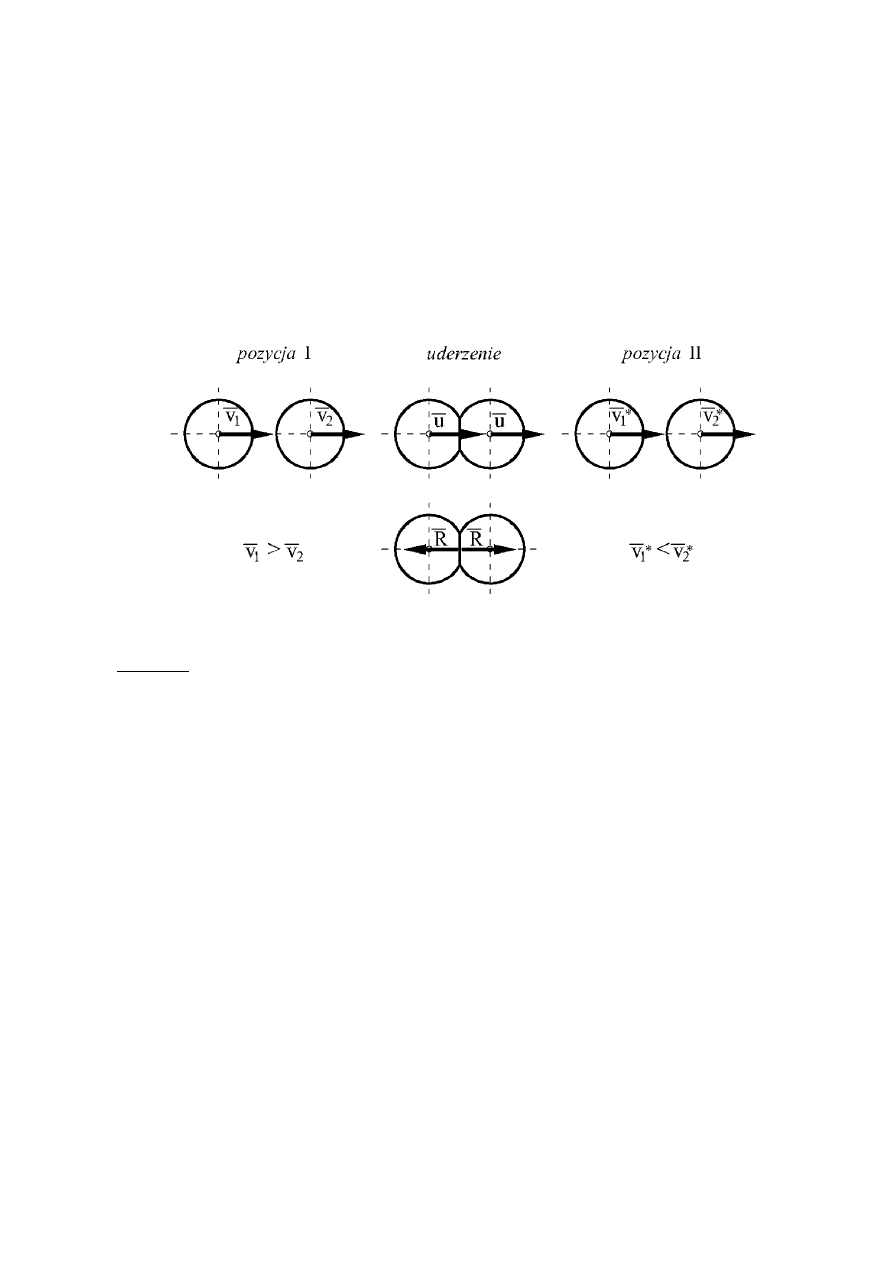
rysunku 1.

Przebieg uderzenia z rysunku 1 można podzielić na dwie fazy. Pierwsza faza trwa od chwili

zetknięcia, aż do chwili wyrównania się prędkości υ

1

, υ

2

. W tym czasie narastają odkształcenia

kontaktowe kul i siły ich wzajemnego oddziaływania, oznaczone przez R. Od chwili wyrównania
się prędkości zaczyna się druga faza. W tym czasie do zera maleją siły wzajemnego oddziaływania
kul. Rozpatrzmy ruch dwóch kul w trakcie uderzenia, tj. gdy istnieją siły wzajemnego
oddziaływania dwóch kul na siebie. Z zasady zachowania pędu masy i popędu siły otrzymujemy
następujące równania dla I i II fazy uderzenia:

gdzie: S’, S” – impuls siły R w I i II fazie uderzenia, m

1

, m

2

– masa kulki pierwszej i drugiej,

u – wspólna prędkość obu kulek, υ

1

, υ

2

– prędkości kulek przed uderzeniem, υ

1

*

, υ

2

*

– prędkości

kulek po uderzeniu, τ’ – czas trwania I fazy uderzenia, τ – całkowity czas uderzenia. Jeżeli

Rys. 1. Schemat uderzenia prostego, środkowego dwóch kul

Definicja: Uderzeniem prostym środkowym nazywamy taki ruch dwóch ciał, gdy prędkości
punktów, w których stykają się ciała, są skierowane wzdłuż wspólnej normalnej do powierzchni
obu ciał, a jednocześnie ta prosta przechodzi przez środki mas .

kula

1

↓

kula 2

↓

I faza uderzenia

→

'

d

'

0

1

1

1

S

t

R

m

u

m

−

=

−

=

−

∫

τ

υ

,

'

d

'

0

2

2

2

S

t

R

m

u

m

=

=

−

∫

τ

υ

(1)

II faza uderzenia

→

"

d

'

1

*

1

1

S

t

R

u

m

m

−

=

−

=

−

∫

τ

τ

υ

,

"

d

'

2

2

S

t

R

u

m

m

=

=

−

∫

τ

τ

*
2

υ

(2)

-3-

założymy, że prędkości kul przed uderzeniem υ

1

, υ

2

są znane to w czterech równiach (1)–(2) mamy

aż pięć niewiadomych. Do ich wyznaczenia potrzebne jest jeszcze jedno równanie, które napiszemy
na podstawie hipotezy Poissona

S”

=

k S’

(3)

gdzie: k – współczynnik restytucji, k

∈ < 0;1 >. Wartość współczynnika restytucji zależy od

materiału z którego wykonane są kule. Mogą wystąpić dwa przypadki graniczne:

• uderzenie idealnie sprężyste k = 1 (S” = S’);

• uderzenie idealnie plastyczne k = 0 (S” = 0).

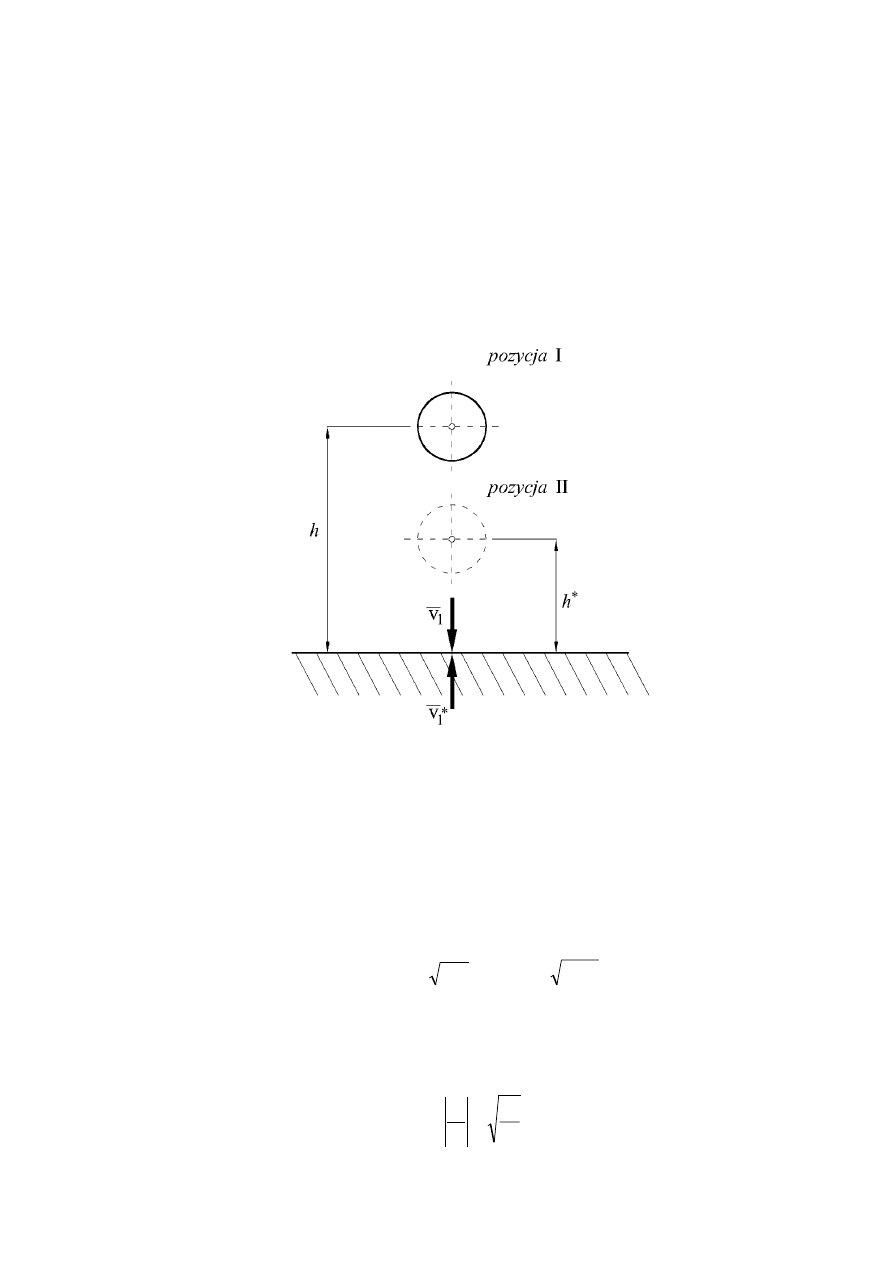
Rozpatrzmy teraz szczegółowo przypadek odbicia się kuli od nieruchomego podłoża,

pokazany na rysunku 2.

Prędkość kuli po uderzeniu w nieruchomą powierzchnię można wyznaczyć z równań (1) – (3). W
tym celu należy uwzględnić w tych równaniach, że υ

2

= υ

2

*

= 0 i m

2

= ∞. Otrzymamy więc

następujące wyrażenie na prędkość kuli po uderzeniu:

υ

1

*

= – k υ

1

(4)

Na podstawie zasady zachowania energii mechanicznej wiemy, że prędkość υ

1

*

i υ

1

opisane są

wzorami

h

g

2

1

=

υ

oraz

*

*

1

g

2 h

=

υ

(5)

gdzie: g – przyśpieszenie ziemskie, h, h

*

– odpowiednio wysokość spadania i odbicia kuli.

Wykorzystując zależności (4) – (5) współczynnik restytucji w przypadku uderzania kuli w
nieruchomą ścianę można zapisać następująco

h

h

k

*

*

1

=

=

1

υ

υ

.

(6)

Rys. 2.

Schemat swobodnego spadania i odbicia kuli od sprężystej,

nieruchomej powierzchni

-4-

3. Opis stanowiska pomiarowego

Podstawowym elementem stanowiska pomiarowego jest para badanych materiałów, złożona z

kulki (1) i płaskiej próbki (4), będącej nieruchomą powierzchnią odbicia. Kulka jest
podtrzymywana za pomocą elektromagnesu (2) na wysokości początkowej h = 1 m. Do pomiaru
wysokości odbicia kulki h

*

od płaskiej powierzchni próbki służy układ pomiarowy, w skład którego

wchodzi liniał pomiarowy (5) oraz kamera cyfrowa (3). Kamera cyfrowa jest sprzężona poprzez
kartę zapisu obrazu z komputerem PC. Plik pomiarowy w formacie *.mpg umożliwia odnalezienie i
zapisanie klatki filmu odpowiadającej położeniu kulki na wysokości odbicia h

*

. Za wysokość

odbicia h

*

uważa się maksymalną wysokość na jaką wzniesie się kulka po odbiciu.

W celu rejestracji obrazu i tzw. poklatkowej jego analizy należy wykorzystać program do

edycji filmów Unlead – VideoStudio v.8. Zapisanie klatki filmu odpowiadającej położeniu kulki na
wysokości odbicia h

*

odbywa się w 3 etapach.

a) Etap 1 to włączenie i wyłączenie rejestracji obrazu za pomocą polecenia „capture video” i

„stop video” (patrz rysunek 4). Operacje tę wykonuje się w zakładce „capture”;

b) Etap 2 to przeprowadzenie tzw. poklatkowej projekcji filmu za pomocą strzałek przewijania

„w lewo” i „ w prawo” (patrz rysunek 5) w celu ustalenia klatki filmu odpowiadającej
najwyższemu położeniu kulki po odbicia. Operacje tę wykonuje się w zakładce „edit”;

c)

Etap 3 to wycięcie właściwej klatki filmu, odpowiadającej wysokości odbicia h

*

za pomocą

polecenia „split video” (patrz rysunek 6).

Rys. 3.

Stanowisko pomiarowe do wyznaczania współczynnika restytucji

–5–

Rys. 4.

Włączanie rejestracji obrazu – polecenie „capture video”

Rys. 5.

Poklatkowa projekcja obrazu – zakładka „edit”

Rys. 6.

Wycinanie klatki filmu – polecenie „split video”

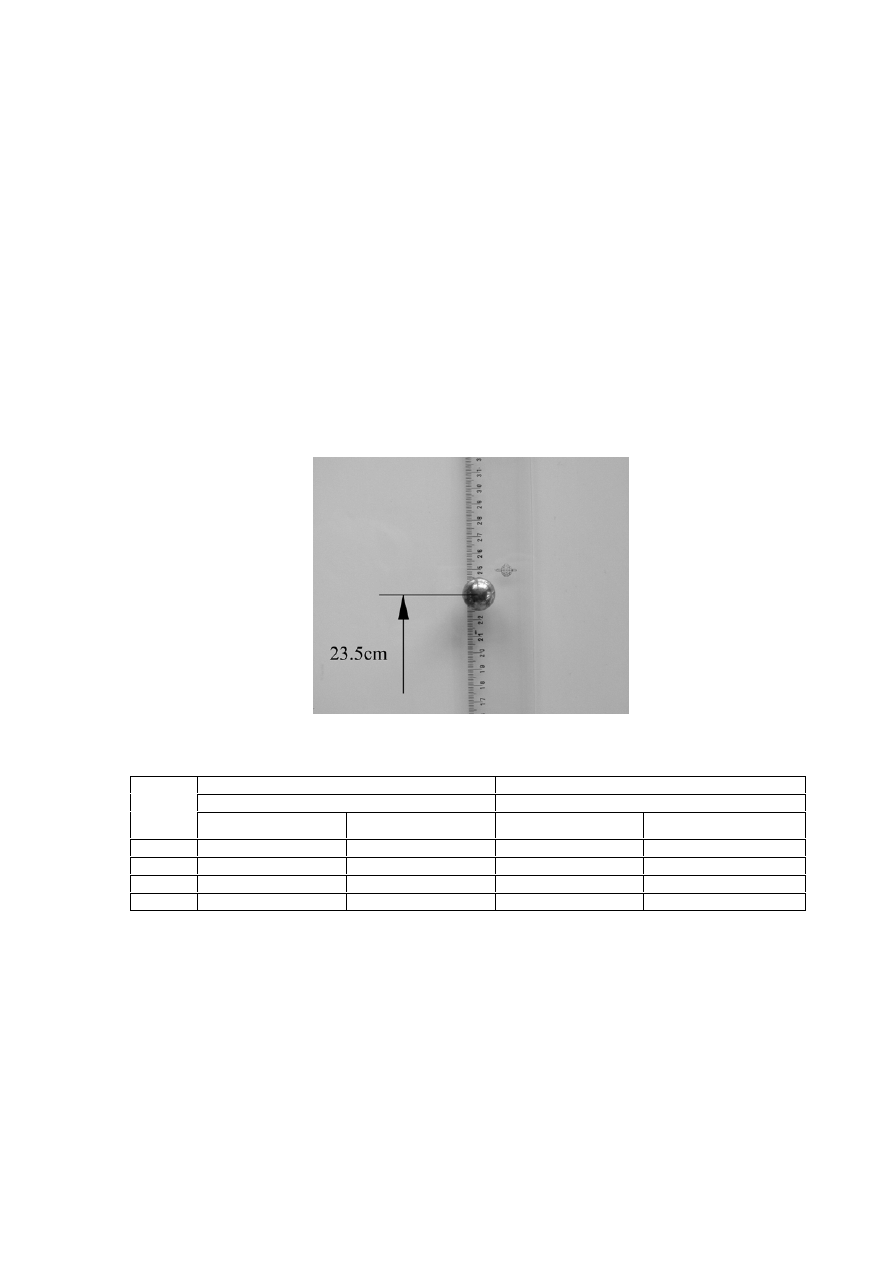
-6-

4. Przebieg

ćwiczenia

a) wypoziomować podstawę stanowiska badawczego;
b) dobrać parę badanych materiałów (kulka + płaska próbka), np. stal – stal, stal – żeliwo, itp;
c) zamocować badaną kulkę na wysokości spadania h = 1 m w uchwycie elektromagnesu;
d) przeprowadzić wstępną próbę (zwolnić uchwyt elektromagnesu) w celu szacunkowego

ustalenia wysokości na której należy zamocować kamerę cyfrową;

e) włączyć rejestrację obrazu i przeprowadzić właściwy pomiar wysokości odbicia h

*

;

f) wyłączyć rejestrację obrazu a następnie pomiary powtórzyć dla innej pary materiałów.

5. Wyniki pomiarów i obliczeń

Wykorzystując wzór (6) obliczyć współczynnik restytucji k dla wybranych par materiałów

przy odbiciu kulki od nieruchomej powierzchni. Wyniki pomiarów i obliczeń zestawić w tabeli 1.
Odczyt wysokości odbicia kulki h

*

wykonać na podstawie właściwej klatki z filmu w sposób

pokazany na rysunku 7 (odległość mierzona od środka ciężkości kulki).

6. Wnioski

Ustosunkować się do możliwości praktycznego wykorzystania wartości współczynnika restytucji k.

7. Literatura

a)

Jerzy Leyko, Mechanika ogólna, T2 – Dynamika, 2002, PWN, Warszawa

b) Anatoliusz Jakowluk, Mechanika techniczna i ośrodków ciągłych. Ćwiczenia laboratoryjne,

1977, PWN, Warszawa

c)

Instrukcja do programu edycji filmów Unlead – VideoStudio v.8.

Rys. 7.

Przykładowy odczyt wysokości odbicia h

*

= 23.5 cm

Tabela 1.

Wyniki pomiarów

Para 1

Para 2

(nazwy) ...................–..........................

(nazwy) ......................–.......................

l.p.

h

*

[mm]

k

h

*

[mm]

k

1

2

3

średnia