Konstrukcje stalowe – sem II
Projekt hali
1
]
[m
3
2
÷
=
d
]
[m
L
h
k
⋅
÷
=
]
14
1
10
1
[
]
[m
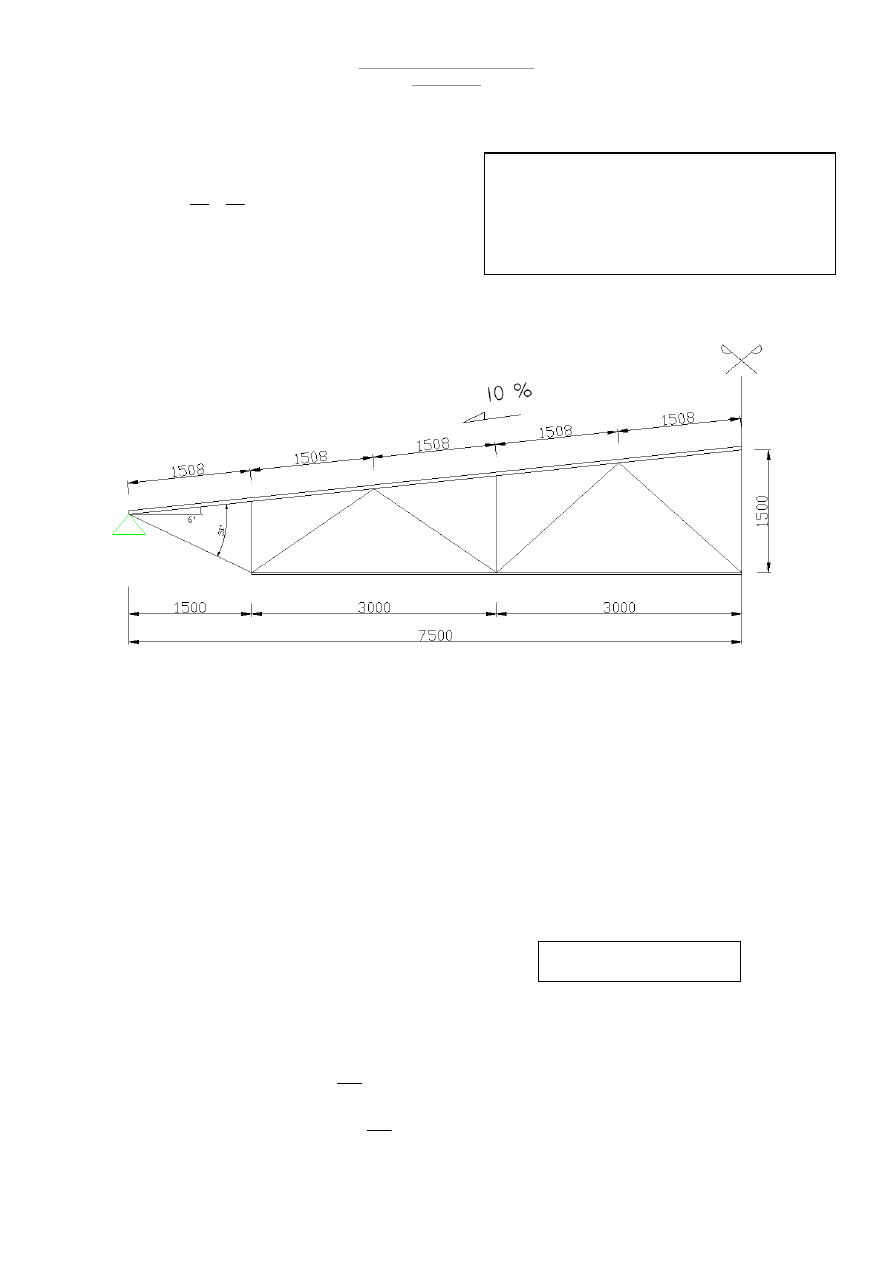
1. Płatew dachowa - rozplanowanie [Rys. 1]
1.1 Geometria wiązara -
Warunki:
Nachylenie połaci - 2 – 10%
Przyjmuje nachylenie połaci dachu α = 6
°
Przyjęte przekroje : [Rys. 2]
3000
=
d
[mm]
1508
=
a
[mm]
1500
1
=
h
[mm]
1.2 Obciążenie od stropodachu
- ciężar stały – [pokrycie dachowe] – płyty warstwowe „REMO”
- obciążenie śniegiem - II strefa klimatyczna
8
,
0
0
,
1
0
,
1
=
=
=
⋅
⋅
⋅
=
α
α
µ
µ
t
e
k
t
e
C
C
S
C
C
S
2
72
,
0
9
,
0
0
,
1
0
,
1
8
,
0
9
,
0
m
kN
S
S
k
=
⋅
⋅
⋅
=
=
2
784
,
0
5
,
1
56
,
0
m
kN
S
S
f
k
=
⋅
=
⋅
=
γ
gdzie : L – rozpiętość w osiach podpór wiązara
d – podział pasa dolnego
a – podział pasa górnego
h
k
– wysokość wiązara
h
1
– wysokość wiązara ponad linia okapu
h
2
– wysokość wiązara pod linia okapu
Eurokod EN 1991-1-3:2003
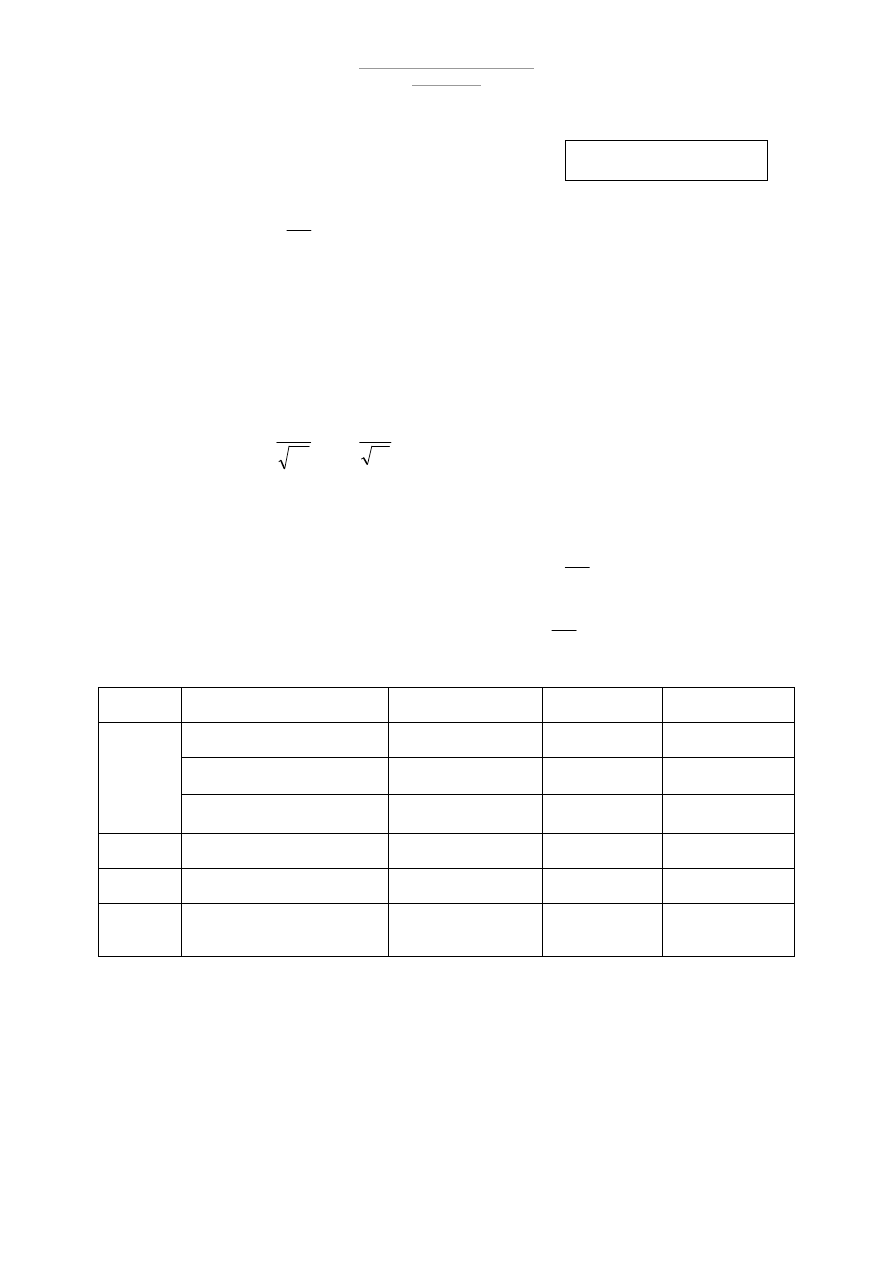
Konstrukcje stalowe – sem II
Projekt hali
2
β
⋅
⋅
⋅
=
C
C
q
p
e
k
k
4
,
0
9
,
0
−
=
−
=
z
z
C
C
- obciążenie wiatrem –
Obciążenie charakterystyczne
2
35
,
0
350
m
kN
Pa
q
k
=
=
Wartość char. ciśnienia prędkości wiatru :
0
=
w
C
Współczynnik ekspozycji
Współczynnik ciśnienia zewnętrznego
Współczynnik podatności porywów wiatru
- wartość logarytmicznego dekrementu tłumienia drgać dla konstrukcji stalowych
∆
= 0,06
- okres drgań własnych :
198
,
0
15
7
,
7
1
,
0
1
,
0
0
=
⋅
=
⋅
=
L
H
T
- Według rysunku 1 PN – 77/B-02011 hala jest nie podatna na działanie porywów wiatru i
β
= 1,8
Obciążenie charakterystyczne dla ściany nawietrznej
2
453
,
0
8
,
1
)
9
,
0
(
8
,
0
35
,
0
m
kN
p
k
−
=
⋅
−
⋅
⋅
=
Obciążenie charakterystyczne dla ściany zawietrznej :
2
20
,
0
8
,
1
)
4
,
0
(
0
,
1
25
,
0
m
kN
p
k
−
=
⋅
−
⋅
⋅
=
Zebranie obciążeń
Lp.
Element
Obciążenie
charakterystyczne
f
γ
Obciążenie
obliczeniowe
1. Ciężar pokrycia
1,19
1,2
1,392
2. Ciężar instalacji
podwieszonych
0,15
1,2
0,18
Obciążenia
Stałe
3. Obciążenie ściagów
0,25
1,2
0,3
q
n
= 0,159
q
o
=1,872
Obciążenia
zmienne
3. Obciążenie śniegiem
0,72
1,5
1,08
4. Obciążenie wiatrem
- strona nawietrzna
- strona zawietrzna
-0,453
-0,20
1,3
-0,634
-0,294
Norma PN – 77/B – 02011
Konstrukcje stalowe – sem II
Projekt hali
3
1.4 Wymiarowanie płatwi zginanych dwukierunkowo
1.4.1 Zebranie obciążeń na kierunki:
Wzdłuż osi X:
m
kN
S
S
m
kN
q
q
m
kN
a
S
S
m
kN
a
q
q
x
x
o
o
62
,
1
6
cos
63
,
1
cos
8
,
2
6
cos
82
,
2
cos
63
,
1
508
,
1
08
,
1
82
,
2
508
,
1
872
,
1
=
⋅
=
⋅
=
=
⋅
=
⋅
=
=
⋅
=
⋅
=
=
⋅
=
⋅
=
o
o
α
α
•
Schemat statyczny :
•
Obliczenia RM – WIN
•
Wykresy Momentów: M
max
= 22,9 kNm
•
Wykresy sił tnących : V
max
= 18kN
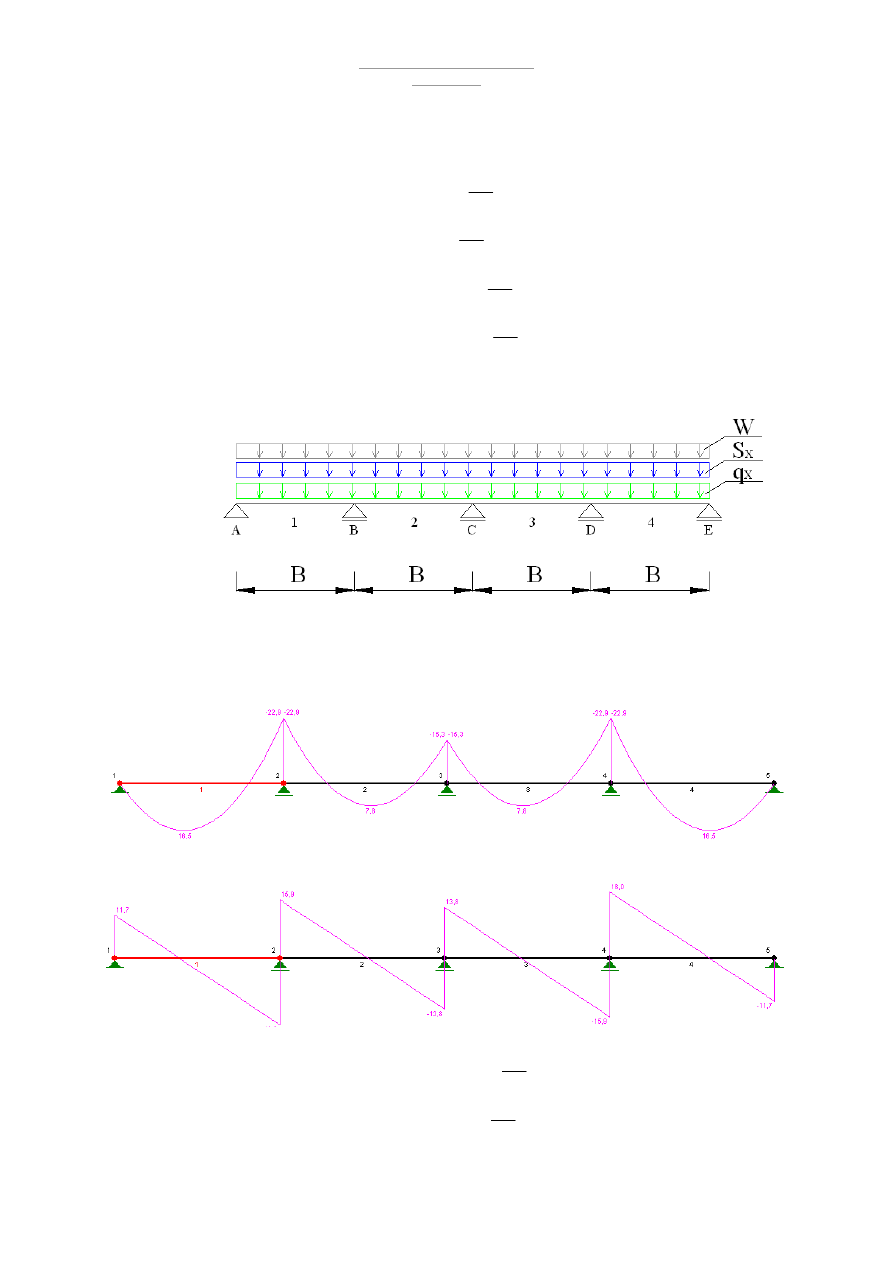
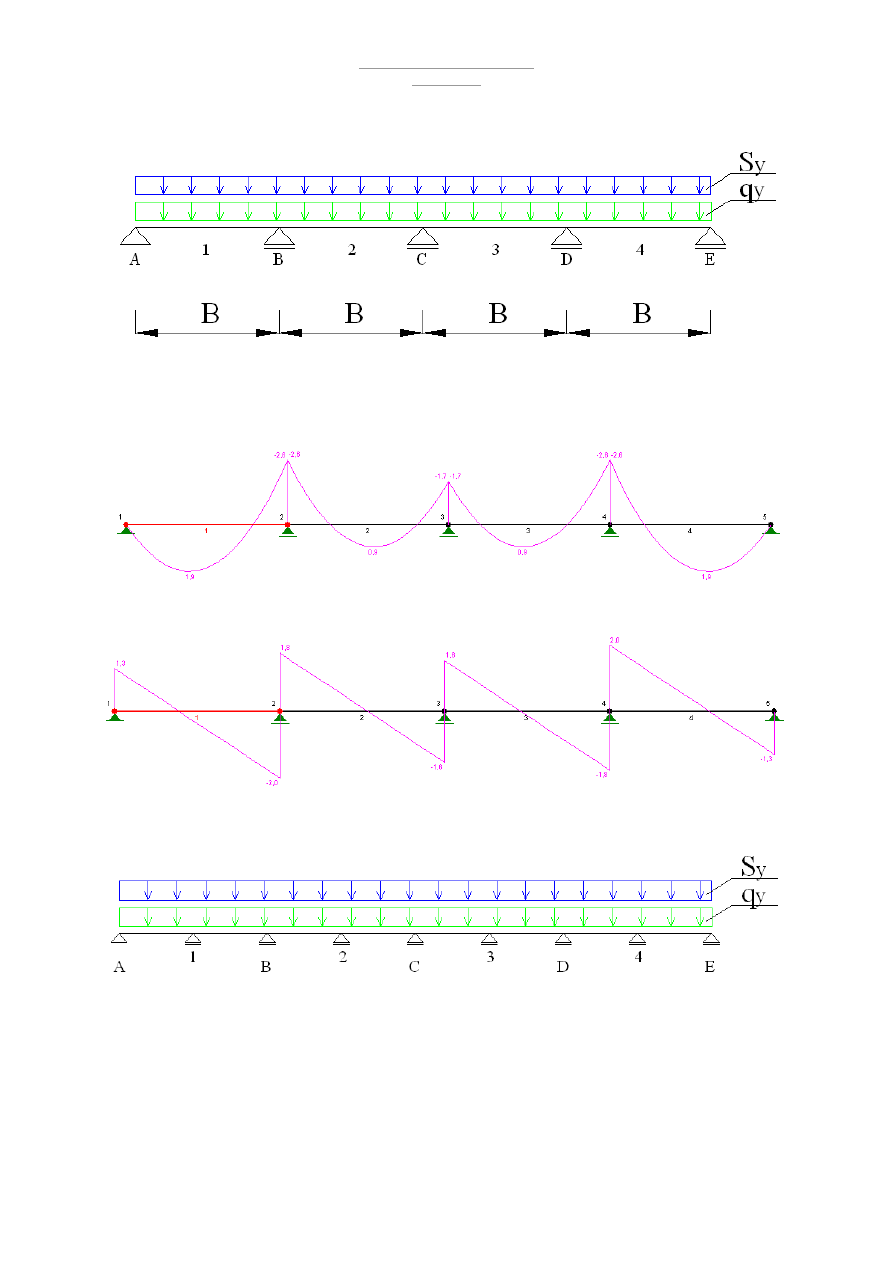
Wzdłuż osi Y:
m
kN
S
S
m
kN
q
q
y
y
17
,
0
6
sin
62
,
1
sin
295
,
0
6
sin
82
,
2
sin
=
⋅
=
⋅
=
=
⋅
=
⋅
=
o
o
α
α
Konstrukcje stalowe – sem II
Projekt hali
4
•
Schemat statyczny
•
Obliczenia RM – WIN
•
Wykresy Momentów: M
max
= 2,6 kNm
•
Wykresy Sił tnących V
max
= 2kN
•
Schemat statyczny po zastosowaniu ściągów
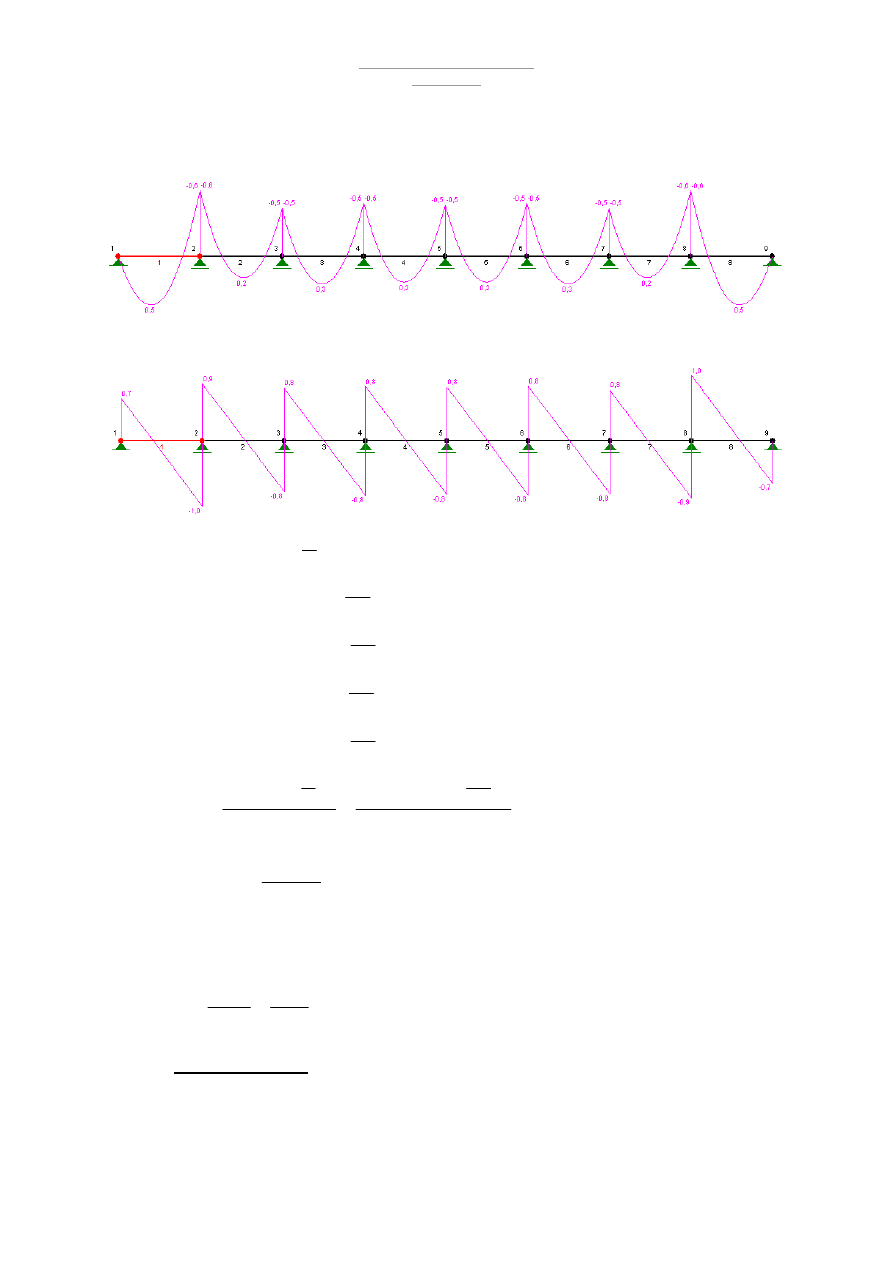
Konstrukcje stalowe – sem II
Projekt hali
5
•
Obliczenia RM – WIN po zastosowaniu ściągów
•
Wykresy Momentów: M
max
= 0,6 kNm
•
Wykres sił tnących V
max
= 1 kN
1.5 Obliczenie sił rozciągających w ściągach
2
)
(
B
q
S
n
S
y
y
⋅
+
=
kN
S
kN
S
kN
S
kN
S
696
,
6
2
2
,
7
)
295
,
0
17
,
0
(
4
022
,
5
2
2
,
7
)
295
,
0
17
,
0
(
3
348
,
3
2
2
,
7
)
295
,
0
17
,
0
(
2
674
,
1
2
2
,
7
)
295
,
0
17
,
0
(
1
4
3
2
1
=
⋅
+
⋅
=
=
⋅
+
⋅
=
=
⋅
+
⋅
=
=
⋅
+
⋅
=
kN
B
q
S
S
y
y
57
,
8
67
cos
2
4
2
2
,
7
)
295
,
0
17
,
0
(
cos
2
4
2
)
(
5
=
⋅
⋅
⋅
+
=
⋅
⋅
⋅
+
=
o
β
1.6 Wstępne przyjęcie przekroju
•
1
max
≤
⋅
R
L
M
M
ϕ
przyjmuje
L
ϕ
= 1
max
M
= 22,90 kNm = 2290 kNcm
235
=
d
f
MPa = 23,5 kN/cm
2
44
,
97
5
,
23
2290
max
=
=
≥
d
x
f
M
W
cm
3
•
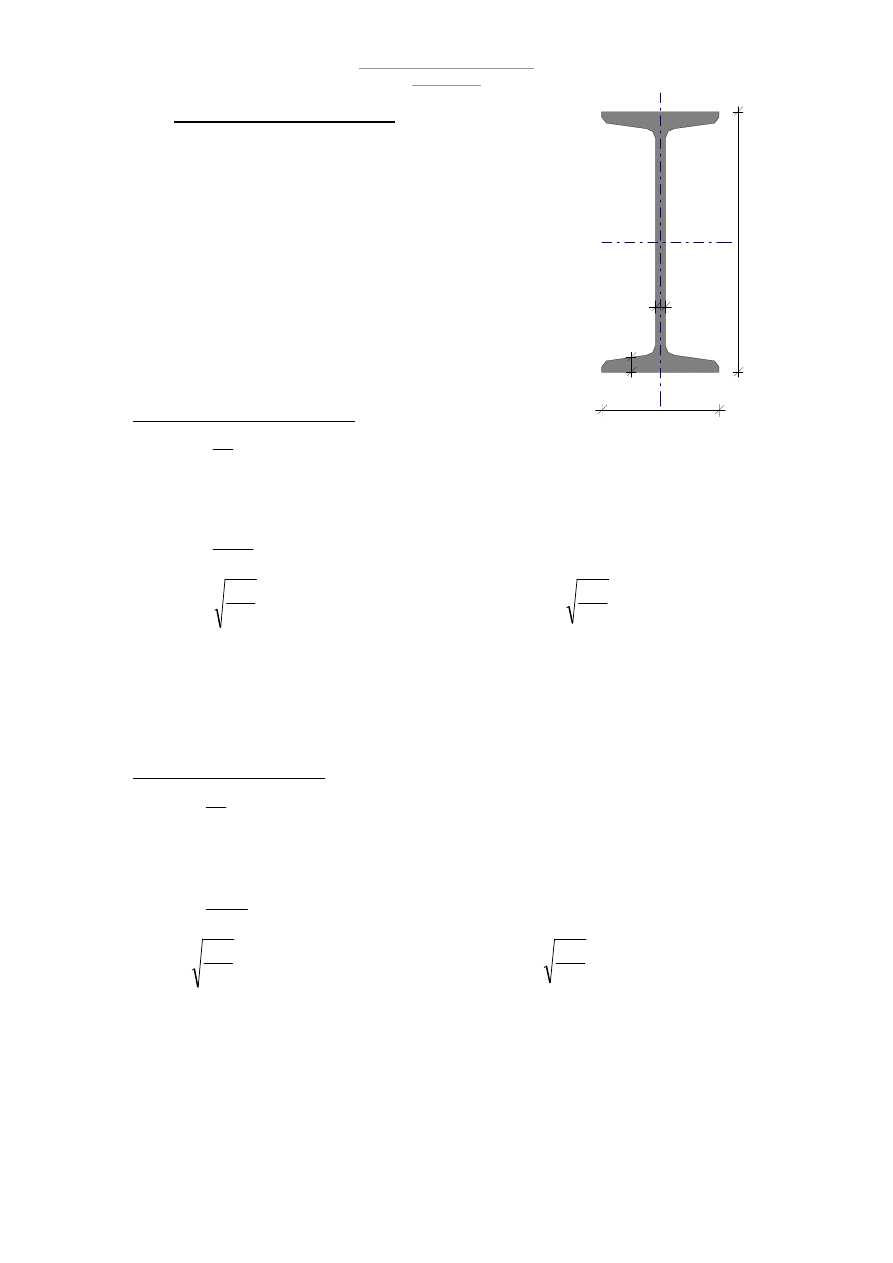
Przyjmuje Dwuteownik I200
Wymiary przekroju
h = 200 mm b
f
= 90 m
t
w
= 7,5 mm t
f
= 11,3 mm
r = 7,5 mm r
1
= 4,5 mm
Konstrukcje stalowe – sem II
Projekt hali
6
y
y
x
x
2
0
0
90
7,5
1
1
,3
Cechy geometryczne przekroju
A = 33,40 cm
2
A
vy
= 15,00 cm
2
A
vx
= 20,34 cm
2
W
x
= 214,0 cm
3
W
y
= 26,00 cm
3
J
x
= 2140 cm
4
J
y
= 117,0 cm
4
i
x
= 8,000 cm i
y
= 1,870 cm
I
ω
= 10400 cm
6
I
Τ
= 14,60 cm
4
W
ω
= 244,0 cm
4
S
x
= 124,0 cm
3
m = 26,20 kg/m
U = 0,709 m
2
/mb
U/A = 212,2 m
-1
1.7 Sprawdzenie przekroju płatwi na zginanie
a) w przęśle
•
określenie klasy przekroju
-
klasa środnika
Określenie smukłości środnika
w
w
s
t
b
=
λ
gdzie:
)
(
2
r
t
h
b
f
w
+
⋅
−
=
=>
mm
b
w
4
,
168
)
5
,
4
3
,
11
(
2
200
=
+
⋅
−
=
45
,
22
5
,
7
4
,
168
=
=
s
λ
ε
λ
⋅
<
33
s
dla klasy 1
d
f
215
=
ε
f
d
dla stali St3S = 235 MPa a więc
956
,
0
235
215
=
=
ε
Sprawdzenie warunku dla klasy 1
55
,
31
956
,
0
33
45
,
22
=
⋅
<
Spełniony
Środnik jest klasy 1
-
klasa półki
Określenie smukłość półki
f
p
p
t
b
=
λ
gdzie :
r
t
s
b
w
p
−
−
⋅
=
)
(
5
,
0
=>
mm
b
p
75
,
36
5
,
4
)
5
,
7
90
(
5
,
0
=
−
−
⋅
=
25
,
3
3
,
11
75
,
36
=
=
p
λ
ε
λ
⋅
<
9
p
dla klasy 1
d
f
215
=
ε
f
d
dla stali St3S = 235 MPa a więc
956
,
0
235
215
=
=
ε
Sprawdzenie warunku dla klasy 1
6
,
8
956
,
0
9
25
,
3
=
⋅
<
Spełniony
Półka jest klasy 1
WNIOSEK: Cały przekrój jest klasy 1
Konstrukcje stalowe – sem II
Projekt hali
7
•
d
x
p
Rx
f
W
M
⋅
⋅
=
α
przyjmuje
p
α
= 1
5029
5
,
23
214
1
=
⋅
⋅
=
Rx
M
kNcm = 50,29 kNm
d
y
p
Ry
f
W
M
⋅
⋅
=
α
przyjmuje
p
α
= 1
611
5
,
23
26
1
=
⋅
⋅
=
Rx
M
kNcm = 6,11kNm
•
Nośność na zginanie
1
1
1
≤
+
⋅
Ry
y
Rx
L
x
M
M
M
M
ϕ
1
11
,
6
6
,
0
29
,
50
90
,
22
≤
+
1
55
,
0
≤
Nośność na zginanie zachowana
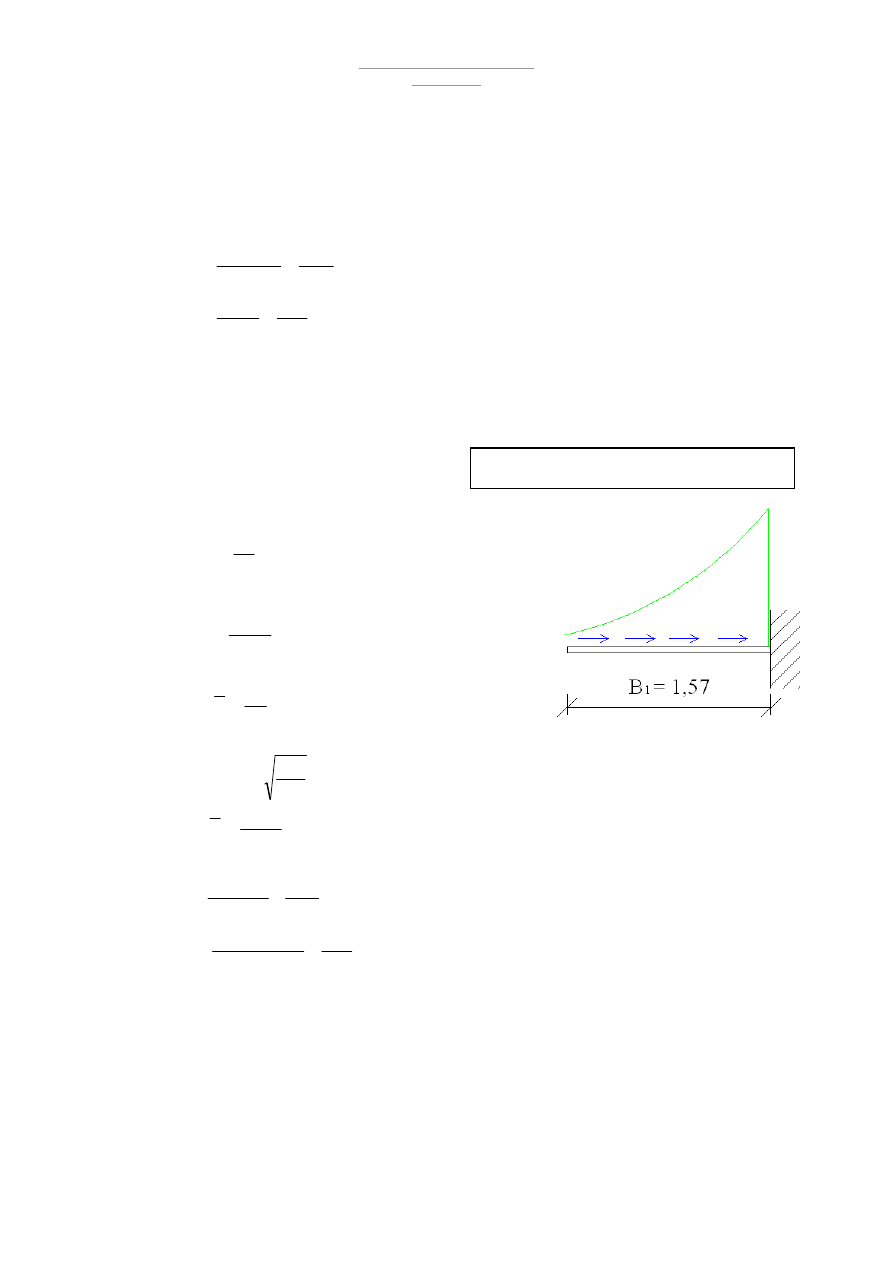
b) na podporze
•
zastępujemy działanie momentu siłą osiową
B = 1,57 m
m
l
l
l
w
w
76
,
1
57
,
1
12
,
1
12
,
1
1
=
⋅
=
⋅
=
•
smukłość giętna pasa ściskanego (dolnego)
yf
w
i
l
=
λ
026
,
0
090
,
0
289
,
0
289
,
0
=
⋅
=
⋅
=
f
yf
b
i
7
,
67
026
,
0
76
,
1
=
=
λ
•
smukłość względna pasa
p
λ
λ
λ
=
842
,
0
34
,
80
7
,
67
34
,
80
235
215
84
=
=
=
=
λ
λ
p
według krzywej „C”
854
,
0
=
L
ϕ
1
1
1
≤
+
⋅
Ry
y
Rx
L
x
M
M
M
M
ϕ
1
11
,
6
6
,
0
29
,
50
854
,
0
9
,
22
≤
+
⋅
1
63
,
0
≤
Nośność na zginanie zachowana
gdzie : l
w
długość wyboczeniowa wspornika

Konstrukcje stalowe – sem II
Projekt hali
8
1.8 Sprawdzenie przekroju płatwi na ścinanie
a ) wzdłuż osi y
1
max
<
R
V
V
kN
V
kN
V
cm
A
f
A
V
R
V
d
V
R
18
45
,
204
5
,
23
15
58
,
0
15
20
75
,
0
58
,
0
max
2
=
=
⋅
⋅
=
=
⋅
=
⋅
⋅
=
1
088
,
0
45
,
204
18
<
=
Nośność zachowana
b ) wzdłuż osi x
1
max
<
R
V
V
kN
V
kN
V
cm
t
b
A
f
A
V
R
f
f
V
d
V
R
1
,
0
23
,
277
5
,
23
34
,
20
58
,
0
34
,
20
13
,
1
9
2
2
58
,
0
max
2
=
=
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
⋅
⋅
=
1
0004
,
0
23
,
277
1
,
0
<
=
Nośność zachowana
1.9 Sprawdzenie nośności na zginanie przy wpływie siły poprzecznej
a) wzdłuż osi y
67
,
122
18
67
,
122
45
,
204
6
,
0
6
,
0
0
0
=
<
=
=
⋅
=
⋅
=
V
V
V
V
xBL
R
nie trzeba uwzględniać wpływu siły poprzecznej
b) wzdłuż osi x
4
,
166
1
,
0
4
,
166
23
,
277
6
,
0
6
,
0
0
0
=
<
=
=
⋅
=
⋅
=
V
V
V
V
xBL
R
nie trzeba uwzględniać wpływu siły poprzecznej
1.10
Sprawdzenie warunku ugięcia płatwi
gr
gr
k
h
x
gr
f
f
cm
l
f
cm
f
S
g
J
E
l
f
f
f
<
=
=
=
=
⋅
⋅
=
⋅
+
⋅
⋅
⋅
⋅
=
⋅
+
⋅
⋅
⋅
⋅
=
≤
1
,
3
200
620
200
27
,
0
00619
,
0
2
,
3368
013
,
0
)
0072
,
0
75
,
0
00159
,
0
5
,
0
(
2140
20500
620
384
5
)
75
,
0
5
,
0
(
384
5
4
4
Warunek ugięcia zachowany.
gdzie: V
R
– nośność obliczeniowa przekroju
na ścinanie
A
V
- pole przekroju czynnego przy
ścinaniu
Konstrukcje stalowe – sem II
Projekt hali
9
1.11. Styk montażowy [Rys. 2]
Rozstawy :
- odległość czoła blachy 30 mm
- rozstaw szeregów 60 mm
Sprawdzenie przykładek
kNm
M
kN
T
1
5
,
8
=
=
α
α
Moment bezwładności środnika :
4
4
3
2140
47
,
298
12
84
,
16
75
,
0
cm
J
cm
J
x
xsr
=
=
⋅
=
kNcm
e
T
M
M
kNcm
J
J
M
M
s
sr
s
x
sr
sr
97
,
64
6
5
,
8
97
,
13
97
,
13
=
⋅
+
=
⋅
+
=
=
⋅
=
α
α
α
α
Siły w śrubach
Od siły poprzecznej :
kN
T
V
125
,
2
4
5
,
8
4
1
=
=
=
α
70
,
2
3
4
3
4
3
97
,
64
70
,
2
3
4
3
4
3
97
,
64
2
2
2
2
=
⋅
+
⋅
⋅
=
⋅
=
=
⋅
+
⋅
⋅
=
⋅
=
sx
a
s
y
xy
a
s
x
S
x
M
F
S
y
M
F
Siła wypadkowa w śrubie A
kN
F
V
F
F
x
y
s
09
,
5
70
,
2
)
125
,
2
70
,
2
(
)
(
2
2
2
2
1
=
+
+
=
+
+
=
1.11
Sprawdzenie nośności ze względu na docisk
t
d
f
S
d
rb
∑
⋅
⋅
⋅
=
α
min
=
α
25
,
4
4
3
12
60
4
3
5
,
2
12
30
1
=
−
=
−
=
=
=
=
d
a
d
a
α
α
kN
S
rb
875
,
52
75
,
0
2
,
1
5
,
23
5
,
2
=
⋅
⋅
⋅
=
875
,
52
09
,
5
1
=
<
=
rb
S
F
Nośność jest spełniona
1.12 Sprawdzenie nośności ze względu na ścięcie trzpienia
kN
S
m
A
R
S
rv
v
m
rv
57
,
33
2
4
2
,
1
33
45
,
0
45
,
0
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
=
π
nośność dla śrub 2 - ciętych
kN
S
F
rv
s
57
,
33
09
,
5
=
<
=
Nośność jest spełniona
Śruby klasy M12 3.6
R
m
= 330 MPa
R
e
= 190 MPa

Konstrukcje stalowe – sem II
Projekt hali
10
2. Dźwigar kratowy
2.1 Schemat statyczny i zebranie obciążeń
2.1.2 Obciążenie stałe A
- ciężar pokrycia
kN
B
a
q
Q
p
01
,
10
2
,
6
508
,
1
392
,
1
1
=
⋅
⋅
=
⋅
⋅
=
- ciężar stężeń
kN
B
a
q
Q
s
80
,
2
2
,
6
508
,
1
3
,
0
2
=
⋅
⋅
=
⋅
⋅
=
- obciążenie instalacjami
kN
B
a
q
Q
i
68
,
1
2
,
6
508
,
1
18
,
0
3
=
⋅
⋅
=
⋅
⋅
=
- obciążenie technologiczne
kN
B
a
q
Q
t
67
,
4
2
,
6
508
,
1
5
,
0
4
=
⋅
⋅
=
⋅
⋅
=
- ciężar płatwi I200
kN
B
q
p
62
,
1
2
,
6
262
,
0
262
,
0
=
⋅
=
⋅
=
SUMA obciążeń
kN
q
q
q
q
q
Q
p
78
,
20
4
3
2
1
=
+
+
+
+
=
2.1.3 Obciążenie śniegiem
- B [połać prawa]
kN
B
d
S
S
k
04
,
10
2
,
6
5
,
1
08
,
1
=
⋅
⋅
=
⋅
⋅
=
- C [połać lewa ]
kN
B
d
S
S
k
04
,
10
2
,
6
5
,
1
08
,
1
=
⋅
⋅
=
⋅
⋅
=
2.1.4 Obciążenie wiatrem
- D [z lewej strony]
połać nawietrzna
kN
B
a
W
n
l
92
,
5
2
,
6
508
,
1
634
,
0
634
,
0
−
=
⋅
⋅
−
=
⋅
⋅
−
=
połać zawietrzna
kN
B
a
W
z
l
74
,
2
2
,
6
508
,
1
294
,
0
294
,
0
−
=
⋅
⋅
−
=
⋅
⋅
−
=
- Słup strona nawietrzna
Współczynnik aerodynamiczny C:
C = C
z
- C
w
= 0,7 - 0 = 0,7
Obciążenie charakterystyczne:
p
k
= q
k
·C
e
·C·
β
= 0,350·1,00·0,7·1,80 =
0,441 kN/m
2
m
kN
h
p
W
s
n
s
73
,
2
2
,
6
441
,
0
=
⋅
=
⋅
=
- Słup strona zawietrzna
Współczynnik aerodynamiczny C:
C = C
z
- C
w
= -0,4 - 0 = -0,4
Obciążenie charakterystyczne:
p
k
= q
k
·C
e
·C·
β
= 0,350·1,00·(-0,4)·1,80 =
-0,252 kN/m
2
m
kN
h
p
W
s
z
s
56
,
1
2
,
6
252
,
0
−
=
⋅
−
=
⋅
=
- E [z prawej strony] - odpowiednio jak w punkcie D
2.1.5
Obciążenie słupów obudowa F
- obciążenie pokryciem
2
392
,
1
m
kN
q
p
=
- rozstaw rygli ściennych
m
c
3
,
1
=
- rozstaw ram
m
B
2
,
6
=
- ciężar jednego rygla ściennego C120
kN
m
mb
kN
q
s
r
844
,
0
3
,
6
134
,
0
=
⋅
=
Obciążenie obudowa ścienna
kN
G
31
,
67
)]
2
,
6
3
,
1
392
,
1
(
844
,
0
[
6
=
⋅
⋅
+
⋅
=
Konstrukcje stalowe – sem II
Projekt hali
11
2.2 Ustalenie schematów statycznych Rys. nr 3
2.3 Obliczenia statyczne za pomocą programu RM-Win dla schematów statyczny z
punktu 2.2
2.4 Wyniki obliczeń statycznych w załączniku Nr 2
2.5 Wykaz sił w danych prętach kratownicy
Nr
Długo
ść
Siły w
pr
ę
tach
Pr
ę
ta
pr
ę
ta [m]
N [max] M [odp] M [max] N [odp]
Wymiarowanie
Pas
górny
1
1,508
324,6
0
4,1
324,6
ś
ciskanie + zginanie
2
1,508
324,2
4,1
4,1
247,3
ś
ciskanie + zginanie
3
1,508
552,8
3,4
3,2
552,8
ś
ciskanie + zginanie
4
1,508
552,8
3,4
3,4
552,8
ś
ciskanie + zginanie
5
1,508
517,6
3,3
3,3
517,6
ś
ciskanie + zginanie
6
1,508
517,6
3,2
3,2
517,6
ś
ciskanie + zginanie
7
1,508
535,9
3,3
3,1
535,9
ś
ciskanie + zginanie
8
1,508
535,9
3,3
3,1
535,9
ś
ciskanie + zginanie
9
1,508
308,9
3,8
3,8
308,9
ś
ciskanie + zginanie
10
1,508
309,2
3,8
0
309,2
ś
ciskanie + zginanie
Pas
dolny
11
3
485,6
4,2
2,0
485,6
rozci
ą
ganie + zginanie
12
3
552,8
4,2
4,2
552,8
rozci
ą
ganie + zginanie
13
3
542,8
4,0
4,0
542,8
rozci
ą
ganie + zginanie
14
3
466
4
4
466
rozci
ą
ganie + zginanie
Słupki
15
0,87
39,2
0
ś
ciskanie
16
1,18
42,5
0
ś
ciskanie
17
1,5
62,7
0
rozci
ą
ganie
18
1,18
38,2
0
ś
ciskanie
19
0,87
35
0
ś
ciskanie
Krzy
ż
ulce
20
1,66
356,9
0
rozci
ą
ganie
21
1,82
197,6
0
ś
ciskanie
22
1,82
77,8
0
rozci
ą
ganie
23
2,01
21,1
0
ś
ciskanie
24
2,01
60,7
0
ś
ciskanie
25
2,01
51,6
0
ś
ciskanie
26
2,01
25,9
0
ś
ciskanie
27
1,82
81,2
0
rozci
ą
ganie
28
1,82
192,4
0
ś
ciskanie
29
1,66
340,1
0
rozci
ą
ganie
Konstrukcje stalowe – sem II
Projekt hali
12
3. Wymiarowanie prętów wiązara
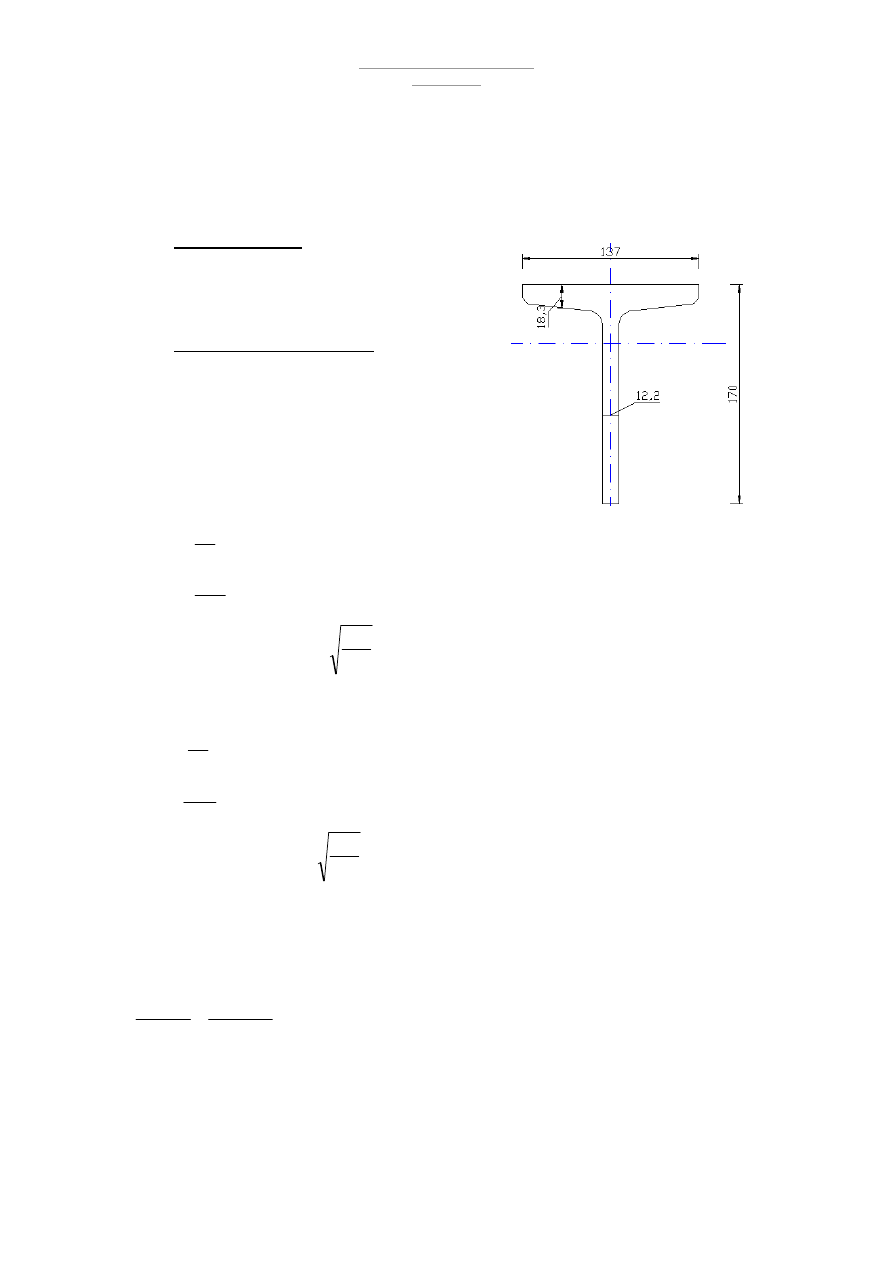
3.1.1 Wymiarowanie pasa górnego
- pas górny jest ściskany siłą N = 552,8 i zginany momentem M = 3,4 kNm
•
Przekrój ½ I340
Dane o przekroju:
Wymiary przekroju
h = 170 mm b
f
= 137 mm
t
w
= 12,2 mm t
f
= 18,3 mm
r = 12,2 mm r
1
= 7,3 mm
e = 4,56 cm
Cechy geometryczne przekroju
A = 43,40 cm
2
A
vy
= 34,04 cm
2
W
x
= 90,60 cm
3
W
y
= 49,20 cm
3
J
x
= 1130 cm
4
J
y
= 337,0 cm
4
i
x
= 5,100 cm i
y
= 2,800 cm
I
= 0 cm
6
I
= 48,70 cm
4
m = 34,05 kg/m
U = 0,586 m
2
/m
•
Ustalenie klasy przekroju
- ustalenie klasy środnika
w
w
s
t
b
=
λ
gdzie
mm
r
t
h
b
f
w
123
)
8
,
10
2
,
16
(
150
)
(
=
+
−
=
+
−
=
38
,
11
8
,
10
123
=
=
s
λ
ε
λ
⋅
<
66
s
gdzie
d
f
215
=
ε
gdzie f
d
dal stali St3S =235 MPa
1
,
63
95
,
0
66
38
,
11
=
⋅
<
Środnik jest klasy 1
- ustalenie smukłości półki
f
p
p
t
b
=
λ
gdzie
mm
r
t
s
b
w
p
75
,
33
8
,
10
)
8
,
10
125
(
5
,
0
)
(
5
,
0
1
=
−
−
⋅
=
−
−
⋅
=
85
,
2
2
,
16
3
,
46
=
=
p
λ
ε
λ
⋅
<
9
p
gdzie
d
f
215
=
ε
gdzie f
d
dal stali St3S =235 Mpa
55
,
8
95
,
0
9
85
,
2
=
⋅
<
Półka jest klasy 1
WNIOSEK : Cały przekrój jest klasy 1
•
Obliczenie nośności elementów ściskanych i zginanych
1
1
∆
−
≤
⋅
+
⋅
Rx
L
x
rc
i
M
M
N
N
ϕ
ϕ
kN
f
A
N
d
rc
15
,
914
5
,
23
9
,
38
1
=
⋅
⋅
=
⋅
⋅
=
ψ
dla przekrojów klasy 1
1
=
ψ

Konstrukcje stalowe – sem II
Projekt hali
13
Wyznaczenie
i
ϕ
18
,
45
67
,
2
8
,
150
8
,
0
29
,
25
77
,
4
8
,
150
8
,
0
=
⋅
=
⋅
=
=
⋅
=
⋅
=
y
y
x
x
i
l
i
l
µ
λ
µ
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
31
,
0
53
,
80
29
,
25
=
=
=
p
x
x
λ
λ
λ
z tablicy 11
944
,
0
=
ix
ϕ
56
,
0
53
,
80
18
,
45
=
=
=
p
y
y
λ
λ
λ
z tablicy 11
807
,
0
=
ix
ϕ
Sprawdzenie nośności na ściskanie
1
74
,
0
15
,
914
807
,
0
8
,
552
1
64
,
0
15
,
914
944
,
0
8
,
552
1
1
<
=
⋅
=
⋅
<
=
⋅
=
⋅
rc
iy
rc
ix
N
N
N
N
ϕ
ϕ
Warunek został spełniony
Sprawdzenie nośności na zginanie
kNm
kNcm
f
W
M
d
x
p
rx
79
,
17
95
,
1778
5
,
23
7
,
75
1
=
=
⋅
⋅
=
⋅
⋅
=
α
1
19
,
0
79
,
17
1
4
,
3
<
=
⋅
=
⋅
Rx
L
x
M
M
ϕ
Składnik poprawkowy
1
∆
[wzór 57 Norma]
1
,
0
25
,
1
2
1
≤
⋅
+
⋅
⋅
⋅
⋅
=
∆
Rx
L
x
rc
i
i
i
M
M
N
N
ϕ
ϕ
λ
ϕ
1
,
0
0103
,
0
79
,
17
1
1
,
4
15
,
914
944
,
0
8
,
552
31
,
0
944
,
0
25
,
1
2
1
≤
=
⋅
⋅
⋅
⋅
⋅
⋅
=
∆
Ogólny warunek
1
1
∆
−
≤
⋅
+
⋅
Rx
L
x
rc
i
M
M
N
N
ϕ
ϕ
98
,
0
93
,
0
0103
,
0
1
19
,
0
74
,
0
<
−
≤
+
Nośność zachowana

Konstrukcje stalowe – sem II
Projekt hali
14
3.1.2 Wymiarowanie pasa dolnego
- pas dolny jest rozciągany siłą N = 552,8 kN i zginany momentem M = 4,2 kNm
•
Przekrój ½ I340
Dane o przekroju:
Wymiary przekroju
h = 170 mm b
f
= 137 mm
t
w
= 12,2 mm t
f
= 18,3 mm
r = 12,2 mm r
1
= 7,3 mm
e = 4,56 cm
Cechy geometryczne przekroju
A = 43,40 cm
2
A
vy
= 34,04 cm
2
W
x
= 90,60 cm
3
W
y
= 49,20 cm
3
J
x
= 1130 cm
4
J
y
= 337,0 cm
4
i
x
= 5,100 cm i
y
= 2,800 cm
I
= 0 cm
6
I
= 48,70 cm
4
m = 34,05 kg/m
U = 0,586 m
2
/m
•
Przekrój jest klasy 1
•
Obliczenie nośności elementów rozciąganych i zginanych
1
<
⋅
+
rx
L
x
rt
t
M
M
N
N
ϕ
L
ϕ
przyjmuje 1 gdyż będą zastosowane ściągi poprzeczne
1
,
2129
5
,
23
60
,
90
1
9
,
1019
5
,
23
4
,
43
=
⋅
⋅
=
⋅
⋅
=
=
⋅
=
⋅
=
d
x
p
rx
d
rt
f
W
M
kN
f
A
N
α
1
73
,
0
29
.
21
2
,
4
9
,
1019
8
,
552
<
=
+
Warunek spełniony
3.1.3
Wymiarowanie słupków elementy ściskane [pręty 15 ,16, 18, 19]
- maksymalna siła działająca w 4 prętach to N = 42,5 kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5,6
•
Dane o przekroju:
Wymiary przekroju
h = 80,0 mm
s = 80,0 mm
g = 5,6 mm
t = 5,6 mm
r = 5,6 mm
Charakterystyka geometryczna przekroju:
J
xg
= 151,0 cm
4
J
yg
=151,0 cm
4
A =16,4 cm
2
J
x
=151,0 cm
4
J
y
=151,0 cm
4
i = 3,03 cm
Konstrukcje stalowe – sem II
Projekt hali
15
1
1
y
y
x
x
50
50
5
0
5
0
4,0
•
Ustalenie klasy przekroju:
- ustalenie klasy ścianek
s
s
s
t
b
=
λ
gdzie
mm
t
h
b
w
w
8
,
68
)]
6
,
5
2
(
80
[
2
)]
2
(
[
2
=
⋅
−
⋅
=
⋅
−
⋅
=
14
,
6
6
,
5
2
8
,
68
=
⋅
=
s
λ
Dla przekrojów rurowych
2
50
ε
λ
⋅
<
s
gdzie
d
f
215
=
ε
gdzie f
d
dal stali St3S =235 MPa
64
,
29
77
,
0
50
14
,
6
2
=
⋅
<
Z uwagi na to, że wszystkie ścianki są takie same cały przekrój jest klasy 1
•
Obliczenie nośności elementu ściskanego siła N = 41,9 kN
1
<
⋅
rc
i
N
N
ϕ
d
Rc
f
A
N
⋅
⋅
=
ψ
dla przekroju klasy 1
1
=
ψ
Określenie współczynnika
i
ϕ
26
,
31
03
,
3
4
,
118
8
,
0
=
⋅
=
⋅
=
x
x
i
l
µ
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
39
,
0
53
,
80
26
,
31
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej b dla przekrojów zamkniętych
970
,
0
=
ix
ϕ
kN
N
Rc
2
,
582
5
,
35
4
,
16
1
=
⋅
⋅
=
1
075
,
0
2
,
582
970
,
0
5
,
42
<
=
⋅
Nośność zachowana
3.1.4
Wymiarowanie słupków element rozciągany [pręt 17]
- maksymalna siła działająca w pręcie to N = 62,7 kN
•
Przekrój tego słupka jest inny niż wszystkich z uwagi na to iż będzie stykiem
montażowym wiązara.
•
Przekrój 2 L 50 x 50 x 4
Cechy geometryczne przekroju
2 kątowniki równoramienne L 50x50x4
Wymiary profilu podstawowego:
a = 50 mm, t = 4,0 mm, r = 7,0 mm,
r
1
= 3,5 mm, e = 1,36 cm,
Charakterystyki profilu podstawowego L 50x50x4
A = 3,890 cm
2
J
x
= 8,970 cm
4
,
J
ξ
= 14,20 cm
4
J
η
= 3,720 cm
4
,
J
x1
= 16,20 cm
4
i
x
= 1,520 cm,
i
ξ
= 1,910 cm
i
η
= 0,980 cm
m = 3,06 kg/m,
U = 0,194 m
2
/m
Konstrukcje stalowe – sem II
Projekt hali
16
Cechy geometryczne przekroju
A = 7,780 cm
2
J
x
= 32,33 cm
4
,
J
y
= 32,33 cm
4
i
x
= 2,039 cm,
i
y
= 2,039 cm
i
1
= 0,980 cm
m = 6,120 kg/m
•
Przekrój klasy 2
•
Obliczenie nośności elementu rozciąganego siła N = 49,2 kN
1
<
rt
t
N
N
kN
f
A
N
d
rt
83
,
182
5
,
23
78
,
7
=
⋅
=
⋅
=
1
36
,
0
83
,
182
7
,
62
<
=
Warunek spełniony
3.1.5
Wymiarowanie krzyżulców ściskanych
3.1.5.1 Pręty 21, 28
- pręt nr 21 ściskany jest siła N = 197,6 kN
- pręt nr 28 ściskany jest siła N = 192,4kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5,6
•
Przekrój klasy 1
•
Obliczenie nośności elementu ściskanego siła N = 197,6 kN
1
<
⋅
rc
i
N
N
ϕ
d
Rc
f
A
N
⋅
⋅
=
ψ
dla przekroju klasy 1
1
=
ψ
Określenie współczynnika
i
ϕ
97
,
47
03
,
3
7
,
181
8
,
0
=
⋅
=
⋅
=
x
x
i
l
µ
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
60
,
0
53
,
80
97
,
47
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej b dla przekrojów zamkniętych
895
,
0
=
ix
ϕ
kN
N
Rc
4
,
385
5
,
23
4
,
16
1
=
⋅
⋅
=
1
57
,
0
4
,
385
895
,
0
6
,
197
<
=
⋅
Nośność zachowana
3.1.5.2 Pręty 23, 26
- pręt nr 23 ściskany jest siła N = 21,1 kN
- pręt nr 26 ściskany jest siła N = 25,9 kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5,6
•
Przekrój klasy 1
•
Obliczenie nośności elementu ściskanego siła N = 25,9 kN

Konstrukcje stalowe – sem II
Projekt hali
17
1
<
⋅
rc
i
N
N
ϕ
d
Rc
f
A
N
⋅
⋅
=
ψ
dla przekroju klasy 1
1
=
ψ
Określenie współczynnika
i
ϕ
12
,
53
03
,
3
2
,
201
8
,
0
=
⋅
=
⋅
=
x
x
i
l
µ
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
65
,
0
53
,
80
12
,
53
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej b dla przekrojów zamkniętych
869
,
0
=
ix
ϕ
kN
N
Rc
4
,
385
5
,
23
4
,
16
1
=
⋅
⋅
=
1
077
,
0
4
,
385
869
,
0
9
,
25
<
=
⋅
Nośność zachowana
3.1.5.3 Pręty 24, 25
- pręt nr 24 ściskany jest siła N = 60,7 kN
- pręt nr 25 ściskany jest siła N = 51,6 kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5,6
•
Przekrój klasy 1
•
Obliczenie nośności elementu ściskanego siła N = 60,7 kN
1
<
⋅
rc
i
N
N
ϕ
d
Rc
f
A
N
⋅
⋅
=
ψ
dla przekroju klasy 1
1
=
ψ
Określenie współczynnika
i
ϕ
12
,
53
03
,
3
2
,
201
8
,
0
=
⋅
=
⋅
=
x
x
i
l
µ
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
65
,
0
53
,
80
12
,
53
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej b dla przekrojów zamkniętych
869
,
0
=
ix
ϕ
kN
N
Rc
4
,
385
5
,
23
4
,
16
1
=
⋅
⋅
=
1
18
,
0
4
,
5385
869
,
0
7
,
60
<
=
⋅
Nośność zachowana
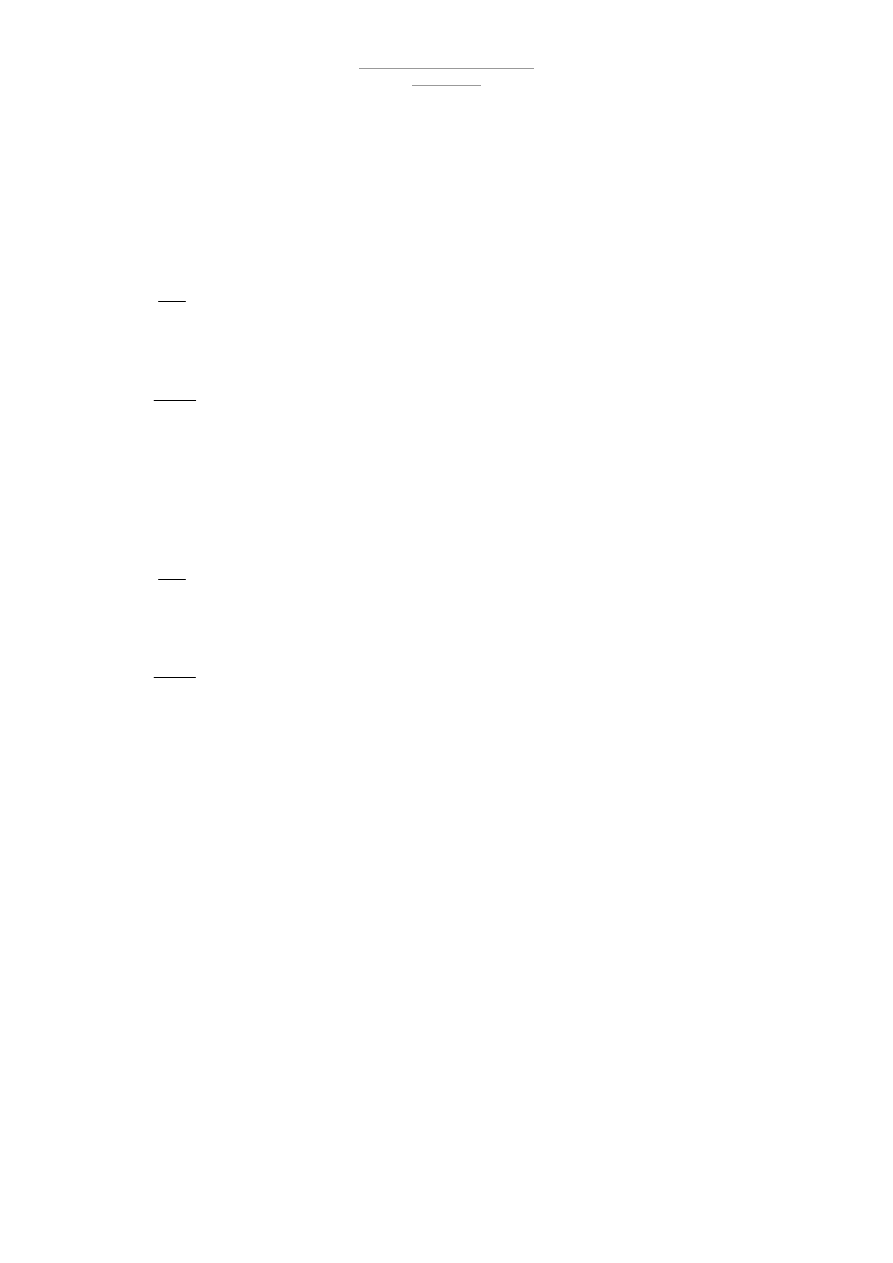
Konstrukcje stalowe – sem II
Projekt hali
18
3.1.6
Wymiarowanie krzyżulców rozciąganych
3.1.6.1 Pręty 20,29
- pręt nr 20 rozciągany jest siła N = 356,9 kN
- pręt nr 29 rozciapany jest siła N = 340,1 kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5
•
Przekrój klasy 1
•
Obliczenie nośności elementu rozciąganego siła N = 356,9 kN
1
<
rt
t
N
N
kN
f
A
N
d
rt
4
,
385
5
,
35
4
,
16
=
⋅
=
⋅
=
1
92
,
0
4
,
385
9
,
356
<
=
Warunek spełniony
3.1.6.1 Pręty 22,27
- pręt nr 22 rozciągany jest siła N = 77,8kN
- pręt nr 27 rozciapany jest siła N = 81,2 kN
•
Przekrój Rurowy prostokątny 80 x 80 x 5,6
•
Przekrój klasy 1
•
Obliczenie nośności elementu rozciąganego siła N = 81,2 kN
1
<
rt
t
N
N
kN
f
A
N
d
rt
4
,
385
5
,
23
4
,
16
=
⋅
=
⋅
=
1
21
,
0
4
,
385
2
,
81
<
=
Warunek spełniony
Konstrukcje stalowe – sem II
Projekt hali
19
4. Wymiarowanie blach węzłowych
4.1 Rodzaje węzłów [ rys. nr 4]
4.2 Węzeł Nr 1 [rys. nr 4.1]
4.2.1 Połączenie krzyżulca z blacha węzłową
Warunki normowe odnośnie wymiarów spoiny
mm
a
mm
mm
a
mm
t
a
t
92
,
3
44
,
2
6
,
5
7
,
0
2
,
12
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
350
35
5
,
3
100
5
,
3
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
Przyjmuje a = 3,5 mm Przyjmuje l = 150 mm
Wymiarowanie spoiny pachwinowej obciążonej osiowo
2
||
||
1
||
8
,
18
5
,
23
8
,
0
cm
kN
f
l
a
P
d
=
⋅
≤
⋅
≤
⋅
=
∑
τ
α
τ
P = 356,9 kN => P
1
= ¼
⋅
356,9 = 89,225 kN
2
||
99
,
16
15
35
,
0
225
,
89
cm
kN
=
⋅
=
τ
Sprawdzenie warunku
2
2
8
,
18
99
,
16
cm
kN
cm
kN
≤
Warunek zachowany
4.2.2 Połączenie pasa górnego z blachą węzłową [Spoina czołowa obciążona osiowo]
Siła ścinająca :
kN
N
W
6
,
324
1
||
=
=
Moment zginający :
kNcm
cm
e
W
M
2
,
1480
56
,
4
6
,
324
||
=
⋅
=
⋅
=
Naprężenia ścinające :
d
f
l
g
W
⋅
≤
⋅
=
||
||
||
α
τ
Naprężenia normalne :
d
x
f
J
x
M
⋅
≤
⋅
=
⊥
⊥
α
σ
Gdzie :
4
3
3
9
,
13691
12
59
8
,
0
12
cm
l
g
J
x
=
⋅
=
⋅
=
cm
l
x
5
,
29
2
59
2
=
=
=
A zatem :
2
2
||
1
,
14
8
,
6
59
8
,
0
6
,
324
cm
kN
cm
kN
<
=
⋅
=
τ
2
2
5
,
23
18
,
3
9
,
13691
5
,
29
2
,
1480
cm
kN
cm
kN
<
=
⋅
=
⊥
σ
α
||
dla R
e
< 255 wynosi 0,8
f
d
= 235 Mpa
P
1
= ½ P gdyż będą 2 kłady spoiny
α
||
dla R
e
< 255 wynosi 0,6
α
⊥
dla R
e
< 255 wynosi 1
f
d
= 235 Mpa
P = ½ P gdyż będą 2 kłady spoiny
Konstrukcje stalowe – sem II
Projekt hali
20
Sprawdzenie warunku :
d
f
≤
+
⊥
2
||
2
α
τ
α
σ
5
,
23
7
,
11
6
,
0
8
,
6
1
18
,
3
2
2
≤
=
+
Warunek zachowany
4.2.3 Wymiarowanie żebra podporowego
Określenie wymiarów żebra
mm
t
mm
mm
h
b
mm
h
s
s
5
50
40
30
287
40
30
300
=
=
+
=
+
=
=
Określenie klasy przekroju żebra
10
5
50
=
=
=
s
s
t
b
t
b
<
3
,
13
95
,
0
14
14
=
⋅
=
⋅
ε
przekrój jest klasy 3
Przekrój zastępczy żebra
2
8
,
17
5
5
,
0
2
8
,
0
8
,
0
20
cm
A
s
=
⋅
⋅
+
⋅
⋅
=
Moment bezwładności względem środnika
4
3
2
3
08
,
53
12
8
,
0
8
,
0
20
)
9
,
2
5
5
,
0
12
5
5
,
0
(
2
cm
J
z
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
Promień bezwładności
cm
A
J
i
s
z
z
98
,
2
8
,
17
08
,
53
=
=
=
Długość wyboczenia żebra
cm
h
l
w
w
24
30
8
,
0
8
,
0
=
⋅
=
⋅
=
Smukłość żebra
05
,
8
98
,
2
24
=
=
=
z
w
z
i
l
λ
Smukłość porównawcza
34
,
80
235
215
84
215
84
=
⋅
=
⋅
=
d
p
f
λ
Smukłość względna
10
,
0
34
,
80
05
,
8
=
=
=
p
z
λ
λ
λ
odczytano z tablicy 11 wg „c”
997
,
0
=
ϕ
Nośność obliczeniowa żebra podporowego
kN
f
A
N
d
s
Rc
3
,
418
5
,
23
8
,
17
1
=
⋅
⋅
=
⋅
⋅
=
ψ
Sprawdzenie warunku nośności żebra podporowego
51
,
0
3
,
418
997
,
0
8
,
212
=
⋅
=
⋅
Rc
A
N
R
ϕ
< 1
Nośność żebra jest zachowana

Konstrukcje stalowe – sem II
Projekt hali
21
4.2.4 Sprawdzenie nośności spoin łączących żebro podporowe
Spoina rozciągana osiowo siłą R
A
= 212,8 kN
Przyjmuje spoine a = 3,5 mm l = 28,7
2
2
||
5
,
23
5
,
22
27
35
,
0
8
,
212
cm
kN
cm
kN
<
=
⋅
=
τ
4.3 Węzeł Nr 2 Kalenicowy [rys 4.2]
4.3.1 Wymiarowanie spoiny pachwinowej łączącej słupek z blachą węzłową
mm
a
mm
mm
a
mm
t
a
t
28
,
0
6
,
1
4
7
,
0
8
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
200
20
2
100
2
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
Pole powierzchni :
2
2
1
1
1
3
3
A
A
A
A
A
A
⋅
+
⋅
⋅
+
=
ψ
Gdzie pole przekroju części przylgowej kątownika brutto
2
1
2
4
,
0
5
cm
A
=
⋅
=
Pole przekroju części odstającej
2
2
89
,
1
2
89
,
3
cm
A
=
−
=
Sprowadzone pole przekroju
2
43
,
3
89
,
1
89
,
1
2
3
2
3
2
cm
A
=
⋅
+
⋅
⋅
+
=
ψ
Obciążenie spoin
kN
P
kN
P
05
,
17
5
36
,
1
7
,
62
64
,
45
5
36
,
1
5
7
,
62
2
1
=
⋅
=
=
−
⋅
=
Potrzebne długości spoin
93
,
6
5
,
23
8
,
0
35
,
0
64
,
45
||
1
1
=
⋅
⋅
=
⋅
⋅
≥
d
f
a
P
l
α
przyjmuje 7 cm
59
,
2
5
,
23
8
,
0
35
,
0
05
,
17
||
2
1
=
⋅
⋅
=
⋅
⋅
≥
d
f
a
P
l
α
przyjmuje 3,5 cm
4.3.2 Wymiarowanie spoiny łączącej blachę węzłową z pasem górnym
Siła ścinająca :
kN
W
27
,
3
84
cos
35
,
31
||
=
⋅
=
Moment zginający :
kNcm
cm
e
W
M
9
,
14
56
,
4
27
,
3
||
=
⋅
=
⋅
=
Gdzie :
4
3
3
13
,
34
12
8
8
,
0
12
cm
l
g
J
x
=
⋅
=
⋅
=
cm
l
x
4
2
8
2
=
=
=
A zatem :
2
2
||
1
,
14
51
,
0
8
8
,
0
27
,
3
cm
kN
cm
kN
<
=
⋅
=
τ
Konstrukcje stalowe – sem II
Projekt hali
22
2
2
5
,
23
39
,
5
13
,
34
4
)
9
,
14
17
,
31
(
cm
kN
cm
kN
<
=
⋅
+
=
⊥
σ
Sprawdzenie warunku :
d
f
≤
+
⊥
2
||
2
α
τ
α
σ
5
,
23
45
,
5
6
,
0
51
,
0
1
39
,
5
2
2
≤
=
+
Warunek zachowany
4.4 Węzeł Nr 3 [rys. 4.3]
•
Warunki normowe odnośnie wymiarów spoiny
mm
a
mm
mm
a
mm
t
a
t
92
,
3
44
,
2
6
,
5
7
,
0
2
,
12
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
350
35
5
,
3
100
5
,
3
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
Przyjmuje a = 3,5 mm Przyjmuje l = 45 mm
•
Wymiarowanie spoiny pachwinowej obciążonej osiowo
2
||
||
1
||
8
,
18
5
,
23
8
,
0
cm
kN
f
l
a
P
d
=
⋅
≤
⋅
≤
⋅
=
∑
τ
α
τ
P = 42,5 kN => P
1
= ¼
⋅
42,5 = 10,62 kN
2
||
74
,
6
5
,
4
35
,
0
62
,
10
cm
kN
=
⋅
=
τ
•
Sprawdzenie warunku
2
2
8
,
18
74
,
6
cm
kN
cm
kN
≤
Warunek zachowany
4.5 Węzeł Nr 4 [rys. 4.4] Połączenie widełkowe
4.5.1 Połączenie krzyżulców Warunek pasem górnym
•
Warunki normowe odnośnie wymiarów spoiny
mm
a
mm
mm
a
mm
t
a
t
92
,
3
44
,
2
6
,
5
7
,
0
2
,
12
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
350
35
5
,
3
100
5
,
3
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
•
Wymiarowanie spoiny pachwinowej obciążonej osiowo
2
||
||
1
||
8
,
18
5
,
23
8
,
0
cm
kN
f
l
a
P
d
=
⋅
≤
⋅
≤
⋅
=
∑
τ
α
τ
•
Pręt numer 23 P = 21,1 kN P
1
= ¼
⋅
21,1 = 5,275 kN
2
||
345
,
3
5
,
4
35
,
0
275
,
5
cm
kN
=
⋅
=
τ
2
2
8
,
18
345
,
3
cm
kN
cm
kN
≤
Warunek zachowany
α
||
dla R
e
< 255 wynosi 0,8
f
d
= 235 Mpa
P
1
= ¼ P gdyż będą 4 kłady spoiny
α
||
dla R
e
< 255 wynosi 0,8
f
d
= 235 Mpa
P
1
= ¼ P gdyż będą 4 kłady spoiny
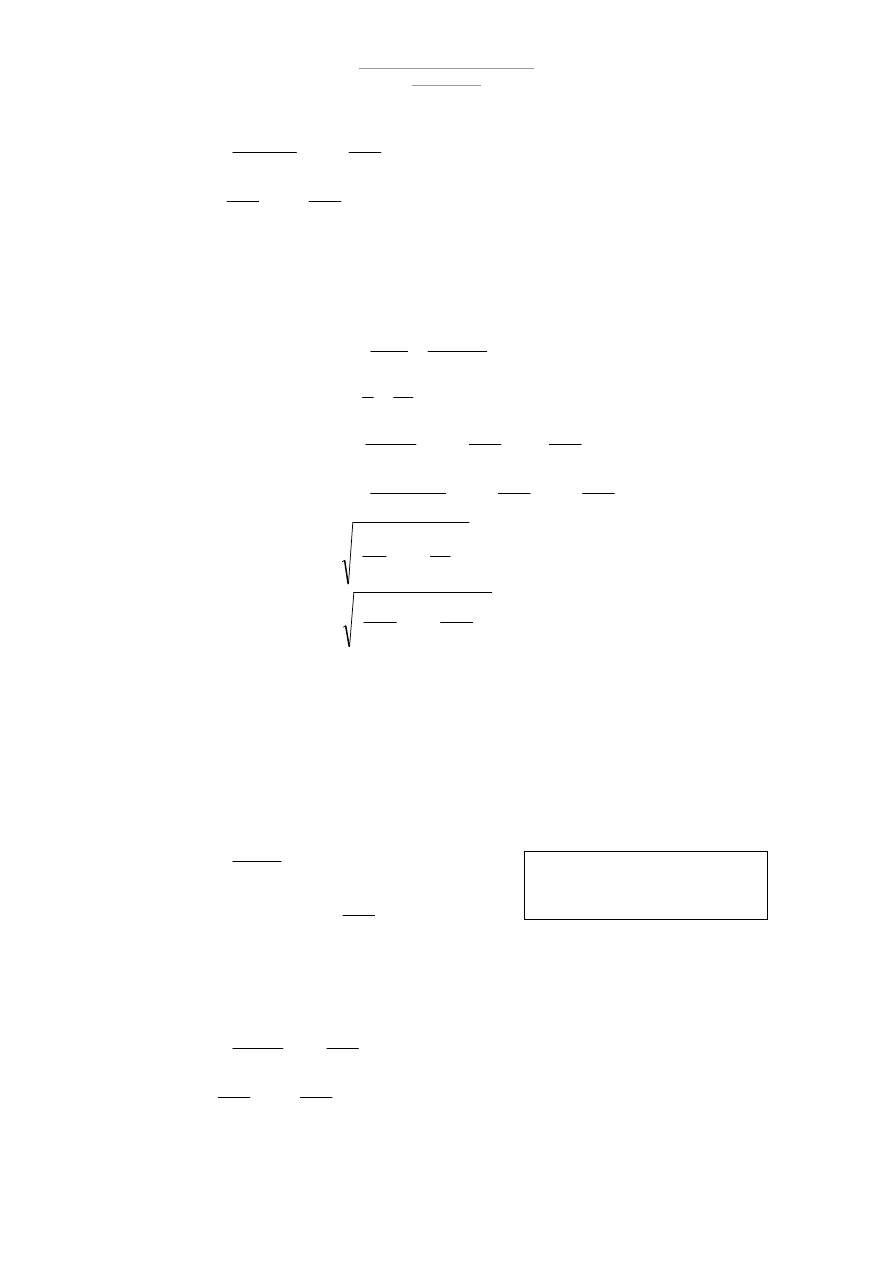
Konstrukcje stalowe – sem II
Projekt hali
23
•
Pręt numer 24 P = 60,7 kN P
1
= ¼
⋅
21,1 = 15,175 kN
2
||
63
,
9
5
,
4
35
,
0
175
.
15
cm
kN
=
⋅
=
τ
2
2
8
,
18
63
,
9
cm
kN
cm
kN
≤
Warunek zachowany
•
Połączenie blachy węzłowej z pasem górnym
Siła ścinająca :
kN
N
N
W
2
,
35
6
,
517
8
,
552
2
1
||
=
−
=
−
=
Moment zginający :
kNcm
cm
e
W
M
51
,
160
56
,
4
2
,
35
||
=
⋅
=
⋅
=
Gdzie :
4
3
3
7
,
11707
12
56
8
,
0
12
cm
l
g
J
x
=
⋅
=
⋅
=
cm
l
x
28
2
56
2
=
=
=
A zatem :
2
2
||
1
,
14
78
,
0
56
8
,
0
2
,
35
cm
kN
cm
kN
<
=
⋅
=
τ
2
2
5
,
23
38
,
0
7
,
11707
28
51
,
160
cm
kN
cm
kN
<
=
⋅
=
⊥
σ
Sprawdzenie warunku :
d
f
≤
+
⊥
2
||
2
α
τ
α
σ
5
,
23
0
,
1
6
,
0
38
,
0
1
78
,
0
2
2
≤
=
+
Warunek zachowany
4.6 Węzeł Nr 5 [rys 4.5]
4.6.1 Połączenie krzyżulców z blachą węzłową
•
Warunki normowe odnośnie wymiarów spoiny
mm
a
mm
mm
a
mm
t
a
t
92
,
3
44
,
2
6
,
5
7
,
0
2
,
12
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
350
35
5
,
3
100
5
,
3
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
•
Wymiarowanie spoiny pachwinowej obciążonej osiowo
2
||
||
1
||
8
,
18
5
,
23
8
,
0
cm
kN
f
l
a
P
d
=
⋅
≤
⋅
≤
⋅
=
∑
τ
α
τ
•
Pręt numer 20 Spoiny przyjęte jak w punkcie 4.2.1
a = 3,5 mm l = 150mm
•
Pręt numer 14 P = 39,2 kN P
1
= ¼
⋅
39,2 = 9,8 kN
2
||
6
,
5
5
35
,
0
8
,
9
cm
kN
=
⋅
=
τ
2
2
8
,
18
6
,
5
cm
kN
cm
kN
≤
Warunek zachowany
•
Pręt numer 21 P = 197,6 kN P
1
= ¼
⋅
197,6 = 49,4 kN
α
||
dla R
e
< 255 wynosi 0,8
f
d
= 235 Mpa
P
1
= ¼ P gdyż będą 4 kłady spoiny
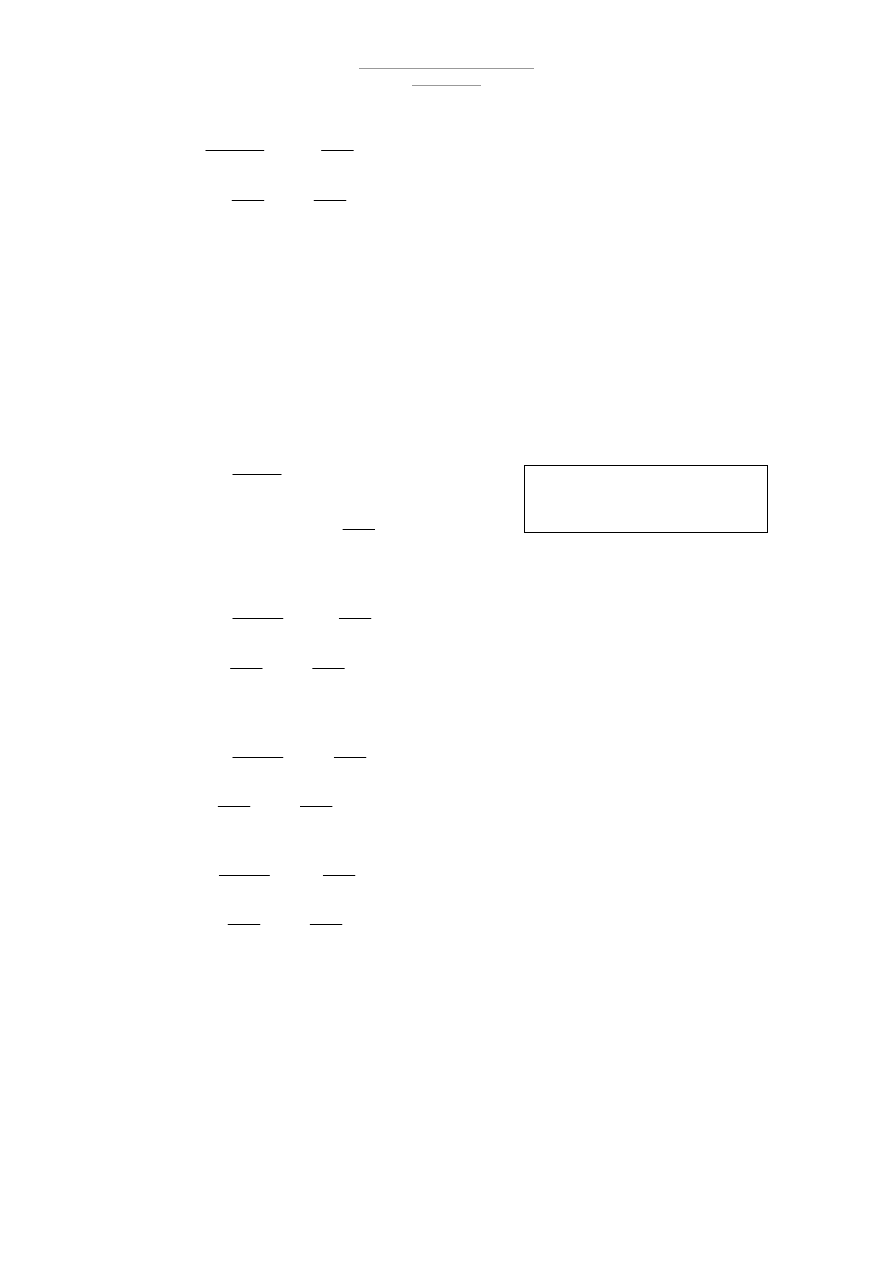
Konstrukcje stalowe – sem II
Projekt hali
24
a = 3,5 mm l = 100mm
2
||
11
,
14
10
35
,
0
4
,
49
cm
kN
=
⋅
=
τ
2
2
8
,
18
11
,
14
cm
kN
cm
kN
≤
Warunek zachowany
4.7 Węzeł Nr 6
4.7.1 Połączenie krzyżulców z blachą węzłową
•
Warunki normowe odnośnie wymiarów spoiny
mm
a
mm
mm
a
mm
t
a
t
92
,
3
44
,
2
6
,
5
7
,
0
2
,
12
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
mm
l
mm
l
a
l
a
i
i
350
35
5
,
3
100
5
,
3
10
100
10
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
•
Wymiarowanie spoiny pachwinowej obciążonej osiowo
2
||
||
1
||
8
,
18
5
,
23
8
,
0
cm
kN
f
l
a
P
d
=
⋅
≤
⋅
≤
⋅
=
∑
τ
α
τ
•
Pręt numer 22 P = 77,8 kN P
1
= ¼
⋅
77,8 = 19,45 kN
2
||
11
,
11
5
35
,
0
45
,
19
cm
kN
=
⋅
=
τ
2
2
8
,
18
11
,
11
cm
kN
cm
kN
≤
Warunek zachowany
•
Pręt numer 23 P = 21,1 kN P
1
= ¼
⋅
21,1 = 5,28 kN
2
||
01
,
3
5
35
,
0
28
,
5
cm
kN
=
⋅
=
τ
2
2
8
,
18
6
,
5
cm
kN
cm
kN
≤
Warunek zachowany
•
Pręt numer 16 P = 42,5 kN P
1
= ¼
⋅
42,5 = 10,62 kN
2
||
07
,
6
5
35
,
0
62
,
10
cm
kN
=
⋅
=
τ
2
2
8
,
18
07
,
6
cm
kN
cm
kN
≤
Warunek zachowany
4.7.2 Połączenie blachy węzłowej z pasem dolnym
Siła ścinająca :
kN
W
9
,
12
42
cos
1
,
21
8
,
552
34
cos
8
,
77
6
,
485
||
−
=
⋅
−
+
⋅
−
−
=
o
o
Moment zginający :
kNm
kNcm
cm
e
W
M
59
,
0
,
8
,
58
56
,
4
9
,
12
||
1
−
=
−
=
⋅
−
=
⋅
=
Moment zginający od sił prostopadłych:
kN
S
54
,
16
42
sin
1
,
21
5
,
42
31
sin
8
,
77
−
=
⋅
−
−
⋅
=
o
o
α
||
dla R
e
< 255 wynosi 0,8
f
d
= 235 Mpa
P
1
= ¼ P gdyż będą 4 kłady spoiny
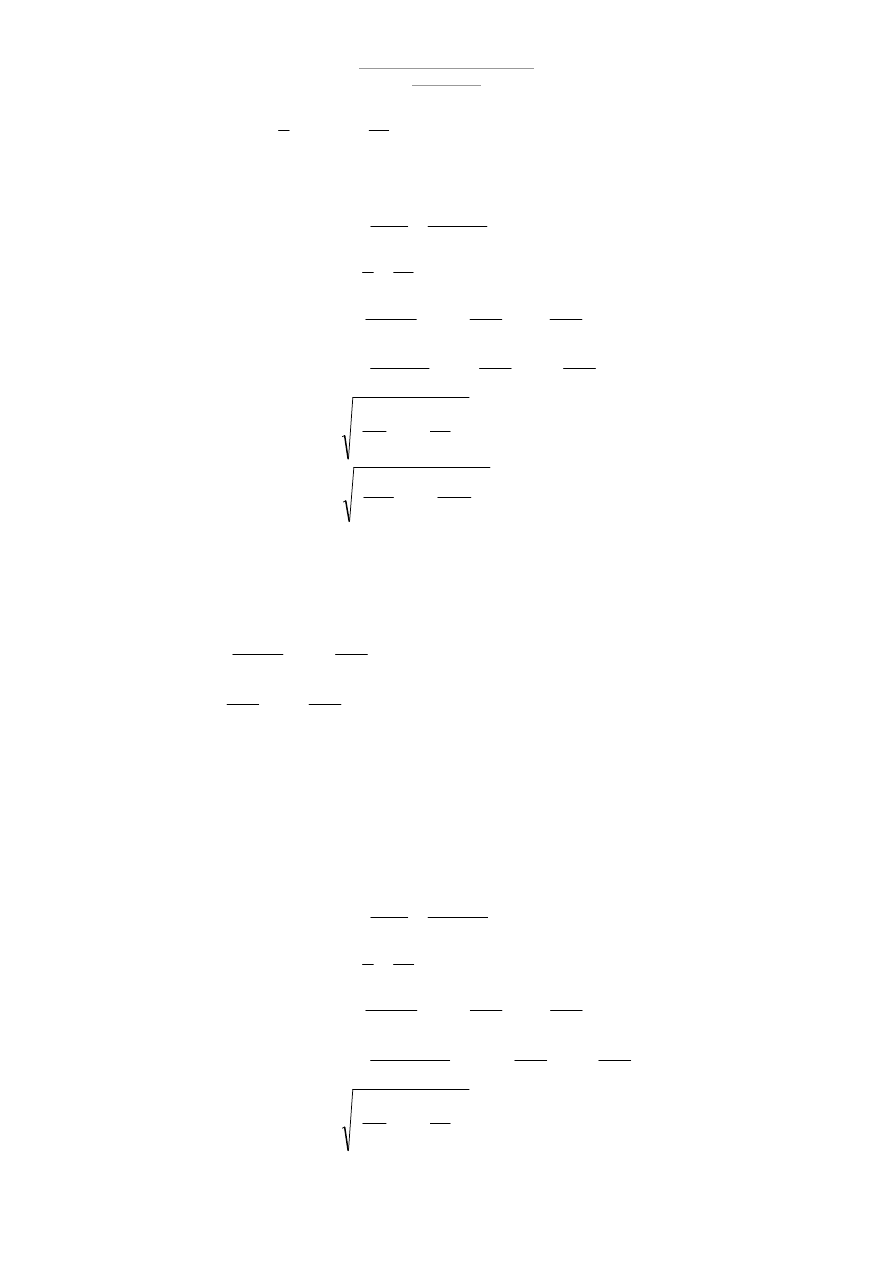
Konstrukcje stalowe – sem II
Projekt hali
25
kNm
kNcm
l
S
M
46
,
5
82
,
545
2
66
54
,
16
2
2
−
=
−
=
⋅
−
=
⋅
=
Moment zginający
kNm
M
M
M
05
,
6
546
,
0
59
,
0
2
1
=
+
=
+
=
Gdzie :
4
3
3
4
,
19166
12
66
8
,
0
12
cm
l
g
J
x
=
⋅
=
⋅
=
m
l
x
33
2
66
2
=
=
=
A zatem :
2
2
||
1
,
14
24
,
0
66
8
,
0
9
,
12
cm
kN
cm
kN
<
=
⋅
=
τ
2
2
5
,
23
04
,
1
4
,
19166
33
605
cm
kN
cm
kN
<
=
⋅
=
⊥
σ
Sprawdzenie warunku :
d
f
≤
+
⊥
2
||
2
α
τ
α
σ
5
,
23
11
,
1
6
,
0
24
,
0
1
04
,
1
2
2
≤
=
+
Warunek zachowany
4.8 Węzeł nr 7 [rys 4.7]
4.8.1 Połączenie krzyżulców z blachą węzłową
Pręt 17 tak jak w punkcie 4.3.1
Pręt 24 P = 60,7 kN P
1
= ¼
⋅
60,7 = 15,17 kN
2
||
66
,
8
5
35
,
0
17
,
15
cm
kN
=
⋅
=
τ
2
2
8
,
18
66
,
8
cm
kN
cm
kN
≤
Warunek zachowany
4.8.2 Połączenie blachy węzłowej z pasem dolnym
Siła ścinająca :
kN
N
W
1
,
45
42
cos
7
,
60
42
cos
1
||
=
⋅
=
⋅
=
Moment zginający :
kNcm
cm
e
W
M
4
,
205
56
,
4
1
,
45
||
=
⋅
=
⋅
=
Moment od siły prostopadłej
kNcm
M
1
,
354
10
35
,
31
1
)
42
sin
7
,
60
(
=
⋅
+
⋅
⋅
=
Gdzie :
4
3
3
2
,
1312
12
27
8
,
0
12
cm
l
g
J
x
=
⋅
=
⋅
=
m
l
x
5
,
13
2
27
2
=
=
=
A zatem :
2
2
||
1
,
14
08
,
2
27
8
,
0
1
,
45
cm
kN
cm
kN
<
=
⋅
=
τ
2
2
5
,
23
75
,
5
2
,
1312
5
,
13
5
,
559
cm
kN
cm
kN
<
=
+
⋅
=
⊥
σ
Sprawdzenie warunku :
d
f
≤
+
⊥
2
||
2
α
τ
α
σ

Konstrukcje stalowe – sem II
Projekt hali
26
5
,
23
71
,
6
6
,
0
08
,
2
1
75
,
5
2
2
≤
=
+
Warunek zachowany
5. Styki montażowe dźwigara [Rys 5]
5.1 Wymiarowanie styku
•
Siły
kN
N
8
,
552
=
kNm
M
3
,
3
=
kN
P
7
,
62
=
•
Wymiarowanie spoin łączących ½ I340 z blacha czołową
Charakterystyka geometryczna spoiny
Pole przekroju :
2
4
,
43 cm
A
s
=
Położenie osi obojętnej:
cm
e
56
,
4
=
Moment bezwładności :
4
1139
cm
J
x
=
Moment statyczny spoiny pasa
3
5
,
90
)
95
,
0
56
,
4
(
83
,
1
7
,
13
cm
S
spx
=
−
⋅
⋅
=
Moment statyczny spoiny środnika
3
2
39
,
94
2
)
56
,
4
17
(
22
,
1
cm
S
spx
=
−
⋅
=
Składowe naprężeń
Naprężenia od siły osiowej (naprężenia średnie)
MPa
A
N
s
N
3
,
127
4
,
43
8
,
552
=
=
=
σ
Naprężenia od zginania
W punkcie 1 (rozciąganie )
MPa
I
y
M
sx
9
,
16
1130
56
,
4
420
1
1
=
⋅
=
⋅
=
σ
W punkcie 2 (rozciąganie )
MPa
I
y
M
sx
1
.
10
1130
)
83
,
1
56
,
4
(
420
1
2
=
−
⋅
=
⋅
=
σ
W punkcie 4 (ściskanie )
MPa
I
y
M
sx
2
,
46
1130
)
56
,
4
17
(
420
1
4
−
=
−
⋅
−
=
⋅
−
=
σ
Naprężenia normalne
MPa
N
2
,
119
=
σ
Naprężenia styczne
W punkcie 2
MPa
a
I
S
P
sx
spx
1
,
41
22
,
1
1130
5
,
90
7
,
62
2
=
⋅
⋅
=
⋅
⋅
=
τ
W punkcie 3
MPa
a
I
S
P
sx
spx
9
,
42
22
,
1
1130
39
,
94
7
,
62
3
=
⋅
⋅
=
⋅
⋅
=
τ
W spoinie poziomej
Współczynnik wytrzymałości spoiny jak dla spoiny rozciąganej
85
,
0
1
15
,
0
1
=
⋅
−
=
⊥
α
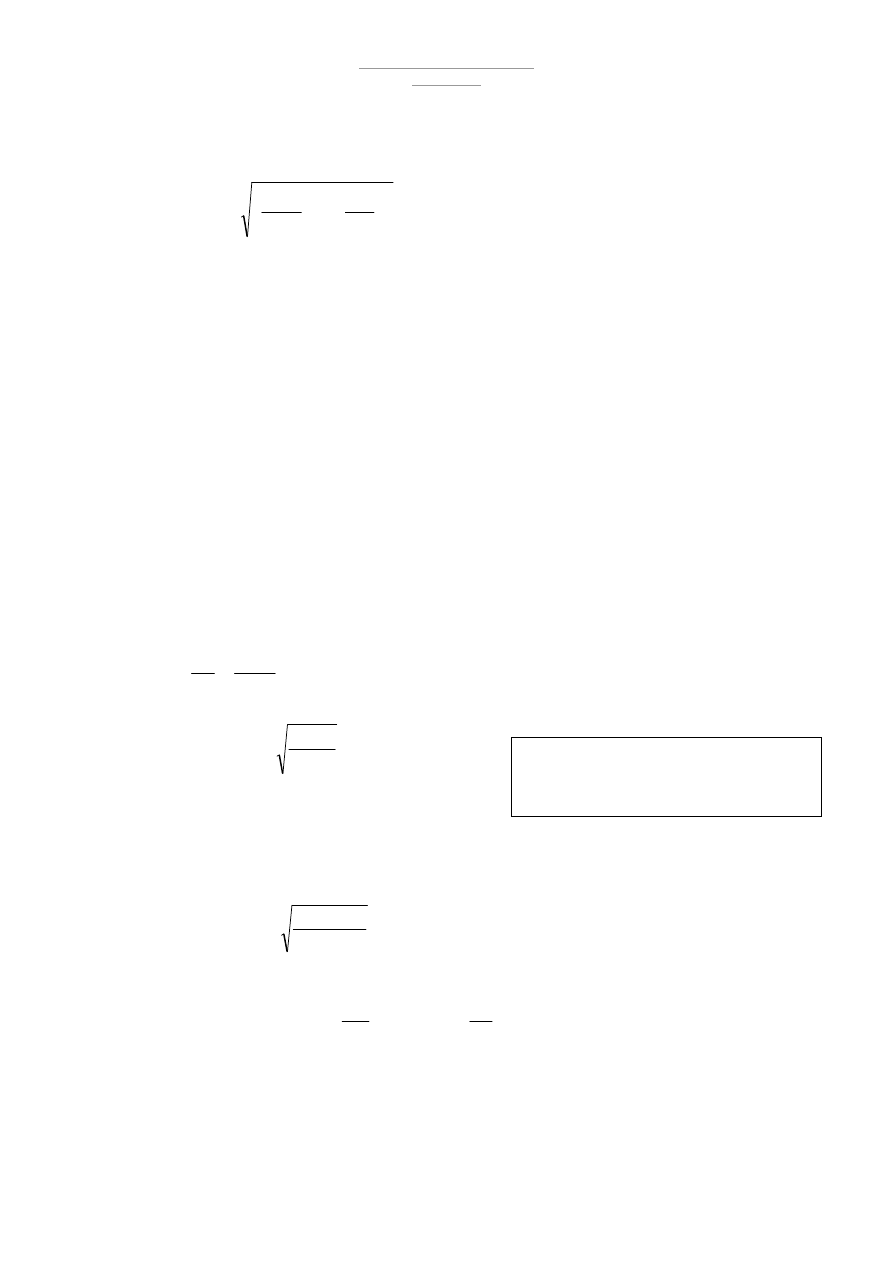
Konstrukcje stalowe – sem II
Projekt hali
27
MPa
f
d
75
,
199
235
85
,
0
5
,
132
1
=
⋅
≤
⋅
≤
⊥
α
σ
Warunek zachowany
W spoinie pionowej
Punkt 2
MPa
235
38
,
144
6
,
0
1
,
41
1
3
,
127
2
2
<
=
+
Warunek zachowany
Punkt 3
MPa
f
d
141
235
6
,
0
9
,
42
||
3
=
⋅
≤
⋅
≤
α
τ
Warunek zachowany
Punkt 4
75
,
199
235
36
1
=
≤
≤
d
f
σ
Warunek zachowany
•
Połączenie śrubowe doczołowe
Dane materiałowe:
- stal pasów górnych St3S -
235
=
d
f
MPa
- stal blach doczołowych St3S
235
=
d
f
dla 16 mm < t < 40 mm
- śruby klasy M20 – 10.9;
kN
S
Rv
150
=
;
MPa
R
m
420
=
2
245mm
A
s
=
- otwory okrągłe średnio dokładne
mm
2
=
∆
mm
d
22
2
20
0
=
+
=
Nośność obliczeniowa śrub :
kN
S
S
Rt
Rr
1
,
141
166
85
,
0
85
,
0
=
⋅
=
⋅
=
Potrzebna ilość śrub
szt
S
N
n
rt
4
91
,
3
1
,
141
8
,
552
≈
=
=
=
Minimalna grubość blachy doczołowej :
d
s
Rt
f
b
S
c
t
⋅
⋅
⋅
=
2
,
1
min
76
70
)
20
18
(
2
18
70
≤
+
⋅
≤
=
=
s
s
b
mm
c
mm
b
cm
t
85
,
0
5
,
23
70
,
0
67
18
,
0
2
,
1
min
=
⋅
⋅
⋅
=
Przyjmuje t = 1,2 cm
Współczynnik efektu dźwigni
min
67
,
2
t
t
−
=
β
258
,
1
5
,
8
12
67
,
2
=
−
=
β
Nośności połączeń rozciąganych kategorii E sprawdza się wg wzoru (85)
Rj
N
N
≤
∑
=
⋅
=
n
i
R
Rj
S
N
1
1
ϖ
Gdzie : c – odległość między brzegiem
otwory a spoina
b
s
- szerokość współdziała blachy
przypadająca na jedna śrubę

Konstrukcje stalowe – sem II
Projekt hali
28
Współczynnik rozdziału obciążenia
Dla dwóch śrub w jednym szeregu m
i
= 2
Dla śrub wewnętrznych przy pasach
ω
i
= 1
Dla śrub zewnętrznych
ω
i
= 0,8
Nośność obliczeniowa połączenia :
kN
N
kN
N
Rj
8
,
552
6
,
597
)
8
,
0
2
1
2
(
166
=
>
=
⋅
+
⋅
⋅
=
Warunek zachowany
Siła ścinająca w śrubie :
kN
kN
n
V
S
v
150
67
,
15
4
7
,
62
max
<
=
=
=
Warunek zachowany
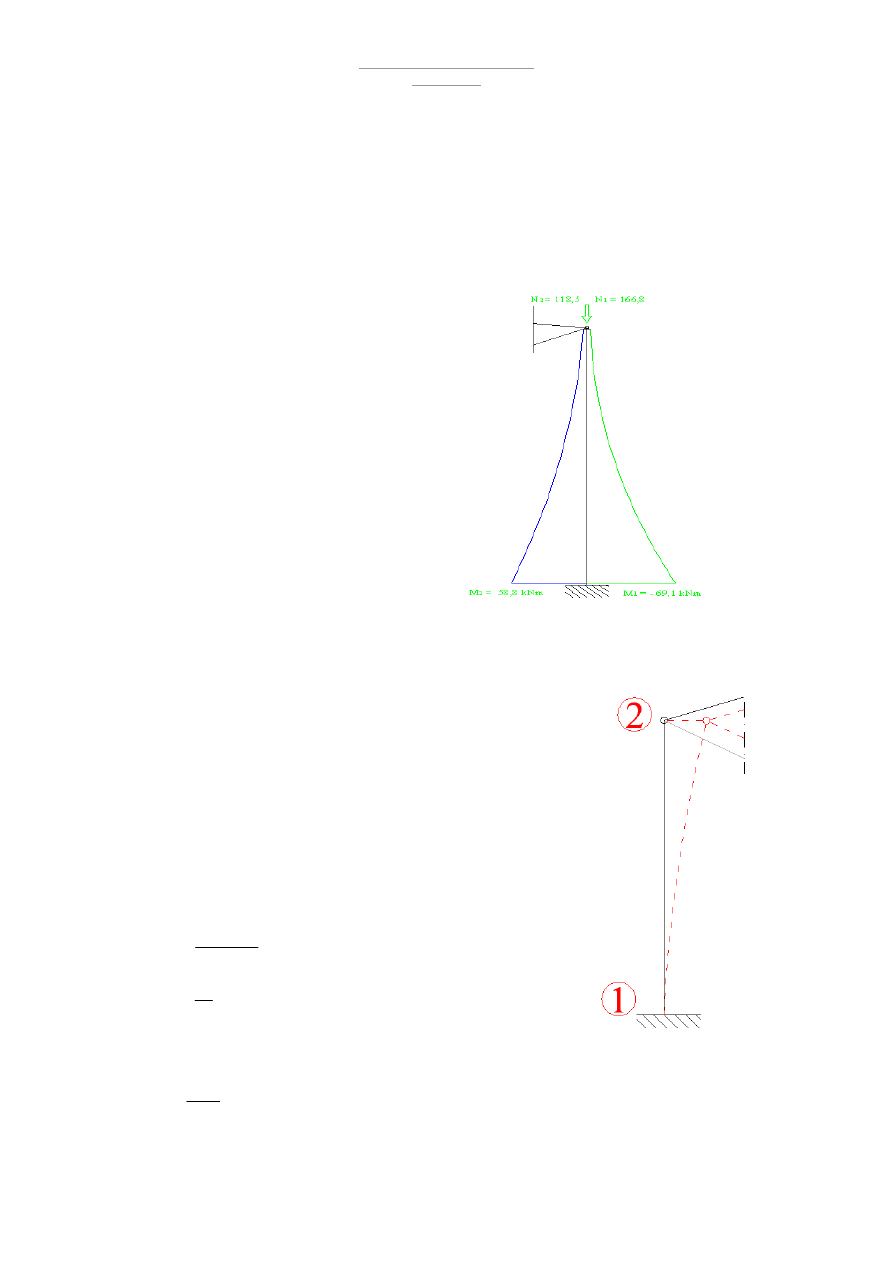
Konstrukcje stalowe – sem II
Projekt hali
29
6.Słup
6.1 Ustalenie sił wewnętrznych
Do wymiarowania przyjęto pary sił:
- schemat I
kNm
M
kN
N
1
,
69
8
,
166
1
1
=
=
- schemat II
kNm
M
kN
N
8
,
58
5
,
118
2
2
=
=
- schemat III
kNm
M
kN
N
1
,
0
8
,
212
3
3
=
=
6.2 Ustalenie współczynników długości wyboczeniowych:
6.2.1 W płaszczyźnie ściany [względem osi Y]
1
=
y
µ
1
1
l
l
l
y
wy
=
⋅
=
µ
6.2.2 W płaszczyźnie układu [względem osi X]
?
=
x
µ
−
l
długość teoretyczna
1
l
l
x
wx
⋅
=
µ
•
Wyznaczenie współczynnika wyboczenia
)
,
(
2
1
χ
χ
µ
µ
=
x
Załącznik 1. Norma [35]
Dla węzła przesuwnego
2
1
,
χ
χ
- podatność węzłów
3
,
0
0
≥
+
=
K
K
K
c
c
i
χ
l
I
K
c
c
=
0
K
- sztywność zamocowania
•
Dla punktu 1 [dla utwierdzenia
0
K
=
c
K
]
3
,
0
5
,
0
2
1
≥
=
=
c
c
K
K
χ
•
Dla punktu 2
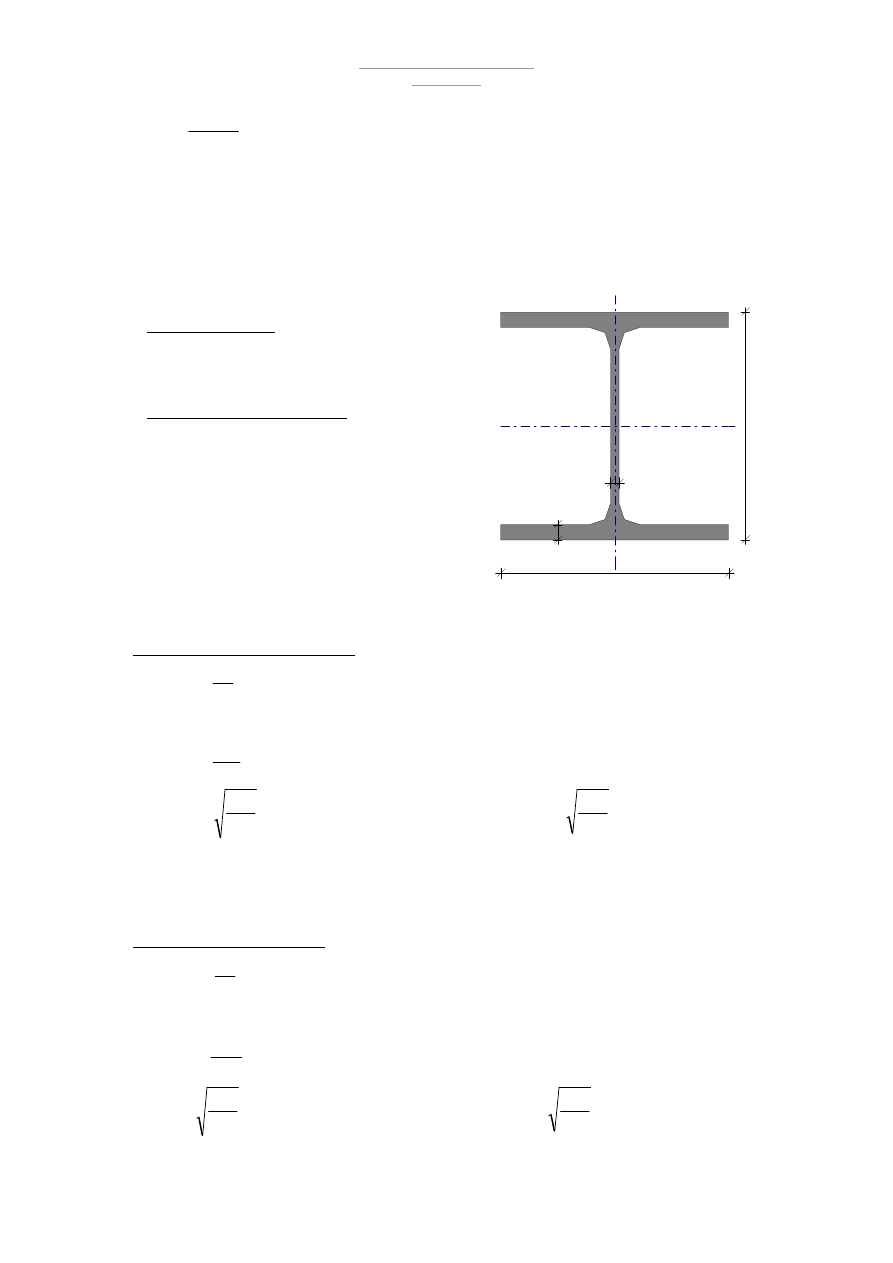
Konstrukcje stalowe – sem II
Projekt hali
30
y
y
x
x
2
6
0
260
10,0
1
7
,5
3
,
0
1
0
2
≥
=
+
=
c
c
K
K
χ
Współczynnik wyboczenia
)
1
;
5
,
0
(
µ
µ
=
x
Z.1-3 [B]
45
,
2
≈
x
µ
6.3 Wymiarowanie słupa HEB 260
Wymiary przekroju
h = 260 mm
b
f
= 260 mm
t
w
= 10,0 mm
t
f
= 17,5 mm
r = 24,0 mm
Cechy geometryczne przekroju
A = 118,0 cm
2
A
vy
= 26,00 cm
2
A
vx
= 91,00 cm
2
W
x
= 1150 cm
3
W
y
= 395,0 cm
3
J
x
= 14920 cm
4
J
y
= 5130 cm
4
i
x
= 11,20 cm
i
y
= 6,580 cm
I
= 753700 cm
6
I
= 124,0 cm
4
W
= 4780 cm
4
S
x
= 641,0 cm
3
m = 93,00 kg/m
U = 1,499 m
2
/mb U/A = 127,0 m
-1
6.3.1 Sprawdzenie klasy przekroju
-
klasa środnika
Określenie smukłości środnika
w
w
s
t
b
=
λ
gdzie:
)
(
2
r
t
h
b
f
w
+
⋅
−
=
=>
mm
b
w
192
)
24
10
(
2
260
=
+
⋅
−
=
2
,
19
10
192
=
=
s
λ
ε
λ
⋅
<
33
s
dla klasy 1
d
f
215
=
ε
f
d
dla stali St3S = 235 MPa a więc
956
,
0
235
215
=
=
ε
Sprawdzenie warunku dla klasy 1
55
,
31
956
,
0
33
26
,
19
=
⋅
<
Spełniony Środnik jest klasy 1
-
klasa półki
Określenie smukłość półki
f
p
p
t
b
=
λ
gdzie :
r
t
s
b
w
p
−
−
⋅
=
)
(
5
,
0
=>
mm
b
p
113
24
)
10
260
(
5
,
0
=
−
−
⋅
=
45
,
6
5
,
17
113
=
=
p
λ
ε
λ
⋅
<
9
p
dla klasy 1
d
f
215
=
ε
f
d
dla stali St3S = 235 MPa a więc
956
,
0
235
215
=
=
ε
Konstrukcje stalowe – sem II
Projekt hali
31
Sprawdzenie warunku dla klasy 1
6
,
8
956
,
0
9
45
,
6
=
⋅
<
Spełniony Półka jest klasy 1
WNIOSEK: Cały przekrój jest klasy 1
6.3.2 Nośności przekroju przy ściskaniu i zginaniu
kN
f
A
N
d
Rc
2773
5
,
23
118
=
⋅
=
⋅
=
kNm
kNcm
f
W
M
d
x
Rc
25
,
270
27025
5
,
23
1150
=
=
⋅
=
⋅
=
Rozpiętość teoretyczna
m
l
911
,
6
0
=
Długość wyboczeniowa w płaszczyźnie ściany
m
l
l
y
y
911
,
6
911
,
6
1
0
=
⋅
=
⋅
=
µ
Długość wyboczeniowa w płaszczyźnie układu
m
l
l
x
x
93
,
16
911
,
6
45
,
2
0
=
⋅
=
⋅
=
µ
Długość przy wyboczeniu skrętnym
m
l
l
911
,
6
911
,
6
1
0
=
⋅
=
⋅
=
ω
ω
µ
Smukłości gięte słupa
Względem osi x
1
,
151
20
,
11
1693
=
=
=
x
x
x
i
l
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
87
,
1
53
,
80
1
,
151
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej b
257
,
0
=
ix
ϕ
Względem osi y
105
58
,
6
1
,
691
=
=
=
y
y
y
i
l
λ
53
,
80
5
,
29
73
,
2
235
10
205
15
,
1
14
,
3
15
,
1
3
=
⋅
=
⋅
⋅
=
⋅
=
d
p
f
E
π
λ
3
,
1
53
,
80
105
=
=
=
p
x
x
λ
λ
λ
z tablicy 11 z krzywej c
415
,
0
=
iy
ϕ
6.3.3
Sprawdzenie nośności na ściskanie
•
Dla schematu I
1
14
,
0
2773
415
,
0
8
,
166
1
23
,
0
2773
257
,
0
8
,
166
1
1
<
=
⋅
=
⋅
<
=
⋅
=
⋅
rc
iy
rc
ix
N
N
N
N
ϕ
ϕ
Warunek został spełniony
•
Dla schematu II
1
1
,
0
2773
415
,
0
5
,
118
1
16
,
0
2773
257
,
0
5
,
118
1
1
<
=
⋅
=
⋅
<
=
⋅
=
⋅
rc
iy
rc
ix
N
N
N
N
ϕ
ϕ
Warunek został spełniony
•
Dla schematu III
Konstrukcje stalowe – sem II
Projekt hali
32
1
18
,
0
2773
415
,
0
8
,
212
1
29
,
0
2773
257
,
0
8
,
212
1
1
<
=
⋅
=
⋅
<
=
⋅
=
⋅
rc
iy
rc
ix
N
N
N
N
ϕ
ϕ
Warunek został spełniony
6.3.4
Sprawdzenie nośności na ściskanie i zginanie
6.3.4.1 Wyznaczenie współczynnika zwichrzenia
L
ϕ
•
Wartość momentu krytycznego
z
y
s
cr
N
N
i
B
M
⋅
⋅
⋅
=
gdzie
818
,
1
55
,
0
1
1
=
=
=
β
B
cm
i
i
i
y
x
s
98
,
12
58
,
6
2
,
11
2
2
2
2
=
+
=
+
=
kN
l
I
E
N
y
y
y
9
,
2170
911
,
6
5130
05
,
2
14
,
3
2
2
2
2
=
⋅
⋅
=
⋅
⋅
=
π
kN
N
N
I
G
l
I
E
i
N
z
z
s
z
7734
)
2
,
99
89
,
31
(
59
)
10
124
10
80
911
,
6
10
753700
10
05
,
2
14
,
3
(
1298
,
0
1
)
(
1
8
6
2
12
8
2
2
2
2
2
=
+
⋅
=
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
⋅
=
−
−
τ
ω
ω
π
9
,
966
7734
9
,
2170
1298
,
0
818
,
1
=
⋅
⋅
⋅
=
cr
M
•
Smukłość przy zwichrzeniu
6
,
0
9
,
966
25
,
270
15
,
1
15
,
1
=
⋅
=
⋅
=
cr
Rc
L
M
M
λ
Współczynnik zwichrzenia z tablicy 11 krzywa a
0
941
,
0
=
L
ϕ
6.3.4.2 Warunki nośności pręta ściskanego i zginanego
1
<
∆
+
⋅
+
⋅
i
Rc
L
Rc
i
M
M
N
N
ϕ
ϕ
•
Składnik poprawkowy
1
∆
[wzór 57 Norma]
1
,
0
25
,
1
2
1
≤
⋅
+
⋅
⋅
⋅
⋅
=
∆
Rx
L
x
rc
i
i
i
M
M
N
N
ϕ
ϕ
λ
ϕ
1
,
0
56
,
0
25
,
270
941
,
0
1
,
69
2773
257
,
0
8
,
166
87
,
1
257
,
0
25
,
1
2
≤
=
⋅
⋅
⋅
⋅
⋅
⋅
=
∆
x
Dla wszystkich schematów przyjmuje
1
,
0
1
=
∆
•
Schemat I
W płaszczyźnie ramy
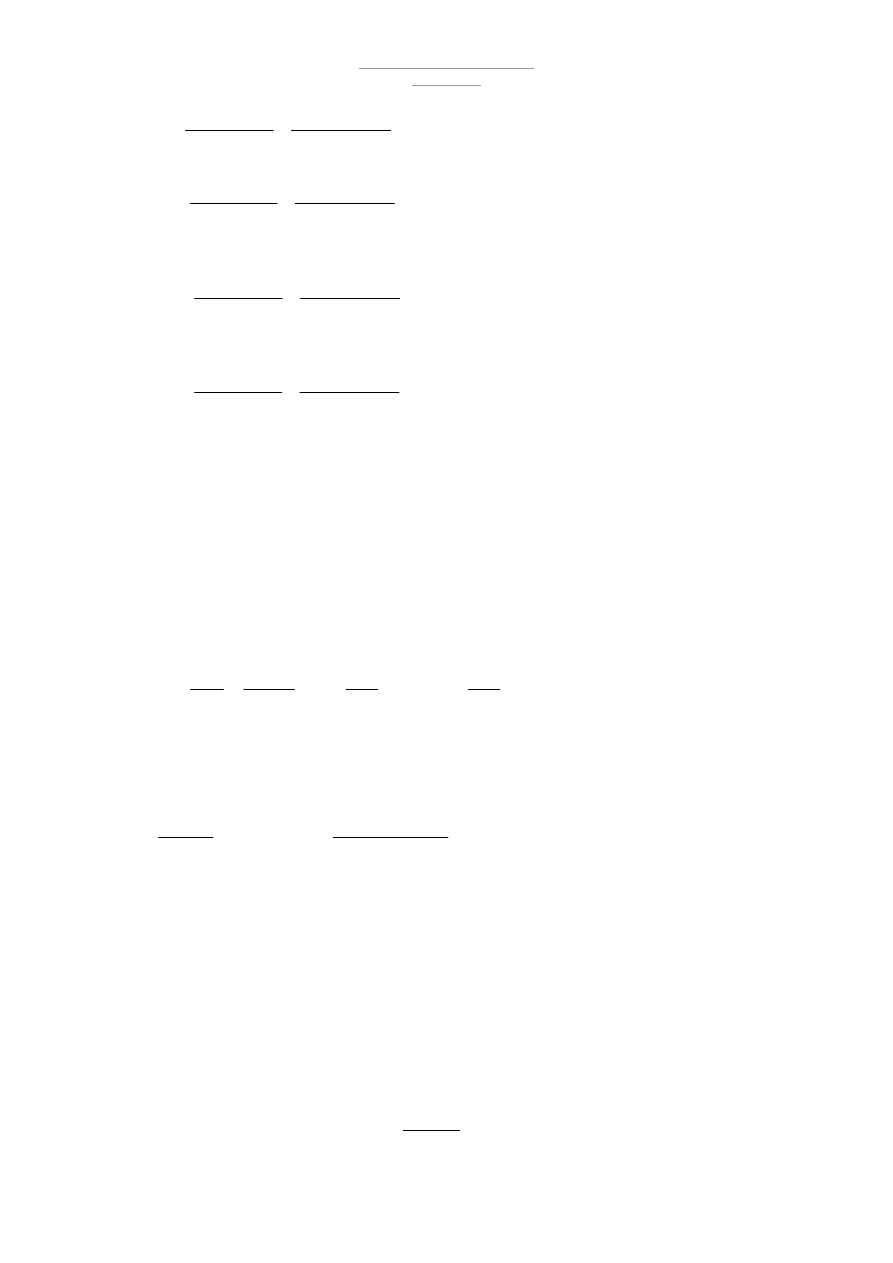
Konstrukcje stalowe – sem II
Projekt hali
33
1
6
,
0
1
,
0
25
,
270
941
,
0
1
,
69
2773
257
,
0
8
,
166
<
=
+
⋅
+
⋅
Warunek został spełniony
W płaszczyźnie układu
1
51
,
0
1
,
0
25
,
270
941
,
0
1
,
69
2773
415
,
0
8
,
166
<
=
+
⋅
+
⋅
Warunek został spełniony
•
Schemat II
W płaszczyźnie ramy
1
6
,
0
1
,
0
25
,
270
941
,
0
8
,
58
2773
257
,
0
5
,
118
<
=
+
⋅
+
⋅
Warunek został spełniony
W płaszczyźnie układu
1
49
,
0
1
,
0
25
,
270
941
,
0
5
,
58
2773
415
,
0
5
,
118
<
=
+
⋅
+
⋅
Warunek został spełniony
6.4 Sprawdzenie nośności przekroju na ścinanie
kN
f
A
V
d
v
R
7
,
261
5
,
23
2
,
19
1
58
,
0
58
,
0
=
⋅
⋅
⋅
=
⋅
⋅
=
02
,
157
7
,
261
6
,
0
1
,
23
6
,
0
1
,
23
0
max
=
⋅
<
⋅
=
<
=
R
V
V
V
Nośność zachowana
7. Obliczenie głowicy słupa
7.1 Określenie wymiarów
blacha głowicy
x
x270
30
270 mm
Naprężenia w spoinie łączącej płytkę centrującą
2
2
1
5
,
23
3
,
21
26
3
,
0
8
,
166
cm
kN
f
cm
kN
l
a
N
d
p
=
<
=
⋅
=
⋅
=
σ
Naprężenia w spoinie łączącej żeberko
mm
a
mm
mm
a
t
a
t
7
6
10
7
,
0
30
2
,
0
7
,
0
2
,
0
min
max
<
≤
⋅
≤
≤
⋅
⋅
≤
≤
⋅
Przyjmuje 6 mm
cm
l
l
f
l
a
N
d
2
,
4
5
,
23
7
,
0
6
,
0
4
8
,
166
||
1
≥
⋅
⋅
⋅
≥
=>
⋅
≤
⋅
∑
α
Przyjmuje l = 5 cm
8. Podstawa słupa stopa utwierdzona
8. 1 Do obliczeń przyjęto najniekorzystniejszy układ sił :
kNm
M
kN
N
1
,
69
8
,
166
1
1
=
=
8.2 Geometria
Wymiary blachy
mm
B
mm
L
400
600
=
=
Przekrój czynny kotew
2
3
,
35 cm
A
=
Wskaźnik wytrzymałości
3
2
24000
6
60
40
cm
W
=
⋅
=
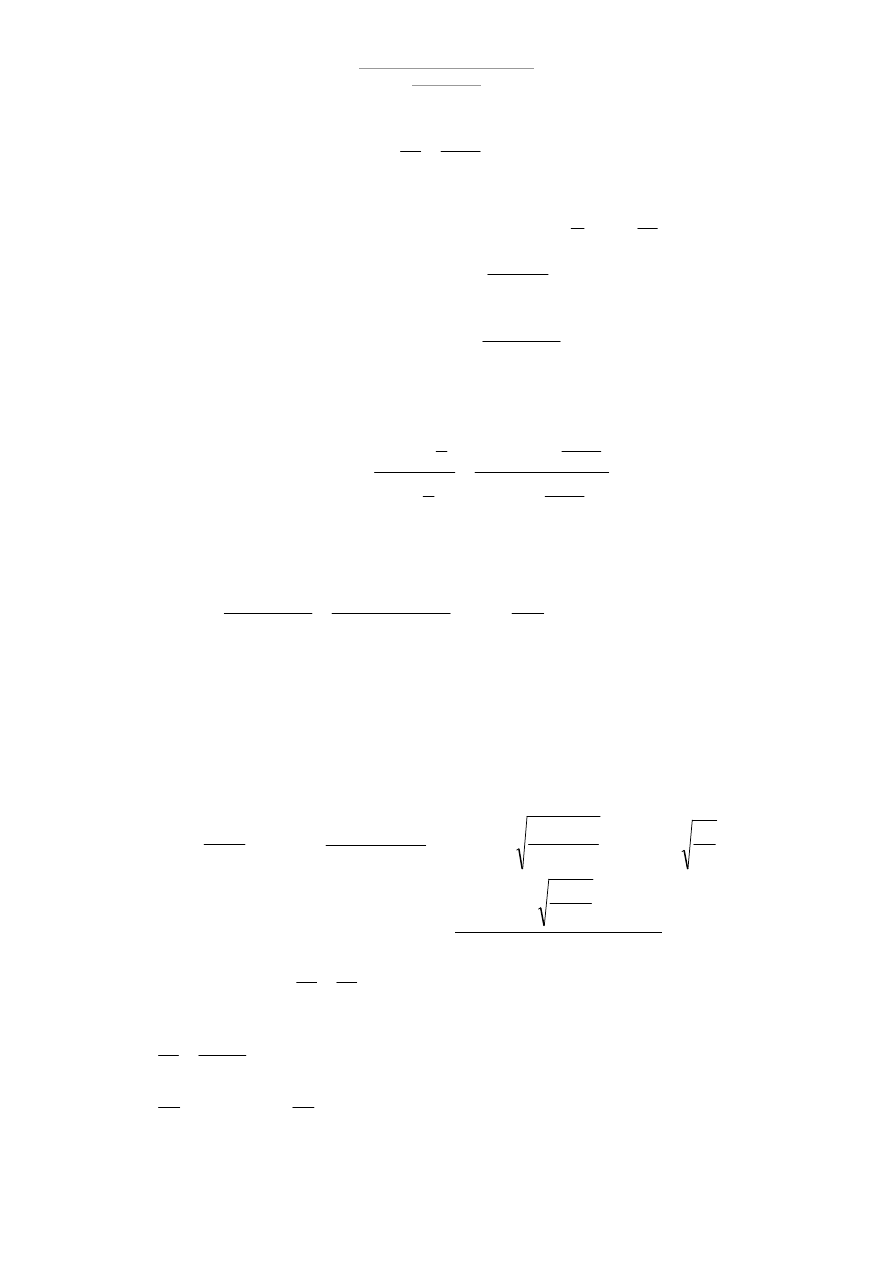
Konstrukcje stalowe – sem II
Projekt hali
34
Ilość kotew
2
=
n
Mimośród obciążenia
cm
m
N
M
e
41
41
,
0
8
,
166
1
,
69
=
=
=
=
Odległość osi kotew od krawędzi ściskanej
cm
L
5
,
51
'
=
Położenie wypadkowej siły ściskającej
cm
L
e
p
11
2
60
41
2
=
−
=
−
=
Zasięg strefy ściskanej :
0
)
)(
(
36
3
2
3
=
−
+
⋅
⋅
⋅
+
⋅
⋅
+
L
x
p
L
B
A
n
x
p
x
Po podstawieniu danych :
0
)
5
,
51
)(
11
5
,
51
(
40
3
,
35
2
36
11
3
2
3
=
−
+
⋅
⋅
⋅
+
⋅
⋅
+
x
x
x
Pierwiastkiem tego równania jest : x = 33,16 cm
Przyjmuje :
Wypadkowa siła rozciągająca w kotwach
kN
x
L
x
p
N
F
t
9
,
90
)
3
16
,
33
5
,
51
(
)
3
16
,
33
11
(
8
,
166
)
3
(
)
3
(
=
−
+
⋅
=
−
+
⋅
=
Warunek nośności zakotwienia [przyjęto śruby S235]
134
67
2
9
,
90
=
⋅
=
⋅
<
=
rt
t
S
n
F
Nośność zachowana
Naprężenia dociskowe na krawędzi stopy :
MPa
cm
kN
B
x
F
N
t
t
c
88
,
3
388
,
0
40
7
,
50
)
9
,
90
8
,
166
(
2
)
(
2
2
=
=
⋅
+
⋅
=
⋅
+
⋅
=
σ
Dla betonu zbrojonego stopy klasy B25 przyjęto f
cd
= 10,6 MPa
Współczynnik rozdziału
ω
=1,0
Warunek nośności
6
,
10
0
,
1
88
,
3
⋅
=
⋅
<
=
cd
c
f
MPa
ω
σ
Nośność zachowana
8.3 Określenie grubości blachy podstawy stopy
Grubość blachy zależy od wielkości momentów zginających wywołana naprężeniami
Płyta A
Naprężenia w płycie A
d
x
A
f
W
M
≤
=
max
σ
=>
d
p
c
f
t
b
≤
⋅
⋅
⋅
⋅
⋅
2
2
1
0
,
1
2
6
0
,
1
σ
d
c
d
c
p
f
b
f
b
t
σ
σ
⋅
⋅
=
⋅
⋅
=
1
2
1
73
,
1
3
cm
b
u
A
65
,
8
5
73
,
1
73
,
1
1
=
⋅
=
⋅
=
= >
cm
t
pA
11
,
1
5
,
23
388
,
0
64
,
8
=
⋅
=
Płyta B
cm
b
cm
l
B
B
17
26
=
=
1
52
,
1
17
26
>
=
=
B
B
b
l
Warunek nie został spełniony, musimy dodać żebro usztywniające
71
,
0
17
125
,
12
=
=
B
B
b
l
Po interpolacji z tabelki odczytujemy u
B
= 0,729
729
,
0
=
B
B
b
u
= >
729
,
0
17
=
B
u
= >
39
,
12
729
,
0
17
=
⋅
=
B
u
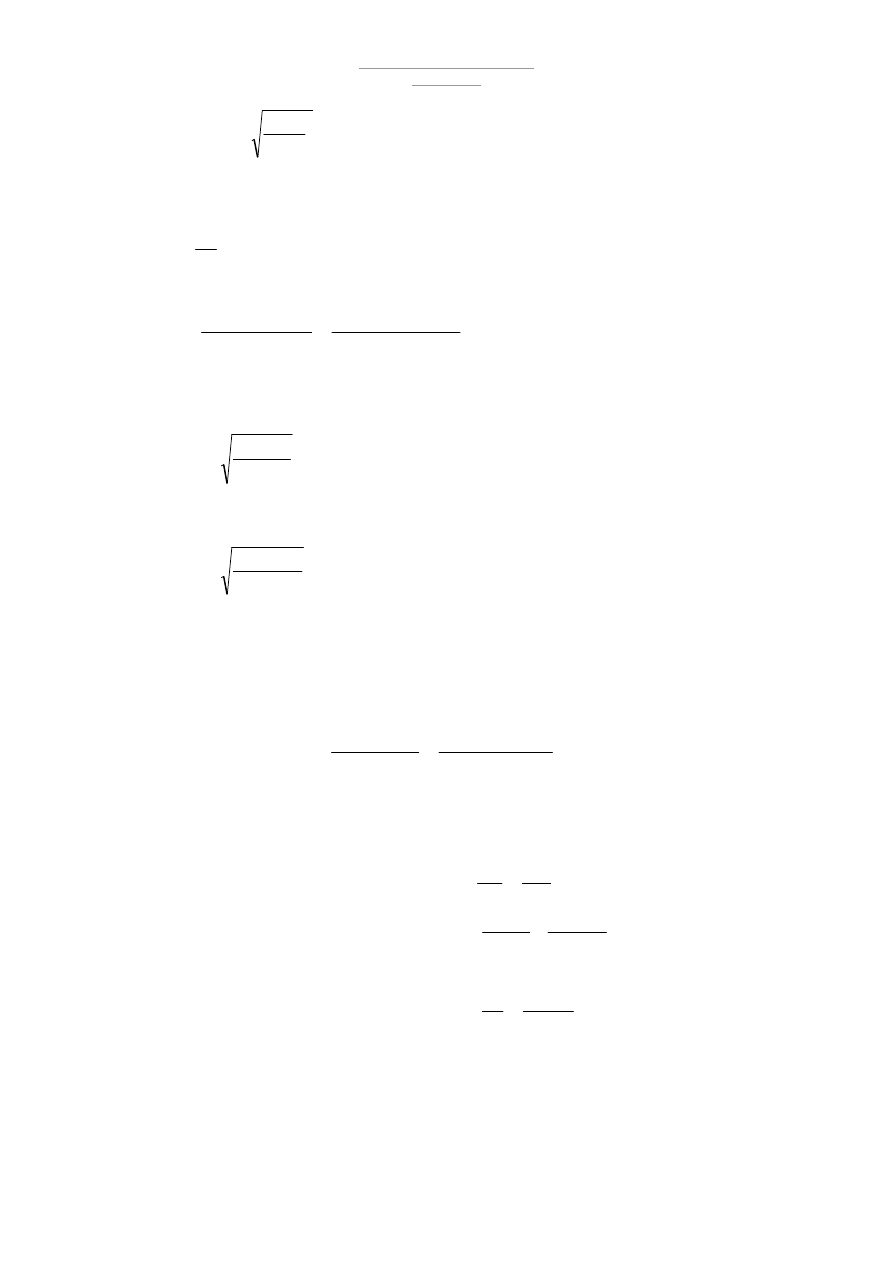
Konstrukcje stalowe – sem II
Projekt hali
35
cm
t
pB
59
,
1
,
5
,
23
388
,
0
39
,
12
=
⋅
=
Przyjmuje grubość płyty 2 cm
Sprawdzenie grubości blachy ze względu na ścięcie
7
,
0
7
,
0
5
,
23
58
,
0
3
14
,
3
9
,
90
58
,
0
58
,
0
>
=
⋅
⋅
⋅
=
⋅
⋅
⋅
≥
⋅
⋅
=
⋅
=
≤
=
p
d
s
t
p
p
s
v
d
dv
v
t
t
f
d
F
t
t
d
A
f
f
A
F
π
π
τ
Sprawdzenie grubości blachy według wzoru 82
48
,
1
48
,
1
5
,
23
8
,
11
9
,
90
7
,
4
2
,
1
118
24
47
2
2
47
6
53
5
,
23
2
,
1
>
=
⋅
⋅
⋅
≥
=
+
⋅
=
+
⋅
=
=
−
=
⋅
⋅
⋅
≥
t
t
d
c
b
mm
c
b
F
c
t
s
s
t
Wnioski: Ostatecznie przyjmuje grubość blachy podstawy 2 cm
8.4 Sprawdzenie naprężeń w blachach węzłowych trapezowych
8.4.1 Określenie wymiarów blachy trapezowej
Wysokość :
cm
f
a
n
N
l
h
d
sp
49
,
3
5
,
23
8
,
0
6
,
0
4
8
,
166
||
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
≥
α
przyjmuje 20 cm
Charakterystyka przekroju :
Pole powierzchni
2
185
75
,
1
20
3
40
2
cm
A
=
⋅
⋅
+
⋅
=
Moment statyczny
3
1
970
1
2
40
10
20
75
,
1
3
cm
S
x
=
⋅
⋅
−
⋅
⋅
⋅
=
Środek ciężkości
cm
A
S
x
x
24
,
5
185
970
1
1
=
=
=
Moment bezwładności przekroju
4
3
3
1
6
,
8906
3
20
3
,
3
3
2
40
cm
J
x
=
⋅
+
⋅
=
4
2
1
9
,
3826
24
,
5
185
6
,
8906
2
cm
x
A
J
J
x
x
=
⋅
−
=
⋅
−
=
Wskaźnik wytrzymałości przekroju
3
2
,
259
76
,
14
9
,
3826
cm
y
J
W
a
x
x
=
=
=
Nośność przekroju
kNm
kNcm
f
W
M
d
x
Rx
912
,
60
2
,
6091
5
,
23
2
,
259
=
=
⋅
=
⋅
=
Moment zginający blachy w płaszczyźnie styku ze słupem
kNm
kNcm
B
a
M
c
426
,
22
22426
5
,
0
40
17
388
,
0
5
,
0
2
2
=
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
σ
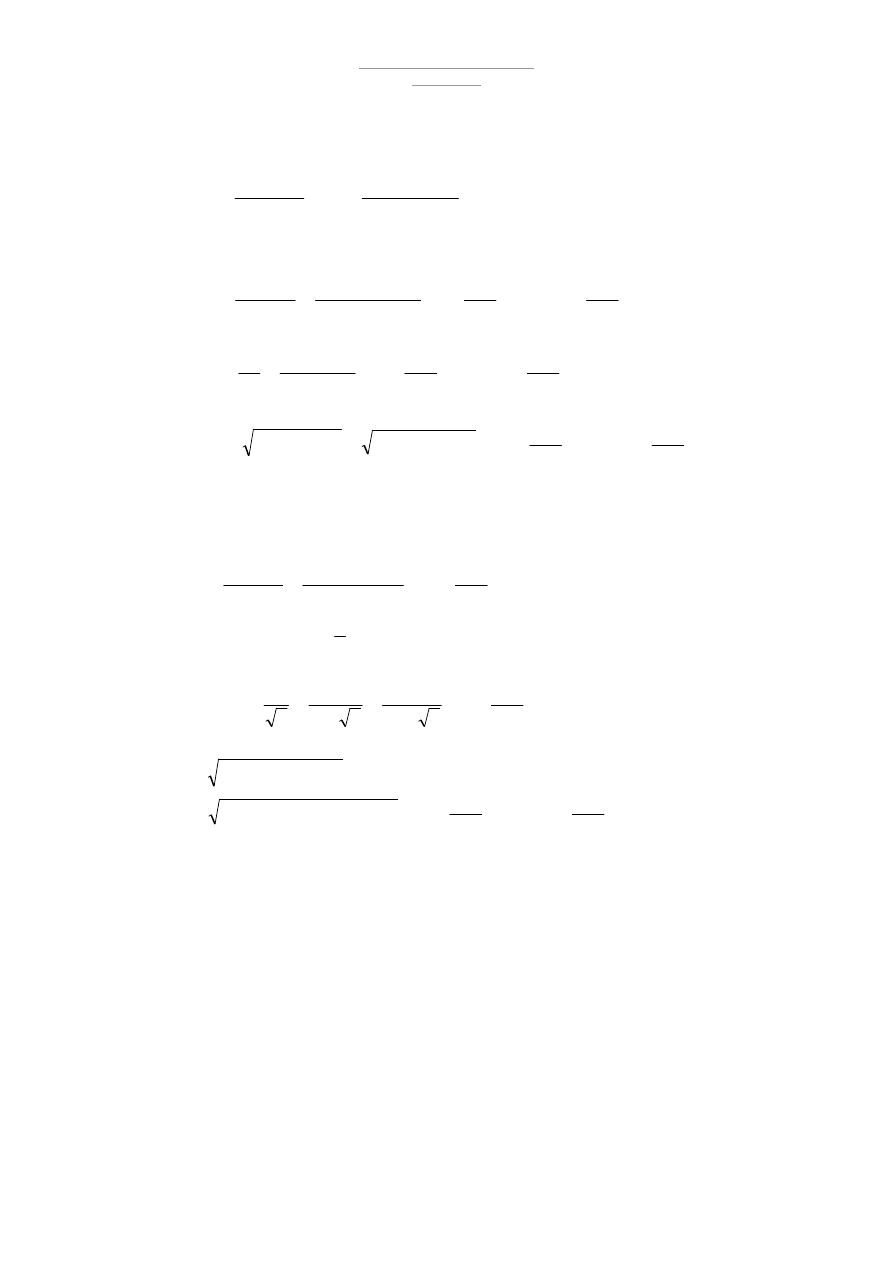
Konstrukcje stalowe – sem II
Projekt hali
36
8.4.2 Sprawdzenie naprężeń
Naprężenia w punkcie A
kN
b
a
W
52
,
128
40
17
189
,
0
1
1
=
⋅
⋅
=
⋅
⋅
=
σ
66
,
67
40
17
2
189
,
0
388
,
0
2
)
(
1
2
=
⋅
⋅
−
=
⋅
⋅
−
=
b
a
W
c
σ
σ
kN
W
W
V
18
,
196
66
,
67
52
,
128
2
1
=
+
=
+
=
α
kNcm
e
W
e
W
M
73
,
1633
9
,
9
66
,
67
5
,
7
52
,
128
2
2
1
1
=
⋅
+
⋅
=
⋅
+
⋅
=
α
2
2
5
,
23
3
,
6
9
,
3826
76
,
14
73
,
1633
cm
kN
f
cm
kN
J
y
M
d
x
A
A
=
<
=
⋅
=
⋅
=
α
σ
Naprężenia ścinające obliczono w sposób uproszczony:
2
2
5
,
23
86
,
1
20
75
,
1
3
18
,
196
cm
kN
f
cm
kN
A
V
d
v
ś
=
<
=
⋅
⋅
=
=
α
τ
Naprężenia zastępcze
2
2
2
2
2
2
5
,
23
07
,
7
86
,
1
3
3
,
6
3
cm
kN
f
cm
kN
d
s
A
z
=
<
=
⋅
+
=
⋅
+
=
τ
σ
σ
Sprawdzenie naprężeń w spoinach poziomych blach trapezowych
Przyjęto : a = 6 mm
2
2
,
133
6
,
0
17
6
6
,
0
60
2
cm
A
s
=
⋅
⋅
+
⋅
⋅
=
Naprężenia ścinające w spoinie
2
||
14
,
7
6
,
0
6
9
,
3826
2
,
499
18
,
197
6
cm
kN
a
J
S
V
x
p
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
α
τ
3
2
,
499
)
2
2
24
,
5
(
40
2
cm
S
p
=
+
⋅
⋅
=
Naprężenia prostopadłe do osi spoiny
2
05
,
1
2
133
18
,
198
2
2
cm
kN
A
V
s
=
⋅
=
⋅
=
=
=
⊥
⊥
α
σ
τ
σ
Naprężenia w złożonym stanie naprężeń
d
f
≤
+
⋅
+
⋅
⊥
⊥
)
(
3
2
2
||
2
τ
τ
σ
χ
2
2
2
2
2
5
,
23
78
,
8
)
05
,
1
14
,
7
(
3
05
,
1
7
,
0
cm
kN
f
cm
kN
d
=
≤
=
+
⋅
+
⋅
Wyszukiwarka
Podobne podstrony:
Projekt hali (konstrukcje?tonowe elementy)
Projekt hali II (konstrukcje?tonowe elementy)
Strona tytuowa, Budownictwo Politechnika Rzeszowska, Rok IV, Konstrukcje Metalowe, Konstrukcje metal
GUP [zmiany], Budownictwo Politechnika Rzeszowska, Rok IV, Konstrukcje Metalowe, Konstrukcje metalow
Projekt hali o konstrukcji stalowej
Projekt Hali Przemysłowej
Dane do projektu hali s5 IPB 2014 2015 (02) (1)
OP TECHN, Budownictwo Politechnika Rzeszowska, Rok IV, Konstrukcje Metalowe, Konstrukcje metalowe II
Siły w prętach kratownicy, Budownictwo Politechnika Rzeszowska, Rok IV, Konstrukcje Metalowe, Konstr
Projekt hali stalowej obliczenia
Projekt Hali Skwara
Projekt Hali Skwara 2
Projekt hali II (konstrukcje?tonowe elementy)
PROJEKT HALI MAGAZYNOWEJ
projekt hali
Projekt Hali z suwnicą na starych normach
Projekt hali stalowej
więcej podobnych podstron