JeĪeli dla danych elementów murowych nie przeprowadzono
badaĔ wytrzymałoĞciowych muru z nich wykonanego,
wytrzymałoĞü charakterystyczną na Ğciskanie muru
projektowanego z tych elementów okreĞliü moĪna według
nastĊpujących zaleĪnoĞci (wg PN-B-03002:1999):
- dla murów na zaprawie zwykłej o

f

m

> 1.0 MPa:

f

k

=

Kf

b

0.65

f

m

0.25

gdzie: K – współczynnik wyraĪony w megapaskalach do
potĊgi 0.10, którego wartoĞü moĪna przyjmowaü równą:

1

potĊgi 0.10, którego wartoĞü moĪna przyjmowaü równą:
0.50 – dla murów z elementów murowych grupy 1,
o 5 MPa ”

f

b

” 40 MPa (dla murów z bloczków z betonu

komórkowego o 2,0 MPa ”

f

b

” 6.0 MPa),

0.45 – dla murów z elementów murowych grupy 2,
o 2.5 MPa ”

f

b

” 15 MPa, (wyjątek: pustaki betonowe)

0.35 – dla murów z elementów murowych grupy 3 i murów
z pustaków betonowych grupy 2 o 2.5 MPa ”

f

b

” 10 MPa,

0.60 – dla murów z bloczków z kamienia naturalnego
o 6 MPa <

f

b

< 120 MPa;

- dla murów na zaprawach lekkich:

f

k

= Ș

2

Kf

b

0.65

f

m

0.25

gdzie: Ș

2

= 0.9 dla murów z elementów murowych grupy 1,

Ș

2

= 0.8 dla murów z elementów murowych grupy 2 i 3;

- dla murów na cienkie spoiny z bloczków
z autoklawizowanego betonu komórkowego:
f

k

=

f

b

0.65

, jeĪeli

f

b

” 2.4 MPa

f

k

= 0.8

f

b

0.65

, jeĪeli

f

b

> 2.4 MPa

- dla murów na słabych zaprawach o

f

m

< 1.0 MPa:

2

- dla murów na słabych zaprawach o

f

m

< 1.0 MPa:

f

k

= 0.1 f

b

– mury z elementów grupy 1,

f

k

= 0.05 f

b

” 0,5 MPa – mury z elementów grupy 2 i 3.

Podane wzory słuĪące do okreĞlenia wytrzymałoĞci

charakterystycznej na Ğciskanie dotyczą murów bez spoiny
podłuĪnej (tj. pionowej spoiny równoległej do powierzchni
Ğciany, która nie wystĊpuje np. w murach jednowarstwowych,
a jest w dwuwarstwowych). ObecnoĞü spoiny podłuĪnej
w murach uwzglĊdniaü naleĪy mnoĪąc wartoĞci

f

k

okreĞlone

z powyĪszych zaleĪnoĞci przez Ș

1

= 0,85.

Postaü wzoru na wytrzymałoĞü
charakterystyczną na Ğciskanie muru na
zaprawie zwykłej lub lekkiej zmieniono w PN-
B-03002:2007 z obowiązującego dotąd w PN-
B-03002:1999

f

k

=

Kf

b

0.65

f

m

0.25

na

f

k

=

Kf

b

0.7

f

m

0.3

zalecany

w EC6 i zmodyfikowano wartoĞci

3

w EC6 i zmodyfikowano wartoĞci
współczynnika K (zaleĪnego od materiału
i grupy).
Rozszerzono mury ze spoinami cienkimi
i obejmują one teraz oprócz elementów
z autoklawizowanego betonu komórkowego
takĪe elementy murowe ceramiczne oraz
elementy silikatowe.

Zmieniono takĪe wzór na wytrzymałoĞü
charakterystyczną muru ze spoinami cienkimi
z elementów murowych ceramicznych grupy 1 i 4,
elementów silikatowych oraz elementów
z autoklawizowanego betonu komórkowego

o

f

b

• 2,4 MPa ze wzoru

f

k

= 0.8

f

b

0.65

na wzór

f

k

=

Kf

b

0.85

, zaĞ dla murów ze spoinami cienkimi

z autoklawizowanego betonu komórkowego

4

z autoklawizowanego betonu komórkowego
o f

b

< 2,4 MPa ze wzoru

f

k

=

f

b

0.65

na wzór

f

k

= 0,8

Kf

b

0.85

Wprowadzono takĪe wzór na wytrzymałoĞü
charakterystyczną muru ze spoinami cienkimi
z elementów murowych ceramicznych grupy 2 i 3

f

k

=

Kf

b

0.7

Zgodnie z PN-B-03002:2007 znormalizowana
wytrzymałoĞü na Ğciskanie

f

b

przyjmowana do wzorów

na obliczanie

f

k

nie powinna byü wiĊksza niĪ:

* w przypadku murów z elementów murowych grupy 1:
- gdy mury wykonane są na zaprawie zwykłej i lekkiej –
75 MPa

- gdy mury wykonane są na cienkie spoiny – 50 MPa

* w przypadku murów z elementów murowych grupy 2 –
35 MPa

5

35 MPa
* w przypadku murów z elementów murowych grupy 3 i 4
– 15 MPa.
WytrzymałoĞü zaprawy na Ğciskanie przyjmowana do
wzorów na

f

k

nie powinna byü wiĊksza niĪ:

a) dla muru na zaprawie zwykłej – 20 MPa oraz

2

f

b

dla elementów murowych grupy 1 i

1

f

b

dla elementów murowych grupy 2, 3 i 4

b) dla muru na zaprawie lekkiej – 10 MPa

WartoĞci współczynnika K zgodnie z PN-B-03002:2007

Element murowy

Rodzaj zaprawy murarskiej

Materiał

Grupa

Zaprawa

zwykła

Zaprawa do

cienkich spoin

Zaprawa

lekka

Ceramika

1

0,45

0,50

0,30

2

0,40

0,60

0,25

3

0,30

0,45

0,20

4

0,30

0,35

0,20

Silikaty

1

0,45

0,55

*)

2

0,40

0,45

*)

1

0,40

*)

*)

6

Beton kruszywowy

1

0,40

*)

*)

2

0,35

*)

*)

3

0,30

*)

*)

4

0,25

*)

*)

Autoklawizowany
beton komórkowy

1

0,45

0,75

0,40

KamieĔ sztuczny

1

0,45

*)

*)

KamieĔ naturalny

1

0,45

*)

*)

*) W praktyce zwykle nie jest stosowane takie połączenie elementu murowego i zaprawy

MODUŁ SPRĉĩYSTOĝCI

JeĪeli nie przeprowadzono odpowiednich badaĔ,
doraĨny moduł sprĊĪystoĞci muru moĪna wg PN-B-
03002: 1999 przyjmowaü jako:
E = Į

c

f

k

gdzie: Į

c

– cecha sprĊĪystoĞci muru.

JeĪeli duĪa dokładnoĞü obliczeĔ nie jest potrzebna,
przyjąü moĪna:

dla murów wykonanych na zaprawie o

f • 5 MPa,

7

dla murów wykonanych na zaprawie o

f

m

• 5 MPa,

z wyjątkiem murów z bloczków z betonu komórkowego –
Į

c

= 1000, przy długotrwałym działaniu obciąĪenia

Į

c,

∞

∞

∞

∞

= 700

dla murów z bloczków z betonu komórkowego,

niezaleĪnie od rodzaju zaprawy, a takĪe dla murów
z innego rodzaju elementów murowych na zaprawie
o

f

m

< 5 MPa – Į

c

= 600, przy długotrwałym działaniu

obciąĪenia Į

c,

∞

∞

∞

∞

= 400.

Długotrwały moduł sprĊĪystoĞci muru E

’

okreĞlamy

wzorem:

E

’

=

=

α

α

α

α

c,’

f

k

gdzie: Ș

E

≤

≤

≤

≤ 1 – współczynnik uwzglĊdniający redystrybucjĊ

sił wewnĊtrznych w konstrukcji oraz stosunek obciąĪenia
działającego długotrwale do obciąĪenia całkowitego,
α

α

α

α

c,’

- cecha sprĊĪystoĞci muru pod obciąĪeniem

długotrwałym.

∞

φ

η

+

α

E

k

c

1

f

8

długotrwałym.
JeĪeli duĪa dokładnoĞü obliczeĔ nie jest wymagana,
moĪna przyjąü Ș

E

= 0.3 i ij

∞

∞

∞

∞

= 1.5 i w związku z tym, za

parametr

α

α

α

α

c,’

przyjmuje siĊ:

- dla murów na zaprawie o

f

m

≥

≥

≥

≥ 5 MPa, z wyjątkiem murów

z bloczków z betonu komórkowego -

α

α

α

α

c,’

= 700,

- dla murów na zaprawie o

f

m

< 5 MPa, i dla murów

z bloczków z betonu komórkowego, niezaleĪnie od rodzaju
zaprawy -

α

α

α

α

c,’

= 400.

JeĪeli duĪa dokładnoĞü obliczeĔ nie jest
wymagana, wg normy PN-B-03002: 1999
przyjąü moĪna współczynnik pełzania
ij

’

= 1.5. Najmniejsze wartoĞci

współczynnika pełzania mają mury z kostki
kamiennej (w literaturze okreĞla siĊ ij

’

= 0

w przypadku takich murów) i elementów

9

w przypadku takich murów) i elementów
ceramicznych (w literaturze okreĞla siĊ
ij

’

= 0.2 ÷ 1.6 w przypadku takich murów),

zaĞ najwiĊksze z elementów wapienno
piaskowych (silikatowych) i betonowych –
nawet ij

’

= 2.0, czyli podobnie jak

w przypadku betonu).

WYTRZYMAŁOĝû CHARAKTERYSTYCZNA

MURU NA ROZCIĄGANIE

-WytrzymałoĞü muru na rozciąganie zaleca siĊ
uwzglĊdniü tylko w przypadku sprawdzenia
noĞnoĞci Ğcian, które nie przenoszą obciąĪeĔ
pionowych, a jedynie obciąĪenie wiatrem.
W zaleĪnoĞci od zorientowania płaszczyzny
działania momentu zginającego wzglĊdem

10

działania momentu zginającego wzglĊdem
płaszczyzny Ğciany rozróĪnia siĊ wytrzymałoĞü
muru na rozciąganie:
przy zginaniu w kierunku prostopadłym do
płaszczyzny Ğciany

f

x

= M/W przy liniowym

rozkładzie naprĊĪeĔ w przekroju
wytrzymałoĞü na rozciąganie osiowe
w płaszczyĨnie Ğciany

f

t

WytrzymałoĞü charakterystyczną muru
na rozciąganie przy zginaniu

f

xk

wyznacza siĊ biorąc pod uwagĊ
(poniĪsza tablica):
- przekrój, w którym nastĊpuje
zniszczenie muru: w przekroju przez
spoiny wsporne

f

lub w przekroju

11

spoiny wsporne

f

xk1

lub w przekroju

prostopadłym do spoin wspornych

f

xk2

- materiał i grupĊ elementów
murowych,
- wytrzymałoĞü Ğrednią zaprawy na
Ğciskanie f

m

.

Charakterystyczne wytrzymałoĞci muru

na rozciąganie przy zginaniu

f

xk

, MPa

(wg PN-B-03002:1999)

Rodzaj

elementów

murowych

f

xk

f

xk1

f

xk2

f

m

< 5

• 5

1

2

5

• 10

Grupa 1 – ceramiczne

0

0,2

0

0,3

0,4

0,4

Grupa 1 – inne niĪ ceramiczne

0

0

0

0,2

0,2

0,3

12

Grupa 1 – inne niĪ ceramiczne

0

0

0

0,2

0,2

0,3

Grupa 1 – ciĊte bloczki z

kamienia naturalnego

0

0

0

0,1

0,2

0,3

Grupa 2 – ceramiczne

0

0,2

0

0,1

0,2

0,2

Grupa 2 – inne niĪ ceramiczne

0

0

0

0,2

0,2

0,3

Grupa 3 – ceramiczne

0

0,2

0

0,1

0,2

0,2

W wypadku Ğcian poddanych
osiowemu rozciąganiu wytrzymałoĞü
charakterystyczna na rozciąganie

f

tk

moĪna przyjmowaü z powyĪszej
tablicy, jak w odniesieniu do
zginania w kierunku prostopadłym

13

zginania w kierunku prostopadłym
do płaszczyzny Ğciany. Przyjąü
naleĪy wartoĞü

f

xk1

lub

f

xk2

w zaleĪnoĞci od kierunku działania
głównych naprĊĪeĔ rozciągających
wzglĊdem spoin wspornych.

W celu zwiĊkszenia noĞnoĞci
konstrukcji murowych stosuje siĊ
zbrojenie. Konstrukcje takie projektuje
siĊ wg PN-B-03340:1999. Do
wykonania murowych konstrukcji
zbrojonych naleĪy stosowaü elementy
murowe zaliczone do grup 1 lub 2 oraz

14

murowe zaliczone do grup 1 lub 2 oraz
zaprawy cementowe lub cementowo –
wapienne o charakterystycznej
wytrzymałoĞci na Ğciskanie nie
mniejszej niĪ 5 MPa (wyznaczonej
zgodnie z PN-85/B-04500).

Beton uĪywany do wypełnienia
w murowych konstrukcjach zbrojonych,
jak teĪ stanowiący czĊĞü składową
konstrukcji murowo – betonowych oraz
murowo – Īelbetowych, powinien byü
klasy co najmniej B15. Stal zbrojeniowa
powinna spełniaü wymagania PN-B-

15

powinna spełniaü wymagania PN-B-
03264:1999.
Parametry wytrzymałoĞciowe muru
potrzebne w projektowaniu murowych
konstrukcji zbrojonych naleĪy okreĞlaü
jak w wypadku muru niezbrojonego,
zgodnie z PN-B-03002:1999.

CzĊĞciowe współczynniki bezpieczeĔstwa w odniesieniu
do konstrukcji murowych ustala siĊ w zaleĪnoĞci od
kategorii kontroli produkcji elementów murowych oraz
kategorii wykonania robót na budowie. RozróĪnia siĊ:
- kategoriĊ A wykonania robót – kiedy roboty murarskie
wykonuje naleĪycie wyszkolony zespół pod nadzorem
mistrza murarskiego, stosuje siĊ zaprawy produkowane
fabrycznie, a jeĪeli zaprawy są przygotowane na budowie,
kontroluje siĊ dozowanie składników, a takĪe

16

kontroluje siĊ dozowanie składników, a takĪe
wytrzymałoĞü zaprawy, jakoĞü robót kontroluje inspektor
nadzoru inwestorskiego,
- kategoriĊ B wykonania robót – kiedy warunki okreĞlające
kategoriĊ A nie są spełnione; w takim przypadku nadzór
nad jakoĞcią robót moĪe sprawowaü osoba odpowiednio
wykwalifikowana, upowaĪniona przez wykonawcĊ.
DecyzjĊ o przyjĊciu kategorii wykonawstwa podejmuje
projektant konstrukcji.

WartoĞci czĊĞciowych współczynników
bezpieczeĔstwa muru, a takĪe zakotwieĔ i kotwi
(stosowanych w zbrojonych konstrukcjach
murowych wg PN-B-03340: 1999), przyjmowane
do obliczeĔ konstrukcji w sytuacjach trwałych
i przejĞciowych, podano w poniĪszej tablicy.
CzĊĞciowe współczynniki bezpieczeĔstwa

17

w odniesieniu do murów dotyczą warunków,
gdy konstrukcje murowe są wykonane zgodnie
z normami, a odchyłki wykonania nie
przekraczają podanych w PN-B-03002:1999.
JeĪeli te warunki nie zostały dotrzymane, to
zaistniałą sytuacjĊ trzeba uwzglĊdniü
w obliczeniach konstrukcji.

W wyjątkowych sytuacjach
obliczeniowych moĪna przyjąü
w odniesieniu do muru Ȗ

m

= 1,3, a do

stali Ȗ

s

= 1,0 (stosowanej

w konstrukcjach zbrojonych) –

18

niezaleĪnie od kategorii produkcji
elementów murowych i kategorii
wykonania. Współczynnik Ȗ

m

w odniesieniu do zakotwieĔ i kotwi
moĪna przyjąü wg poniĪszej tablicy.

WartoĞci czĊĞciowych współczynników
bezpieczeĔstwa Ȗ

m

muru i zakotwieĔ

(wg PN-B-03002:1999 i PN-B-03340:1999)

Wyszczególnienie

Kategoria wykonania

robót

A

B

Kategoria I produkcji elementów murowych

1,7

2,2

19

Kategoria I produkcji elementów murowych

1,7

2,2

Kategoria II produkcji elementów murowych

2,0

2,5

Zakotwienie, wytrzymałoĞü na rozciąganie

i Ğciskanie kotewek murowych

2,5

2,5

Zakotwienie stali zbrojeniowej

1,7

2,2

Uwaga. WartoĞü Ȗ

m

w odniesieniu do betonu wypełniającego

przyjmuje siĊ odpowiednio do kategorii kontroli produkcji
elementów murowych w strefie muru wypełnianej betonem

WartoĞci czĊĞciowych współczynników
bezpieczeĔstwa dla muru Ȗ

m

(wg PN-B-03002:2007)

Materiał

Kategorie

wykonania robót

A

B

Mury

wykonane

z

elementów

murowych

kategorii I i zaprawy projektowanej

1,7

2,0

Mury

wykonane

z

elementów

murowych

2,0

2,2

20

Mury

wykonane

z

elementów

murowych

kategorii I i zaprawy przepisanej

2,0

2,2

Mury

wykonane

z

elementów

murowych

kategorii II i dowolnego rodzaju zaprawy

2,2

2,5

Zakotwienie stali zbrojeniowej

2,0

2,2

Stal zbrojeniowa

1,15

NadproĪa prefabrykowane zgodnie z PN-EN

845-2

1,7

WytrzymałoĞci obliczeniowe muru
moĪna okreĞliü ze wzorów:
- na Ğciskanie

f

d

=

f

k

/ Ȗ

m

- na Ğcinanie w kierunku równoległym
do spoin wspornych

f

vd

=

f

vk

/ Ȗ

m

- na Ğcinanie w kierunku prostopadłym

21

- na Ğcinanie w kierunku prostopadłym
do spoin wspornych

f

vvd

=

f

vvk

/ Ȗ

m

- na rozciąganie przy zginaniu
f

xd

=

f

xk

/ Ȗ

m

- na rozciąganie osiowe
f

td

=

f

tk

/ Ȗ

m

JeĪeli pole przekroju elementu
konstrukcji murowej jest mniejsze niĪ
0,30 m

2

(przy gruboĞci muru 0,25 m

filarek o szerokoĞci < 1,2 m), to
wytrzymałoĞci obliczeniowe okreĞlone
wg powyĪszychwzorów naleĪy podzieliü
przez współczynnik Ș wg poniĪszej

22

przez współczynnik Ș

A

wg poniĪszej

tablicy.

Pole
przekroju
muru, m

2

0,09

0,12

0,20

• 0,30

Ș

A

2,00

1,43

1,25

1,00

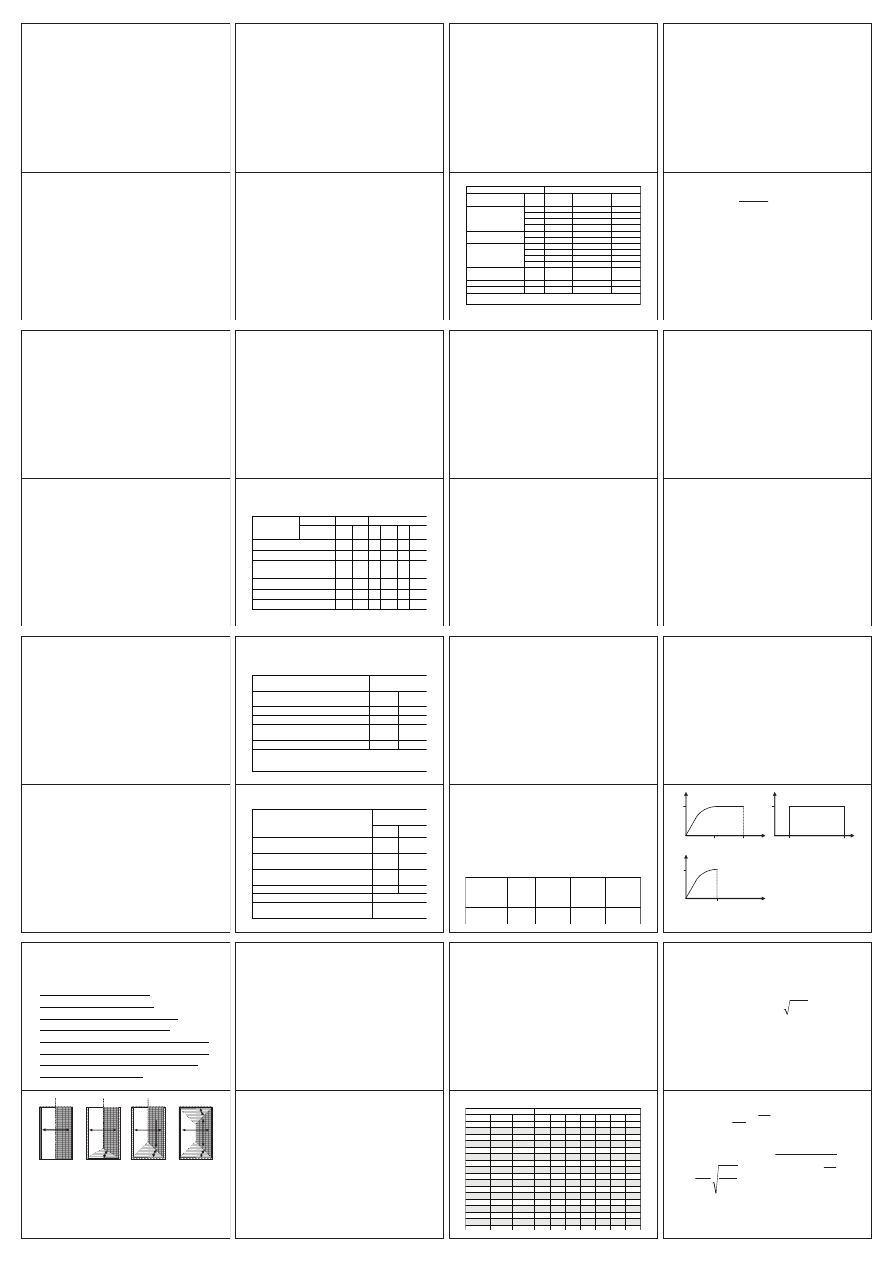
OdkształcalnoĞü muru

ZaleĪnoĞü miĊdzy naprĊĪeniem ı i odkształceniem
jednostkowym İ muru moĪna przyjmowaü:
- mur wykonany z elementów grupy 1 i 2 –
paraboliczno-prostokątna funkcja z İ

1

= 0,002 i İ

u

=

0,0035 - wykres ı(İ) w postaci paraboli madryckiej
(rys. a)
- obliczanie noĞnoĞci przekroju zginanego lub

23

- obliczanie noĞnoĞci przekroju zginanego lub
mimoĞrodowo Ğciskanego muru wykonanego z
elementów grupy 1 i 2 – moĪna siĊ równieĪ
posługiwaü funkcją o wykresie prostokątnym (rys. b)
- mury wykonane z elementów grup 3 i 4
charakteryzują siĊ zwykle zaleĪnoĞcią ı(İ) bez półki
poziomej. W takim przypadku moĪna przyjąü, Īe jest
to funkcja paraboliczna z İ

1

= İ

u

= 0,002 (rys. c).

a) ı

b) ı

f

d

f

d

İ

İ

İ

1

=0,002

İ

u

=0,0035

0,2İ

u

İ

u

c) ı

24

ZaleĪnoĞci miĊdzy naprĊĪeniem (ı), a odkształceniem (İ) muru:

a) paraboliczno-prostokątna, b) prostokątna, c) paraboliczna

f

d

İ

İ

1

=İ

u

=0,002

ObciąĪenie pionowe od stropów
wyznacza siĊ zgodnie z zasadami
podanymi na poniĪszym rysunku.
JeĪeli strop przylega do
nieoddylatowanej Ğciany
samonoĞnej, to do obciąĪenia

25

samonoĞnej, to do obciąĪenia
pionowego tej Ğciany naleĪy
doliczyü obciąĪenie z trójkąta stropu
wg rys. b lub zastĊpczo – obciąĪenie
z pasma stropu szerokoĞci równej
0,3 rozpiĊtoĞci stropu.

Rozdział obciąĪenia ze stropu na Ğciany

a)

b)

c)

d)

30

o

45

o

45

o

45

o

26

Rozdział obciąĪenia ze stropu na Ğciany

konstrukcyjne : a) strop zbrojony jednokierunkowo,
b) strop zbrojony jednokierunkowo przylegający do

Ğciany samonoĞnej, c) strop zbrojony

dwukierunkowo, oparty na trzech Ğcianach noĞnych,

d) strop zbrojony dwukierunkowo, oparty na

czterech Ğcianach noĞnych; strzałkami oznaczono

kierunek zbrojenia stropu

Stan graniczny noĞnoĞci Ğcian
obciąĪonych głównie pionowo sprawdza
siĊ z warunku

N

Sd

” N

Rd

w którym:

N

Sd

– wartoĞü obliczeniowa

obciąĪenia pionowego Ğciany,
N

Rd

– noĞnoĞü obliczeniowa Ğciany.

NoĞnoĞü sprawdza siĊ w przekrojach pod

27

NoĞnoĞü sprawdza siĊ w przekrojach pod
i nad stropem oraz w Ğrodkowej strefie
Ğciany, z uwzglĊdnieniem geometrii Ğcian,
mimoĞrodowego działania obciąĪenia
pionowego i właĞciwoĞci materiałowych
muru. W Ğcianach z otworami naleĪy takĪe
sprawdzaü noĞnoĞü nadproĪy.

Wyznaczając miejsce przyłoĪenia obliczeniowego
obciąĪenia pionowego

N

Sd

, naleĪy uwzglĊdniü

niezamierzony mimoĞród przypadkowy

e

a

=

h/300 (lecz

nie mniej niĪ 10 mm), w którym

h jest wysokoĞcią

Ğciany wyraĪoną w mm. NoĞnoĞü obliczeniową Ğciany
wyznacza siĊ ze wzorów:
- w przekroju pod stropem górnej kondygnacji

N

1R,d

oraz w przekroju nad stropem dolnej kondygnacji

N

2R,d

28

2R,d

N

iR,d

= ij

i

Af

d

w którym:

i = 1 – w przypadku przekroju pod stropem,

i = 2 – w przypadku przekroju nad stropem,
ij

i

– współczynnik redukcyjny, zaleĪny od mimoĞrodu

e

i

, na którym w rozpatrywanym przekroju działa

obliczeniowa siła pionowa

N

d

, oraz od mimoĞrodu

niezamierzonego

e

a

,

A – pole przekroju,

f

d

– wytrzymałoĞü obliczeniowa muru na Ğciskanie

- w Ğrodkowej strefie Ğciany
N

mR,d

= ij

m

Af

d

,

w którym:
ij

m

– współczynnik redukcyjny

wyraĪający wpływ efektów drugiego
rzĊdu na noĞnoĞü Ğciany, zaleĪny od

29

mimoĞrodu początkowego

e

0

= e

m

,

smukłoĞci Ğciany

h

eff

/

t, zaleĪnoĞci ı(İ)

muru i czasu trwania obciąĪenia,
A – pole przekroju,
f

d

– wytrzymałoĞü obliczeniowa muru na

Ğciskanie

Współczynnik redukcyjny noĞnoĞci ij

m

Współczynnik smukłoĞci h

eff

/t dla

MimoĞród e

m

α

α

α

α

c

= 1000

Į

c,’

=700

Į

c,’

=400

0,05t

0,10t

0,15t

0,20t

0,25t

0,30t

0,33t

0

0

0

0,90

0,80

0,70

0,60

0,50

0,40

0,34

1

0,8

0,6

0,90

0,80

0,70

0,60

0,50

0,40

0,34

2

1,6

1,3

0,90

0,80

0,70

0,60

0,50

0,40

0,34

3

2,4

1,9

0,90

0,80

0,70

0,60

0,50

0,40

0,34

4

3,3

2,6

0,90

0,80

0,70

0,60

0,49

0,39

0,33

5

4,2

3,2

0,89

0,79

0,69

0,59

0,49

0,39

0,33

6

5,0

3,8

0,88

0,78

0,68

0,58

0,48

0,39

0,33

30

6

5,0

3,8

0,88

0,78

0,68

0,58

0,48

0,39

0,33

7

5,9

4,4

0,88

0,77

0,67

0,57

0,47

0,37

0,31

8

6,7

5,1

0,86

0,76

0,66

0,56

0,45

0,35

0,29

9

7,5

5,7

0,85

0,75

0,65

0,54

0,44

0,34

0,28

10

8,4

6,3

0,84

0,73

0,63

0,53

0,42

0,32

0,26

11

9,2

7,0

0,82

0,72

0,61

0,51

0,40

0,30

0,24

12

10,0

7,6

0,80

0,70

0,59

0,49

0,38

0,28

0,22

13

10,9

8,2

0,79

0,68

0,57

0,47

0,36

0,26

0,20

14

11,7

8,8

0,77

0,66

0,55

0,45

0,34

0,24

0,18

15

12,5

9,5

0,75

0,64

0,53

0,42

0,32

0,22

0,16

16

13,4

10,1

0,72

0,61

0,51

0,40

0,30

0,20

0,15

Podane w powyĪszej tablicy wartoĞci
współczynnika ij

m

wyznaczono dla Ș

E

= 0.3

i ij

’

= 1.5. JeĪeli stosuje siĊ inne wartoĞci Ș

E

i ij

’

, wówczas wartoĞci ij

m

przyjmuje siĊ

z powyĪszej tablicy dla

α

α

α

α

c

= 1000 i

h

eff

/

t

pomnoĪonego przez 0,0316

∞

α

,

c

31

gdzie

α

α

α

α

c,’

- cecha sprĊĪystoĞci muru pod

obciąĪeniem długotrwałym, Ș

E

≤

≤

≤

≤ 1 –

współczynnik uwzglĊdniający redystrybucjĊ
sił wewnĊtrznych w konstrukcji oraz
stosunek obciąĪenia działającego
długotrwale do obciąĪenia całkowitego.

WartoĞci w tablicy obliczono ze wzoru:

ij

m

=

gdzie:

e – podstawa logarytmu naturalnego,

u =

2

2

2

1

u

m

e

t

e

−

−

−

−

¸¸¸¸

¹¹¹¹

····

¨¨¨¨

©©©©

§§§§

−

−

−

−

e

17

.

1

73

.

0

063

.

0

m

−

−

λ

32

Ȝ =

WartoĞci ij

m

, podane w tablicy odnoszą siĊ do

murów z elementów wszystkich czterech
grup, z tym, Īe dla murów z elementów grupy
3 i 4 obowiązuje dodatkowo warunek: ij

m

≤

≤

≤

≤ ij

i

t

e

17

.

1

73

.

0

m

−

∞

α

,

c

eff

1

t

h

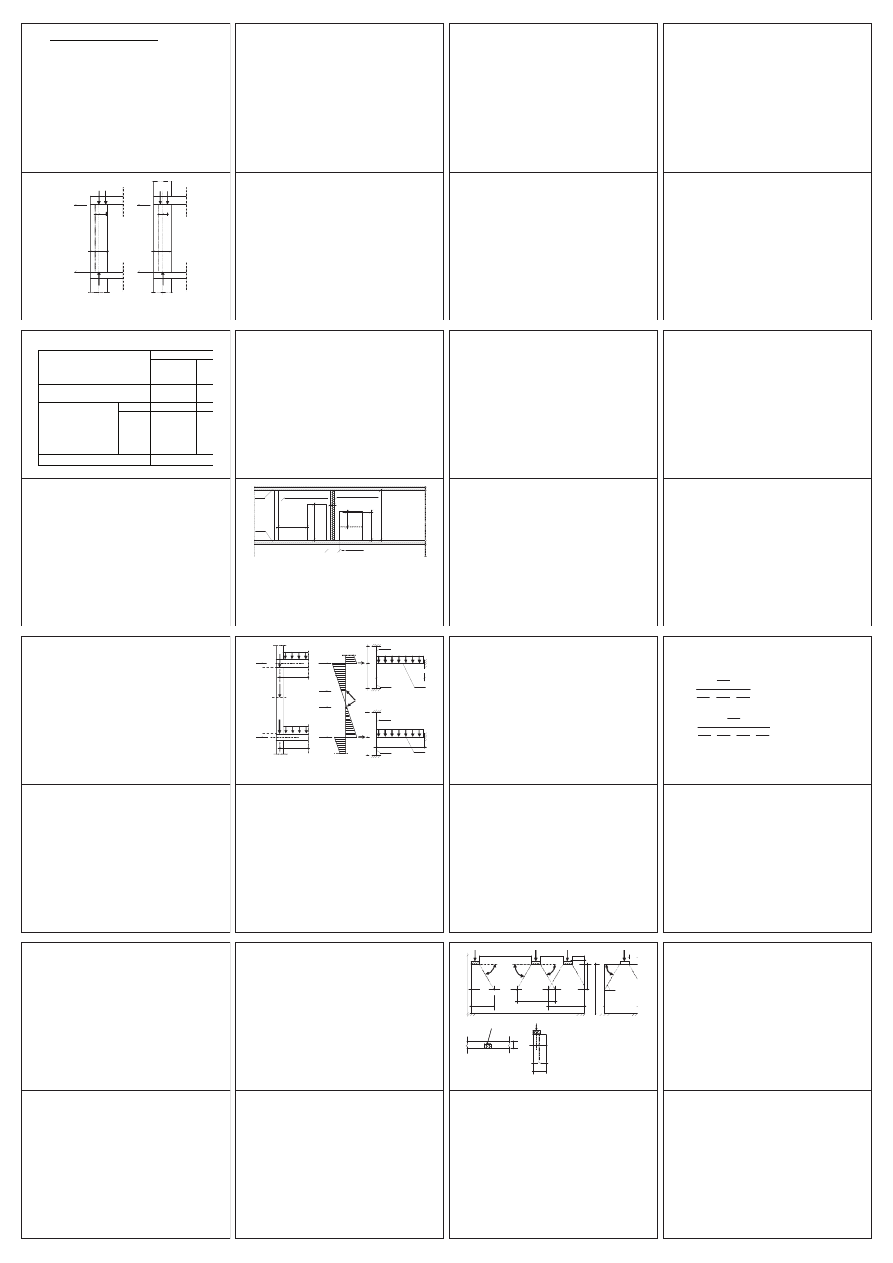
W MODELU PRZEGUBOWYM obliczania
Ğcian obciąĪonych głównie pionowo,
moĪna przyjąü:
a) na najwyĪszej kondygnacji:
- w przekroju pod stropem siła z dachu
N

0d

działa w stosunku do nominalnej osi

Ğciany na mimoĞrodzie e

a

, a obciąĪenie

33

Ğciany na mimoĞrodzie e

a

, a obciąĪenie

od stropu

N

sl,d

- na mimoĞrodzie 0,4 t +

e

a

,

- w przekroju nad

stropem dolnej

kondygnacji siła

N

2d

, stanowiąca sumĊ

N

0d

i

N

sl,d

- oraz ciĊĪaru Ğciany, działa na

mimoĞrodzie e

a

, (por. rysunek poniĪej)

a) N

0d

N

sl,d

b) N

0d

N

sl,d

e

a

0, 4t

e

a

t/3

h

1

h

1

34

Model przegubowy Ğciany zewnĊtrznej: a) Ğciana

najwyĪszej kondygnacji, b) Ğciana niĪszych kondygnacji

t

t

N

2d

N

2d

b) w przypadku Ğcian niĪszych
kondygnacji:
- w przekroju pod stropem siła
z górnych kondygnacji

N

0d

działa na

mimoĞrodzie

e

a

, a obciąĪenie od

stropu

N

- na mimoĞrodzie 0,33 t

35

stropu

N

sl,d

- na mimoĞrodzie 0,33 t

+ e

a

,

- w przekroju nad stropem dolnej
kondygnacji – analogicznie jak
w przypadku Ğciany najwyĪszej
kondygnacji.

NoĞnoĞü Ğciany najwyĪszej
kondygnacji naleĪy sprawdzaü
w przekroju pod stropem górnej
kondygnacji na moment

M

1d

,

a w przekroju nad stropem dolnej

36

kondygnacji na moment

M

2d

.

Momenty te okreĞla siĊ
z zaleĪnoĞci:
M

1d

=

N

0d

·

e

a

+ N

sl,d

·(0,4

t + ea),

M

2d

=

N

2d

·

e

a

NoĞnoĞü Ğciany niĪszych
kondygnacji naleĪy sprawdzaü
w przekroju pod stropem górnej
kondygnacji na moment

M

1d

,

a w przekroju nad stropem dolnej

37

kondygnacji na moment

M

2d

.

Momenty te okreĞla siĊ
z zaleĪnoĞci:
M

1d

=

N

0d

·

e

a

+ N

sl,d

·(0,33

t + e

a

),

M

2d

=

N

2d

·

e

a

Aby okreĞliü wartoĞü ij

m

(wg tablicy

lub ze wzoru) konieczne jest m. in.
wyznaczenie zastĊpczego
mimoĞrodu początkowego

e

m

,

równego co do wartoĞci u dołu
i góry modelowego prĊta Ğciany

38

i góry modelowego prĊta Ğciany
e

m

= (0,6

M

1d

+ 0,4

M

2d

)/

N

md

,

gdzie: |M

1d

| > |M

2d

|,

N

md

– wartoĞü

obliczeniowa siły pionowej
w połowie wysokoĞci Ğciany

JeĪeli na ĞcianĊ działa
bezpoĞrednio obciąĪenie poziome,
to mimoĞród

e zwiĊksza siĊ

o mimoĞród dodatkowy
e

m,w

= M

wd

/

N

md

, gdzie:

M

wd

– wartoĞü

obliczeniowa momentu zginającego

39

obliczeniowa momentu zginającego
w połowie wysokoĞci Ğciany,
obliczona jak dla belki swobodnie
podpartej; w wypadku obciąĪenia
w

d

rozłoĪonego równomiernie

M

wd

= w

d

h

1

2

/8

WysokoĞü efektywną Ğciany

h

eff

oblicza

siĊ ze wzoru

h

eff

=

ρ

ρ

ρ

ρ

h

ρ

ρ

ρ

ρ

n

h, w którym:

ρ

ρ

ρ

ρ

h

– współczynnik zaleĪny od

przestrzennego usztywnienia budynku
(poniĪsza tablica),

ρ

ρ

ρ

ρ

n

– współczynnik

zaleĪny od usztywnienia wzdłuĪ jej
krawĊdzi (dwóch, trzech lub czterech),

40

krawĊdzi (dwóch, trzech lub czterech),
h – wysokoĞü kondygnacji równa: przy
posługiwaniu siĊ modelem przegubowym
– wysokoĞci kondygnacji w Ğwietle, przy
posługiwaniu siĊ modelem ciągłym –
wysokoĞü kondygnacji w osiach modelu
ramy (

h

1

).

WartoĞü współczynnika ȡ

h

Rodzaj konstrukcji z uwagi na

usztywnienie przestrzenne

Rodzaj stropów

z betonu
z wieĔcami

Īelbetowymi

inne

Konstrukcja usztywniona przestrzennie

w sposób eliminujący przesuw poziomy

1,0

1,25

Konstrukcja bez Ğcian

3 i wiĊcej

1,25

1,50

41

Konstrukcja bez Ğcian

usztywniających, przy
czym liczba Ğcian
prostopadłych do kierunku
działania obciąĪenia
poziomego, przyjmujących
to obciąĪenie wynosi

3 i wiĊcej

1,25

1,50

2

1,50

2,0

ĝciany wolno stojące

2,0

ĝciany moĪna uwaĪaü za usztywnione
wzdłuĪ krawĊdzi pionowej, jeĪeli:
- są połączone wiązaniem murarskim lub
za pomocą zbrojenia ze Ğcianami
usztywniającymi usytuowanymi do nich
prostopadle, wykonanymi z muru
o podobnych właĞciwoĞciach

42

o podobnych właĞciwoĞciach
odkształceniowych,
- długoĞü Ğcian usztywniających jest nie
mniejsza niĪ 0,2 wysokoĞci Ğciany,
a gruboĞü nie mniejsza niĪ 0,3 gruboĞci
Ğciany usztywnianej i nie mniejsza niĪ
180 mm.

W przypadku Ğciany
usztywniającej z otworami zaleca
siĊ, aby długoĞü czĊĞci Ğciany
miĊdzy otworami, przyległej do
Ğciany usztywnianej, była nie

43

mniejsza niĪ podano na
poniĪszym rysunku, a Ğciana
usztywniająca siĊgała poza otwór
na długoĞü nie mniejszą niĪ 1/5
wysokoĞci kondygnacji.

strop Ğciana usztywniająca Ğciana usztywniana

> h/5 h

1

h

2

h

2

h

strop

h

2

– wysokoĞü

otworu

okiennego lub
drzwiowego

t

h

h

≥

+

2

)

(

5

1

2

1

t

44

Minimalna długoĞü Ğciany usztywniającej z otworami

Alternatywnie Ğciany mogą byü równieĪ usztywniane przez
elementy inne niĪ Ğciany murowane, pod warunkiem, Īe
sztywnoĞü tych elementów jest równowaĪna ze sztywnoĞcią
murowanej Ğcianie usztywniającej, o której mowa powyĪej,
a obie Ğciany połączone są ze Ğcianą usztywnianą za pomocą
Ğciągów lub kotew, zaprojektowanych tak, aby zdolne były
przenieĞü siły Ğciskające lub rozciągające, które mogą siĊ
pojawiü w połączeniu.

t

≥

2

5

Za wartoĞü

ρ

n

moĪna przyjmowaü:

a) dla Ğcian podpartych u góry i u dołu, kiedy
stropy oparte są na Ğcianie za poĞrednictwem
wieĔca Īelbetowego o szerokoĞci równej
gruboĞci Ğciany lub nie mniejszej niĪ gruboĞü
stropu, mają zbrojenie podporowe zdolne do
przeniesienia momentu zamocowania stropu

45

przeniesienia momentu zamocowania stropu
w Ğcianie, Ğrednie naprĊĪenie obliczeniowe
Ğciany

σ

cd

• 0,25 MPa, a mimoĞród e

1

działania obciąĪenia pionowego w przekroju

Ğciany pod stropem e

1

” 0,33 t

ρ

ρ

ρ

ρ

2

= 0,75

,

w pozostałych przypadkach

ρ

ρ

ρ

ρ

2

= 1,00.

b) dla Ğcian podpartych u góry i u dołu
i usztywnionych wzdłuĪ jednej krawĊdzi
pionowej (z jedną swobodną krawĊdzią
pionową):
- jeĪeli h ” 3,5 l, wartoĞü obliczoną ze

wzoru:

ρ

ρ

ρ

ρ

3

=

ρ

ρ

ρ

ρ

2

/[1 + (

ρ

ρ

ρ

ρ

2

h/3

l

)

2

],

46

wzoru:

ρ

ρ

ρ

ρ

3

=

ρ

ρ

ρ

ρ

2

/[1 + (

ρ

ρ

ρ

ρ

2

h/3

l

) ],

w którym

ρ

ρ

ρ

ρ

2

jak podano wyĪej,

- jeĪeli h > 3,5 l, wartoĞü obliczoną ze

wzoru

ρ

ρ

ρ

ρ

3

=

1,5 l/h > 0,3

w którym l – odległoĞü krawĊdzi swobodnej
od osi Ğciany usztywniającej,

c) dla Ğcian podpartych u góry i u dołu oraz
wzdłuĪ obu krawĊdzi pionowych:
- jeĪeli h ” l, wartoĞü obliczoną ze wzoru:
ρ

ρ

ρ

ρ

4

=

ρ

ρ

ρ

ρ

2

/[1 + (

ρ

ρ

ρ

ρ

2

h/l)

2

], w którym

ρ

ρ

ρ

ρ2 jak podano

w a) powyĪej,
- jeĪeli h > l, wartoĞü obliczoną ze
wzoru

ρ

ρ

ρ

ρ

4

= 0,5 l/h

47

4

W przypadku, gdy Ğciany są usztywnione
wzdłuĪ obu krawĊdzi pionowych i l

≥ 30 t lub

gdy Ğciany są usztywnione wzdłuĪ jednej
krawĊdzi pionowej i l

≥ 15 t, gdzie t jest

gruboĞcią Ğciany usztywnionej - Ğciany takie
naleĪy uwaĪaü za usztywnione tylko u góry
i u dołu.

Zaleca siĊ, aby smukłoĞü

h

eff

/

i (lub

wyraĪona jako

h

eff

/

t) Ğcian

konstrukcyjnych była nie wiĊksza niĪ:
h

eff

/

i

≤

≤

≤

≤ 87,5 (h

eff

/

t

≤

≤

≤

≤ 25) – w przypadku

Ğcian z murów na zaprawie f

m

≥

≥

≥

≥ 5 MPa,

z wyjątkiem murów z autoklawizowanego
betonu komórkowego,

48

betonu komórkowego,
h

eff

/

i

≤

≤

≤

≤ 63 (h

eff

/

t

≤

≤

≤

≤ 18) – w przypadku Ğcian

z autoklawizowanego betonu
komórkowego, niezaleĪnie od rodzaju
zaprawy, a takĪe murów z innego rodzaju
elementów murowych, na zaprawie
f

m

< 5 MPa.

MODEL CIĄGŁY

Modelem ciągłym naleĪy siĊ posługiwaü,
kiedy stropy oparte są na Ğcianie za
poĞrednictwem wieĔca Īelbetowego
o szerokoĞci równej gruboĞci Ğciany lub nie
mniejszej niĪ wysokoĞü stropu, mają
zbrojenie podporowe zdolne do przeniesienia
momentu zamocowania stropu w Ğcianie,

49

momentu zamocowania stropu w Ğcianie,
Ğrednie naprĊĪenie obliczeniowe Ğciany

σ

σ

σ

σ

cd

• 0,25 MPa, a mimoĞród e

i

działania

obciąĪenia pionowego w przekroju Ğciany pod
stropem e

i

” 0,33 t (gdzie t jest gruboĞcią

Ğciany). W przeciwnym przypadku naleĪy
posługiwaü siĊ modelem przegubowym.

Przy wyznaczaniu wielkoĞci

e

i

lub

e

m

naleĪy takĪe

uwzglĊdniaü obciąĪenie poziome, oddziaływujące
bezpoĞrednio na rozpatrywaną ĞcianĊ.
Przy posługiwaniu siĊ modelem ciągłym
współczynnik ij

i

wyznacza siĊ odpowiednio do

wartoĞci mimoĞrodu

e

i

działania obciąĪenia

pionowego, którą obliczaü moĪna ze wzoru:
e

i

=

M

id

/

N

id

+

M

wd

/

N

id

+

e

a

• 0,05 t

w którym:

M – obliczeniowy moment zginający

50

i

id

id

wd

id

a

w którym:

M

id

– obliczeniowy moment zginający

w przekroju Ğciany pod stropem (

M

1d

) lub nad

stropem (

M

2d

), wynikający z obciąĪenia Ğciany

stropem,

N

id

– obliczeniowa siła pionowa w

rozpatrywanym przekroju,

M

wd

– obliczeniowy

moment zginający wywołany obliczeniowym
obciąĪeniem poziomym oddziałującym bezpoĞrednio
na ĞcianĊ,

e

a

– mimoĞród przypadkowy

a)

b)

E

2

I

2

h

2

M

1d

h

2

N

1d

L

3

2 h

1

/5

L

3

h

1

E

1

I

1

E

3

I

3

N

md

M

m1

h

1

h

1

/5

M

md

= M

m1

lu b M

m2

M

m2

51

Wyznaczanie wartoĞci M

1d

i M

2d

w modelu ciągłym: a) zewnĊtrzna Ğciana

noĞna, b) momenty wywołane mimoĞrodowym obciąĪeniem Ğciany stropami,
c) uproszczone modele obliczeniowe do wyznaczania wartoĞci M

id

E

1

I

1

h

1

N

2d

2h

1

/5

h

5

L

4

M

2d

h

5

L

4

E

5

I

5

E

4

I

4

WartoĞü momentu

M

id

wyznaczaü moĪna

dla kaĪdego z wĊzłów ramy oddzielnie, jak
na powyĪszym rysunku, przyjmując
w uproszczeniu, Īe schodzące siĊ w wĊĨle
Ğciany i strop są niezarysowane
i zachowują siĊ liniowo sprĊĪyĞcie.
WartoĞci

E

i

modułu sprĊĪystoĞci muru

52

WartoĞci

E

i

modułu sprĊĪystoĞci muru

i betonu przyjmuje siĊ jak dla obciąĪenia
krótkotrwałego. SztywnoĞü stropów
gĊstoĪebrowych moĪna przyjmowaü
w przybliĪeniu od 0,80 (stropy
wielokanałowe) do 0,33 (stropy belkowe)
sztywnoĞci stropu pełnego.

WartoĞci momentów zginających,
wyznaczone na podstawie analizy ramowej
przy załoĪeniu sztywnych połączeĔ Ğciana –
strop, mają zawyĪoną wartoĞü. Rzeczywiste
połączenia Ğcian murowych ze stropami
charakteryzują siĊ wiĊkszą lub mniejszą
podatnoĞcią, zaleĪną miĊdzy innymi od

53

podatnoĞcią, zaleĪną miĊdzy innymi od
sposobu oparcia stropu na Ğcianie oraz
rozkładu i wartoĞci naprĊĪeĔ Ğciskających.
PodatnoĞü połączeĔ Ğcian murowych ze
stropami moĪna uwzglĊdniaü, redukując
wartoĞü momentów

M

id

odpowiednio do

wyników badaĔ doĞwiadczalnych.

W przypadku, gdy szerokoĞü wieĔca
za poĞrednictwem którego strop
opiera siĊ na Ğcianie jest nie
mniejsza niĪ gruboĞü Ğciany lub
wysokoĞü przekroju stropu –
obowiązuje wartoĞü mniejsza, do

54

obowiązuje wartoĞü mniejsza, do
obliczeĔ przyjąü moĪna moment
zginający w przekroju nad i pod
stropem równy 0,85 wartoĞci
uzyskanej z analizy sprĊĪystej
modelu ramy.

JeĪeli nie prowadzi siĊ analiz numerycznych, to wartoĞü momentu
przywĊzłowego przy górnej krawĊdzi Ğciany

M

1d

wyznaczaü moĪna

z zaleĪnoĞci:
- dla Ğciany obciąĪonej jednostronnie stropem

M

1d

=

· 0,85

M

o3

- dla Ğciany obciąĪonej dwustronnie stropem

3

3

3

2

2

2

1

1

1

1

1

1

h

I

E

h

I

E

h

I

E

h

I

E

+

+

+

+

+

+

+

+

55

- dla Ğciany obciąĪonej dwustronnie stropem

M

1d

=

· 0,85 (

M

o3

-

M

o4

)

Moment wĊzłowy

M

o

w przypadku stropu obciąĪonego

równomiernie obciąĪeniem obliczeniowym

q

d

wyznaczyü moĪna:

- dla przĊsła o rozpiĊtoĞci l

3

M

o3

=

q

3d

l

3

2

/12

- dla przĊsła o rozpiĊtoĞci l

4

M

o4

=

q

4d

l

4

2

/12

4

4

4

3

3

3

2

2

2

1

1

1

1

1

1

h

I

E

h

I

E

h

I

E

h

I

E

h

I

E

+

+

+

+

+

+

+

+

+

+

+

+

WartoĞci momentów zginających
od obciąĪenia poziomego
wyznaczaü naleĪy jak dla belki
ciągłej. Kiedy oddziałujące
bezpoĞrednio na ĞcianĊ

56

obliczeniowe obciąĪenie poziome
jest obciąĪeniem równomiernie
rozłoĪonym

w

d

, za wartoĞü

M

wd

przyjmowaü moĪna:
M

wd

= w

d

h

1

2

/16

Gdy zaleĪnoĞü ı(İ) moĪna wyraziü za
pomocą paraboli madryckiej lub funkcji
podobnej, tak jak ma to miejsce w przypadku
murów z elementów murowych grupy 1 i 2
(z wyjątkiem murów z autoklawizowanego
betonu komórkowego), wartoĞü
współczynnika ij

i

przyjmuje siĊ równą:

57

współczynnika ij

i

przyjmuje siĊ równą:

ij

i

= 1 – 2

e

i

/

t

W przypadku elementów murowych grupy 3

i 4 oraz murów z autoklawizowanego betonu
komórkowego, których zaleĪnoĞü ı(İ) nie
ma półki poziomej, zaleca siĊ przyjmowaü

ij

i

= 1/(1+5

e

i

/

t)

WartoĞü współczynnika ij

m

wyznacza siĊ jak

dla prĊta podpartego przegubowo
o wysokoĞci efektywnej

h

eff

obciąĪonego siłą

N

md

działającą na mimoĞrodzie

e

m

, którego

wartoĞü oblicza siĊ ze wzoru:
e

m

=

M

md

/

N

md

+

M

wd

/

N

md

+

e

a

• 0,05 t

w którym

M

md

– najwiĊkszy moment

58

md

obliczeniowy w Ğrodkowej 1/5 wysokoĞci
Ğciany, zaleĪny od wartoĞci M

1d

i

M

2d

,

M

wd

–

obliczeniowy moment zginający w połowie
wysokoĞci Ğciany, wywołany obliczeniowym
obciąĪeniem poziomym oddziałującym
bezpoĞrednio na ĞcianĊ,

N

md

– obliczeniowa

siła pionowa w połowie wysokoĞci Ğciany

Wpływ długotrwałego
działania obciąĪenia na
noĞnoĞü Ğciany
uwzglĊdnia siĊ
przyjmując do

59

przyjmując do
wyznaczenia wartoĞci ij

m

długotrwały moduł
sprĊĪystoĞci muru E

’

.

ĝciany obciąĪone siłą skupioną

JeĪeli Ğciana wykonana z elementów murowych
grupy 1 i spełniająca wymagania konstrukcyjne
stawiane Ğcianom noĞnym poddana jest
obciąĪeniu skupionemu, naleĪy sprawdziü
warunek

N

Sd

” N

Rd

przyjmując

N

Rd

= ȕ

A

b

f

d

w którym ȕ – współczynnik wyraĪający wpływ

60

w którym ȕ – współczynnik wyraĪający wpływ
siły skupionej okreĞlany ze wzoru:
ȕ = (1+0,3a

1

/

h

c

) (1,5 – 1,1

A

b

/

A

eff

)

lecz nie wiĊkszy niĪ mniejsza z wartoĞci:
1,25 +

a

1

/2

h

c

lub 1,5

a

1

– odległoĞü od krawĊdzi Ğciany do

najbliĪszej krawĊdzi pola oddziaływania
obciąĪenia skupionego (por. rysunek poniĪej);

N

Sd

N

Sd

N

Sd

N

Sd

a

1

60

o

60

o

60

o

60

o

h

c

/2

h

6 0

o

h

c

l

eff

l

eff

l

eff

l

eff

a

1

61

ĝciana

poddana

obciąĪeniu

skupionemu

N

Sd

A

b

≤ t/4

RZUT

PRZEKRÓJ

t

t

h

c

– wysokoĞü Ğciany do poziomu obciąĪenia;

A

b

– pole oddziaływania obciąĪenia

skupionego;
A

eff

– efektywne pole przekroju Ğciany

o wymiarach l

eff

·

t;

l

eff

– efektywna długoĞü okreĞlona w połowie

wysokoĞci Ğciany lub pilastra;
N

– obliczeniowe obciąĪenie skupione.

62

N

Sd

– obliczeniowe obciąĪenie skupione.

Stosunek A

b

/A

eff

nie moĪe byü wiĊkszy niĪ

0,45
W przypadku Ğcian wykonanych z elementów
murowych grupy 2, 3 i 4, lokalne obliczeniowe
naprĊĪenie Ğciskające nie powinno byü
wiĊksze niĪ

f

d

(tj. ȕ = 0)

Gdy bezpoĞrednio pod obciąĪeniem
skupionym w Ğcianie wykonana
została warstwa muru z elementów
murowych grupy 1 o wysokoĞci co
najmniej równej gruboĞci Ğciany
i nie mniejszej niĪ 200 mm oraz

63

i nie mniejszej niĪ 200 mm oraz
długoĞci nie mniejszej niĪ trzy
długoĞci na której przyłoĪone jest to
obciąĪenie, przyjąü moĪna, Īe
obciąĪenie skupione rozkłada siĊ
pod kątem 60

o

(poprzedni rysunek).

Zaleca siĊ, aby siła skupiona
znajdowała siĊ w stosunku do
płaszczyzny Ğrodkowej Ğciany
w odległoĞci nie wiĊkszej niĪ 0,25

t.

Poza sprawdzeniem stanu

64

granicznego noĞnoĞci z warunku
N

Sd

” N

Rd

, dla N

Rd

z warunku

N

Rd

= ȕ

A

b

f

d

sprawdziü naleĪy

równieĪ warunki

N

iR,d

= ij

i

Af

d

i

N

mR,d

= ij

m

Af

d

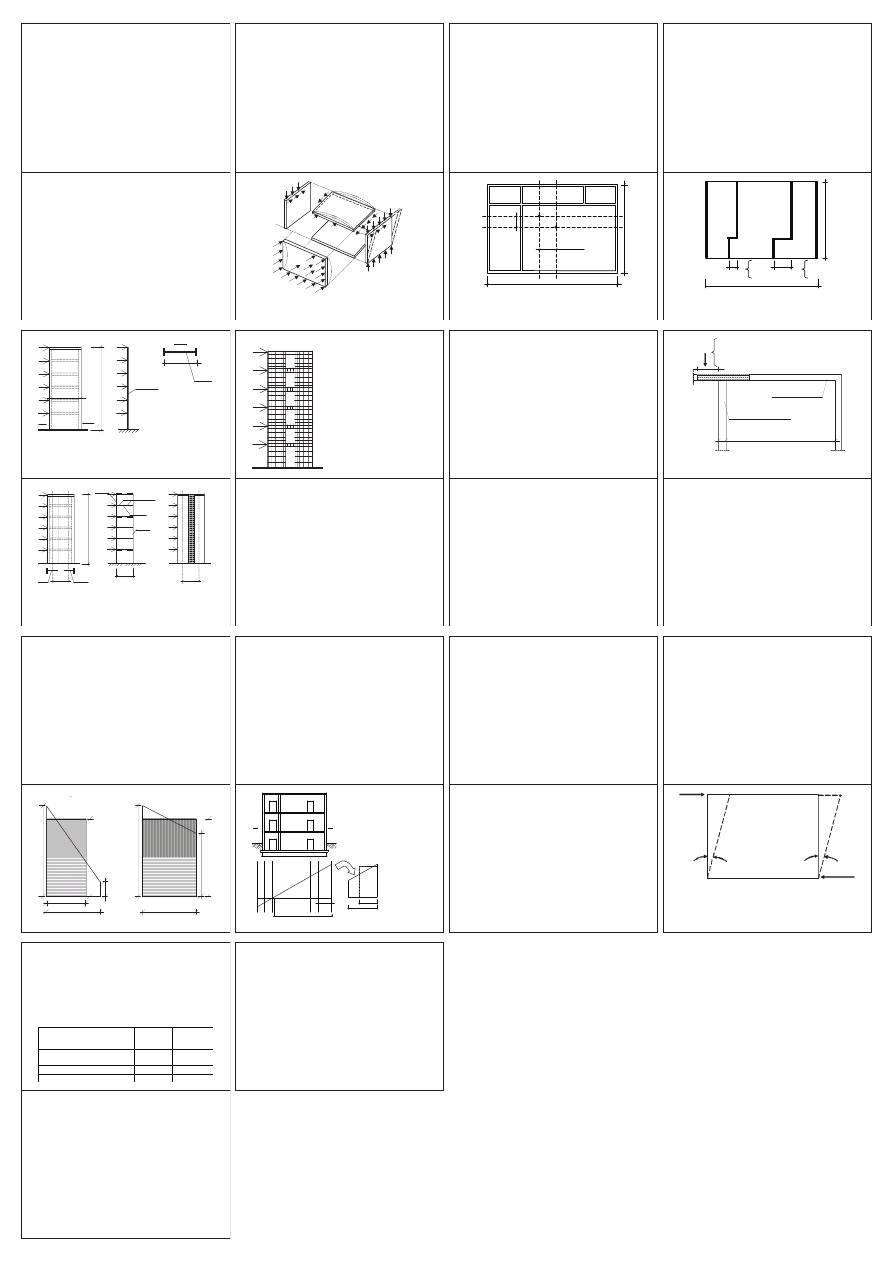
ĝciany usztywniające

W obliczeniach Ğcian usztywniających
uwzglĊdnia siĊ – poza siłami
wewnĊtrznymi wywołanymi obciąĪeniem
pionowym – siły wewnĊtrzne (momenty
i siły styczne) działające w płaszczyĨnie
Ğciany wynikające z przestrzennej pracy

65

Ğciany wynikające z przestrzennej pracy
budynku. Z uwagi na rodzaj oddziaływaĔ
wywołujących te siły rozróĪnia siĊ:
- Ğciany usztywniające z uwagi na
obciąĪenie poziome;
- Ğciany usztywniające z uwagi na
przemieszczenia pionowe podłoĪa.

Do obliczeĔ konstrukcji budynków ze
stropami Īelbetowymi lub sprĊĪonymi
przyjmowaü moĪna, Īe całe
obciąĪenie poziome oddziałujące na

ĝciany usztywniające z uwagi na

obciąĪenie poziome

66

obciąĪenie poziome oddziałujące na
budynek rozkłada siĊ na
poszczególne Ğciany usztywniające,
proporcjonalnie do ich sztywnoĞci na
zginanie z uwzglĊdnieniem obecnoĞci
otworów w Ğcianach.

Zakłada siĊ przy tym, Īe kierunek obciąĪenia
poziomego jest równoległy do Ğcian
usztywniających, w związku z czym wyznacza
siĊ oddzielnie siły w Ğcianach
usztywniających, usytuowanych w kierunku
podłuĪnym i poprzecznym.
JeĪeli stropy nie są dostatecznie sztywne, aby

67

uwaĪaü je za sztywne tarcze (np. w przypadku
niezmonolityzowanych stropów z elementów
prefabrykowanych), za siły poziome
oddziałujące na ĞcianĊ usztywniającą zaleca
siĊ uwaĪaü siły przekazywane przez stropy,
z którymi Ğciana usztywniająca jest
bezpoĞrednio połączona.

Strop

Strop

Ğciana

Ğ

ciana

usztywniająca

68

Schemat przekazywania siĊ sił od poziomego

parcia wiatru na Ğciany usztywniające

Ğciana
frontowa

wiatr

usztywniająca

JeĪeli Ğciany usztywniające są rozmieszczone
asymetrycznie lub jeĪeli z innego powodu siła
wypadkowa z poziomych obciąĪeĔ lub
oddziaływaĔ na budynek działa mimoĞrodowo
w stosunku do Ğrodka ciĊĪkoĞci rzutu Ğcian
usztywniających, na mimoĞrodzie wiĊkszym

69

niĪ 0,05 długoĞci wzglĊdnie szerokoĞci
budynku (rysunek poniĪej), naleĪy uwzglĊdniü
wpływ obrotu ustroju usztywniającego na
rozdział obciąĪenia na poszczególne Ğciany
usztywniające oraz wpływ skrĊcenia całego
budynku na jego sztywnoĞü przestrzenną.

” 0,05 B O

1

O

B

” 0,05L

70

Zasada rozmieszczania Ğcian usztywniających budynku:

O

1

– Ğrodek geometryczny rzutu Ğcian usztywniających,

O – Ğrodek geometryczny rzutu budynku

” 0,05L

L

ĝciana usztywniająca moĪe byü na swojej
długoĞci załamana w planie (rysunek poniĪej)
jeĪeli odcinek usytuowany prostopadle do jej
płaszczyzny:
- nie jest dłuĪszy niĪ 1,2 m;
- nie jest dłuĪszy niĪ 0,2 długoĞci obliczanej
Ğciany;
- nie zawiera otworu drzwiowego wzglĊdnie

71

- nie zawiera otworu drzwiowego wzglĊdnie
okiennego;
- jest powiązany z pozostałymi odcinkami Ğciany
zgodnie z wymaganiami dotyczącymi Ğcian
usztywniających.
JeĪeli którykolwiek z powyĪszych warunków nie
jest spełniony, ĞcianĊ taką naleĪy obliczaü jako
dwa niezaleĪne (niepowiązane ze sobą) pasma.

B

1

B

2

B

3

B

4

B

72

ĝciana usztywniająca załamana w planie: B1, B2 i B4

– Ğciana traktowane jako jedno pasmo, B3 – Ğciana

obliczana jako dwa niezaleĪne pasma

1,2 m

1,2 m

0,2 B

0,2 B

L

”

>

a)

A-A

L

I

H

EI

L

73

Modele obliczeniowe Ğcian

usztywniających: a) bez otworów –

prĊt wspornikowy;

A

A

b)

E

1

I

1

b1)

b2)

E

r

I

r

=

E

3

I

3

H

E

2

I

2

8

74

Modele obliczeniowe Ğcian usztywniających:
b) z szeregiem otworów; 1 – rama zastĊpcza,

2 - model pasmowy z połączeniem ciągłym

L

(1)

I

1

L

(1)

I

2

L

(1)

Modele

obliczeniowe Ğcian

usztywniających:

b) z szeregiem

otworów:

b3)

75

otworów:

3 – podział tarczy

Ğciennej na

elementy do
analizy MES

ĝcianĊ poprzeczną prostopadłą do Ğcian
usztywniających przyjmowaü moĪna jako
półkĊ w przekroju poprzecznym Ğciany,
zwiĊkszającą jej sztywnoĞü i noĞnoĞü.
ZwiĊkszenie to uwzglĊdniaü moĪna
w obliczeniach pod warunkiem, Īe
wysokoĞü Ğciany jest nie wiĊksza niĪ

76

wysokoĞü Ğciany jest nie wiĊksza niĪ
podwójna jej długoĞü oraz, Īe połączenie
Ğciany usztywniającej ze Ğcianą
poprzeczną ma dostateczną noĞnoĞü
z uwagi na wystĊpujące tu siły Ğcinające,
półka nie ulegnie wyboczeniu na swojej
długoĞci.

JeĪeli w obliczeniach Ğciany
usztywniającej uwzglĊdnia siĊ
współpracĊ czĊĞci Ğciany poprzecznej
moĪe byü potrzebne obliczeniowe
sprawdzenie połączenia obu Ğcian. Gdy
nie są one połączone przez przewiązanie

77

elementów murowych przyjąü naleĪy, Īe
całą siłĊ poprzeczną przyjmuje wieniec
Īelbetowy łączący obie Ğciany
w poziomie stropu. NoĞnoĞü wieĔca na
Ğcinanie oblicza siĊ zgodnie z PN-B-
03264.

Zaleca siĊ, aby długoĞü półki
przyjmowana do obliczeĔ nie była
wiĊksza niĪ najmniejsza z nastĊpujących
wartoĞci (rysunek poniĪej):
- 0,20 wysokoĞci całkowitej obliczanej
Ğciany usztywniającej (h

tot

),

78

tot

- 0,5 odległoĞci od sąsiedniej Ğciany
usztywniającej (l

s

);

- odległoĞci od krawĊdzi Ğciany;
- 0,5 wysokoĞci kondygnacji w Ğwietle
(

h);

- szeĞciokrotnej gruboĞci półki (

t).

h

t ot

/5

min

1/2 l

s

h/2
6t

Ğciana poprzeczna

79

Sposób okreĞlania długoĞci Ğciany poprzecznej

współpracującej ze Ğcianą usztywniającą

Ğciana usztywniająca

t

l

s

WystĊpujące w Ğcianach poprzecznych
otwory o rozpiĊtoĞci mniejszej niĪ

h/4 lub

l

s

/4 mogą byü w obliczeniach pominiĊte,

natomiast w przypadku otworów
o wiĊkszej rozpiĊtoĞci ich krawĊdzie
naleĪy traktowaü jako koĔce Ğciany.
JeĪeli Ğciana usztywniająca przenosi

80

JeĪeli Ğciana usztywniająca przenosi
takĪe inne obciąĪenia pionowe poza
ciĊĪarem własnym z jednej kondygnacji,
jej noĞnoĞü naleĪy sprawdziü z uwagi na
obciąĪenie pionowe oraz z uwagi na
obciąĪenie poziome działające
w płaszczyĨnie Ğciany.

Obliczeniowe sprawdzanie Ğcian usztywniających

ĝciany usztywniające sprawdza siĊ z uwagi na
obciąĪenia pionowe z warunku

N

Sd

” N

Rd

w przekroju

nad i pod stropem oraz w Ğrodkowej czĊĞci Ğciany,
przyjmując za wartoĞü

N

Sd

sumĊ:

N

Sd

=

N

vd

+

N

hd,

gdzie

N

vd

– siła pionowa, spowodowana obliczeniowym

obciąĪeniem pionowym,

N

hd

- siła pionowa, działająca

w płaszczyĨnie Ğciany, spowodowana obliczeniowym
obciąĪeniem poziomym.

81

obciąĪeniem poziomym.
Gdy róĪnica naprĊĪeĔ na krawĊdziach wydzielonego
pasma o szerokoĞci b

o

, powstałych w wyniku łącznego

działania obciąĪenia pionowego i poziomego wynosi:
σ

σ

σ

σ

1

-

σ

σ

σ

σ

2

• 0,33 σ

σ

σ

σ

1

, przy czym

σ

σ

σ

σ

1

>

σ

σ

σ

σ

2

, siła

N

Sd

odpowiada

wypadkowej bryły równomiernie rozłoĪonych
naprĊĪeĔ

σ

σ

σ

σ

0

wystĊpujących w wydzielonym paĞmie

Ğciany N

Sd

=

σ

σ

σ

σ

0

b

0

t = 0,83

σ

σ

σ

σ

1

b

0

t (rysunek poniĪej).

a) ı

1

– ı

2

> 0. 33ı

1

(ı

1

>ı

2

)

b)

ı

1

– ı

2

< 0.33 ı

1

ı

0

= 0.83ı

1

ı

0

= 0. 5(ı

1

+ı

2

)

ı

1

ı

0

ı

1

ı

0

82

Rozkład naprĊĪeĔ przyjmowanych do wyznaczenia siły N

Sd

ı

2

ı

2

b

0

l

l

Gdy naprĊĪenia na krawĊdziach
wydzielonego pasma o szerokoĞci

b

0

spełniają warunek

σ

σ

σ

σ

1

-

σ

σ

σ

σ

2

< 0,33

σ

σ

σ

σ

1

przyjmuje siĊ

N

Sd

=

σ

σ

σ

σ

0

b

0

t = 0,5(

σ

σ

σ

σ

1

+

σ

σ

σ

σ

2

)

b

0

t

Dla czĊĞci Ğciany, gdzie w wyniku
łącznego działania obciąĪenia poziomego

83

i pionowego wystĊpują naprĊĪenia
rozciągające, przyjmuje siĊ

N

Sd

= 0.

Za szerokoĞü pasma obliczeniowego

b

0

naleĪy przyjmowaü:
-

b

0

=

b, gdy b ” 1,0 m;

-

b

0

= 1,0 m, gdy

b > 1,0 m.

Sposób

wyznaczenia

miarodajnej

wartoĞci siły

N

Sd

A

A

L

a) przekrój miarodajny

84

N

Sd

a) przekrój miarodajny

σ

σ

σ

σ

1

σ

σ

σ

σ

0

σ

σ

σ

σ

2

b

b

0

b

l

c

b) wypadkowy wykres naprĊĪeĔ pionowych od

c) hipotetyczne pasmo o szerokoĞci b

0

równoczesnego działania obciąĪeĔ pionowych i poziomych i bryła naprĊĪeĔ

σ

σ

σ

σ

0

do wyznaczenia siły N

Sd

NoĞnoĞü Ğciany z uwagi na siły poziome
działające w jej płaszczyĨnie, sprawdza siĊ
z warunku:

V

Sd

” V

Rd

gdzie:

V

Sd

– obliczeniowa siła Ğcinająca

wywołana działaniem sił poziomych
w płaszczyĨnie Ğciany – równoznaczna
z wypadkową bryły naprĊĪeĔ Ğcinających od
obliczeniowych wartoĞci oddziaływaĔ;

85

obliczeniowych wartoĞci oddziaływaĔ;
V

Rd

– noĞnoĞü obliczeniowa sprawdzanego

przekroju Ğciany równa:
V

Rd

=

f

vd

t l

c

f

vd

– wytrzymałoĞü obliczeniowa muru na

Ğcinanie w kierunku równoległym do spoin
wspornych;

t – gruboĞü Ğciany, l

c

– długoĞü

Ğciskanej czĊĞci przekroju poprzecznego Ğciany.

JeĪeli Ğciana usztywniająca nie przenosi
innego obciąĪenia pionowego poza
ciĊĪarem własnym z jednej kondygnacji,
sprawdziü naleĪy nieprzekroczenie
dopuszczalnej wielkoĞci kąta granicznego
odkształcenia postaciowego Ğciany Ĭ

adm

86

adm

wywołanego obciąĪeniem działającym
w jej płaszczyĨnie. JeĪeli Ğciana taka jest
Ğcianą zewnĊtrzną, naleĪy sprawdziü
dodatkowo jej noĞnoĞü z uwagi na
obciąĪenie poziome działające
prostopadle do płaszczyzny Ğciany.

STAN GRANICZNY UĩYTKOWALNOĝCI

KONSTRUKCJI MUROWYCH

ĝciany usztywniające sprawdza siĊ z uwagi
na nieprzekroczenie dopuszczalnej wielkoĞci
kąta Ĭ

adm

z ogólnego warunku: Ĭ

Sd

” Ĭ

adm

gdzie: Ĭ

Sd

– kąt odkształcenia postaciowego

obliczony dla charakterystycznych wartoĞci

87

obliczony dla charakterystycznych wartoĞci
poziomych sił Ğcinających

V

Sk

(rysunek

poniĪej) równy Ĭ

Sd

=

V

Sk

/0,2

EA

E – moduł sprĊĪystoĞci muru;
A – przekrój poziomy Ğciany;
Ĭ

adm

– dopuszczalna wartoĞü kąta

odkształcenia postaciowego

V

Sk

88

Model obliczeniowy do wyznaczenia

kąta odkształcenia postaciowego

Ĭ

Sd

Ğciany usztywniającej

obciąĪonej poziomo

Ĭ

Sd

Ĭ

Sd

V

Sk

WartoĞci Ĭ

adm

przyjmowaü moĪna dla murów

z wypełnionymi spoinami pionowymi
z poniĪszej tablicy, a dla murów
z niewypełnionymi spoinami pionowymi –
wartoĞci z tej samej tablicy, lecz zmniejszone
o 50%.

Dopuszczalne wartoĞci kąta odkształcenia

89

Dopuszczalne wartoĞci kąta odkształcenia

postaciowego Ĭ

adm

w miliradianach (mm/m)

Rodzaj elementów murowych

Zaprawa

cementowa

Zaprawa
cementowo-

wapienna

Grupa 1, poza bloczkami z betonu

komórkowego

0,4

0,5

Grupa 2, 3 i 4

0,3

0,4

Bloczki z betonu komórkowego

0,2

0,3

NoĞnoĞü nadproĪy murowych stanowiących
łącznik pasm pionowych Ğciany
usztywniającej sprawdza siĊ z warunku:
V

Sd

/0,75

th

n

” f

vd

gdzie:

V

Sd

– obliczeniowa siła Ğcinająca

w nadproĪu; udział pionowego obciąĪenia
nadproĪa obciąĪonego stropem z reguły

90

pomija siĊ;

t – gruboĞü Ğciany;

h

n

– wysokoĞü nadproĪa łącznie z wieĔcem;

f

vd

– wytrzymałoĞü obliczeniowa muru na

Ğcinanie.
JeĪeli warunek

V

Sd

/0,75

th

n

” f

vd

nie jest

spełniony, zaprojektowaü naleĪy nadproĪe
Īelbetowe.

ĝciany usztywniające z uwagi na

przemieszczenia pionowe podłoĪa

Przy sprawdzaniu konstrukcji budynku poddanego
przemieszczeniom pionowym podłoĪa moĪna przyjąü
w uproszczeniu, Īe deformacje pionowe podłoĪa pod
budynkami w całoĞci przekazywane są na Ğciany
usztywniające.
W obliczeniach deformacji budynku poddanego
wpływom pionowych przemieszczeĔ podłoĪa, naleĪy

91

wpływom pionowych przemieszczeĔ podłoĪa, naleĪy
w miarĊ moĪliwoĞci uwzglĊdniü współpracĊ budynku
z podłoĪem zarówno stosując metody uproszczone jak
i modele analityczne, posługując siĊ programami
opartymi na metodzie elementów skoĔczonych (MES).
JeĪeli w obliczanych Ğcianach usztywniających
wystĊpują otwory drzwiowe i/lub okienne to naleĪy je
uwzglĊdniaü przy wyznaczaniu sztywnoĞci giĊtnej
Ğciany oraz stanu jej deformacji.