GEOMETRIA I GRAFIKA INŻYNIERSKA

(5)

WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI

KATEDRA URZĄDZEŃ ELEKTRYCZNYCH I TECHNIKI ŚWIETLNEJ

10. PRZEKROJE

    Jednym  z  elementów  rysunku  technicznego  są  przekroje.  Służą  przede
wszystkim  uwidocznieniu  szczegółów  obiektu  niewidocznych  w  rzutach
prostokątnych.  Przekrojów  brył  można  dokonywać  zarówno  na  rzutach
prostokątnych jak i rzutach aksonometrycznych.
   Przecięcia na rzutach prostokątnych wykonujemy najczęściej płaszczyznami
pionowo- lub poziomo- rzutującymi.
    Płaszczyzny którymi dokonujemy przecięć nazywamy płaszczyznami

siecznymi lub tnącymi

.

10.1. Przykłady przekrojów na rzutach prostokątnych

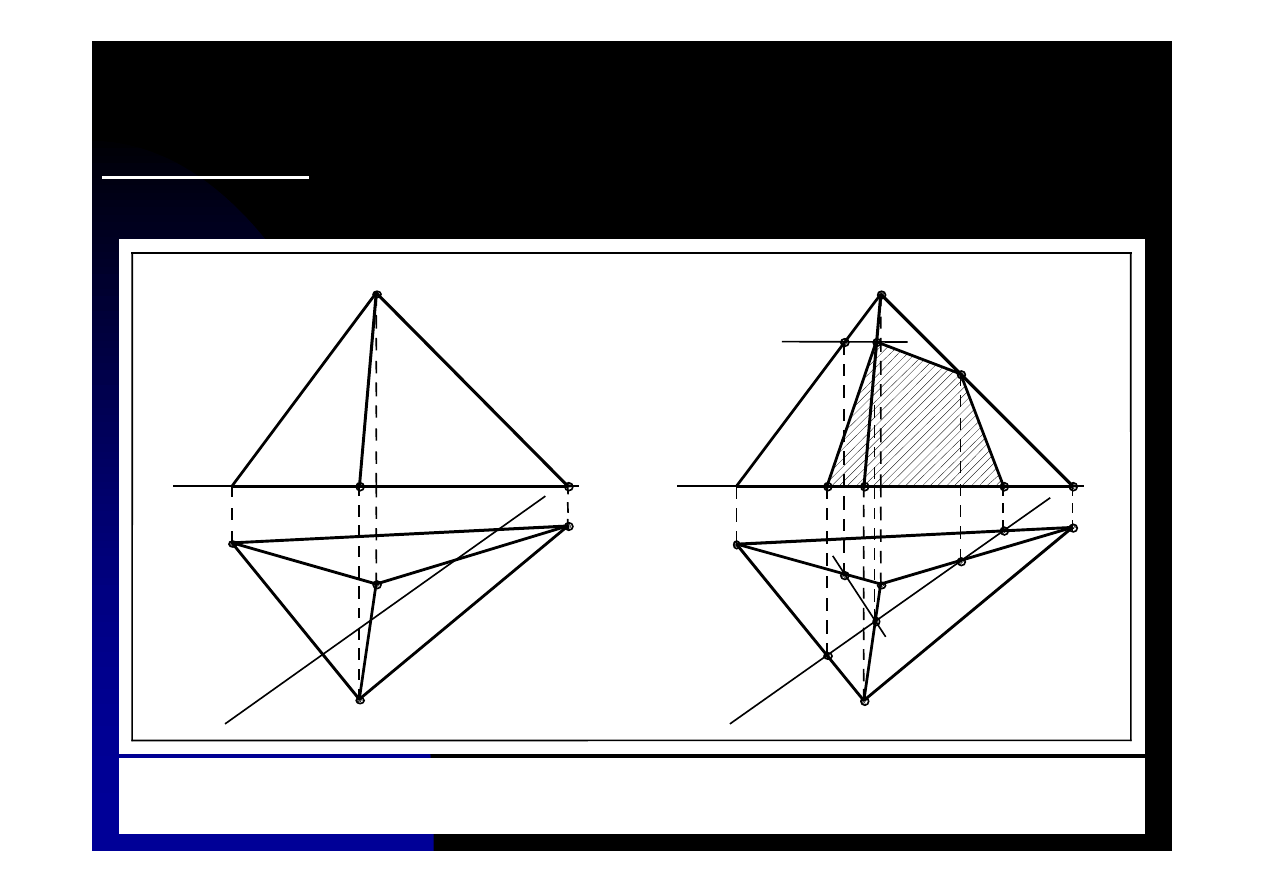
Zadanie 10.1. Ostrosłup dany dwoma rzutami przeciąć płaszczyzną

 

αααα

prostopadłą do rzutni poziomej.

C'

3'

4'

3"

4"

C"

A'

C'

W'

2"

1"

5"

A"

B"

W"

b)

a)

W"

C"

B"

A"

1'

2'

5'

B'

α

'

α

'

B'

W'

A'

x

x

x

Rys. 10.1. Rysunek do zadania 10.1: rzuty ostrosłupa i płaszczyzny tnącej (a) oraz sposób
wykonania przekroju (b)

Zaznaczamy rzuty poziome punktów przecięcia ostrosłupa przez płaszczyznę 

α

 (1”, 2”,

3”  i  4”).  Znajdujemy  rzuty  pionowe  punktów  przecięcia  za  pomocą  prostych
rzutujących wiedząc, że muszą leżeć na odpowiadających im krawędziach ostrosłupa.
Wyznaczenie  punktu  2”  może  być  jednak  mało  dokładne  gdyż  krawędź  B’W’  jest
prawie prostopadła do x. Punkt 2” można wyznaczyć w sposób następujący:

- przez punkt 2’ prowadzimy prostą leżącą na ścianie ABW ostrosłupa równolegle
do  krawędzi  AB.  Rzut  pionowy  punktu  przecięcia  prostej  z  krawędzią  AW  (5”)
można wyznaczyć już dokładnie.
- ponieważ rzut pionowy pomocniczej prostej musi być również równoległy do
rzutu pionowego krawędzi AB, łatwo wyznaczamy położenie punktu 2”.

Krawędzie rzutu pionowego przekroju znajdujemy łącząc ze sobą punkty 1”, 2”, 3” i
4”.

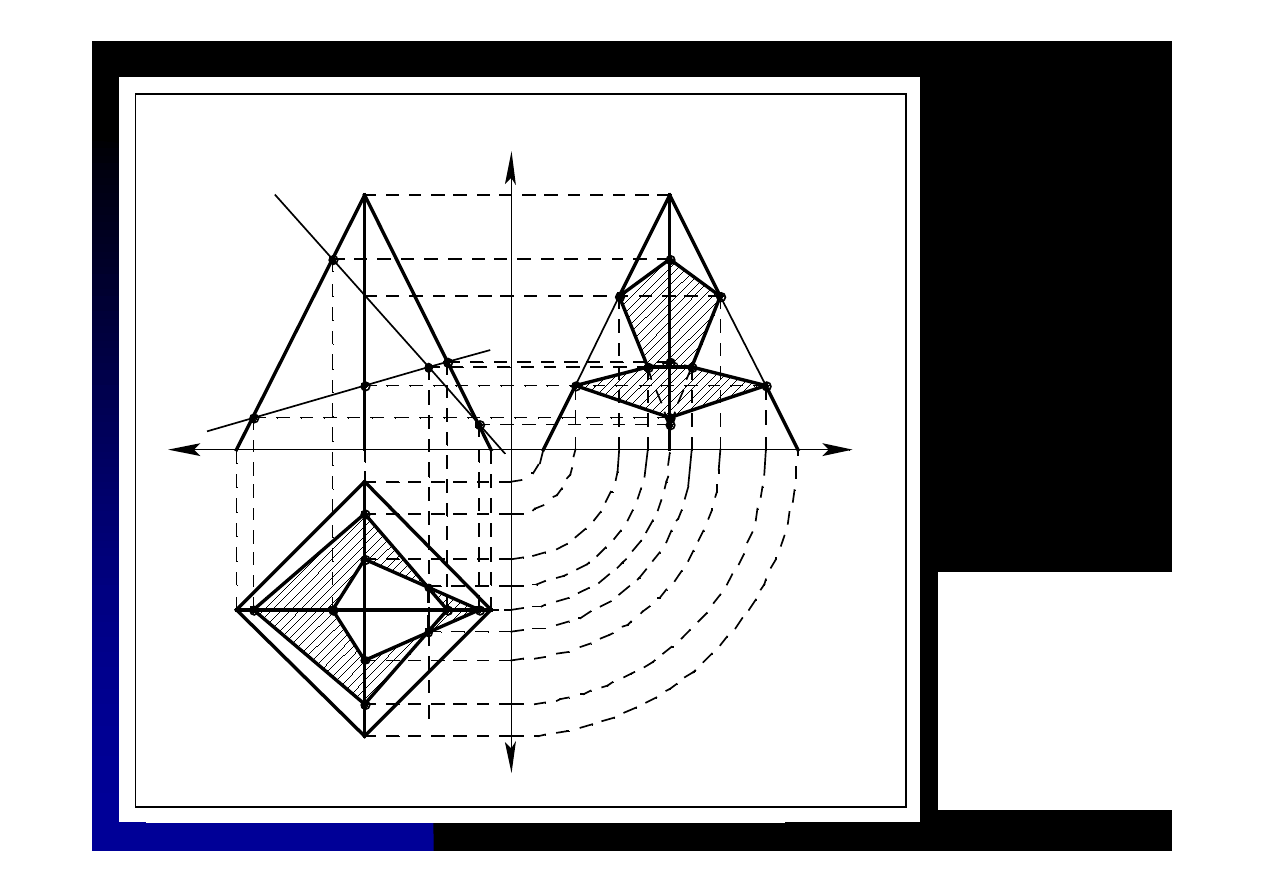
Zadanie 10.2. W ostrosłupie czworokątnym prawidłowym o danych
rzutach  wyciąć  otwór  ograniczony  dwoma  płaszczyznami 

αααα

  i 

ββββ

prostopadłymi do rzutni pionowej.

A'

C'

D'

x

β

"

α

"

C"

A"

B'

D" B"

W'

W"

z

C"'

W"'

y

A"'

B"'

D"'

y

Rys. 10.2. Rzuty główne ostrosłupa oraz płaszczyzn 

α

 i 

β

prostopadłych do rzutni pionowej

Rys. 8.2. Rzut aksonometryczny ukadu osi

Rys. 10.2a. Rzuty
główne ostrosłupa
z wyciętym
fragmentem przez
dwie płaszczyzny
prostopadłe do
rzutni pionowej

z

y

x

β

"

α

"

D'

W"

W"'

y

10"

8"

7"

6"

5"

4"

3"

2"

D"'

C"'

A"'

B"'

C"

A"

B'

D" B"

A'

C'

W'

2"'

8"'

9"'

10"'

4"'

6"'

7"'

5"'

3"'

1"'

2'

8'

4'

6'

1'

10'

9'

7'

5'

3'

1"

9"

Zadanie 10.3. Przeciąć graniastosłup o podstawie prostokątnej
płaszczyzną 

α

(1,2,3) określoną trzema punktami leżącymi na jego

krawędziach.

10.2. Przykłady przekrojów na rzutach aksonometrycznych

z

2

5

y

y

1

G

G

z

H

3

E

F

B

A

P

6

x

4

a)

b)

E

H

3

D

F

E

C

B

A

x

1

2

Rys. 10.3. Przekrój graniastosłupa płaszczyzną określoną przez trzy punkty

α

(1, 2 ,3)

Punkty 1 i 2 leżą przynależą jednocześnie do ściany ABFE graniastosłupa i do
płaszczyzny tnącej – przez te dwa punkty musi więc przechodzić krawędź
przecięcia. Ściana DCGH jest równoległa do ściany ABFE zatem krawędzie
przecięcia tych ścian muszą być równoległe – stąd punkt 4. Punkt P należy do
płaszczyzny tnącej bo do tej płaszczyzny należy krawędź przecięcia z płaszczyzną
‘zy’ – możemy wyznaczyć zatem następny punkt (5) należący do przekroju.
Krawędź 3-6 musi być równoległa do krawędzi 2-5, a krawędź 1-6 do krawędzi 4-5
(na mocy niezmiennika rzutowania równoległego). Zadanie ilustruje rysunek 10.3.

z

2

5

y

y

1

G

G

z

H

3

E

F

B

A

P

6

x

4

a)

b)

E

H

3

D

F

E

C

B

A

x

1

2

Rys. 10.3.
Powtórzenie

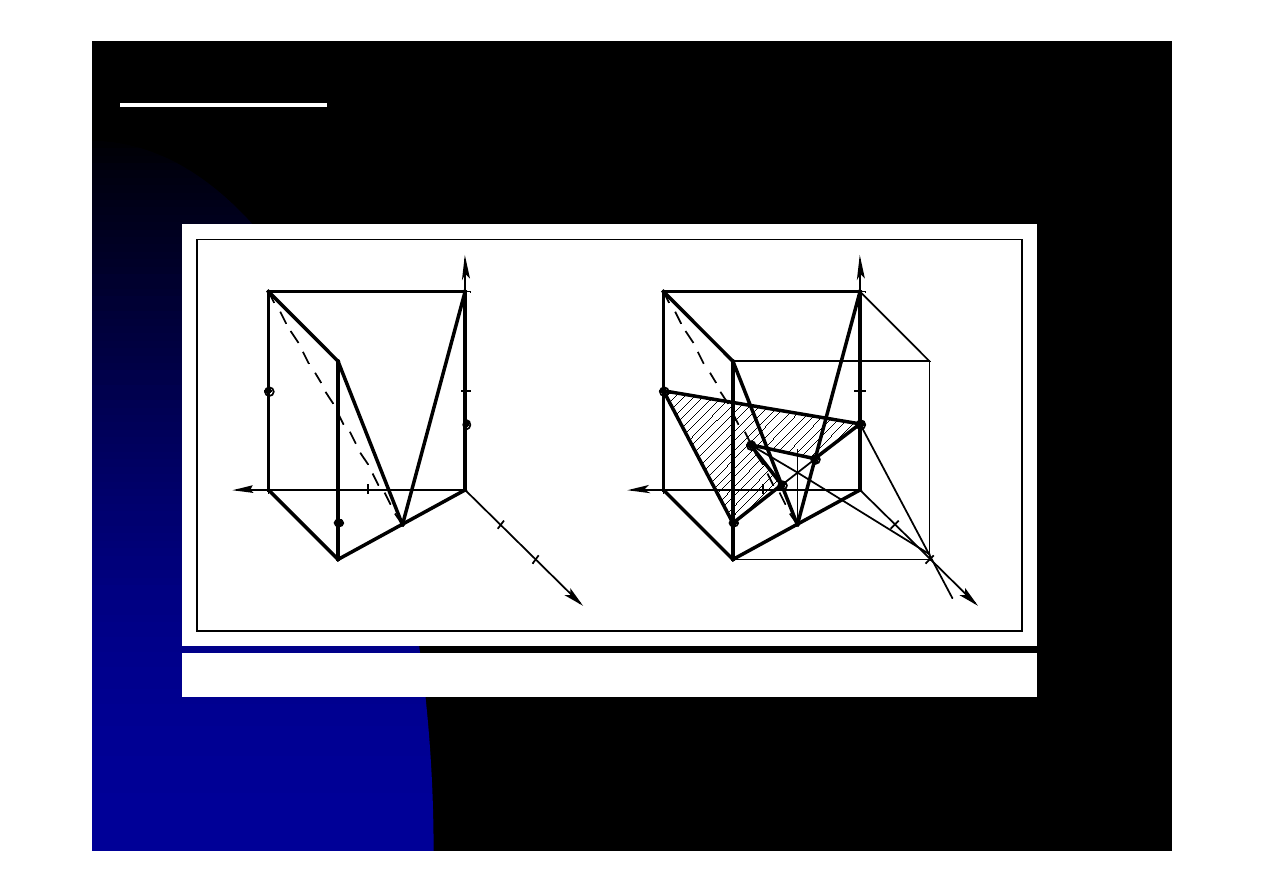
Zadanie 10.4. Wykreślić aksonometrię przekroju bryły płaszczyzną
określoną trzema punktami leżącymi na jej krawędziach 

α

(1,2,3).

Bryła powstała przez wycięcia z sześcianu.

2

3

1

A

u

z

1

2

3

u

y

0

u

y

u

x

0

u

x

u

z

W zadaniu 10.4 problemem jest wyznaczenie punktu na krawędzi narysowanej
linią kreskową (krawędź niewidoczna).

Rys. 10.4. Przekrój bryły płaszczyzną określoną przez trzy punkty 

α

(1, 2 ,3)

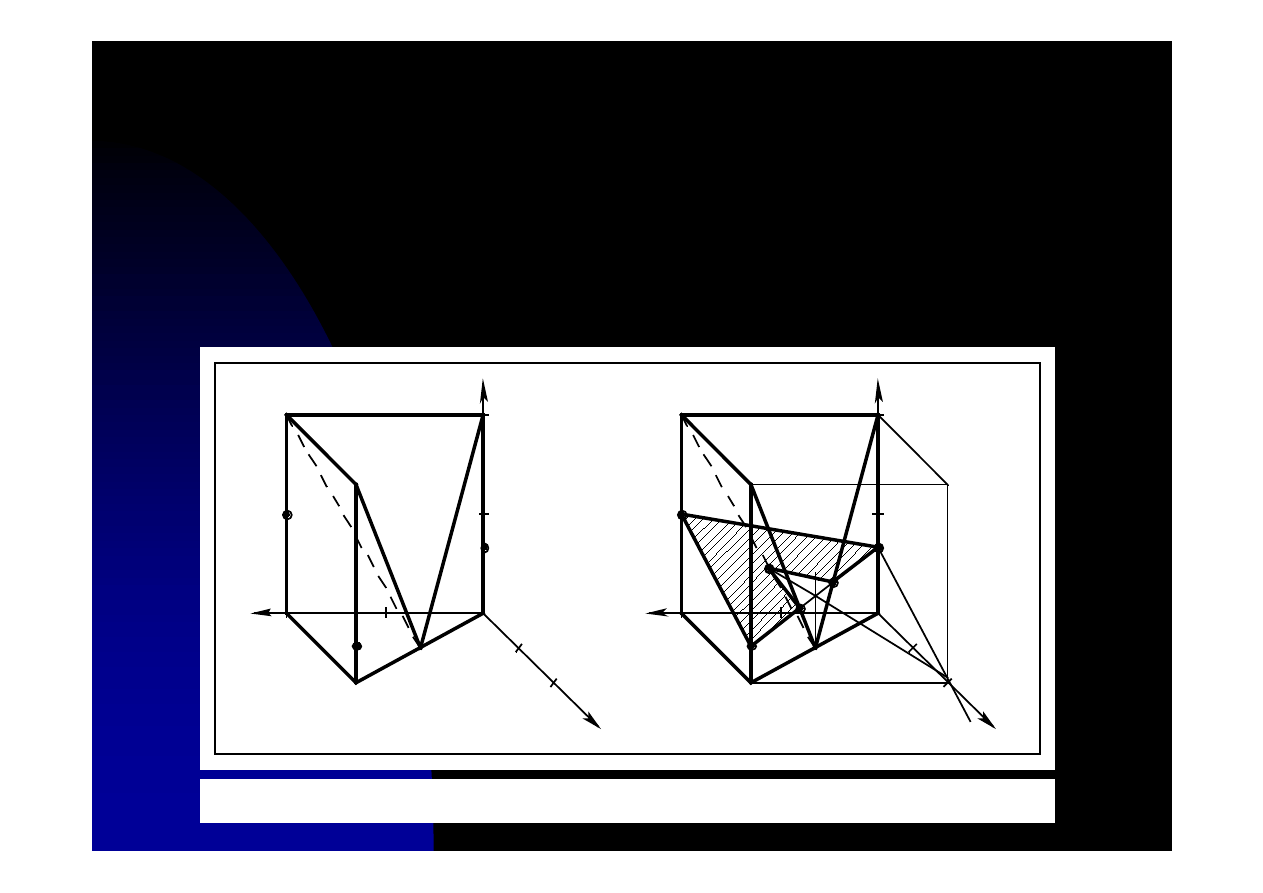
Rys. 10.4. Powtórzenie

Wiedząc, że bryła powstała przez wycięcia z sześcianu możemy naszkicować
krawędzie tego sześcianu. Punkt A wyznaczamy przez poprowadzenie prostej z
punktu 3 równoległej do krawędzi 1-2 aż do przecięcia z krawędzią (nieistniejącą)
sześcianu. Drugi punkt wynikający z przecięcia prostej prostopadłej do podstawy i
krawędzi 2-3 pozwala na poprowadzenie prostej przecinającej się z krawędzią
narysowaną linią kreskową w poszukiwanym punkcie. Prosta ta leży na hipotetycznej
płaszczyźnie prostopadłej do podstawy i przechodzącej przez przekątną podstawy.

2

3

1

A

u

z

1

2

3

u

y

0

u

y

u

x

0

u

x

u

z

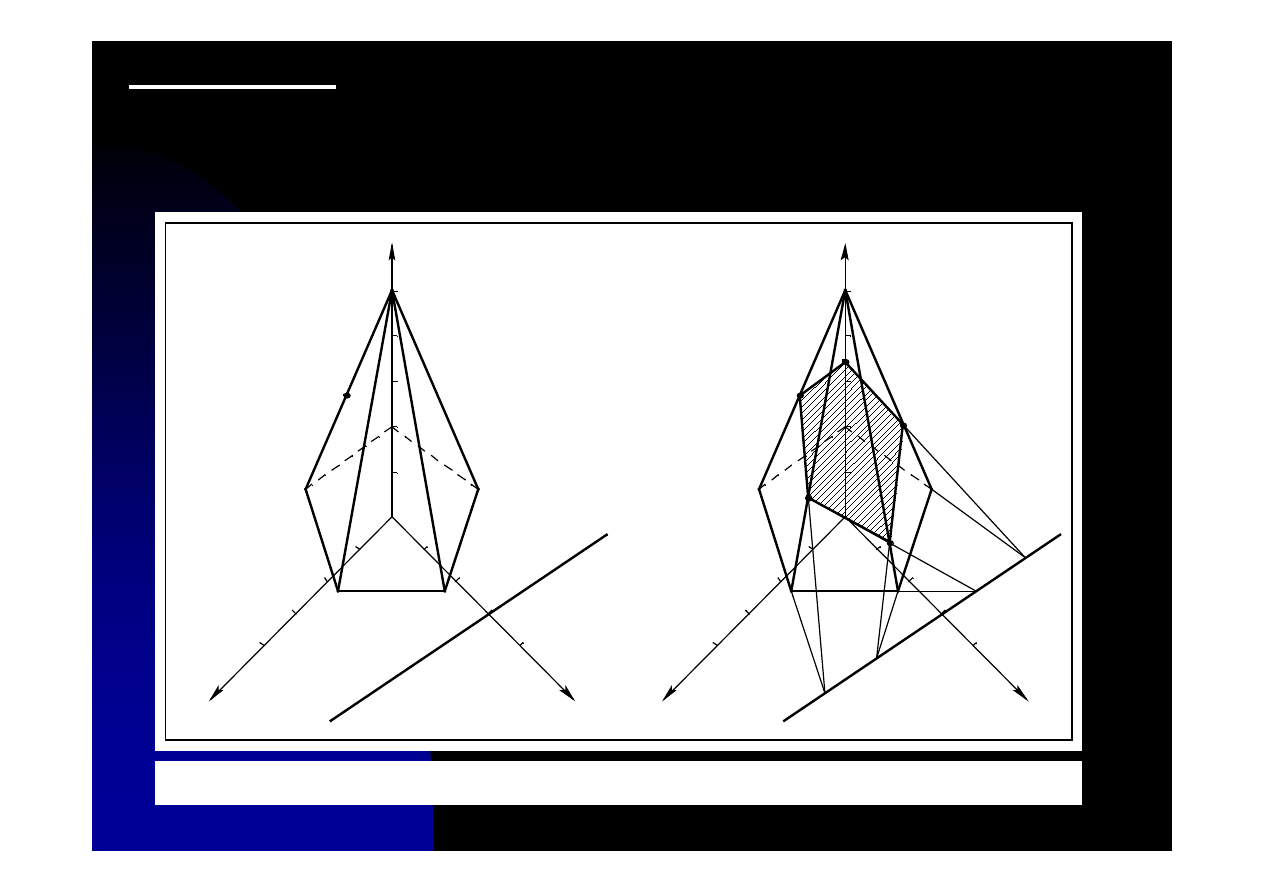
Zadanie 10.5. Wykreślić aksonometrię przekroju ostrosłupa
płaszczyzną określoną przez prostą leżącą w płaszczyźnie jego
podstawy i punkt leżący na jego krawędzi (rys. 10.5a).

z

a)

1

z

b)

5

1

D

3

k

2

C

A

y

x

k

y

x

B

4

Rys. 10.5. Sposób przecięcia ostrosłupa płaszczyzną określoną przez punkt i prostą

   Przy wyznaczaniu przekroju wykorzystujemy
fakt, że krawędzie trzech przecinających się
płaszczyzn zbiegają się w jednym punkcie (tak
jak płaszczyzny wyznaczone przez osie układu
prostokątnego mają jeden wspólny punkt w
ś

rodku układu współrzędnych). Punkty A, B, C i

D są punktami jednocześnie należącymi do
płaszczyzny tnącej (leżą na prostej k), do
płaszczyzny ‘xy’ oraz do płaszczyzny określanej
przez kolejne ściany ostrosłupa.
   I tak, ponieważ punkt 1 i punkt A należą do
płaszczyzny tnącej i do płaszczyzny wyznaczonej
przez ścianę ostrosłupa, to krawędź przecięcia
tych płaszczyzn musi przechodzić przez prostą
łączącą te punkty – w ten sposób wyznaczamy
punkt 2.
   W podobny sposób wyznaczamy następne
punkty należące do przekroju. Dla lepszego
uwidocznienia powierzchnię przecięcia
zakreskowano.

z

b)

5

1

D

3

k

2

C

A

y

x

B

4

Rys. 10.5b. Powtórzenie

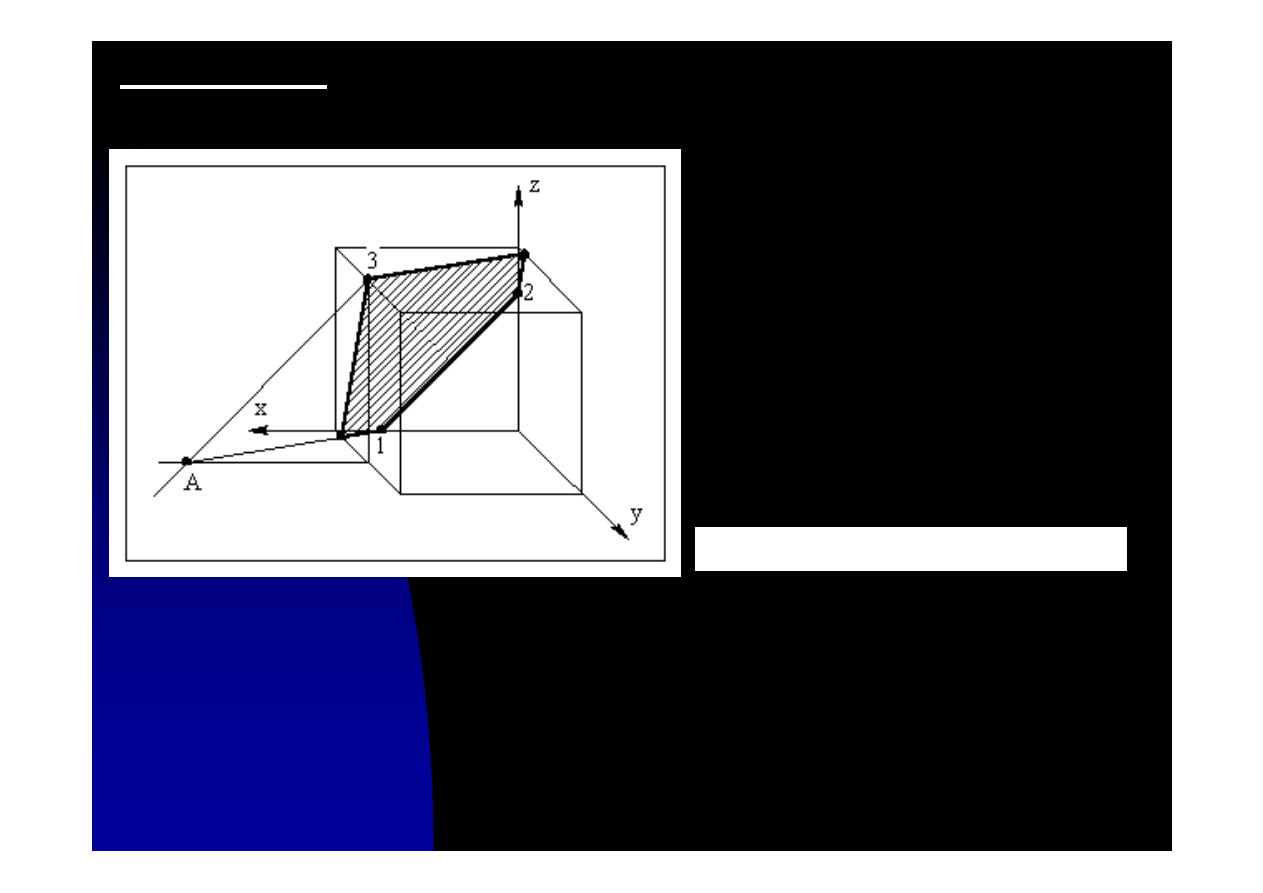
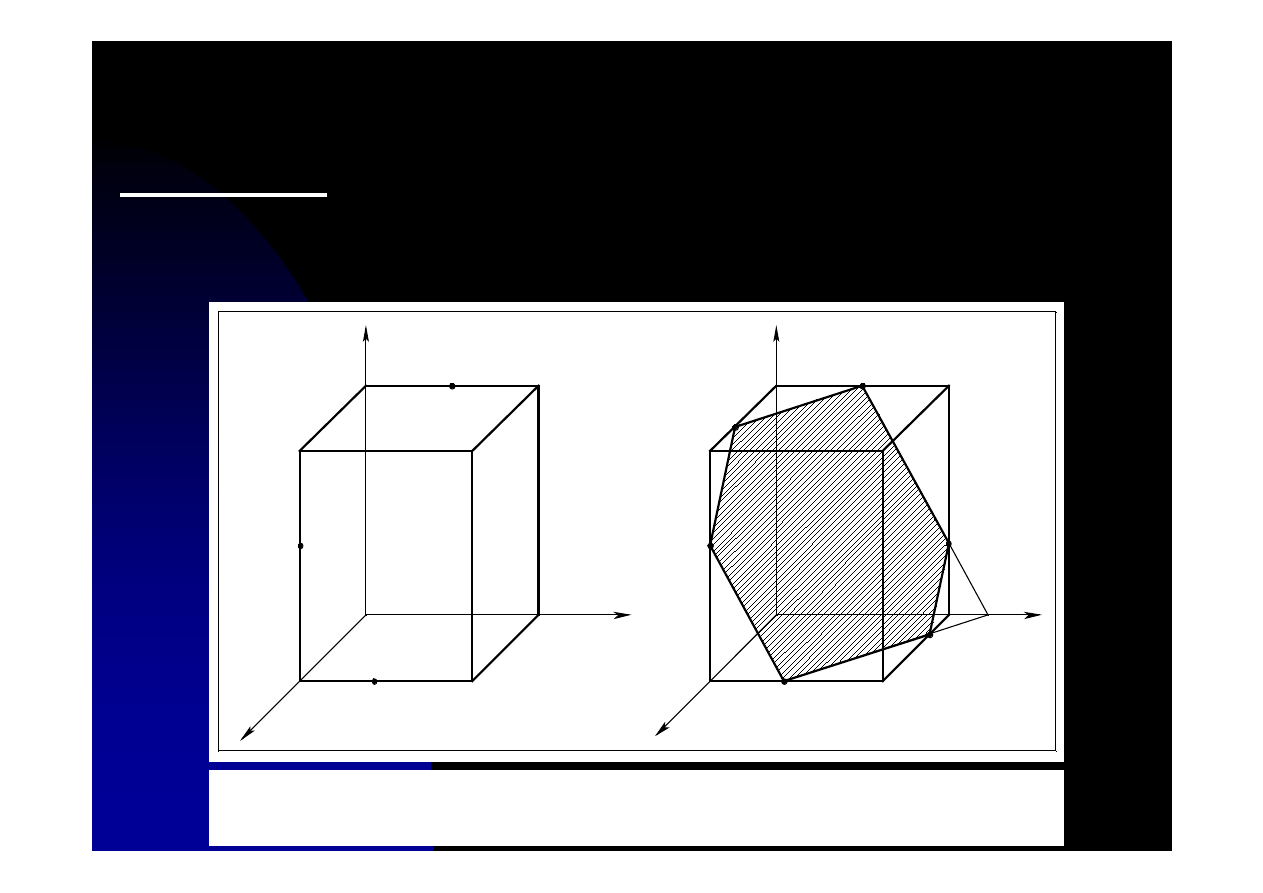
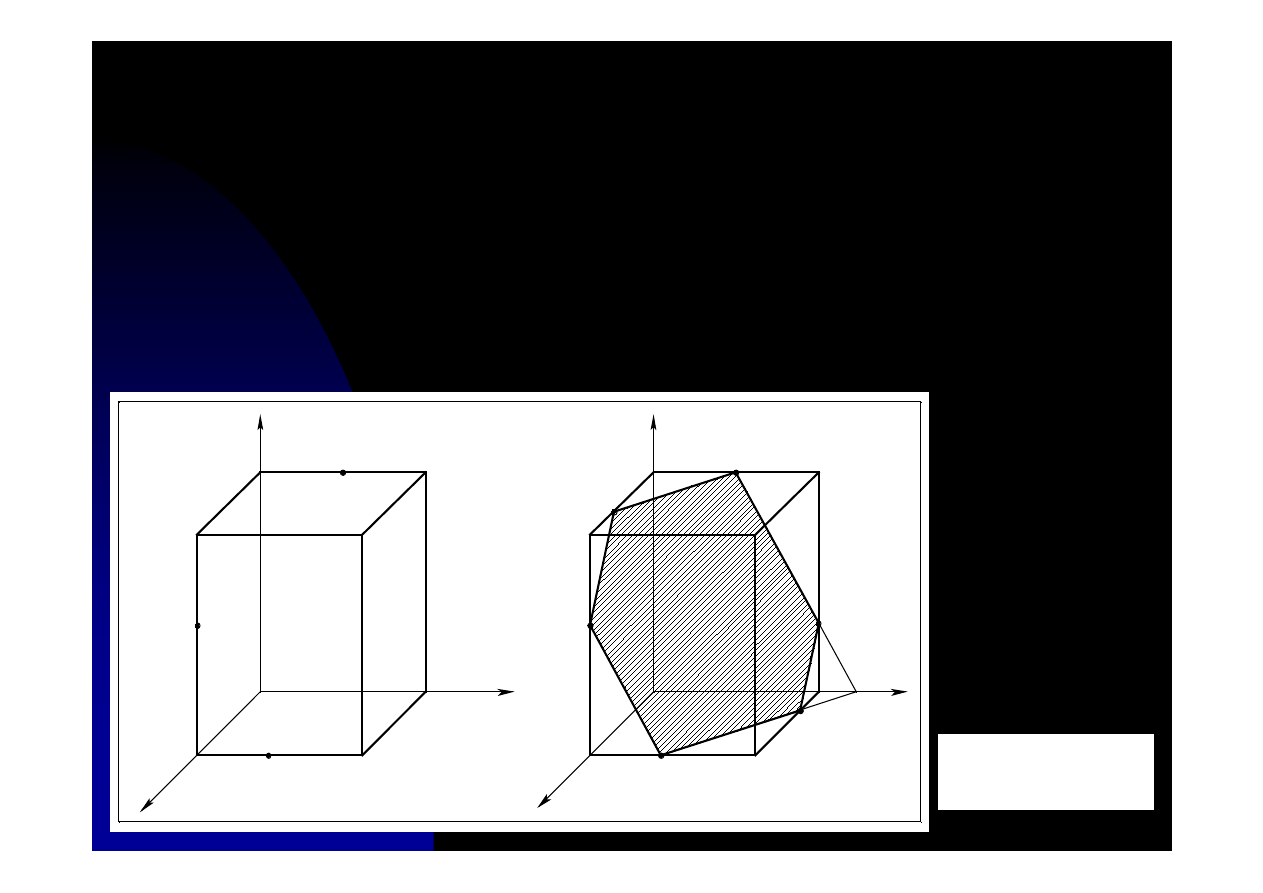
Zadanie 10.6. Przeciąć sześcian płaszczyzną określoną trzema
punktami leżącymi na jego krawędziach 

α

(1,2,3).

Po wyznaczeniu krawędzi 1-2
stajemy przed problemem
wyznaczenia kolejnej krawędzi.
Zadanie jest przykładem
zastosowania pomocniczej
płaszczyzny – w tym przypadku
przechodzącej przez punkt 3 i
prostopadłej do podstawy.
Płaszczyzna ta przecina płaszczyznę
xy w prostej równoległej do osi x.

Ponieważ płaszczyzna ta jest równoległa do płaszczyzny xz (tylnej ściany sześcianu) to
krawędź przecięcia jej przez płaszczyznę tnącą (3-A) musi być równoległa do krawędzi
1-2. Otrzymujemy punkt A leżący na płaszczyźnie xy i należący do płaszczyzny tnącej.
Drugim punktem mającym takie cechy jest punkt 1. Prosta przechodząca przez te dwa
punkty wyznaczy nam krawędź przecięcia podstawy sześcianu. Pozostałe krawędzie
jest już łatwo wyznaczyć korzystając z równoległości krawędzi przecięć na
płaszczyznach równoległych.

Rys. 10.6. Ilustracja do zadania 10.6

11. PRZENIKANIE OBIEKTÓW GEOMETRYCZNYCH

Wykonując przekroje brył płaszczyznami mieliśmy do czynienia z przenikaniem się
dwóch  obiektów  geometrycznych  -  bryły  i  płaszczyzny.  Wyznaczanie  przekroju
polegało na znalezieniu elementów wspólnych dwóch obiektów.

Zbiór  punktów  wspólnych  dla  dwóch  wielościanów  nazywamy 

linią  przenikania

tych wielościanów

.

Wykonując przekroje brył płaszczyznami ( w poprzednim rozdziale) wyznaczaliśmy
właśnie linię przenikania płaszczyzny z bryłą. Jeżeli bryła ta była wielościanem, to
linią przenikania był wielokąt przestrzenny lub, czasami, dwa lub więcej wielokątów
na które linia przenikania się rozpada.

11.1. Przenikanie się wielokątów

Dla ułatwienia będziemy wyznaczać linie przenikania figur płaskich których boki są
odcinkami prostych czyli wielokątów.  Przenikanie np. kół wykonuje się wprowa-
dzając siatkę prostokątną lub kwadratową, czyli też sprowadzając zagadnienie do
przenikania wielokątów.
W przypadku przecinania wielokąta płaszczyzną, linią przenikania jest część krawę-
dzi przecięcia  się dwóch płaszczyzn  –  płaszczyzny  tnącej  i  płaszczyzny  wyznaczo-
nej przez wielokąt. Odcinek ten jest wspólny dla tych dwóch obiektów geometrycz-
nych.

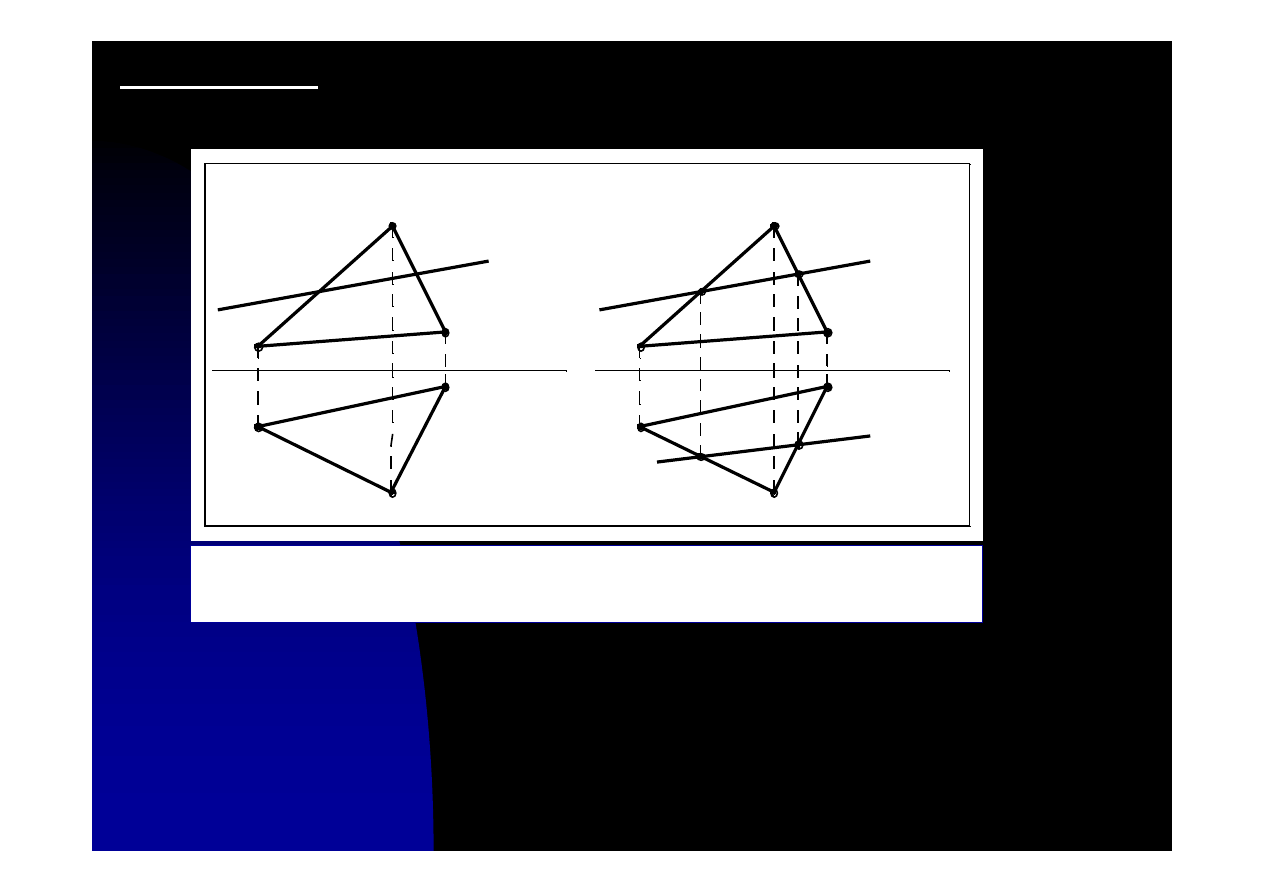
Zadanie 11.1. Przeciąć trójkąt, dany dwoma rzutami, płaszczyzną 

α

prostopadłą do rzutni pionowej.

A"

C"

α

''

B"

a)

A'

C'

x

A"

A'

b)

C'

2'

1"

2"

B"

x

1'

B'

B'

α

''=p''

p'

C"

Płaszczyzna 

α

 przecina boki trójkąta AB i BC w punktach 1 i 2. Rzuty pionowe tych

punktów, 1” i 2”, leżą na rzutach pionowych tych boków trójkąta. Rzuty poziome tych
punktów muszą leżeć na rzutach pionowych tych boków.
Prosta p (o rzutach p’ i p”) jest krawędzią przecięcia płaszczyzny 

α

 i płaszczyzny

trójkąta ABC. Odcinek 1-2 jest linią przenikania.

Rys. 11.1. Rysunek do zadania 11.1. a) dane dwa rzuty trójkąta i płasz-
czyzny 

α

, b) sposób rozwiązania zadania

Powyższy przykład ilustruje sposób wyznaczania linii przenikania figur płaskich w przypadku
gdy jedna z nich zajmuje szczególne położenie względem rzutni (prostopadłość). Rzut krawędzi
przecięcia płaszczyzn wyznaczonych przez figury może być bezpośrednio odczytany z rzutu w
którym rzut płaszczyzny jest prostą.

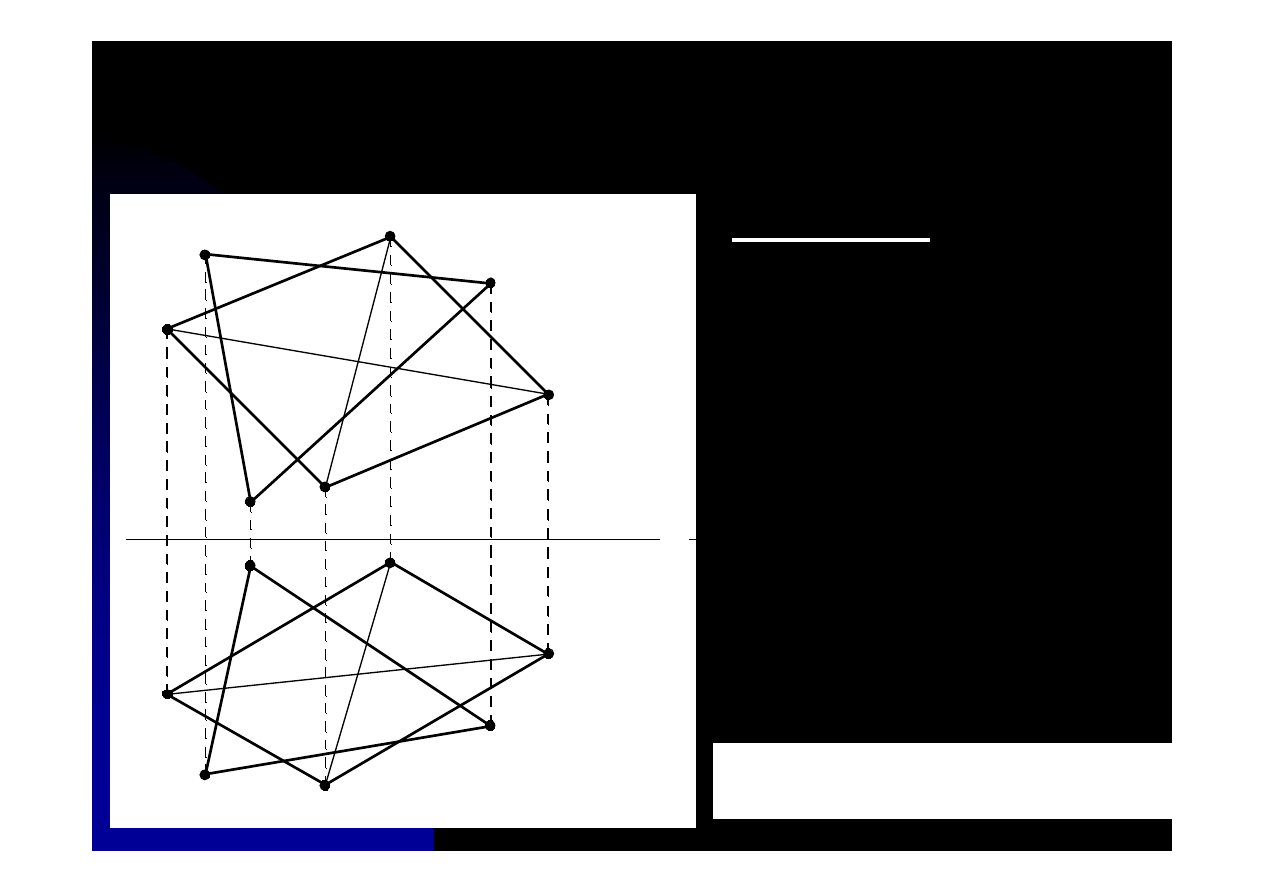
Zadanie 11.2. Wyznaczyć
rzuty linii przenikania dwóch
wielokątów znajdujących się
w położeniu ogólnym
względem rzutni.

Q"

P"

S"

A"

R"

x

C"

B"

Q'

A'

S'

R'

P'

B'

C'

Rys. 11.2. Rzuty pionowy i poziomy
trójkąta i czworokąta płaskiego

Należy wyznaczyć punkty
przebicia czworokąta PQRS przez
boki AC i AB trójkąta ABC:

1"

B"

R"

S"

x

A"

N"

4"

2"

M"

n''

Q"

P"

C"

B'

β

'=n'

R'

A'

3"

m''

2'

N'

4'

M'

1'

P'

S'

α

'=m'

C'

Q'

3'

-  przez  boki  AC  i  AB  trójkąta  prowa-
dzimy  płaszczyzny  poziomo  rzutujące 

α

i 

β

, przecinają one boki PS i PQ oraz PQ i

RS  czworokąta  w  punktach  1,  2  i 3,  4.
Rzuty  tych  punktów  leżą  na  odpowied-
nich rzutach boków czworokąta,
-  krawędzie  przecięć  czworokąta  i  płasz-
czyzn 

α

 i 

β

 to proste m i n. Rzuty piono-

we tych prostych pozwalają na wyznacze-
nie rzutów pionowych punktów przebicia
czworokąta  przez  boki  trójkąta.  Są  to
punkty M” i N” leżące na rzutach boków
trójkąta.  Znajdujemy  rzuty  poziome  tych
punktów  prowadząc  proste  rzutujące  do
rzutów  poziomych  boków  AC  i  AB
trójkąta,
- odcinek MN jest linią przenikania.

Widoczność  krawędzi  można  ustalić  porównując  np.  wysokości  punktów  A,  P  i Q.  Bok  PQ
znajduje się powyżej boków AB i AC trójkąta.
Przedstawiony sposób wyznaczania linii przenikania polega na wyznaczeniu punktów przebicia
jednego wielokąta przez boki drugiego.

Rys. 11.2b. Sposób wyznaczania linii
przenikania wielokątów

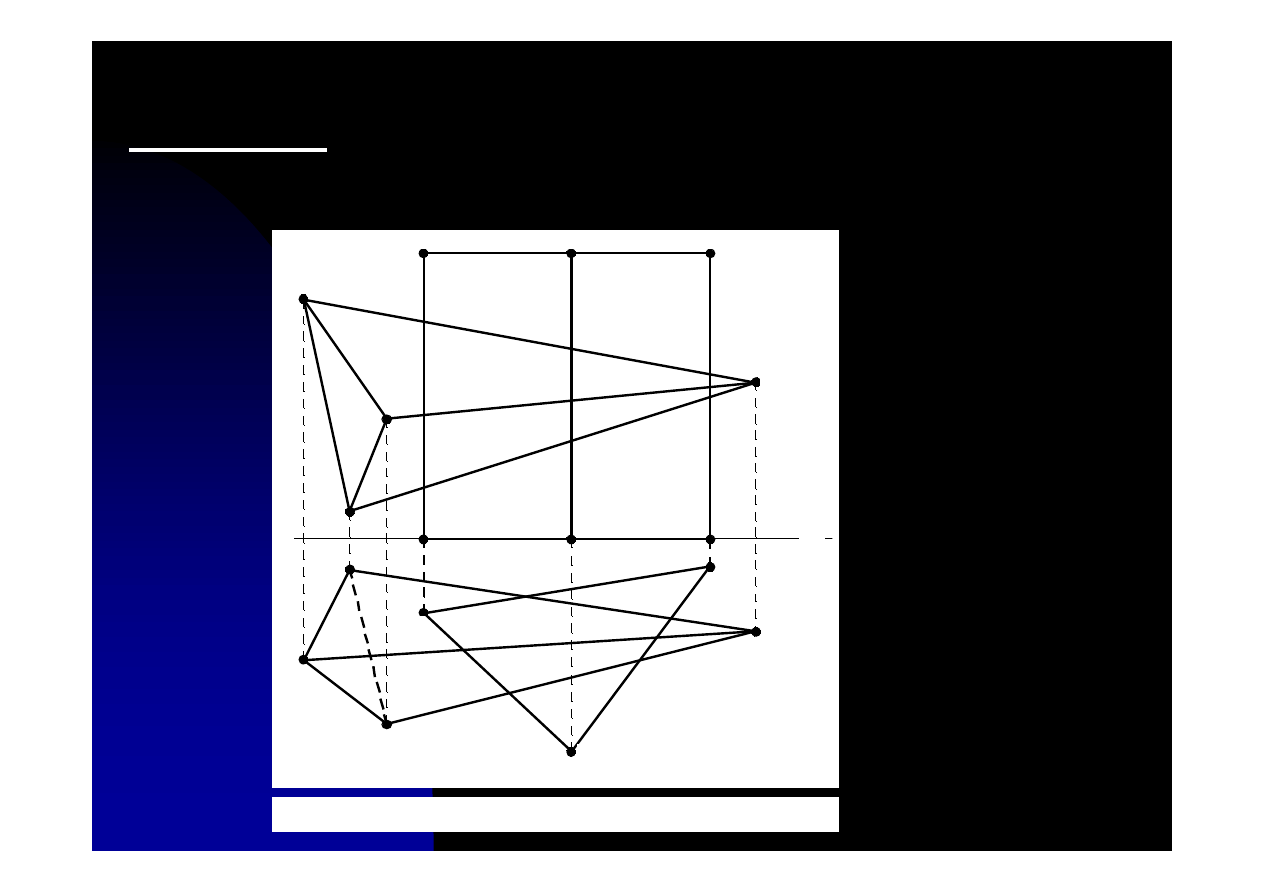
11.2. Przenikanie wielościanów

Zadanie 11.3. Wyznaczyć przenikanie graniastosłupa z ostrosłupem
przy danych dwóch rzutach tych obiektów.

Q"

P"

A"

C"

B"

a"

c"

b"

W"

a'

P'

A'

C'

W'

R"

x

Q'

c'

b' B'

R'

Rys. 11.3. Rzuty pionowy i poziomy dwóch brył

L"

P"

1"

b"

a"

R"

8"

5"

3"

Q"

C"

2"

B"

A"

7"

6"

W"

c"

4"

5'

1'

C'

P'

x

R'

b'

7'

2'

4'

3'

W'

6'

c'

L'

Q'

A'

a'

8'

B'

α

'

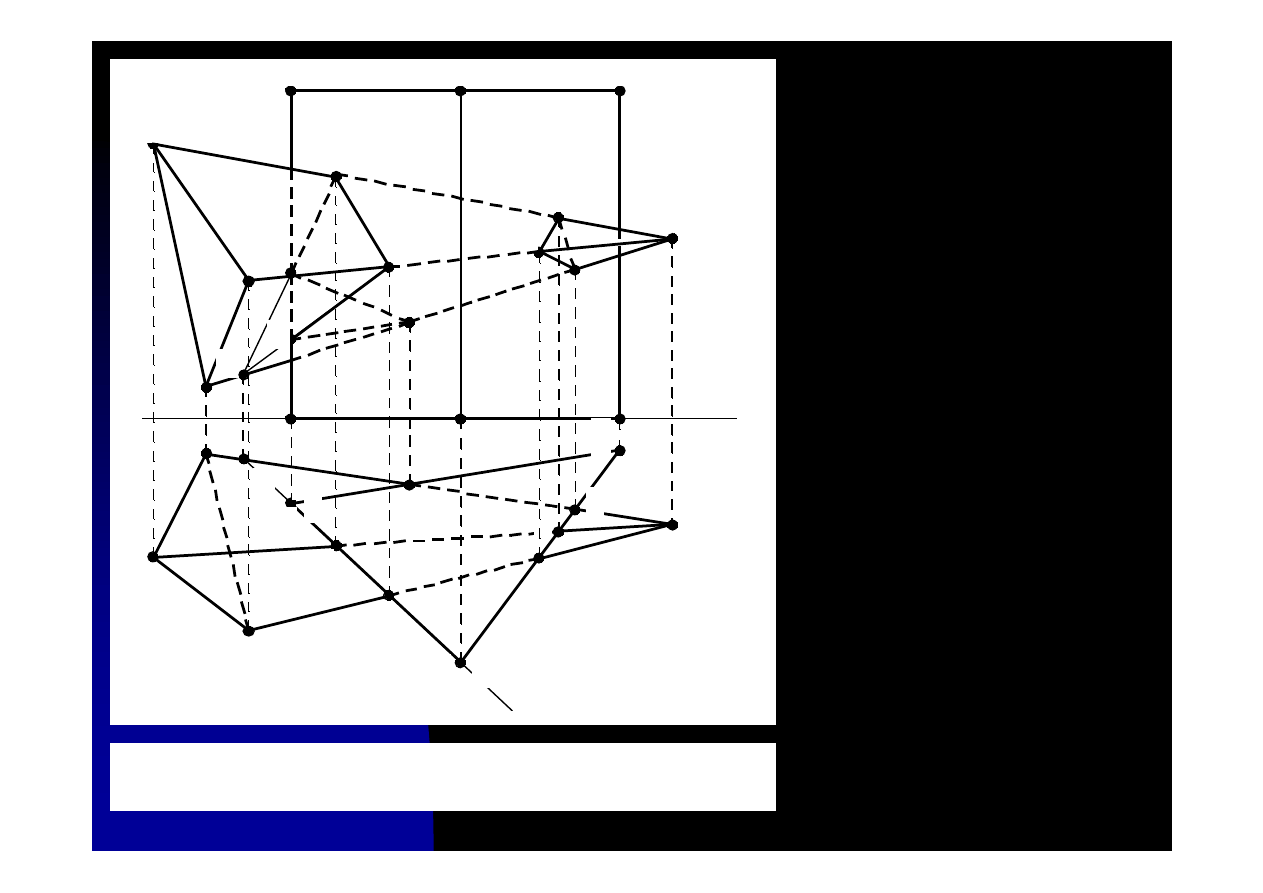
-  krawędziami  bocznymi  ostro-
słupa PW, QW i RW przebijamy
poziomo  rzutujące  ściany  bocz-
ne  graniastosłupa.  otrzymujemy
punkty:

1=PW

∩

ab

  (

ab

  -  płaszczyzna

wyznaczona przez proste a i b)

2=PW

∩

bc,    3=QW

∩

ac,

4=QW

∩

bc,    5=RW

∩

ab,

6= RW

∩

bc.

Rzuty pionowe i poziome punk-
tów pokazuje rysunek 11.3b.
- poziomo-rzutująca płaszczyzna

α

,  wyznaczona  przez  proste  ab,

przecina  krawędź  QW  ostrosłu-
pa  w  punkcie  L.  Punkty  1  i  L
oraz  5  i  L  leżą  na  tej  samej
płaszczyźnie 

α, 

zatem punkty te

będą wyznaczać krawędzie prze-
cięcia  ścian  ostrosłupa  i  grania-
stosłupa.  Punkty  7  i  8  leżące  na
krawędzi a pozwalają na wykre-
ś

lenie brakujących krawędzi 3-8

i 3-7.

Rys. 11.3b. Wyznaczanie linii przenikania ostrosłupa
i graniastosłupa

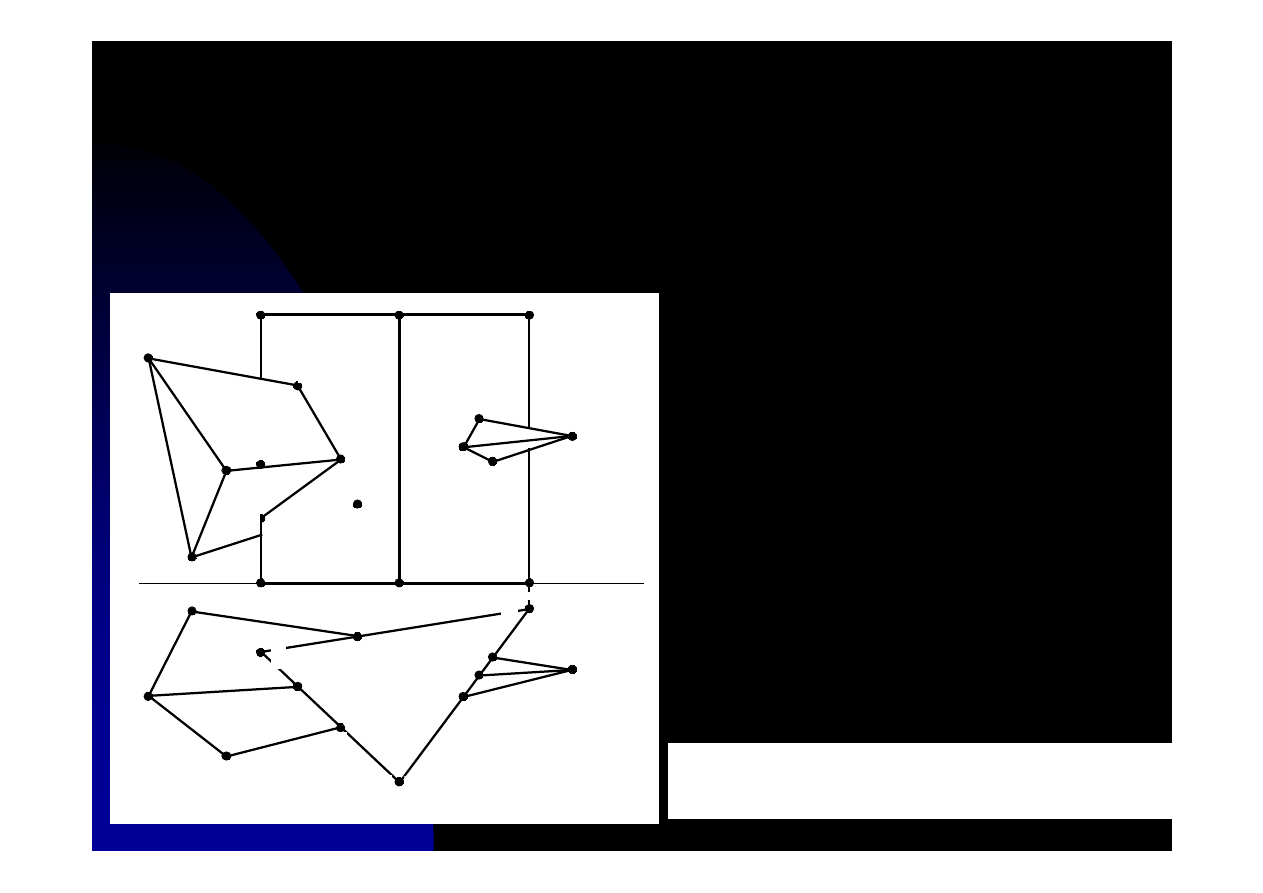
Wyznaczanie linii przenikania jest trudniejsze niż wyznaczanie przekrojów brył. Przy
przekrojach brył płaszczyzną szukane punkty należące do przekroju leżą na krawę-
dziach bryły (w przypadku wielościanów), punkty łamanej przenikania leżą również na
ś

cianach brył. Należy zatem łączyć sposoby wykonywania przekrojów ze sposobami

wyznaczania punktów przebicia płaszczyzny i prostej.

W'

A'

3'

4'

2'

7'

C'

1'

C"

B"

6'

x

A"

R"

5"

c'

8'

B'

b'

R'

a'

5'

W"

6"

2"

3"

8"

1"

4"

P"

Q'

P'

Q"

7"

a"

b"

c"

Rys. 11.3c. Widok przenikania brył po usu-
nięciu linii niewidocznych i pomocniczych

Dziękuję za uwagę