1

Teoria zbiorów.

Zadanie 1. Które z następujących zbiorów są sobie równe?

A = {x, y, z}, B = {z, y, z, x}, C = {y, x, y, z}, D = {y, z, x, y}.

Zadanie 2. Udowodnić, że B\A = B ∩ A

C

.

Zadanie 3. Udowodnić, że następujące trzy stwierdzenia są równoważne:

A ⊆ B, A ∩ B = A, A ∪ B = B.

Zadanie 4. Zilustrować prawa DeMorgana na diagramach Venna.

Zadanie 5. Udowodnić, że (A ∪ B)\(A ∩ B) = (A\B) ∪ (B\A).

Zadanie 6. Po przeprowadzeniu ankiety wśród 120 studentów otrzymano nastę-

pujące wyniki:

65 studentów przegląda codziennie portal A,

20 przegląda codziennie A i B

45 studentów przegląda codziennie portal B,

25 przegląda codziennie A i C

42 studentów przegląda codziennie portal C,

15 przegląda codziennie B i C

• Znaleźć liczbę studentów, którzy przeglądają przynajmniej jeden por-

tal dziennie.

• Wypełnić odpowiedni diagram Venna (wpisać odpowiednią liczbę

w jeden z 8 obszarów dla przecięcia trzech zbiorów).

• Znaleźć liczbę studentów, którzy przeglądają dokładnie jeden portal

dziennie.

Zadanie 7. Przedstawić na diagramie Venna następujące stwierdzenia:

• S

1

: wszyscy moi przyjaciele są muzykami

• S

2

: Adam jest moim przyjacielem

• S

3

: żaden z moich sąsiadów nie jest muzykiem

Odpowiedzieć na pytanie: czy Adam jest moim sąsiadem?

Zadanie 8. Korzystając z praw algebry zbiorów udowodnić:

• (A ∩ B) ∪ (A ∩ B

C

) = A

• A ∪ B = (A ∩ B

C

) ∪ (A

C

∩ B) ∪ (A ∩ B)

• A\(A\B) = A ∩ B

• A\(B ∩ C) = (A\B) ∪ (A\C)

• A\(B\(C\D)) = (A\B) ∪ ((A ∩ C)\D)

Zadanie 9. Znaleźć wszystkie podziały zbioru S = {a, b, c, d}.

1

2

Zasada indukcji matematycznej.

Zadanie 1. Udowodnić, że suma pierwszych n dodatnich liczb jest równa

1
2

n(n + 1).

Zadanie 2. Udowodnić, że suma pierwszych n dodatnich liczb nieparzystych jest

równa n

2

.

Zadanie 3. Udowodnić poniższe stwierdzenia:

• 1 + 2 + 2

2

+ . . . + 2

n

= 2

n+1

− 1

• 2 + 4 + 6 + . . . + 2n = n(n + 1)

• 1 + 4 + 7 + . . . + 3n − 2 =

n(3n−1)

2

• 1

2

+ 2

2

+ 3

2

+ . . . n

2

=

n(n+1)(2n+1)

6

•

1

1·3

+

1

3·5

+

1

5·7

+ . . . +

1

(2n−1)(2n+1)

=

n

2n+1

•

1

1·5

+

1

5·9

+

1

9·13

+ . . . +

1

(4n−3)(4n+1)

=

n

4n+1

• 1 · 1 + 2 · 3 + 3 · 7 + . . . + n(2

n

− 1) = (n − 1)2

n+1

+ 2 −

n(n+1)

2

Zadanie 4. Udowodnić następujące podzielności:

• 5|7

n

− 2

n

• 3|n

3

− 4n + 6

• 6|n(n + 1)(2n + 1)

• 6|10

n

+ 4

n

− 2

• 15|3m

5

+ 5m

3

+ 7m

• 133|11

n+1

+ 12

2n−1

• 4|3

n

+ 1, dla n = 123456789

• 5|2

n

+ 3

n

, dla n = 2

12345

− 1

Zadanie 5. Skorzystać z tego, że 1 + 2 + 3 + . . . + n =

1
2

n(n + 1) aby udowodnić,

że 1

3

+ 2

3

+ 3

3

+ . . . n

3

= (1 + 2 + 3 + . . . + n)

2

.

2

3

Podstawy logiki - rachunek zdań.

Zadanie 1. Wyznaczyć tabele prawdy dla następujących funkcji:

• p ∨ (q → (p ∧ ¬q)

• ¬p → (¬q ∧ (p ↔ q))

• ¬(r → q) ↔ (¬q ∨ (p ∧ ¬q)

Zadanie 2. Korzystając z praw algebry zdań, pokazać, że:

• ¬(p ∨ q) ∨ (¬p ∧ q) = ¬p

Zadanie 3. Sprawdzić, czy podane zdanie logiczne jest sprzecznością:

• (p ∧ q) ∧ ¬(p ∨ q)

Zadanie 4. Sprawdzić, czy podane zdanie logiczne jest tautologią:

• (p → q) ∨ (r ↔ (¬q → r))

Zadanie 5. Czy zdanie logiczne z zad. 4 jest równoważne ze zdaniem:

• ((r ∨ q) ⊕ r) ∧ (¬q ∧ p)

Zadanie 6. Zapisać poniższe zdania bez użycia stwierdzenie warunkowego:

• ”Jeżeli przeczytasz tą książkę to będziesz więcej wiedział”

• ”Jeżeli podniosą wam zarobki i złotówka się umocni to jeżeli będziesz

miał ochotę to pojedziesz na wakacje za granicę”

Zadanie 7. Które z podanych zdań są sobie równoważne?

• p → q

• q → p

• ¬p → ¬q

• ¬q → ¬p

Zadanie 8. Wiadomo, że zdania p → q, ¬p → r oraz r → (p ∨ q) są prawdziwe.

Co można powiedzieć o zdaniach p, q, r?

Zadanie 9. Wiadomo, że zdanie ¬p ∧ q jest fałszywe. Co można powiedzieć o

zdaniu (p ∨ ¬q) ∧ (q → p) ∧ (q → (¬p → p))?

Zadanie 10. Wiadomo, że zdanie (p

1

→ (p

2

→ (p

3

→ . . . (p

n

→ q) . . .))) jest

fałszywe. Co można powiedzieć o zdaniach p

1

, p

2

, . . . , p

2

, q?

Zadanie 11. Niech A = {1, 2, 3, 4, 5}. Które z podanych zdań są prawdziwe a

które fałszywe?

• (∃x ∈ A)(x + 3 = 10)

3

• (∀x ∈ A)(x + 3 < 10)

• (∃x ∈ A)(x + 3 < 5)

• (∀x ∈ A)(x + 3 ≤ 7)

Zadanie 12. Niech U = {1, 2, 3} będzie zbiorem uniwersalnym. Które z poda-

nych zdań są prawdziwe a które fałszywe?

• ∃x∀y, x

2

< y + 1

• ∀x∃y, x

2

+ y

2

< 12

• ∀x∀y, x

2

+ y

2

< 12

Zadanie 13. Zanegować poniższe zdania logiczne:

• ∃x∀y, p(x, y)

• ∀x∀y, p(x, y)

• ∃y∃x∀x, p(x, y, z)

Zadanie 14. Czy stwierdzenie p(x): ”x > 7” jest predykatem dla następujących

zbiorów

• N
• Z

−

• C
• R

2

= R × R

Zadanie 15. Jako uniwersum przyjmijmy zbiór N. Czy podane stwierdzenie jest

zdaniem logicznym czy predykatem?

• ∀x∃z, x + y < x + z

• ∀x∃z, x + y < y + z

Zadanie 16. Zapisać podane zdanie w postaci symbolicznej.

• ”Nie istnieje największa liczba pierwsza”. Przyjąć, że Q(x, y) oznacza

”x > y” oraz P (x) oznacza ”x jest liczbą pierwszą”. Nie definiować
innych predykatów.

4

4

Relacje.

Zadanie 1. Ile jest różnych relacji ze zbioru A = {a, b, c} do B = {1, 2}?

Zadanie 2. Dla zbiorów A = {1, 2, 3, 4} i B = {x, y, z} oraz relacji

R = {(1, y), (1, z), (3, y), (4, x), (4, z)}

wyznaczyć:

• macierz relacji

• diagram strzałkowy relacji

• relację odwrotną R

−1

• dziedzinę i zakres relacji

Zadanie 3. Niech A = {1, 2, 3}, B = {a, b, c} i C = {x, y, z} oraz relacje

R = {(1, b), (2, a), (2, c)} , S = {(a, y), (b, x), (c, y), (c, z)}

• wyznaczyć złożenie relacji R ◦ S za pomocą diagramów strzałkowych

• wyznaczyć macierze M

R

, M

S

, M

R

M

S

(porównać z macierzą M

R◦S

)

Zadanie 4. Dana jest relacja na zbiorze A = {1, 2, 3, 4}:

R = {(1, 1), (2, 2), (2, 3), (3, 2), (4, 2), (4, 4)}

• narysować diagram relacji

• znaleźć relacje R

2

Zadanie 5. Dane są następujące relacje na zbiorze A = {1, 2, 3}:

R = {(1, 1), (1, 2), (2, 3), (3, 1), (3, 3)} , S = {(1, 2), (1, 3), (2, 1), (3, 3)}

• znaleźć R ∪ S, R ∩ S, R

C

• R ◦ S

• S

2

Zadanie 6. Niech R będzie relacją zdefiniowaną na zbiorze liczb naturalnych N

jako xRy wtedy i tylko wtedy, jeżeli x + 3y = 12

• wypisać relację R w postaci zbioru par uporządkowanych

• znaleźć dziedzinę i zakres relacji R

• znaleźć R

−1

• znaleźć złożenie relacji R ◦ R

5

Zadanie 7. Rozważmy następujące pięć relacji na zbiorze A = {1, 2, 3}:

R = {(1, 1), (1, 2), (1, 3), (3, 3)} ,

∅

S = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3)}

A × A

T = {(1, 1), (1, 2), (2, 2), (2, 3)}

Które z relacji są (a) zwrotne, (b) symetryczne, (c) antysymetryczne, (d)
przechodnie?

Zadanie 8. Dane są pewne relacje na zbiorze liczb naturalnych N :

(a) “x jest większe od y”

(c) x + y = 10

(b) “xy jest kwadratem pewnej liczby całkowitej”

(d) x + 4y = 10

Które z relacji są (a) zwrotne, (b) symetryczne, (c) antysymetryczne, (d)
przechodnie?

Zadanie 9. Podać przykład relacji R na zbiorze A = {1, 2, 3}, takiej, że

• R jest jednocześnie symetryczna i antysymetryczne

• R nie jest symetryczna i nie jest antysymetryczna

• R jest przechodnia ale R ∪ R

−1

nie jest przechodnia

Zadanie 10. Niech C będzie pewną kolekcją relacji S na zbiorze A oraz T będzie

przecięciem relacji S z C, tj. T =

T(S|S ∈ C)

• udowodnić, że jeżeli każda relacja S jest symetryczna, to T jest sy-

metryczna

• udowodnić, że jeżeli każda relacja S jest przechodnia, to T jest prze-

chodnia

Zadanie 11. Niech R i S będą pewnymi relacjami na zbiorze A. Zakładając,

że zbiór A ma przynajmniej trzy elementy, które z poniższych stwierdzeń
są prawdziwe a które fałszywe. Jeżeli stwierdzenie jest fałszywe to należy
podać kontrprzykład dla zbioru A = {1, 2, 3}.

• jeżeli R i S są symetryczne to R ∩ S jest symetryczna

• jeżeli R i S są symetryczne to R ∪ S jest symetryczna

• jeżeli R i S są zwrotne to R ∩ S jest zwrotna

• jeżeli R i S są zwrotne to R ∪ S jest zwrotna

• jeżeli R i S są przechodnie to R ∪ S jest przechodnia

• jeżeli R i S są antysymetryczne to R ∪ S jest antysymetryczna

• jeżeli R jest antysymetryczna to R

−1

jest antysymetryczna

• jeżeli R jest zwrotna to R ∩ R

−1

nie jest pusta

• jeżeli R jest symetryczna to R ∩ R

−1

nie jest pusta

6

5

Relacje równoważności, porządki, funkcje.

Zadanie 1. Udowodnić, że jeżeli R jest relacją równoważności na zbiorze A, to

R

−1

jest również relacją równoważności na zbiorze A.

Zadanie 2. Udowodnić, że kongruencja x ≡ y(mod m) jest relacją równoważno-

ści dla dowolnej ustalonej liczby całkowitej m > 1.

Zadanie 3. Niech A będzie zbiorem liczb całkowitych różnych od zera. Pokazać,

że relacja ≈ na zbiorze A × A, zdefiniowana jako

(a, b) ≈ (c, d) jeżeli ad = bc

jest relacją równoważności.

Zadanie 4. Niech R będzie następującą relacją równoważności na na zbiorze

A = {1, 2, 3, 4, 5, 6}:

R = {(1, 1) , (1, 5) , (2, 2) , (2, 3) , (2, 6) , (3, 2) , (3, 3) , (3, 6) , (4, 4) ,

(5, 1) , (5, 5) , (6, 2) , (6, 3) , (6, 6)}

Znaleźć podział A/R oraz klasy równoważności relacji R.

Zadanie 5. Niech S = {1, 2, 3, . . . , 18, 19} oraz R będzie relacją zdefiniowaną na

S jako “xy jest kwadratem pewnej liczby całkowitej”.

• Udowodnić, że R jest relacją równoważności.

• Podać kasę abstrakcji [1].

• Wypisać wszystkie klasy abstrakcji z więcej niż jednym elementem.

Zadanie 6. Niech S = {1, 2, 3, . . . , 9} oraz R będzie relacją zdefiniowaną na

A × A jako:

(a, b) R (c, d) jeżeli a + d = b + c

• Udowodnić, że R jest relacją równoważności.

• Podać kasę abstrakcji [(2, 5)].

Zadanie 7. Pokazać, że relacja

4 na liczbach zespolonych C, zdefiniowana jako

a + bi 4 c + di wtedy i tylko wtedy, gdy a ≤ c ∧ b ≤ d jest częściowym
porządkiem ale nie jest porządkiem liniowym.

Zadanie 8. Rozważmy zbiór liczb całkowitych Z. Zdefiniujmy relację aRb jeżeli

b = a

r

dla pewnej liczby całkowitej r > 0. Pokazać, że R jest częściowym

porządkiem na Z.

Zadanie 9. Niech X = {1, 2, 3, 4}. Która z poniższych relacji jest funkcją z X

do X.

• f = {(2, 3) , (1, 4) , (2, 1) , (3, 2) , (4, 4)}

• g = {(3, 1) , (4, 2) , (1, 1)}

• h = {(2, 1) , (3, 4) , (1, 4) , (2, 1) , (4, 4)}

7

Zadanie 10. Niech funkcje f , g i h ze zbioru V = {1, 2, 3, 4} będą zdefiniowane

następująco: f (n) = 5 − n, g(n) = 3, h = {(1, 2) , (2, 3) , (3, 4) , (4, 1)}.
Które z nich są iniekcją, surjekcją, bijekcją?

Zadanie 11. Niech funkcje f , g i h z N do N będą zdefiniowane następująco:

f (n) = n + 2, g(n) = 2

n

, h(n) = liczba dodatchich dzielników n. Które

z nich są iniekcją, surjekcją, bijekcją? Znaleźć zbiór {x|h(x) = 2}.

Zadanie 12. Które z poniższych funkcji są iniekcją, surjekcją, bijekcją?

• f : Z

2

→ Z, taka że f(n, m) = n − m

• g : Z

2

→ Z

2

, taka że g(n, m) = (n, m)

• h : Z × (Z\ {0}) → Q, taka że h(n, m) =

n

m

• k : Z → Z

2

, taka że k(n) = (n, n)

8

6

Teoria grafów.

Zadanie 1. Dla grafu przedstawionego na poniższym rysunku:

B

C

A

D

E

• Zapisać zbiory V i E z formalnej definicji grafu (G = (V, E)).

• Podać rząd każdego wierzchołka. Podać liczbę krawędzi.

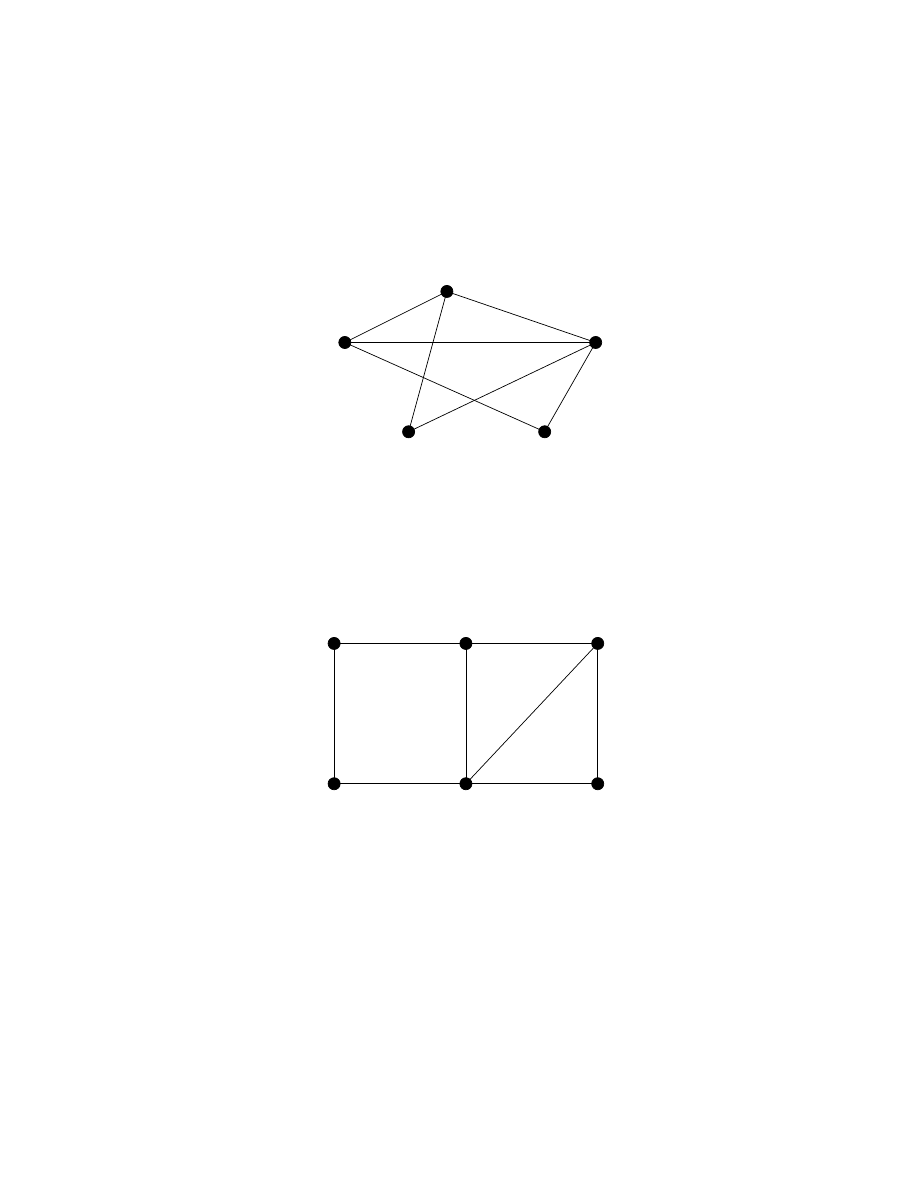
Zadanie 2. Dla grafu G przedstawionego na poniższym rysunku:

B

A

C

E

D

F

• Podać wszystkie ścieżki proste z A do F .

• Podać d(A, F ).

• Podać diam(G).

• Podać wszystkie cykle które zawierają wierzchołek A.

• Podać wszystkie cykle w grafie G.

9

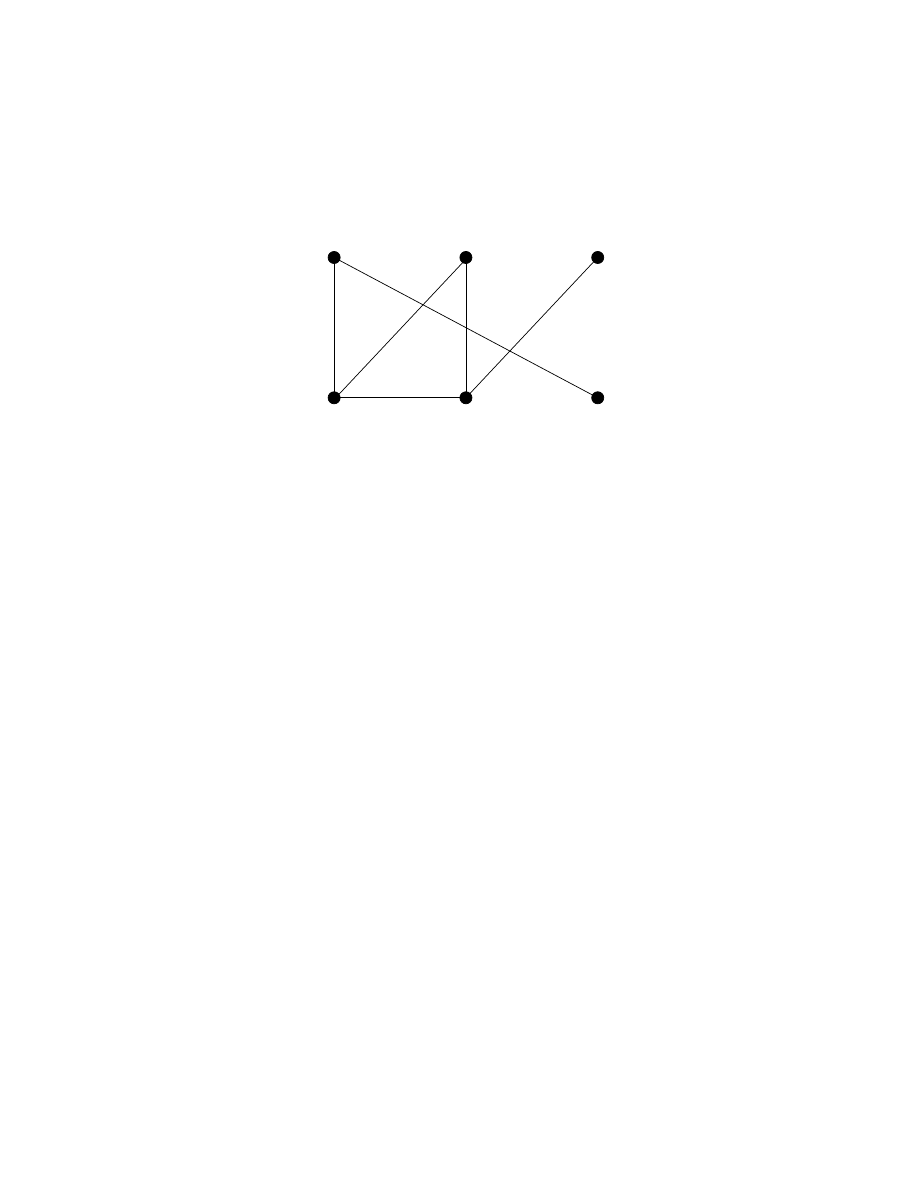
Zadanie 3. Dla grafu G przedstawionego na poniższym rysunku:

B

A

C

X

Y

Z

Znaleźć:

• Wszystkie ścieżki proste z A do C.

• Wszystkie cykle.

• Podgraf H generowany przez V

0

= {B, C, X, Y }

• G − Y

• Wszystkie punkty artykulacji.

• Wszystkie mosty.

Zadanie 4. Dla grafu z Zad. 2 znaleźć wszystkie podgrafy, które otrzymamy po

usunięciu każdego z wierzchołków. Czy graf ten ma jakieś punkty artyku-
lacji.

Zadanie 5. Narysować dwa różne (nie izomorficzne) grafy regularne stopnia 3:

(a) z ośmioma wierzchołkami

(b) z dziewięcioma wierzchołkami

Zadanie 6. Dla grafu pełnego K

n

(a) Znaleźć diam(G).

(b) Znaleźć liczbę krawędzi w grafie G.

(c) Znaleźć stopień każdego wierzchołka.

(d) Dla jakich wartości n graf K

n

jest grafem regularnym?

Zadanie 7. Dla grafu dwudzielnego pełnego K

m,n

(a) Znaleźć diam(G).

(b) Znaleźć liczbę krawędzi w grafie G.

(c) Czy istnieją dwa różne grafy K

m,n

i K

m

0

,n

0

, które są homeomorficzne?

10

Zadanie 8. Niech n − kostka, oznaczana jako Q

n

, będzie grafem o 2

n

wierzchoł-

kach, które opisane są n bitowymi ciągami binarnymi. Dwa wierzchołki
grafu Q

n

są połączone krawędzią, jeżeli ich opis różni się tylko na jednym

bicie.

(a) Narysować grafy Q

2

i Q

3

.

(b) Znaleźć diam(Q

n

).

(c) Znaleźć stopień wierzchołków w Q

n

.

(d) Znaleźć liczbę krawędzi w grafie Q

n

.

Zadanie 9. Niech n − cykl, oznaczany jako C

n

, będzie grafem składającym się

tylko z jednego cyklu o długości n.

(a) Narysować grafy C

3

i C

6

.

(b) Znaleźć liczbę krawędzi i liczbę wierzchołków w grafie C

n

.

(c) Znaleźć diam(C

n

).

Zadanie 10. Jeśli to możliwe, narysować planarną reprezentację poniższych gra-

fów. W przeciwnym przypadku, korzystając z tw. Kuratowskiego, pokazać
że to niemożliwe .

B

A

C

D

E

F

B

F

C

D

E

A

B

A

C

D

E

F

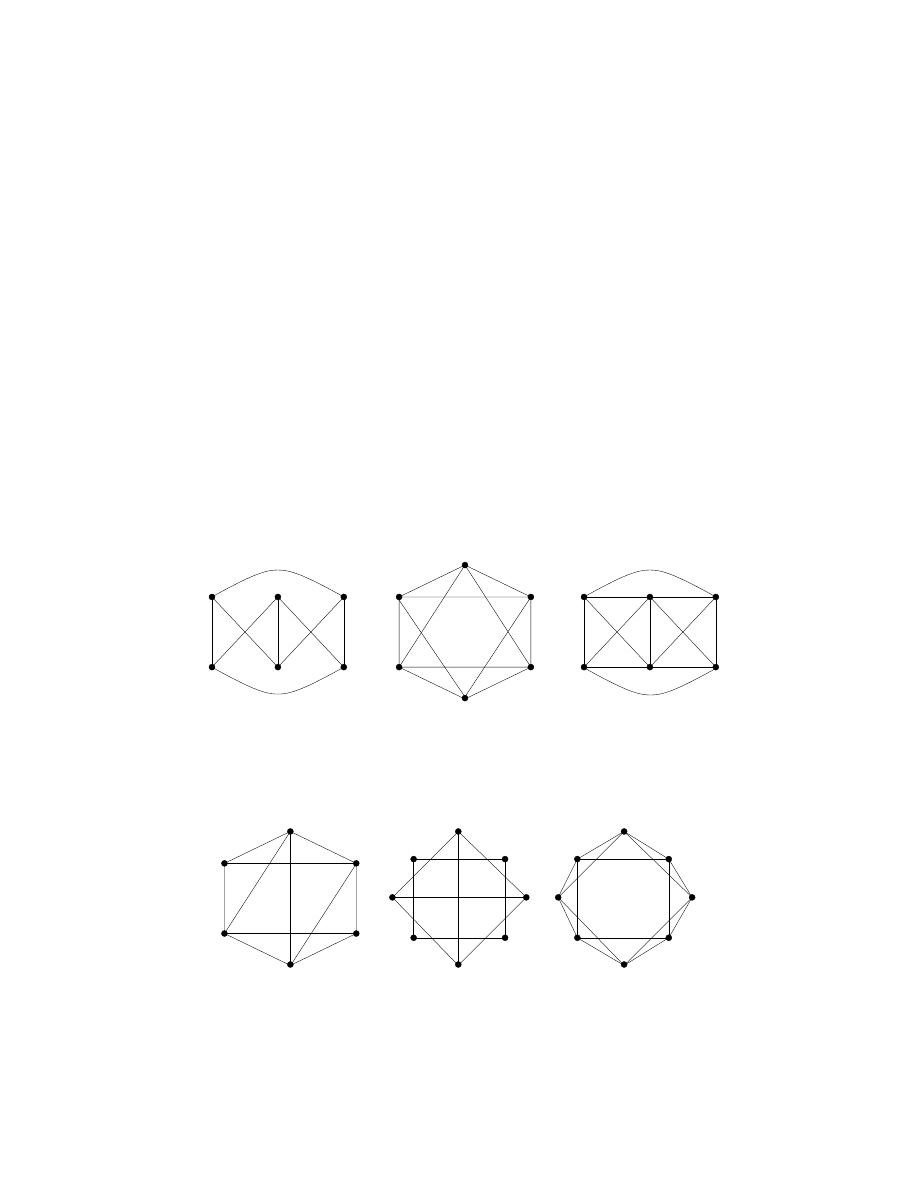
Zadanie 11. Jeśli to możliwe, narysować planarną reprezentację poniższych gra-

fów. W przeciwnym przypadku, korzystając z tw. Kuratowskiego, pokazać
że to niemożliwe .

11

7

Drzewa

Zadanie 1. Narysować wszystkie nie izomorficzne drzewa o 6 wierzchołkach.

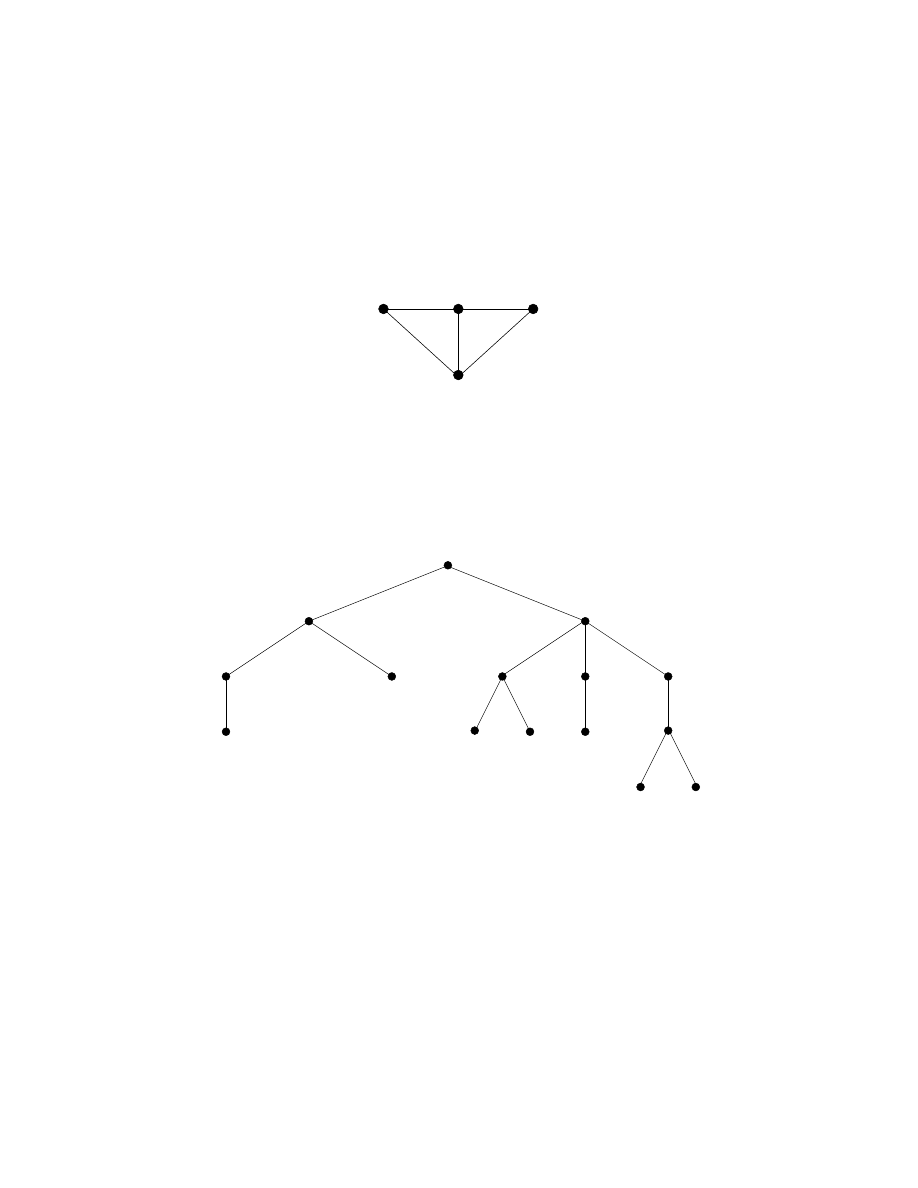
Zadanie 2. Dla grafu przedstawionego na rysunku narysować wszystkie drzewa

rozpinające.

Zadanie 3. Dla drzewa T przedstawionego na poniższym rysunku podać:

(a) Ścieżki z korzenia R do węzłów: H, F, M. Podać poziom tych węzłów.

(b) Dzieci węzła B oraz wszystkich potomków węzła A.

(c) Liście w drzewie.

R

A

B

C

D

F

E

G

H

I

J

K

L

M

N

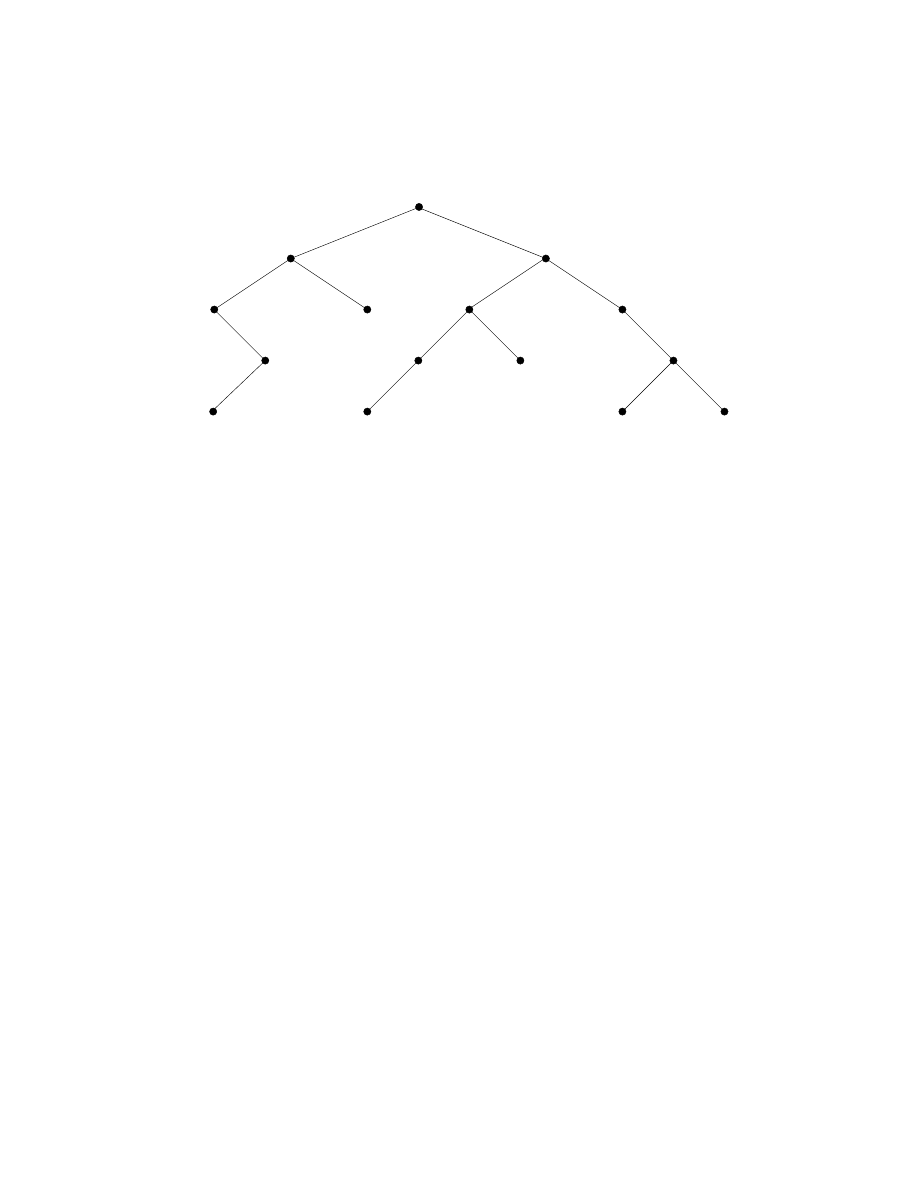
Zadanie 4. Dane jest drzewo binarne T przedstawione na poniższym rysunku.

Podać:

(a) głębokość (wysokość) drzewa,

(b) przejście zgodnie z algorytmem preorder,

(c) przejście zgodnie z algorytmem inorder,

(d) przejście zgodnie z algorytmem postorder.

12

R

A

B

C

D

E

F

G

H

I

J

K

L

M

N

Zadanie 5. Drzewo binarne T ma dziewięć węzłów. Narysować T jeżeli wiadomo,

że:

• przejście preorder to: G, B, Q, A, C, P , D, E, R, oraz

• przejście inorder to: Q, B, C, A, G, P , E, D, R.

Zadanie 6. Załóżmy, że przejścia preorder i inorder przez pewne drzewo T są

następujące:

• preorder: G, B, Q, A, C, K, F , P , D, E, R, H, oraz

• inorder: Q, B, K, C, F , A, G, P , E, D, H, R.

Wyznaczyć drzewo T . Podać głębokość drzewa T .

Zadanie 7. Rozważmy wyrażenie

(a) E = (2x + y)(5a − b)

3

,

(b) E = (x + 3y)

4

(a − 2b).

Narysować drzewo binarne opisujące to wyrażenie (∗ — mnożenie, / —
dzielenie, ↑ — potęgowanie). Zapisać wyrażenie E w notacji polskiej.

13

Zadanie 8. Rozważmy drzewo T przedstawione na poniższym rysunku.

57

39

42

47

26

13

29

34

66

81

74

68

95

Dlaczego drzewo T jest binarnym drzewem poszukiwań? Opisać algorytm
wstawiania elementu 38.

Zadanie 9. Dane jest n posortowanych elementów A

1

, A

2

, . . . , A

n

(A

1

< A

2

<

. . . < A

n

). Opisać drzewo binarne T jakie powstanie podczas wstawiania

kolejno elementów A

1

, A

2

, . . . ,. Jaka jest głębokość wynikowego drzewa?

Zadanie 10. Wyznaczyć binarne drzewo poszukiwań powstałe po wstawianiu

kolejno następujących liter alfabetu:

J , R, D, G, W , E, M , H, P , A, F , Q.

Zadanie 11. Wyznaczyć binarne drzewo poszukiwań powstałe po:

(a) usunięciu węzła M ,

(b) usunięciu węzła D,

z drzewa otrzymanego w Zadaniu 10.

Zadanie 12. Wyznaczyć binarne drzewo poszukiwań powstałe w wyniku kolej-

nego wstawiania następujących elementów:

50, 33, 44, 22, 77, 35, 60, 40.

14

Zadanie 13. Rozważmy binarne drzewo poszukiwań T przedstawione na poniż-

szym rysunku.

50

25

75

22

40

60

90

15

30

44

80

33

(a) Jak będzie wyglądało drzewo T po kolejnym wstawieniu do niego

elementów 20, 55, 88?

(b) Jak będzie wyglądało drzewo T po kolejnym usunięciu z niego ele-

mentów 22, 25, 75?

15