Podstawy programowania

wykład 13

Dr inż. Jakub Bauman

[e-mail]

Odwrotna notacja polska

Dr inż. Jakub Bauman

[e-mail]

Odwrotna notacja polska

Odwrotna notacja polska (ONP, ang. Reverse Polish
Notation, RPN) – jest sposobem zapisu wyrażeń
arytmetycznych, w którym znak wykonywanej operacji
umieszczony jest po operandach (zapis postfiksowy), a nie
pomiędzy nimi jak w konwencjonalnym zapisie
algebraicznym (zapis infiksowy) lub przed operandami jak w
zwykłej notacji polskiej (zapis prefiksowy). Zapis ten
pozwala na całkowitą rezygnację z użycia nawiasów w
wyrażeniach, jako że jednoznacznie określa kolejność
wykonywanych działań.

Zalety ONP

ONP bardzo ułatwia wykonywanie na komputerze obliczeń
z nawiasami i zachowaniem kolejności działań. Zarówno
algorytm konwersji notacji konwencjonalnej (infiksowej) na
odwrotną notację polską (postfiksową), jak i algorytm
obliczania wartości wyrażenia danego w ONP są bardzo
proste i wykorzystują stos.

Historia ONP

Odwrotna notacja polska została opracowana przez
australijskiego naukowca Charlesa Hamblina jako
„odwrócenie” beznawiasowej notacji polskiej Jana
Łukasiewicza na potrzeby zastosowań informatycznych.

Zastosowania ONP

Jest używana w niektórych językach programowania (np.
FORTH, Postscript) oraz w niektórych kalkulatorach
naukowych (np. Hewlett-Packard, National Semiconductor).
Programy komputerowe kompilujące program dokonują
analizy wyrażenia arytmetycznego, przekształcając je na ciąg
instrukcji odpowiadający odwrotnej notacji polskiej.
Wyrażenie to jest obliczane podczas wykonywania programu.

Przykłady wyrażeń w ONP



a+b ≡ a b +



(a+b)*d ≡ a b+d *



(a+(b*c)≡ abc*+



(a+b)*(c+d)≡ a b +c d +*



((a+b)*((c+(d+e))

(e+ f )

)))≡ a b +c d e++ e f + ^*



1. Analizuj wyrażenie po jednym elemencie (stałej, zmiennej lub ograniczniku).



2. Jeśli ten element jest:



a) stałą lub nazwą zmiennej – przekaż go na wyjście;



b) operatorem:



− jeśli priorytet badanego operatora jest wyższy od priorytetu operatora zajmującego szczyt stosu lub jeśli stos
jest pusty – dopisz go na stos;



− jeśli na szczycie stosu znajduje się operator o wyższym lub równym priorytecie – odczytaj ze stosu i prześlij na
wyjście wszystkie operatory o priorytecie wyższym bądź równym aż do wystąpienia na szczycie stosu operatora o
priorytecie niższym od priorytetu operatora nadchodzącego z wejścia; element badany dopisz na stos;



c) nawiasem:



− jeśli trafiłeś na nawias otwierający – dopisz go na stos;



− jeśli trafiłeś na nawias zamykający: zdejmij wszystkie operatory ze stosu i przekaż je na wyjście aż do trafienia na
nawias otwierający; nawiasów nie wypisuj na wyjście.



3. Jeśli badane wyrażenie



a) nie zostało wyczerpane – wróć do punktu pierwszego;



b) zostało wyczerpane – odczytaj wszystkie operatory ze stosu i przekaż je na wyjście
automatu.

Algorytm konwersji na ONP

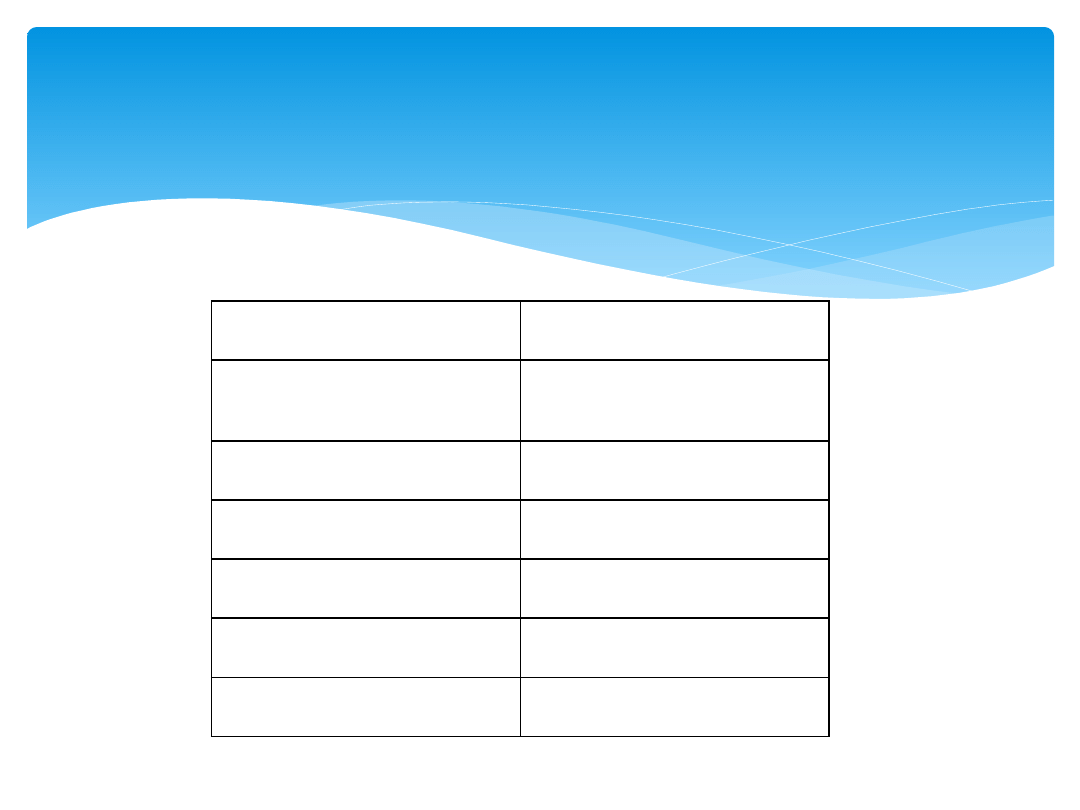
operator

priorytet

funkcja

lg,sin, exp

5

potęgowanie

4

* ÷ ~

3

+ -

2

= (przypisanie)

1

(

0

Priorytety operatorów

Przykład zamiany na ONP

Krok

Wejście

Stos

Wyjście

1

x

x

2

+

+

3

3

+

3

4

*

+ *

5

z

+ *

z

6

–

–

* +

7

2

–

2

8

*

– *

9

3

– *

3

10

/

– /

*

11

k

– /

k

12

koniec

/ –

Wyrażenie arytmetyczne: x + 3 * z – 2 * 3 / k

Wyrażenie w notacji ONP: x 3 z * + 2 3 * k / –

Do czego to potrzebne?

Na przykład po to, żeby móc na swoje potrzeby
stworzyć bardziej zaawansowany kalkulator. Trudno
by nam było obliczyć zadanie zapisane nie w RPN.
Musielibyśmy szukać, które zadania mają wyższy
priorytet i je najpierw przeliczać (trzeba by najpierw
obliczyć wszystko w nawiasach).
Natomiast zadania zapisane w ONP w takim
przypadku łatwiej się oblicza.

Obliczanie wyrażenia zapisanego

w ONP

1. Analizuj wyrażenie po jednym elemencie (stałej, zmiennej lub

ograniczniku).

2. Jeśli ten element jest:

a) stałą lub nazwą zmiennej – dopisz go na stos;
b) operatorem – zdejmij ze stosu właściwą dla danego operatora

ilość argumentów, wykonaj na nich obliczenia, uzyskany wynik
dopisz na stos;

3. Jeśli badane wyrażenie

a) nie zostało wyczerpane – wróć do punktu pierwszego;
b) zostało wyczerpane – wartość znajdująca się na stosie to wynik

obliczeń.

Przykład

Krok

Wejście

Operacja

Stos

1

6

6

2

3

6 3

3

/

6 / 3

2

4

2

2 2

5

5

2 2 5

6

+

2 + 5

2 7

7

*

2 * 7

14

Wyrażenie: 6 3 / 2 5 + *

Wartość wyrażenia: 14



Zamień następujące wyrażenia na notację ONP, a
następnie oblicz wartość wyrażenia:



(10+2)*5+(3-1)/2



7*(10-(1 +4)*2)-1



8+3+1-4*(12 +2*2)/2



(9*9-1)/10-2*3



4-5+6*2-8*(1+3)

Zadania do rozwiązania

Pytania

Dyskusja

Dziękuję za uwagę!

Dr inż. Jakub Bauman

[e-mail]