
Chemia teoretyczna
2012/13
prof. Marek Kręglewski
mkreg@amu.edu.pl
1

Plan wykładu
•
Obliczenia kwantowo-chemiczne dla cząsteczek
•
Podział energii całkowitej na elektronową, wibracyjną i rotacyjną
•
Energia cząsteczki w podstawowym i wzbudzonym stanie elektronowym
•
Drgania cząsteczki
– Oscylator harmoniczny
– Oscylator anharmoniczy
– Oscylator dwuwymiarowy
•
Rotacja cząsteczki
– Rotator sztywny
– Obsadzenia stanów – rozkład Boltzmana
– Multipletowość stanów
•
Oddziaływanie materii z promieniowaniem elektromagnetycznym
•
Widma rotacyjne
– Cząsteczki liniowe
– Cząsteczki typu bąka sferycznego, symetrycznego i asymetrycznego
– Wyznaczanie geometrii cząsteczki
•
Widma wibracyjno-rotacyjne
– Reguły Francka-Condona
– Pasma widmowe
– Podstawienie izotopowe
•
Widma wibronowe
•
Widma NMR
2

Postulaty mechaniki kwantowej
1. System w pełni opisany przez funkcję falową
2. Obserwable są reprezentowane przez operatory spełniające warunki komutacji
3. Wartość średnia obserwabli jest równa jej wartości oczekiwanej
jeżeli ψ jest funkcją własną operatora , ω jego wartością własną, to
t
r
r
,
,
,
2
1
q
i
p
q
/
,
0
'
,
0
'
,
,
'
'
p
p
q
q
i
p
q
q
d
d
*
*
ˆ
ˆ
d
d
*
*
ˆ
3

Postulaty mechaniki kwantowej
4. Prawdopodobieństwo znalezienia cząstki w elemencie objętości dτ wokół punktu r
jest proporcjonalne do
5. Ewolucja systemu jest opisana czasowo zależnym równaniem Schrӧdingera
Hamiltonian H czasowo niezależny prowadzi do funkcji falowej ψ czasowo niezależnej
będącej rozwiązaniem czasowo niezależnego równania Schrӧdingera
Funkcja stanu stacjonarnego
gdzie (ψ* ψ) nie zmienia się w czasie
d
r
r
d
r
*
2
V
T
H
t
i
ˆ
ˆ
ˆ
E
H
ˆ
/
,
iEt
e
r
t
r
4
Równanie Schrӧdingera
)
(
2
2
2
2
x
V
E
mv
p
m
p
mv
T
E
E
E
E
pot
x
x
x
x
kin
pot
kin
cał
)
(
ˆ
2
ˆ
ˆ
ˆ
2
ˆ
ˆ
ˆ
ˆ
ˆ
2
2
2
2
2
2
2
2
x
V
x
m
T
x
x
i
x
i
p
x
i
p
m
p
T
V
T
H
x
x
x
Obserwable
Wielkości fizyczne
Operatory
E
H
ˆ
5
Cząstka w pudle potencjału
0
a
x
I
V=
II
V=0
III
V=
0
0
ˆ
ˆ
x
x
E
H
E
H
III
I
III
III
III
I
I
I
2
2
2
2
2
n
ma
E
x
a
n
a
x
E
dx
d
m
E
H
II
n
II
II
II
II
II
sin
2
2
ˆ
2
2
2
V
I
=V
III
=
cząstka nie
może się tu znaleźć
x
a
n
a
a
n
dx
d
x
a
n
a
a
n
dx
d
II
II
sin
2
cos
2
2
2
2
2
2
Sprawdzenie rozwiązania:
x
a
n
a
E
x
a
n
a
a
n
m
sin
2
sin
2
2
2
2
2
2
n
=1,2,...
6
Cząstka w pudle potencjału
n
3
2
1
2
2
2
2
1
2ma
2
2
2
2
2
2ma
2
2
2
2
3
2ma
0
a
Normalizacja funkcji falowej
a
N
a
N
a
N
a
n
n
a
x
N
dx
a
n
dx
N
dx
x
a
n
N
x
a
n
N
a
a
a
a
a
n
2
2
1
2
1
2
sin
2
1
2
cos
1
sin
sin
2
2
0
2
1
0
2
1
2
0
0
2
1
2
1
2
0
2
2
W punktach x=0 i x=a
funkcje przyjmują wartość 0,
taką jaką mają funkcje w
obszarach x<0 i x>a.
Porównaj wartość N z postacią
funkcji falowej na poprzednim
slajdzie.
2
2
cos
1
sin
2
Prawdopodobieństwo
znalezienia się cząstki w
obszarze <0,a> wynosi 1.
7
Cząstka w pudle potencjału
Ortogonalność funkcji falowych
m
n
gdy
m
n
gdy
dx
a
m
n
0
1
0
*
0
sin
sin
sin
sin
cos
cos
cos
cos
sin
sin
1
0
0
1
0
0
1
0
2
1
2
0
2
2
m
n
m
n
x
x
dx
x
dx
x
dx
x
x
dx
x
x
m
n
a
m
n
a
a
a
a
m
n
m
n
a
a
a
m
n
m
n
a
a
a
a
m
n
a
a
m
n
a
a
a
m
n
a
m
n
a
a
a
m
a
a
n
a
Oznacza to, że cząstka nie
może równocześnie
znajdować się w dwóch
różnych stanach
stacjonarnych
cos
cos
sin
sin
2
1
8

Cząstka w pudle potencjału
2
2
2
2
0
2
0
2
2
2
0
2
0
2
2
2
0
0
2
2
2
2
sin
2
sin
2
2
sin
2
sin
sin
2
2
sin
2
sin
2
sin
2
2
sin
2
n
ma
dx
x
a
n
a
dx
x
a
n
a
n
m
a
dx
x
a
n
a
dx
x
a
n
dx
d
x
a
n
m
a
dx
x
a
n
a
x
a
n
a
dx
x
a
n
a
dx
d
m
x
a
n
a
E
a
a
a
a
a
a
0
2
sin
1
cos
sin
2
sin
2
sin
2
0
0
0
dx
x
a
n
a
n
i
a
dx
x
a
n
x
a
n
a
n
i
a
dx
x
a
n
a
dx
d
i
x
a
n
a
p
a
a
a
x
2
2
2
2
0
2
2
0
2
2
2
0
2
2
2
2
2
cos
1
2
1
2
sin
2
sin
2
sin
2
n
a
dx
x
a
n
a
n
a
dx
x
a
n
a
n
a
dx
x
a
n
a
dx
d
x
a
n
a
p
a
a
a
x
Obliczenia średnich kwantowo-mechanicznych (wartości oczekiwanych)
Energia
Pęd
Kwadrat pędu
9
Cząstka w pudle potencjału
2
2
2
0
2
2
2
2
2
2
0
0
3
0
0
2
0
3
0
2
0
2
0
2
2
0
2
2
2
1
3
1
2
sin
2
2
2
3
2
cos
2
1
2
cos
2
1
3
2
sin
2
2
1
2
sin
2
1
3
1
2
cos
2
1
2
2
1
2
sin
2
sin
2
sin
2
n
a
x
a
n
n
a
n
a
n
a
a
dx
x
a
n
n
a
n
x
a
n
n
a
x
n
a
dx
x
a
n
x
n
a
a
x
a
n
n
a
x
a
x
a
dx
x
a
n
x
a
dx
x
a
dx
x
a
n
x
a
dx
x
a
n
a
x
x
a
n
a
x
a
a
a
a
a
a
a
a
a
a
2
2
2
cos
2
2
1
2
sin
2
2
1
2
2
sin
2
2
1
2
sin
2
sin
2
sin
2
0
2
2
0
0
0
2
0
a
a
a
x
a
n
n
a
x
a
a
dx
x
a
n
n
a
x
a
x
a
n
n
a
x
x
a
dx
x
a
n
x
a
dx
x
a
n
a
x
x
a
n
a
x
a
a
a
a
a
4
2
3
1
4
2
1
12
1
2
1
4
1
3
1
0
2
2
1
3
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
n
n
n
n
n
a
n
a
n
a
p
p
x
x
p
p
x
x
p
p
p
p
x
x
x
x
p
p
x
x
p
x
p
p
p
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Sprawdzenie zasady nieoznaczoności Heisenberga dla cząstki w pudle:
Położenia
Kwadratu położenia
10

Zasada wariacyjna
Wartość oczekiwana energii <E> jest równa wartości własnej energii E stanu
podstawowego, jeżeli <E> obliczamy stosując funkcję będącą dokładnym
rozwiązaniem równania Schrӧdingera dla stanu podstawowego.
Jeżeli stosujemy funkcję przybliżoną, to zawsze <E> jest większa od energii
stanu podstawowego.
Wniosek ogólny dla obliczeń przybliżonych:
wśród różnych funkcji przybliżonych szukamy takich, które dają najniższą
wartość średnią energii
Sprawdźmy tę zasadę na przykładzie cząstki w pudle:
11
Cząstka w pudle potencjału
2
2
4
2
3
2
2
1
sin
2
x
a
Nx
x
x
a
Nx
x
x
a
Nx
x
x
a
Nx
x
x
a
n
a
x
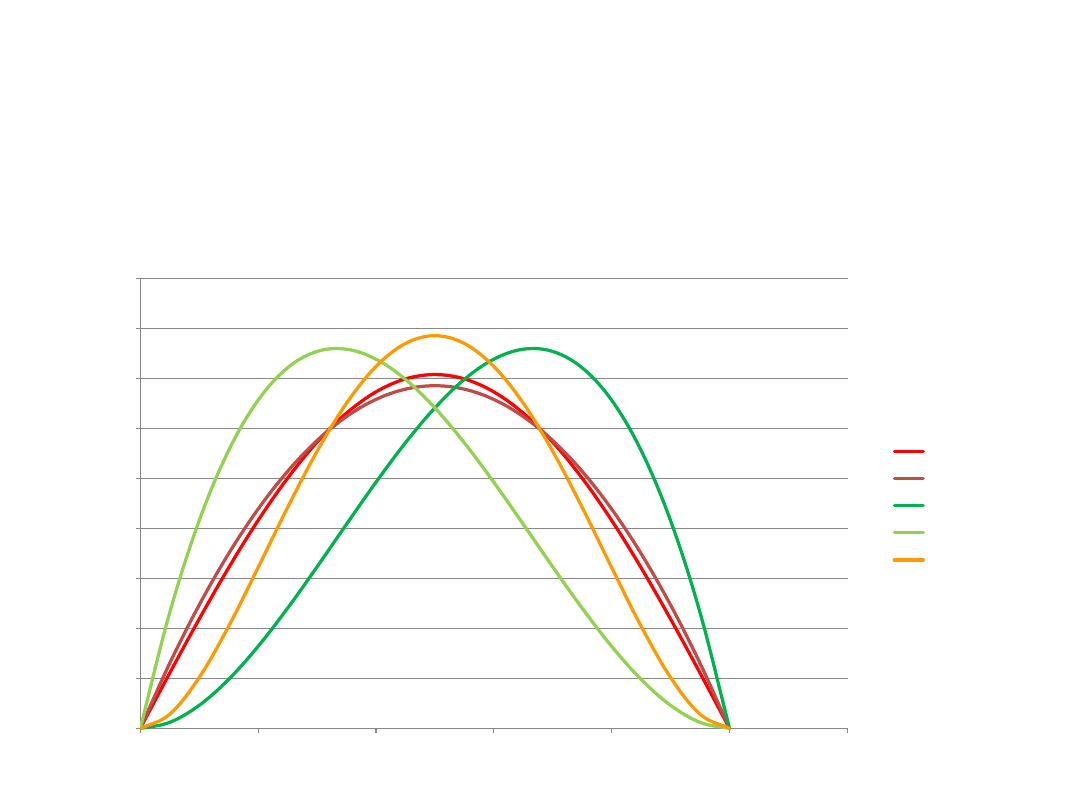
Funkcja własna (dokładna)
Funkcje próbne (przybliżone):
x
a
x
a
x
a
N
a
N
a
N
a
a
a
N
x
x
a
x
a
N
dx
x
ax
x
a
N
dx
x
a
x
N
a
a
a
5
1
5
5
2
5
2
5
5
5
2
0
5
4
3
2
2
0
4
3
2
2
2
0
2
2
30
30
30
1
30
5
4
2
3
5
4
2
3
2
x
a
x
a
x
a
N
a
N
a
N
a
a
a
N
x
x
a
x
a
N
dx
x
ax
x
a
N
dx
x
a
x
N
a
a
a
2
7
2
7
7
2
7
2
7
7
7
2
0
7
6
5
2
2
0
6
5
4
2
2
0
2
2
2
105
105
105
1
105
7
3
5
7
6
2
5
2
2
7
3
7
7
2
7
2
7
7
7
7
7
2
0
7
6
5
2
4
3
3
4
2
0
6
5
4
2
3
3
2
4
2
0
2
2
2
105
105
105
1
105
7
3
2
5
6
3
7
6
4
5
6
4
4
3
4
6
4
x
a
x
a
x
a
N
a
N
a
N
a
a
a
a
a
N
x
x
a
x
a
x
a
x
a
N
dx
x
ax
x
a
x
a
x
a
N
dx
x
a
x
N
a
a
a
1
630
5
1
3
2
7
6
2
1
9
1
5
6
4
7
6
8
4
9
4
6
4
4
2
4
4
9
2
9
2
0
5
4
6
3
7
2
8
9
2
0
4
4
5
3
6
2
7
8
2
0
7
6
2
5
3
8
6
2
4
4
2
0
2
2
2
2
a
N
a
N
x
a
x
a
x
a
x
a
x
N
dx
x
a
x
a
x
a
ax
x
N
dx
ax
x
a
x
a
x
x
a
x
a
N
dx
x
a
x
N
a
a
a
a
2
2
9
4
9
9
2
630
630
630
x
a
x
a
x
a
N
a
N
Normalizacja funkcji przybliżonych:
12
Cząstka w pudle potencjału
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0
0.2
0.4
0.6
0.8
1
1.2
sin
f1
f2
f3
f4
Wykresy funkcji dokładnej i funkcji próbnych (a=1)
13
Cząstka w pudle potencjału
2
2
2
2
2
0
2
2
0
2
2
2
0
2
2
2
2
87
,
9
2
2
cos
1
2
1
2
2
sin
2
2
sin
2
2
sin
2
ma
ma
dx
x
a
a
m
a
dx
x
a
a
m
a
dx
x
a
a
dx
d
m
x
a
a
a
a
a
2
2
2
1
2ma
E
2
2
9
4
2
7
3
2
7
2
5
1
630
105
105
30
sin
2
x
a
x
a
x
x
a
x
a
x
x
a
x
a
x
x
a
x
a
x
x
a
a
x
2
2
0
3
2
2
5
0
2
5
5
0
2
2
2
5
2
10
3
2
2
30
2
30
30
2
30
ma
x
x
a
m
a
dx
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
2
2
0
5
4
3
2
2
7
0
4
3
2
2
2
7
0
2
2
7
2
7
0
2
2
2
2
7
2
14
5
6
4
8
3
2
2
105
6
8
2
2
105
6
2
2
105
105
2
105
ma
x
x
a
x
a
m
a
dx
x
ax
x
a
m
a
dx
x
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a
2
2
0
5
4
3
2
2
3
2
7
0
4
3
2
2
3
2
7
0
2
2
7
2
7
0
2
2
2
2
2
7
2
14
5
6
4
16
3
14
2
4
2
105
6
16
14
4
2
105
6
4
2
105
105
2
105
ma
x
x
a
x
a
x
a
m
a
dx
x
ax
x
a
x
a
m
a
dx
x
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a
2
2
2
2
0
7
6
5
2
4
3
3
4
2
9
0
6
5
4
2
3
3
2
4
2
9
2
2
0
2
2
2
9
2
2
9
0
2
2
2
2
2
9
2
12
7
12
6
36
5
38
4
16
3
2
2
630
7
12
6
36
5
38
4
16
3
2
2
630
12
36
38
16
2
2
630
12
12
2
2
630
630
2
630
ma
m
a
x
x
a
x
a
x
a
x
a
m
a
dx
x
ax
x
a
x
a
x
a
m
a
dx
x
ax
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a
14
Dwuwymiarowe pudło potencjału
x
y
a
b
0
V=0
V=
V=
V=
V=
y
b
k
b
x
a
n
a
y
x
b
k
a
n
m
E
k
n
k
n
sin
2
sin
2
,
2
,
2
2
2
2
2
2
,
Stany zdegenerowane:
gdy a=b,
wtedy E
1,2=
E
2,1
Dwa stany opisane
różnymi funkcjami mają
tę samą energię.
y
a
a
x
a
a
y
x
a
a
m
E
2
sin
2
sin
2
,
2
1
2
2
,
1
2
2
2
2
2
2
2
,
1
y
a
a
x
a
a
y
x
a
a
m
E
sin
2
2
sin
2
,
1
2
2
1
,
2
2
2
2
2
2
2
1
,
2
15
Dwuwymiarowe pudło potencjału
Inne przykłady:
a=2
b=4
1/a
2
1/b
2
n
x
n
y
E
0.25
0.0625
2
2
1.25
0.25
0.0625
1
4
1.25
0.25
0.0625
3
2
2.5
0.25
0.0625
1
6
2.5
y
b
n
b
x
a
n
a
y
x
b
n
a
n
m
E
y
x
n
n
y
x
n
n
y
x
y
x
sin
2
sin
2
,
2
,
2
2
2
2
2
2
,
m
2
2
2
16
Hamiltonian molekularny H
2
R
r
E
R
r
H
r
e
r
e
r
e
r
e
r
e
m
R
e
M
M
H
B
B
A
A
e
B
B
A
A
,
,
ˆ
2
2
2
ˆ
2
2
1
2
2
2
1
2
12
2
2
2
2
1
2
2
2
2
2
2
R
r
12
r
B2
r
A1
r
B1
r
A2
A
2
1
B
Przybliżenie adiabatyczne:
(Borna-Oppenheimera)
R
R
r
R
r
vr
e
;
,
Pełna funkcja falowa przedstawiona jako iloczyn funkcji elektronowej i funkcji dla
ruchu jąder.
R
r
e
;
funkcja opisuje rozkład elektronów dla chwilowej konfiguracji jąder R
R
vr
funkcja opisuje rozkład jąder – ich odległość R i kierunek wektora R
17
Równanie elektronowe
R
R
R
r
R
E
R
r
H
R
e
r
e
r
e
r
e
r
e
r
e
m
H
e
e
e
e
B
B
A
A
e
e
;
;
ˆ
2
ˆ
2
2
2
1
2
2
2
1
2
12
2
2
2
2
1
2
R
R
e
E
e
E
H
D
e
D
0
½h
18
Równanie wibracyjno-rotacyjne
R
E
R
R
H
R
E
M
M
H
vr
vr
vr
vr
e
B
B
A
A
vr
ˆ
2
2
ˆ
2
2
2
2
Separacja ruchu wibracyjnego i rotacyjnego:
,
,
r
v
vr
R
R
,
,
,
,
,
,
ˆ
r
r
r
r
v
v
v
v
E
H
R
E
R
R
H
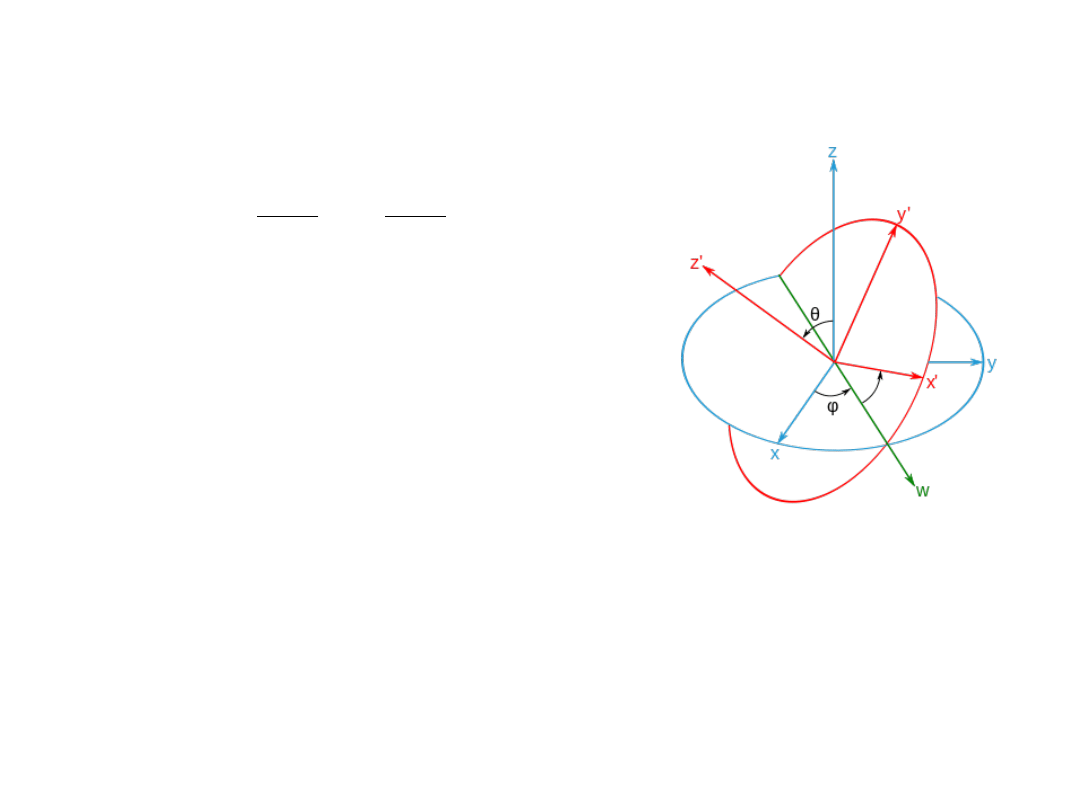
Kąty Eulera
Energia całkowita cząsteczki w przybliżeniu adiabatycznym
E = E
e
+ E
v
+ E
r
19
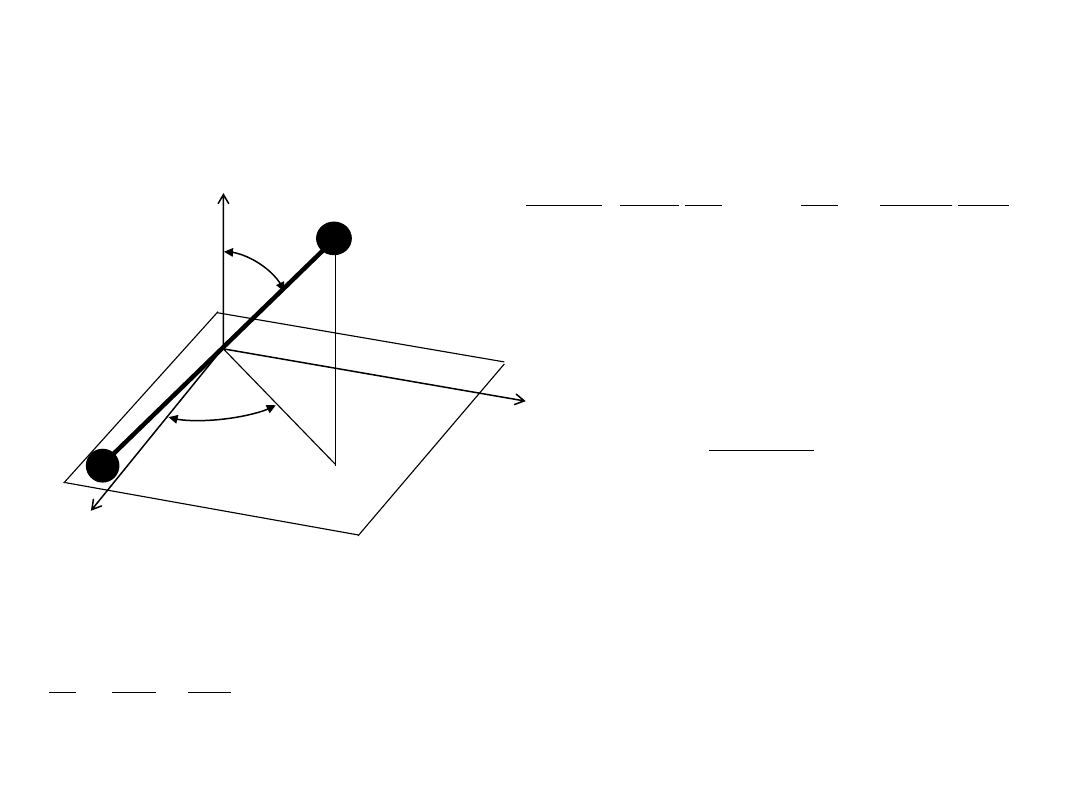
Rotator sztywny (E
r
)
z
x
y
R
θ
φ
2
2
2
2
2
sin
1
sin
sin
1
2
ˆ
R
H
r
,
,
,
ˆ
M
J
r
M
J
r
Y
E
Y
H
1
2
2
2
J
J
R
J
E
r
J= 0, 1, 2, ...
M=-J, -J+1,...,0,..., J
a
b
b
a
m
m
1
1
1
masa zredukowana:
(2J+1) – krotna degeneracja każdego stanu rotacyjnego
20
Rotator sztywny (E
r
)
1
2
2
2
J
J
R
J
E
r
J= 0, 1, 2, ...
Stała rotacyjna B
I
R
B
2
2
2
2
2
1
J
BJ
E
J
Moment bezwładności
2
R
I
21
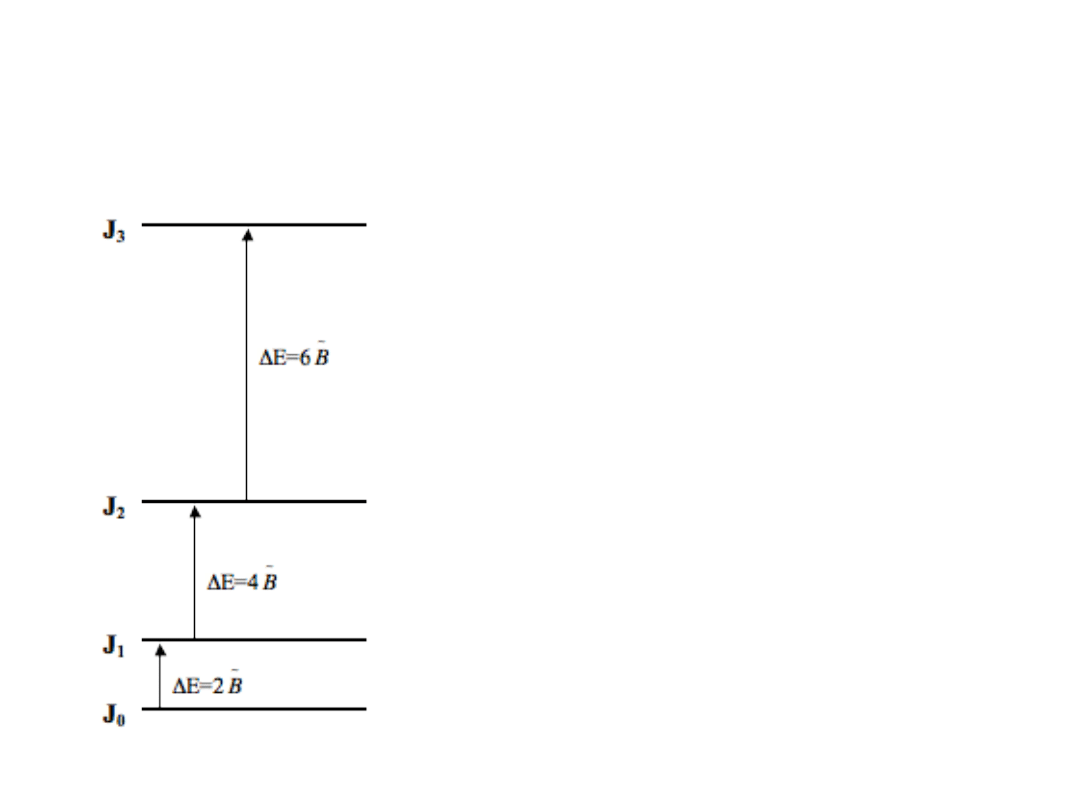
Poziomy energetyczne rotatora
1
J
BJ
E
J
22

Moment bezwładności - CO
2
n
i
i
i
i
x
z
y
m
I
1
2
2
Współrzędne jąder mierzone w
układzie środka masy cząsteczki
z
1
3
2
1,16 A
I= 7,1501E-42 kg*m
2
B= 7,7772E-28 J
B/(hc) = 0,3915 cm
-1
B*c = 1,1737E+06 s
-1
= 1,1737 MHz
Stałe:
mu = 1,660538921E-27 kg
ħ = 1,0545919E-34 J*s
c = 299792400 m/s
hc = 1,9865E-25 J*m = 1,9865E-27 J*cm
23
Rotacja bryły sztywnej
x
z
y
0
2
0
2
0
2
0
ˆ
ˆ
ˆ
2
1
ˆ
zz
z
yy
y
xx
x
rot
I
J
I
J
I
J
H
Bąk symetryczny
0
0
0
0
0
0
/
zz
yy
xx
zz
yy
xx
I
I
I
I
I
I
Bąk asymetryczny
0
0
0
zz
yy
xx
I
I
I
Bąk sferyczny
0
0
0
zz
yy
xx
I
I
I
Rotator liniowy
0
,
0
0
0
zz
yy
xx
I
I
I
wydłużony/spłaszczony
24

Stałe rotacyjne
C
B
A
I
C
I
B
I
A
C
B
A
2
2
2
2
2
2
Wyrażone w jednostkach energii (Joule)
Aby wyrazić je w cm-1 należy każdą podzielić przez (hc)
C
B
A
cI
h
C
cI
h
B
cI
h
A
C
B
A
2
2
2
8
8
8
25

Energia rotacji bąka symetrycznego
wydłużonego
0
0
0
zz
yy
xx
I
I
I
2
0
0
0
2
,
1
1
1
2
k
I
I
I
J
J
E
yy
zz
yy
k
J
k = -J, -J+1, ... , J
B
A
I
B
I
A
B
A
2
2
2
2
2
,
1
k
B
A
J
BJ
E
k
J
Przykład: chlorometan
26

Energia rotacji bąka symetrycznego
spłaszczonego
0
0
0
zz
yy
xx
I
I
I
2
0
0
0
2
,
1
1
1
2
k
I
I
I
J
J
E
yy
zz
yy
k
J
k = -J, -J+1, ... , J
B
C
I
B
I
C
B
C
2
2
2
2
2
,
1
k
B
C
J
BJ
E
k
J
Przykład: benzen
27
Bąki symetryczne
2
0
,
1
k
B
A
J
BJ
E
a
k
J
2
0
,
1
k
B
C
J
BJ
E
c
k
J
B
A
B
C
wydłużony
spłaszczony
28
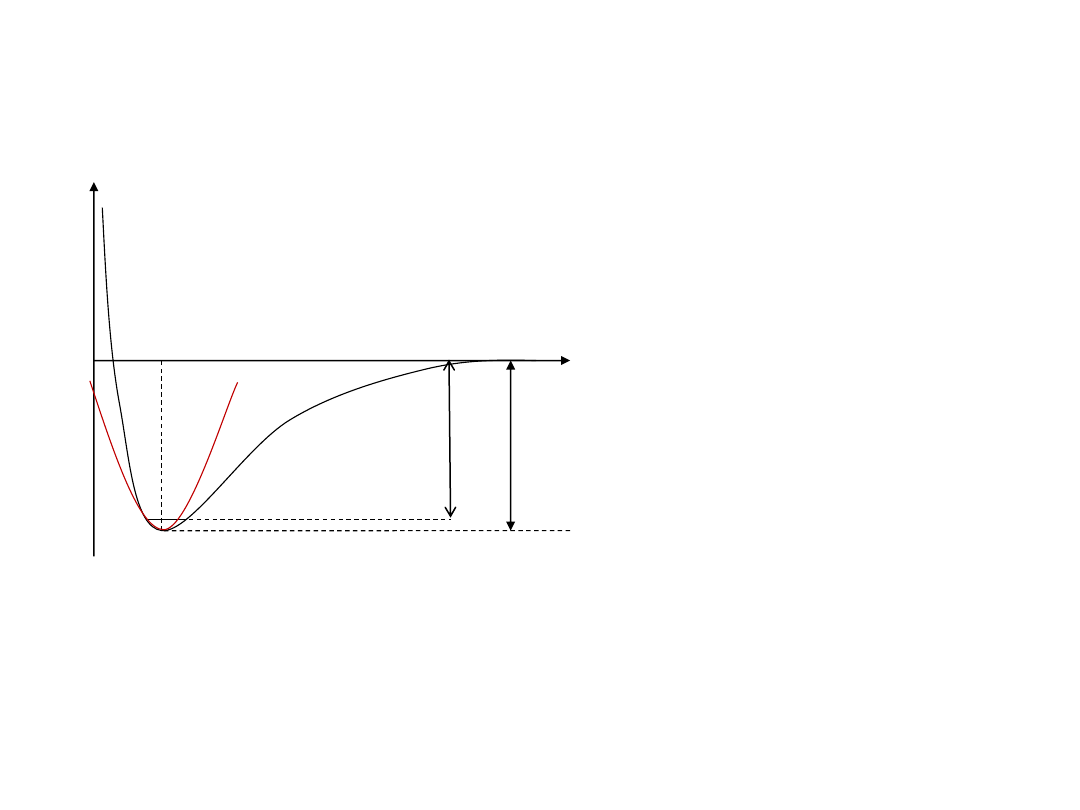
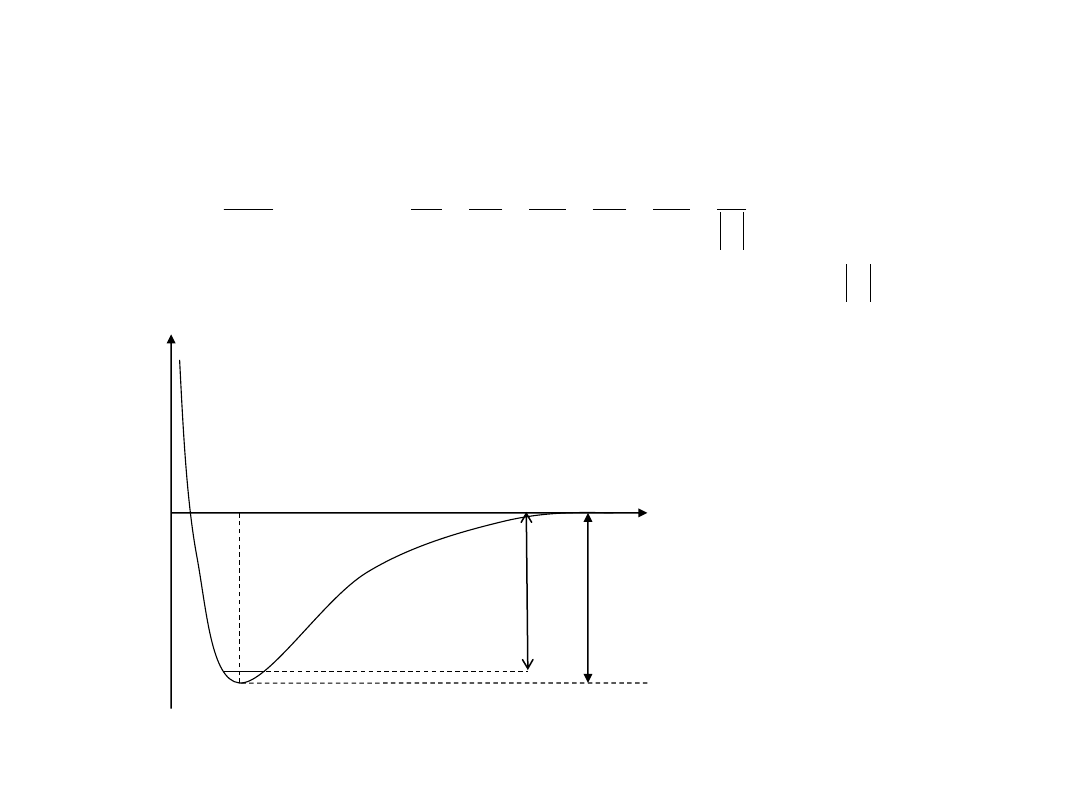
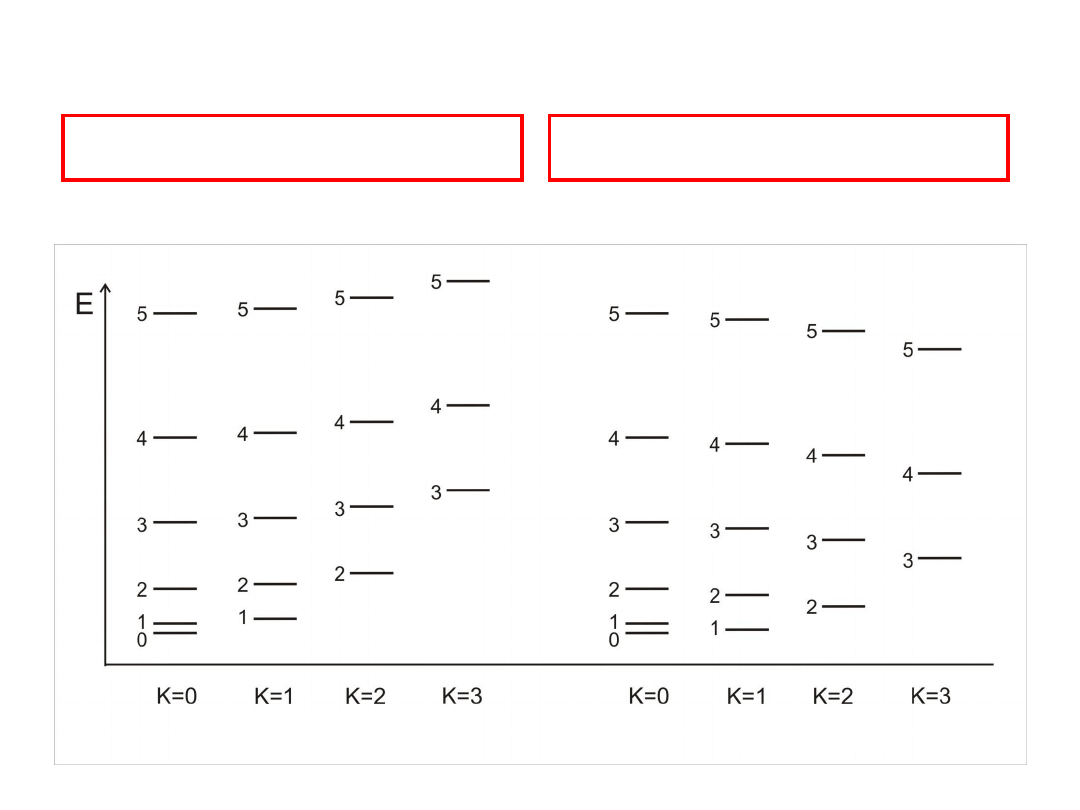
Energia wibracyjna (E
v
)
R
R
e
E
e
E
H
D
e
D
0
½h
W pobliżu minimum krzywą
energii potencjalnej
przybliżamy parabolą, co
prowadzi do równania
Schrӧdingera dla oscylatora
harmonicznego
29
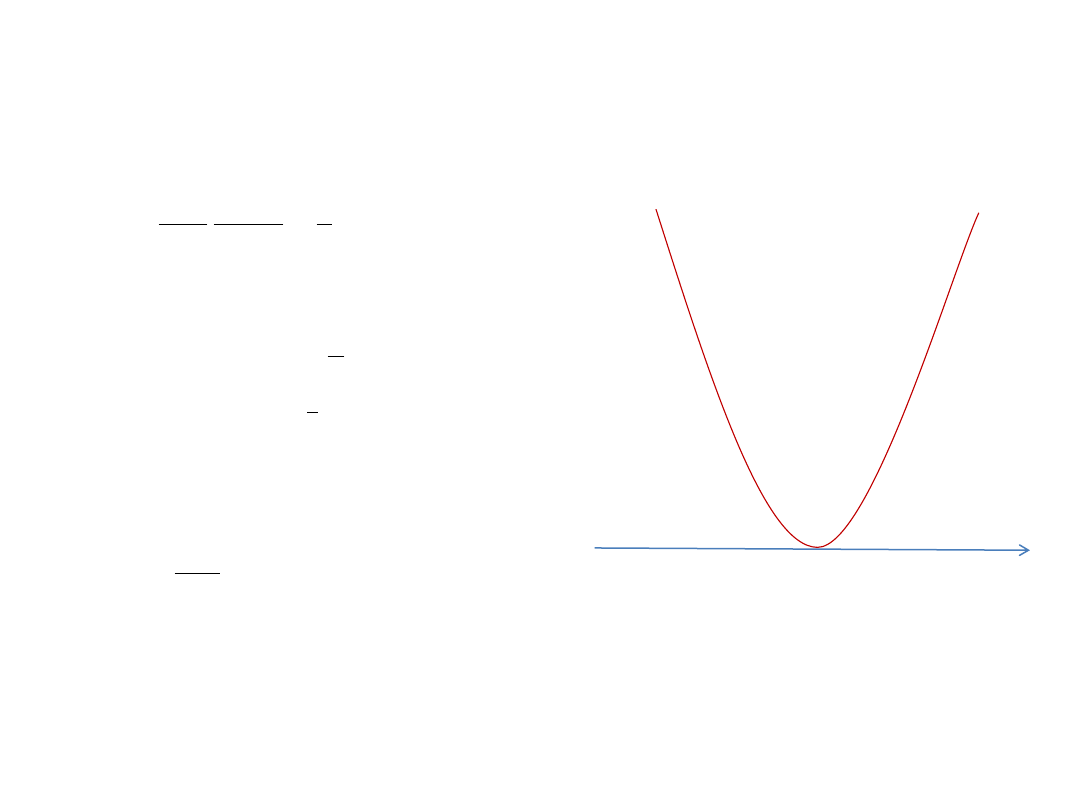
Oscylator harmoniczny
E
kx
dx
d
m
2
2
1
2
2
2
2
x
H
e
x
n
E
n
x
n
2
2
1
2
1
h
h
2
2
x
30
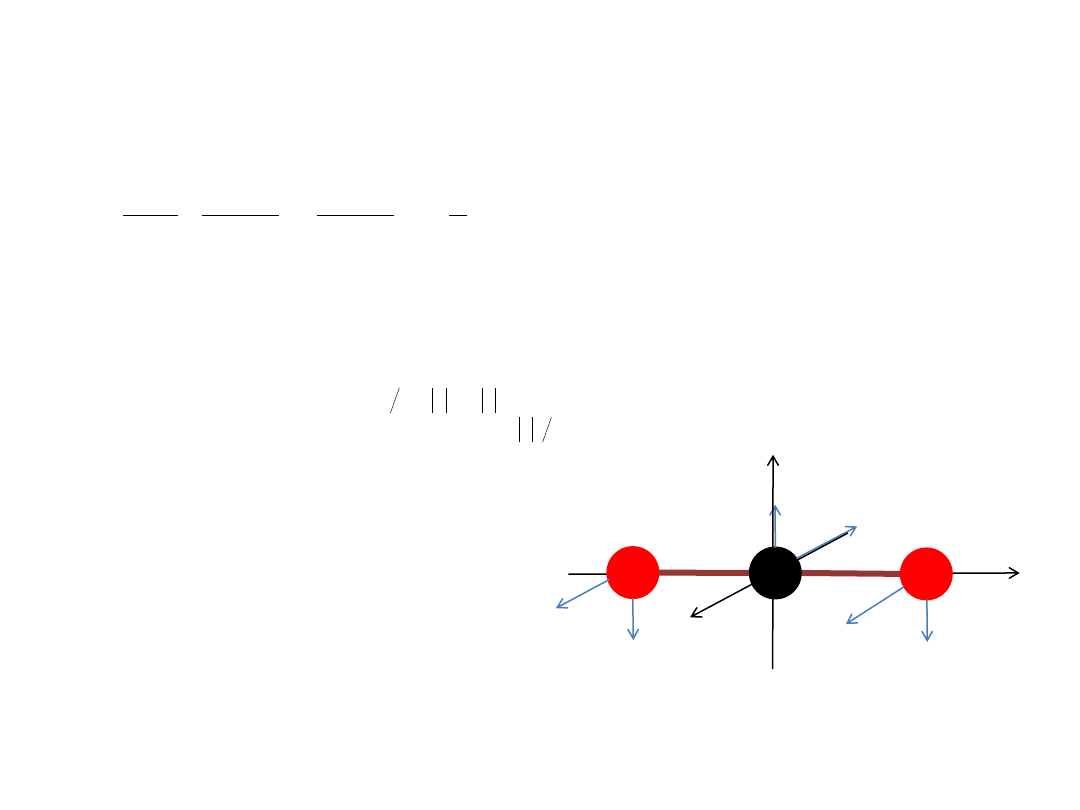
Oscylator harmoniczny 2-wymiarowy
il
l
l
n
l
r
l
n
l
n
e
r
L
r
e
N
r
r
y
r
r
x
E
y
x
k
dy
d
dx
d
m
2
2
.
,
2
2
2
1
2
2
2
2
2
2
,
2
0
sin
0
cos
2
n
n
n
n
l
n
n
E
,
2
,...,
2
,
,...
2
,
1
,
0
1
y
x
z
31

Współrzędne wibracyjne
3N
współrzędnych dla przemieszczeń jąder w układzie
(x,y,z)
to
3N
-
6
niezależnych współrzędnych wibracyjnych
+
3
współrzędne translacyjne
+
3
współrzędne rotacyjne
6
warunków Eckarta
oznacza:
1) cząsteczkowy układ współrzędnych związany ze środkiem
masy cząsteczki
2) osie układu (x,y,z) powiązane z elementami geometrycznymi
cząsteczki
z
y
x
N
i
d
i
,
,
,
,
,
2
,
1
;
6
3
,
,
2
,
1
;
N
k
r
k
N
i
i
i
a
m
1
0
N
i
i
i
i
d
a
m
1
0
)
(
32

Hamiltonian wibracyjny
funkcja falowa
równanie
Układ 3N-6 niezależnych oscylatorów harmonicznych HO (we
współrzędnych normalnych
Q
)
0
0
0
6
3
1
2
6
3
1
2
0
2
2
1
2
v
v
v
N
k
k
k
N
k
k
v
E
Q
Q
)
(
)
(
)
(
6
3
2
1
0
6
3
2
1
N
v
v
v
v
Q
Q
Q
N
6
3
1
2
1
)
6
3
(
)
2
(
)
1
(
0
N
k
k
N
v
v
v
v
v
h
E
E
E
E
energia
dwuwymiarowy (zdegenerowany) HO
trójwymiarowy (zdegenerowany) HO
1
k
v
h
2
3
k
v
h
33
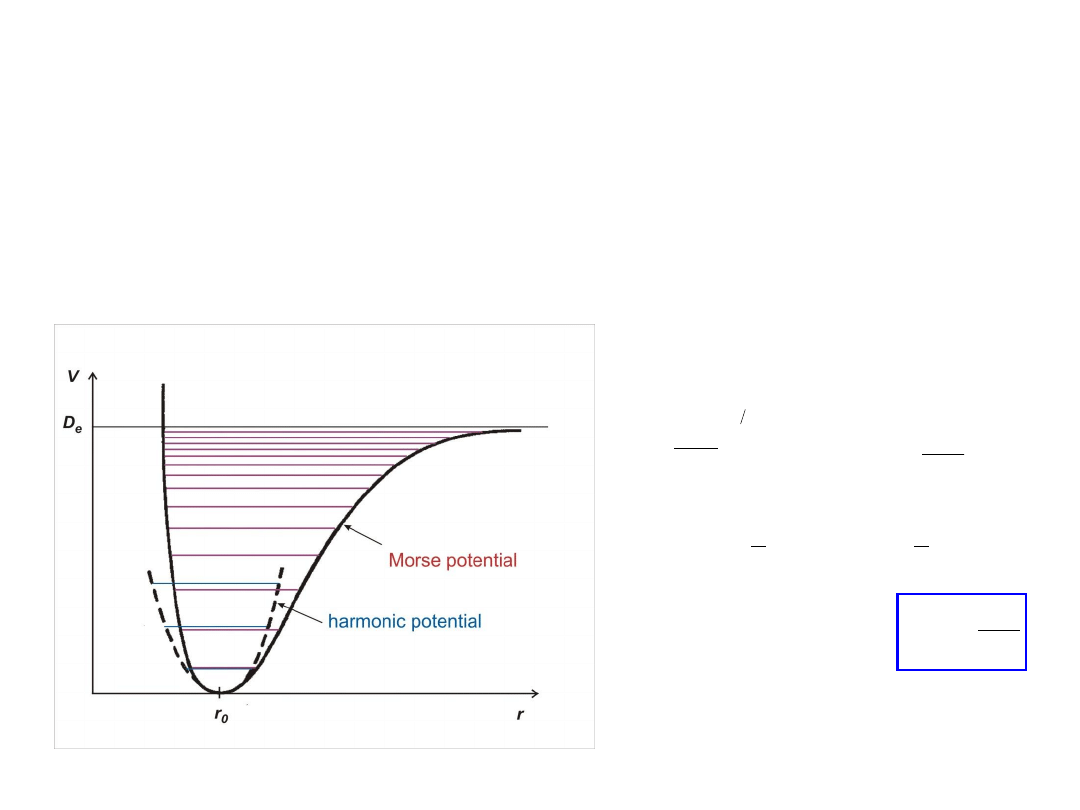
Wibracje w potencjale Morse’a
dokładne rozwiązanie równania Schrödingera z potencjałem Morse’a
potencjał Morse – bliższy rzeczywistości niż harmoniczny
uwzględnia anharmoniczność i energię dysocjacji
2
0
1
)
(
r
r
e
e
D
r
V
2
1
2
e
D
k
e
v
x
v
v
E
2
2
1
2
1
2
e
x
0
2
2
r
r
V
k
34
Hamiltonian wibracyjno-rotacyjny dla
dwuatomowej cząteczki
2
2
2
2
1
2
1
1
)
1
(
,
J
DJ
J
BJ
x
v
v
J
v
E
e
rot
vib
człon harmoniczny
człon anharmoniczny wynikający z
nieharmonicznego potencjału
człon opisujący rotację
sztywnej cząsteczki
człon uwzględniający
niesztywność cząsteczki
35
Wibracyjne reguły wyboru
x
v=0
v=1
v=2
v=3
v=4
v=+1
Oznaczenie przejścia
v’
v”
stan wyższy
stan niższy
Przejście podstawowe
(fundamental bands):
v’
v” = 1
0
Przejścia gorące (hot bands):
v’
v” = 2
1
v’
v” = 3
2
Gdy potencjał jest anharmoniczny możliwe także przejścia
v=+2, +3,
nadtony (overtones), np. v’
v” = 2
0
36
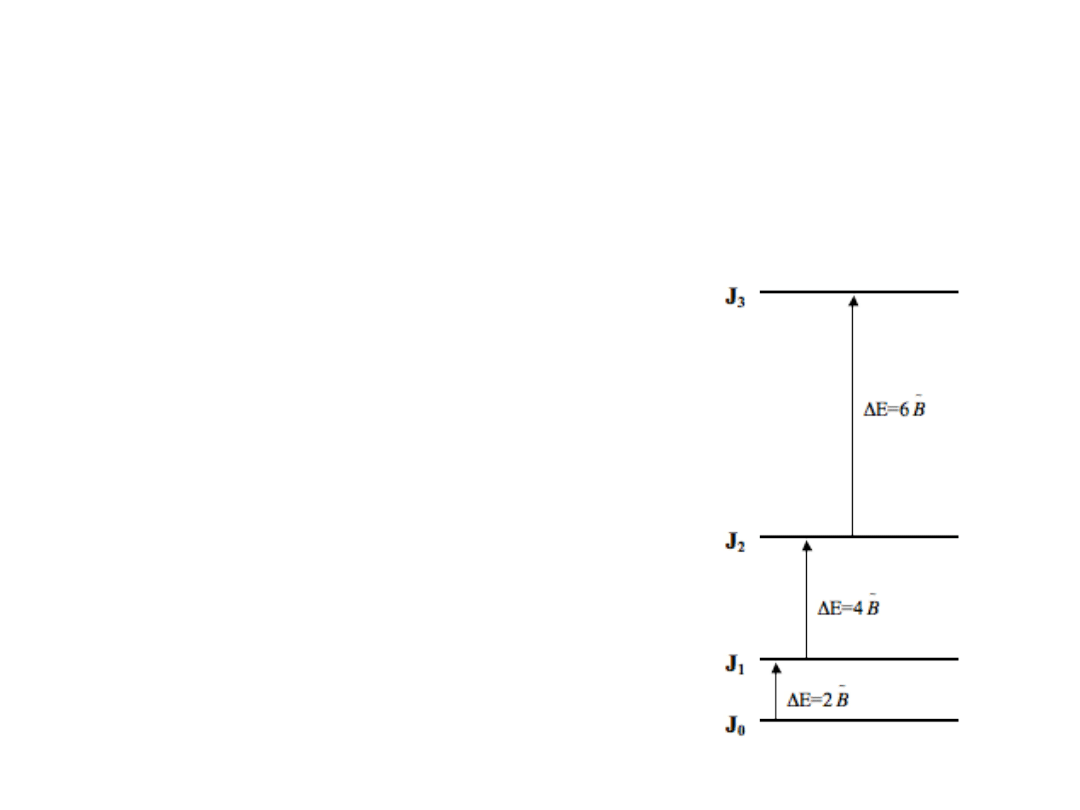
Rotacyjne reguły wyboru
Przejścia w ramach jednego stanu wibracyjnego
J=+1
37
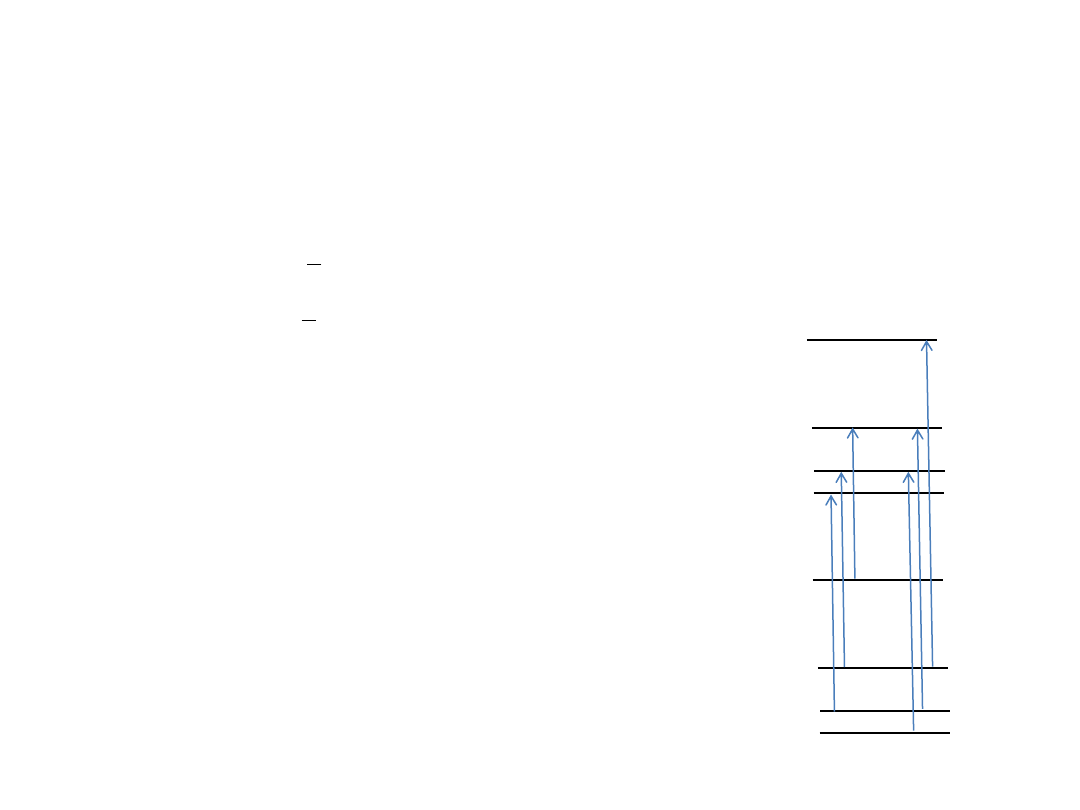
Przejścia wibracyjno-rotacyjne
v=+1
J=
1
2
2
0
2
3
2
2
0
2
1
1
'
)
1
(
'
,
1
1
"
)
1
(
"
,
0
J
J
D
J
J
B
v
J
E
J
J
D
J
J
B
v
J
E
rot
vib
rot
vib
v=0
v=1
J”
J’
3
2
1
0
3
2
1
0
Gałąź P:
v=+1 , J-1
J
Gałąź R:
v=+1 , J+1
J
...
"
'
2
"
'
"
'
"
'
1
"
)
1
(
"
1
'
)
1
(
'
,
0
1
,
1
3
2
0
2
2
2
2
0
J
D
D
J
D
D
B
B
J
B
B
v
J
J
D
J
J
B
J
J
D
J
J
B
v
J
E
J
E
E
rot
vib
rot
vib
...
1
'
4
"
'
1
'
4
'
2
1
"
)
1
(
"
2
1
'
2
)
1
(
'
,
0
1
,
1
0
2
2
2
2
0
J
J
D
B
B
J
D
B
v
J
J
D
J
J
B
J
J
D
J
J
B
v
J
E
J
E
E
rot
vib
rot
vib
P R
38
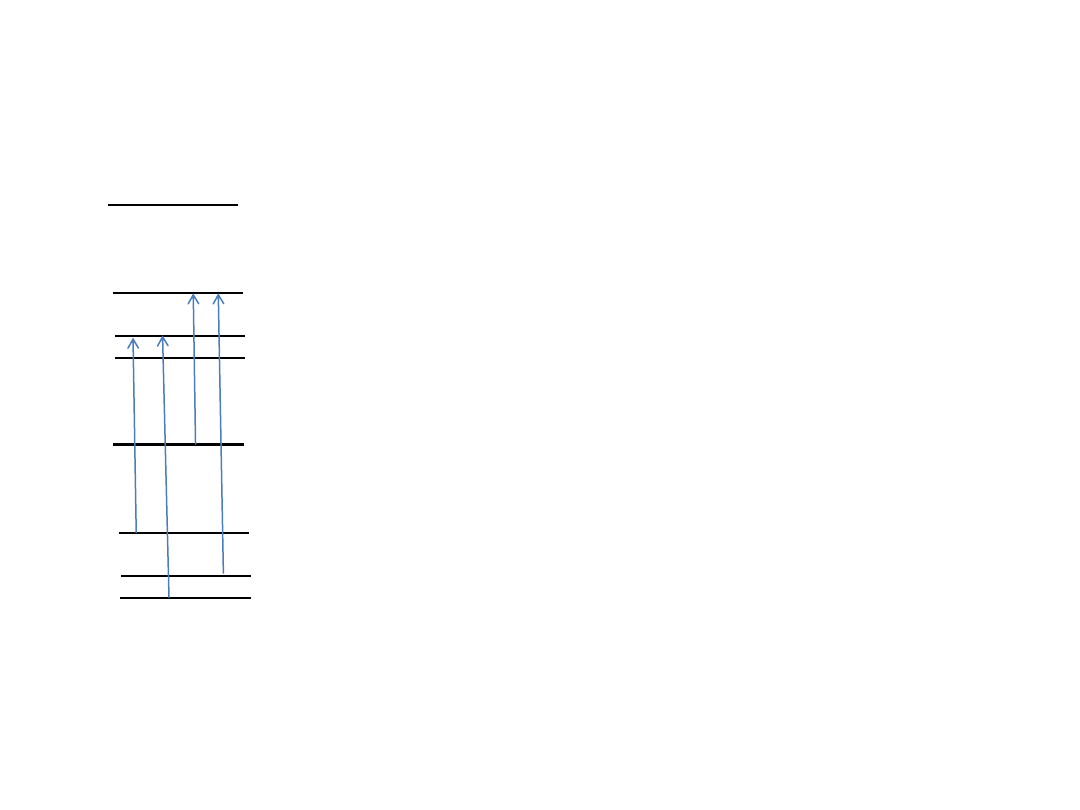
Kombinacje różnicowe w stanie
podstawowym
v=0
v=1
J”
J’
3
2
1
0
3
2
1
0
P(2)
R(0)
P(3)
R(1)
Różnice energii E(v,J) w stanie podstawowym:
E(0,2)-E(0,0)=R(0)-P(2)
E(0,3)-E(0,1)=R(1)-P(3)
E(0,4)-E(0,2)=R(2)-P(4)
...
E(0,J+2)-E(0,J)=B
0
[(J+2)(J+3)-J(J+1)]-
-D
0
[(J+2)
2
(J+3)
2
-J
2
(J+1)
2
]=
=R(J)-P(J+2)
Obserwując dostatecznie dużo przejść w
gałęziach P i R mających wspólne poziomy we
wzbudzonym stanie wibracyjnym, można
określić metodą najmniejszych kwadratów stałe
rotacyjne B
0
i D
0
dla stanu podstawowego.
GSCD – Ground State Combination Differences
39

GSCD – przykład
12
C
16
O
P
v'
J'
v"
J"
R
v'
J'
v"
J"
R-P(exp)
obl
(e-o)^2
2135.5473 2
1
1
2
2147.0823 2
1
1
0
11.5350
11.5349
3.53E-09
2131.6326 2
2
1
3
2150.8571 2
2
1
1
19.2245
19.2244
7.74E-09
2127.6832 2
3
1
4
2154.5967 2
3
1
2
26.9135
26.9131
1.23E-07
2123.6999 2
4
1
5
2158.3008 2
4
1
3
34.6009
34.6009
1.52E-09
2119.6819 2
5
1
6
2161.9694 2
5
1
4
42.2875
42.2873
6.16E-08
2115.6301 2
6
1
7
2165.6022 2
6
1
5
49.9721
49.9720
5.07E-09
2111.5442 2
7
1
8
2169.1991 2
7
1
6
57.6549
57.6549
1.44E-12
2107.4244 2
8
1
9
2172.7599 2
8
1
7
65.3355
65.3356
4.67E-09
2103.2709 2
9
1
10
2176.2846 2
9
1
8
73.0137
73.0137
1.93E-09
2099.0838 2
10
1
11
2179.7730 2
10
1
9
80.6892
80.6891
4.58E-09
2094.8635 2
11
1
12
2183.2249 2
11
1
10
88.3614
88.3614
1.6E-09
2090.6098 2
12
1
13
2186.6402 2
12
1
11
96.0304
96.0304
6.92E-10
2086.3231 2
13
1
14
2190.0188 2
13
1
12
103.6957
103.6956
3.61E-09
2082.0034 2
14
1
15
2193.3603 2
14
1
13
111.3569
111.3569
2.04E-09
2077.6508 2
15
1
16
2196.6648 2
15
1
14
119.0140
119.0140
1.37E-11
2073.2656 2
16
1
17
2199.9322 2
16
1
15
126.6666
126.6665
1.01E-08
2068.8479 2
17
1
18
2203.1620 2
17
1
16
134.3141
134.3142
3.86E-09
2064.3980 2
18
1
19
2206.3547 2
18
1
17
141.9567
141.9567
9.85E-11
2059.9158 2
19
1
20
2209.5094 2
19
1
18
149.5936
149.5938
3.62E-08
2055.4015 2
20
1
21
2212.6266 2
20
1
19
157.2251
157.2252
4.77E-09
2050.8552 2
21
1
22
2215.7057 2
21
1
20
164.8505
164.8505
1.11E-09
2046.2770 2
22
1
23
2218.7466 2
22
1
21
172.4696
172.4696
1.1E-10
2041.6677 2
23
1
24
2221.7494 2
23
1
22
180.0817
180.0820
1.19E-07
2037.0262 2
24
1
25
2224.7141 2
24
1
23
187.6879
187.6876
8.75E-08
2032.3539 2
25
1
26
2227.6397 2
25
1
24
195.2858
195.2860
3.1E-08
2027.6500 2
26
1
27
2230.5270 2
26
1
25
202.8770
202.8769
1.79E-08
2022.9153 2
27
1
28
2233.3754 2
27
1
26
210.4601
210.4600
1.41E-08
∑= 5.46E-07
B0=
1.922527
D0= 6.112E-06
40
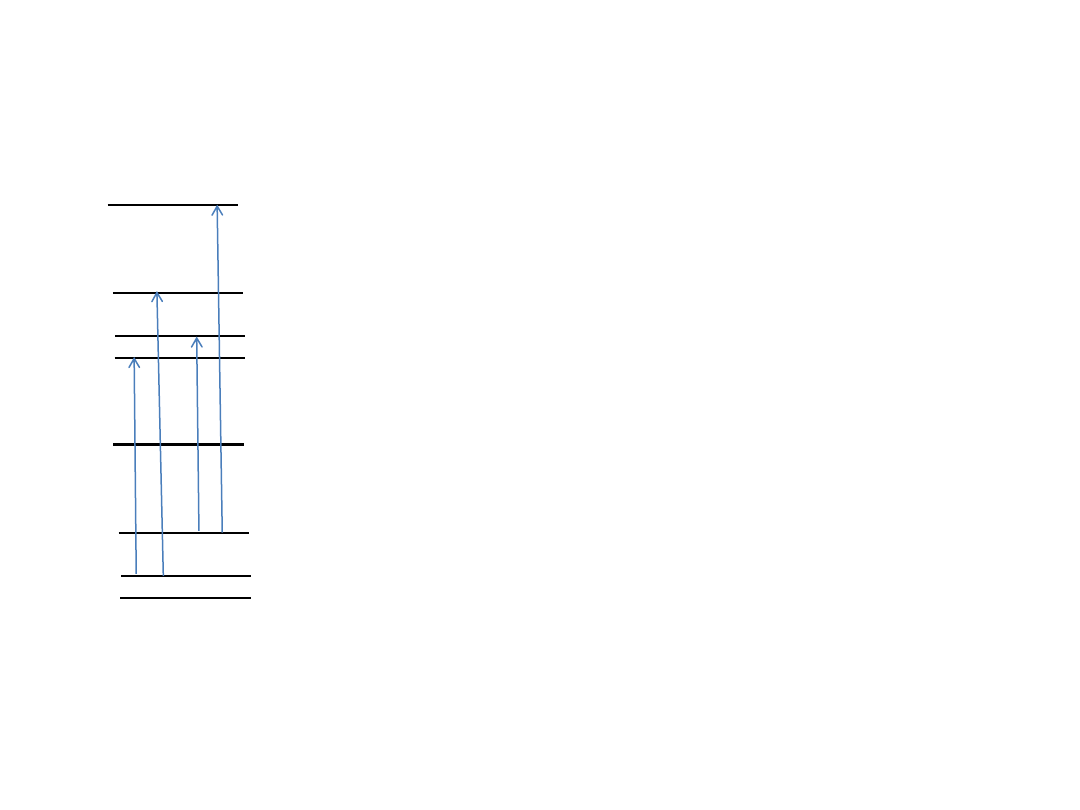
Kombinacje różnicowe w stanie
wzbudzonym
v=0
v=1
J”
J’
3
2
1
0
3
2
1
0
P(1)
R(1)
P(2)
R(2)
Różnice energii E(v,J) w stanie wzbudzonym:
E(1,2)-E(1,0)=R(1)-P(1)
E(1,3)-E(1,1)=R(2)-P(2)
E(1,4)-E(1,2)=R(3)-P(3)
...
E(1,J+1)-E(1,J-1)=B
1
[(J+1)(J+2)-(J-1)J]-
-D
1
[(J+1)
2
(J+2)
2
- (J-1)
2
J
2
]=
=R(J)-P(J)
Obserwując dostatecznie dużo przejść w
gałęziach P i R mających wspólne poziomy we
podstawowym stanie wibracyjnym, można
określić metodą najmniejszych kwadratów stałe
rotacyjne B
1
i D
1
dla stanu wzbudzonego.
USCD – Upper State Combination Differences
41

USCD – przykład
12
C
16
O
P
v'
J'
v"
J"
R
v'
J'
v"
J"
R-P(exp)
obl
(e-o)^2
2135.5473 2
1
1
2
2154.5967 2
3
1
2
19.0494
19.0494 1.27E-10
2131.6326 2
2
1
3
2158.3008 2
4
1
3
26.6682
26.6681 6.85E-09
2127.6832 2
3
1
4
2161.9694 2
5
1
4
34.2862
34.2858 1.45E-07
2123.6999 2
4
1
5
2165.6022 2
6
1
5
41.9023
41.9022
1E-08
2119.6819 2
5
1
6
2169.1991 2
7
1
6
49.5172
49.5170 5.41E-08
2115.6301 2
6
1
7
2172.7599 2
8
1
7
57.1298
57.1298 7.55E-10
2111.5442 2
7
1
8
2176.2846 2
9
1
8
64.7404
64.7405 7.57E-09
2107.4244 2
8
1
9
2179.7730 2
10
1
9
72.3486
72.3487 2.75E-09
2103.2709 2
9
1
10
2183.2249 2
11
1
10
79.9540
79.9540 9.24E-10
2099.0838 2
10
1
11
2186.6402 2
12
1
11
87.5564
87.5563 5.26E-09
2094.8635 2
11
1
12
2190.0188 2
13
1
12
95.1553
95.1553 2.48E-09
2090.6098 2
12
1
13
2193.3603 2
14
1
13
102.7505 102.7505 2.75E-11
2086.3231 2
13
1
14
2196.6648 2
15
1
14
110.3417 110.3418 9.82E-09
2082.0034 2
14
1
15
2199.9322 2
16
1
15
117.9288 117.9288 1.47E-09
2077.6508 2
15
1
16
2203.1620 2
17
1
16
125.5112 125.5113 1.68E-08
2073.2656 2
16
1
17
2206.3547 2
18
1
17
133.0891 133.0890 1.45E-08
2068.8479 2
17
1
18
2209.5094 2
19
1
18
140.6615 140.6615 2.85E-11
2064.3980 2
18
1
19
2212.6266 2
20
1
19
148.2286 148.2286 3.43E-10
2059.9158 2
19
1
20
2215.7057 2
21
1
20
155.7899 155.7899 2.17E-09
2055.4015 2
20
1
21
2218.7466 2
22
1
21
163.3451 163.3453 3.87E-08
2050.8552 2
21
1
22
2221.7494 2
23
1
22
170.8942 170.8943 1.91E-08
2046.2770 2
22
1
23
2224.7141 2
24
1
23
178.4371 178.4368 1.04E-07
2041.6677 2
23
1
24
2227.6397 2
25
1
24
185.9720 185.9723 1.04E-07
2037.0262 2
24
1
25
2230.5270 2
26
1
25
193.5008 193.5007 1.49E-08
2032.3539 2
25
1
26
2233.3754 2
27
1
26
201.0215 201.0216 2.61E-09
2027.6500 2
26
1
27
2236.1849 2
28
1
27
208.5349 208.5346 6.31E-08
2022.9153 2
27
1
28
2238.9549 2
29
1
28
216.0396 216.0397 6.02E-09
∑= 6.33E-07
B1= 1.905024
D1= 6.113E-06
42
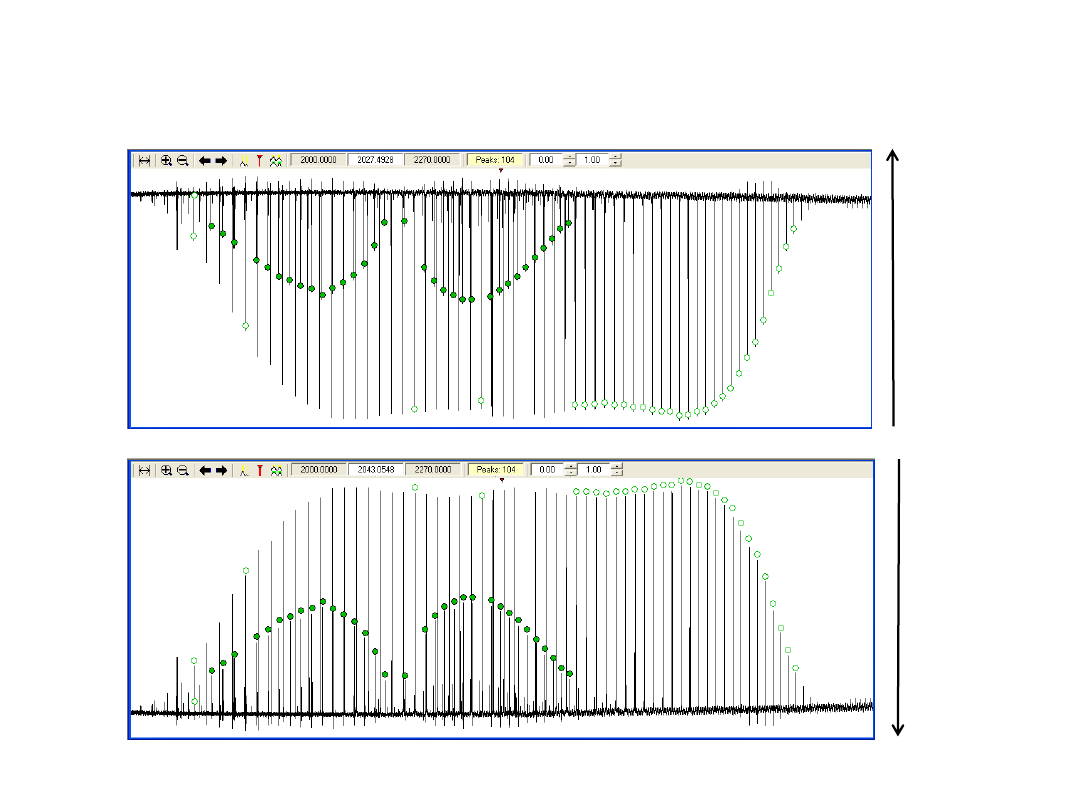
Wyznaczanie środka pasma ν
0
v=0
v=1
J”
J’
3
2
1
0
3
2
1
0
P(2) R(1)
Środek pasma:
ν
0
= P(J) – E(1,J-1) + E(0,J)
ν
0
= R(J) – E(1,J+1) + E(0,J)
ν
0
= P(J) – B
1
(J-1)J+D
1
(J-1)
2
J
2
+B
0
J(J+1) -D
0
J
2
(J+1)
2
ν
0
= R(J) – B
1
(J+1)(J+2)+D
1
(J+1)
2(
J+2)
2
+B
0
J(J+1) -D
0
J
2
(J+1)
2
Obliczenia wartości ν
0
prowadzi się dla każdego przejścia
w pasmach P i R i oblicza z nich wartość średnią.
43

ν
0
- przykład dla
12
C
16
O
P
v'
J'
v"
J"
nu
R
v'
J'
v"
J"
nu
B0= 1.922527
2135.5473 2
1
1
2
2143.2722
2147.0823 2
1
1
0
2143.2723
D0= 6.11E-06
2131.6326 2
2
1
3
2143.2721
2150.8571 2
2
1
1
2143.2722
B1= 1.905024
2127.6832 2
3
1
4
2143.2719
2154.5967 2
3
1
2
2143.2722
D1= 6.11E-06
2123.6999 2
4
1
5
2143.2722
2158.3008 2
4
1
3
2143.2722
2119.6819 2
5
1
6
2143.2720
2161.9694 2
5
1
4
2143.2723
nu= 2143.2722
2115.6301 2
6
1
7
2143.2722
2165.6022 2
6
1
5
2143.2723
2111.5442 2
7
1
8
2143.2722
2169.1991 2
7
1
6
2143.2722
2107.4244 2
8
1
9
2143.2722
2172.7599 2
8
1
7
2143.2722
2103.2709 2
9
1
10 2143.2722
2176.2846 2
9
1
8
2143.2722
2099.0838 2
10
1
11 2143.2721
2179.7730 2
10
1
9
2143.2722
2094.8635 2
11
1
12 2143.2722
2183.2249 2
11
1
10 2143.2722
2090.6098 2
12
1
13 2143.2722
2186.6402 2
12
1
11 2143.2722
2086.3231 2
13
1
14 2143.2722
2190.0188 2
13
1
12 2143.2723
2082.0034 2
14
1
15 2143.2722
2193.3603 2
14
1
13 2143.2721
2077.6508 2
15
1
16 2143.2721
2196.6648 2
15
1
14 2143.2721
2073.2656 2
16
1
17 2143.2721
2199.9322 2
16
1
15 2143.2722
2068.8479 2
17
1
18 2143.2720
2203.1620 2
17
1
16 2143.2720
2064.3980 2
18
1
19 2143.2722
2206.3547 2
18
1
17 2143.2722
2059.9158 2
19
1
20 2143.2722
2209.5094 2
19
1
18 2143.2720
2055.4015 2
20
1
21 2143.2723
2212.6266 2
20
1
19 2143.2722
2050.8552 2
21
1
22 2143.2722
2215.7057 2
21
1
20 2143.2722
2046.2770 2
22
1
23 2143.2720
2218.7466 2
22
1
21 2143.2721
2041.6677 2
23
1
24 2143.2724
2221.7494 2
23
1
22 2143.2721
2037.0262 2
24
1
25 2143.2721
2224.7141 2
24
1
23 2143.2724
2032.3539 2
25
1
26 2143.2723
2227.6397 2
25
1
24 2143.2721
2027.6500 2
26
1
27 2143.2721
2230.5270 2
26
1
25 2143.2722
2022.9153 2
27
1
28 2143.2721
2233.3754 2
27
1
26 2143.2722
2236.1849 2
28
1
27 2143.2723
2238.9549 2
29
1
28 2143.2720
2241.6858 2
30
1
29 2143.2719
44
Widmo
13
C
16
O
T=1
T=0
T=0
T=1
45

Widmo
13
C
16
O
Transmisja
0
I
I
T
I – natężenie światła przechodzącego przez próbkę
I
0
– natężenie światła padającego na próbkę
Absorbancja
I
I
T
A
0
log
1
log
Absorbancja określa, jaka część promieniowania została pochłonięta:
A=0 przeszło całe promieniowanie T=1
A=
całe promieniowanie zostało pochłonięte T=0
Spektrometry rejestrują na ogół widma w skali transmisji.
46

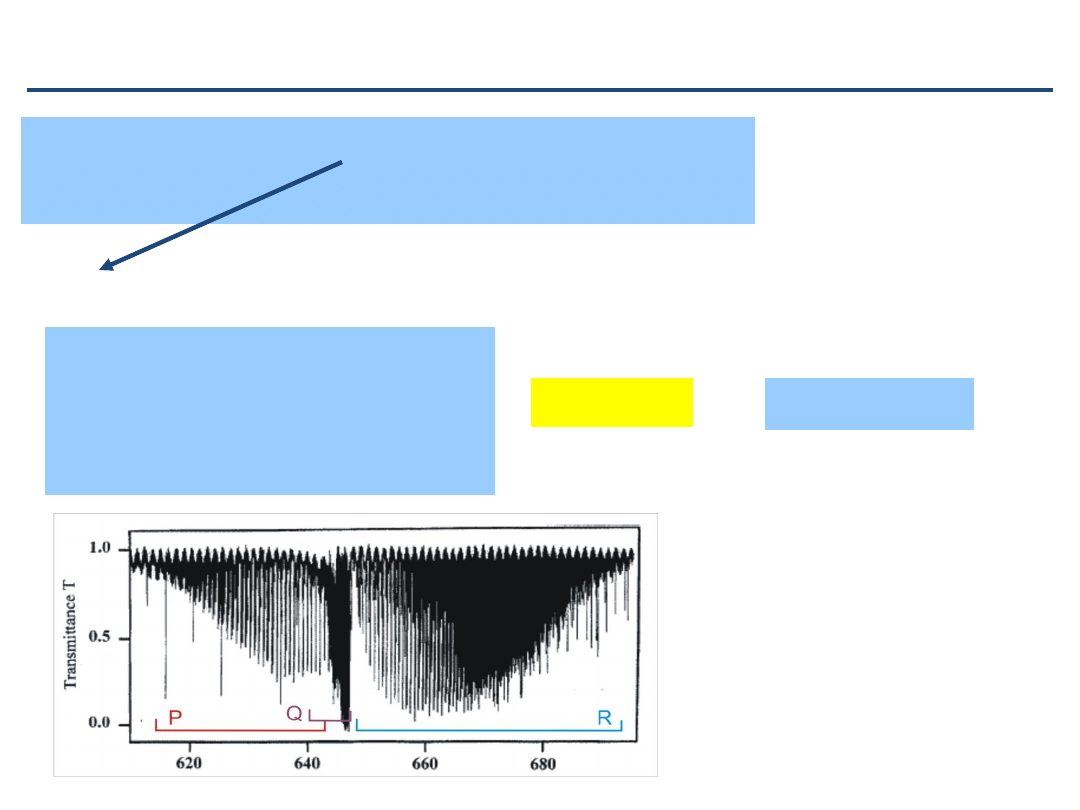
Widmo
13
C
16
O
Analiza gałęzi P i R pasma podstawowego drgania rozciągającego daje
następujące wyniki:
B
0
= 1,837964 cm
-1
B
1
= 1,821605 cm
-1
D
0
= 5,575*10
-6
cm
-1
D
1
= 5,571*10
-6
cm
-1
ν
0
= 2096,0680 cm
-1
Przypomnijmy:
Stąd:
Sprawdźmy:
Jest to dowód, że obserwowane słabsze pasmo jest drganiem rozciągającym
w cząsteczce
13
C
16
O.
I
R
B
2
2
2
2
2
046119
,
1
16
12
16
*
12
16
13
16
*
13
16
12
16
13
16
12
2
0
16
13
2
0
16
12
0
16
13
0
16
13
0
16
12
0
O
C
O
C
O
C
R
O
C
R
O
C
I
O
C
I
O
C
B
O
C
B
046009
,
1
837964
,
1
922527
,
1
16
13
0
16
12
0
O
C
B
O
C
B
47

Intensywność przejść rotacyjnych
kT
E
v
v
rot
wib
rot
e
J
P
I
1
2
2
"
'
,
Przejścia rotacyjne w ramach podstawowego stanu wibracyjnego
kT
E
rot
rot
e
J
I
1
2
2
Przejścia wibracyjno- rotacyjne z podstawowego stanu wibracyjnego
(2J+1) – stopień degeneracji stanu niższego
k = 1.380658E-23 J/deg (stała Boltzmana)
T – temperatura w skali Kelvina
48
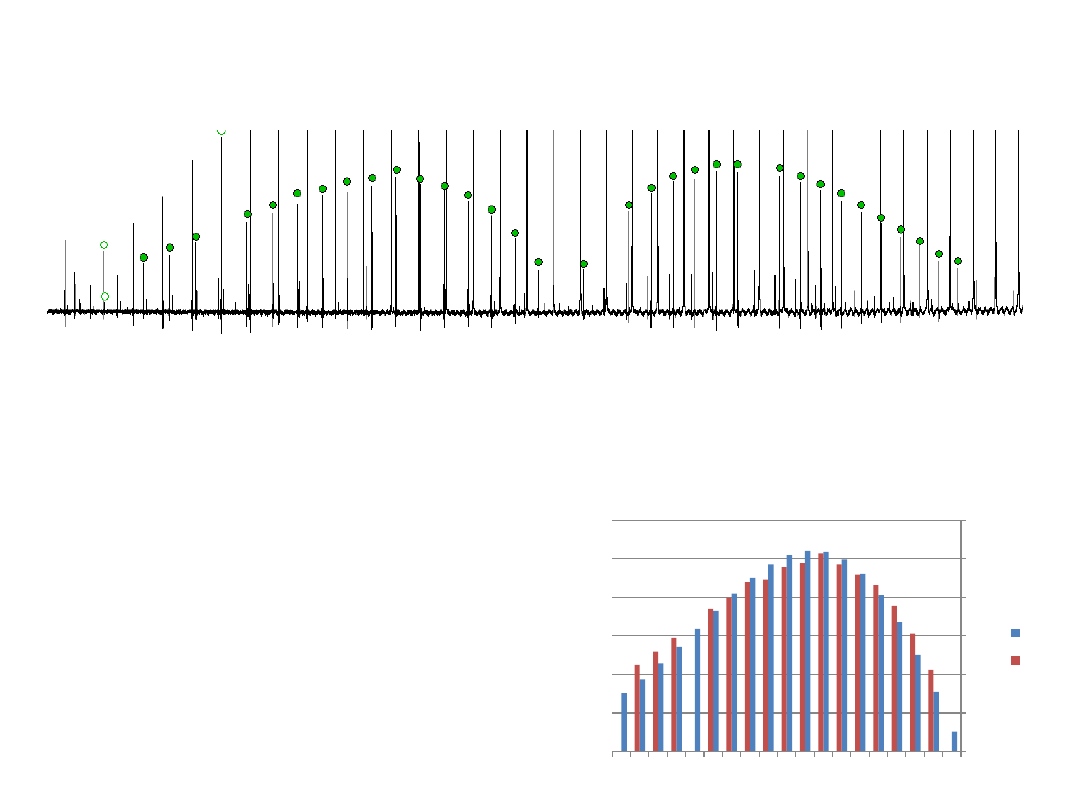
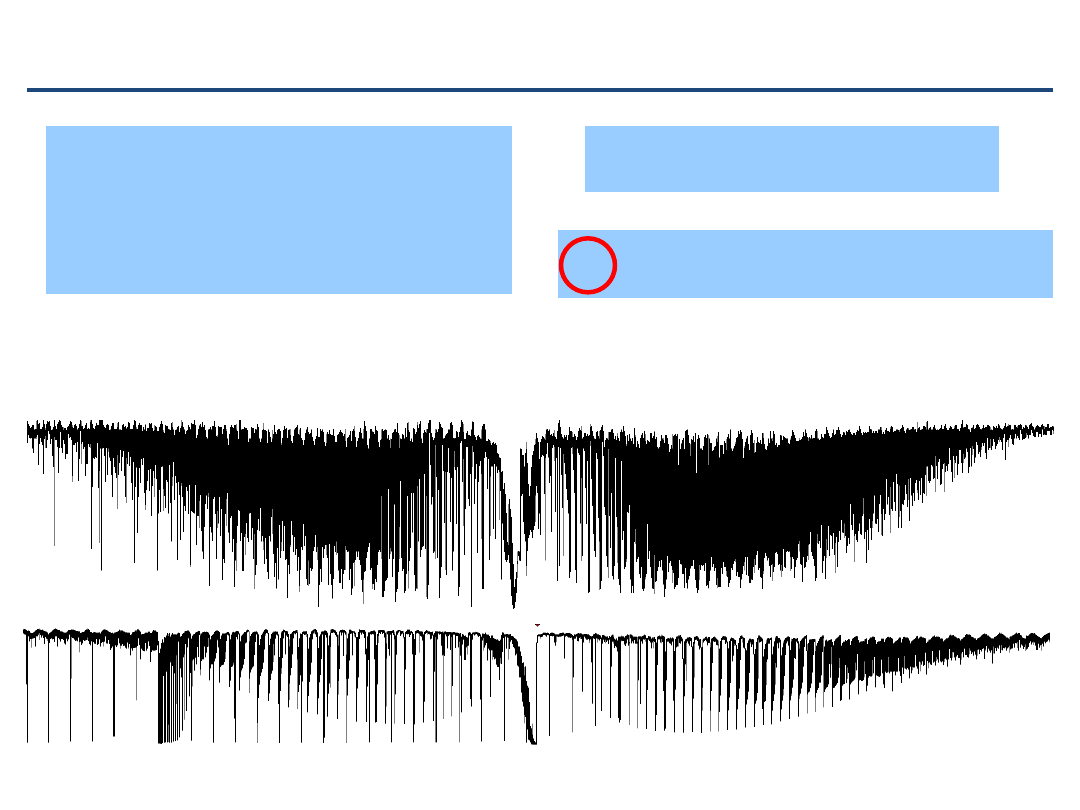
Wyznaczenie temperatury rotacyjnej z widma
13
C
16
O
Gałąź P
J
E(J)
Int_obl
Int_exp_P
(e-o)^2
0
0 0.052421
1
3.675905 0.154936 0.211749 0.003228
2
11.02758 0.250642 0.305692
0.00303
3
22.05476 0.335554 0.378366 0.001833
4
36.75704 0.406458
0.43172 0.000638
5
55.13389 0.461109 0.459239
3.5E-06
6
77.18464 0.498335 0.485285
0.00017
7
102.9085 0.518045 0.514058 1.59E-05
8
132.3045 0.521143 0.489271 0.001016
9
165.3716 0.509364 0.479119 0.000915
10
202.1085 0.485063 0.446468
0.00149
11
242.5141 0.450972 0.439332 0.000135
12
286.5867 0.409966 0.399873 0.000102
13
334.3247 0.364839 0.370603 3.32E-05
14
385.7265 0.318137
15
440.7902 0.272024 0.294809 0.000519
16
499.5136 0.228215 0.259272 0.000965
17
561.8949 0.187949 0.224834
0.00136
Korzystamy z dodatku Solver
k=
6.95E-01 cm-1/K
T=
354.81365 K
kT=
246.60924 cm-1
N=
0.0524209
0
0.1
0.2
0.3
0.4
0.5
0.6
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Obl
Exp
49

Hamiltonian wibracyjno-rotacyjny dla
bąka symetrycznego C
3v
Stany wibracyjne
•
Poziomy wibracyjne o symetrii A
1
v
n
= 0, 1, 2, …
•
Wyższe poziomy wibracyjne
v
t
= 1
±1
, 2
0,
±2
, 3
±1, ±3
•
Poziomy kombinacyjne
v
t
= 1
±1
,
v
t
’
= 1
±1
Stany wibracyjno-rotacyjne
kl
k
J
J
A
k
D
k
J
J
D
J
J
D
k
B
A
J
BJ
E
l
k
J
E
K
J
v
K
JK
J
wib
rot
wib
2
4
2
2
2
2
)
1
(
2
1
1
)
1
(
,
,
50
51
Hamiltonian
rotacyjny zerowego rzędu
Energia rotacyjna
– nie zależy od znaku k
dwukrotna degeneracja z wyjątkiem
k = 0,
można
użyć liczbę kwantową
K = |k|
-
nie zależy od m
(2J+1)
-krotna degeneracja
2
0
1
k
B
A
J
BJ
E
rot
Funkcje rotacyjne bąka symetrycznego są używane jako funkcje bazowe przy
obliczaniu stanów wibracyjno-rotacyjnych (także cząsteczek typu bąka
asymetrycznego)
k
J ,
Funkcje rotacyjne

52
Rotacyjne reguły wyboru
Własności operatora momentu pędu
rotacyjne reguły wyboru = dozwolone
zmiany rotacyjnych liczb kwantowych przy przejściach pomiędzy stanami
wibracyjnymi cząsteczki
1
J
1
,
0
J
Przejścia czysto rotacyjne (bez zmiany stanu
wibracyjnego)
Ogólne przejścia wibracyjno-rotacyjne
Zapis spektroskopowy
J = -1
gałąź P
J = 0
gałąź Q
J = +1
gałąź R
53
Rotacyjne reguły wyboru
Łączna symetria części wibracyjnej i rotacyjnej funkcji falowej decyduje o wartości
całki momentu przejścia
1
,
0
k
Reguła podstawowa – zależy od orientacji wektora momentu dipolowego
0
0
z
k
0
,
1
y
x
k
z
y
x
r
A
r
v
v
z
y
x
r
v
A
r
v
,
,
''
0
'
0
''
0
'
0
,
,
''
0
''
0
'
0
'
0
0
TM
I
Reguły wyboru w cząsteczkach o symetrii C
3v
E
E
A
A
2
1
cosinus kąta między kierunkiem
pola elektromagnetycznego a
momentem dipolowym
składowa cząsteczkowego
momentu dipolowego
54
Rotacyjne reguły wyboru
z
y
x
r
A
r
v
v
z
y
x
r
v
A
r
v
,
,
''
0
'
0
''
0
'
0
,
,
''
0
''
0
'
0
'
0
0
TM
I
czynniki H
önla-Londona
1
2
1
1
2
1
1
1
1
1
1
1
1
2
1
1
1
2
1
1
2
0
1
1
1
1
1
0
2
J
K
J
K
J
J
K
J
K
J
J
K
J
K
J
J
J
J
K
J
K
J
J
J
J
K
J
K
J
J
J
J
K
J
J
J
K
J
K
J
J
K
J
K
J
J
K
J
K
J
J
K
K
K

55
Symetria funkcji wibracyjnych
Symetria stanów wibracyjnych
A
1
/ E
w cząsteczce o symetrii C
3v
odpowiada
symetrii podstawowego stanu wzbudzonego (v=1)
Nadtony lub stany kombinacyjne posiadają symetrię będącą iloczynem prostym
symetrii stanów składowych
)
(
)
(
)
(
6
3
6
3
2
2
1
1
0
N
vib
N
vib
vib
vib
q
q
q
Drganie niezdegenerowane (A
1
) v
s
= n
6
3
2
1
)
(
)
(
)
(
6
3
6
3
2
2
1
1
N
v
N
vib
N
v
vib
v
vib
vib
q
q
q
1
1
1
1
A
A
A
A
n
v
s
Drganie zdegenerowane (E) v
t
= 2
E
A
E
E
1
2
t
v
E
A
A
E
E
E
2
1
3
t
v
v
t
= 3
56
Dipolowe reguły wyboru
z
y
x
o
r
A
o
r
o
v
o
v
z
y
x
o
r
o
v
A
o
r
o
v
,
,
''
'
''
'
,
,
''
''
'
'
0
TM
I
Wibracyjny moment przejścia
Czynniki H
önla-Londona
r
r
e
r
e
Q
Q
Elektryczne przybliżenie harmoniczne
1
vib
vib
A
0
/
A
A
1
1
k
e
k
z
q
q
Pasmo równoległe
Pasmo prostopadłe
E
0
/
E
A
,
vib
vib
1
k
e
k
y
x
q
q
57
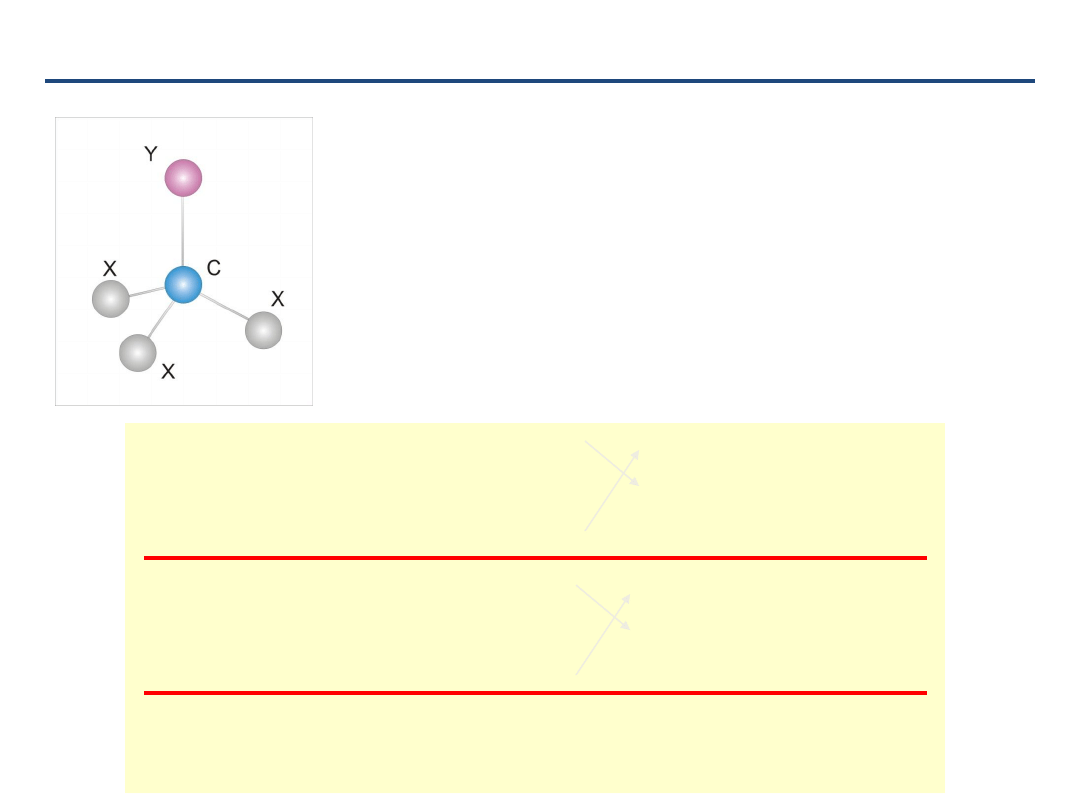
Poziomy wibracyjne cząsteczki CX
3
Y
3N-6
wibracyjnych stopni swobody
= 15
dla N=5
3 niezdegenerowane drgania
A
1
+ 3 zdegenerowane drgania
E
X/Y =
H / halogen
podstawiony metan
5.675
/
0.1893
/155.358
1820
.
5
/GHz)
(cm
10.348
/
0.3452
25.536
/
0.8518
/GHz)
(cm
503
bend
asym
CF
1183
rock
CH
1152
stretch
asym
CF
1468
bend
asym
CH
3025
rock
CH
2999
stretch
asym
CH
E
700
bend
sym
CF
1050
stretch
CF
1141
stretch
sym
CF
1459
bend
sym
CH
3025
stretch
CH
2917
stretch
sym
CH
A
1
-
1
-
3
3
6
3
3
5
3
4
3
3
3
3
2
3
1
1
C
B
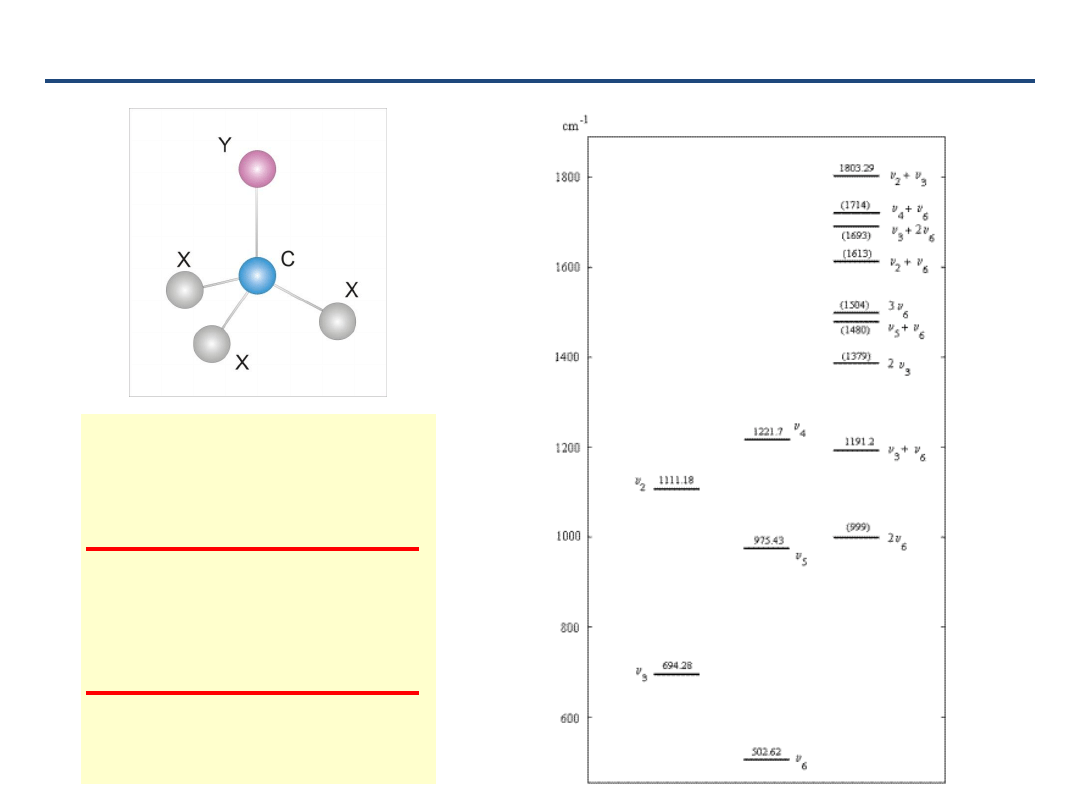
58
Poziomy wibracyjne CDF
3
1888
.
0
/GHz)
(cm
0.3309
/GHz)
(cm
503
a
CF
975
astr
CF
1222
rock
CD
E
694
sb
CF
1111
sstr
CF
2261
str
CD
A
1
-
1
-
3
6
3
5
4
3
3
3
2
1
1
C
B

59
Przejścia rotacyjne
Powyższe wyrażenie może być użyte dla opisu
czysto rotacyjnego
przejścia
(w ramach jednego stanu wibracyjnego)
4
2
2
2
2
1
1
)
1
(
,
k
D
k
J
J
D
J
J
D
k
B
A
J
BJ
k
J
E
K
JK
J
rot
k
J
E
k
J
E
k
J
rot
rot
rot
,
,
1
,
2
3
1
2
1
4
)
1
(
2
,
k
J
D
J
D
J
B
k
J
JK
J
rot
Reguły wyboru
J = +1
k = 0
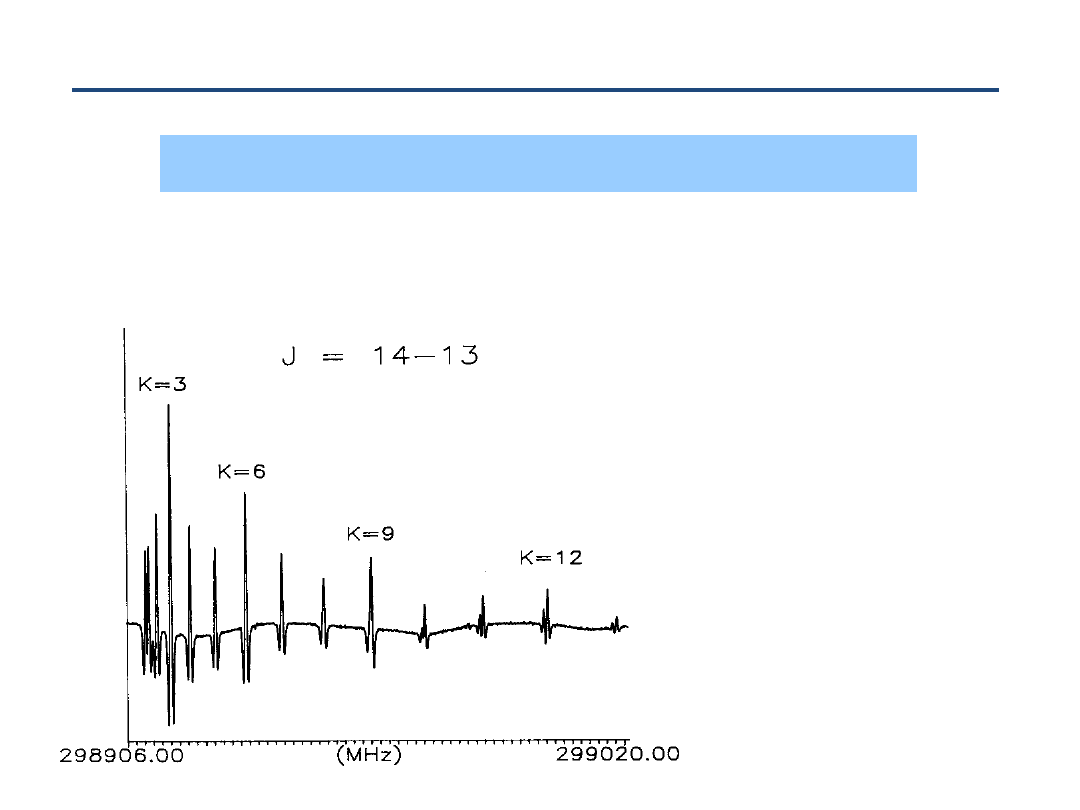
60
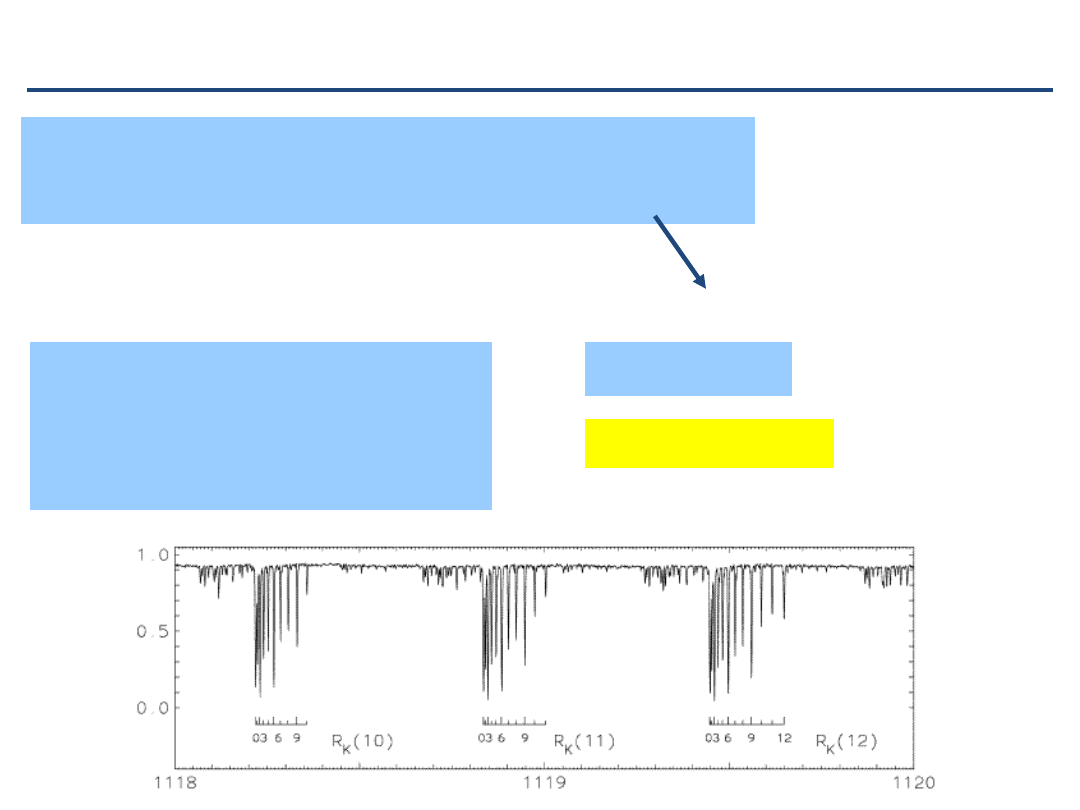
Widmo rotacyjne NF
3
Struktura rotacyjna podstawowego stanu wibracyjnego NF
3
2
3
1
2
1
4
)
1
(
2
,
k
J
D
J
D
J
B
k
J
JK
J
rot
Uwaga:
stała
D
JK
określa odstępy
pomiędzy liniami dla
różnych K
D
JK
= -22.77 kHz
(Cazzoli et al.)
!
C
3v
wagi spinowe
(linie z K podzielnym
przez 3 intensywniejsze
od pozostałych)
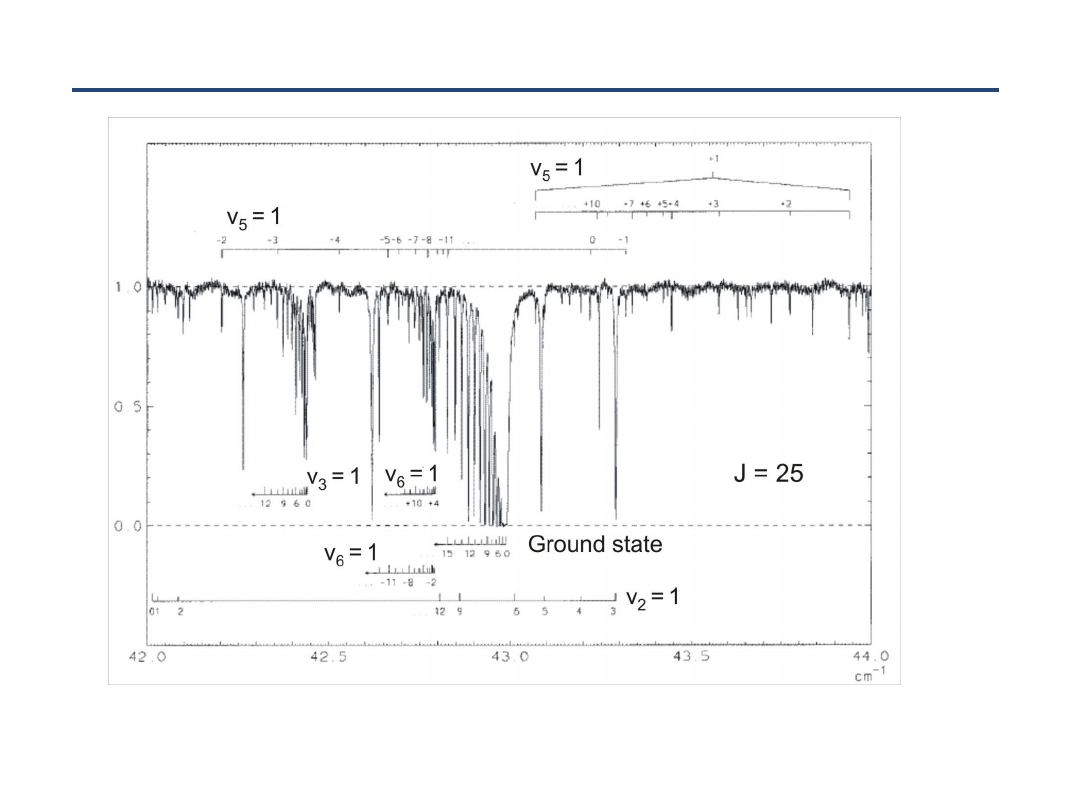
61
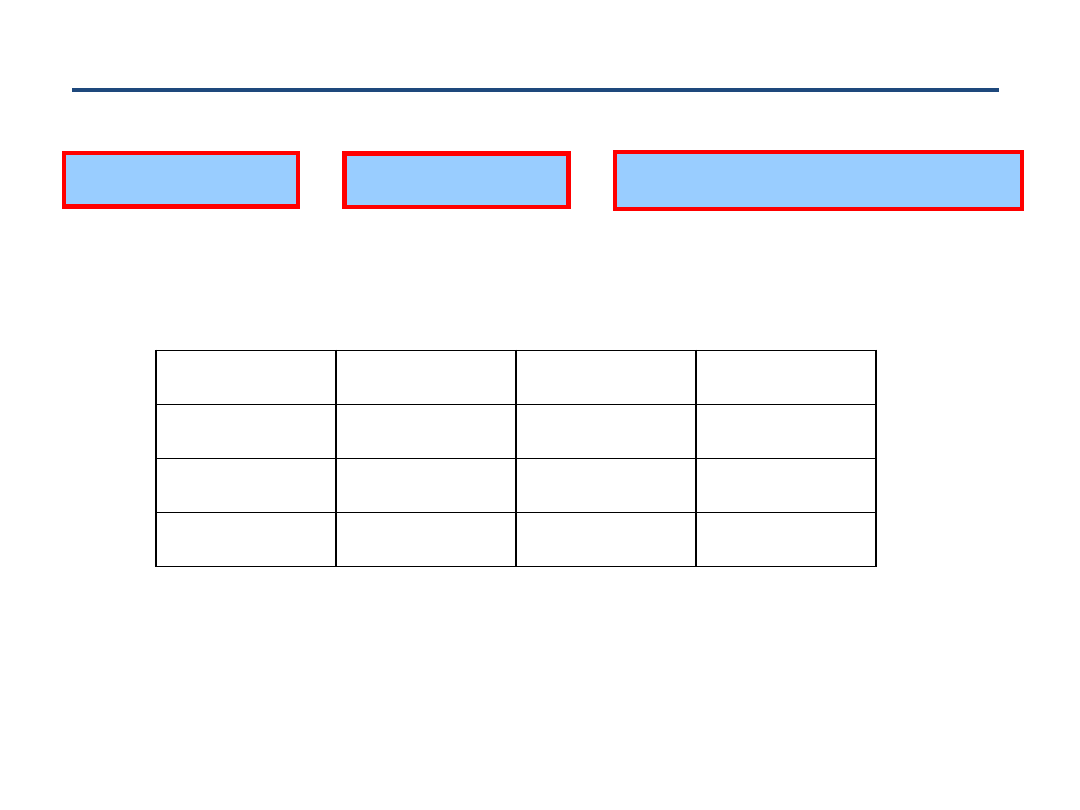
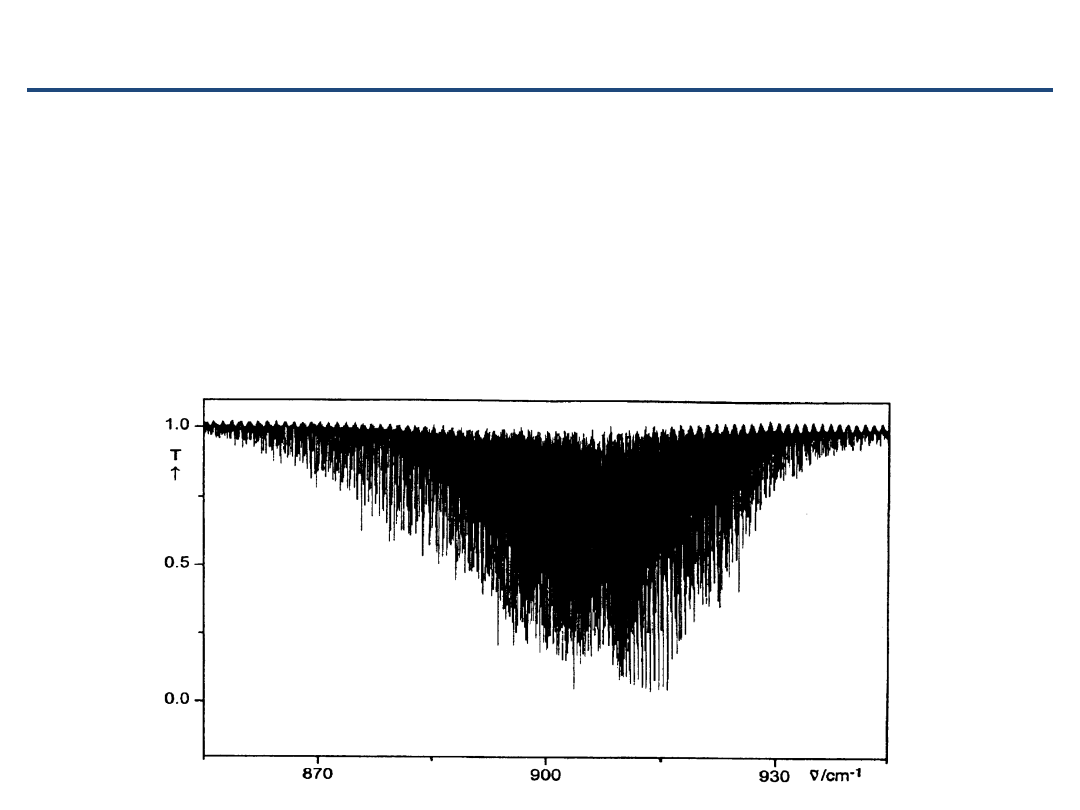
Widmo rotacyjne w dalekiej podczerwieni FIR
Uwaga: liczne
‘satelity wibracyjne’ = widma rotacyjne we wzbudzonych stanach
wibracyjnych (fragment widma CH
3
F with
D
JK
~ 390 kHz
(Papou
šek et al.))
Wibracyjno-
rotacyjne reguły wyboru C
3v
1
,
0
J
Zapis spektroskopowy
1
,
0
k
...
,
6
,
3
,
0
l
k
k= -1
k= 0
k= +1
J = -1
P
P
K
(J)
Q
P
K
(J)
R
P
K
(J)
J = 0
P
Q
K
(J)
Q
Q
K
(J)
R
Q
K
(J)
J = +1
P
R
K
(J)
Q
R
K
(J)
R
R
K
(J)
62

63
Równoległe pasmo wibracyjno-rotacyjne
Rozpatrzmy przejście
v
n
= 1
0
(drganie o symetrii A
1
)
pasmo
równoległe
z
K = 0
oraz
J = 0,
1
k
J
v
E
k
J
v
E
k
J
v
k
J
v
rot
wib
rot
wib
rot
wib
,
,
,
,
,
,
,
,
~
4
2
2
2
2
0
1
1
)
1
(
k
D
k
J
J
D
J
J
D
k
B
A
J
J
B
E
E
v
K
v
JK
v
J
v
v
wib
rot
wib
4
0
2
0
2
2
0
2
0
0
4
2
2
2
2
0
1
1
)
1
(
1
1
)
1
(
,
,
~
k
D
k
J
J
D
J
J
D
k
B
A
J
J
B
k
D
k
J
J
D
J
J
D
k
B
A
J
J
B
E
k
J
v
K
JK
J
v
K
v
JK
v
J
v
v
wib
rot
wib
64
Szczegóły pasma równoległego
Gałęzie P,Q,R (
J = -1, 0, +1)
2
0
0
)
1
(
)
1
(
,
,
~
k
B
A
B
A
J
J
B
J
J
B
E
k
J
v
v
v
vib
rot
vib
1
)
1
(
2
:
1
:
1
2
:
J
BJ
J
B
R
J
BJ
Q
J
BJ
BJ
P
B
B
Uwaga :
B
3
< B
0
powoduje,
że gałąź Q zanika w kierunku
niższych liczb falowych
(
przykład: pasmo
3
czasteczki CDF
3
)
B
v
v
B
B
0
65
Szczegóły pasma równoległego
gałęzie
P,Q,R
(
J = -1, 0, +1)
2
0
0
)
1
(
)
1
(
,
,
~
k
B
A
B
A
J
J
B
J
J
B
E
k
J
v
v
v
vib
rot
vib
1
)
1
(
'
2
:
1
:
1
'
2
:
J
BJ
J
B
R
J
BJ
Q
J
BJ
J
B
P
struktura
k
gałęzi
P,Q,R
2
k
B
A
B
B
A
)
(
66
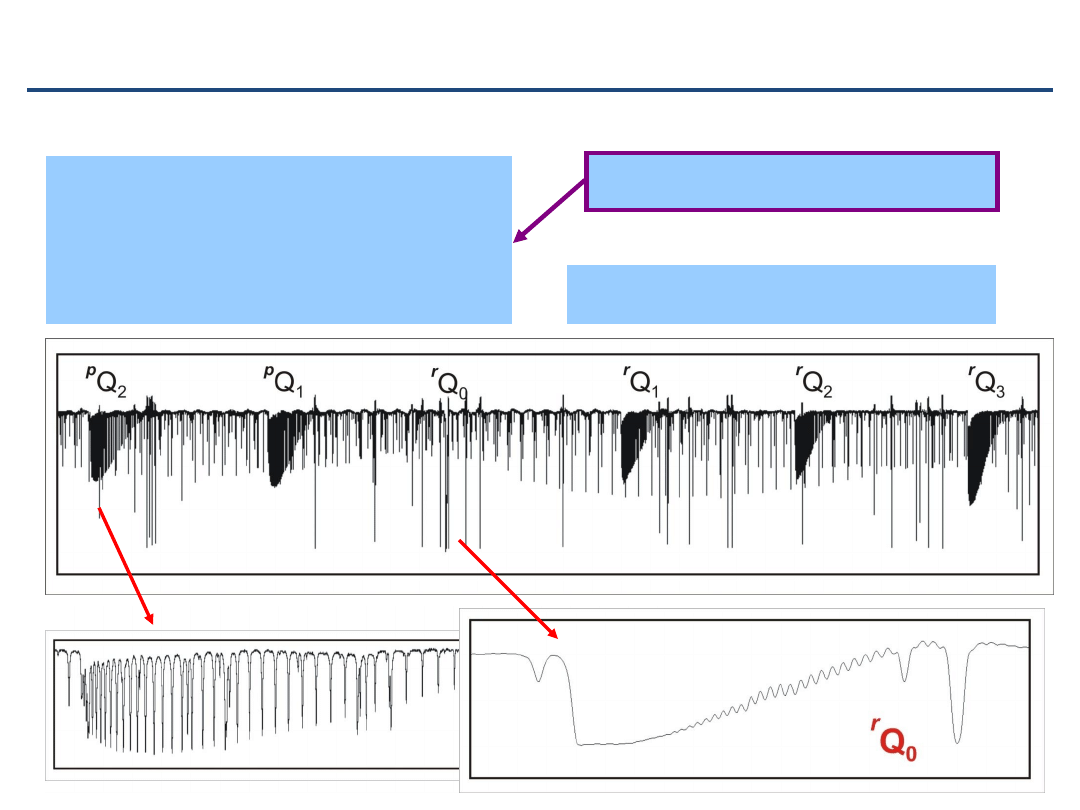
Ogólny kształt pasma prostopadłego
•
gałęzie
Q
nie są stłoczone w jednym zakresie, ale rozciągają
się w całym obszarze gałęzi
P
i
R
•
Różny rozkład intensywności pomiędzy gałęziami (czynniki
H
önla-Londona)
NF
3
3
band
67
Szczegóły pasma prostopadłego
1
)
1
(
'
2
:
1
:
1
'
2
:
J
BJ
J
B
R
J
BJ
Q
J
BJ
J
B
P
2
0
K
B
A
B
A
t
K
A
B
A
t
2
68
Szczegóły pasma prostopadłego
1
)
1
(
'
2
:
1
:
1
'
2
:
J
BJ
J
B
R
J
BJ
Q
J
BJ
J
B
P
K
A
B
A
t
2
2
0
K
B
A
B
A
t
Przypadkowa zgodność stałych – pasmo prostopadłe
6
wygląda jak pasmo
równoległe
3
CDF
3
pasmo
6
CDF
3
pasmo
3

Reguły wyboru
Intensywność przejścia proporcjonalna do kwadratu całki momentu przejścia:
2
"
'
Z
I
Z – kierunek drgań wektora elektrycznego fali elektromagnetycznej
Symbol
││
oznacza całkowanie po całej przestrzeni zmiennych
zZ
z
yZ
y
xZ
x
Z
xZ
– cosinus kąta między osią Z a osią x układu związanego z cząsteczką
μ
α
– składowa momentu dipolowego α= x,y,z w układzie cząsteczkowym
z
y
x
Q
Q
k
k
k
,
,
...
0
0
Składowe momentu dipolowego rozwinięte po współrzędnych normalnych Q
k
69
Reguły wyboru 2
"
'
,
,
"
'
0
"
'
0
"
'
"
'
"
"
"
'
'
'
"
'
r
Z
r
z
y
x
k
w
k
w
e
k
e
w
w
e
e
r
w
e
Z
r
w
e
Z
Q
Q
Jakie przejścia są dozwolone ze względu na symetrię?
Badamy, czy wyrażenie podcałkowe jest pełnosymetryczne, tzn. czy Γ ϵ A’
'
"
'
"
'
A
Z
Z
W przybliżeniu Borna-Oppenheimera funkcję stanu można przedstawic jako
iloczyn funkcji elektronowej, wibracyjnej i rotacyjnej, a moment dipolowy
rozwinąć w szereg współrzędnych normalnych:
70
Reguły wyboru 3
'
"
'
0
"
'
0
0
A
e
e
e
e
Dozwolone przejście czysto elektronowe
'
"
'
'
"
'
"
'
0
"
'
0
A
Q
A
Q
Q
Q
k
w
w
k
e
e
w
k
w
e
k
e
Dozwolone przejście czysto elektronowe -
wibracyjne
'
"
'
0
"
'
A
Z
r
r
r
Z
r
Dozwolone przejście rotacyjne
71
Jak określić symetrię?
Operacja
Grupa punktowa
Grupa PI
Tożsamość
Obrót o 180°
Odbicie w płaszczyźnie yz
Odbicie w płaszczyźnie xz
E
C
2
σ
yz
σ
xz
E
(12)
E*
(12)*
Porównanie grupy punktowej i grupy permutacji-inwersji (PI) na przykładzie
cząsteczki wody
y
z
x
3
2
1
72
Grupa symetrii C
2v
Tabela charakterów dla grupy C
2v
PI
E
(12)
E*
(12)*
Przykład
C
2v
E
C
2
σ
yz
σ
xz
funkcji
A
1
1
1
1
1
z
A
2
1
1
-1
-1
R
z
B
1
1
-1
-1
1
x, R
y
B
2
1
-1
1
-1
y, R
x
reprezentacje nieprzywiedlne
73
Symetria funkcji całkowitej
spin
r
w
e
total
Ψ
spin
to funkcja spinowa jąder atomów zamieniających sie miejscami w
wyniku działania operacji symetrii.
Przykład 1: H
2
O
jądra H są fermionami, zatem: (12) Ψ
total
= -Ψ
total
Ψ
total
należy do reprezentacji B
1
lub B
2
, bo znak funkcji Ψ
total
dla operacji *
nie jest określony
Bazowe funkcje spinowe
E
(12)
E*
(12)*
α(1)α(2)
α(1)α(2)
α(2)α(1)
α(1)α(2)
α(2)α(1)
α(1)β(2)
α(1)β(2)
α(2)β(1)
α(1)β(2)
α(2)β(1)
α(2)β(1)
α(2)β(1)
α(1)β(2)
α(2)β(1)
α(1)β(2)
β(1)β(2)
β(1)β(2)
β(2)β(1)
β(1)β(2)
β(2)β(1)
Г
spin
(symetria funkcji spinowej)
4
2
4
2
74
Symetria funkcji całkowitej
Reprezentacja przywiedlna (redukowalna) funkcji spinowej składa się z
następujących reprezentacji nieprzywiedlnych:
Г
spin
= 3 A
1
+ B
2
E
(12)
E*
(12)*
A
1
1
1
1
1
A
1
1
1
1
1
A
1
1
1
1
1
B
2
1
-1
1
-1
suma
4
2
4
2
Г
spin
4
2
4
2
75
Jądrowe wagi statystyczne
spin
r
w
e
total
Całkowita funkcja falowa dla H
2
O musi należeć do reprezentacji B
1
lub B
2
.
Jeżeli funkcja Ψ
e
Ψ
w
Ψ
r
ma określona symetrię ( należy do określonej reprezentacji
nieprzywiedlnej), to przez jaką funkcję spinową musi być pomnożona, aby
całkowita funkcja zawierała reprezentacje B
1
lub B
2
?
Г
ewr
Г
spin
B
1
lub B
2
Г
ewr
Г
spin
Г
total
waga
A
1
B
2
B
2
1
A
2
B
2
B
1
1
B
1
3A
1
B
1
3
B
2
3A
1
B
2
3
Przejścia ze stanów o symetrii B
1
lub B
2
będą 3 razy bardziej
intensywne niż przejścia ze stanów o symetrii A
1
lub A
2
.
76
Wagi statystyczne w
12
C
16
O
2
Spin dla jądra
16
O wynosi 0 – to jest bozon, σ(
16
O)=0
(12) Ψ
total
= +Ψ
total
Ψ
total
należy do reprezentacji A
1
lub A
2
w grupie C
2v
.
Bazowe funkcje spinowe
E
(12)
E*
(12)*
σ(1) σ(2)
σ(1) σ(2) σ(2) σ(1)
σ(1) σ(2)
σ(2) σ(1)
σ(1) σ(2)
σ(1) σ(2) σ(2) σ(1)
σ(1) σ(2)
σ(2) σ(1)
σ(2) σ(1)
σ(1) σ(2) σ(2) σ(1)
σ(1) σ(2)
σ(2) σ(1)
σ(1) σ(2)
σ(1) σ(2) σ(2) σ(1)
σ(1) σ(2)
σ(2) σ(1)
Г
spin
(symetria funkcji spinowej)
4
4
4
4
Rozkład Г
spin
na reprezentacje nieprzywiedlne:
Г
spin
= 4 A
1
77

Wagi statystyczne w
12
C
16
O
2
Pamiętajmy, że Ψ
total
należy do reprezentacji A
1
lub A
2
w grupie C
2v
.
Г
ewr
Г
spin
Г
total
waga
A
1
4A
1
A
1
4
A
2
4A
1
A
2
4
B
1
brak
brak
0
B
2
brak
brak
0
Przejścia ze stanów o symetrii A
1
lub A
2
posiadają tę samą intensywność,
a przejścia ze stanów o symetrii B
1
lub B
2
są wzbronione.
Dla cząsteczki liniowej funkcje rotacyjne dla J parzystych posiadają
symetrię Σ
g
+
,
a dla J nieparzystych Σ
g
-
,
odpowiadające symetrii A
1
i B
1
w grupie C
2v
.
Jeżeli badamy przejścia rotacyjne ze stanu elektronowego o symetrii A
1
,
stanu wibracyjnego o symetrii A
1
, to obserwować będziemy tylko
przejścia rotacyjne ze stanów o J parzystym.
78
Tabela charakterów dla grupy D
∞h
E
2C
∞
...
∞σ
v
i
2S
∞
...
∞C'
2
funkcje
liniowe,
obroty
funkcje
kwadratowe
Skorelowane
reprezentacje
grupy C
2v
A
1g
=Σ
+
g
1
1
...
1
1
1
...
1
x
2
+y
2
, z
2
A
1
A
2g
=Σ
-
g
1
1
...
-1
1
1
...
-1
R
z
B
1
E
1g
=Π
g
2 2cos(φ)
...
0
2
-2cos(φ)
...
0
(R
x
, R
y
)
(xz, yz)
E
2g
=Δ
g
2 2cos(2φ) ...
0
2
2cos(2φ)
...
0
(x
2
-y
2
, xy)
E
3g
=Φ
g
2 2cos(3φ) ...
0
2
-2cos(3φ)
...
0
...
...
...
...
...
...
...
...
...
A
1u
=Σ
+
u
1
1
...
1
-1
-1
...
-1
z
B
2
A
2u
=Σ
-
u
1
1
...
-1
-1
-1
...
1
A
2
E
1u
=Π
u
2 2cos(φ)
...
0
-2
2cos(φ)
...
0
(x, y)
E
2u
=Δ
u
2 2cos(2φ) ...
0
-2
-2cos(2φ)
...
0
E
3u
=Φ
u
2 2cos(3φ) ...
0
-2
2cos(3φ)
...
0
...
...
...
...
...
...
...
...
...
79
Wyszukiwarka
Podobne podstrony:
2 chemia teoretyczna
chemia teoretycznaB sprawko1
Chemia teoretyczna
Widmo liniowe lub dyskretne, Chemia, Teoretyczna
Chemia teoretyczna wykład
2 chemia teoretyczna
mechanika-test-odp, Chemia budowlana, Geometria wykreślna, Mechanika teoretyczna
xdzfgxh, Chemia budowlana, Geometria wykreślna, Mechanika teoretyczna
wykladChK-03, Chemia UŁ, teoretyczna wykład
wykladChK-10, Chemia UŁ, teoretyczna wykład
ZAGADNIENIA TEORETYCZNE ĆW.7-8, Studia TOŚ, chemia analityczna-labor. semestr III
wykladChK-11, Chemia UŁ, teoretyczna wykład
cw5-adsorpcja, adsorp-teoret, CHEMIA FIZYCZNA
Wstęp teoretyczny, chemia w nauce i gospodarce Uł, semestr V, sprawozdania chemia fizyczna i anality
ZAGADNIENIA TEORETYCZNE ĆW.1-3, Studia TOŚ, chemia analityczna-labor. semestr III
Wstęp teoretyczny 3, chemia fizyczna
wykladChK-15, Chemia UŁ, teoretyczna wykład
Zagadnienia teoretyczne 41, POLITECHNIKA ŁÓDZKA, Technologia Żywności i Żywienia Człowieka, semestr
więcej podobnych podstron