
Chemia teoretyczna
2011/2012

Zagadnienia
I
. Podstawy eksperymentalne mechaniki kwantowej
1.
Rozkład widmowy ciała doskonale czarnego
2.
Zjawisko fotoelektryczne
3.
Efekt Comptona
4.
Widmo atomu wodoru
II. Podstawowe
pojęcia mechaniki kwantowej
1.
Hipoteza de
Broglie’a
2.
Dualizm falowo-korpuskularny
3.
Zasada nieoznaczoności
4.
Funkcja falowa
5.
Normalizacja funkcji falowej
6.
Gęstość prawdopodobieństwa
7.
Operatory położenia i pędu
8.
Operator energii całkowitej
9.
Średnia kwantowo-mechaniczna
10.
Równanie Schrödingera

Zagadnienia
III. Proste modele chemii kwantowej
1.
Ruch cząstki swobodnej
2.
Cząstka w pudle jednowymiarowym
a) kształt potencjału
b) zszywanie funkcji falowej na granicy obszarów
c) normalizacja funkcji falowej
d) energia cząstki w pudle
e) prawdopodobieństwo zaobserwowania cząstki w różnych częściach pudła potencjału
f) obliczenie średniej kwantowo-mechanicznej położenia i pędu
g) zasada wariacyjna
3.
Cząstka w pudle dwuwymiarowym
a) Separacja
dwuwymiarowego równania Schrödingera
b) Iloczynowa
postać funkcji falowej
c) Energia
cząstki
d) Degeneracja
stanów
4.
Przejście przez barierę potencjału

Zagadnienia
IV. Atom wodoru
1.
Operator energii potencjalnej w atomie wodoru
2.
Współrzędne środka masy
3.
Separacja ruchu translacyjnego od ruchów względnych
4.
Układ współrzędnych sferycznych
5.
Element objętości dV dla całki we współrzędnych sferycznych
6.
Schemat rozwiązania równania
7.
Zbiór liczb kwantowych dla atomu wodoru
8.
Wykres gęstości radialnej dla stanów 1s i 2s
V. Atom wieloelektronowy
1.
Doświadczenie Sterna-Gerlacha
2.
Zasada nierozróżnialności jednakowych cząstek
3.
Podstawowe własności bozonów i fermionów
4.
Zakaz Pauliego
5.
Hamiltonian dla atomu wieloelektronowego
w przybliżeniu nieskończenie ciężkiego jądra
6.
Atom helu
a)
Funkcja falowa w przybliżeniu jednoelektronowym
b)
Spinorbitale atomowe
c)
Stany singletowe i tripletowe atomu helu
7.
Atomy
więcej niż dwuelektronowe
a)
Wykładnikowa postać funkcji falowej
b)
Poziomy energetyczne atomu w atomie wieloelektronowym
c)
Wypadkowy spin układu elektronów
d)
Reguła Hunda dla degeneracji orbitalnej

Zagadnienia
VI. Cząsteczka H
2
+
1.
Definicja cząsteczki
2.
Hamiltonian cząsteczki
3.
Orbitale molekularne a orbitale atomowe
4.
Wariacyjne
rozwiązanie równania Schrödingera dla cząsteczki
5.
Całka nakrywania
6.
Całka rezonansowa
7.
Orbitale
wiążące i antywiążące
8.
Energia
całkowita cząsteczki H
2
+
a)
odległość równowagowa R
e
b)
energia
wiązania D
e
9.
Zastosowanie metody wariacyjnej do cząsteczki H
2
+
10. Atom zjednoczony

Zagadnienia
VII. Cząsteczki dwuatomowe
1.
Cząsteczka wodoru
a)
Hamiltonian dla cząsteczki wodoru
b)
Diagram korelacyjny dla cząsteczki wodoru (atom zjednoczony a atomy rozdzielone)
c)
Całki kulombowskie i wymienne
2.
Wiązania σ i π w cząsteczce i ich symetria
3.
Odpychanie walencyjne
4.
Cząsteczki dwuatomowe heterojądrowe
5.
Orbitale zhybrydyzowane
6.
Efektywność mieszania orbitali atomowych

Zagadnienia
VIII. Obliczenia ab initio
1.
Metoda Hartree-Focka
2.
Wyznacznikowe funkcje falowe Slatera
3.
Orbitale Gaussowskie a Slaterowskie
4.
Metoda liniowych kombinacji orbitali atomowych (LCAO)
5.
Centrowanie orbitali atomowych
6.
Metoda Hartree-Focka
dla układów zamkniętopowłokowych
7.
Metoda pola samouzgodnionego (SCF LCAO MO)
8.
Orbitale HOMO i LUMO
9.
Bazy orbitali atomowych
10.
Korelacja ruchów elektronów
11. Energia korelacji
12.
Metoda oddziaływania konfiguracji (CI)
13.
Metoda sprzężonych klasterów (CC)
14.
Rachunek zaburzeń Møllera-Plesseta (MP2)

Zagadnienia
IX. Metoda
Hückla
1.
Założenia metody Hückla
2.
Separacja
π – σ
3.
Metoda LCAO MO w metodzie
Hückla
4.
Całki kulombowskie i wymienne w metodzie Hückla
5.
Budowa wyznacznika wiekowego
6.
Wartości własne energii i odpowiadające im funkcje własne
7.
Wzbudzenie HOMO
– LEMO
8.
Gęstość elektronowa i rząd wiązania
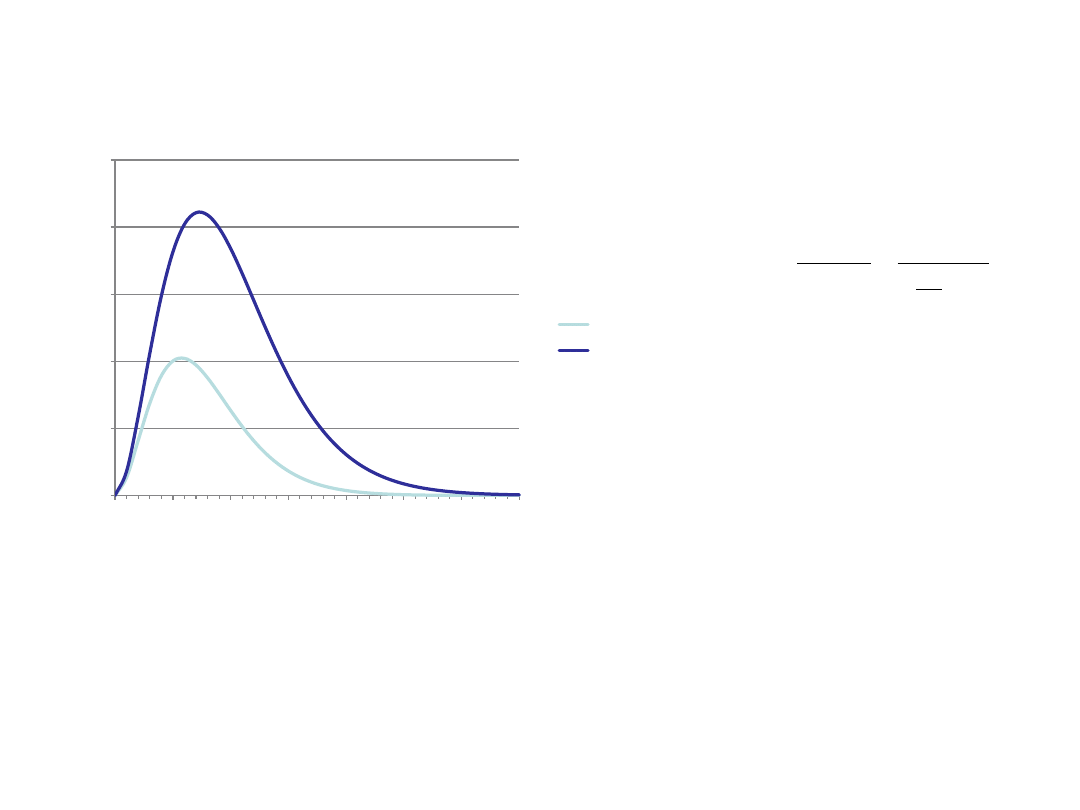
Widmo ciała doskonale czarnego
0
100
200
300
400
500
0
500
1000
1500
2000
2500
3000
3500
u(20)
u(100)
1
8
,
3
2
kT
h
e
h
c
T
u
Gęstość energii
promieniowania:
Hipoteza Plancka (1900):
ΔE=hν (kwant promieniowania)
h = 6,62∙10
-34
J s c = 2,99792458∙10
8
m s
-1
k = 1,380662∙10
-23
J K
-1
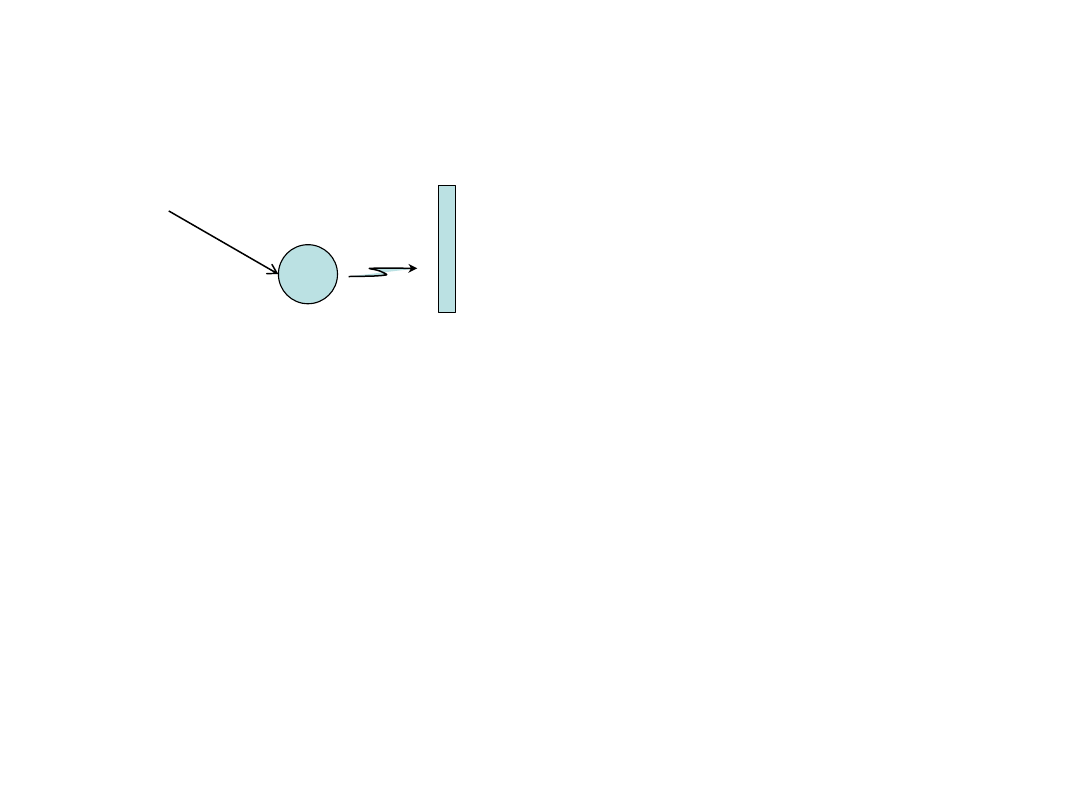
Efekt fotoelektryczny
(-) (+)
iskra
h
ν
Prawa Lenarda (1899 rok)
1)
Liczba wyzwalanych elektronów
proporcjonalna do natężenia
promieniowania
2)
Maksymalna prędkość elektronów
zależy od częstości promieniowania,
nie od jego natężenia
Wzór Einsteina (1905 rok):
hν = ½ m
e
v
2
+ W
Zn
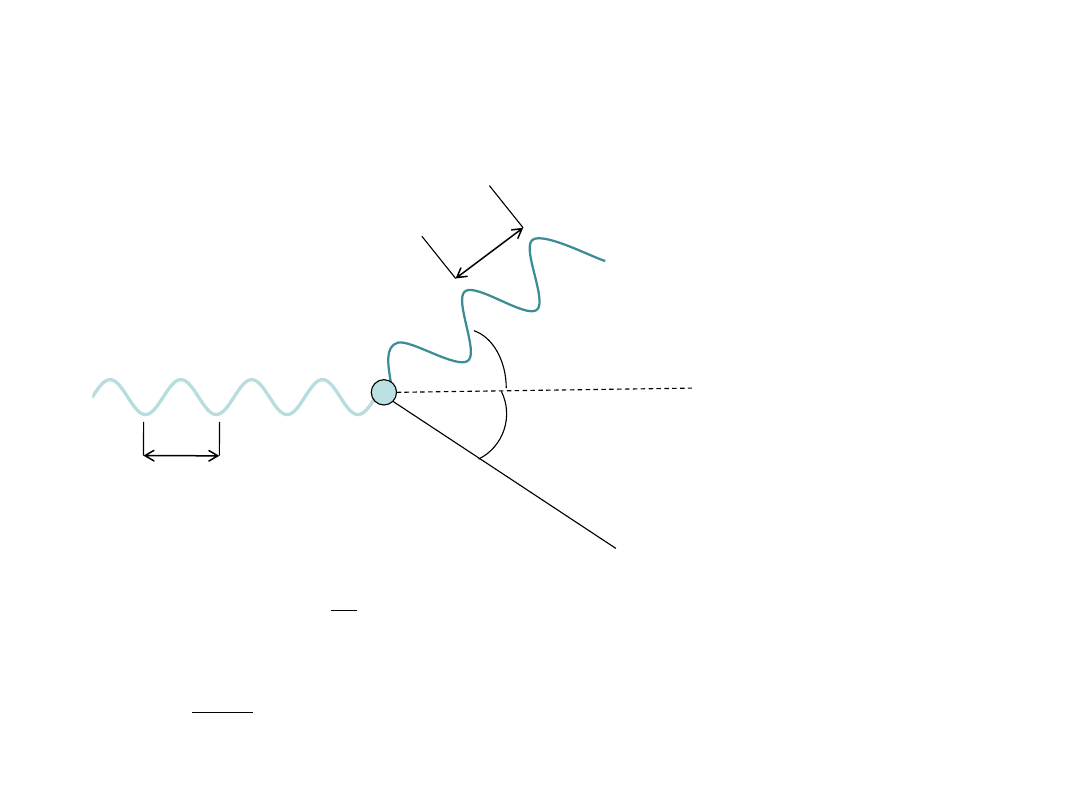
Efekt Comptona
θ
φ
λ
λ’
m
e
v
m
c
m
h
e
11
2
10
0242
,
0
2
sin
2
λ’ > λ
p
e
= m
e
v
p
f
= h/
λ
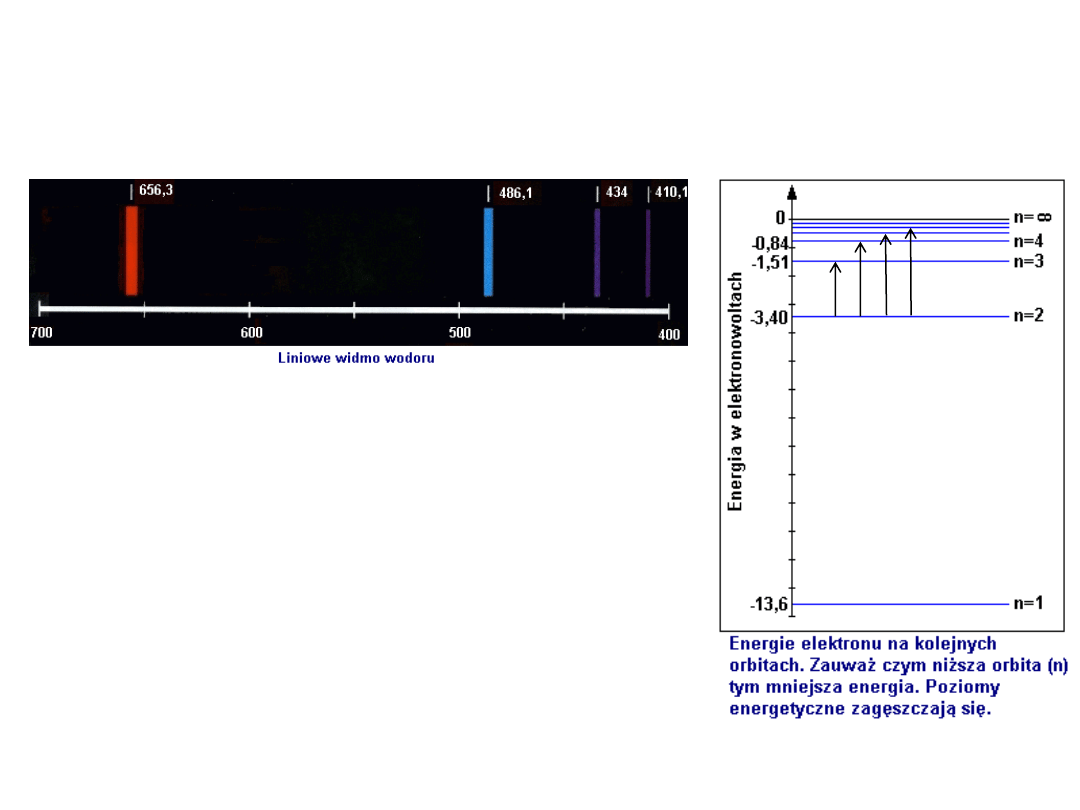
Widmo atomu wodoru
ΔE = T
i
– T
j
λ = hc / ΔE
nm
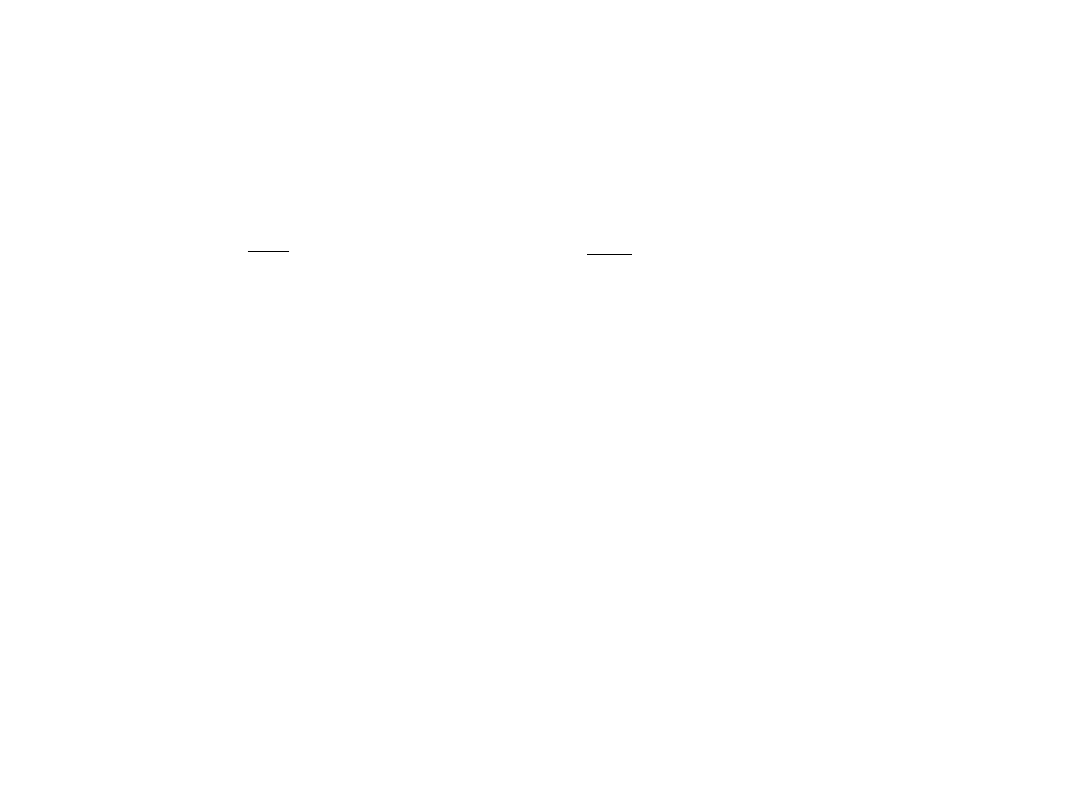
Hipoteza de
Broglie’a
h
p
m = 100g v = 20 m/s p = 2 kg m /s
h = 6,62∙10
-34
J s c = 2,99792458∙10
8
m /s
λ = 6,62 ∙10
-34
/ 2 m = 3,31∙10
-25
nm
p
h
Dualizm falowo-korpuskularny

Zasada nieoznaczoności
h
x
p
x
h
t
E
1923 - Werner Heisenberg
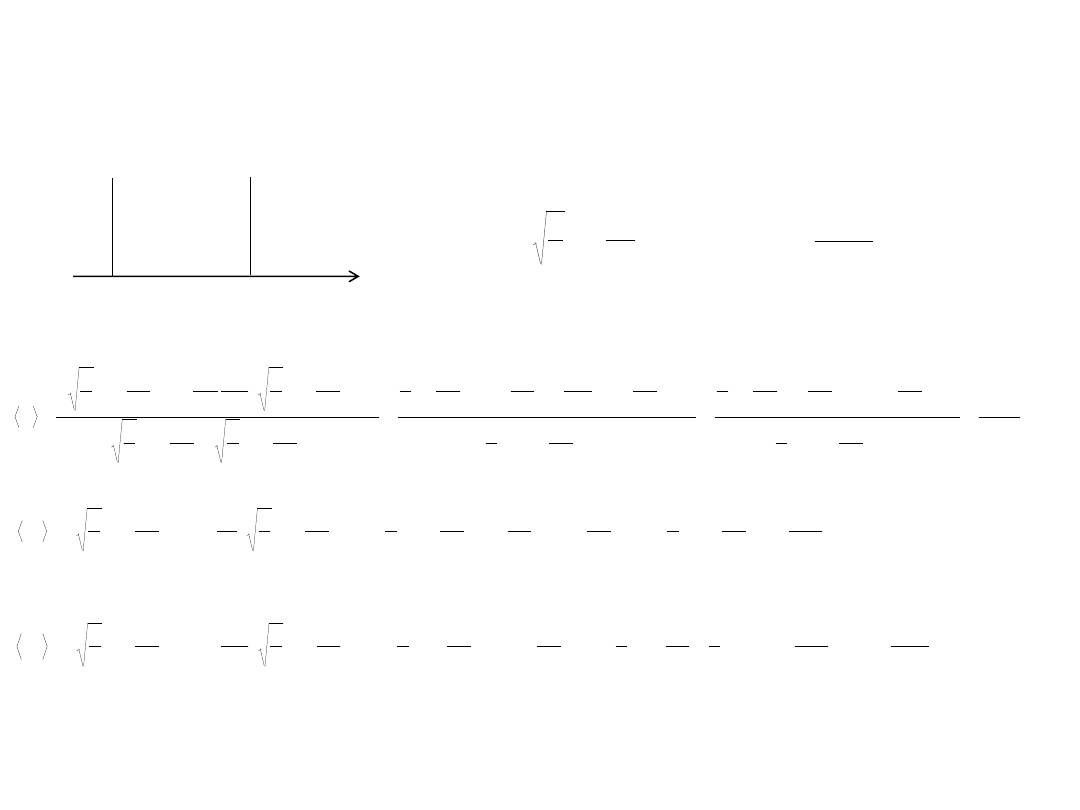
Cząstka w pudle potencjału
0
a
x
I
V=
II
V=0
III
V=
0
sin
2
0
ˆ
x
x
a
n
a
x
x
E
H
III
II
I
2
2
2
2
2
n
ma
E
2
2
2
2
0
2
0
2
2
2
0
2
0
2
2
2
0
0
2
2
2
2
sin
2
sin
2
2
sin
2
sin
sin
2
2
sin
2
sin
2
sin
2
2
sin
2
n
ma
dx
x
a
n
a
dx
x
a
n
a
n
m
a
dx
x
a
n
a
dx
x
a
n
dx
d
x
a
n
m
a
dx
x
a
n
a
x
a
n
a
dx
x
a
n
a
dx
d
m
x
a
n
a
E
a
a
a
a
a
a
0
2
sin
1
cos
sin
2
sin
2
sin
2
0
0
0
dx
x
a
n
a
n
i
a
dx
x
a
n
x
a
n
a
n
i
a
dx
x
a
n
a
dx
d
i
x
a
n
a
p
a
a
a
x
2
2
2
2
0
2
2
0
2
2
2
0
2
2
2
2
2
cos
1
2
1
2
sin
2
sin
2
sin
2
n
a
dx
x
a
n
a
n
a
dx
x
a
n
a
n
a
dx
x
a
n
a
dx
d
x
a
n
a
p
a
a
a
x
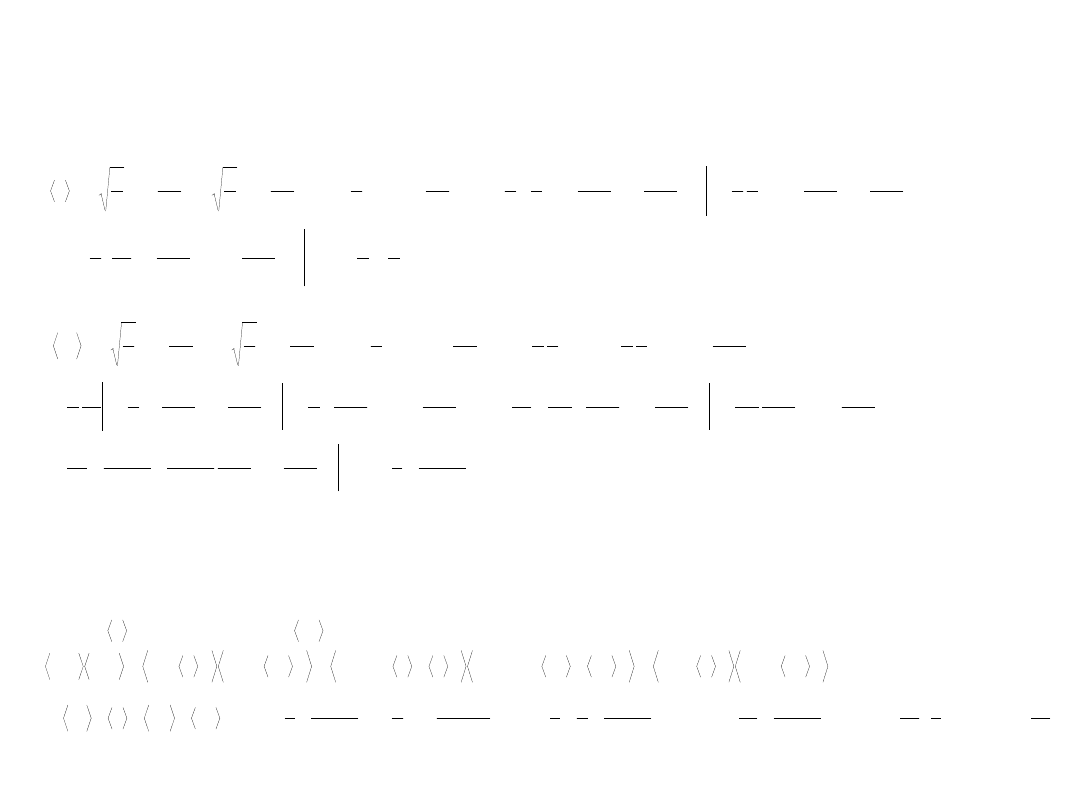
Cząstka w pudle potencjału
2
2
2
0
2
2
2
2
2
2
0
0
3
0
0
2
0
3
0
2
0
2
0
2
2
0
2
2
2
1
3
1
2
sin
2
2
2
3
2
cos
2
1
2
cos
2
1
3
2
sin
2
2
1
2
sin
2
1
3
1
2
cos
2
1
2
2
1
2
sin
2
sin
2
sin
2
n
a
x
a
n
n
a
n
a
n
a
a
dx
x
a
n
n
a
n
x
a
n
n
a
x
n
a
dx
x
a
n
x
n
a
a
x
a
n
n
a
x
a
x
a
dx
x
a
n
x
a
dx
x
a
dx
x
a
n
x
a
dx
x
a
n
a
x
x
a
n
a
x
a
a
a
a
a
a
a
a
a
a
2
2
2
cos
2
2
1
2
sin
2
2
1
2
2
sin
2
2
1
2
sin
2
sin
2
sin
2
0
2
2
0
0
0
2
0
a
a
a
x
a
n
n
a
x
a
a
dx
x
a
n
n
a
x
a
x
a
n
n
a
x
x
a
dx
x
a
n
x
a
dx
x
a
n
a
x
x
a
n
a
x
a
a
a
a
a
4
2
3
1
4
2
1
12
1
2
1
4
1
3
1
0
2
2
1
3
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
n
n
n
n
n
a
n
a
n
a
p
p
x
x
p
p
x
x
p
p
p
p
x
x
x
x
p
p
x
x
p
x
p
p
p
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Sprawdzenie zasady nieoznaczoności Heisenberga dla cząstki w pudle:
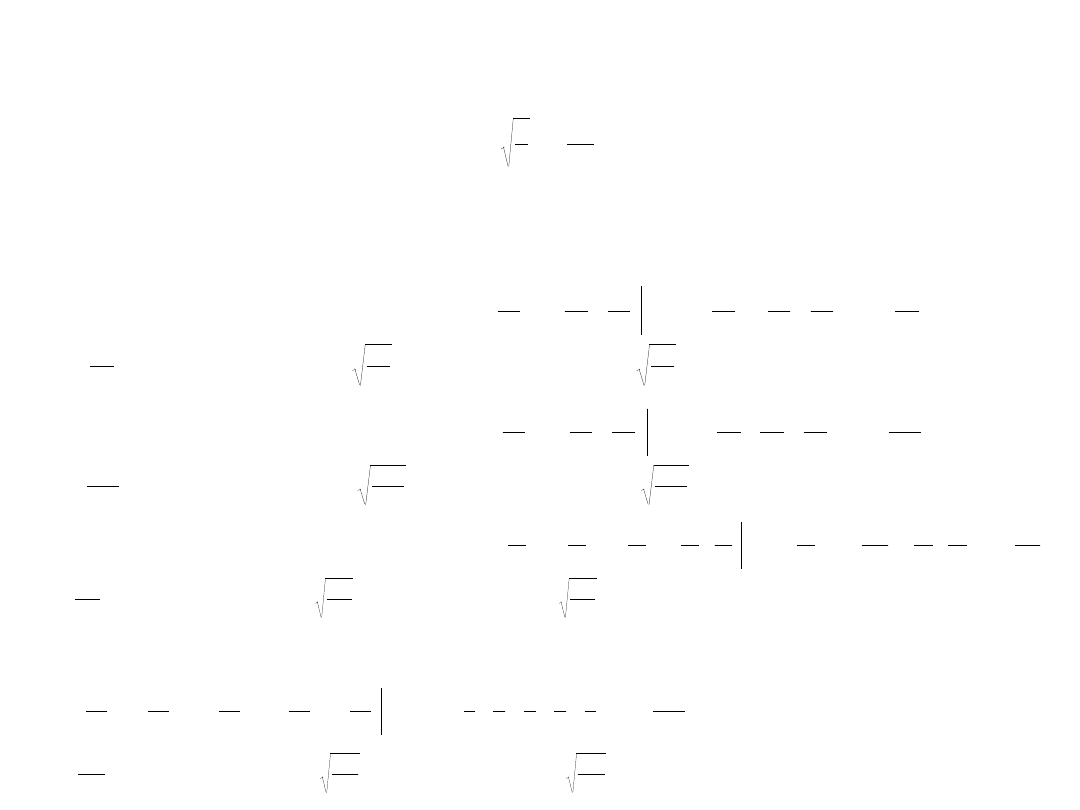
Cząstka w pudle potencjału
2
2
4
2
3
2
2
1
sin
2
x
a
Nx
x
x
a
Nx
x
x
a
Nx
x
x
a
Nx
x
x
a
n
a
x
Funkcja własna (dokładna)
Funkcje próbne (przybliżone):
x
a
x
a
x
a
N
a
N
a
N
a
a
a
N
x
x
a
x
a
N
dx
x
ax
x
a
N
dx
x
a
x
N
a
a
a
5
1
5
5
2
5
2
5
5
5
2
0
5
4
3
2
2
0
4
3
2
2
2
0
2
2
30
30
30
1
30
5
4
2
3
5
4
2
3
2
x
a
x
a
x
a
N
a
N
a
N
a
a
a
N
x
x
a
x
a
N
dx
x
ax
x
a
N
dx
x
a
x
N
a
a
a
2
7
2
7
7
2
7
2
7
7
7
2
0
7
6
5
2
2
0
6
5
4
2
2
0
2
2
2
105
105
105
1
105
7
3
5
7
6
2
5
2
2
7
3
7
7
2
7
2
7
7
7
7
7
2
0
7
6
5
2
4
3
3
4
2
0
6
5
4
2
3
3
2
4
2
0
2
2
2
105
105
105
1
105
7
3
2
5
6
3
7
6
4
5
6
4
4
3
4
6
4
x
a
x
a
x
a
N
a
N
a
N
a
a
a
a
a
N
x
x
a
x
a
x
a
x
a
N
dx
x
ax
x
a
x
a
x
a
N
dx
x
a
x
N
a
a
a
1
630
5
1
3
2
7
6
2
1
9
1
5
6
4
7
6
8
4
9
4
6
4
4
2
4
4
9
2
9
2
0
5
4
6
3
7
2
8
9
2
0
4
4
5
3
6
2
7
8
2
0
7
6
2
5
3
8
6
2
4
4
2
0
2
2
2
2
a
N
a
N
x
a
x
a
x
a
x
a
x
N
dx
x
a
x
a
x
a
ax
x
N
dx
ax
x
a
x
a
x
x
a
x
a
N
dx
x
a
x
N
a
a
a
a
2
2
9
4
9
9
2
630
630
630
x
a
x
a
x
a
N
a
N
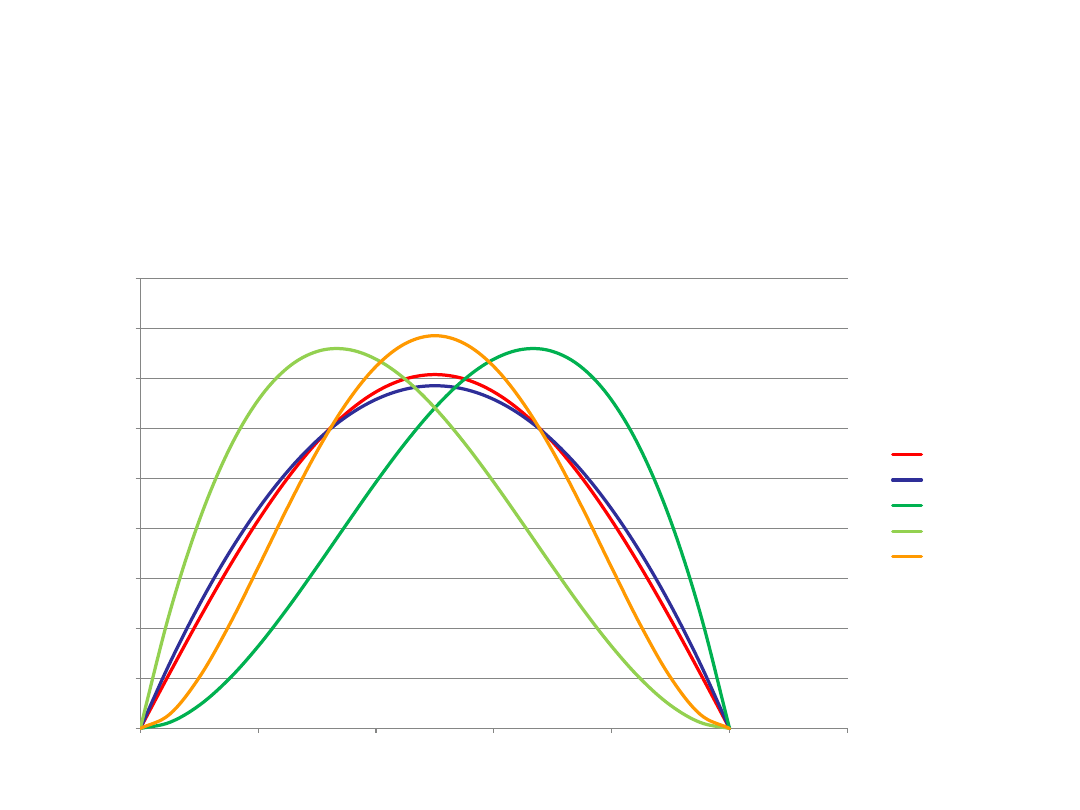
Cząstka w pudle potencjału
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0
0.2
0.4
0.6
0.8
1
1.2
sin
f1
f2
f3
f4
Wykresy funkcji dokładnej i funkcji próbnych
Cząstka w pudle potencjału
2
2
2
2
2
0
2
2
0
2
2
2
0
2
2
2
2
87
,
9
2
2
cos
1
2
1
2
2
sin
2
2
sin
2
2
sin
2
ma
ma
dx
x
a
a
m
a
dx
x
a
a
m
a
dx
x
a
a
dx
d
m
x
a
a
a
a
a
2
2
2
1
2ma
E
2
2
9
4
2
7
3
2
7
2
5
1
630
105
105
30
sin
2
x
a
x
a
x
x
a
x
a
x
x
a
x
a
x
x
a
x
a
x
x
a
a
x
2
2
0
3
2
2
5
0
2
5
5
0
2
2
2
5
2
10
3
2
2
30
2
30
30
2
30
ma
x
x
a
m
a
dx
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
2
2
0
5
4
3
2
2
7
0
4
3
2
2
2
7
0
2
2
7
2
7
0
2
2
2
2
7
2
14
5
6
4
8
3
2
2
105
6
8
2
2
105
6
2
2
105
105
2
105
ma
x
x
a
x
a
m
a
dx
x
ax
x
a
m
a
dx
x
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a
2
2
0
5
4
3
2
2
3
2
7
0
4
3
2
2
3
2
7
0
2
2
7
2
7
0
2
2
2
2
2
7
2
14
5
6
4
16
3
14
2
4
2
105
6
16
14
4
2
105
6
4
2
105
105
2
105
ma
x
x
a
x
a
x
a
m
a
dx
x
ax
x
a
x
a
m
a
dx
x
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a
2
2
2
2
0
7
6
5
2
4
3
3
4
2
9
0
6
5
4
2
3
3
2
4
2
9
2
2
0
2
2
2
9
2
2
9
0
2
2
2
2
2
9
2
12
7
12
6
36
5
38
4
16
3
2
2
630
7
12
6
36
5
38
4
16
3
2
2
630
12
36
38
16
2
2
630
12
12
2
2
630
630
2
630
ma
m
a
x
x
a
x
a
x
a
x
a
m
a
dx
x
ax
x
a
x
a
x
a
m
a
dx
x
ax
a
x
a
x
m
a
dx
x
a
x
a
dx
d
m
x
a
x
a
a
a
a
a

Dwuwymiarowe pudło potencjału
x
y
a
b
0
V=0
V=
V=
V=
V=
y
b
k
b
x
a
n
a
y
x
b
k
a
n
m
E
k
n
k
n
sin
2
sin
2
,
2
,
2
2
2
2
2
2
,
Stany zdegenerowane:
a=b
Wtedy E
1,2=
E
2,1
y
a
a
x
a
a
y
x
a
a
m
E
2
sin
2
sin
2
,
2
1
2
2
,
1
2
2
2
2
2
2
2
,
1
y
a
a
x
a
a
y
x
a
a
m
E
sin
2
2
sin
2
,
1
2
2
1
,
2
2
2
2
2
2
2
1
,
2
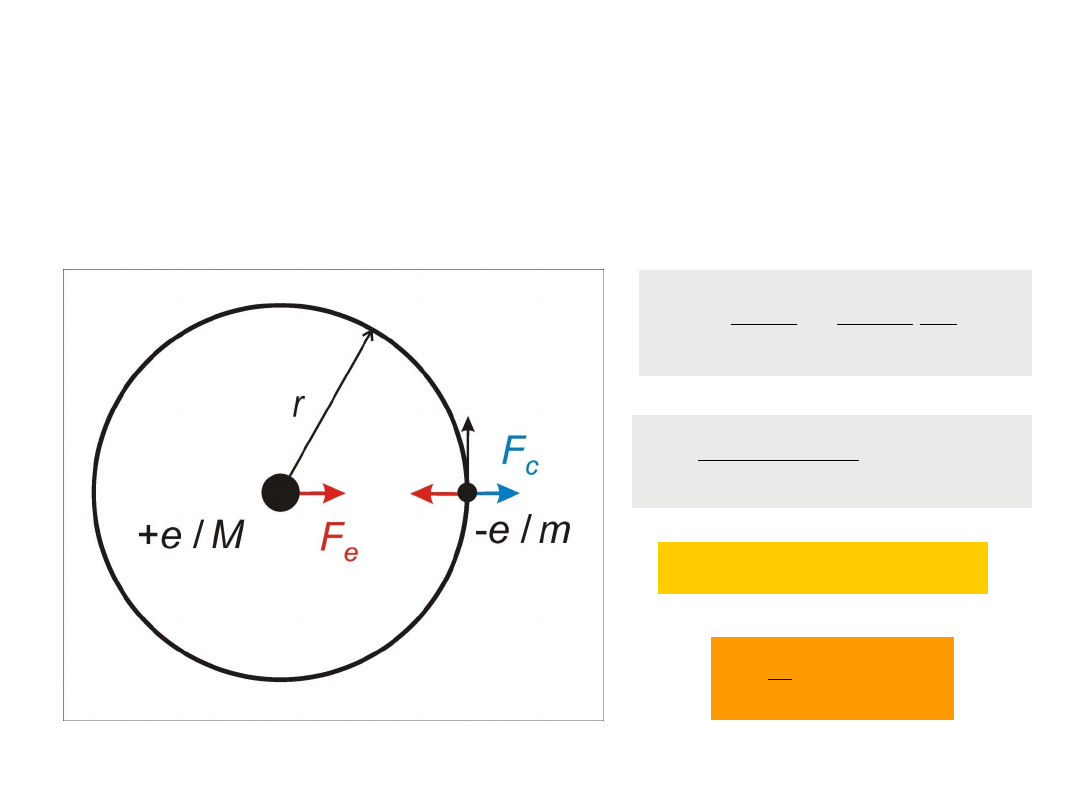
Atom wodoru
– opis klasyczny
e
c
F
r
e
r
m
F
2
2
0
2
4
1
v
1
15
10
.
6
1
s
T
1
6
2
/
1
0
10
.
2
4
v
ms
mr
e
eV
V
T
E
6
.
13
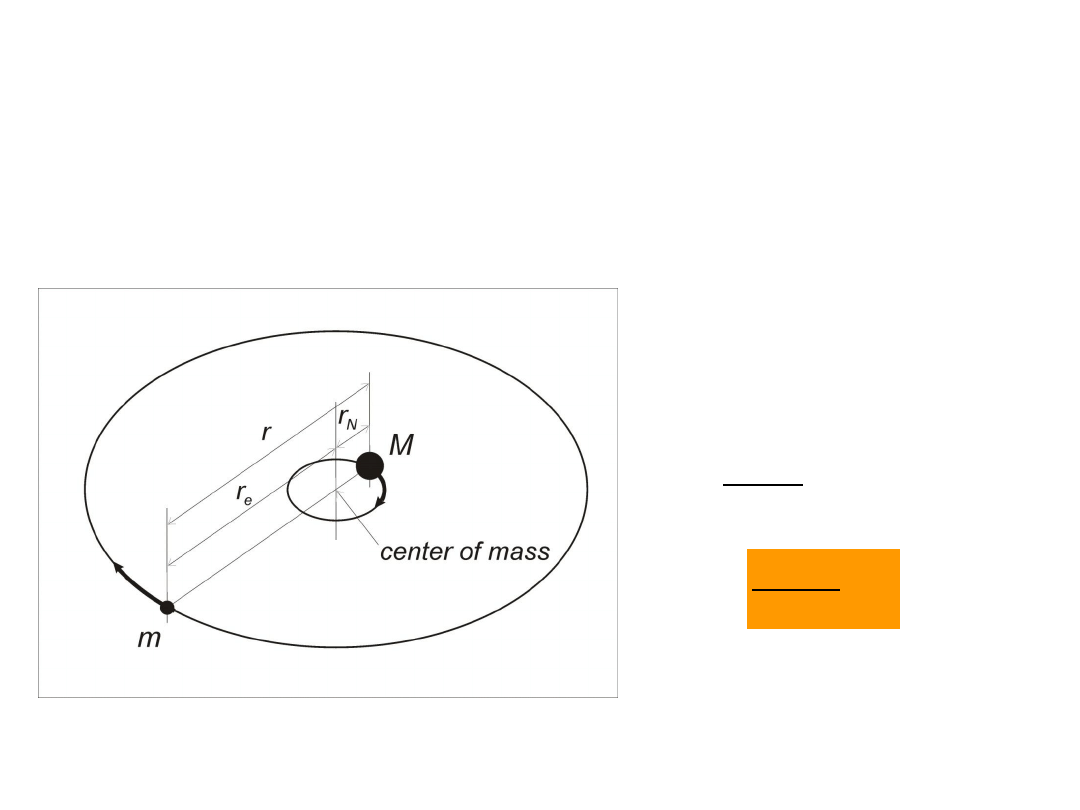
Zredukowana masa 2 ciał
ruch zredukowanej (efektywnej) masy wokół
środka masy
N
e
N
e
r
r
r
Mr
mr
n
r
M
r
m
N
e
2
2
n
r
M
m
mM
2
M
m
mM
m
/
0.99945 (H)
0.99972 (D)
Atom wodoru
2
2
2
2
2
2
2
2
2
2
2
e
z
y
x
r
r
e
z
y
x
2
H
ˆ
Równanie Schrödingera:
)
z
,
y
,
x
(
E
)
z
,
y
,
x
(
H
ˆ
e
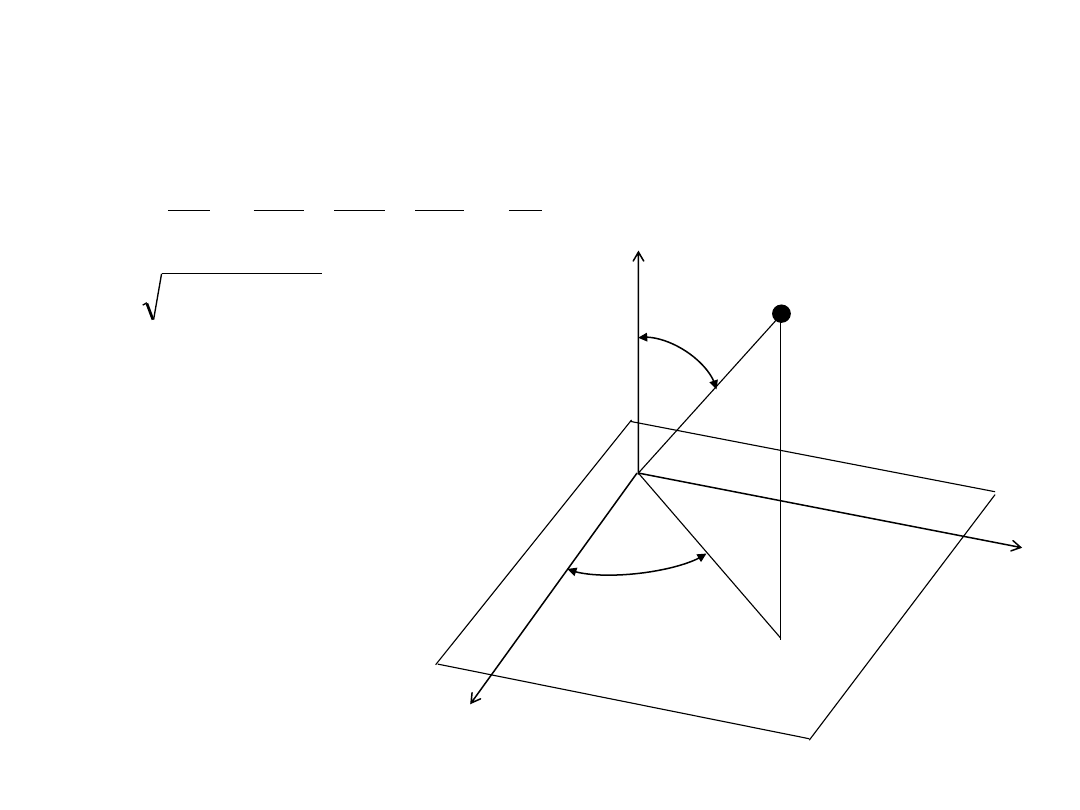
Współrzędne sferyczne:
x = r sin
θ cosφ
y = r sin
θ sinφ
z = r cos
θ
z
P
x
y
r
θ
φ
Atom wodoru 1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ˆ
e
j
e
j
e
j
e
e
e
e
j
j
j
j
z
z
y
y
x
x
r
r
e
z
y
x
m
z
y
x
M
H
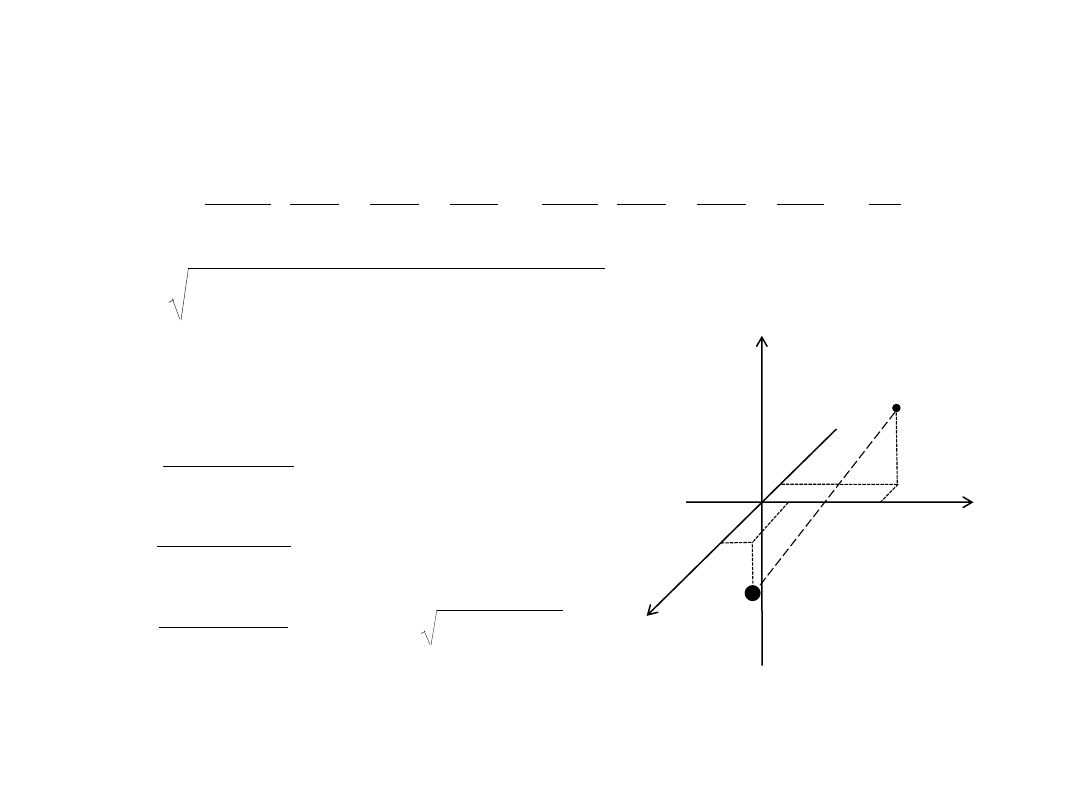
Współrzędne
środka masy:
e
j
e
e
j
j
e
j
e
e
j
j
e
j
e
e
j
j
m
M
z
m
z
M
Z
m
M
y
m
y
M
Y
m
M
x
m
x
M
X
Współrzędne
względne:
2
2
2
z
y
x
r
z
z
z
y
y
y
x
x
x
j
e
j
e
j
e
x
z
y
j
e
x
e
x
j
z
j
y
j
z
e
y
e
r
e
e
e
j
j
j
c
e
e
e
j
j
j
z
y
x
z
y
x
E
z
y
x
z
y
x
H
,
,
,
,
,
,
,
,
,
,
ˆ
Atom wodoru 1a
M
m
x
X
M
m
x
X
M
m
x
M
X
M
m
M
x
X
M
m
x
m
X
M
m
m
x
M
x
m
x
X
M
m
M
x
X
M
m
M
x
X
M
m
M
x
x
X
M
m
m
x
X
M
m
m
x
X
M
m
m
x
x
X
M
m
M
x
x
x
X
x
X
x
x
X
M
m
m
x
x
x
X
x
X
x
j
e
j
e
j
j
j
e
e
e
1
1
1
2
2
2
1
2
1
2
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Transformacja hamiltonianu do współrzędnych środka masy i względnych
Podobnie dla współrzędnych Y , Z, y, z:
r
e
z
y
x
Z
Y
X
m
M
H
e
j
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ˆ
Atom wodoru 2
r
e
z
y
x
Z
Y
X
m
M
H
e
j
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ˆ
Równanie Schrödingera po separacji:
)
,
,
(
)
,
,
(
ˆ
,
,
,
,
ˆ
z
y
x
E
z
y
x
H
Z
Y
X
E
Z
Y
X
H
e
tr
tr
ruch translacyjny atomu
ruch względny jądra i elektronu
E
c
=E
tr
+E
z
y
x
Z
Y
X
z
y
x
Z
Y
X
z
y
x
z
y
x
e
e
e
j
j
j
,
,
,
,
,
,
,
,
,
,
,
,
,
,
H
tr
H
e
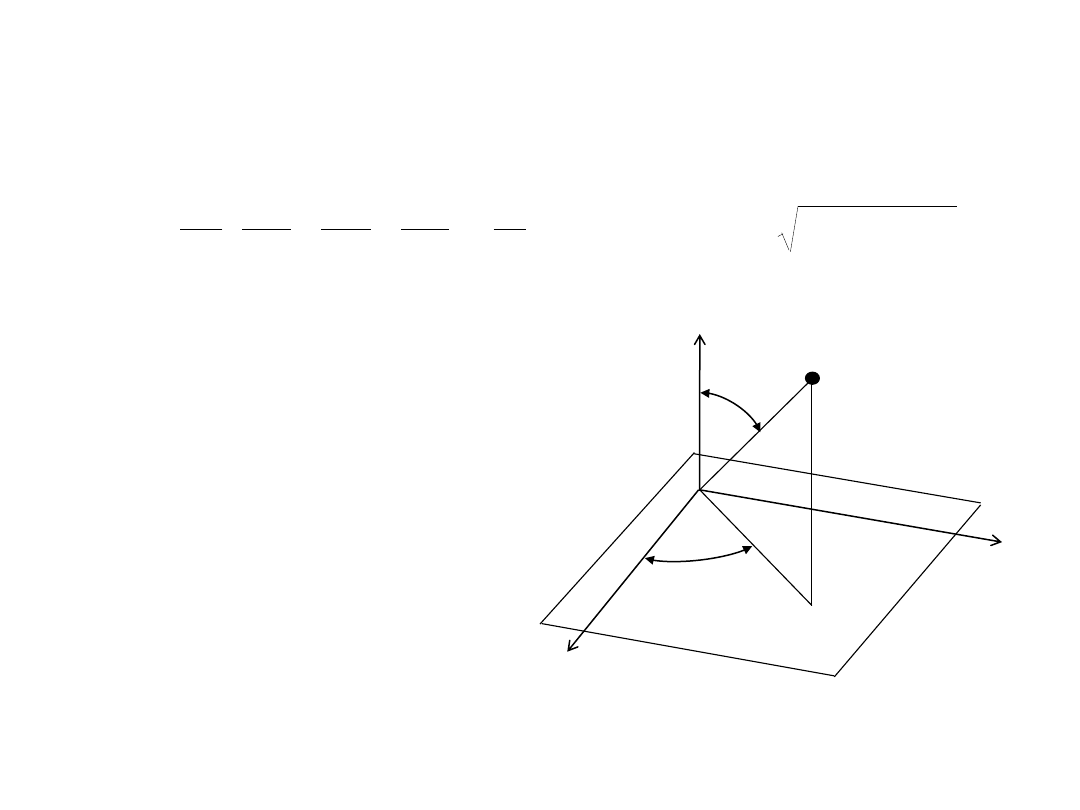
Atom wodoru 3
Równanie Schrödingera:
)
z
,
y
,
x
(
E
)
z
,
y
,
x
(
H
ˆ
e
Współrzędne sferyczne:
x = r sin
θ cosφ
y = r sin
θ sinφ
z = r cos
θ
r
e
z
y
x
H
e
2
2
2
2
2
2
2
2
2
ˆ
2
2
2
z
y
x
r
0≤r<
, 0
≤θ≤π, 0≤φ<2π
z
P
x
y
r
θ
φ
Atom wodoru 4
r
e
sin
1
sin
sin
1
r
r
r
r
2
H
ˆ
2
2
2
2
2
2
2
e
)
,
,
r
(
E
)
,
,
r
(
H
ˆ
e
)
r
(
R
)
,
,
r
(
Po separacji układ 3 równań:
r
R
E
r
R
r
e
1
l
l
r
r
r
r
2
1
l
l
sin
m
sin
sin
1
m
i
nlm
n
nlm
2
2
2
2
lm
lm
2
2
2
m
m
równanie we
współrzędnych
sferycznych
równanie:
azymutalne
horyzontalne
radialne

Atom wodoru 5
Warunki brzegowe generujące liczby kwantowe
Równanie azymutalne:
2
m=0,
±1, ±2, ±3, …
Równanie horyzontalne:
całkowalna z kwadratem l=0, 1, 2, 3, …
m=-l,-
l+1,…,0,…,+l
Równanie radialne:
R(r)
całkowalna z kwadratem n=1, 2, 3, …
l=0,1,…,n-1
2
2
2
4
1
2
n
R
n
e
E
Energia atomu wodoru
1
2
4
109677
2
cm
e
R
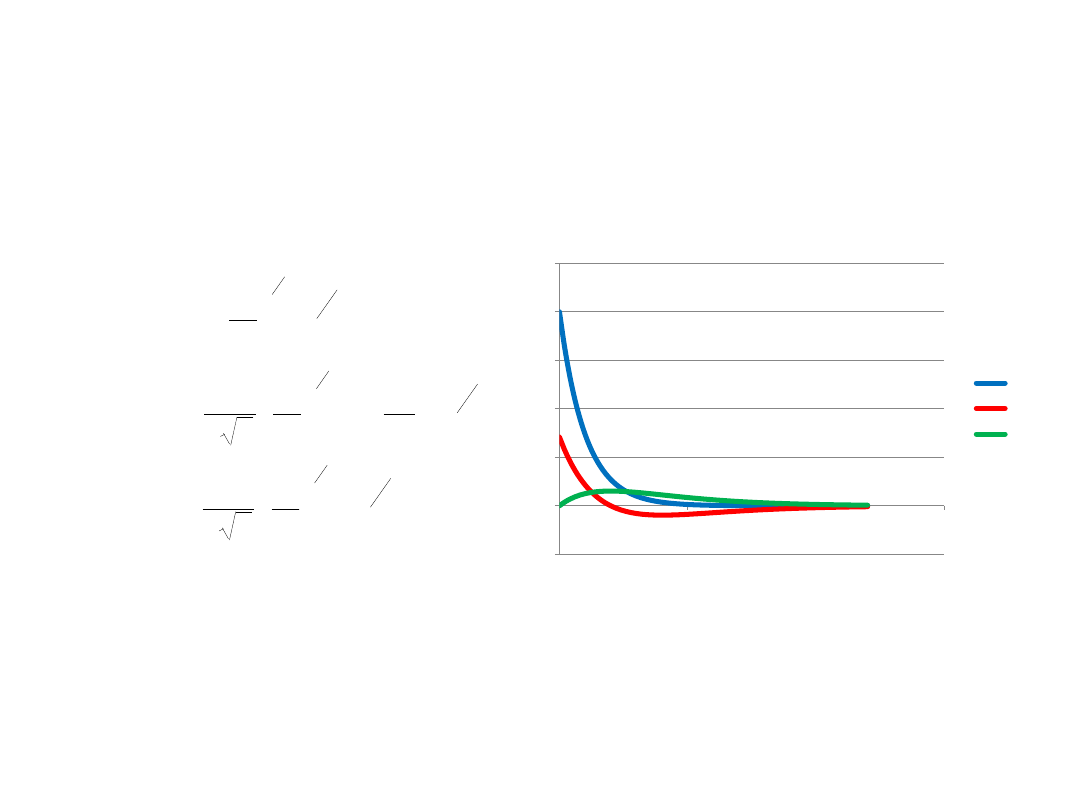
Atom wodoru 6
Funkcje falowe dla atomu wodoru
,
)
(
)
,
,
(
m
l
nl
nlm
Y
r
R
r
Funkcje radialne:
0
2
5
0
2
3
0
2
3
2
0
21
2
0
0
20
0
10
6
2
1
)
(
2
2
2
1
)
(
2
)
(
a
Zr
a
Zr
a
Zr
re
a
Z
r
R
e
a
Zr
a
Z
r
R
e
a
Z
r
R
a
0
= 0,529 Ǻ = 0,529 · 10
-10
m promień Bohra
-0.5
0
0.5
1
1.5
2
2.5
0
5
10
15
R10
R20
R21
a
0
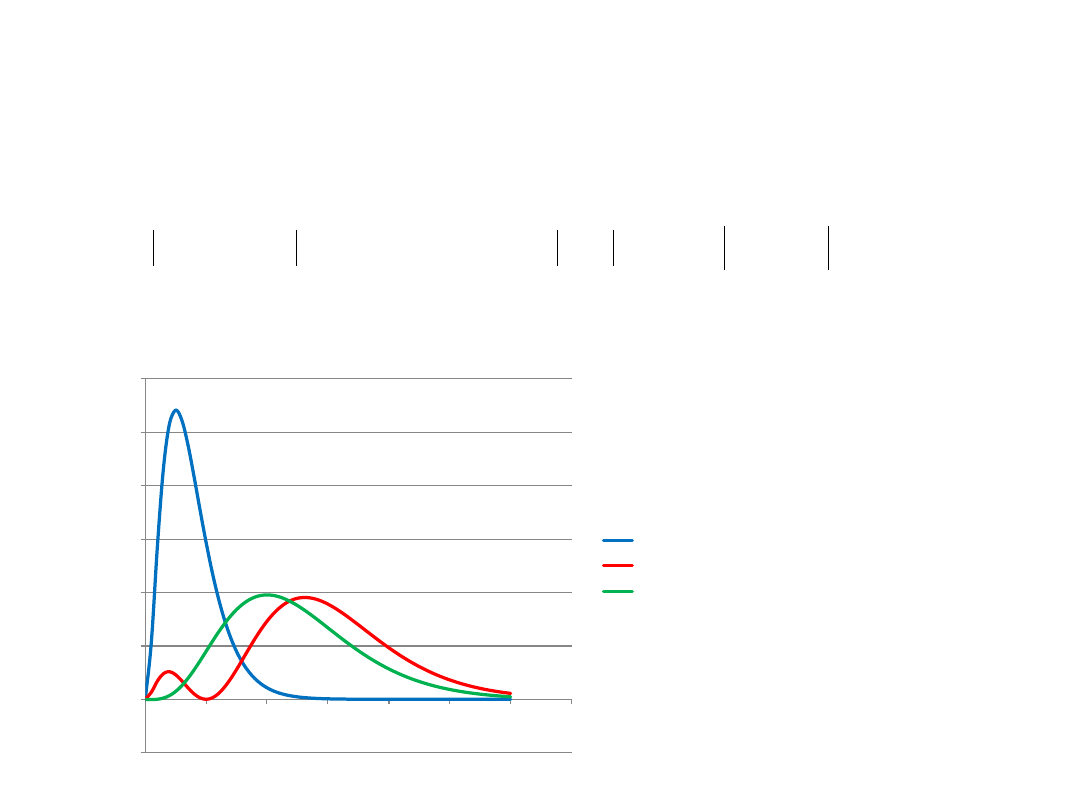
Atom wodoru 7
Radialna gęstość prawdopodobieństwa:
R
2
(r) r
2
Element objętości :
dV = dx dy dz = r
2
sin
θ dr dθ dφ
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0
2
4
6
8
10
12
14
(R10*r)^2
(R20*r)^2
(R21*r)^2
Ciekawe:
Dla l=n-1 jedno
jedyne maksimum
dla r=n
2
*a
0
Całka normalizacji:
0
0
2
0
2
2
2
2
0 0
2
0
2
1
sin
,
sin
,
,
d
d
Y
dr
r
r
R
d
d
dr
r
r
m
l
nlm
Atom wodoru 8
Warstwica orbitalu: zbiór wszystkich punktów w przestrzeni, którym
odpowiada ta sama, zadana wartość orbitalu, ε.
Kontur orbitalu (powierzchnia graniczna orbitalu): powierzchnia najmniejszej
figury geometrycznej, na zewnątrz której wartość orbitalu jest wszędzie
mniejsza co do modułu od zadanej, małej, dodatniej wartości.
Kontur gęstości prawdopodobieństwa: powierzchnia najmniejszej figury
geometrycznej, na zewnątrz której gęstość prawdopodobieństwa jest
wszędzie mniejsza co do modułu od zadanej, małej, dodatniej wartości ε.
Dla orbitalu 1s:
3
3
0
0
2
3
0
3
ln
2
0
Z
a
Z
a
r
e
a
Z
a
Zr
Gdy
ε = 0,01 a
0
-3
, wówczas:
r=1,73 a
0
dla atomu wodoru,
r=1,38 a
0
dla jonu He
+
,
r=1,13 a
0
dla jonu Li
2+
.
Atom wodoru 9
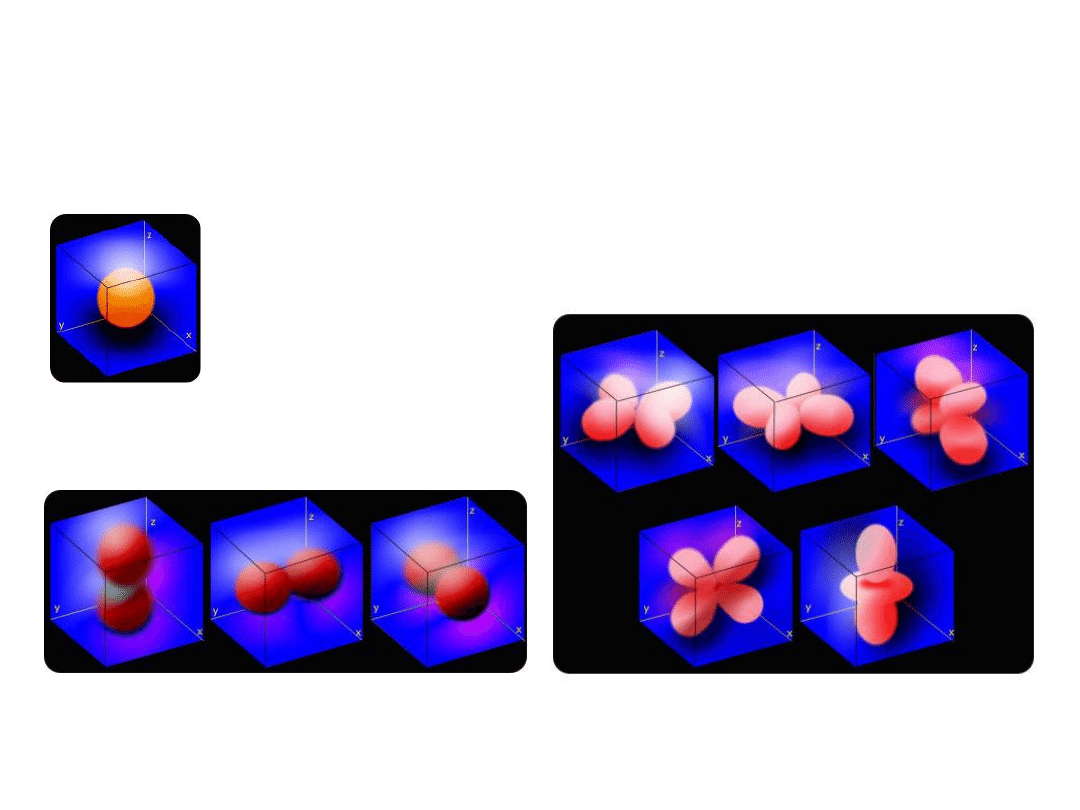
Jakościowe kontury orbitali typu s, p, d
s
p
z
p
y
p
x
d
x2-y2
d
xy
d
xz
d
yz
d
z2
Atom wodoru 10
Kombinacje liniowe orbitali atomowych
Orbitale atomowe
i
a
Zr
p
i
a
Zr
p
s
a
Zr
p
s
a
Zr
s
s
a
Zr
s
e
re
N
e
re
N
a
Z
N
re
N
a
Z
N
e
a
Zr
N
a
Z
N
e
N
sin
2
1
sin
2
1
4
1
cos
2
4
1
2
1
0
0
2
5
0
2
3
0
2
3
0
2
2
1
21
2
2
211
0
2
2
2
210
0
2
2
0
2
200
0
1
1
100
0
0
0
0
0
0
2
2
2
2
2
2
2
2
2
2
2
2
1
21
211
1
21
211
sin
sin
2
sin
2
cos
sin
2
sin
2
2
2
1
a
Zr
p
a
Zr
p
i
i
a
Zr
p
y
a
Zr
p
a
Zr
p
i
i
a
Zr
p
x
ye
N
re
N
i
e
e
re
N
p
xe
N
re
N
e
e
re
N
p
i
Spin
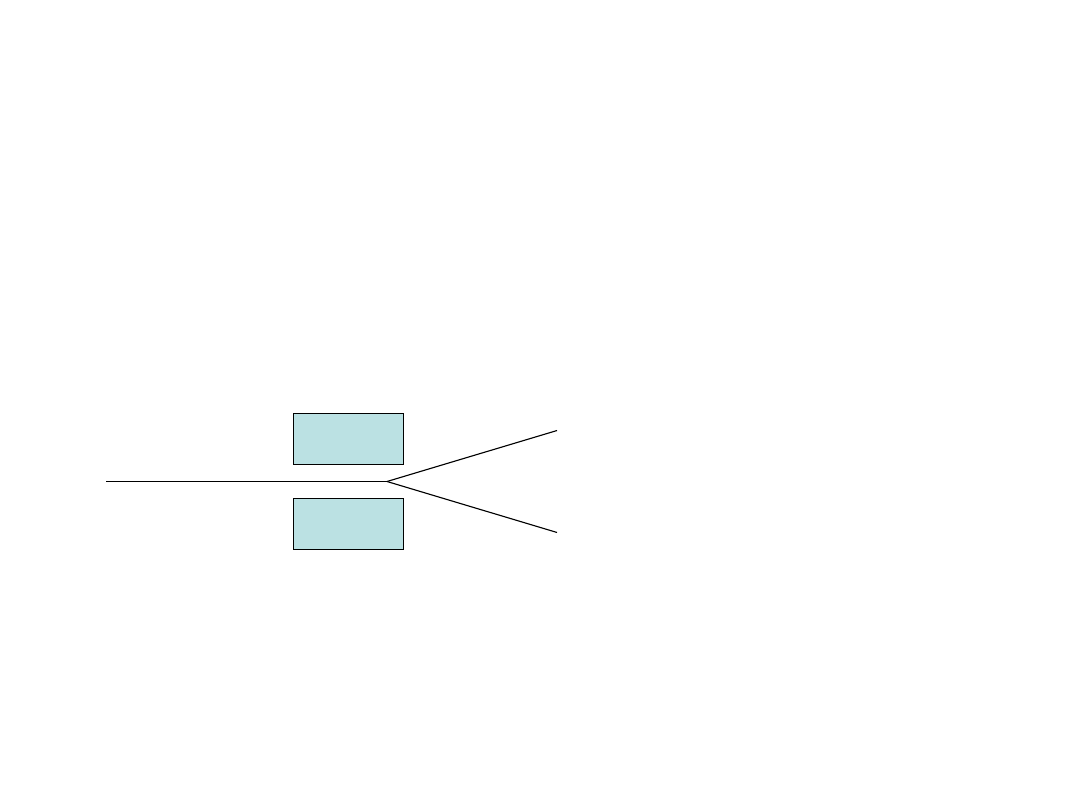
Doświadczenie Sterna Gerlacha
Wiązka atomów srebra przepuszczana przez pole magnetyczne
Konfiguracja elektronowa srebra
Ag: 1s
2
/2s
2
2p
6
/3s
2
3p
6
3d
10
/4s
2
4p
6
4d
10
/5s
1
m
s
= +
½
m
s
= -
½
magnes
Spinorbital
s
s
m
nlm
nlmm
Stany elektronu
α
β
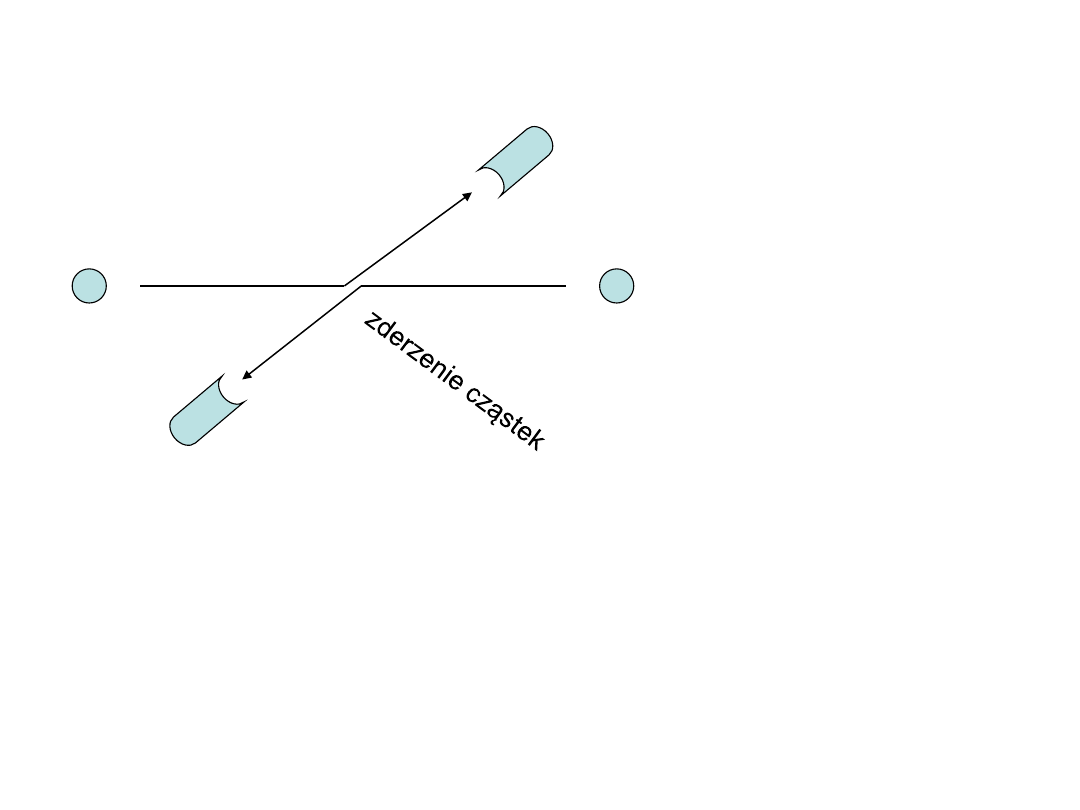
Zasada nierozróżnialności jednakowych cząstek
a,b
– cząstki
1,2 - detektory
a
b
2
1
Prawdopodobieństwo zarejestrowania cząstek różnych P
1
=|
φ
a
(1)
φ
b
(2)|
2
P
2
=|
φ
a
(2)
φ
b
(1) |
2
Gdy cząstki jednakowe P
1
= P
2
, zatem
φ
a
(1)
φ
b
(2) =
± φ
a
(2)
φ
b
(1)
Cząstki interferują ze sobą

Zasada nierozróżnialności jednakowych cząstek
Amplituda rozpraszania jednakowych cząstek:
Bozony
φ
a
(1)
φ
b
(2) +
φ
a
(2)
φ
b
(1)
spin całkowity
Fermiony
φ
a
(1)
φ
b
(2) -
φ
a
(2)
φ
b
(1)
spin połowkowy
Funkcja falowa dla fermionów jest antysymetryczna:
Φ(1,2,3,…) = - Φ(2,1,3,…)
Jeżeli fermiony zajmują te same stany czyli 1=2, to φ
a
(1)
φ
b
(1) -
φ
a
(1)
φ
b
(1)
≡ 0
Jest to treść zakazu Pauliego.
Funkcja falowa dla bozonów jest symetryczna
Bozony dążą do obsadzenia tego samego stanu – stąd nadciekłość helu
4
He
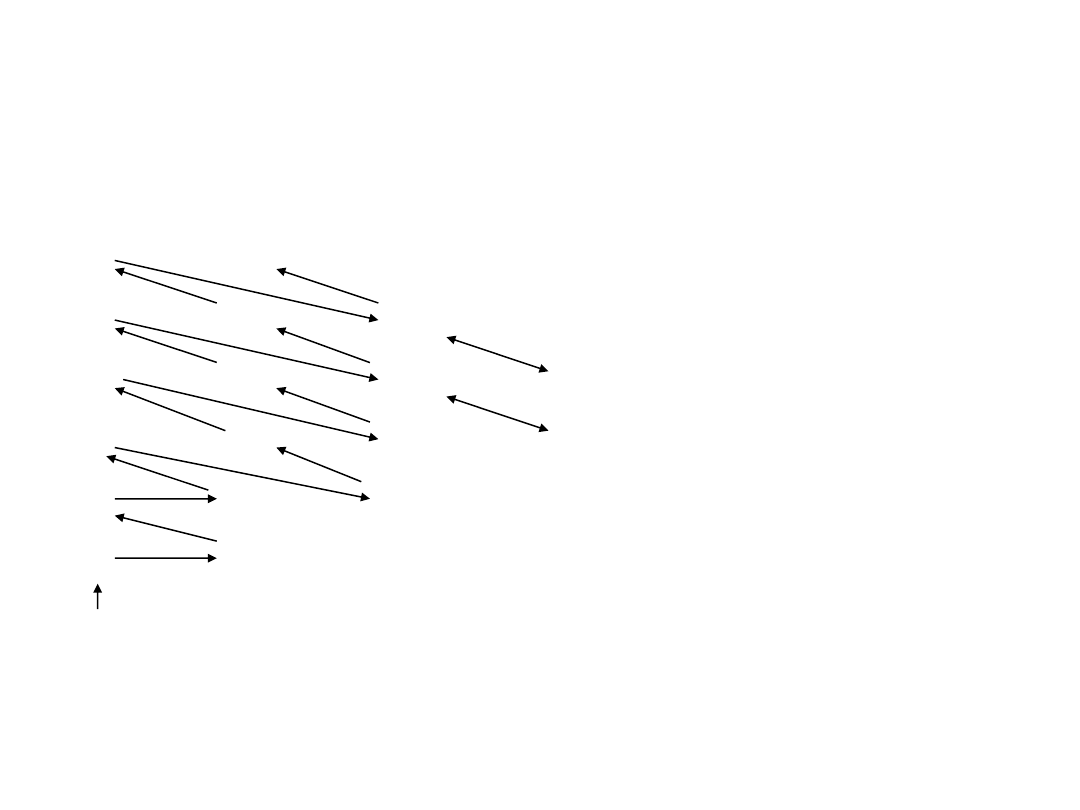
Atom wieloelektronowy
7s
7p
6s
6p
6d
5s
5p
5d
5f
4s
4p
4d
4f
3s
3p
3d
2s
2p
1s
Powłoki elektronowe:
n = 1,2,3,… → K,L,M,…
l = 0,1,2,…→ s,p,d,…
Reguła Hunda:
W wypadku degeneracji
orbitalnej najniższą energię ma
stan o maksymalnej
multipletowości
Atomy wieloelektronowe
Term widmowy
2S+1
L
J
2S+1 to multipletowość, gdzie S to całkowity spin orbitalu
Jak wyznaczyć L, J, S ? J = L+S, L+S-1, … , |L-S|
Atom węgla C konfiguracja elektronowa 1s
2
2s
2
2p
2
Zapełnione powłoki dają S = 0
l
1
l
2
s
1
s
2
m
1
m
2
M
L
L
M
S
S
1
1
+
½ -½
1 1
2
2
0
0
½
½
1 0
1
1
+1,0,-1
,
0
1
½
½
1 -1
0
0
+1,0,-1
,
0
0
+
½ -½
0 0
0
0
½
½
0 -1
-1
+1,0,-1
,
0
+
½ -½
-1 -1
-2
0
Termy:
3
P
2
,
3
P
1
,
3
P
0
,
1
D
2
,
1
S
0
Atom helu 1
12
2
2
2
1
2
2
2
2
2
2
2
2
2
2
2
2
1
2
2
1
2
2
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ˆ
r
e
r
e
r
e
z
y
x
m
z
y
x
m
z
y
x
M
H
e
e
j
j
j
j
12
2
2
2
1
2
2
2
1
2
2
2
2
2
2
2
ˆ
r
e
r
e
r
e
m
m
M
H
e
e
j
j
12
2
2
1
2
2
2
2
ˆ
r
e
r
e
m
H
i
i
i
e
e
Hamiltonian elektronowy w przybliżeniu
nieskończenie ciężkiego jądra
2
1
2
,
1
2
1
Przybliżenie jednoelektronowe
1
1
1
1
1
1
Spinorbital=orbital*funkcja_spinowa
1
,
2
2
,
1
1
2
1
2
1
,
2
2
1
2
1
2
,
1
1
2
2
1
1
2
2
1
Antysymetryzowana funkcja wieloelektronowa
i
E
i
i
H
r
e
m
i
H
n
n
n
i
i
e
e
ˆ
2
2
ˆ
2
2
Hamiltonian jednoelektronowy
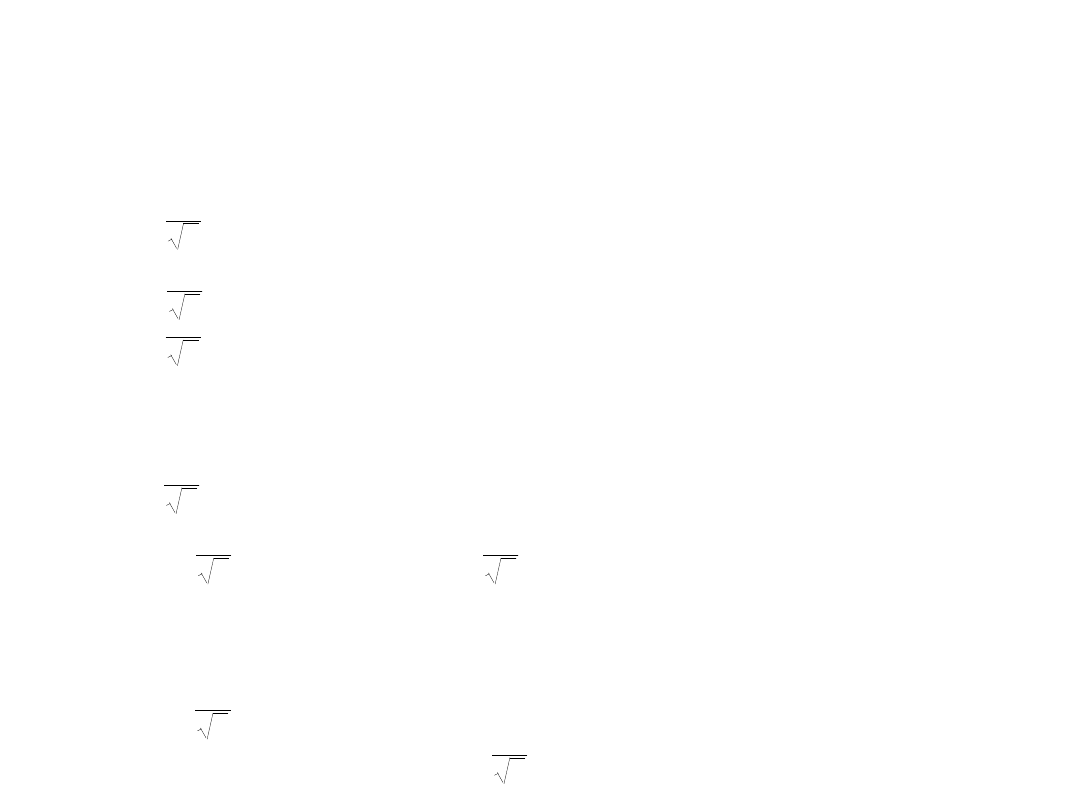
Atom helu 2
2
,
1
2
,
1
2
,
1
1
,
2
2
1
2
1
2
1
2
,
1
1
,
2
2
1
2
1
2
1
2
,
1
1
2
2
1
1
2
2
1
a
a
s
s
Funkcja spinorbitalna= funkcja przestrzenna* funkcja spinowa
Symetria funkcji przestrzennej
1
,
2
2
1
2
1
2
1
2
,
1
1
,
2
2
1
2
,
1
1
,
2
2
1
2
,
1
1
,
2
2
1
2
1
2
1
2
,
1
s
s
s
s
s
s
a
a
Symetria funkcji spinowej
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
,
1
2
1
2
1
2
1
2
1
2
1
2
1
2
,
1
1
2
2
1
tryplet
1
2
2
1
singlet
oraz
Funkcje
singletowa (S=0)
i trypletowa (S=1)
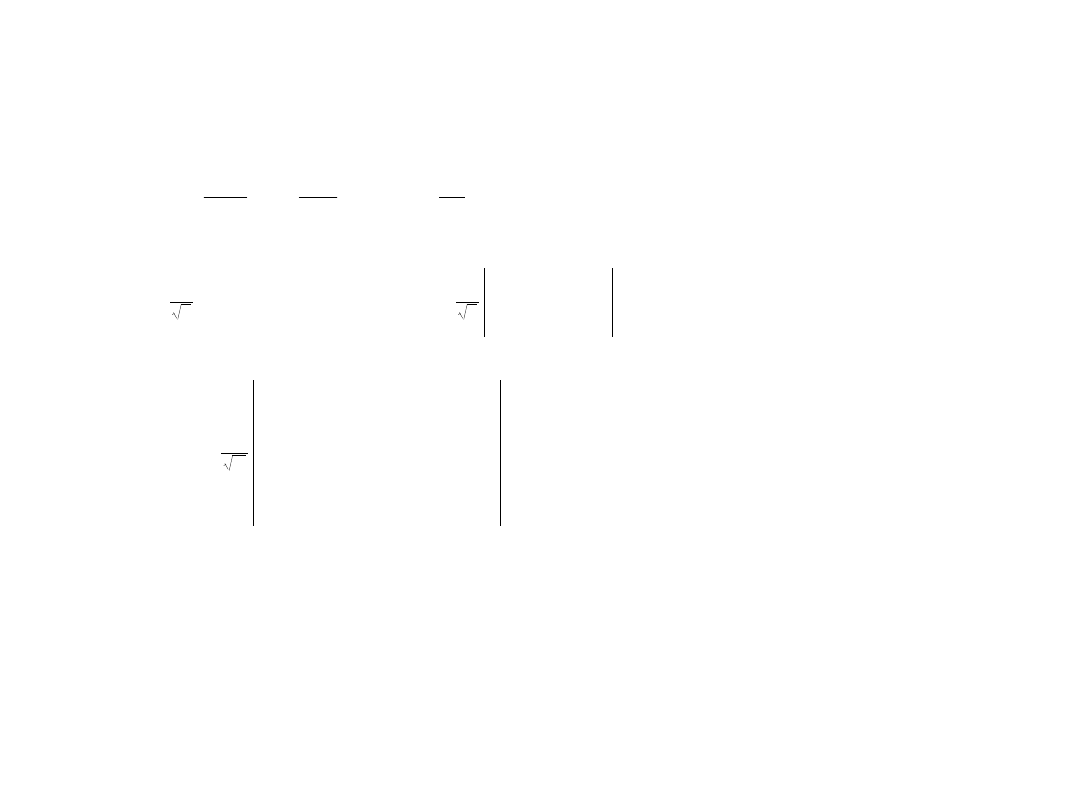
Atom wieloelektronowy
1
1
1
2
1
2
2
2
ˆ
n
i
n
i
j
ij
n
i
i
i
e
e
r
e
r
ne
m
H
2
1
2
1
2
1
2
1
2
,
1
2
2
1
1
2
1
1
2
2
1
2
1
Wyznacznikowa postać
antysymetryzowanej funkcji
falowej dla atomu helu
n
n
n
n
n
n
n
n
...
2
1
...
...
...
...
...
2
1
...
2
1
,...,
2
,
1
2
2
2
1
1
1
!
1
Antysymetryzowana funkcja dla
układu n elektronów spełniająca
zakaz Pauliego
– podstawa
przybliżenia jednoelektronowego
E
HF
: Energia Hartree-Focka
– najniższa energia uzyskana w ramach
przybliżenia jednoelektronowego
E
korelacji
= E
dokładna
– E
HF
Energia korelacji

Metoda wariacyjna
Jak rozwiązać równanie Schrödingera, gdy nieznana jest postać dokładna
funkcji falowej? Szukamy energii najbliższej energii stanu podstawowego i
odpowiadającej jej przybliżonej funkcji falowej.
dV
S
dV
H
H
c
dV
dV
H
E
H
j
i
ij
j
i
ij
N
i
i
i
*
*
1
*
*
ˆ
ˆ
ˆ
Jeżeli Φ jest tożsame z ψ, to ε jest równe E
0
.
Jeżeli Φ jest przybliżeniem ψ, to ε jest większe od E
0
.
Metoda kombinacji liniowych:
Najlepszej funkcji
Φ szukamy w postaci kombinacji
liniowej funkcji
φ
i
, które nazywamy bazą funkcyjną.
Minimalizując ε ze względu na współczynniki c
i
:
N
i
dla
S
H
c
H
c
i
j
ij
ij
j
ii
i
,...,
1
0
N
i
dla
c
i
,...,
1
0
uzyskujemy układ N równań na współczynniki c
i
:
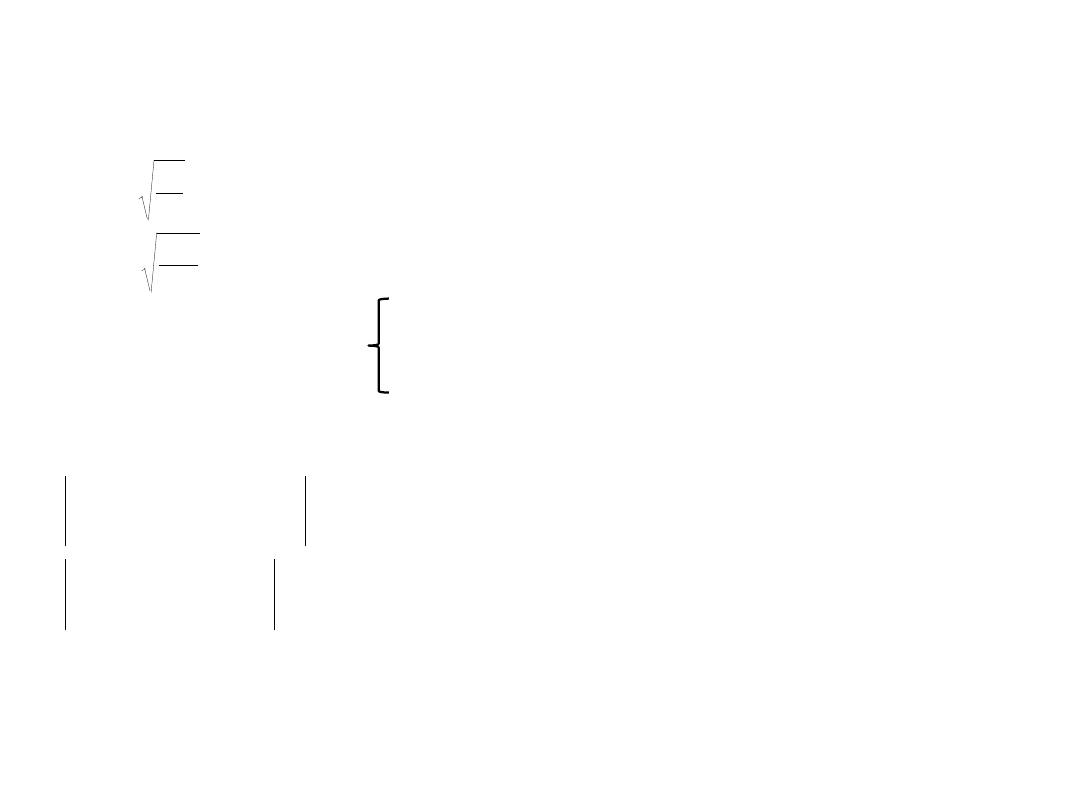
Metoda wariacyjna dla cząstki w pudle (1)
x
c
x
c
x
x
a
x
a
x
x
a
x
a
x
2
2
1
1
2
2
9
2
7
1
630
30
Funkcje bazowe
φ
1
i
φ
2
są unormowane, tzn.
S
11
=1 i S
22
=1.
Układ równań wiekowych:
0
0
22
2
21
21
1
12
12
2
11
1
H
c
S
H
c
S
H
c
H
c
Warunki istnienia rozwiązań układu równań liniowych jednorodnych:
0
0
22
12
12
11
21
12
21
12
22
21
21
12
12
11
H
S
H
S
H
H
S
S
S
H
H
H
S
H
S
H
H
Normalizacja funkcji
Φ(x):
1
2
1
2
2
1
2
2
2
1
2
1
2
1
2
2
2
2
2
1
2
1
2
2
2
1
1
2
*
S
c
c
c
c
dx
c
c
dx
c
dx
c
dx
x
c
x
c
dx
x
dx
x
x

Metoda wariacyjna dla cząstki w pudle (2)
0
0
22
2
12
1
12
2
11
1
H
c
S
H
c
S
H
c
H
c
0
22
12
12
11
H
S
H
S
H
H
S
H
H
c
c
S
c
c
c
c
12
11
1
2
2
1
2
2
2
1
1
2
S
H
H
H
S
S
H
H
H
S
H
H
H
H
S
H
H
S
H
H
H
H
H
H
S
S
H
H
H
H
H
H
S
H
H
H
S
S
H
H
H
12
22
11
2
2
12
22
11
2
1
12
22
12
11
22
11
2
12
2
22
11
2
12
22
11
2
2
12
22
11
2
12
22
11
12
22
11
2
2
2
12
22
11
2
1
2
1
2
1
2
1
4
4
1
4
2
0
2
1
0
Dla każdej wyznaczonej energii
ε
1
lub
ε
2
rozwiązujemy układ
równań na współczynniki c
1
i c
2
.
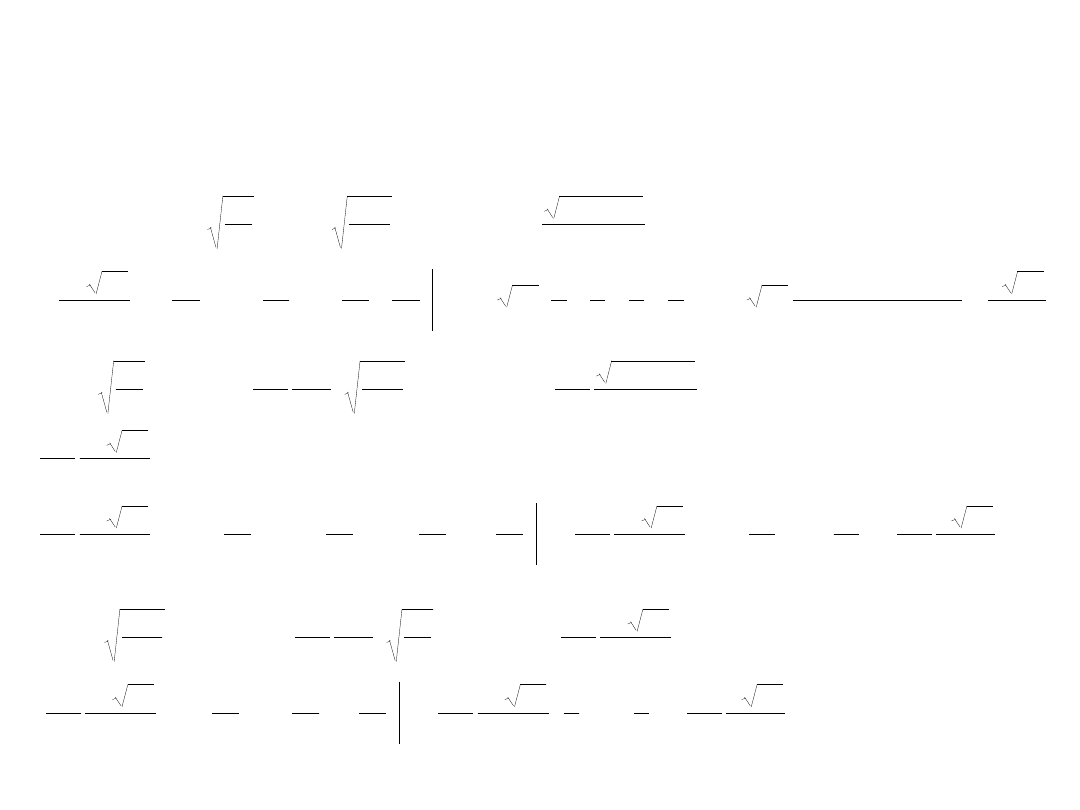
Metoda wariacyjna dla cząstki w pudle (3)
Obliczenie całek w równaniach:
14
21
3
140
20
70
84
35
21
30
7
1
2
1
5
3
4
1
21
30
7
6
3
5
3
4
21
30
3
3
630
*
30
630
30
0
7
6
5
2
4
3
7
0
3
2
2
3
3
0
7
2
2
9
5
21
12
a
a
a
x
x
a
x
a
x
a
a
dx
x
ax
x
a
a
x
a
dx
x
a
x
a
x
a
x
a
S
S
S
2
2
2
2
0
5
4
3
2
2
3
7
2
0
4
3
2
2
3
2
2
3
7
2
0
2
2
2
0
7
2
2
2
9
2
2
2
5
12
21
2
2
5
12
6
3
14
1
21
30
2
5
12
4
24
3
14
2
2
21
30
2
12
12
2
12
12
2
21
30
2
12
12
2
630
*
30
2
630
2
30
a
m
a
m
x
x
a
x
a
x
a
a
m
dx
x
ax
x
a
ax
x
a
x
a
a
m
dx
x
ax
a
x
ax
a
m
dx
x
a
x
a
dx
d
m
x
a
x
a
H
a
a
a
a
2
2
2
2
0
5
4
3
2
7
2
0
4
3
2
2
0
7
2
5
2
2
2
2
2
9
21
21
2
2
5
2
1
3
2
21
30
2
5
2
4
4
3
2
21
30
2
2
2
21
30
2
30
2
630
a
m
a
m
x
x
a
x
a
a
m
dx
x
ax
x
a
a
m
dx
x
a
x
a
dx
d
m
x
a
x
a
H
a
a
a
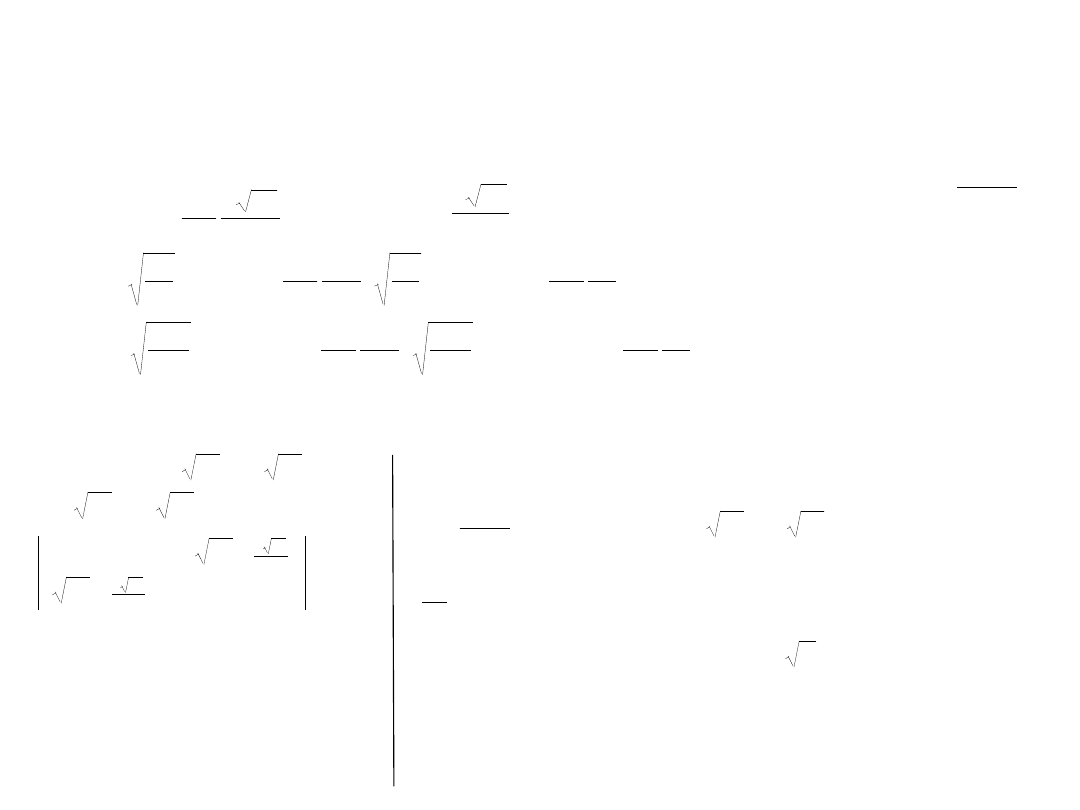
Metoda wariacyjna dla cząstki w pudle (4)
Obliczenie całek w równaniach:
14
21
3
S
2
2
21
12
21
2
2
a
m
H
H
2
2
0
2
2
9
2
2
2
2
2
9
22
2
2
0
5
2
2
2
5
11
12
2
630
2
630
10
2
30
2
30
a
m
dx
x
a
x
a
dx
d
m
x
a
x
a
H
a
m
dx
x
a
x
a
dx
d
m
x
a
x
a
H
a
a
Układ równań wiekowych:
0
12
21
2
21
2
10
0
)
12
(
14
/
21
3
21
2
0
)
14
/
21
3
21
2
(
10
14
21
3
14
21
3
2
1
2
1
c
c
c
c
13025038
,
102
)
2
/
28
(
*
295017884
,
3
4
869719621
,
9
)
2
/
28
(
*
295017884
,
3
4
295017884
,
3
7
/
76
36
*
28
/
1
*
4
16
0
36
4
28
1
0
21
*
4
12
*
10
14
/
21
*
3
*
21
*
2
*
2
12
10
196
21
*
9
1
2
1
2
2
Rozwiązanie:
Całki energetyczne
wyrażamy w jednostkach
2
2
2ma
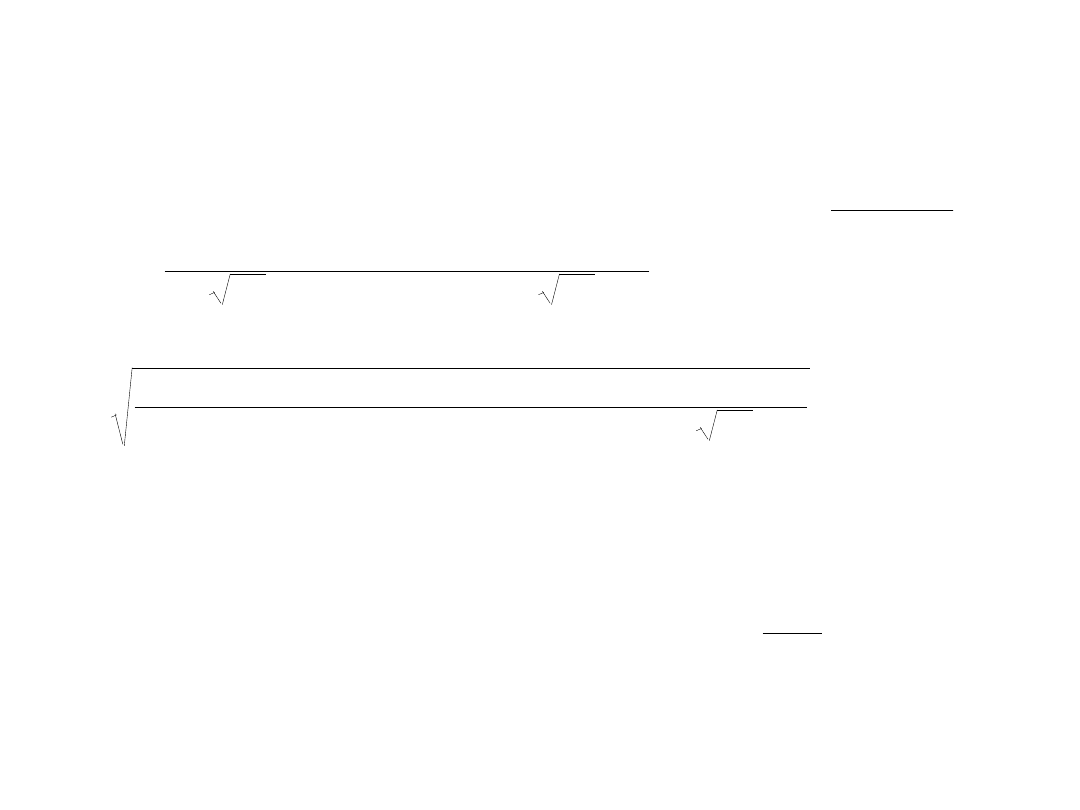
Metoda wariacyjna dla cząstki w pudle (5)
Obliczenie współczynników kombinacji liniowej:
2
1
1
2
1
2
1
1
2
1
2
1
19882025
,
0
80405626
,
0
19882025
,
0
80405626
,
0
14
/
21
*
2
*
247271562
,
0
*
2
247271562
,
0
1
1
247271562
,
0
14
/
21
*
3
*
869719621
,
9
21
*
2
869719621
,
9
10
869719621
,
9
c
c
c
c
c
c
c
S
H
H
c
c
S
c
c
c
c
12
11
1
2
2
1
2
2
2
1
1
2
Dokładna wartość E
1
dla cząstki w pudle [w jednostkach ]
1
1
2
1
869604401
,
9
E
E
2
2
2ma
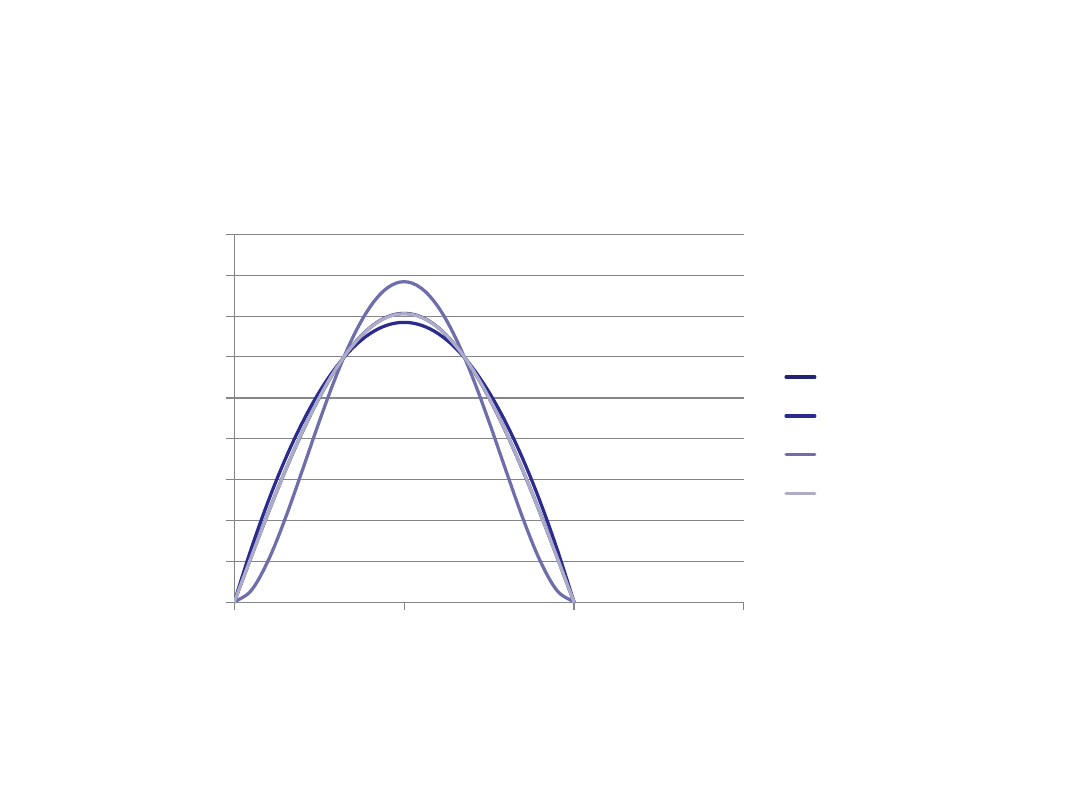
Metoda wariacyjna dla cząstki w pudle (6)
Wykresy funkcji:
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0
0.5
1
1.5
sin
f1
f2
f1+f2
Funkcja sin(x) i kombinacja liniowa funkcji
φ
1
i
φ
2
pokrywają się w skali rysunku
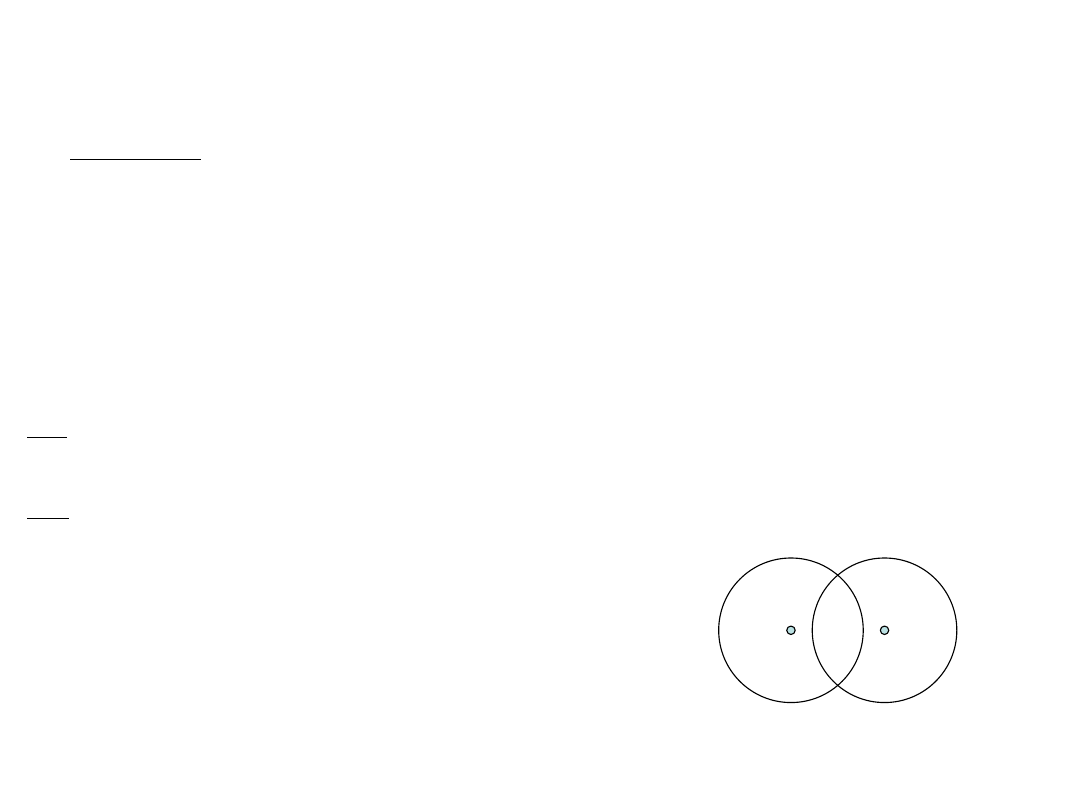
Jon H
2
+
0
E
H
c
SE
H
c
0
SE
H
c
E
H
c
H
c
2
H
c
2
S
c
2
c
2
E
H
c
2
H
c
2
S
c
2
c
2
E
H
H
H
c
2
H
c
2
S
c
2
c
2
S
c
c
2
c
c
c
H
c
2
H
c
2
S
c
2
c
2
S
c
c
2
c
c
c
H
c
c
2
H
c
H
c
S
c
c
2
c
c
dV
H
ˆ
c
c
2
dV
H
ˆ
c
dV
H
ˆ
c
dV
c
c
2
dV
c
dV
c
dV
c
c
H
ˆ
c
c
dV
c
c
dV
H
ˆ
dV
dV
dV
H
ˆ
aa
2
ab
1
ab
2
aa
1
ab
1
aa
2
1
2
ab
2
aa
1
2
1
bb
aa
ab
1
bb
2
1
2
2
1
2
2
2
1
2
ab
2
aa
1
2
1
2
1
2
2
2
1
1
ab
2
1
bb
2
2
aa
2
1
2
1
2
2
2
1
b
a
2
1
b
b
2
2
a
a
2
1
b
a
2
1
2
b
2
2
2
a
2
1
b
2
a
1
b
2
a
1
2
b
2
a
1
*
*
*
*
S
a
b
Jon H
2
+
E
E
S
H
R
E
H
S
H
H
E
S
H
H
E
H
H
SE
E
H
H
SE
E
SE
H
E
H
SE
H
E
H
SE
H
E
H
SE
H
E
H
E
H
SE
H
SE
H
E
H
ab
n
H
aa
ab
aa
ab
aa
ab
aa
ab
aa
ab
aa
ab
aa
ab
aa
ab
aa
aa
ab
ab
aa
1
0
0
1
1
0
0
2
1
2
2
Z identyczności obu centrów a i b wynika
2
1
2
2
2
1
c
c
czyli
c
c
S
2
2
1
N
N
c
c
E
dla
S
2
2
1
N
N
c
c
E
dla
b
a
b
1
a
1
b
a
b
1
a
1
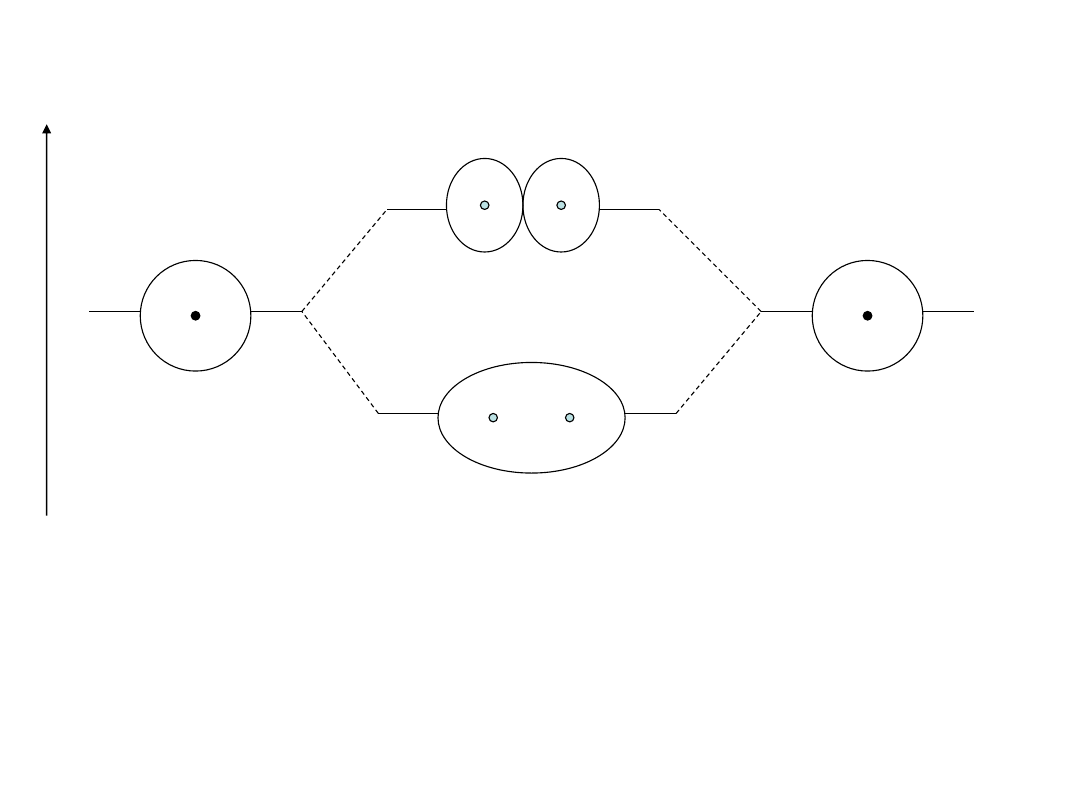
Jon H
2
+
E
E
H
E
H
atom a
atom b
χ
a
χ
b
E
-
E
+
+
+
-
Ψ
+
orbital wiążący
Ψ
-
orbital antywiążący
Jeżeli R maleje, to |H
ab
|
rośnie
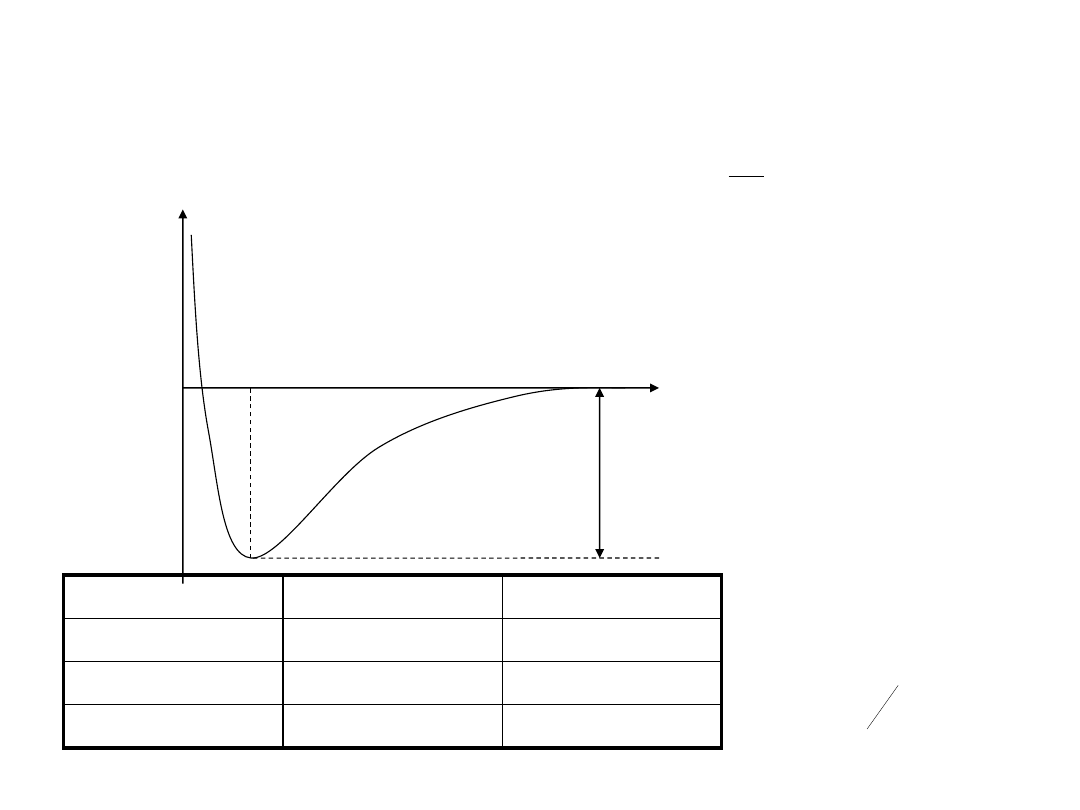
Jon H
2
+
Energia całkowita cząsteczki :
R
e
E
2
c
R
R
e
E
E
H
D
e
D
e
R
e
Doświadczalne
2,793 eV
1,057
Å
Obliczone
1,78 eV
1,32
Å
Obliczone war
2,35 eV
1,06
Å
24
,
1
e
N
0
a
r
a
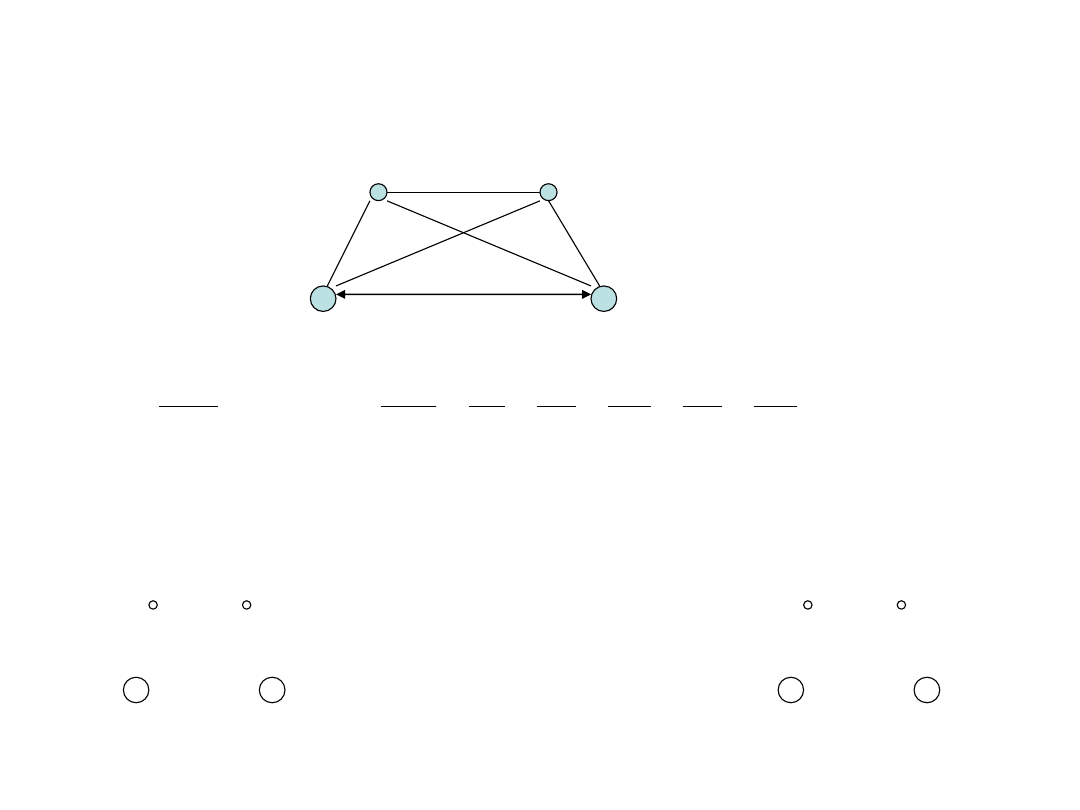
Cząsteczka H
2
2
2
1
2
2
2
1
2
12
2
2
2
2
2
1
2
2
B
B
A
A
AB
e
r
e
r
e
r
e
r
e
r
e
R
e
m
H
ˆ
2
1
1
B
A
R
r
12
r
B2
r
A1
r
B1
r
A2
A
2
1
B
Przybliżenie Borna-Oppenheimera: R
AB
= const
Przybliżenie jednoelektronowe:
A
2
1
B
1
2
2
B
A
A
1
2
B
2
2
1
1
c
c
Cząsteczka H
2
1
2
2
1
1
2
2
1
2
2
1
1
2
2
1
1
B
A
B
A
B
B
A
A
N
N
Wyznacznik Slatera
Energia średnia:
2
1
12
2
2
1
12
2
1
1
2
2
1
2
1
1
2
2
1
1
2
2
1
1
1
2
1
2
2
dV
dV
r
e
K
dV
dV
r
e
J
dV
r
e
Z
m
h
V
K
J
h
E
j
*
i
j
*
i
ij
j
*
j
i
*
i
ij
i
A
A
A
e
*
i
ii
p
i
nn
p
i
p
i
j
ij
ij
ii
e

Bazy funkcyjne 1
n
...
...
...
...
...
n
...
n
...
n
,...,
,
n
n
n
!
n
2
1
2
1
2
1
2
1
2
2
2
1
1
1
1
Metoda Hartree-Focka- Roothana SCF-LCAO-MO
Przybliżenie jednoelektronowe:
Metoda LCAO (Linear Combination of Atomic Orbitals)
Funkcje jednoelektronowe jako liniowe kombinacje funkcji bazy:
m
j
j
ij
i
c
1
1
1

Bazy funkcyjne 2
W cząsteczce: rozwinięcie orbitali molekularnych φ
i
(r)
na funkcje bazowe - orbitale atomowe
χ
j
(r)
m
j
j
ij
i
r
c
r
1
Orbitale atomowe
χ
j
(r
) są zazwyczaj centrowane na jądrach atomowych
Orbital atomowy AO = część radialna × część kątowa
,
Y
r
R
,
,
r
r
lm

Bazy funkcyjne 3
Część kątowa l=
0
1
2
3
s
p
d
f
AO grupujemy w powłoki o określonym l mające tę samą część radialną
Część radialna – 2 rodzaje baz:
slaterowskie = wielomian(r) * exp(-
αr)
gaussowskie = wielomian(r) * exp(-
αr
2
)
Właściwą asymptotykę dla małych i dużych r mają funkcje slaterowskie,
ale obliczenia całek z r
12
są bardzo czasochłonne i dlatego stosuje się
częściej funkcje gaussowskie.

Skontraktowane bazy gaussowskie
K
k
k
jk
j
r
G
a
r
1
gdzie:
χ
j
jest skontraktowanym orbitalem typu gaussowskiego CGTO
G
k
jest prymitywnym orbitalem Gaussa PGTO
Współczynniki rozwinięcia ustalone przez twórców oprogramowania, nie
podlegają optymalizacji w trakcie obliczeń SCF.

Wybór baz funkcyjnych
Baza minimalna (single zeta SZ)
po jednej funkcji radialnej R(r) dla orbitalu danej
podpowłoki
Przykład:
atom C 1s
2
2s
2
2p
2
Baza: jedna funkcja radialna dla reprezentacji orbitalu 1s
jedna funkcja radialna dla reprezentacji orbitalu 2s
jedna funkcja radialna dla reprezentacji orbitalu 2p
Czyli 5 funkcji bazy
χ
1s
,
χ
2s
,
χ
2px
,
χ
2py
,
χ
2pz

Wybór baz funkcyjnych
Baza double zeta (DZ)
po dwie funkcje radialne R(r) dla orbitalu danej
podpowłoki
Przykład:
atom C 1s
2
2s
2
2p
2
Baza: dwie funkcje radialne dla reprezentacji orbitalu 1s
dwie funkcje radialne dla reprezentacji orbitalu 2s
dwie funkcje radialne dla reprezentacji orbitalu 2p
Czyli 10 funkcji bazy
χ
1s;1
,
χ
1s;2
,
χ
2s;1
,
χ
2s;2
,
χ
2px;1
,
χ
2px;2
,
χ
2py;1
,
χ
2py;2
,
χ
2pz;1
,
χ
2pz;2

Wybór baz funkcyjnych
Baza double zeta valence (DZV)
po jednej funkcji radialnej R(r
) dla orbitali powłok wewnętrznych
po dwie funkcje radialne R(r
) dla orbitali powłok walencyjnych
Przykład:
atom C 1s
2
2s
2
2p
2
Baza: jedna funkcja radialna dla reprezentacji orbitalu 1s
dwie funkcje radialne dla reprezentacji orbitalu 2s
dwie funkcje radialne dla reprezentacji orbitalu 2p
Czyli 9 funkcji bazy
χ
1s
,
χ
2s;1
,
χ
2s;2
,
χ
2px;1
,
χ
2px;2
,
χ
2py;1
,
χ
2py;2
,
χ
2pz;1
,
χ
2pz;2

Wybór baz funkcyjnych
Analogicznie baza triple zeta valence (TZV)
po jednej funkcji radialnej R(r
) dla orbitali powłok wewnętrznych
po trzy funkcje radialne R(r
) dla orbitali powłok walencyjnych
Przykład:
atom C 1s
2
2s
2
2p
2
Baza: jedna funkcja radialna dla reprezentacji orbitalu 1s
trzy funkcje radialne dla reprezentacji orbitalu 2s
trzy funkcje radialne dla reprezentacji orbitalu 2p
Czyli 13 funkcji bazy
χ
1s
,
χ
2s;1
,
χ
2s;2
,
χ
2s;3
,
χ
2px;1
,
χ
2px;2
,
χ
2px;3
,
χ
2py;1
,
χ
2py;2
,
χ
2py;3
,
χ
2pz;1
,
χ
2pz;2
,
χ
2pz;2

Wybór baz funkcyjnych
Funkcje polaryzacyjne
– dodatkowe funkcje dla orbitali nieobsadzonych
Przykład:
atom C 1s
2
2s
2
2p
2
Baza double zeta valence polaryzacyjna(DZVP)
Baza: jedna funkcja radialna dla reprezentacji orbitalu 1s
dwie funkcje radialne dla reprezentacji orbitalu 2s
dwie funkcje radialne dla reprezentacji orbitalu 2p
jedna funkcja radialna dla reprezentacji orbitali 3d
Czyli 15 funkcji bazy
1funkcja 1s, 2 funkcje 2s, 2 funkcje 2px, 2 funkcje 2py, 2 funkcje 2pz,
dodatkowo 6 funkcji 3d (d
xy
, d
yz
, d
xz
, d
x2
, d
y2
, d
z2
)

Wybór baz funkcyjnych
Funkcje dyfuzyjne
– dodatkowe funkcje radialne o małym wykładniku tzn.
rozciągające się daleko od jąder
Stosowane dla anionów

Bazy
Pople’owskie
6-31G VDZ
funkcje rdzenia: 1 kontrakcja z 6 prymitywów Gaussowskich
funkcje walencyjne: 2 kontrakcje (z 3 i 1 prymitywów)
3-21G
VDZ
tyle samo kontrakcji lecz mniej prymitywów
6-311G VTZ
funkcje rdzenia: 1 kontrakcja z 6 prymitywów Gaussowskich
funkcje walencyjne: 3 kontrakcje (z 3, 1 i 1 prymitywów)

Bazy
Pople’owskie
Dla większych baz uzupełnienie o funkcje polaryzacyjne (o wyższym l)
6-31G* = 6-31(d) = VDZP
funkcje rdzenia: 1 kontrakcja z 6 prymitywów Gaussowskich
funkcje walencyjne: 2 kontrakcje (z 3 i 1 prymitywów)
funkcje polaryzacyjne: 1 kontrakcja z 1 prymitywu
Funkcje dyfuzyjne:
6-31+G*
j.w
. + funkcja o niskim wykładniku (dalekozasięgowa)

Podsumowanie
Dobra baza
– należy poszukiwać wskazówek w literaturze lub własnym
doświadczeniu (różne bazy dla różnych własności)
Rutynowe obliczenia
– bazy ≥ VDZP
Bazy Gaussowskie:
-
Pople’owskie 6-311G(d)
(dla H zwykle nie dodajemy funkcji polaryzacyjnych p)
-
dla obliczeń z uwzględnieniem korelacji (MP2, CI)
correlation consistent cc-pVnZ
(n=D,T,Q,5,…)
augmented aug-cc-pVnZ
Wyszukiwarka
Podobne podstrony:
wykladChK-03, Chemia UŁ, teoretyczna wykład
wykladChK-10, Chemia UŁ, teoretyczna wykład
wykladChK-11, Chemia UŁ, teoretyczna wykład
wykladChK-15, Chemia UŁ, teoretyczna wykład
wykladChK-12, Chemia UŁ, teoretyczna wykład
wykladChK-13, Chemia UŁ, teoretyczna wykład
wykladChK-07, Chemia UŁ, teoretyczna wykład
wykladChK-14, Chemia UŁ, teoretyczna wykład
wykladChK-04, Chemia UŁ, teoretyczna wykład
wykladChK-09, Chemia UŁ, teoretyczna wykład
wykladChK-05, Chemia UŁ, teoretyczna wykład
wykladChK-01, Chemia UŁ, teoretyczna wykład
wykladChK-02, Chemia UŁ, teoretyczna wykład
chemia organiczna wykład 6
Chemia medyczna wykład 1
Chemia fizyczna wykład 11
Cząsteczka (VB), CHEMIA, semestr 1, chemia ogólna, wykłady
chemia fizyczna wykłady, sprawozdania, opracowane zagadnienia do egzaminu Sprawozdanie ćw 7 zależ
2 chemia teoretyczna
więcej podobnych podstron