Spin

Z momentem pędu elektronu w atomie (lub cząsteczce), podobnie jak z momentem pędu każdego innego ładunku, związany jest pewien moment magnetyczny. Okazuje się, że w mechanice kwantowej, nawet w sytuacji, gdy moment pędu (orbitalny) elektronu jest równy zeru (jak np. dla elektronu opisywanego orbitalem typu s), elektron wykazuje pewien własny moment pędu (o innej naturze).

Tego rodzaju moment pędu, tzw. wewnętrzny moment pędu, nazywamy spinem.

Konsekwencją faktu, że elektron posiada określony spin (kręt) jest pojawienie się magnetycznego momentu elektronu.

Spinem nazywamy dodatkowy wewnętrzny moment pędu, który nie jest związany z ruchem orbitalnym elektronu.

Początkowo podejrzewano, że spin elektronu wynika z ruchu obrotowego elektronu wokół własnej osi (stąd angielskie słowo „spin” i polskie słowo „kręt”). Okazuje się jednak, że gdyby spin elektronu wynikał rzeczywiście z ruchu wirowego elektronu (wokół własnej osi), elektron musiałby obracać się z prędkością 300 razy większą od prędkości światła, co jak wiadomo ze szczególnej teorii względności Einsteina, jest niemożliwe.

Wniosek: spin elektronu nie ma odpowiednika w fizyce klasycznej

Spin (czyli spinowy moment pędu) ma charakterystykę podobną w sensie matematycznym do orbitalnego momentu pędu elektronu.

A zatem:

1. Spinowy moment pędu (S), podobnie jak orbitalny moment pędu (M) jest wielkością wektorową: S=i∙S_x+j∙S_y+k∙S_z

2. Zgodnie z zasadą nieokreśloności Heisenberga, możliwe jest jednoczesne wyznaczenie (pomiar) kwadratu całkowitego spinu (S²) oraz składowej zetowej spinu (S_z).

Podobnie jest dla orbitalnego momentu pędu, dla którego możemy jednocześnie wyznaczyć tylko kwadrat długości (M²) i jedną składową (umownie: zetową) M_z.

3. Rzut wektora spinu na wyróżnioną oś układu współrzędnych wynosi m_sħ (podobnie jak rzut wektora M na pewną oś wynosi mħ).

4. Rzut wektora spinu na wyróżnioną oś układu wynosi zawsze +½ ħ albo -½ ħ (czyli m_s=½ lub m_s= -½).

5. Kwadrat spinu elektronu jest zawsze równy ¾ ħ², natomiast kwadrat orbitalnego momentu pędu wynosi l(l+1)ħ².

6. Przez analogię do orbitalnego momentu pędu, kwadrat spinu zapisujemy jako ½∙(½+1)ħ albo s∙(s+1)ħ

(gdzie s=½).

Wprowadzamy zatem dla elektronu w atomie dwie nowe (dodatkowe) liczby kwantowe, które określają jego spin:

magnetyczną spinową liczbę kwantową m_s (odpowiednik magnetycznej liczby kwantowej m), oraz

spinową liczbę kwantową s (odpowiednik orbitalnej liczby kwantowej l).

Dopuszczalne wartości liczb kwantowych s i m_s :

s=½ m_s=±½

Stan elektronu w atomie jest zatem opisywany zestawem pięciu liczb kwantowych: n, l, m, s, m_s

Ponieważ jednak wartość liczby kwantowej s wynosi dla elektronu zawsze ½, podawanie tej liczby nie jest konieczne (tylko dla elektronu!).

Wniosek: opis stanu elektronu za pomocą funkcji falowej ψ_nlm(r,θ,φ) nie jest wystarczający i dlatego wprowadzamy jeszcze funkcję spinową σ, która zależy od liczb kwantowych s i m_s i dla której argumentem jest tzw. współrzędna spinowa.

Ponieważ s=½, zamiast pisać σ_sms zapisujemy w skrócie σ_ms

Ponadto, ponieważ m_s=±½, możliwe są jedynie dwie funkcje spinowe: σ_½ oraz σ_-½

Wobec tego stosujemy zapis α (dla σ_½) oraz β (dla σ_-½).

σ_½ ≡ α σ_-½ ≡ β

Czyli:

Jeżeli wartość spinowej magnetycznej liczby kwantowej m_s

wynosi ½ mówimy, że elektron opisywany jest spinową funkcją α.

Podobnie, jeżeli wartość spinowej magnetycznej liczby kwantowej m_s wynosi -½ mówimy, że elektron opisywany jest spinową funkcją β.

Możemy zatem zapisać dwa dodatkowe równania własne dla atomu wodoru:

Po zamianie symboli i wprowadzeniu s=½ mamy dla kwadratu spinu

oraz

natomiast dla składowej zetowej wektora spinu:

oraz

Pełny opis elektronu w atomie jest dany przez iloczyn funkcji ψ_nlm(r,θ,φ) (zależącej od współrzędnych przestrzennych) oraz funkcji σ_sms (zależącej od współrzędnej spinowej).

Funkcję ψ_nlm(r,θ,φ) nazywamy przestrzenną funkcją falową albo orbitalem.

Funkcję σ_sms nazywamy spinową funkcją falową.

Iloczyn funkcji przestrzennej ψ i funkcji spinowej σ nazywamy spinorbitalem. A zatem spinorbital φ jest dany przez wyrażenie:

φ_nlmsms = ψ_nlm(r,θ,φ)∙ σ_sms

Ponieważ z jednego orbitala ψ można uzyskać dwa spinorbitale:

ψ∙α oraz ψ∙β, mówimy często o „orbitalach alfa” (czyli ψ∙α) lub „orbitalach beta” (czyli ψ∙β).

Elektron opisywany spinową funkcją α oznaczamy przez ↑

natomiast elektron opisywany spinową funkcją β przez ↓

Orbital oznaczamy zazwyczaj symbolem □

Warto pamiętać, że nie tylko elektrony obdarzone są spinem. Spin posiadają również np. neutrony oraz jądra atomowe (co jest wykorzystywane w różnych dziedzinach chemii, fizyki i medycyny).

Spin w układach wieloelektronowych

W układach gdzie występuje więcej niż jeden elektron, liczby kwantowe związane ze spinem zapisujemy przez analogię jako

S oraz M_s. Mówimy wówczas o całkowitym wektorze spinu (dotyczącym jednocześnie wszystkich elektronów).

Liczba S dla układu wieloelektronowego wynika z różnicy między elektronami opisywanymi funkcją α i funkcją β.

Jeżeli np. tyle samo elektronów w układzie opisywanych jest funkcjami α i β, to całkowity spin S wynosi 0.

Jeżeli różnica wynosi 1 (np. mamy trzy elektrony α i dwa β lub odwrotnie), to całkowity spin S wynosi ½.

Jeżeli różnica wynosi 2 (np. mamy trzy elektrony β i jeden α lub odwrotnie), to całkowity spin S wynosi 1 (... i tak dalej).

Liczbę M_s dla układu wieloelektronowego obliczamy poprzez

sumowanie (po wszystkich elektronach) liczb m_s

Multipletowość układu określamy obliczając wartość 2∙S+1.

Np. dla S=0 , multipletowość wynosi 1 (gdyż 2∙0+1=1)

Mówimy wówczas o stanie singletowym.

Dla S=½ , multipletowość wynosi 2 (gdyż 2∙½+1=2)

Mówimy wówczas o stanie dubletowym.

Dla S=1 , multipletowość wynosi 3 (gdyż 2∙1+1=3)

Mówimy wówczas o stanie trypletowym.

Dla S=1½ , multipletowość wynosi 4 (gdyż 2∙1½+1=4)

Mówimy wówczas o stanie kwartetowym. (... i tak dalej).

Multipletowość nazywamy degeneracją spinową, gdyż określa ona ile jest możliwych wartości rzutu wektora całkowitego spinu (na określony kierunek w przestrzeni). Jeżeli całkowity spin określa liczba kwantowa S to mamy właśnie 2S+1 możliwych wartości rzutu.

Oczywiście dla układu jednoelektronowego, mamy S=s=½, czyli będzie to zawsze stan o multipletowości 2 (stan dubletowy, dublet).

Operatory związane ze spinem

Ponieważ spin nie ma odpowiednika w fizyce klasycznej, operatorów spinu nie można utworzyć w oparciu o reguły Jordana.

Dlatego, konstruujemy je (na zasadzie postulatu) w taki sposób, aby obliczane wartości średnie składowej zetowej oraz kwadratu wektora spinu były zgodne z doświadczeniem:

Pamiętając, że spin jest wektorem: S=i∙S_x+j∙S_y+k∙S_z

definiujemy następujące operatory składowych spinu (poprzez podanie w jaki sposób działają one na funkcje spinowe α i β) :

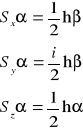
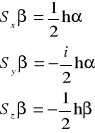
Przybliżenie Borna-Oppenheimera

Atom wodoru (jony wodoropodobne) - najbardziej skomplikowane układy, dla których równanie Schrödingera można rozwiązać w sposób dokładny.

Przybliżenie Borna-Oppenheimera zakłada, że jądra atomowe są „nieskończenie ciężkie”, czego konsekwencją jest to, że funkcja falowa cząsteczki jest iloczynem funkcji elektronowej (zależnej parametrycznie od położenia jąder) i funkcji falowej jądrowej.

A zatem, rozwiązujemy problem własny dla funkcji zależącej od położenia elektronów, dla zadanego (zamrożonego) położenia jąder. Uzasadnienie: wobec niewielkiej masy elektronów w porównaniu z masą jąder, rozkład elektronów w cząsteczce zależy w przybliżeniu od chwilowego rozkładu jąder, natomiast nie zależy on od ruchu jąder.

Hamiltonian elektronowy

Na podstawie przybliżenia BO można zdefiniować tzw. hamiltonian elektronowy:

gdzie T_el oznacza energię kinetyczną elektronów, U_j-el jest energią potencjalną oddziaływania elektronów z jądrami (przyciąganie kulombowskie), U_el-el jest energią potencjalną wzajemnego oddziaływania elektronów (odpychanie kulombowskie), U_j-j jest energią potencjalną wzajemnego oddziaływania jąder (odpychanie kulombowskie).

Hamiltonian elektronowy w porównaniu z pełnym hamiltonianem nie zawiera członu T_j odpowiadającego za energię kinetyczną jąder.

Przybliżenie BO jest powszechnie stosowane we współczesnej chemii kwantowej.

Energia elektronowa

Wartość własna (energia) w równaniu Schrödingera z hamiltonianem elektronowym (tzw. elektronowe równanie Schrödingera) nazywana jest energią elektronową (E^el).

Po rozwiązaniu powyższego równania i uzyskaniu E^el (dla określonej konfiguracji jąder) możemy otrzymać energię całkowitą E poprzez dodanie do E^el członu odpowiadającego odpychaniu międzyjądrowemu.

Przybliżenie jednoelektronowe

Po wprowadzeniu przybliżenia BO mamy do czynienia z zagadnieniem własnym
. Jest ono jednak w dalszym ciągu zbyt skomplikowane i niezbędne jest wprowadzenie kolejnego przybliżenia, opartego na modelu cząstek niezależnych.

W przybliżeniu jednoelektronowym każdemu elektronowi w atomie (lub cząsteczce) przyporządkowujemy jednoelektronową funkcję falową nazywaną spinorbitalem.

W tym ujęciu, ruch każdego z elektronów rozpatrujemy niezależnie.

Zakaz Pauliego (pierwsze sformułowanie)

W układzie wieloelektronowym nie może być dwóch elektronów znajdujących się w jednakowym stanie.

Alternatywnie:

Żadne dwa elektrony nie mogą być opisane takim samym spinorbitalem (czyli takim samym zespołem liczb kwantowych określających spinorbital).

Metoda Hartree - iloczynowa funkcja falowa

A zatem, np. dla układu trzech elektronów (atom litu) mielibyśmy pełną funkcję falową ψ=φ₁(1)∙φ₂(2)∙φ₃(3) , gdzie φ_k(k) oznacza k-ty spinorbital opisujący ruch k-tego elektronu (czyli zależący od współrzędnych k-tego elektronu).

Założenie iloczynowej funkcji falowej (niepoprawne) jest intuicyjne i wynika z tego, że prawdopodobieństwo zdarzeń niezależnych jest równe iloczynowi prawdopodobieństw.

Na iloczynowej funkcji falowej oparta była stosowana w przeszłości metoda Hartree.

Wada metody Hartree: postać funkcji falowej jest sprzeczna z zasadą nieodróżnialności cząstek identycznych (pamiętamy, że funkcja opisująca układ elektronów musi być antysymetryczna względem permutacji elektronów). Funkcja iloczynowa nie wykazuje natomiast żadnej symetrii względem permutacji elektronów (patrz ćwiczenia).

Wyznacznik Slatera

Okazuje się, że wyznacznikowa funkcja falowa posiada odpowiednią symetrię (tzn. jest antysymetryczna względem permutacji elektronów), jak również ma inne, wygodne własności.

Wyznacznik zbudowany ze spinorbitali, który można następnie rozwinąć w antysymetryczną funkcję falową, nazywamy wyznacznikiem Slatera

Wyznacznik Slatera dla układu n­-elektronowego:

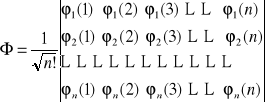
(sposób konstrukcji wyznacznika Slatera dla dowolnej konfiguracji elektronowej - patrz ćwiczenia).

Np. dla układu dwuelektronowego, wyznacznik jest bardzo prosty:

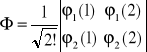
i można go rozwinąć otrzymując funkcję:

Własności funkcji wyznacznikowej

1. Poprawna symetria względem permutacji elektronów (antysymetryczność) - uzasadnienie: zamiana (permutacja) dwóch elektronów byłaby równoważna zamianie kolumn wyznacznika, co jak wiadomo z algebry liniowej, powoduje zmianę znaku.

2. Unormowanie - uzasadnienie: współczynnik 1/√n! zapewnia unormowanie funkcji wyznacznikowej.

3. Spełnianie zakazu Pauliego - uzasadnienie: jeżeli mielibyśmy dwa elektrony opisywane tym samym orbitalem, to dwa wiersze wyznacznika byłyby jednakowe, czyli wyznacznik byłby równy zeru (co wynika z własności matematycznych wyznacznika). Funkcja falowa równa tożsamościowo zeru jest niemożliwa, gdyż oznaczałoby to, że opisywany układ nie istnieje.

Przybliżenie jednoelektronowe - stanowi podstawę spojrzenia na strukturę elektronową atomów i molekuł, na nim opierają się takie pojęcia jak: orbitale, konfiguracja elektronowa, powłokowy model atomu, energie orbitalne, itp.

Zakaz Pauliego (drugie sformułowanie)

Dwa elektrony nie mogą znajdować się w tym samym miejscu przestrzeni konfiguracyjno-spinowej (czyli w tym samym miejscu przestrzeni konfiguracyjnej (x,y,z) i spinowej (ten sam spin: ↑ lub ↓).

Całka kulombowska J, całka wymienna K i całka rdzeniowa I

Rozwiązanie równania Schrödingera z hamiltonianem elektronowym (w przybliżeniu BO i w przybliżeniu jedno-elektronowym) prowadzi m.in. do trzech rodzajów całek, które pojawiają się w wyrażeniu na energię elektronową:

Całka J_pq, nazywana całką kulombowską:

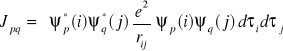
Całka K_pq, nazywana całką wymienną:

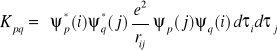
Całka I_p, nazywana całką rdzeniową:

Definicje tych całek będą wykorzystane przy omawianiu

metody Hartree-Focka.

Konfiguracje elektronowe atomów

Konfiguracją elektronową nazywamy przyporządkowanie elektronów określonym poziomom energetycznym.

Patrz podręcznik Kołosa, rozdział 8:

(i) energie orbitalne, (ii) powłoki i podpowłoki elektronowe, (iii) układy zamkniętopowłokowe, (iv) układy otwartopowłokowe, (v) reguły Hunda.

Termy atomowe i molekularne

Termami atomowymi (molekularnymi) nazywamy rzeczywiste (obserwowane w spektroskopii) poziomy energetyczne atomu (molekuły).

Wyznaczanie termów atomowych dla danej konfiguracji elektronowej - patrz ćwiczenia oraz podręcznik Kołosa (rozdział 9)

87

---