Metoda zaburzeń

Metodę zaburzeń (rachunek zaburzeń) stosuje się zazwyczaj wtedy, gdy hamiltonian badanego układu daje się przedstawić w postaci:

oraz spełnione są dwa następujące warunki:

1. Operator
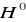
   , nazywany hamiltonianem niezaburzonym, musi być taki, aby równanie Schrödingera z tym hamiltonianem można było rozwiązać ściśle

2. Operator
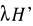
   , nazywany zaburzeniem, musi być mały (parametr zaburzeniowy λ musi być niewielką liczbą).

Rachunek zaburzeń można sformułować na wiele sposobów. Zajmiemy się sformułowaniem Rayleigha-Schrödingera niezależnym od czasu.

Rachunek zaburzeń Rayleigha-Schrödingera

(niezależny od czasu)

Cel: wyznaczenie przybliżonych rozwiązań równania Schrödingera z całkowitym hamiltonianem, czyli

Pełny hamiltonian
zależy od parametru λ, a więc rozwiązania pełnego równania Schrödingera (z tym hamiltonianem) również zależą od λ.

Parametr λ jest z definicji niewielki, co umożliwia rozwinięcie zarówno ψ_n jak i E_n w szereg według potęg λ :

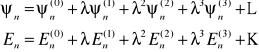
W krótszym zapisie mamy (to samo):

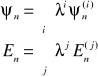
Im mniejszy jest parametr λ (czyli im mniejsze jest zaburzenie) tym szybciej zbieżne są oba te szeregi.

Podstawiamy oba powyższe rozwinięcia do równania

(gdzie
) :

, czyli

Oczywiste jest, że powyższe równanie jest spełnione gdy współczynniki przy jednakowych potęgach λ po lewej i po prawej stronie równania są sobie równe.

97