W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

1

1

K

K

I

I

N

N

E

E

M

M

A

A

T

T

Y

Y

K

K

A

A

P

P

Ł

Ł

Y

Y

N

N

U

U

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

R

R

U

U

C

C

H

H

O

O

Ś

Ś

R

R

O

O

D

D

K

K

A

A

C

C

I

I

Ą

Ą

G

G

Ł

Ł

E

E

G

G

O

O

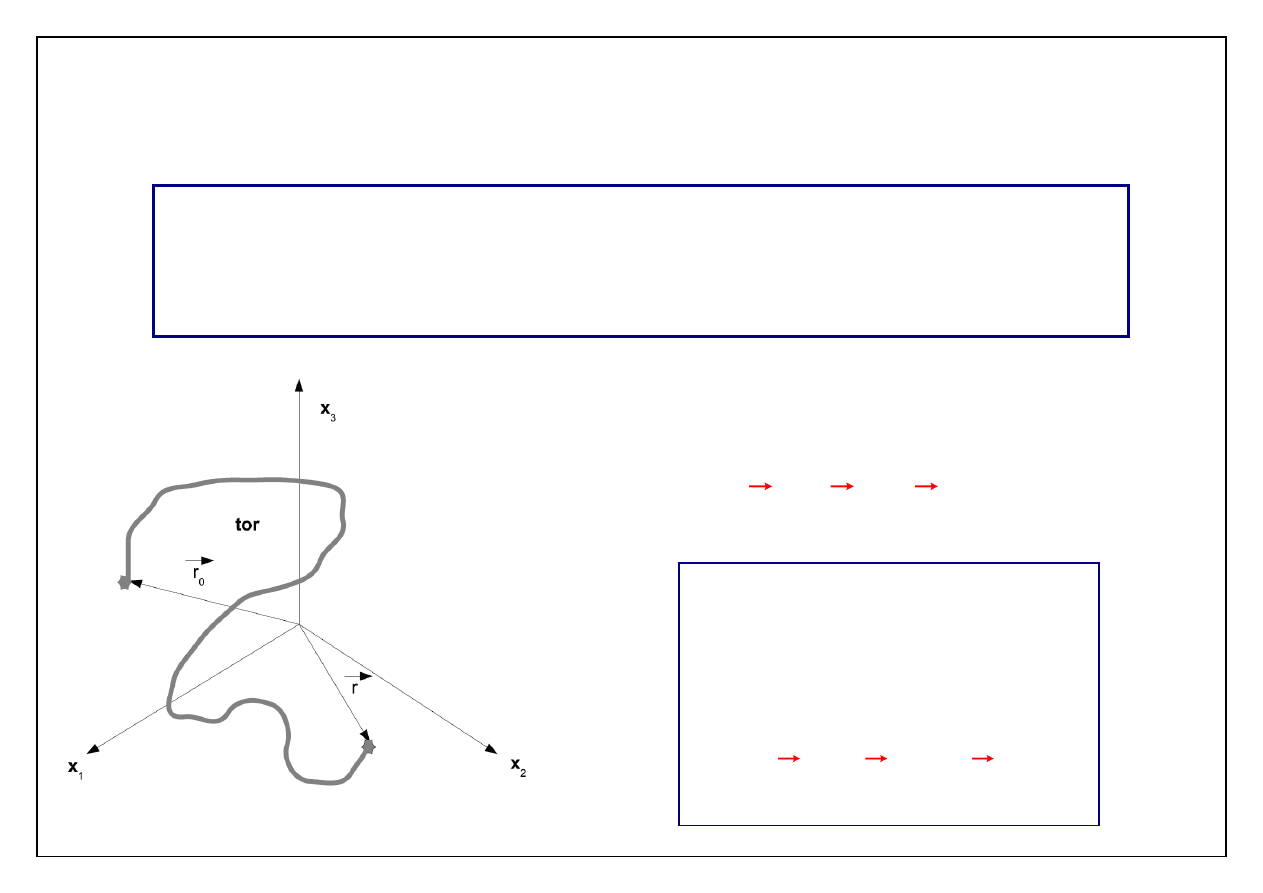
Ośrodek ciągły jest utworzony przez ciągły zbiór punktów
materialnych

– w każdym punkcie przestrzeni znajduje się punkt

materialny ośrodka

Wybrany punkt materialny porusza

się, więc zmienia się jego położenie

o

r

r(t, r )



TOR

– linia zakreślona

przez

poruszający

się

punkt materialny.
Początek toru określa:

o

o

r(0, r )

r



Prędkość poruszającego się punktu:

o

o

r(t, r )

v

v(t, r )

t









Przyspieszenie punktu materialnego:

2

o

o

o

2

v(t, r )

r(t, r )

a

a(t, r )

t

t















Warunek:

wiadomo gdzie punkt materialny znajdo

wał się w chwili początkowej

Eliminacja niedogodności:

o

o

r

r (t, r)



wstawiamy do

o

o

(t, r)

v

v(t, r )

v(t, r

)





Złożenie daje

v

v(t, r)



czyli pole wektorowe zależne od czasu i położenia (wektorowa
funkcja miejsca)

t = t

1

prędkości wybranego punktu

prędkość dowolnego punktu

D

D

W

W

A

A

O

O

P

P

I

I

S

S

Y

Y

R

R

U

U

C

C

H

H

U

U

P

P

Ł

Ł

Y

Y

N

N

U

U

Zmienne Lagrange’a

Zmienne

o

o

o

o

(x , y , z )

t, r

czyli czas oraz współrzędne miejsca, w którym

rozważany punkt znajdował się w chwili początkowej

Zmienne Eulera

Zmienne

(x, y, z)

t, r

czyli czas oraz współrzędne miejsca, w którym

jest w danej chwili poruszający się punkt

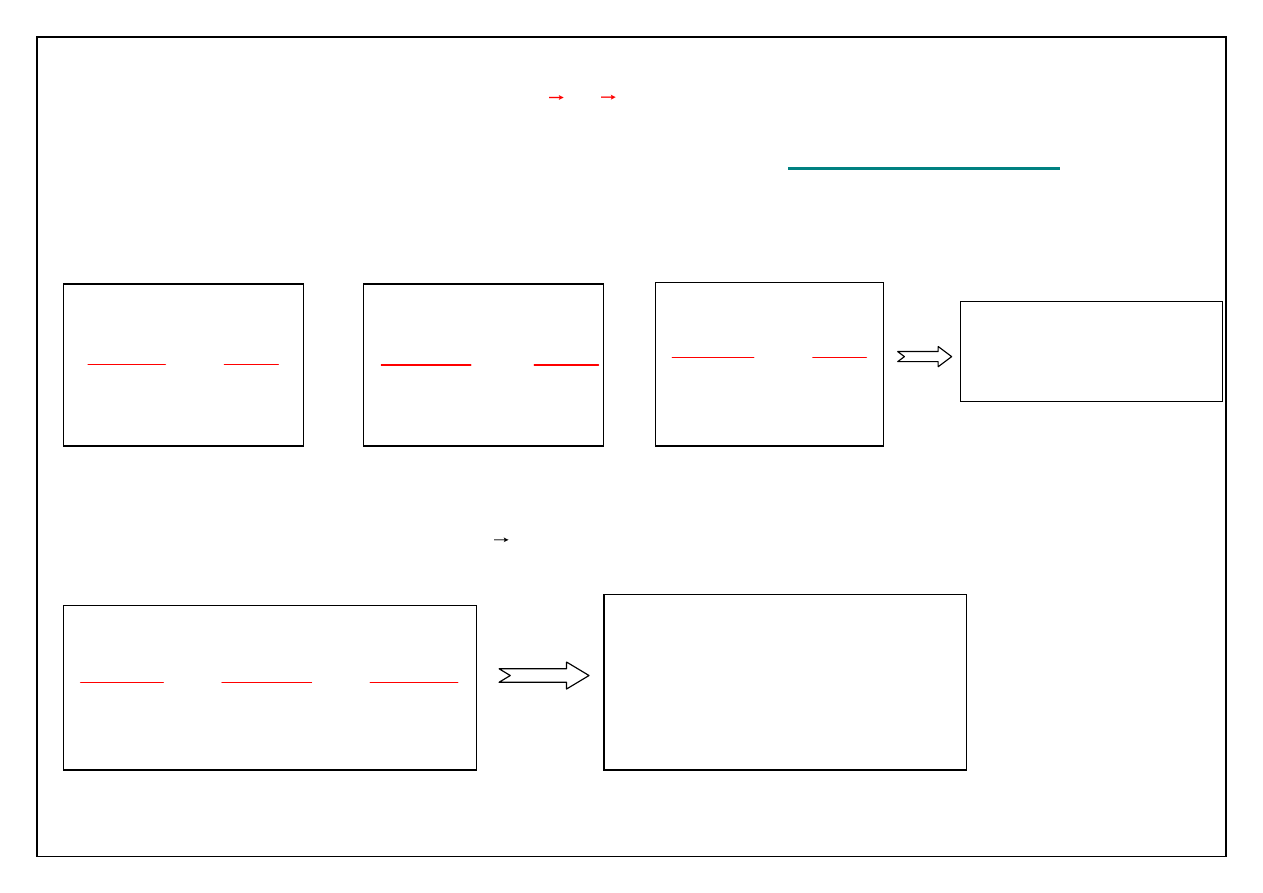
Załóżmy, że w każdym miejscu przestrzeni i w każdym czasie
znamy wektory prędkości

v(t, r)

. Linie, do których w wybranej

chwili wektory te będą styczne nazywamy

LINIAMI PRĄDU

Cosinusy kierunkowe LINII PRĄDU:

ds

–

długość elementarnego odcinka linii

v

– moduł (długość) wektora

v

1

1

dx

v

ds

v



2

2

dx

v

ds

v



3

3

dx

v

ds

v



3

1

2

1

2

3

dx

dx

dx

v

v

v





Równanie linii prądu
(krawędziowe)

po wyrugowaniu
długości łuku i modułu
prędkości

Równania
parametryczne

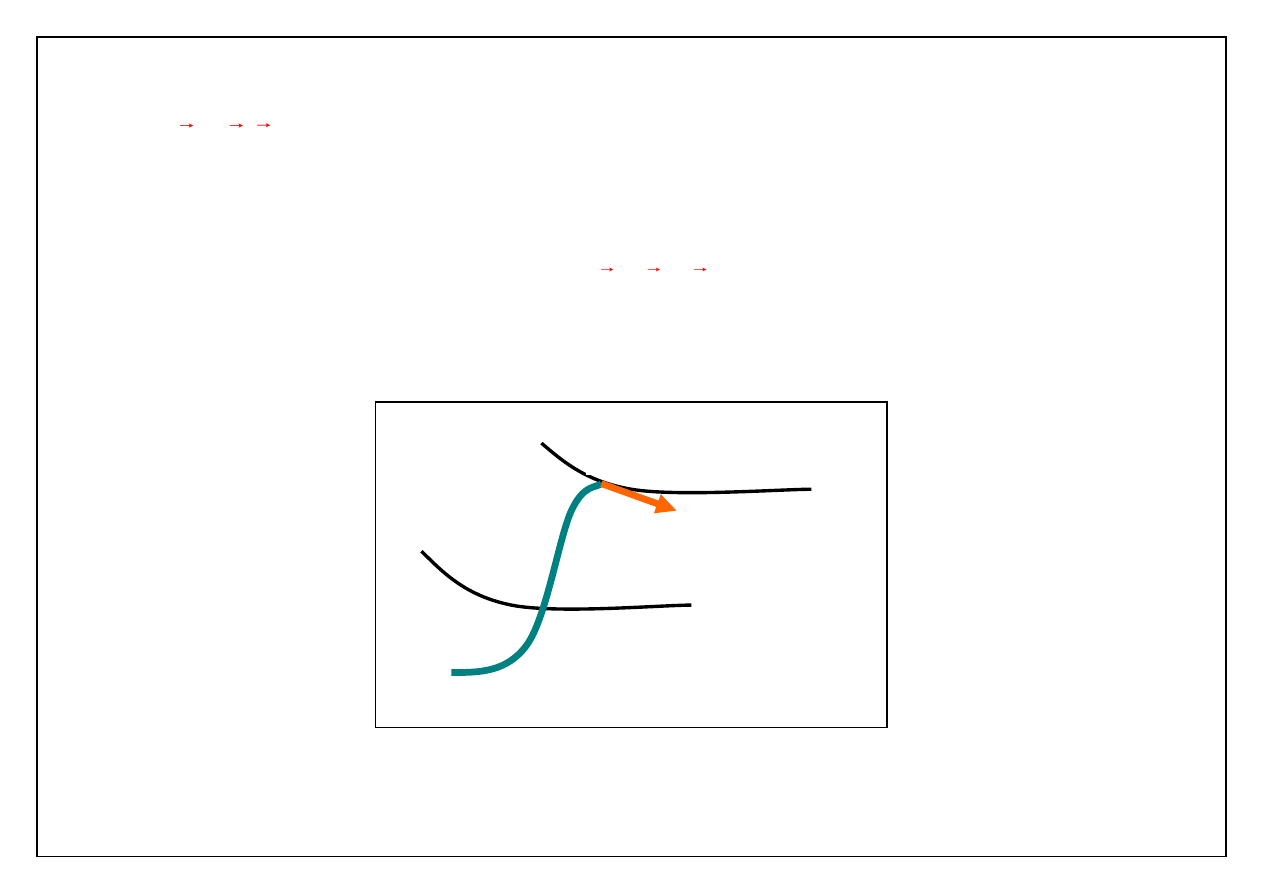
Gdy pole prędkości nie zmienia się w czasie linie prądu są niezmienne. Zatem

jeśli

v

v(r)



niezależna od czasu

TORY i LINIE PRĄDU SĄ

NIEROZRÓŻNIALNE

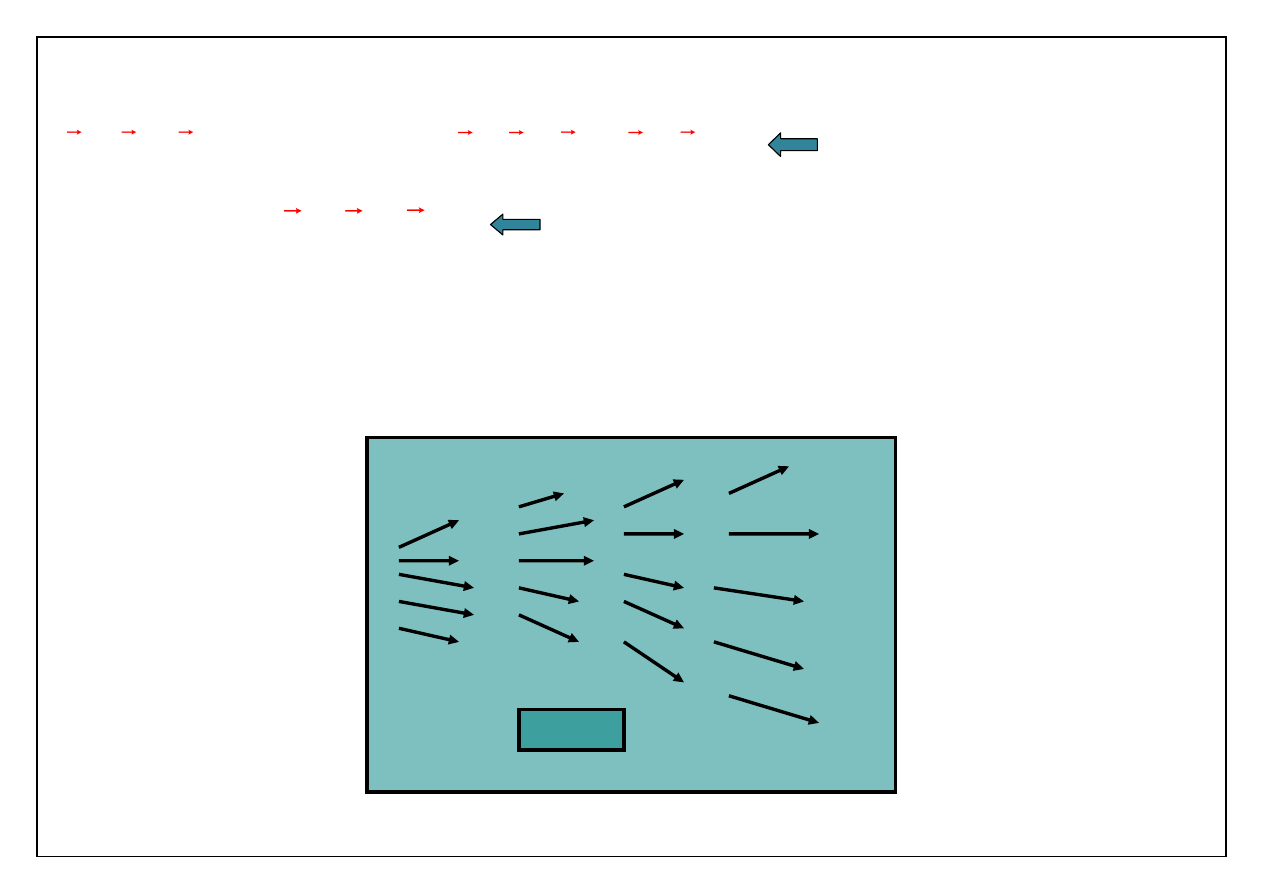
Gdy pole prędkości zależy od czasu

v

v(t, r)



TOR

jest na swym końcu zawsze

styczny do

LINII PRĄDU

(jest obwiednią chwilowych linii prądu).

tor

linia prądu w chwili t

linia prądu w chwili t

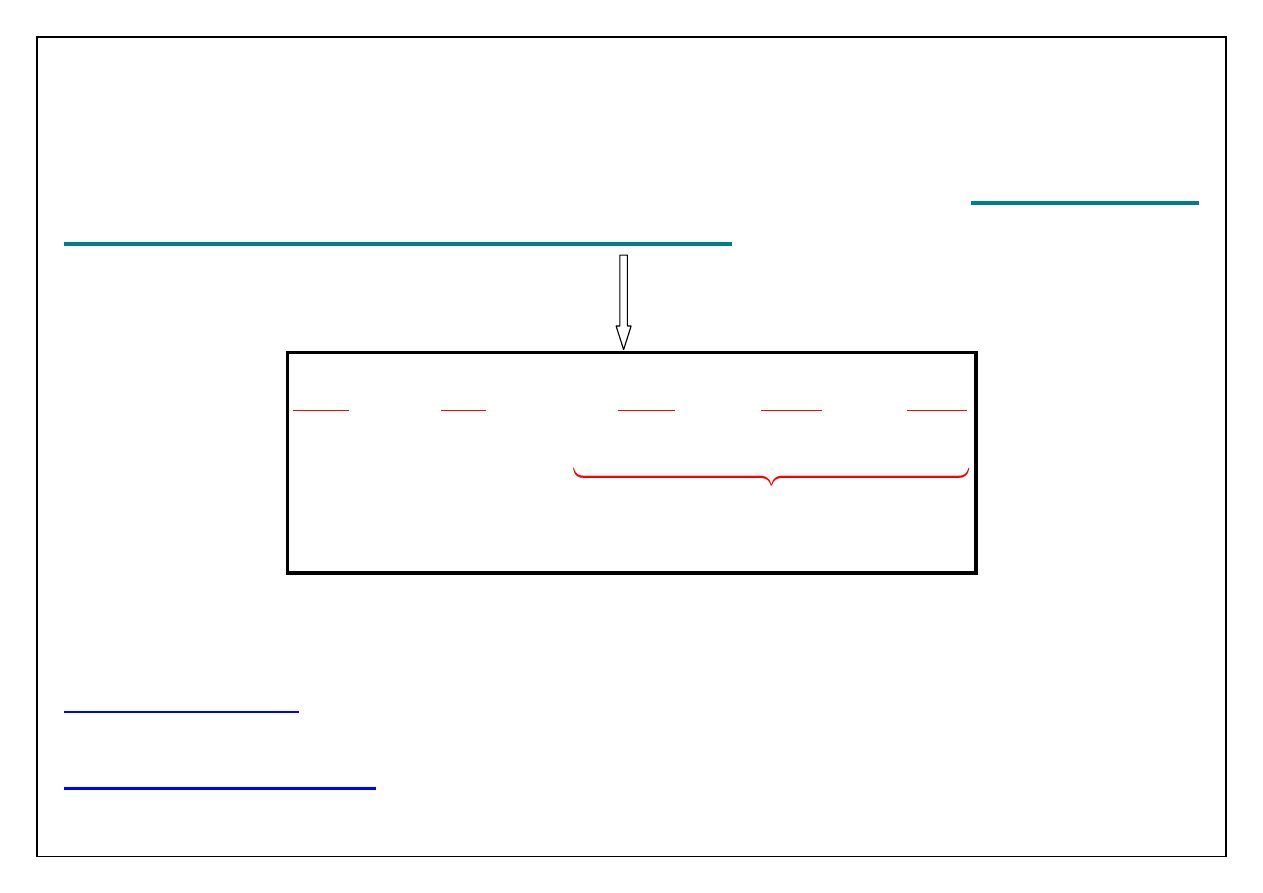
Niech

1

2

3

f

f (t, x (t), x (t), x (t))



będzie funkcją określającą wielkość

fizykalną opisującą poruszający się ośrodek ciągły. Pochodna
względem czasu takiej funkcji nosi nazwę

POCHODNEJ

SUBSTANCJALNEJ lub MATERIALNEJ

1

2

3

1

2

3

pochodna

pochodna

loka ln a

konwekcyjna

f

f

f

x

x

x

f

v

v

v

t

df

dt

























pochodna lokalna -

określa zmianę funkcji

f

wynikającą z upływu czasu

pochodna konwekcyjna

–

opisuje

zmianę funkcji

f

wynikającą z ruchu

ośrodka ciągłego

POCHODNA SUBSTANCJALNA

zapisana przy użyciu konwencji

sumacyjnej

k

k

f

f

v

t

x

df

dt









 

Z

definiujmy operator różniczkowania zwany nablą. Oznacza się

go symbolem



.

1

2

3

1

2

3

e

e

e

grad

x

x

x







 













Zapiszmy

POCHODNĄ SUBSTANCJALNĄ

używając operatora



.

f

v

)f

t

df

(

dt







 

dla k=1,2 ,3

P

P

R

R

Z

Z

Y

Y

S

S

P

P

I

I

E

E

S

S

Z

Z

E

E

N

N

I

I

E

E

W

W

Z

Z

M

M

I

I

E

E

N

N

N

N

Y

Y

C

C

H

H

E

E

U

U

L

L

E

E

R

R

A

A

Przyspieszenie

a

jest polem wektorowym zależnym od czasu i

położenia. Otrzymujemy go licząc pochodną substancjalną z pola
prędkości

k

k

v

v

v

t

x

a









 

C

zęść konwekcyjną można zapisać przy użyciu iloczynu skalarnego

prędkości i operatora nabla

.

v

v

)v

t

a

(







 

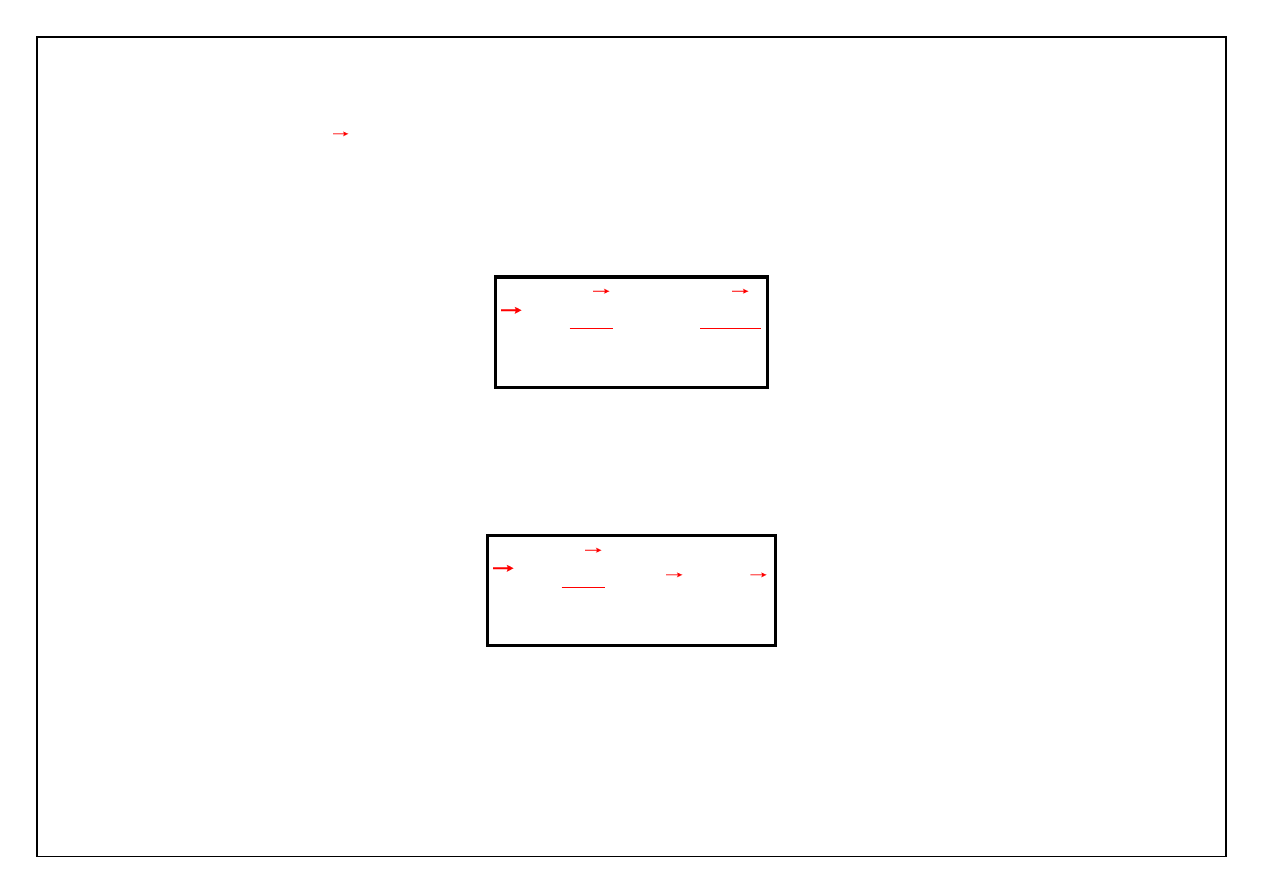
Aby policzyć składową przyspieszenia

i

a

korzystamy ze wzoru

dla k=1,2 ,3

i

i

i

k

k

v

v

v

t

x

a













pamiętając o konwencji sumacyjnej po

k

.

K

K

R

R

Ó

Ó

T

T

K

K

I

I

E

E

U

U

Z

Z

U

U

P

P

E

E

Ł

Ł

N

N

I

I

E

E

N

N

I

I

E

E

:

:

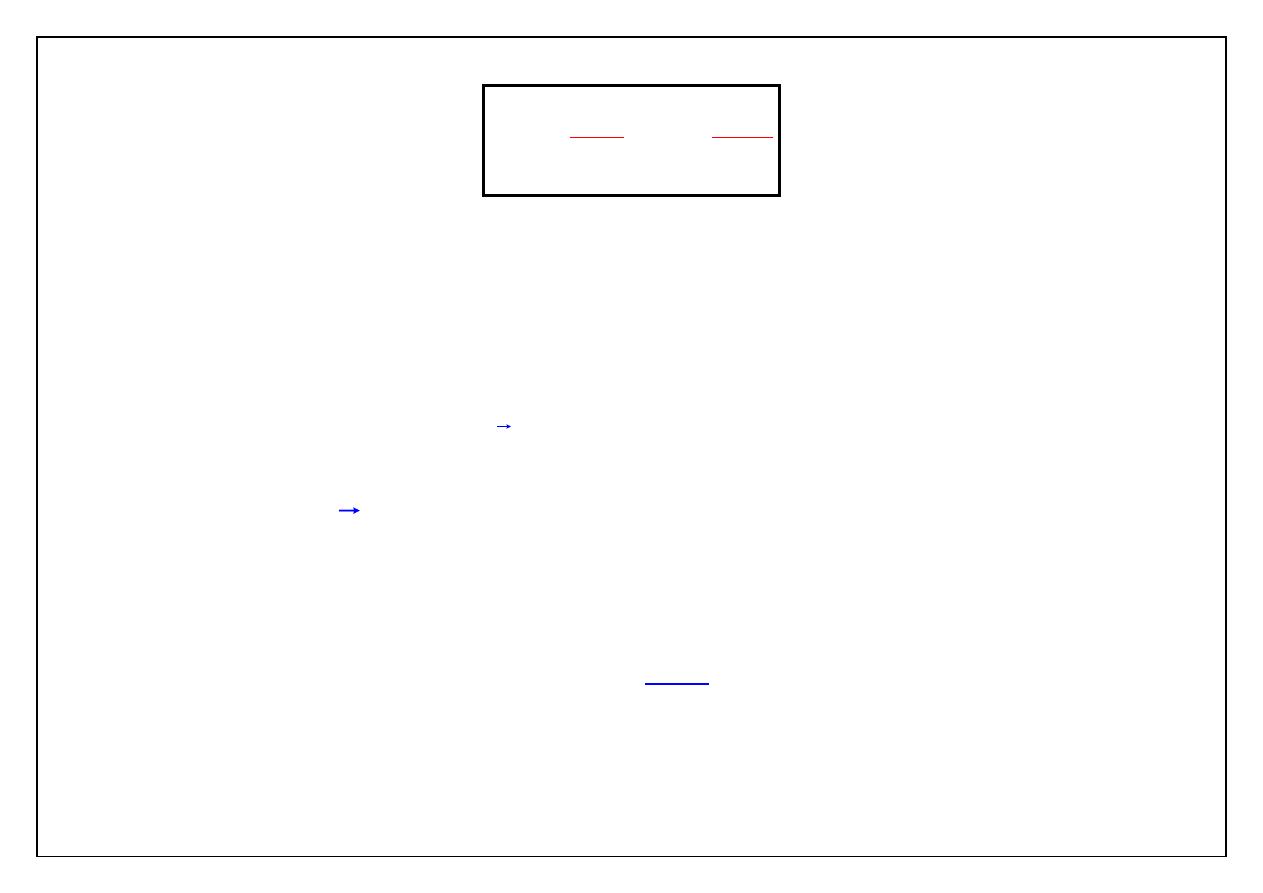
Iloczyn skalarny

prędkości

v

i wektora nabla



1

1

2

2

3

3

(v

)

v

v

v

   

  

gdzie

k

k

x



 



Iloczyn skalarny zawierający nablę



nie jest przemienny!

dla i=1,2 ,3

3

1

2

1

2

3

v

v

v

(

v)

(v

)

x

x

x







 

















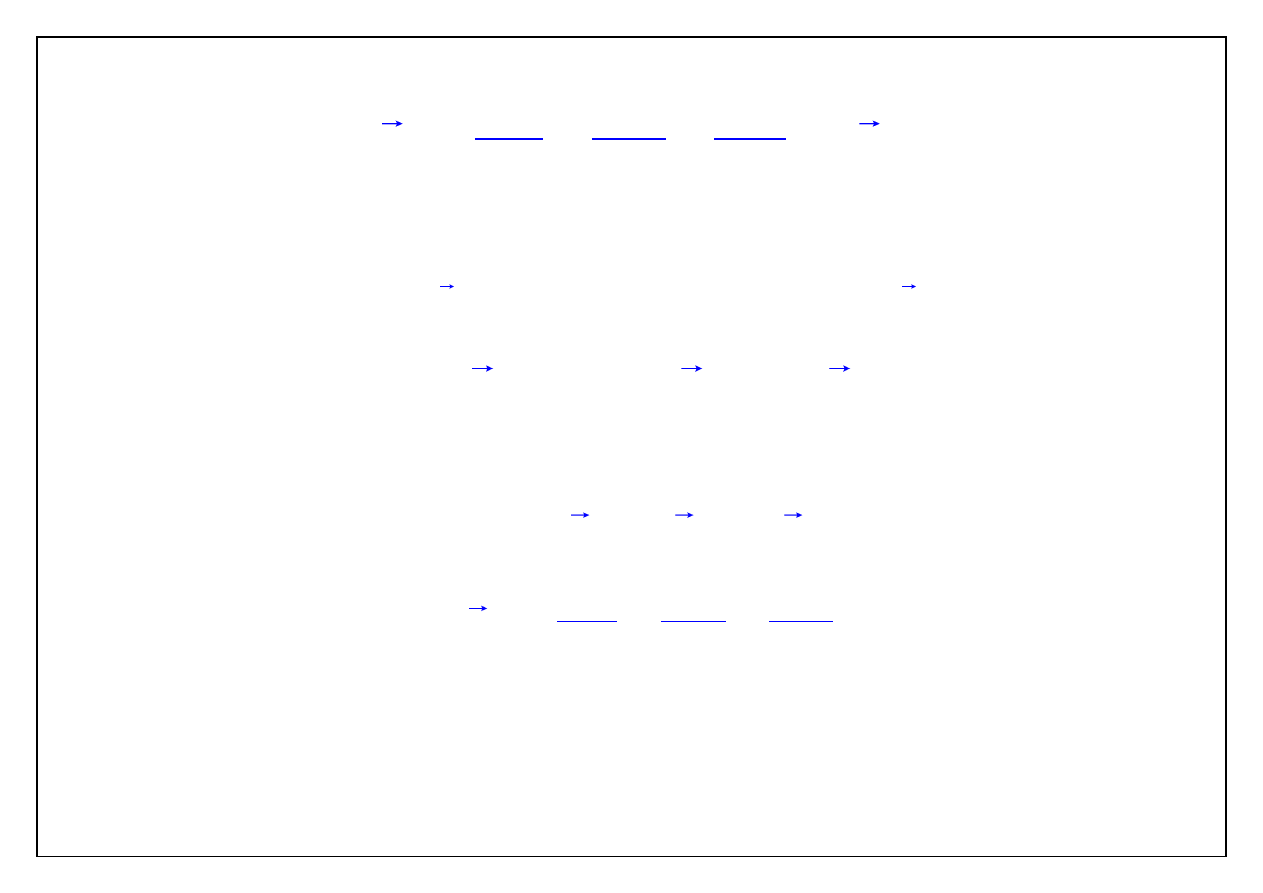
Iloczyn wektorowy



i

v

n

osi nazwę rotacji wektora

v

v

grad v

rot v

 

 

1

2

3

1

2

3

1

2

3

e

e

e

rot v

x

x

x

v

v

v







































Wektor

-

Tensor -

ik i k

T e e



i i

e

A

A



i

A

-

składowe wektora,

i

e

-

wersory kartezjańskiego układu

współrzędnych.

ik

T

-

składowe tensora,

i

k

e , e

- wersory

Uwaga

i

e

nie mnożymy przez

k

e

!