Politechnika Łódzka

Centrum Nauczania Matematyki i Fizyki

Ćwiczenie O3_A8
Badanie aktywności optycznej.

Cel ćwiczenia

Celem ćwiczenia jest:

1. Zademonstrowanie zjawiska aktywności optycznej.
2. Wyznaczenie współczynnika skręcalności właściwej sacharozy.
3. Wyznaczenie zależności współczynnika skręcalności właściwej sacharozy od

długości fali.

Wstęp.

Substancję nazywamy optycznie czynną (aktywną) jeśli płaszczyzna polaryzacji światła

liniowo spolaryzowanego zmienia swoją orientację w przestrzeni podczas przechodzenia światła
przez tę substancję. W przypadku przechodzenia światła liniowo spolaryzowanego przez roztwór
substancji aktywnej optycznie, kąt o jaki obróci się płaszczyzna polaryzacji światła zależy od ilości
cząsteczek substancji rozpuszczonej, jakie światło napotyka na swej drodze a zatem od długości
przebywanej w roztworze drogi oraz od stężenia roztworu. Wielkość kąta skręcenia płaszczyzny
polaryzacji światła

α

opisuje prawo Biota. W przypadku roztworu substancji optycznie czynnej

(w nieaktywnym optycznie rozpuszczalniku) prawo to ma postać:



=

k d C

(1)

gdzie: k - skręcalność właściwa substancji
d - droga przebyta przez światło w roztworze
C - stężenie roztworu

Wielkość k występująca we wzorze (1), zwana skręcalnością właściwą, określa kąt skręcenia

płaszczyzny polaryzacji światła po przejściu fali świetlnej przez warstwę roztworu o jednostkowej
grubości i jednostkowym stężeniu (określonych w wybranych jednostkach). Wielkość ta zależy
przede wszystkim od rodzaju substancji optycznie czynnej zawartej w roztworze a także od rodzaju
rozpuszczalnika, z którego sporządzony jest roztwór, temperatury i długości fali światła.

Wartość skręcalności właściwej substancji aktywnej optycznie zawartej w roztworze można

zatem wyznaczyć mierząc kąt obrotu płaszczyzny polaryzacji

α

światła po przebyciu drogi d

w roztworze o znanym stężeniu C.

Przebieg pomiaru

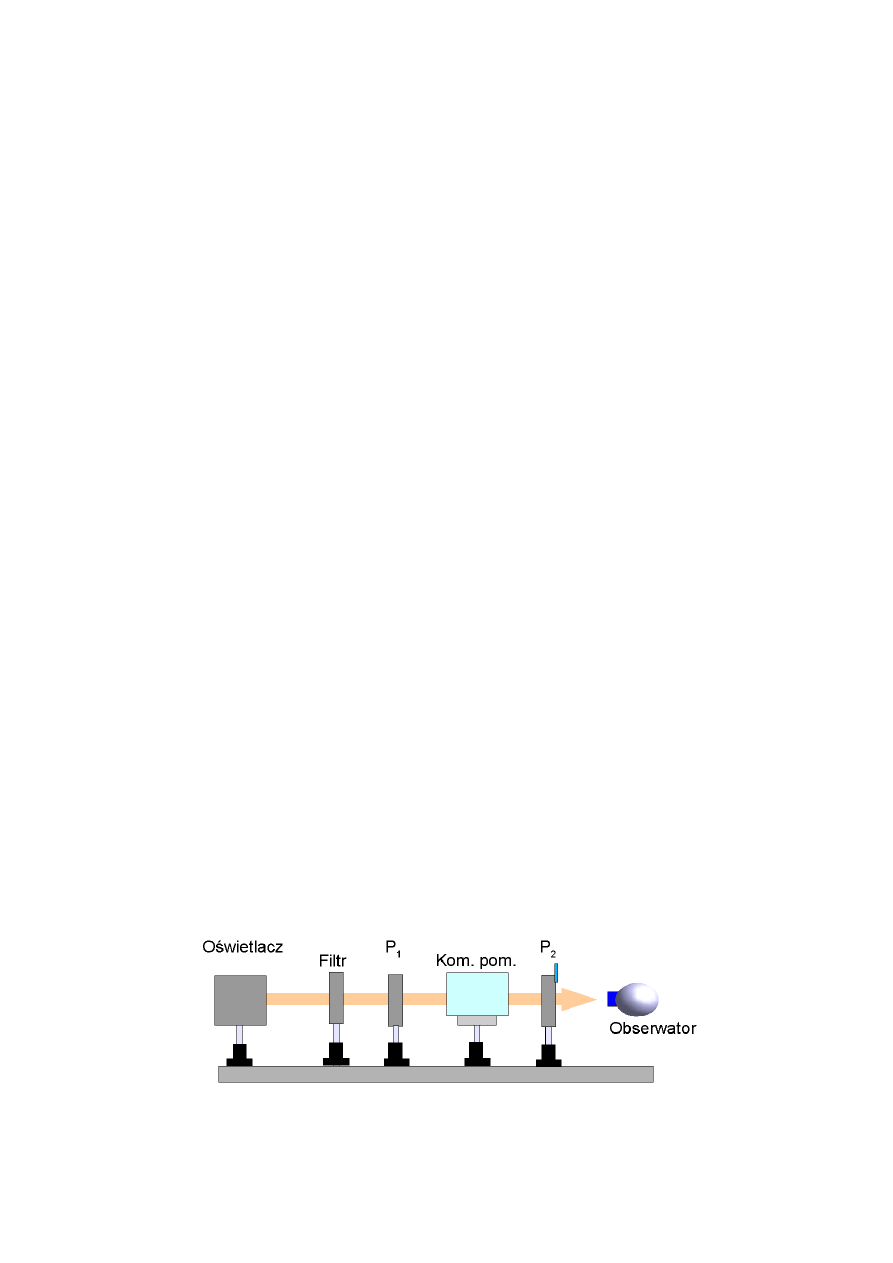
Rys. 1. Układ pomiarowy

1

Wykorzystywany podczas ćwiczenia układ pomiarowy przedstawiono na rysunku 1. Układ

składa się z oświetlacza emitującego białe światło, filtra, polaryzatora P

1

, komórki pomiarowej

zawierającej badany roztwór oraz drugiego polaryzatora P

2

. Filtr zastosowano w celu zawężenia

zakresu długości fal w wiązce przechodzącej przez komórkę pomiarową. Polaryzator P

2

przepuszcza światło o jednej, określonej płaszczyźnie polaryzacji. Konstrukcja polaryzatora P

1

jest

inna. Polaryzator ten składa się z dwóch połówek. Płaszczyzny przepuszczania obu połówek
polaryzatora są inne. Różnica wynosi kilka stopni. Dzięki takiej konstrukcji, niespolaryzowane
światło padające na polaryzator rozdzielone zostaje na dwie spolaryzowane wiązki o różnych
płaszczyznach polaryzacji.

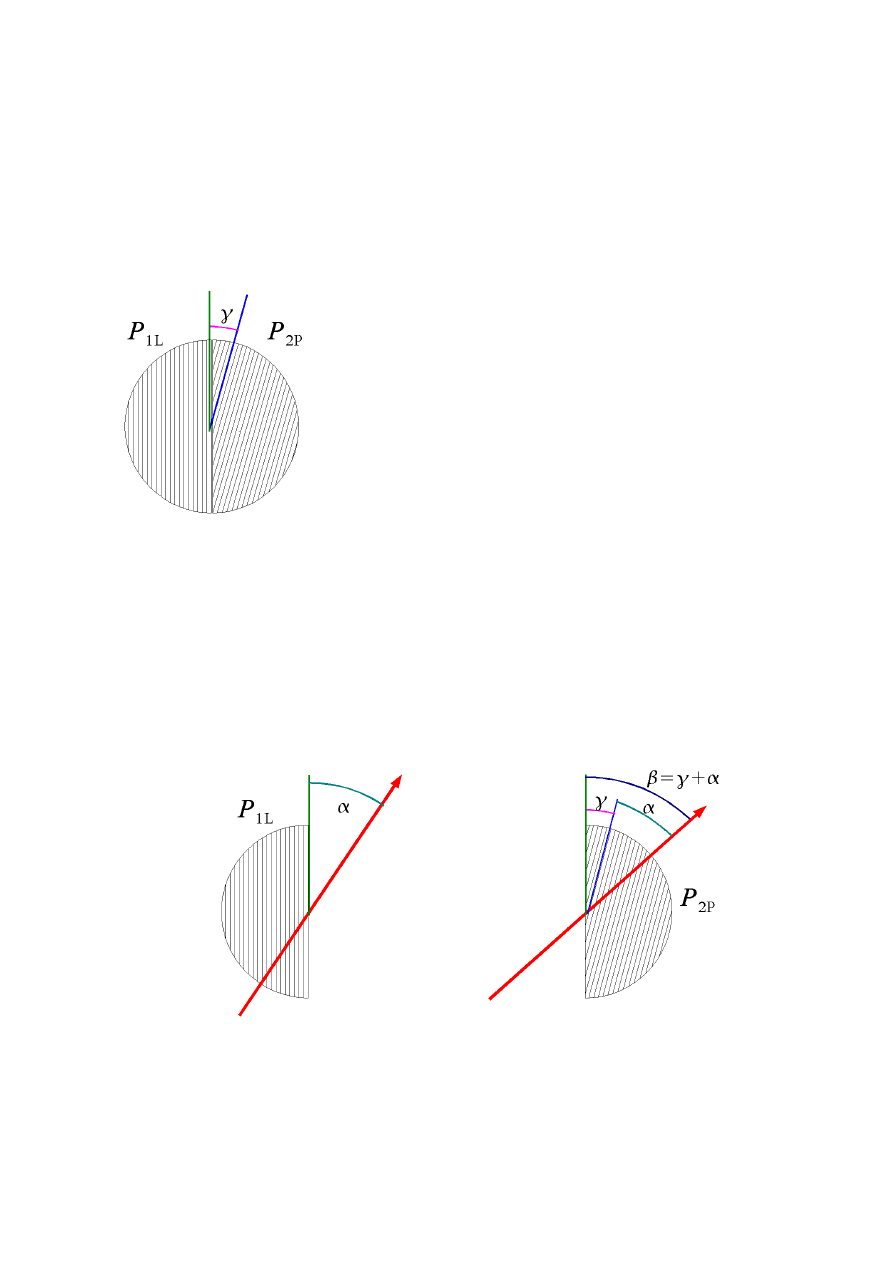
Rys. 2. Konstrukcja polaryzatora P

1

.

UWAGA! Linie narysowane na obu częściach
polaryzatora pokazują jedynie jaki rodzaj
polaryzacji jest przez dany polaryzator
przepuszczany. Nie mają one żadnego związku z
prawdziwą budową każdej z części
polaryzatora.

W przypadku polaryzatora przedstawionego na rysunku 2 światło po przejściu lewej części

jest spolaryzowane pionowo zaś światło w prawej części ma płaszczyznę polaryzacji odchyloną od
pionu o kąt

γ .

Jeżeli tak przygotowana wiązka przejdzie przez ośrodek w którym kąt skręcenia wynosi

α

to w lewej części płaszczyzna polaryzacji będzie odchylona od pionu o kąt

α

zaś w prawej części

o kąt



=







(2)

Rys. 3. Nachylenie płaszczyzny polaryzacji światła po przejściu przez polaryzator P

1

i ośrodek,

który skręcił płaszczyznę polaryzacji światła o kąt

α

.

Po przejściu przez badany ośrodek, światło pada na drugi polaryzator (P

2

). Natężenie I

światła spolaryzowanego liniowo po przejściu przez polaryzator, zgodnie z prawem Malusa, wynosi

2

I

=

I

0

cos

2





 (3)

gdzie I

0

jest natężeniem światła padającego zaś



jest kątem pomiędzy płaszczyzną

przepuszczania polaryzatora a płaszczyzną polaryzacji wiązki padającej. Ponieważ płaszczyzna
polaryzacji wiązki światła padającej na polaryzator P

2

jest w każdej połówce inna więc z godnie

z prawem Malusa, natężenia wiązek wyjściowych będą różne (rys. 4a). Obserwator będzie widział,
że obie połowy pola widzenia mają różną jasność. Pokręcając polaryzatorem P

2

można osiągnąć

stan, w którym obie połówki pola widzenia mają jednakową jasność (rys. 4b)

(a)

(b)

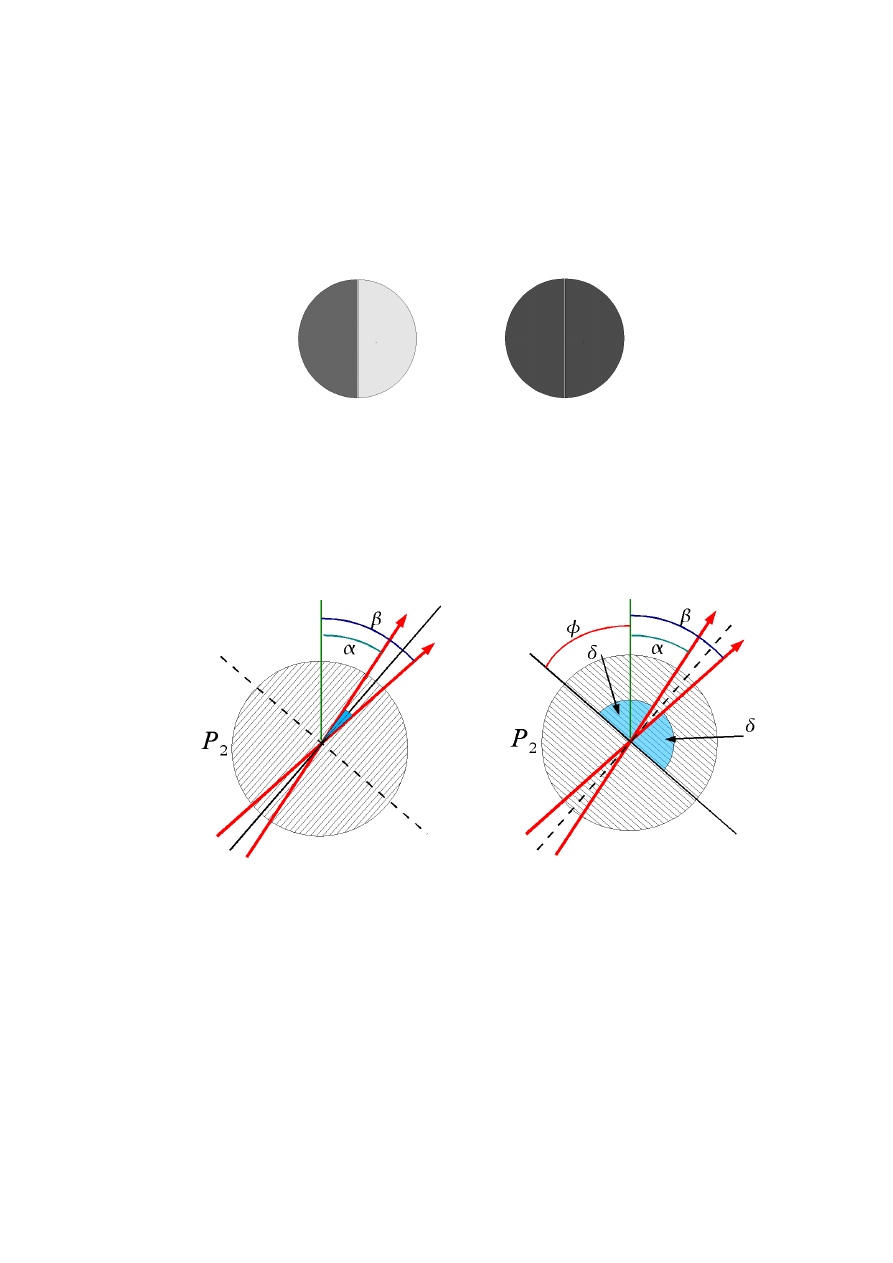
Rys. 4. Obraz widziany przez obserwatora w zależności od ustawienia polaryzatora P

2

.

Istnieją dwa położenia polaryzatora P

2

, w których jasność obu połówek jest jednakowa.

W pierwszym (rys. 5a), płaszczyzna przepuszczania polaryzatora P

2

tworzy jednakowe, małe

kąty z płaszczyznami polaryzacji obu wiązek. Zgodnie z wzorem (3) natężenie światła
przechodzącego przez polaryzator P

2

dla obu polaryzacji jest jednakowe i bliskie natężeniu

wejściowemu. Z uwagi na dużą jasność obu połówek pola widzenia, trudno jest dokładnie
zauważyć moment, w którym jasność obu połówek jest taka sama.

(a)

(b)

Rys. 5. Dwa położenia polaryzatora P

2

, w których jasność obu połówek jest jednakowa.

W drugim położeniu (rys. 5b) płaszczyzna przepuszczania polaryzatora P

2

także tworzy

jednakowe kąty z płaszczyznami polaryzacji obu wiązek. Jednak kąty te (

δ

) są duże więc

intensywność światła przechodzącego jest znacznie mniejsza. W takiej sytuacji łatwiej zauważyć
moment kiedy obie połówki pola widzenia mają tę samą jasność.

Jak widać (rysunek 5b) kąt

φ

, jaki w tej sytuacji tworzy płaszczyzna przepuszczania

polaryzatora P

2

z pionem, wynosi

=−

(4)

Jednocześnie można zauważyć, że

−=

(5)

3

Na podstawie równania (2) wiemy, że

−=

więc równanie (5) przyjmuje postać

=

(6)

Łącząc równania (4) i (6) otrzymamy, że kąt

φ

jaki tworzy płaszczyzna przepuszczania polaryzatora

P

2

z pionem wynosi

 = − = −

2

−  = 

2

− 

2

− 

(7)

Jeżeli dokonamy pomiaru dla pustego układu (czyli bez cieczy optycznie aktywnej) to kąt

=0

i kąt jaki tworzy płaszczyzna przepuszczania polaryzatora P

2

z pionem wynosi wtedy

0 =  −  = −

2

−  = 

2

− 

2

(8)

Na podstawie (7) i (8) otrzymujemy

 − 0 =−

(9)

Wystarczy więc dla pustego układu znaleźć położenie, w którym obie połówki pola widzenia

są jednakowo oświetlone a następnie umieścić w układzie badaną substancję. Kąt o jaki trzeba
będzie przekręcić polaryzator P

2

aby obie połówki pola widzenia miały ponownie jednakową

jasność jest szukanym kątem

α

o jaki ośrodek aktywny skręcił płaszczyznę polaryzacji

przechodzącego przez ośrodek światła. (Zastanów się co oznacza znak minus).

Kąt

α

o jaki ośrodek aktywny skręcił płaszczyznę polaryzacji, przechodzącego przez

ośrodek światła, zależy od długości próbki d, stężenia roztworu C i długości fali użytego światła

λ

.

Jeśli ustalimy długość fali światła korzystając z filtra i użyjemy substancji o znanym stężeniu C to
jedynym parametrem wpływającym na kąt skręcenia płaszczyzny polaryzacji

α

będzie długość

próbki d.
Jeśli oznaczymy

k C

=const= A

to na podstawie (1)

=k d C= A d

(10)

W taki razie zależność kąta skręcenia od długości próbki powinna być liniowa a współczynnik
nachylenia prostej

d 

wynosi

A

=k C

(11)

Aby znaleźć współczynnik skręcalności k dla danej substancji należy wykonać pomiary kąta

skręcenia

α

dla różnych długości ośrodka aktywnego optycznie d. Na podstawie wykresu zależności





d

 można znaleźć współczynnik nachylenia prostej A i korzystając z zależności (11) obliczyć

współczynnik skręcalności właściwej k z wzoru

k

=

A

C

(12)

4

Kolejność czynności

1. Pierwszy pomiar wykonaj bez badanej substancji i bez komórek pomiarowych.

●

Włącz źródło światła.

●

Polaryzator P

1

ustaw tak by łączenie dwóch połówek polaryzatora było w przybliżeniu

pionowe.

●

Kręcąc polaryzatorem P

2

znajdź położenie, w który obie połówki mają jednakową

jasność. Przy właściwym ustawieniu polaryzatora P

2

niewielkie jego obroty powodują

wyraźne zmiany jasności obu połówek pola widzenia (tzn. zamianę miejscami połówki
jasnej i ciemnej).

●

Na skali polaryzatora P

2

odczytaj wartość kąta

0

. Nie próbuj "zerować" skali.

Pamiętaj, że we wzorze (9) i tak występuje różnica kątów.

2. Zmierz wewnętrzne wymiary wszystkich komórek pomiarowych wykorzystywanych

w ćwiczeniu.

3. Wypełnij komórki pomiarowe roztworem dostarczonym przez obsługę laboratorium.
4. Wstawiaj komórki do układu pomiarowego w taki sposób aby otrzymać jak najwięcej różnych

wartości łącznej długości drogi, którą światło przechodzi przez badany roztwór.

5. Dla każdej kombinacji komórek pomiarowych

●

Zanotuj łączną długość badanego ośrodka d.

●

Kręcąc polaryzatorem P

2

znajdź położenie, w którym obie połówki mają jednakową

jasność

●

Na skali polaryzatora P

2

odczytaj wartość kąta

d 

6. Powtórz czynności 4-5 dla różnych długości fali przechodzącego światła (dla różnych filtrów)
7. Po zakończeniu wszystkich pomiarów opróżnij i umyj komórki, wyłączyć oświetlacz

i uporządkuj stanowisko. Roztwór wlej do naczynia w którym go otrzymałeś!!

Opracowanie sprawozdania

Sprawozdanie powinno zawierać:

1. Krótki opis przeprowadzonych pomiarów (bez wymieniania wykonywanych czynności)

2. Tabele zawierające zmierzone wartości kąta skręcenia

α

, długości ośrodka aktywnego

optycznego d oraz dane użytych filtrów.

3. Wykresy



=

f



d

=





d

−





0

 dla każdego filtra (każdej długości fali).

4. Obliczenia współczynników nachylenia (A) prostych

= f d 

metodą najmniejszych

kwadratów oraz błędu

∆α

współczynników nachylenia A.

5. Obliczenia skręcalności właściwej

k

=

A

C

dla każdego filtra.

6. Zestawienie, na jednym wykresie, prostych

= f d 

dla wszystkich wykorzystanych

filtrów. Zaznacz koniecznie kolory filtrów na wykresie.

5

7. Obliczenie błędu skręcalności właściwej z wzoru

k =k



 A

A 

C

C



8. Wyniki końcowe w postaci

k

=

k

±

k

dla każdego z filtrów.

9. Dyskusję wyników.

Literatura

1. S. Szczeniowski, Fizyka doświadczalna, PWN cz. IV, Optyka,
2. B. Jaworski, A.Dietłaf, Kurs fizyki, PWN, tom III
3. J. Karniewicz, T. Sokołowski, Podstawy fizyki laboratoryjnej, skrypt PŁ
4. H. Szydłowski, Pracownia fizyczna, PWN

6