
Przesyłanie sygnałów
analogowych
Wykład 4
Modulacje amplitudy i kąta
Wytwarzanie i sygnałów zmodulowanych i demodulacja
Korzyści z modulacji kątowych
Modulacje nośnej impulsowej
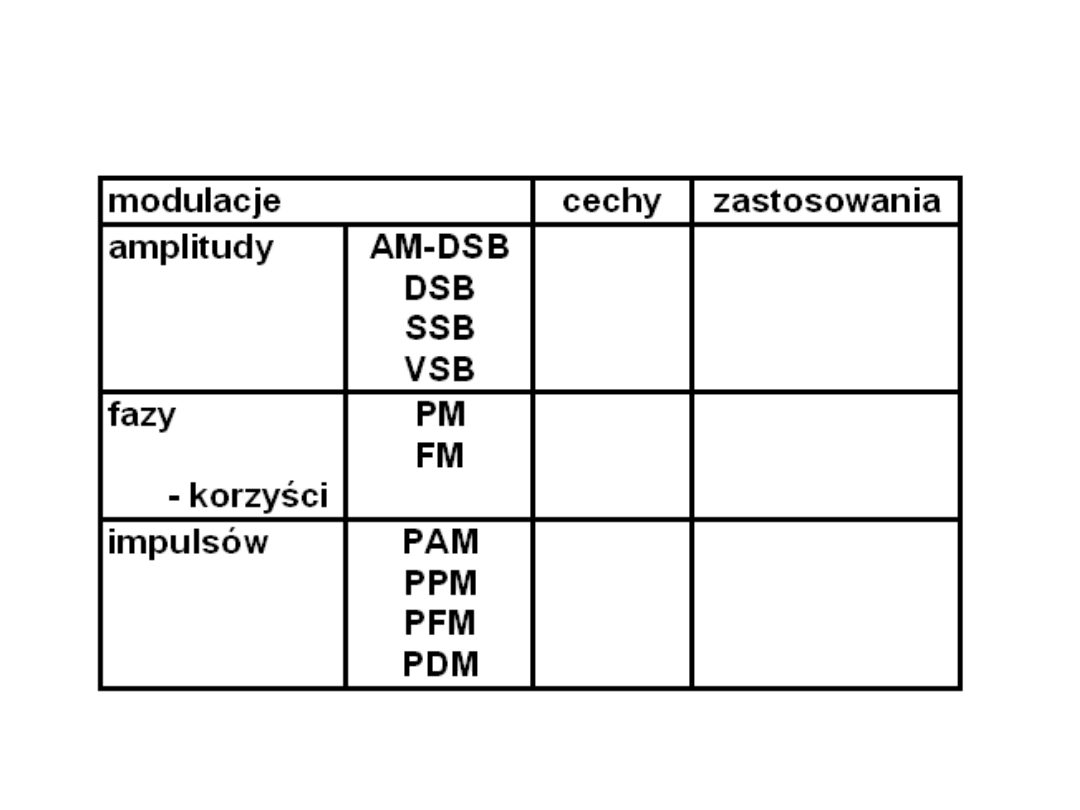
Porównanie modulacji analogowych
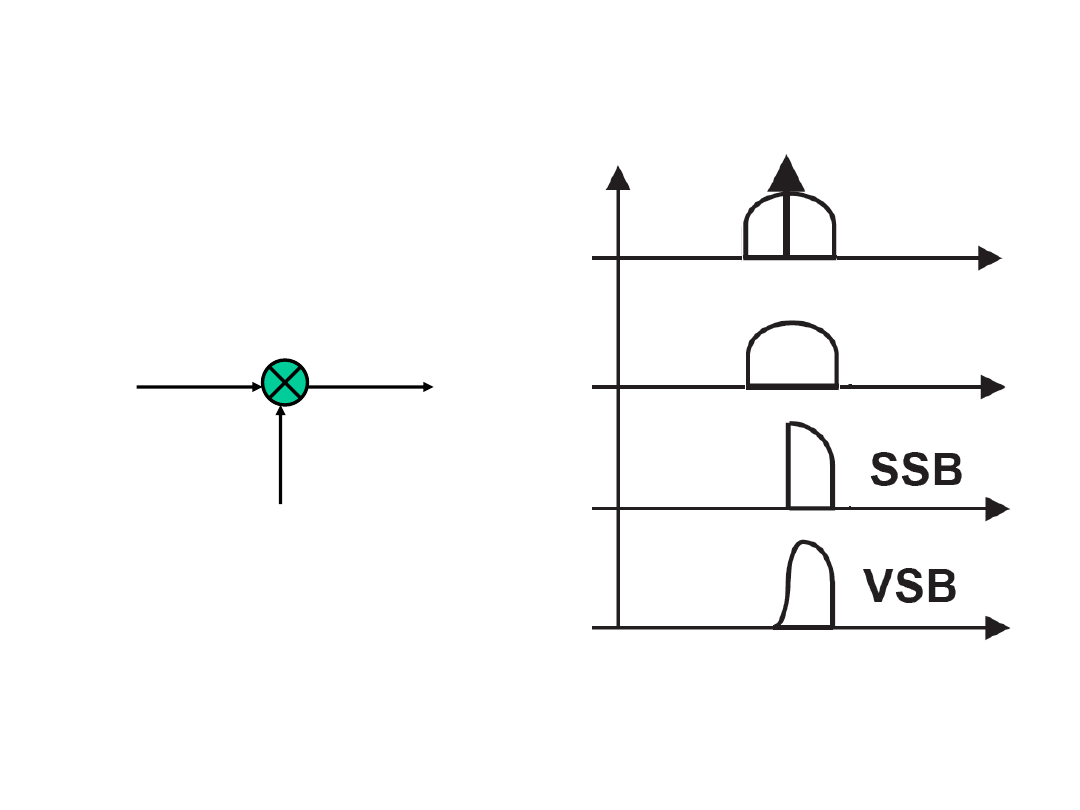
Modulacje amplitudy nośnej harmonicznej
•Modulacja dwuwstęgowa z nośną
(DSB)
•Modulacja dwuwstęgowa bez nośnej
(SC DSB)
•Modulacja jednowstęgowa
(SSB)
•Modulacja jednowstęgowa z resztkową wstęgą boczną
(VSB)
x(t)
c(t) = cos (2
f
0
t
)
g(t)=x(t)
·c(t)
Modulacja amplitudy [nośnej
harmonicznej] =
operacja iloczynu
sygnału modulującego z nośną
harmoniczną
DSB
SC DSB
Modulacja amplitudy DSB
g(t
)=A
·[ 1+m·
x
(t) ]
·
cos(2
f
0
t)
Modulacja dwuwstęgowa z nośną (DSB)
f0
2B
S
G
(f)
2 x
szersze
pasmo
wstęga dolna
wstęga górna
B
X(f)
0<m
1 -
wsp. głebokości modulacji
Modulacje SC DSB i SSB
Modulacja dwuwstęgowa bez nośnej (SC DSB)
g(t)
=A
·
x(t)
·
cos(2
f
0
t)
f0
2B
S
G
(f)
wstęga dolna
wstęga górna
f0
B
S
G
(f)
pasmo = 1 x B
np. wstęga górna
Modulacja jednowstęgowa (SSB)
2 x szersze
pasmo
g
USB
(t)=A/2[
x(t)
cos (
2
f
0
t
)
-
x(t)
sin(
2
f
0
t
)
]
^
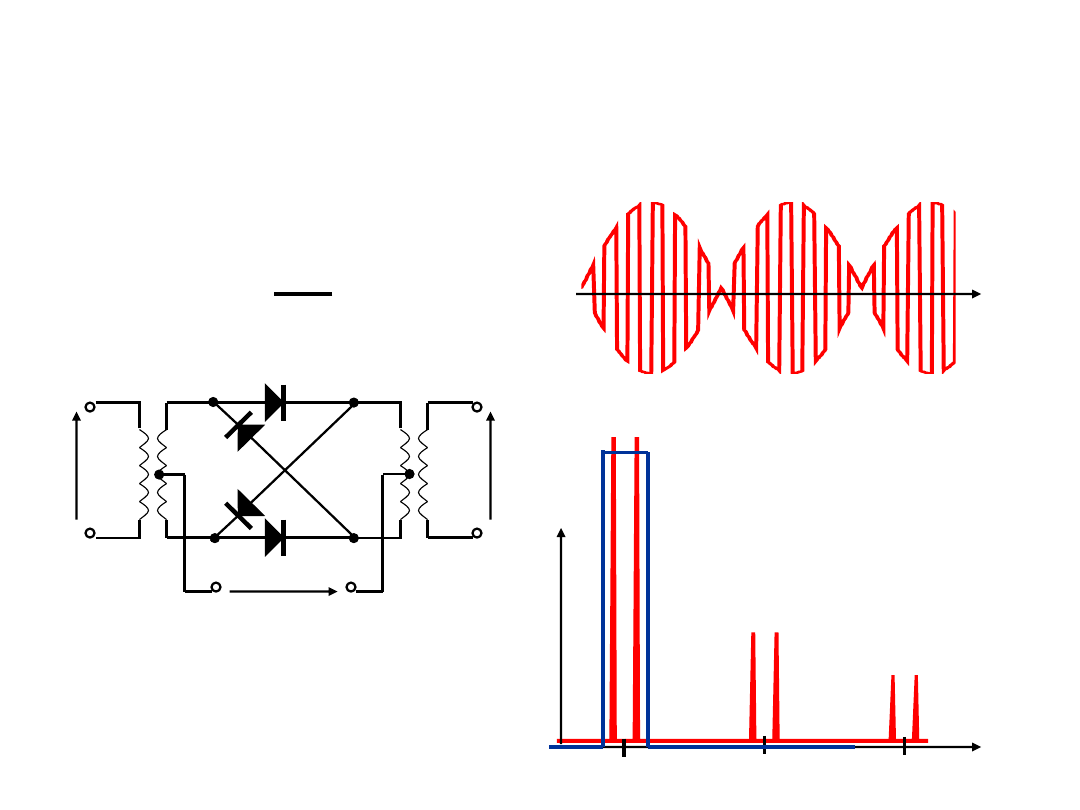
Wytwarzanie sygnałów zmodulowanych DSB SC
c(t)
x(t)
g(t)
t
f
0
3f
0
5f
0
Wytwarzanie sygnałów zmodulowanych amplitudowo
Modulator pierścieniowy
(podwójnie zrównoważony)
g(t)
=4A/
·
x(t)
·
cos[(2k-1) 2
f
0
t]
(-1)
k-1
2k-1
k=1
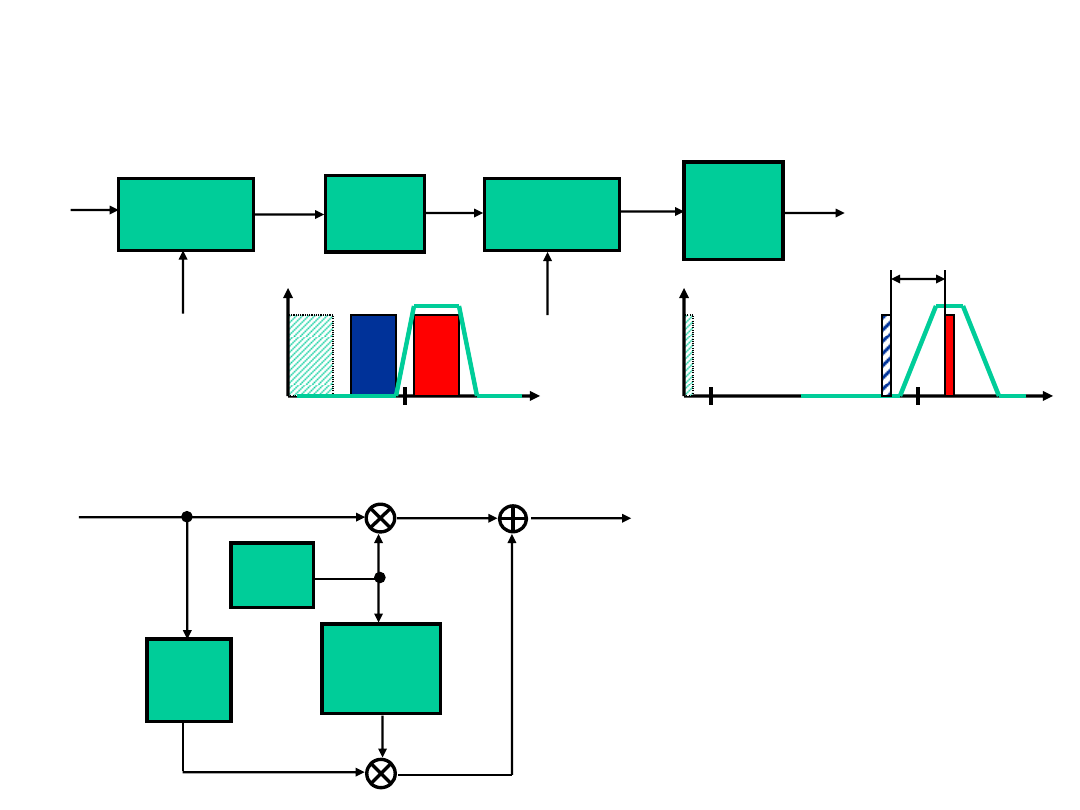
Wytwarzanie sygnałów zmodulowanych SSB SC metodą filtracji
Wytwarzanie sygnałów zmodulowanych amplitudowo
Przesuw
nik fazy
-90
º
Gene
rator
Tr.
Hilberta
cos(2
f
0
t
)
sin(2
f
0
t)
g
USB
(t)
x(t)
x(t)
^
+
-
Wytwarzanie sygnałów zmodulowanych SSB SC metodą fazową
Modulator
zrównoważony
Filtr
f
1
.B+ f
1
Filtr
f
2
.B+ f
1
+ f
2
Modulator
zrównoważony
x(t)
cos(2
f
1
t)
cos(2
f
2
t)
f
2
f
1
f
1
f
1
2f
1
f
2
g
USB
(t)=
½[
x(t)
cos(
2
f
0
t)
-
x(t)
sin (
2
f
0
t)
]
^
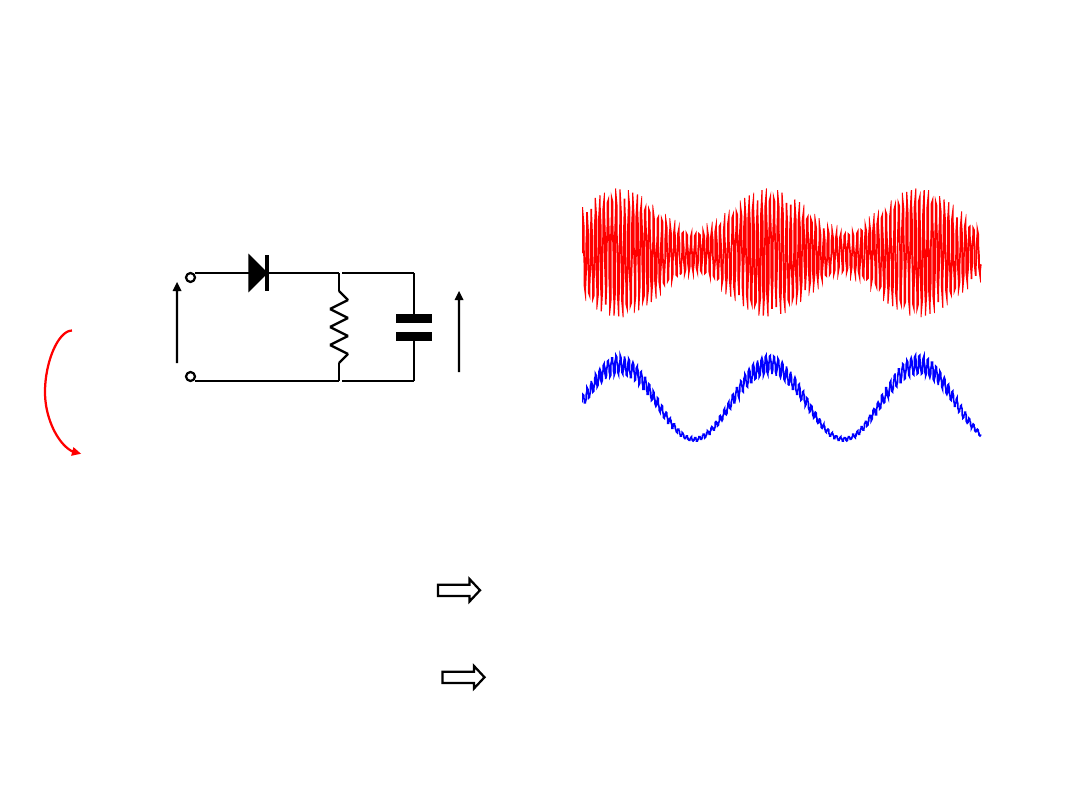
Demodulacja sygnałów zmodulowanych amplitudowo
Detektor obwiedni (AM - DSB)
sygnał
AM
sygnał
m.cz.
x(t)
Acos(2
f
0
t)
+z(t)
1
º A[1+mx(t)] >> z(t)
praktyczna możliwość detekcji
2
º A[1+mx(t)] << z(t)
na wyjściu demodulatora tylko szum
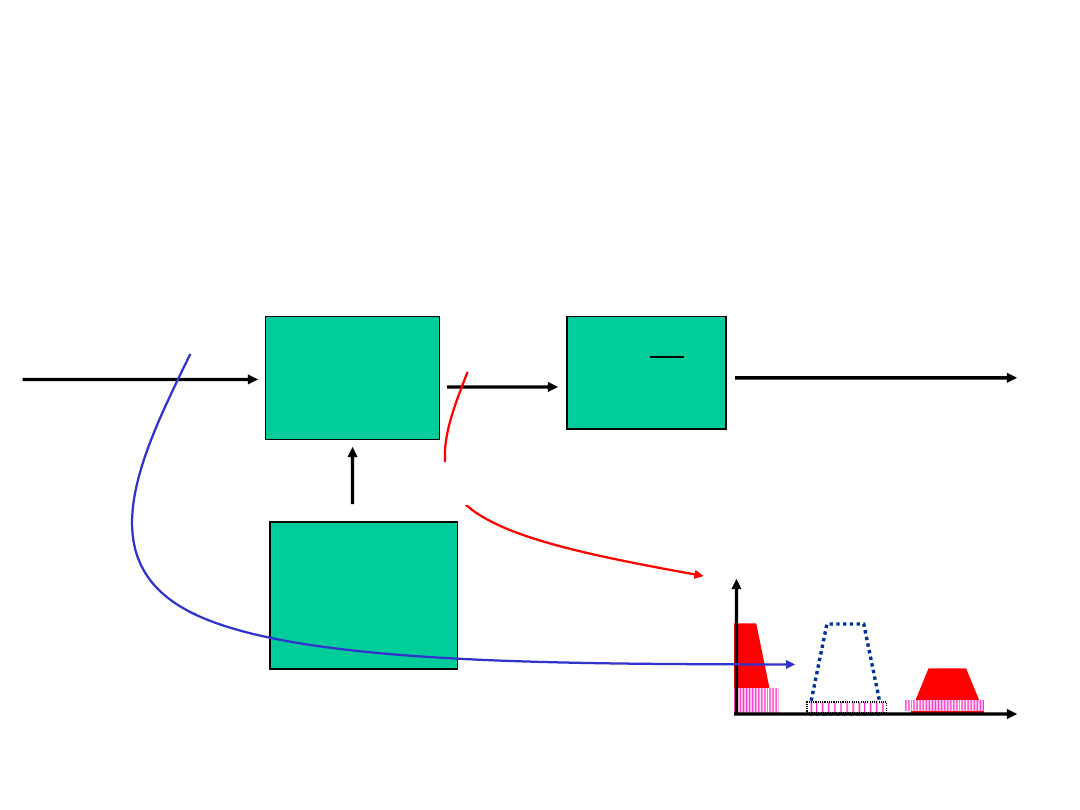
Demodulacja sygnałów zmodulowanych amplitudowo
Detektor koherentny (AM
– DSB SC )
modulator
zrównoważony
FDP
x
d
(t) =
½AA
g
cos(
0
-
g
)
·
x(t)
x(t)
A
cos(2
f
0
t+
0
)
+z(t)
A
g
cos(2
f
g
t+
g
)
S
m
(f)
-2f
0
2f
0
0
Generator
stabilizowany
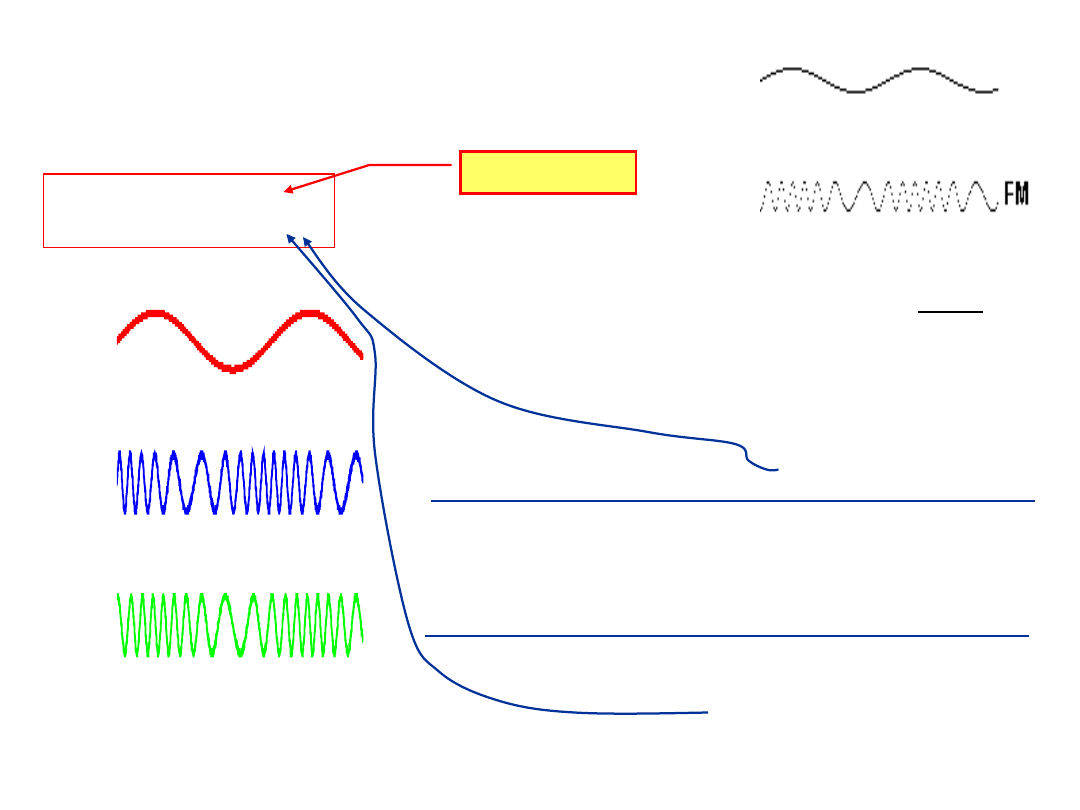
g(t)=A
·
cos[
(t)]
g
PM
(t)
g
FM
(t)
x(t)
Funkcja x(t)
• Modulacja fazy (PM)
(t)= 2
f
0
t + k
p
x(t)
• Modulacja częstotliwości (FM)
f(t)= f
0
+ k
f
x(t)
(t)= 2
f
0
t + 2
k
f
x(
)d
0
t
częstotliwość chwilowa
f(t) =
Te same właściwości energetyczne i widmowe
(t)
t
Modulacje kąta nośnej harmonicznej
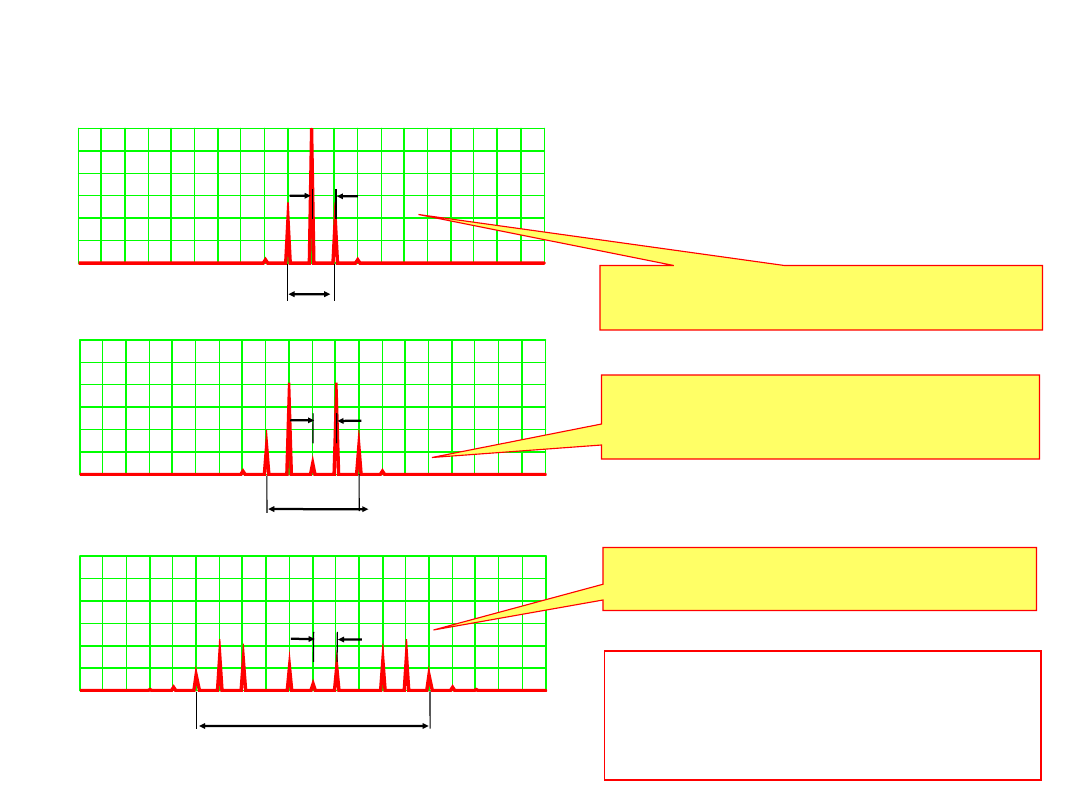
Modulacja częstotliwości sygnałem harmonicznym
2
f
B
f
0
B
f
0
B
2
f
f
0
2
f
S
g
(f)
S
g
(f)
S
g
(f)
Nieskończona liczba prążków wokół
f
0
rozmieszczonych co B
Wzrost dewiacji - zmniejszenie mocy
nośnej i rozłożenie mocy na pozostałe
prążki
Wzrost dewiacji
– poszerzenie pasma
B
T
= 2(
f + B)
- praktyczna
szerokość pasma
f
– dewiacja (amplituda zmian
częstotliwości np. 150kHz)
B
T
>> B
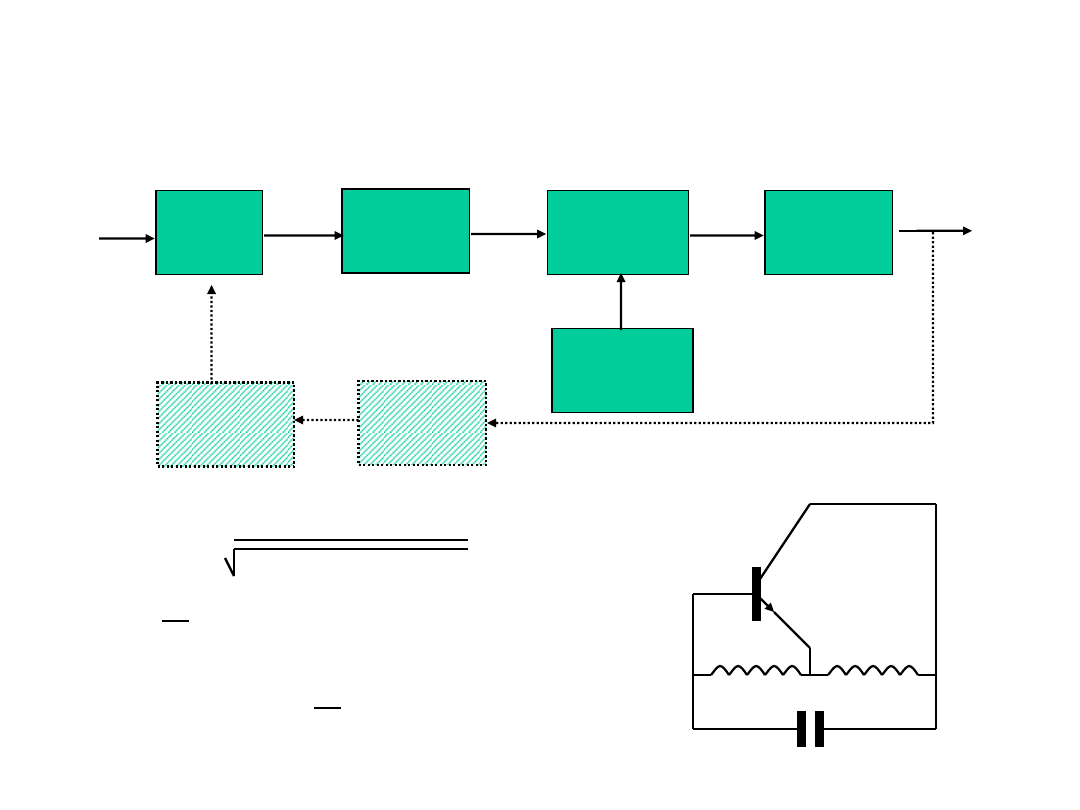
Wytwarzanie sygnałów zmodulowanych częstotliwościowo
VCO
Powielacz
częstotliwości
Mieszacz
(modulator AM)
Filtr
pasmowy
Generator
stabilizowany
dyskryminator
częstotliwości
Filtr
dolnopasmowy
i wzmacniacz
x(t)
g(t)
C
L
1
L
2
f(t)=
(L
1
+ L
2
)[ C
0
+
Cx(t) ]
1/2
C
C
0
<<1
f(t)
f
0
[ 1 - x(t) ]
C
2C
0
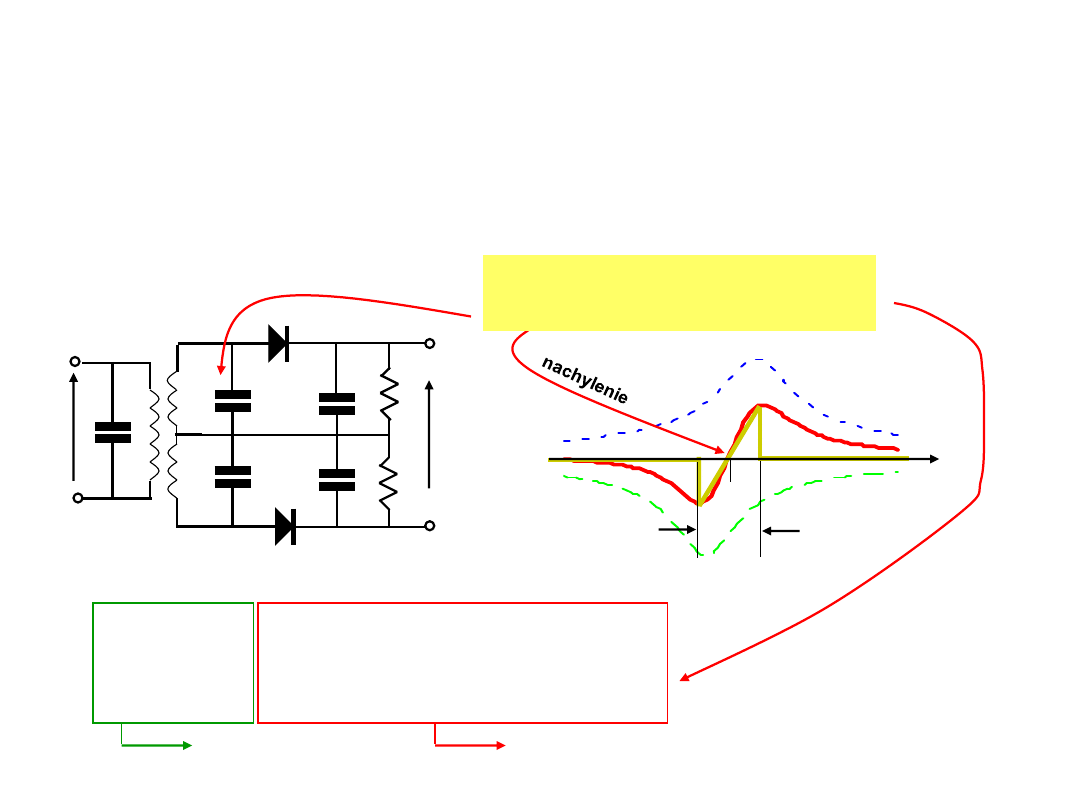
Demodulacja sygnałów zmodulowanych kątowo
Zrównoważony dyskryminator częstotliwości
g(t)
4
Aak
f
·x(t)
[1+k
x(t)
]
cos[2
f
0
t + 2
k
f
x(
)d
+
½
]
0
t
f
0
B
T
wytworzenie sygnału o
zmodulowanej amplitudzie
nośna
modulacja ampl
Korzyść z użycia modulacji kątowych
Zakłócenia (szumy) po demodulacji maleją ze wzrostem amplitudy
nośnej!
moc szumu po demodulacji (N
wy
) jest
odwrotnie proporcjo-
nalna
do SNR
we
przed demodulacją
Acos(
0
t)+z
we
(t)=Acos(
0
t)+z
I
(t)cos(
0
t)+ z
Q
(t)sin(
0
t)
Acos(
0
t)+z
Q
(t)sin(
0
t)=
A
2
+[z
Q
(t)]
2
cos[
0
t+
z
(t)]
z
(t)=arcsin
z
Q
(t)
A
2
+[z
Q
(t)]
2
z
Q
(t)
A
z
wy
(t)= =
1
A
d
z
(t)
dt
dz
Q
(t)
dt
N
wy
(f)
= j2
f
·
Z
Q
(f)
Szum powodowany chwilową
modulacją częstotliwości wskutek
szumu na wejściu demodulatora:
widmo szumu
1
A
B
|N
wy
(f)|
2
f
4
2
f
2
N
we
A
2
·
B
N
we
/B
B
B
T
N
we
(f)
f
N
we
Korzyść z użycia modulacji kątowych
SNR
wy
poprawia się wraz ze wzrostem
poszerzenia pasma
w
stosunku do B
– wymiana pasma na SNR
N
wy
= 2
2
B
2
N
we
½A
2
S
wy
=
f
2
=
¼B
T
2
SNR
wy
= SNR
we@B
1
8
2
B
T
2
B
2
Modulacje analogowe nośnej impulsowej
g(t)=
A
k
u(t
– kT - t
k
;
k
)
k=-
A
k
- amplituda k-tego impulsu
t
k
-
położenie k-tego impulsu
k
- czas trwania k-tego impulsu
T - okres
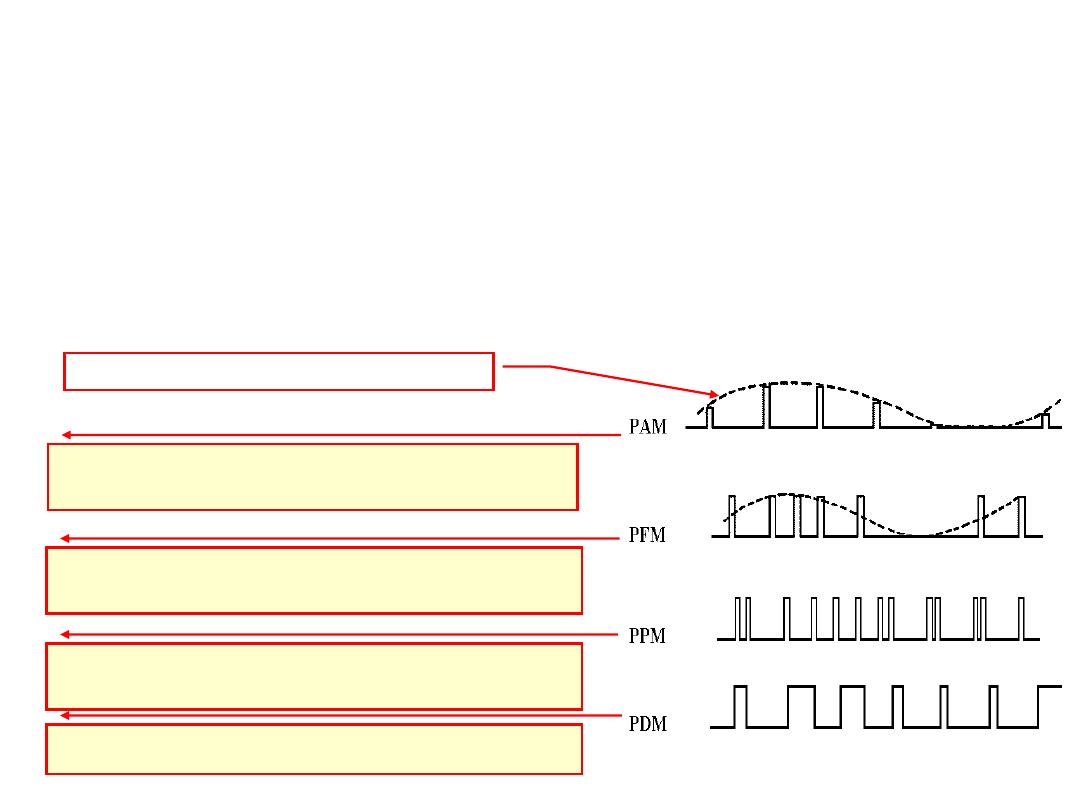
Modulacja amplitudy impulsów
A
k
x(kT)
Modulacja szerokości impulsów
k
x(kT)
Modulacja położenia impulsów
t
k
x(kT)
Modulacja częstotliwości impulsów
1/T
k
x(t)
Przebiegi zmodulowanych impulsów
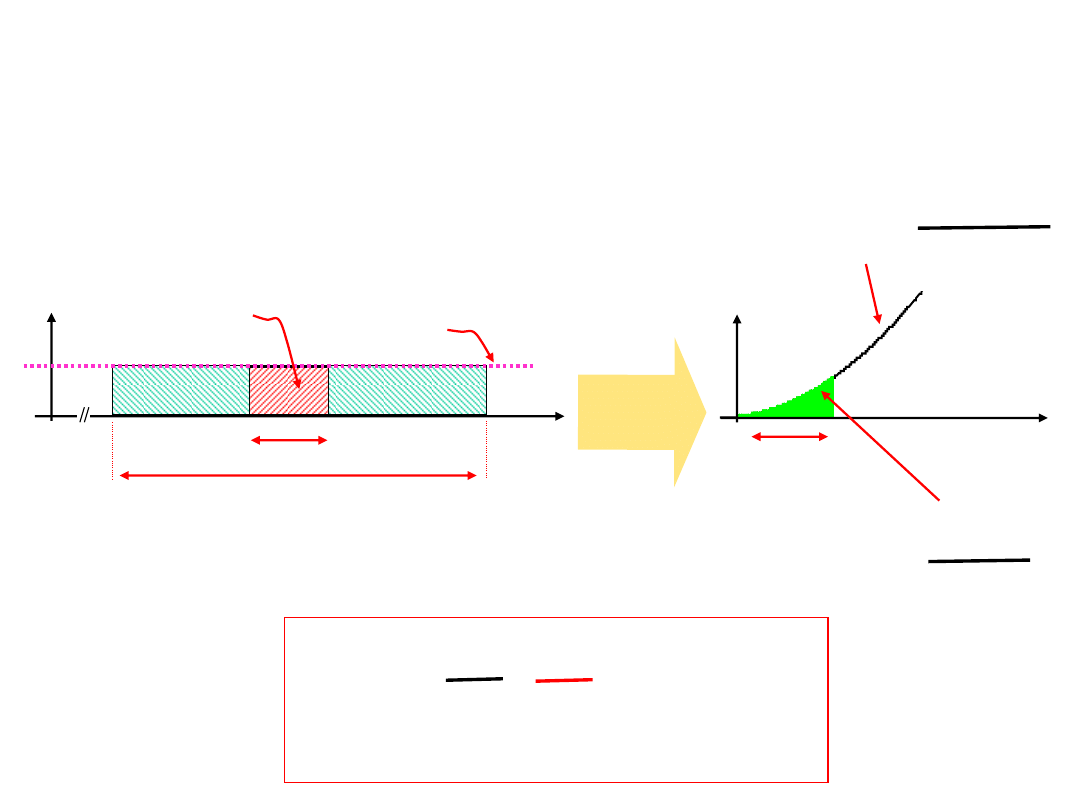
Szerokość pasma widma sygnałów modulacji impulsów
1/
B
2B
S
g
(f)
f
Szerokość pasma zmodulowanych
impulsów >>B!
Dla PAM i PDM początkowa część
widma 0
f
B odpowiada widmu
sygnału modulującego
1/T
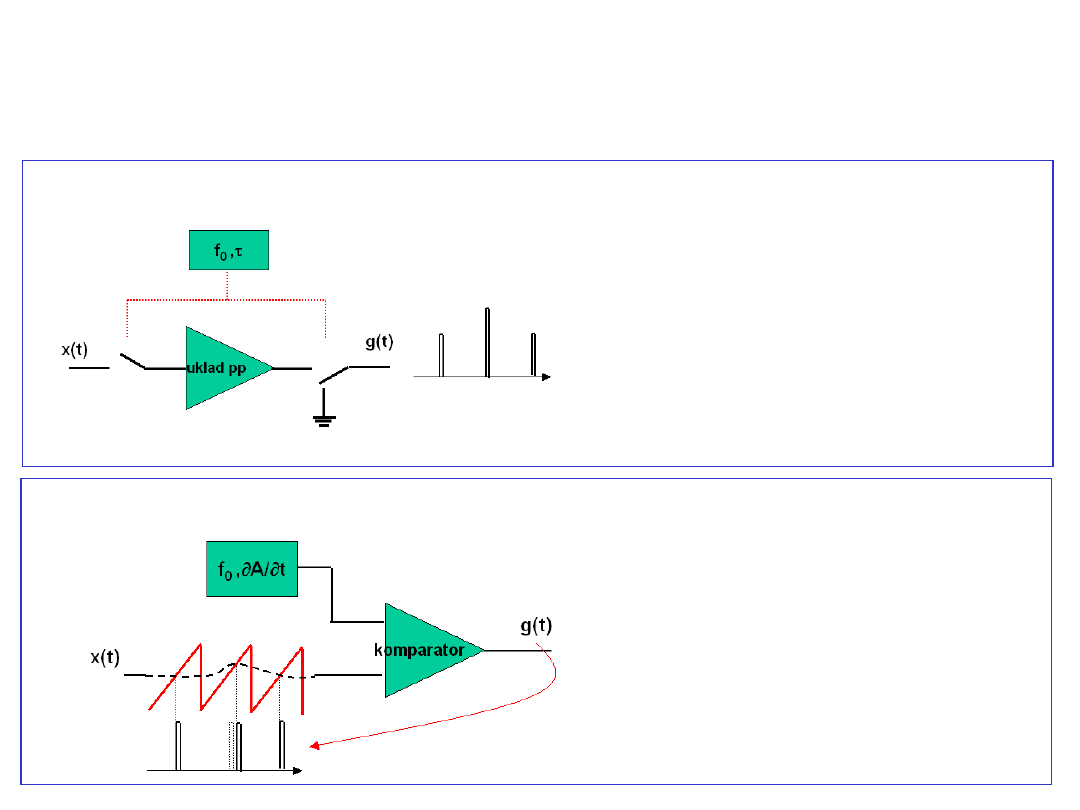
Wytwarzanie i demodulacja sygnałów modulacji
impulsów
• Modulator PAM
• Demodulator PAM
Filtr dolnoprzepustowy
• Modulator PPM
• Demodulator PPM
Konwerter na PDM
+
Filtr dolnoprzepustowy
- zysk modulacyjny odniesiony
SNR
d
B
x
SNR
c
B
T
Porównanie właściwości modulacji
Zysk modulacyjny
Zysk modulacyjny opisuje poprawę odporności na
szum wskutek zastosowania modulacji
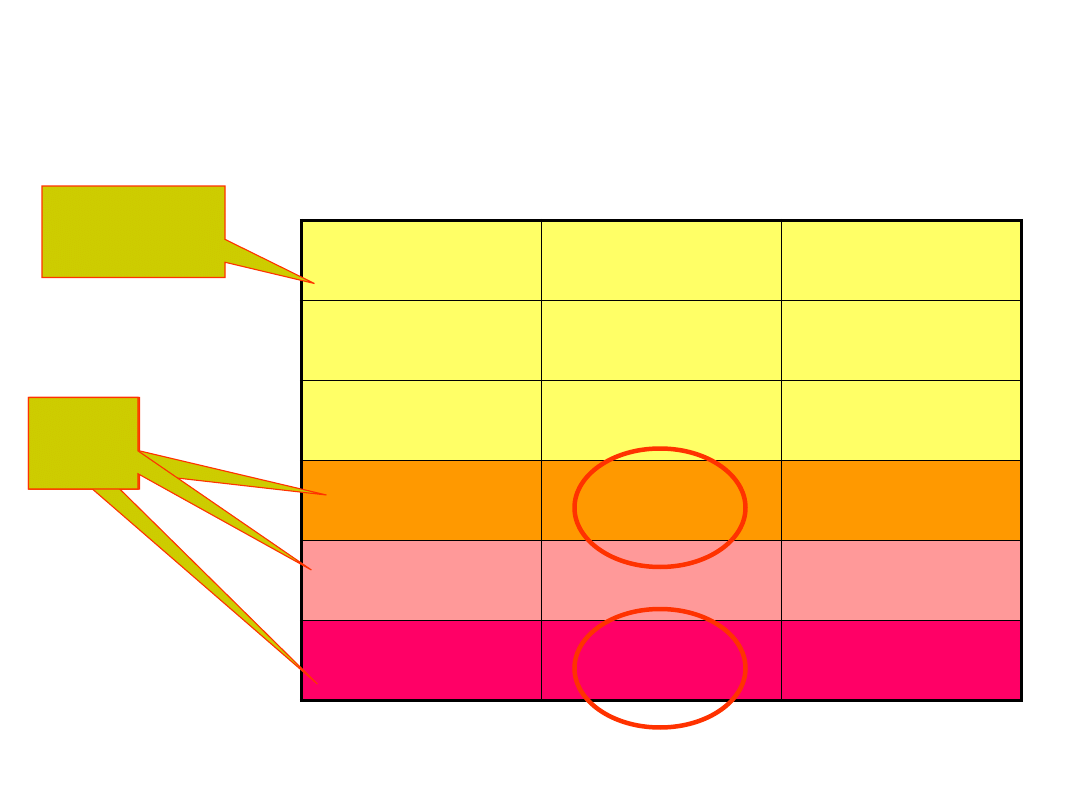
Porównanie właściwości modulacji
Zysk modulacyjny
AM-DSB
½
2B
m
AM-
DSB-SC
2B
m
AM-
SSB-SC
B
m
FM*
Duży *
2(
f+B
m
)
PAM
>>2B
m
PPM*
Duży *
>>2B
m
1
1
1
niska
sprawność
energetyczna
szerokie
pasmo
zysk
pasmo
* tym większy im większy B
T
/B
m
Podsumowanie
Następny wykład:
Przesyłanie
sygnałów cyfrowych
Obowiązująca literatura
do bieżącego wykładu:
•S. Haykin, „Systemy
telekomunikacyjne t. 1” s.
126-192
•A. Wojnar, „Teoria
sygnałów”, s. 159 – 177
Wyszukiwarka
Podobne podstrony:
15 Powt rzenie wyk ead 15id 16 Nieznany
Dermatologia wyk ead 18 11 Nieznany
PRËBKOWANIE SYGNAúËW ANALOGOWYCH1, II ElektrycznyGrupa ˙wiczeniowa 5
Wyk�ad ekonometryczne+ ++metody+heurystyczne analogowe+ +cz II ppt
NAGÅAÅNIANIE DLA KAÅ»DEGO PRZESYÅANIE SYGNAÅÃW
EDI wyk
Wyk ad 5 6(1)
zaaw wyk ad5a 11 12
Wyk 02 Pneumatyczne elementy
Automatyka (wyk 3i4) Przel zawory reg
więcej podobnych podstron