1
Ć
wiczenie 4
PRÓBA ROZCIĄGANIA –
WYZNACZANIE MODUŁU SPRĘŻYSTOŚCI E ORAZ UMOWNYCH
GRANIC: SPRĘŻYSTOŚCI R
r0,05
(R
0,05
) I PLASTYCZNOŚCI R
r0,2
(R
0,2
)
Opracował: dr inż. Marek Gontarczyk
1. Wstęp
Z próby rozciągania metali (wykonywanej jako tzw. ścisła próba rozciągania) można wy-
znaczyć
−
dla stali węglowej
−
poza wielkościami R
eH
, R
eL
, R
m
, dodatkowo wielkości cechu-
jące materiał pod względem wytrzymałościowym i sprężystym:
−
umowna granica sprężystości przy wydłużeniu trwałym R
r0,05
(według poprzednich ozna-
czeń: umowna granica sprężystości R
0,05
),
−
umowna granica plastyczności przy wydłużeniu trwałym R
r0,2
(według poprzednich
oznaczeń: umowna granica plastyczności R
0,2
),
−
moduł sprężystości E (tzw. moduł sprężystości podłużnej – podstawowa stała sprężysta,
określająca zdolność do odkształcania materiału izotropowego w zakresie liniowo – sprę-
ż
ystym pracy materiału.
Próbę wykonuje się według Polskiej Normy: PN−EN 10002−1: 2004 Metale. Próba roz-
ciągania. Metoda badania w temperaturze otoczenia.
2. Cel ćwiczenia
2.1. Cel ogólny
Celem ogólnym jest zapoznanie się ze sposobem przeprowadzenia tzw. ścisłej próby roz-
ciągania, sposobem prowadzenia pomiarów, zapoznanie się ze zjawiskiem histerezy spręży-
stej, nabycie umiejętności wyznaczania wielkości charakterystycznych R
r0,05
(R
0,05
),
R
r 0,2
(R
0,2
) i E dla stali węglowej.
2.2. Cele szczególne
1. Wyznaczenie wielkości charakteryzujących stal pod względem wytrzymałościowym
(umowne granice sprężystości i plastyczności przy wydłużeniu trwałym: R
r0,05
i R
r0,2
)
oraz modułu sprężystości E,
2. Wykonanie dla próbki stalowej wykresów: histerezy sprężystej:
σ
(
ε
) – w zakresie li-
niowo – sprężystym oraz naprężenie – wydłużenie
σ
(
ε
) i naprężenie – wydłużenie
trwałe
σ
(
ε
pl
).
3. Definicje
3.1. Umowna granica sprężystości przy wydłużeniu trwałym
0
05
,
0
05
,
0
S
F
R
r
r
=
[MPa =10
6
N/m
2
].
(1)
3.2. Umowna granica plastyczności przy wydłużeniu trwałym
0
2
,
0
2
,
0
S
F
R
r
r
=
[MPa].
(2)
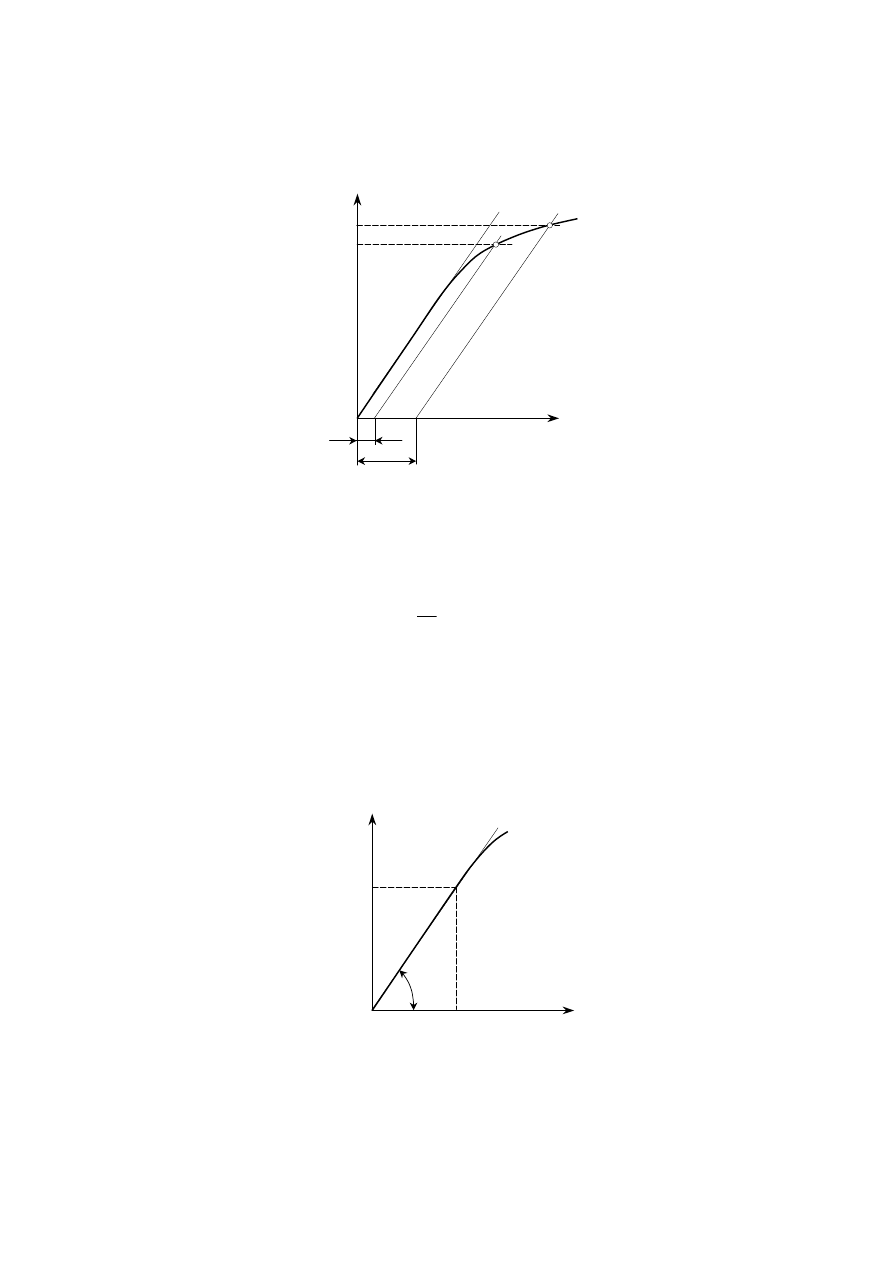
2
Są to wartości naprężeń przy jednoosiowym rozciąganiu, przy których po zdjęciu siły
wydłużenie trwałe początkowej długości pomiarowej L
0
jest równe umownej wartości (odpo-
wiednio: 0,05% i 0,2%) – (rys. 1)
Rys. 1. Umowna granica sprężystości R
0,05
i umowna granica plastyczności R
0,2
3.3. Moduł sprężystości podłużnej E
Moduł sprężystości E w zakresie odkształceń sprężystych i proporcjonalnych definiuje
się moduł jako stosunek naprężenia normalnego σ przy jednoosiowym stanie napięcia do od-
powiadającego mu wydłużenia względnego ε (rys. 2)
1
1
ε
σ
=
E
[MPa = 10
6
N/m
2
].
(3)
Graficzna interpretacja modułu E: jest to współczynnik kierunkowy prostoliniowego od-
cinka wykresu rozciągania σ = F(ε) i jest równy co do wartości liczbowej tangensowi kąta
α
nachylenia prostoliniowej części wykresu rozciągania.
Uwaga 1: W przypadku odkształceń sprężystych i nie proporcjonalnych, kiedy wykres
rozciągania nie wykazuje odcinka o przebiegu prostoliniowym (jak w przypadku żeliwa lub
stali sprężynowej), oblicza się moduł sprężystości styczny lub sieczny.
Rys. 2. Moduł sprężystości E – w zakresie odkształceń sprężystych i proporcjonalnych
ε
[%]
σ
y
O
0,05
R
0,2
M
0,2
N
R
0,05
ε
σ
y
O
α
ε
1
σ
1
3
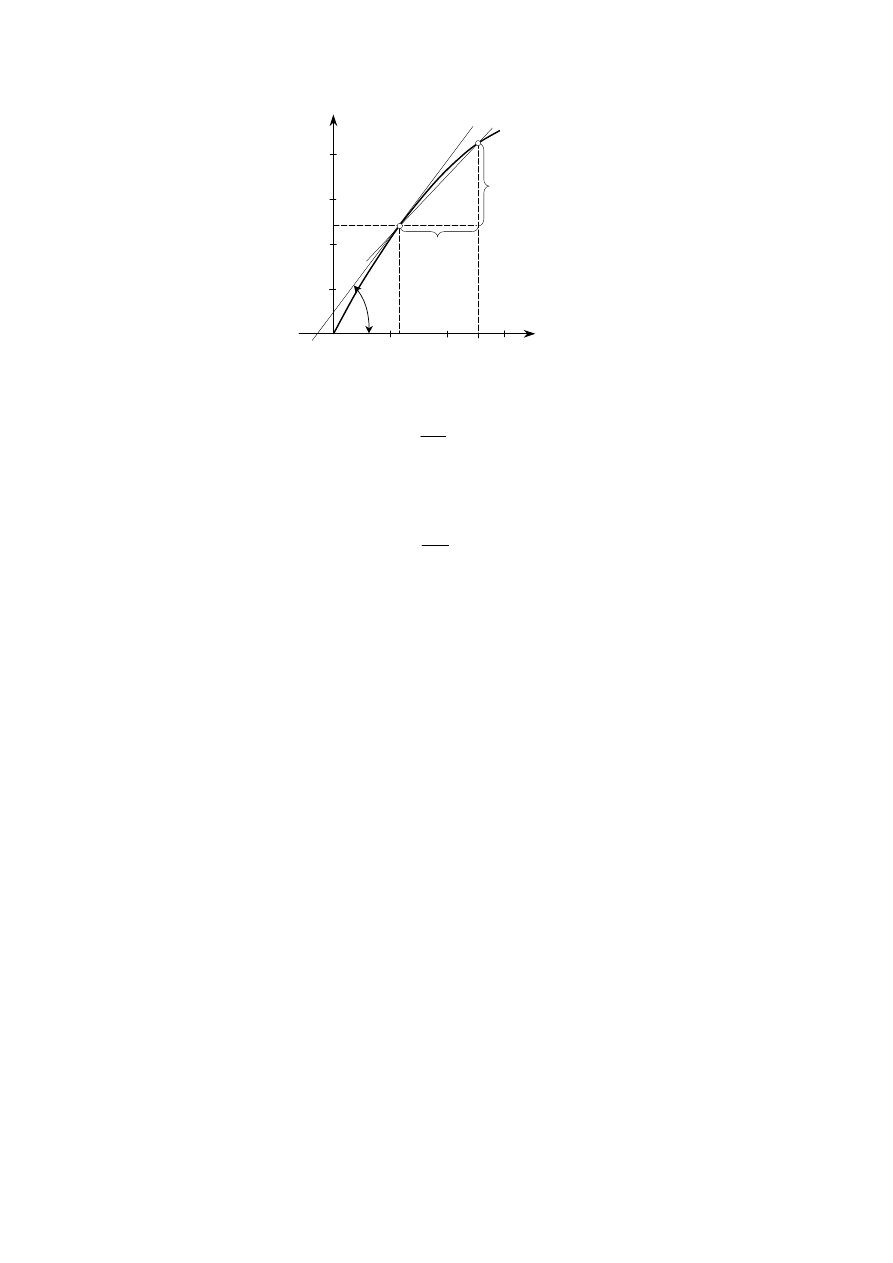
Rys. 3. Moduł styczny E
t
i moduł sieczny E
s
Moduł styczny E
t
definiuje się jako
ε
σ
d
d
E
t
=
[MPa].
(4)
E
t
jest równy tangensowi kąta nachylenia stycznej do krzywej rozciągania w określonym
punkcie (rys. 3, graficzna interpretacja modułu E
t
).
Moduł sieczny E
s
definiuje się jako
ε
σ
∆
∆
=
s
E
[MPa].
(5)
E
s
jest równy tangensowi kąta nachylenia siecznej krzywej rozciągania poprowadzonej przez
2 punkty wykresu (rys. 3). Moduły E
t
i E
s
wyznacza się w zakresie obciążeń odpowiadających
naprężeniom w przedziale 10%
÷
90% umownej granicy sprężystości.
Uwaga 2: W niektórych zagadnieniach analitycznych wytrzymałości materiałów stosuje
się pojęcia: modułu stycznego lub siecznego – w odniesieniu do zakresu odkształceń poza
zakresem sprężystości – wówczas definicje i graficzne interpretacje modułów są analogiczne
jak podano wyżej (jednak nie są to już moduły sprężystości).
4. Zasada dokładnego pomiaru wydłużeń
Pomiaru wydłużeń z dużą dokładnością dokonuje się przy użyciu tensometrów.
Zależnie od budowy i zasady działania można wyróżnić tensometry: mechaniczne, me-
chaniczno – optyczne, elektrooporowe, indukcyjne i inne.
Dla uzyskania wyników pomiarowych z dużą dokładnością w zakresie małych wydłużeń
stosuje się tensometry mechaniczno – optyczne.
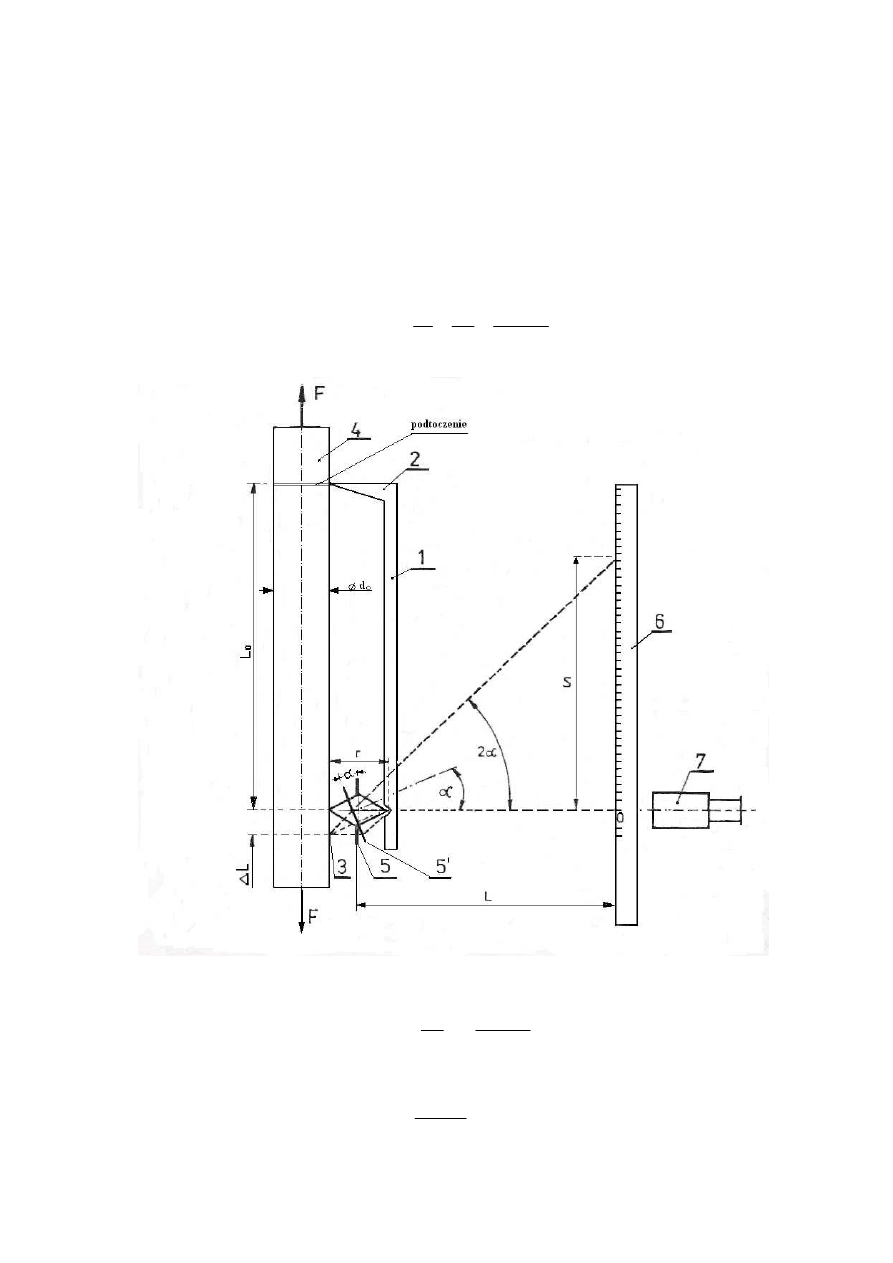
Na rys. 4 podano zasadę działania tensometru mechaniczno – optycznego systemu Mar-
tensa, stosowanego w ćwiczeniu. Tensometr składa się z pionowego pręta (szabelki 1), za-
kończonego z jednego końca ostrzem stałym (2), które montuje się w małym podtoczeniu
obwodowym próbki (4). Na drugim końcu pręt posiada wycięcie, w którym oparty jest pry-
zmat (ruchome ostrze) (3). Ostrza (2) i (3) wraz z prętem (1) są dociskane do rozciąganej
próbki (4) obejmami ze sprężynami. Z pryzmatem (3) jest połączone lusterko (5) – przy po-
mocy tzw. strzemiączka, usytuowanego poziomo. Bazę pomiarową L
0
wyznacza na próbce
odległość między ostrzami stałym i ruchomym.
Przy wydłużeniu próbki równym
∆
l
ostrze ruchome – pryzmat (3) obraca się w wycięciu
pręta (szabelki 1) o kąt
α
, razem z nim o taki sam kąt obraca się lusterko (5) – do położenia
(5’). W odległości L od pryzmatu, równolegle do próbki, jest umieszczona listwa pomiarowa
(6) z podziałką milimetrową. Przez lunetę (7) obserwuje się, odbitą w lusterku podziałkę li-
stwy pomiarowej. Przy próbce nie odkształconej widoczne jest „0” podziałki, a przy wydłu-
ε⋅
10
−3
[MPa]
O
1
∆ε
=1,3
⋅
10
−3
50
ε
0
100
A
B
150
200
E
t
E
s
∆σ
=100 MPa
2
3
σ
α
4
ż
onej o
∆
l odczyt jest równy S. Zależność między wydłużeniem
∆
l a przekątną pryzmatu r
jest równa
∆
l = r·sin
α
Obrót lusterka o kąt
α
powoduje obrót promienia optycznego o kąt 2
α
, stąd otrzymuje się
S = L·tg2
α
.
Ponieważ kąt
α
jest bardzo mały, to z wystarczającą dokładnością można przyjąć: sin
α
≈
α
,
tg2
α
≈ 2
α
; wówczas:
∆
l = r
α
; S = L·2
α
.
Stosunek S
⁄∆
l, nazywany powiększeniem (przekładnią tensometru), dla L = 1000 mm oraz
r = 4 mm, jest równy:
500
4
1000
2
2
=
⋅
=
=
∆
=
r
L
l
S
n
.
(6)
Ry
s. 4. Schemat tensometru mechaniczno
−
optycznego Martensa
Z powyższych zależności otrzymuje się
S
S
S
L
r
l
1
500
1000
2
4
2
−
=
⋅
=
=
∆
.
(7)
Ponieważ stosuje się zdwojony układ tensometrów, to otrzymuje się odczyty S
1
i S
2
(po
przeciwnych stronach próbki). Przyjmując średnią z pomiarów:
2
2
1
S
S
S
+
=
(8)
5
eliminuje się błąd wynikający z ewentualnej mimośrodowości obciążenia próbki. Stąd wyra-
ż
enie na przyrost długości odcinka pomiarowego przyjmuje postać:
(
)
2
1
3
10
S
S
l
+
=
∆
−
,
(9)
gdzie wszystkie wielkości są wyrażone w [mm].
5. Metoda wyznaczania wielkości E, R
r 0,05
i R
r0,2
5.1. Moduł sprężystości E
−−−−
materiał o charakterystyce liniowo
−−−−
sprężystej
Korzystamy ze zbioru punktów w układzie
σ
(
ε
) (naprężenie
−−−−
wydłużenie względne cał-
kowite); współrzędne punktów są zawarte w tabeli 1.
Po naniesieniu punktów w układzie współrzędnych ustalamy zbiór punktów znajdujących
się w zakresie liniowo –sprężystym charakterystyki materiału; pomijamy ostatni punkt z tego
zakresu. W przypadku, kiedy punkty ułożone są na linii prostej, obliczamy moduł E jako:
1
2
1
2
ε
ε
σ
σ
ε
σ
−
−
=
∆
∆
=
E
,
(10)
gdzie odległość punktów 2 i 1jest możliwie duża. Natomiast kiedy wyniki pomiarów są obar-
czone większymi błędami i występują odchylenia punktów od zakładanej linii prostej, można
otrzymać wynik w pewnym stopniu niezależny od błędów, przyjmując (rys. 5):
1. punkty pomiarowe z zakresu 10
÷
90% przedziału liniowego;
2. z pominięciem punktów znacznie odległych od zakładanej linii prostej.
Wówczas
−−−−
dla n + 1 uwzględnianych punktów – moduł E można obliczyć jako:
∑
=
−
−
−
−
=
n
i
i
i
i
i
n
E
1
1
1
1
ε
ε
σ
σ
.
(11)
Rys. 5. Obliczanie modułu E – odchylenia punktów od linii prostej (n = 5)
ε
σ
y
i=1
punkt pomini
ę
ty
0,9
σ
H
0,1
σ
H
σ
i
σ
0
ε
0
ε
i
i=2
i=3
i=4
i=5
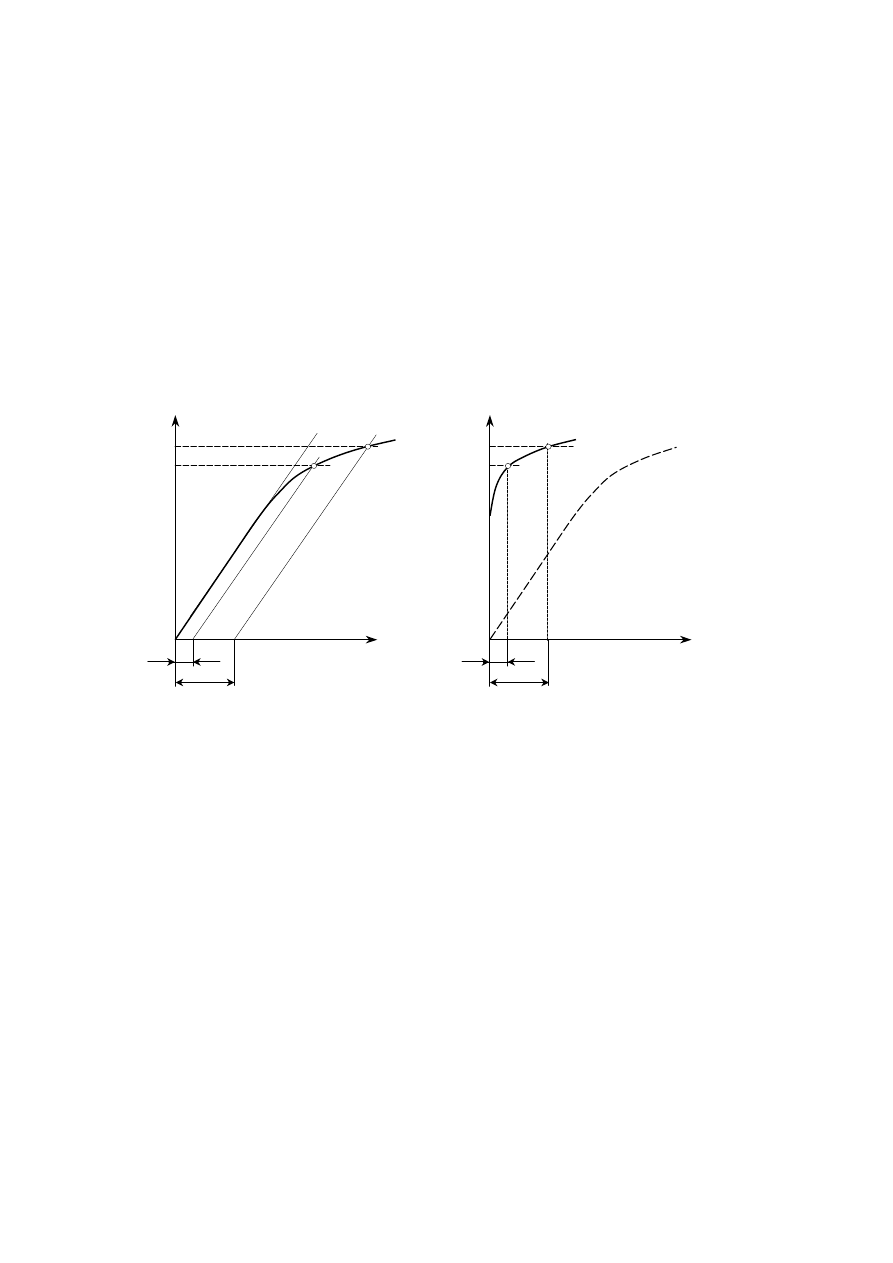
6
5.2. Umowne granice: sprężystości i plastyczności (przy wydłużeniu trwałym)
Umowne granice: sprężystości i plastyczności wyznacza się sposobem graficznym, po
uprzednim narysowaniu odpowiedniego wykresu
σ
(
ε
) lub
σ
(
ε
)
pl
−
(rys. 6):
−
metodą obciążania:
−
z wykorzystaniem wykresu
σ
(
ε
), tj. naprężenie
−
wydłużenie cał-
kowite. W tym celu na osi odciętych zaznacza się odpowiednią wartość wydłużenia
względnego (0,05% lub 0,2%) i prowadzi się z tego punktu linię prostą równoległą do
początkowego, liniowo – sprężystego odcinka wykresu – do przecięcia z wykresem.
Rzędną tego punktu jest szukana wartość naprężenia charakterystycznego
(R
r0,05
lub R
r0,2
);
−
metodą odciążania:
−
z wykorzystaniem wykresu
σ
(
ε
pl
), tj. naprężenie
−
wydłużenie
trwałe (plastyczne). W tym celu na osi odciętych zaznacza się wartość wydłużenia
względnego (0,05% lub 0,2%) i prowadzi się z tego punktu linię prostą pionową
−
do
przecięcia z wykresem. Rzędną tego punktu jest szukana wartość naprężenia charakte-
rystycznego (R
r0,05
lub R
r0,2
).
Rys. 6. Wyznaczanie umownych granic: a) – metodą obciążania,
b) – metodą odciążania
Uwaga 1. Wykresy
σ
(
ε
) i
σ
(
ε
)
pl
wyznaczamy dla naprężeń większych od
σ
0
(naprężenia
wstępnego). Konieczność stosowania napięcia wstępnego, któremu odpowiada wartość na-
prężenia
σ
0
, wynika z używania maszyny wytrzymałościowej typu wagowego. W ten sposób
w maszynie likwiduje się luzy w układzie dźwigniowym maszyny.
Uwaga 2. Dla wyznaczenia umownych granic R
r0,05
i R
r0,2
stosowana jest w ćwiczeniu
metoda obciążania – ze względu na większą dokładność uzyskiwanych wyników.
6. Zjawisko histerezy sprężystej
Histereza sprężysta polega na tym, że po odciążeniu próbki uprzednio obciążonej naprę-
ż
eniami
σ
(w zakresie uznawanym za sprężysty), obserwujemy niewielkie odkształcenie
ε
H
,
które w krótkim czasie zanika. Odkształcenie to można uznać za trwałe – jako uzyskane po
odciążeniu, jednak z drugiej strony – jako samoodwracalne – można zaliczyć do odkształceń
sprężystych.
Efekt histerezy można wyjaśnić w oparciu o polikrystaliczną strukturę metalu. Powsta-
wanie odkształceń trwałych w objętości próbki, rozpatrywane w kategoriach mikroskopo-
wych, jest związane z występowaniem dyslokacji struktury (przeskoku atomów) i przemiesz-
czania się tych dyslokacji w pewnych uprzywilejowanych płaszczyznach, zwanych płaszczy-
znami poślizgu. Odkształcenie plastyczne powstanie wtedy, gdy kierunki przeskoków (pośli-
zgów) zostaną uporządkowane – w tym celu niezbędne jest zaistnienie pewnej wartości na-
ε
[%]
σ
y
σ
0
0,05
R
0,2
M
0,2
N
R
0,05
ε
[%]
σ
y
σ
0
0,05
R
0,2
M
0,2
N
R
0,05
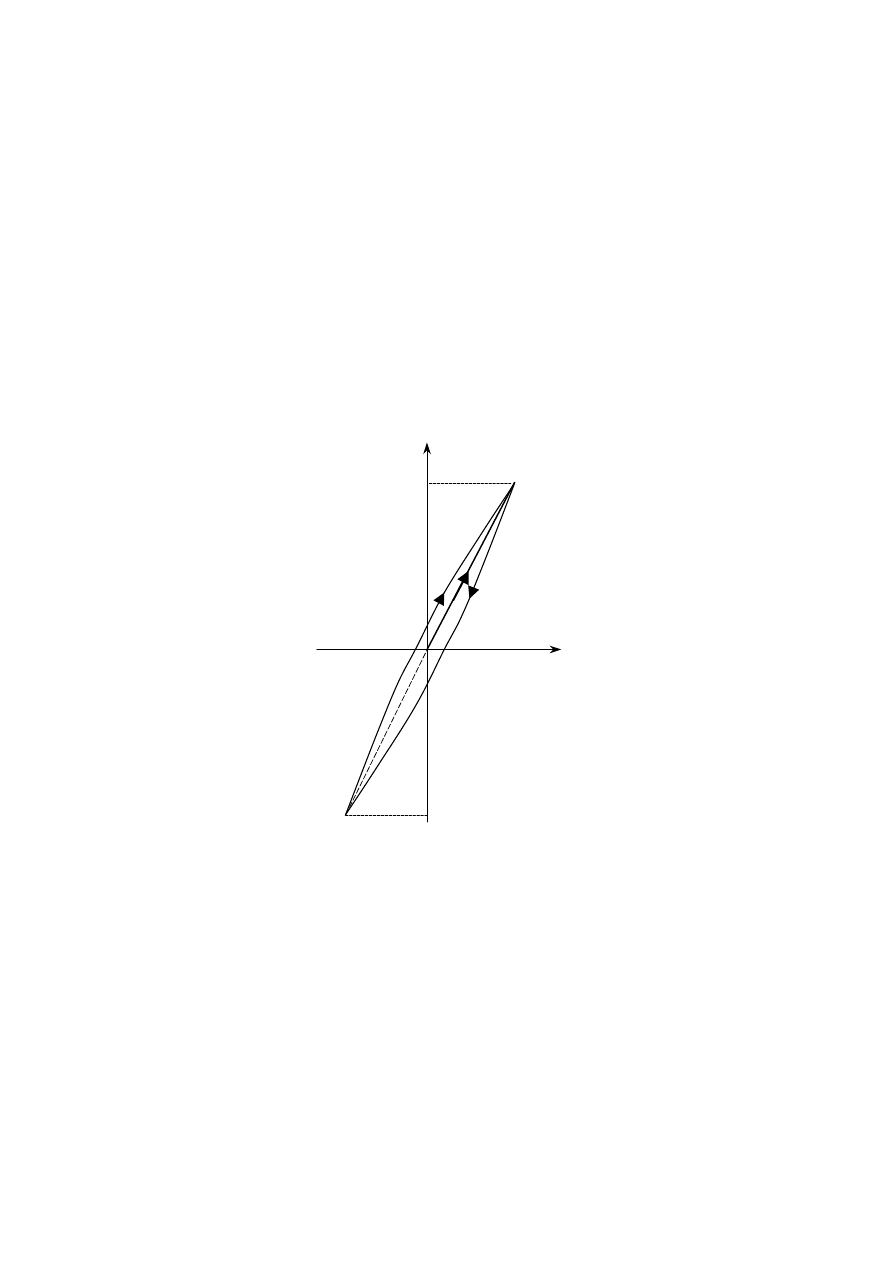
7
prężenia stycznego w płaszczyźnie poślizgu. Inaczej mówiąc – dla zaistnienia odkształcenia
trwałego konieczne jest wcześniejsze działanie na dany kryształ przez pewien czas sił ze-
wnętrznych, powodujących sprężyste odkształcenie postaciowe.
Powstałe odkształcenie histerezy było odkształceniem trwałym, jednak nie przebiegło
ono całkowicie – była to początkowa faza przemieszczania się dyslokacji przez płaszczyzny
poślizgów. Ze względu na to, że obciążanie przerwano, odkształcenie zatrzymało się przed
zakończeniem przeskoku całej warstwy atomów. Wobec tego powstał stan naprężenia wstęp-
nego, podczas którego sieci krystaliczne dążyły do uporządkowania. Nastąpiła w tym czasie
odbudowa sieci, przywracająca poprzedni porządek – w rezultacie powstałe częściowo od-
kształcenie trwałe zostało zlikwidowane. Obserwowane początkowo odkształcenie trwałe
cofnęło się.
Pole pętli histerezy sprężystej przedstawia pracę, jaka zostaje wykonana nad próbką w
jednym pełnym cyklu obciążania (naprężenia zmieniają się od 0 do
σ
, następnie do −
σ
po-
nownie do
σ
(rys. 7). Praca histerezy sprężystej – ze względu na to, że przemiana jest nieod-
wracalna – zamienia się częściowo w pracę niszczenia sił spójności, a częściowo w energię
cieplną.
Rys. 7. Pętla histerezy sprężystej
7. Przeprowadzenie próby
Próbę wykonuje się na maszynie wytrzymałościowej typu wagowego. Próbka i układ
pomiarowy tensometru zostają zamontowane w maszynie przed ćwiczeniem.
Czynności, które należy wykonać w celu uzyskania danych do wykresów:
−
histerezy sprężystej i
−
zależności naprężenie – wydłużenie:
σ
(
ε
) oraz
σ
(
ε
)
pl
są następujące:
1. sprawdzić dane maszyny, zakres obciążenia i nastawienie obciążenia wstępnego
(P = 200daN), sprawdzić średnicę próbki,
2. sprawdzić, czy widoczna jest pozioma nić pajęcza lunet – na tle wystarczająco ostrego
obrazu listew pomiarowych – ewentualnie skorygować obraz przy pomocy pokrętła przy
okularze; sprawdzić pokrywanie się zera z nicią pajęczą lunety, ewentualnie skorygować
położenie „0” dolnym pokrętłem lunet,
−
σ
σ
σ
ε
8
3. obciążyć próbkę siłą równą podwójnej wartości siły wstępnej i odczytać przy pomocy
lunet wskazania na obu listwach pomiarowych (skalach) – równe S
1
i S
2
.
4. Wykonywać kolejne pomiary, stosując:
do wykresu histerezy – przyrosty obciążenia równe ok. 300
÷
400 daN przy obciążaniu
(w zakresie sprężystym), a przy odciążaniu – przejście przez identyczne wartości obcią-
ż
eń jak przy obciążaniu, w odwrotnej kolejności; wyniki pomiarów wpisuje się do tabeli
1; do wykresów
σ
(
ε
) oraz
σ
(
ε
)
pl
przyrosty obciążenia równe ok. 300
÷
400 daN w zakre-
sie sprężystym, a poza tym zakresem – ok. (200
÷
50) daN; wyniki pomiarów wpisuje się
do tabeli 2.
Uwaga: pomiary wykonane pod obciążeniem pozwalają obliczyć wydłużenie całkowite
odcinka pomiarowego, natomiast część pomiarów wykonujemy przy odciążeniu do siły
wstępnej (200 daN) – wówczas otrzymuje się wydłużenie trwałe, odpowiadające obciążeniu,
od którego nastąpił powrót.
5. Pomiary do wykresów
σ
(
ε
) oraz
σ
(
ε
)
pl
należy przerwać, kiedy wartość wydłużenia trwa-
łego odcinka pomiarowego przekroczy 0,2% (dla tensometru Martensa odpowiednikiem
wydłużenia
ε
= 0,2% jest suma wskazań S
1
+ S
2
= 200 mm) lub – kiedy skale listew po-
miarowych obserwowane w lunetach zaczną się przesuwać przy stałym obciążeniu
(próbka płynie).
7. Dla l
0
= 100 mm , L = 1000 mm i r = 4 mm wydłużenie względne każdego punktu po-
miarowego (całkowite i trwałe) oblicza się ze wzoru (9), zaś wydłużenie bezwzględne z
poniższego wzoru:
(
)
0
2
1
3
10
l
S
S
+
=
−
ε
, [%] (12)
gdzie:
∆
l, S
1
, S
2
wyrażone są w mm.
8. Przykład obliczeniowy
Wyznaczyć moduł sprężystości E oraz umowne granice sprężystości i plastyczności przy
wydłużeniu trwałym (R
r0,05
i R
r0,2
) na podstawie wyników pomiarów podanych w tabeli poni-
ż
ej – metodą obciążania – dla próbki o średnicy d = 8,5 mm (S
0
= 56,745 mm
2
).
Tabela 1. Dane do przykładu obliczeniowego
Lp.
F
S
1
+S
2
ε
ε
pl
σ
−
[daN]
[mm]
[%]
[%]
[MPa]
1
200
0
0
−
35,2
2
500
27,2
0,0272
−
88,1
3
800
53,9
0,0539
−
141,0
4
1200
88,4
0,0884
−
211,5
5
1500
115,2
0,1152
−
264,3
6
1800
142,2
0,1422
−
317,2
7
2000
169,8
0,1698
−
352,4
8
2300
191,2
0,1912
−
405,3
9
200
4,3
−
0,0043
405,3
10
2450
211
0,211
−
431,8
11
2550
232
0,232
−
449,4
12
200
13,6
−
0,0136
449,4
13
2600
249
0,249
−
458,2
14
2650
253,9
0,2539
−
467,0
15
2700
299
0,299
−
475,8
16
200
58,2
−
0,0582
475,8
17
2870
436
0,436
−
505,8
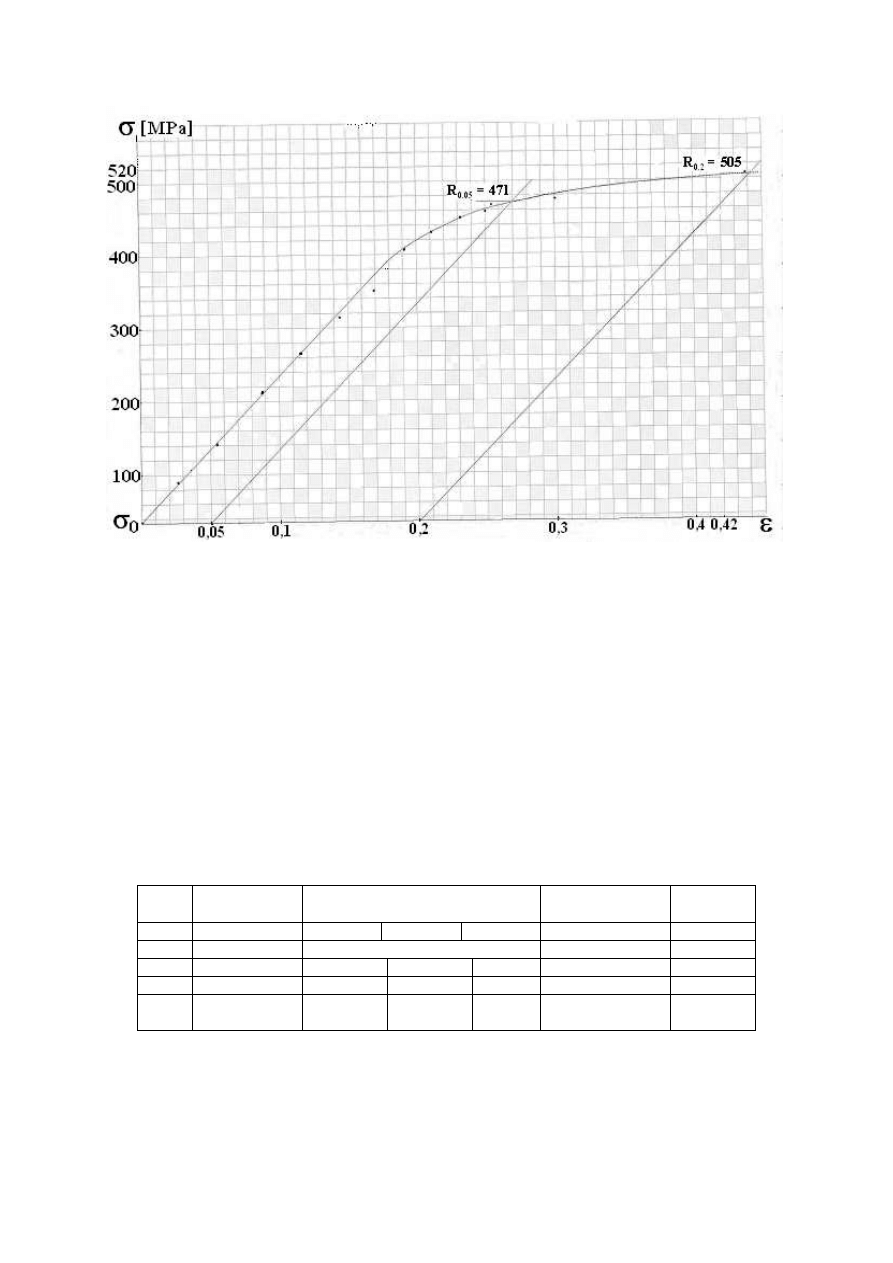
9
Rys. 8. Wykres
σ
(
ε
) dla przykładu obliczeniowego
9. Wykonanie sprawozdania
Sprawozdanie należy wykonać według punktów:
1. tytuł i cele ćwiczenia,
2. definicje: modułu sprężystości oraz umownych granic sprężystości i plastyczności,
3. schemat tensometru Martensa – rysunek z objaśnieniami części składowych,
4. podać metody wyznaczania E, R
r0,05
i R
r0,2
– stosowane w ćwiczeniu,
5. podać zestawienie wyników badań i wielkości obliczanych w tabelach pomiarowych 1 i
2; pod tabelą pomiarową 2 podać przykład obliczenia wartości z jednego wiersza,
6. narysować wykresy:
σ
(
ε
) – ¼ pętli histerezy sprężystej,
7.
σ
(
ε
)– naprężenie – wydłużenie całkowite i
σ
(
ε
)
pl
, naprężenie – wydłużenie trwałe,
8. wykonać obliczenie wielkości charakterystycznych, stanowiących cel ćwiczenia; zapisać
wyniki w sprawozdaniu.
Tabela pomiarowa 1. Pomiary do wyznaczenia histerezy sprężystej
Lp.
Siła
rozciągająca F
Odczyty na skalach
Wydłużenie
względne
ε×
10
3
Naprężenie
σ
= F/S
0
S
1
S
2
S
1
+ S
2
[daN]
[mm]
[%]
[MPa]
1
200
0
0
0
0
2
600
…
…
…
…
…
…
…
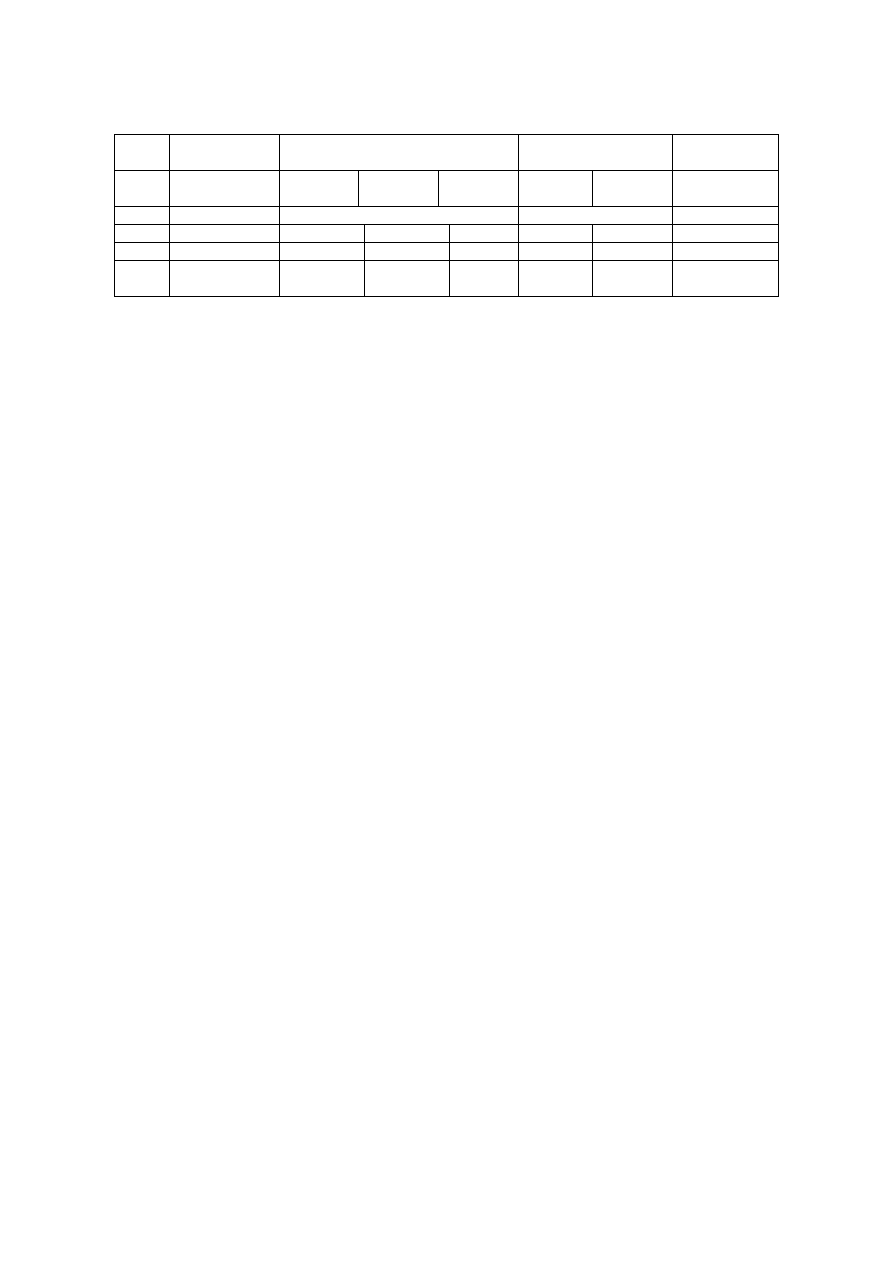
10
Tabela pomiarowa 2. Pomiary do wykresów
σ
(
ε
) oraz
σ
(
ε
)
pl
Lp.
Siła
rozciągająca F
Odczyty na skalach
Wydłużenie względne
Naprężenie
σ
= F/S
0
S
1
S
2
S
1
+ S
2
całkowite
ε×
10
3
plastyczne
ε
pl
×
10
3
[daN]
[mm]
[%]
[MPa]
1
200
0
0
0
0
2
600
…
…
…
…
…
…
…
…