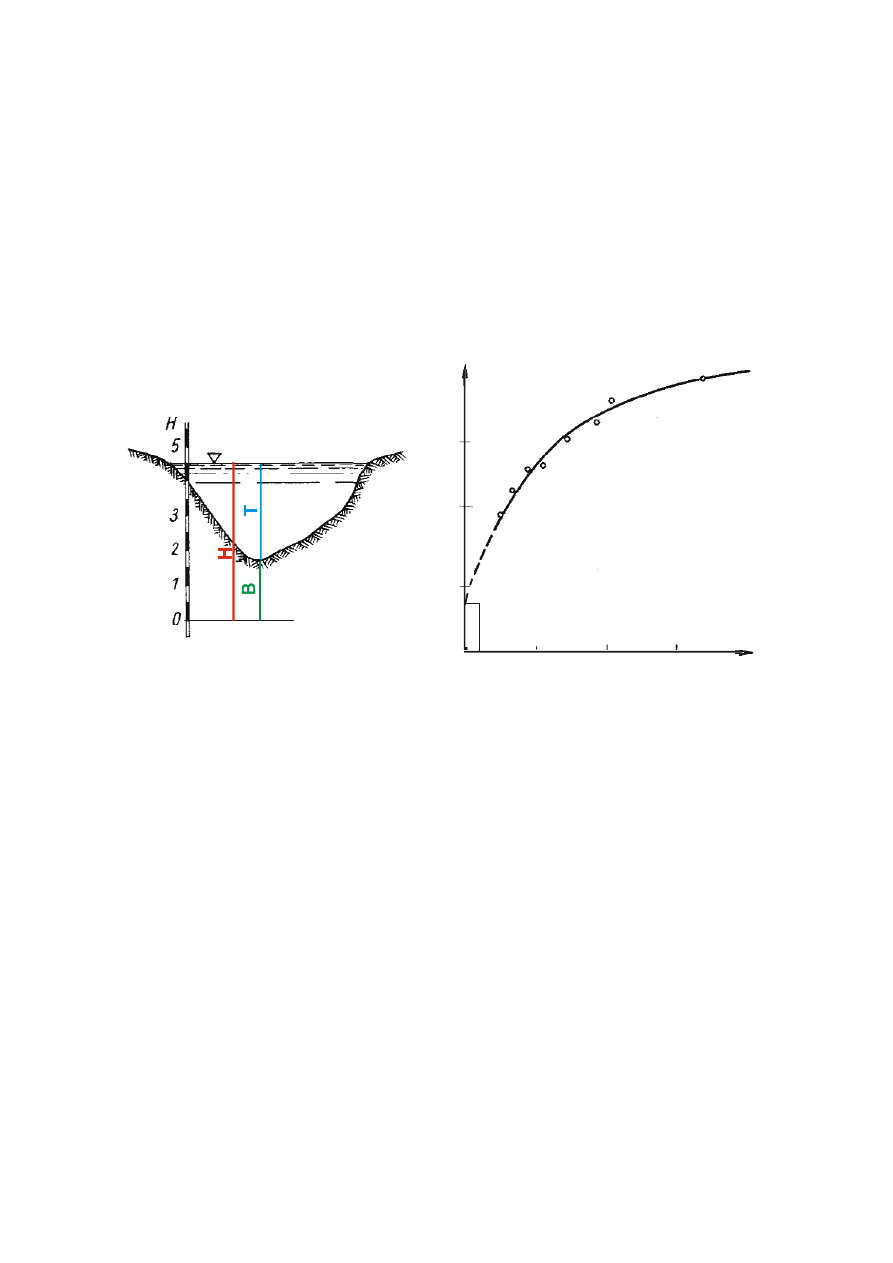
KRZYWA KONSUMCYJNA

KRZYWA KONSUMCYJNA albo KRZYWA PRZEPŁYWU (krzywa K) jest to

krzywa przedstawiająca związek pomiędzy stanem wody w rzece (H), a przepływem (Q).

Q = f(H)

(l)

Krzywa konsumcyjna jest parabolą wyższego rzędu, a krzywizna jej zależy od wykładnika
potęgowego, który z kolei zależny jest od kształtu przekroju (profilu) poprzecznego rzeki.

0

100

200

300

Q[m3/s]

50

100

150

H [

cm

]

B

KONSTRUOWANIE KRZYWEJ KONSUMCYJNEJ

Znajomość zależności pomiędzy stanami i przepływami wody pozwala na określanie

wielkości przepływów na podstawie obserwacji stanów wody na wodowskazie. Jest więc krzywa
konsumcyjna jedną z najważniejszych w praktyce hydrologicznej.
Krzywa konsumcyjna powstaje przez naniesienie w układzie prostokątnym punktów
otrzymanych poprzez pomiar przepływów przy różnych stanach wody w danym przekroju.

Najczęściej punkty te wykazują pewien rozrzut spowodowany m.in. przez:
1. zmiany poziomu zera wodowskazu,
2. zmiany przekroju poprzecznego rzeki,
3. ruchy dna (odkładanie materiału, wymywanie),
4. zmiany spadku zwierciadła wody,
5. sezonowe zmiany przekroju (zarastanie roślinnością w lecie, zjawiska lodowe w zimie)

Każdorazowo należy przeanalizować warunki w jakich pomiar został wykonany. Jeśli zmiany w
przekroju poprzecznym są znaczące, zachodzi konieczność opracowania nowej krzywej. Krzywa
konsumcyjna wyznaczona dla okresu poza zarastaniem i zlodzeniem nosi nazwę KRZYWEJ
PODSTAWOWEJ.

Krzywa obejmująca całą strefę zmienności przepływów od punktu dennego - zerowego do
przepływu najwyższego znanego, to KRZYWA ZUPEŁNA.

KRZYWA ODCINKOWA obejmuje część amplitudy wahań przepływów.


RÓWNANIA KRZYWEJ KONSUMCYJNEJ

W praktyce hydrologicznej krzywe przepływu opisuje się różnymi typami równań, najczęściej
równaniami paraboli n-tego stopnia.

Równanie Harlachera (1883 r. ):

Q = a(H- B)

n

(2)

Równanie Bubendeya:

Q = a

0

+ a

1

H + a

2

H

2

+ ... + a

n

H

n

(3)

W praktyce opuszcza się wyrazy o wyższych potęgach. poprzestając na równaniu drugiego
stopnia:

Q =a+bH+cH

2

(4)

gdzie w równaniach (2, 3, 4) :

Q – przepływ [m

3

/s],

a, b, c, n, a

0

, a

1

. . . . a

n

- parametry równania,

H - stan wody na wodowskazie [cm],
B - różnica rzędnych zera wodowskazu i dna teoretycznego [cm].

Napełnienie w przekroju T [cm]:

T = H - B

(5)

Stałą B można wyznaczyć z pomiarów w korycie lub teoretycznie np. metodą Głuszkowa:
Na odręcznie wykonanej krzywej wybieramy dwa możliwie najbardziej odległe od siebie punkty
o współrzędnych (H

1,

Q

1

) i (H

2

, Q

2

). Obliczamy średnią geometryczną

2

1

3

Q

Q

Q

=

oraz z

wykresu odczytujemy stan wody H

3

. Jeśli wartości par współrzędnych podstawimy do równania

ogólnego (2), otrzymamy 3 równania szczególne, w których za Q

3

podstawiamy

2

1

Q

Q

i po

prostych przekształceniach otrzymujemy:

2

1

3

2

1

2

3

H

H

2H

H

H

H

B

−

−

×

−

=

(6)

Uzyskaną wielkość B należy sprawdzić nanosząc na wykres krzywej konsumcyjnej.

Następnie należy wyznaczyć wartość parametrów a i n.
Znając wartość B, równanie (2) możemy zapisać:

Q = aT

n

(7)

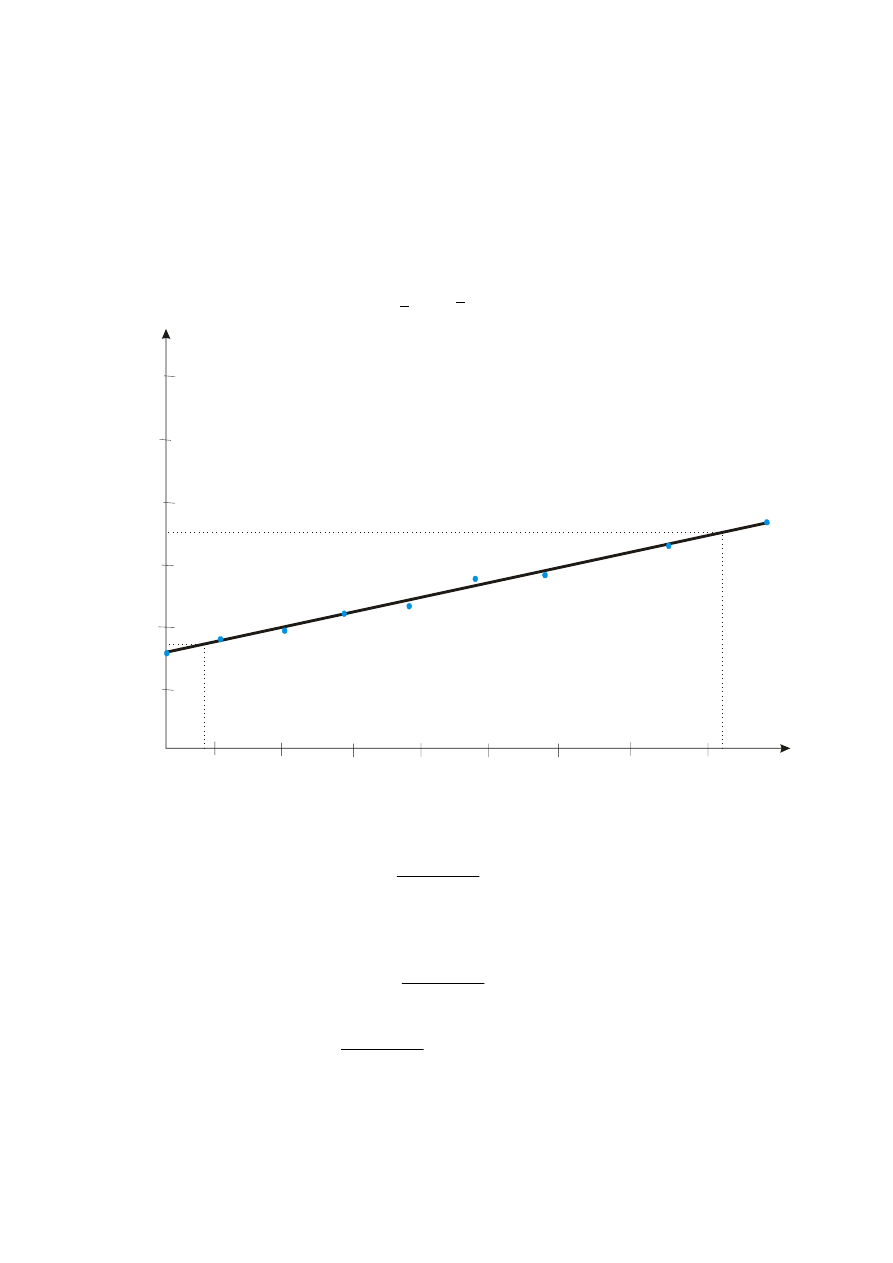
Aby wyznaczyć parametry a i n równanie (7) logarytmujemy stronami:

lg Q = lg a + n lg T

(8)

Parametry a i n można wyznaczyć metodą analityczno-wykreślną. Nanosząc wartości lg Q i lg T
otrzymujemy szereg punktów, które wyrównujemy linią prostą (czasem dwoma prostymi), której
równanie obliczamy wybierając dwa punkty (lgQ

l

. lgT

l

) i (lgQ

2

, lgT

2

). Równanie prostej

przechodzącej przez te dwa punkty ma postać:

b

Q

lg

a

T

lg

+

=

(9)

log Q

log T

1.5

2.0

2.5

3.0

2.0

2.5

3.0

3.5

log Q1

log Q2

log T1

log T2

log T =

0.129

logQ +

1.369

Parametry równania krzywej konsumcyjnej można określić z równania:

(

)

1

1

2

1

2

1

lgT

lgT

lgT

lgT

lgQ

lgQ

lgQ

lgQ

−

−

−

=

−

(10)

skąd po przekształceniach otrzymujemy:

1

1

2

1

2

1

lgT

lgT

lgT

lgQ

lgQ

lgQ

lga

−

−

−

=

(11)

1

2

1

2

lgT

lgT

lgQ

lgQ

n

−

−

=

(12)

Parametry a i n określić można także metodą najmniejszych kwadratów, rozwiązując układ
dwóch równań normalnych względem lg a i n:

∑

∑

+

=

m

1

m

1

lgT

n

mlga

lgQ

(13)

( )

∑

∑

∑

+

=

m

1

m

1

m

1

2

lgT

n

lgT

lga

lgT)

(lgQ

m - ilość punktów użytych do obliczeń.

m

T

lg

n

Q

lg

a

lg

m

1

m

1

∑

∑

−

=

(14)

W efekcie końcowym otrzymamy równanie krzywej konsumcyjnej w postaci:

Q = 0.00025 (H+ B)

2.565