Byczkowski A, 1999. Hydrologia /t.1/ Wydawca:SGGW

Krzywa natężenia przepływu (konsumcyjna)

Pojęcia ogólne

Dotychczas przedmiotem rozważań były stany wody i metodyka ich opracowywania. Dawniej, w okresie rozwoju
służb hydrologicznych, gdy wyniki ich działalności wykorzystywane były głównie dla celów żeglugi i dróg
wodnych, znajomość stanów wody była wystarczająca dla praktyki inżynierskiej. Obecnie, gdy gospodarka wodna
obejmuje szeroki wachlarz zagadnień technicznych i gospodarczych, konieczna jest znajomość nie tylko stanów
wody w rzekach, lecz również - i to przede wszystkim - przepływów wody w rzekach. Ma to szczególne znaczenie
wtedy, gdy naturalny reżim rzek zostaje zmieniony przez budowle piętrzące oraz inne urządzenia i obiekty
gospodarki wodnej. Regulowanie odpływem rzecznym jeszcze bardziej czyni niezbędnym operowanie
wartościami przepływów.
Przepływy mierzone są na posterunkach sieci hydrologicznej w sposób sporadyczny, zazwyczaj kilka lub
kilkanaście razy w ciągu roku. Jedynie w nielicznych zlewniach badawczych bądź też w przekrojach
kontrolujących pracę szczególnie ważnych obiektów gospodarki wodnej przepływy mierzone są codziennie lub
też rejestrowane w sposób ciągły. Natomiast stany wody obserwowane są systematycznie częstokroć w sposób
ciągły przez cały rok hydrologiczny.
Z tej przyczyny od lat stosuje się w hydrologii metodę polegającą na określaniu przepływów na podstawie
wyników pomiarów stanów wody ze związku statystycznego, jaki istnieje między zmierzonymi jednocześnie
wartościami przepływu i stanu wody Q=f(H).
Analizując związek między natężeniem przepływu a stanem wody, należy stwierdzić, że stan wody, będąc miarą
napełnienia koryta, stanowi skutek wywołany przez przyczynę, jaką jest masa wody płynąca korytem rzeki,
pochodząca z wód opadowych, roztopowych oraz z wód podziemnych. W tej sytuacji jako zmienną niezależną
(argument) należałoby traktować przepływ Q, a jako zmienną zależną (funkcja) - stan wody H = <p (Q). W
praktyce interesuje nas jednak zależność odwrotna, tj. związek Q =f(H), ponieważ to stany wody są znane, a nie
natężenie przepływu. Tak sformułowana zależność jest dużym uproszczeniem zagadnienia, ponieważ natężenie
przepływu, poza stanem wody, zależy jeszcze od wielu innych czynników. Ogólna postać równania związku
powinna być przyjmowana jako:
Q=f(H,i,F,m,-x)
gdzie:
i — spadek zwierciadła wody [%] [-],
F — powierzchnia przekroju poprzecznego [m],
m — współczynnik szorstkości koryta,
X — obwód zwilżony [m].
Pozostałe oznaczenia j w.

Zależność tę można upraszczać w warunkach przepływu swobodnego w korytach jednorodnych do
przytoczonej na początku postaci Q =f(H). Uproszczenie takie nie może być stosowane w warunkach
ruchu nieustalonego (np. podpiętrzenie stanów wody, przejście fali powodziowej). W tych wszystkich
przypadkach do omawianego związku wprowadza się dodatkowa, zmienną, najczęściej
charakteryzującą wpływ spiętrzenia stanów wody bądź zmianę spadku zwierciadła wody. Zmienna,
taka. może być spadek zwierciadła wody i, stan wody na recypiencie H lub wielkość spiętrzenia
stanów ∆H. Równanie związku przyjmuje wówczas postać:
Q=f(H*m)
gdzie: m — zmienna charakteryzująca wpływ zmian w profilu podłużnym zwierciadła wody.
Graficznym obrazem lego związku jest krzywa natężenia przepływu lub krótko -przepływu. Krzywa ta
była i jest jeszcze do dziś przez wielu praktyków nazywana krzywą konsumcyjną. Jest to nazwa
zwyczajowa, wywodząca się z tradycji austriackiego Centralnego Biura Hydrograficznego, nie
wyjaśniająca istoty omawianej zależności. Nieraz można spotkać w polskiej literaturze inne nazwy

określające związek pomiędzy stanem i przepływem, jak np. krzywa objętości lub krzywa k.
Wykres krzywej przepływu w układzie współrzędnych prostokątnych powstaje przez odłożenie na osi
poziomej wartości natężenia przepływu Q, a na osi pionowej odpowiadających im wartości stanów
wody H (lub napełnienia przekroju, czy też rzędnych zwierciadła wody). W literaturze obcej (np.
francuskiej) można spotkać odwrotny opis osi współrzędnych (oś pozioma - stany wody, oś pionowa -
natężenie przepływu).

3.3.2. Kształt krzywej przepływu
Natężenie przepływu, można -jak wiadomo - wyrazić jako iloczyn:
Q = Fv
gdzie:
F — czynna powierzchnia przekroju poprzecznego [m],
v — średnia prędkość w przekroju [m/s].
Obydwa składniki wzoru można wyrazić jako funkcje stanów wody:


F =f

1

,(H) oraz v=f

2

(H) czyli

Q=f

1

(H)f

2

(H)

Koryta naturalne zazwyczaj rozszerzają się wraz ze wzrostem napełnienia. Dla takich koryt funkcja
F= f

1

(H) ma kształt wypukły ku górze. Odwrotny kierunek wykresu oznaczać by musiał, że przekrój

zwęża się ku górze, co może zdarzać się jedynie
Krzywa przepływu (konsumcyjna)Rysunek.

Wykres związków: a- krzywej natężenia
przepływu Q = f

1

(H), b- krzywej powierzchni

przekroju F=f

2

(H), c- krzywej prędkości

przepływu v= f

3

(H)

Rysunek 3.32.
Przekrój
poprzeczny cieku
zwężający się ku
górze

[m/s]

w przypadku rzek górskich, płynących pod nawisami skalnymi (rys. 3.32) lub też przewodów
zamkniętych o przekroju kołowym, eliptycznym lub owalnym. W przekrojach naturalnych w miarę
wzrostu stanów wody H powierzchnia przekroju poprzecznego F wzrasta szybciej niż liniowo.
Funkcja v =f

2

(/H) w korytach rozszerzających się ku górze, przy nieznacznie zmieniającym się spadku

zwierciadła wody, i, jest również funkcja rosnąca wraz ze wzrostem stanów wody H. Funkcja Q =f(H)
jest na ogół funkcją rosnącą szybciej niż liniowo, ponieważ, natężenie przepływu Q zgodnie ze
wzorem jest iloczynem funkcji f

1

(H) i f

2

(H).

Z przeprowadzonych rozważali wynika, że krzywa przepływu ma kształt krzywej potęgowej o
wykładniku n>\. Równanie krzywej można określić na podstawie rozważań teoretycznych bądź na
podstawie wyników pomiarów natężenia przepływu. Teoretycznie równanie krzywej można
wyprowadzić dla przekrojów poprzecznych o kształcie figur geometrycznych, jak np. prostokąt,

wycinek paraboli, trójkąt.
Pole przekroju poprzecznego o kształcie prostokątnym oblicza się z zależności:

F =Bh

s

gdzie:
F — pole przekroju poprzecznego korytu [m

2

],

b — szerokość koryta [m],
h

s

— głębokość średnia [m].

Prędkość średnią w przekroju można wyrazić za pomocą wzorów hydraulicznych, np. wzoru
Chezy'ego:
v=c i

-0,5

h

s

0,5

gdzie:
v — prędkość średnia w przekroju [m/s],
c — współczynnik prędkości,
i — spadek zwierciadła wody [m/km],
h

s

— jak we wzorze poprzednim.

W tym przypadku we wzorze Chezy'ego przyjmuje się głębokość średnią zamiast promienia
hydraulicznego R

h

, ponieważ dla koryt naturalnych jest zazwyczaj spełniony warunek:

B > 10h

s

Po podstawieniu tego warunku do wzoru otrzymuje się następujące równanie:

gdzie: k

i

= Bci

-0,5

.

Podobne rozważania można przeprowadzić dla przekroju o kształcie wycinka paraboli,
trójkąta itp. Prowadzą one do wniosku, że stopień krzywej wzrasta w miarę zwiększania
się stosunku B/h

o

- szerokości koryta B do głębokości maksymalnej h

o

- oraz zmniejszania

się stosunku h

s

/h

o

.Prawidłowość tę przedstawia tabela.

W ogólnym przypadku równanie krzywej przybiera postać:
Q = kh

n

s

Krzywe przepływu koryt naturalnych
Punkty szczególne krzywej przepływu. Kształt krzywej przepływu koryta naturalnego zależy w
pierwszym rzędzie od kształtu przekroju poprzecznego oraz od spadku zwierciadła wody. Na wykresie
krzywej przepływu można wyróżnić kilka punktów szczególnych: punkt denny, punkty załomu,
punkty brzegowe, punkt graniczny łożyska.

Krzywa przepływu (konsumcyjna) 243
Tabela. Wartości ilorazów B/h

0

i h

s

/h

0

dla różnych kształtów przekrojów poprzecznych (m=B/h

s

)

Kształt przekroju

B/h

0

h

s

/h

0

n

Prostokątny

m

1

1,5

Paraboliczny

3/2 m

2/3

2,0

Trójkątny

2 m

1/2

2,5

Q[m

3

/s]

Rysunek. Punkty szczególne krzywej przepływu
Punkt dermy krzywej wyznacza stan wody, przy którym przepływ Q jest równy zeru. Stan ten nosi
często nazwę stałej B.
Punkty załomu wyznaczone są. przez przecięcie się skarpy brzegowej z rzędną koryta niskiej wody.
Jeżeli przekrój ma kształt regularny, punkty załomu nie występują.
Punkt brzegowy znajduje się na poziomie stanu brzegowego, tj. stanu wody odpowiadającego
położeniu krawędzi brzegu koryta. Stan ten wyznacza się na podstawie analizy przekrojów
poprzecznych. Ponieważ zarówno brzeg lewy, jak i prawy nie zawsze leżą na jednakowej wysokości,
więc na krzywej będzie się obserwować dwa lub jeden punkt brzegowy. Punkty brzegowe w profilu
podłużnym rzeki mogą układać się również na różnej wysokości. W tej sytuacji jako miarodajny
przyjmuje się przeciętny stan brzegowy na odcinku rzeki w rejonie wodowskazu. Przy stanach wody
wyższych od stanu brzegowego (H > H

brzeg

), krzywa przepływu zmienia swój kształt, a wykres staje

się bardziej płaski. Związane jest to ze wzrostem szerokości przekroju poprzecznego powyżej wody
brzegowej. Powoduje to większy przyrost przepływu na jednostkę stanów wody niż przyrost
przepływu poniżej stanu brzegowego w obrębie koryta rzeki.
Punkty brzegowe krzywej przepływu występują w przekrojach złożonych. Krzywe przepływu w
przekrojach zwartych nie mają punktów brzegowych.
Punkt graniczny łożyska rzeki odpowiada najwyższemu stanowi obserwowanemu w danym profilu
wodowskazowym w okresie obserwacji WWW.
Krzywa przepływu obejmująca cały obszar zmienności stanów wody od zera przepływu aż do
najwyższego obserwowanego stanu wody nosi nazwę krzywej zupełnej.
W odróżnieniu od niej, krzywa poprowadzona w jednej tylko strefie lub też obejmująca niecały przedział
zmienności stanów wody zwana jest krzywą odcinkową.
Wyrównywanie krzywych przepływu
Punkty pomiarowe naniesione na wykres w układzie osi współrzędnych prostokątnych H0Q nie leżą dokładnie
na krzywej, lecz układają, się z pewnym (większym lub mniejszym) rozrzutem. Do wyznaczania krzywej
wyrównującej punkty pomiarowe służą metody, które można podzielić na dwie grupy: analityczne i graficzne.
Metody analityczne
W praktyce hydrologicznej krzywe przepływu opisuje się różnymi typami równań. Najczęściej są to dwa
równania:
—

równanie krzywej potęgowej n-tego stopnia z wierzchołkiem w początku układu osi

współrzędnych (równanie Harlachera z 1883 r.):
Q = a(H-B)

n

gdzie:
a, n — parametry krzywej,
B — stan na wodowskazie, przy którym Q = 0;
—

ogólne równanie paraboli n-tego stopnia (równanie Bubendeya):

Q=a

0

+ a

1

H+ a

2

H

3

+ ...+a

n

H

n

gdzie: a

0

, a

1

..., a„ — parametry krzywej.

Oprócz tych znanych i od dawna stosowanych równań krzywych przepływu można znaleźć propozycje
wprowadzenia innych krzywych aproksymujących wyniki pomiarów. Smolik (1970) zaproponował do tego

celu równanie krzywej wykładniczej w postaci:
Q = ab

H

gdzie: a, b — parametry krzywej.
Równanie Harlachera. Spośród wymienionych równań krzywa potęgowa n-tego stopnia najlepiej oddaje kształt
krzywej przepływu. Zgodnie z założeniem równanie Harlachera jest równaniem krzywej, której wierzchołek
pokrywający się z punktem dennym krzywej znajduje się w początku układu współrzędnych:

y = ax

n

Zazwyczaj jednak początek układu współrzędnych (H = O i Q = 0) nie pokrywa się z punktem dennym
krzywej, którego współrzędne wynoszą H = B i Q = 0. W tej sytuacji oś poziomu układu współrzędnych (oś Q)
przesuwa się równolegle po osi pionowej, aż do punktu dennego. Otrzymuje się wówczas nowy układ
współrzędnych:
x'=x-a

gdzie:
x' — współrzędna punktu w nowym układzie równa T,
x — współrzędna punktu w pierwotnym układzie równa H,
a — miara przesunięcia osi poziomej do początku nowego układu współrzędnych równa B.
Wprowadzając oznaczenia stosowane w hydrologii:
T=-H-B

podstawiając równanie do równania 3.42, otrzymuje się:
Q = a T

n

Wyznaczanie stałej B. Odcięte punktu dennego krzywej przepływu, czyli odczyt na wodowskazie, przy którym
2 = 0, można określać różnymi metodami opierającymi się na pomiarach terenowych bądź na konstrukcjach
graficznych. Najczęściej określa się B następującymi metodami:
z przekroju poprzecznego cieku,
z profilu podłużnego dna,
metodą Gruszkowa, metodą prób z wykresu krzywej przepływu w podziałce logarytmicznej.
Metody te można podzielić na terenowe i kameralne. W miarę posiadanych materiałów hydrometrycznych
należy stosować metody oparte na danych terenowych.
Metody terenowe. Najprostszym sposobem określania stałej B jest wykorzystanie do tego celu przekroju
poprzecznego w profilu wodowskazowym. Znając stan wody na wodowskazie H oraz głębokość maksymalną
h

max

, określa się wartość B z różnicy

B=H-h

max

Określanie stałej 8 na podstawie przekroju

poprzecznego cieku.
Wartości B określone na podstawie kilku pomiarów przepływu różnią się
zazwyczaj między sobą, ponieważ pomiary przepływu (a zatem i
pomiary przekroju poprzecznego) wykonywane są nie w profilu

wodowskazowym, ale w różnych przekrojach położonych w góro lub w dół od wodowskazu. Tylko w
nielicznych przypadkach obiera się jeden stały profil pomiarowy. Ponadto w rzekach o dnie zbudowa-
nym z piasku i żwiru, nawet znajdującym się w stanie równowagi, mogą zachodzić niewielkie zmiany
położenia średniego poziomu dna w obydwóch kierunkach. Z tej przyczyny wartość B oblicza się jako
średnich ze wszystkich wartości różnic H - h

max

obliczonych na podstawie wyników pomiarów

przepływu:

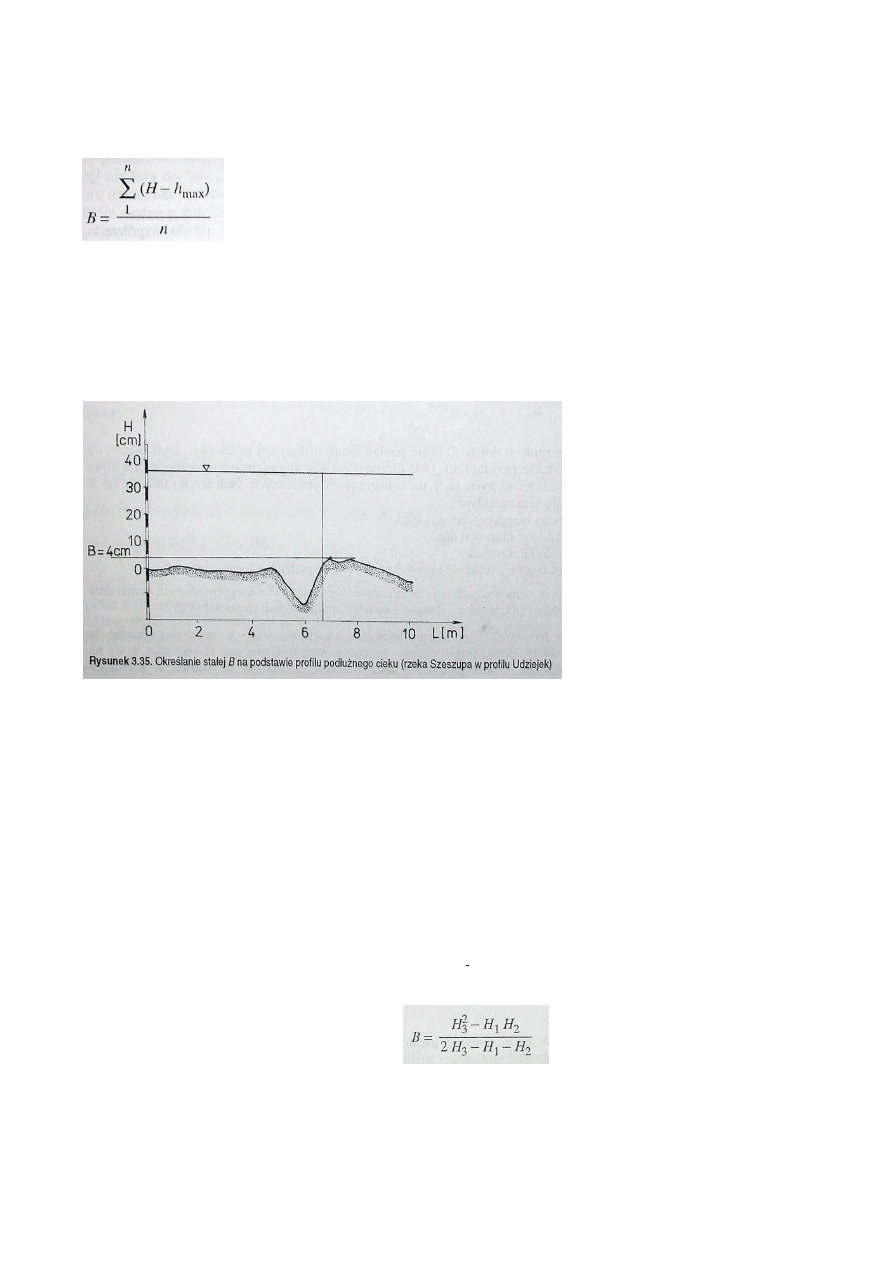
Taki sposób postępowania jest słuszny, jeżeli koryto rzeki jest regularne, a dno układa się ze stałym
spadkiem równoległym do zwierciadła wody. Często jednak w dnie rzeki istnieją, lokalne zagłębienia,
wyboje i odsypiska. Wodowskazy mogą, znajdować się w profilach, w których występują lokalne
zagubienia dna, wypełnionych wodą również i wtedy, gdy Q = 0. W takich przypadkach określenie
stałej B jest możliwe

Rysunek 3.35. Określanie stałej B na
podstawie profilu podłużnego cieku
(rzeka Szeszupa w profilu Udziejek)
jedynie na podstawie analizy
profilu podłużnego dna,
poprowadzonego w punktach o
największej głębokości. Zwykle
jest to profil w linii nurtu.
Wartość stałej B wyznacza się
albo z wykresu profilu
podłużnego, rzutując największy
wyniosłość dna (najmniejsza

głębokość) na podziałkę wodowskazu, albo analitycznie ze wzoru:
H – min h

max

– L

i

gdzie: min h

max

— najmniejsza z głębokości maksymalnych w przekrojach [m],

L — odległość od wodowskazu punktu, w którym zmierzono najmniejsza wartość
H

max

[m],

I - spadek zwierciadła wody na odcinku L [m/km].
Metody kameralne. Jeżeli nie dysponuje się profilem poprzecznym i podłużnym oraz jeżeli nie można
skorzystać ze wzoru 3.48, to do wyznaczenia stałej B należy stosować sposoby kameralne, opierające
się na konstrukcjach graficznych lub graficzno-analitycznych.
Metoda Głuszkowa. Najczęściej podawana w literaturze metoda Głuszkowa opiera się na odręcznie
wyrównanej krzywej przepływu. Na krzywej tej obiera się dwa punkty leżące w pobliżu skrajnych
punktów pomiarowych o współrzędnych H

1

, Q

l

i H

2

,

Q2

. Oblicza się średnia, geometryczna,

przepływów Q

1

i Q

2

,równą Q

3

= √Q

1

*Q

2

, a następnie z wyrównanej odręcznie krzywej określa się

odpowiadający jej stan wody H

3

. Otrzymuje się w ten sposób trzeci punkt na krzywej o współrzędnych

H

3

,Q

3

. Wartość stałej B oblicza się ze wzoru:

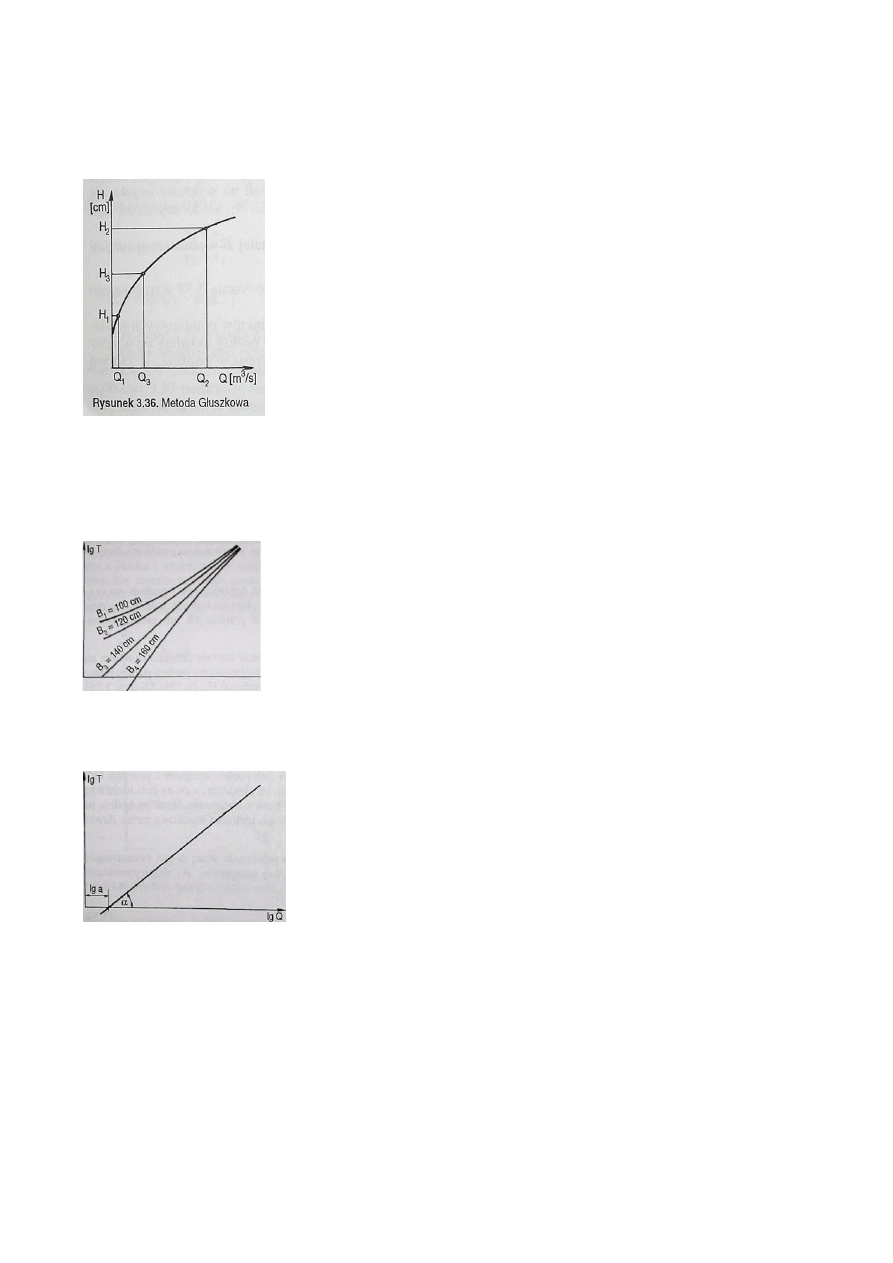
Rysunek 3.36. Metoda Głuszkowa
Metoda Głuszkowa może dawać w praktyce dobre wyniki pod warunkiem właściwego
odręcznego wyrównania punktów pomiarowych i prawidłowego doboru punktów l i 2. Krzywa
przepływu może mieć punkty załamali (lub punkty brzegowe), powyżej których zmienia się jej
charakter, a co za tym idzie i jej równanie. Jeżeli punkt 2 przyjmuje się powyżej punktu
załamania, leżeć on będzie na krzywej o innym równaniu. W takich przypadkach metoda
Głuszkowa może dawać wyniki niewłaściwe, a nawet zupełnie nierealne.
Metoda prób. Innym kameralnym sposobem wyznaczania stałej B jest zastosowanie
logarytmicznego przekształcenia równania krzywej przepływu. Po zlogarytmowaniu równania
otrzymuje się:
Ig Q = Ig a + n Ig T

Przyjmując Ig Q = y i Ig T= x oraz Ig α = A, otrzymuje się równanie prostej y = A + nx.
Obraz taki otrzyma się, jeżeli stała B została właściwie określona, tzn. początek przesuniętego równolegle układu współrzędnych
znajduje się w punkcie dennym. Jeżeli stała B nie została właściwie określona, wierzchołek krzywej nie znajdzie się w początku
układu, a punkty pomiarowe naniesione na skale logarytmiczna nie ułożą się według linii prostej. Stosując omawiana metodę, w
przybliżeniu wyznacza się stałą B, ekstrapolując odręcznie wykres krzywej przepływu. Określona w ten sposób stała B podstawia się
do równania i określa wartości napełnień przekroju T oraz nanosi punkly pomiarowe o

Rysunek. Określenie stałej B metodą prób, współrzędnych T i Q na wykres w skali logarytmicznej.
Jeżeli stała B została przyjęta prawidłowo, to otrzyma się na wykresie linię prosta.. Jeżeli na wykresie
uzyska się krzywa, wówczas droga prób przyjmuje się różne wartości B, aż do uzyskania linii prostej.

Sposobu tego można również używać do weryfikacji stałej B
wyznaczonej innymi metodami.
Określenie parametrów a i n. Wartości parametrów równania
wyrażającego krzywa przepływu można określić graficznie i
analitycznie. Metoda graficzna polega na odręcznym wyrównaniu
punktów pomiarowych naniesionych na wykres w skali logarytmicznej*
- w tej skali punkty układają się wzdłuż linii prostej (rys. 3.38). Wartość
Ig a odczytuje się z wykresu w punkcie, w którym (Rysunek. Graficzny
sposób wyznaczania parametrów równania krzywej przepływu)

wyrównana prosta przecina oś pozioma - punkt przecięcia ma współrzędne lg T = O i lg Q = Ig a.
Parametr n określa się jako cotangens kata a zawartego między osią Ig g a wyrównana prostą:
Jeżeli nie dysponujemy skalą logarytmiczną, to nanosi si« na wykres logarytmy wartości T i Q, tj. lg r i
lg Q.
Sposób ten znajduje zastosowanie, jeżeli w zasięgu sporządzonego wykresu znajduje się punkt przecięcia prostej
logarytmicznej z osią poziomu. W ogólnym przypadku stosuje się metodę graficzno-analityczną.