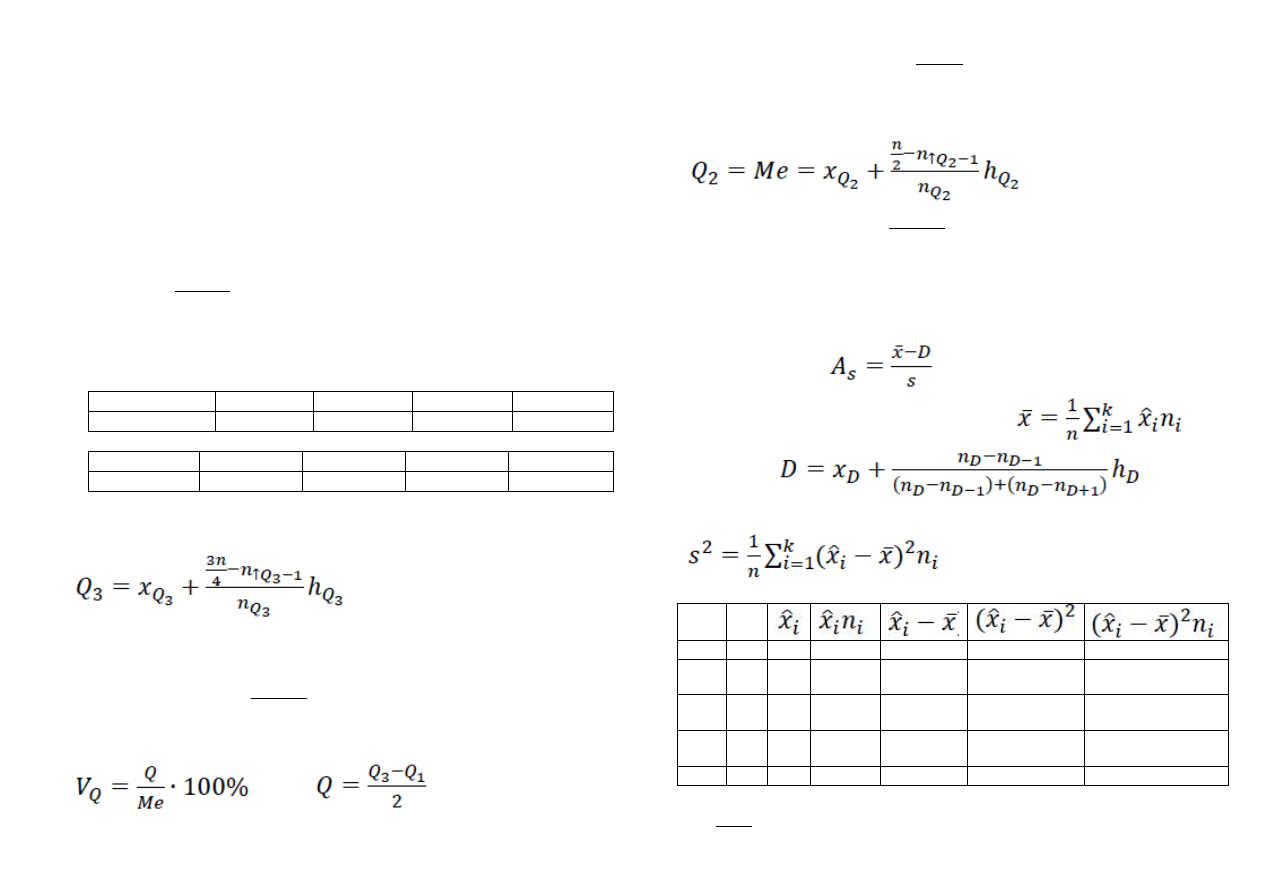
Do pozycyjnych miar położenia należą m.in.:
a. Średnia harmoniczna
b. Dominanta
c. Odchylenie ćwiartkowe
Jeżeli indeks dynamiki przyjmuje wartość 5,2 to zjawisko:
a. Wzrosło o 5,2%
b. Wzrosło o 420%
c. Wzrosło o 520%
Wyjaśnienie: przy indeksie równym 1 (czyli 100%) poziom zjawiska nie uległ
zmianie, dlatego trzeba odjąć te 100%. Ja niestety zaznaczyłam C….
Jeśli każdy wariant cechy zwiększymy o 6 to wariancja:
a) Zwiększy się 6 -krotnie
b) Nie zmieni się
c) Zwiększy się o 6
odszkodowanie
0-40
40-80
80-120
120-160
liczba firm
27
43
19
11
kumulacja
27
70
89
100
pozycje:
Q
1
Me, D
Q
3
Zad. 9. 75% firm zapłaciło co najmniej …… tys. zł odszkodowania.
Czyli wyznaczamy Q
3
Pozycja trzeciego kwartyla: (27+43+19+11)*3/4 = 75 czyli w przedziale 3
(80-120).
Zad. 10. Coś o odniesieniu do mediany (czyli obliczyć V
Q
)
Kwartyl trzeci już mamy z poprzedniego zadania: 90,53.
A więc: Q = (90,53 - 37,04) : 2 = 26,745 = 26,75
I takim sposobem: V
Q
= (26,75 * 100%) : 61,4 = 43,56677 = 43,57%
Zad. 11. Współczynnik asymetrii dla zróżnicowania odszkodowań
wynosi … .
Czyli co mamy policzyć:
Nasz współczynnik:
Średnią arytmetyczną dla sz. rozdz. przedz.:
Dominantę:
Odchylenie standardowe, a więc wariancję:
x
i
n
i
0-40
27
20
540
-45,6
2079,36
56142,72
40-
80
43
60
2580
-5,6
31,36
1348,48
80-
120
19
100
1900
34,4
1183,36
22483,84
120-
160
11
140
1540
74,4
5535,36
60888,96
100
6560
140 864,00
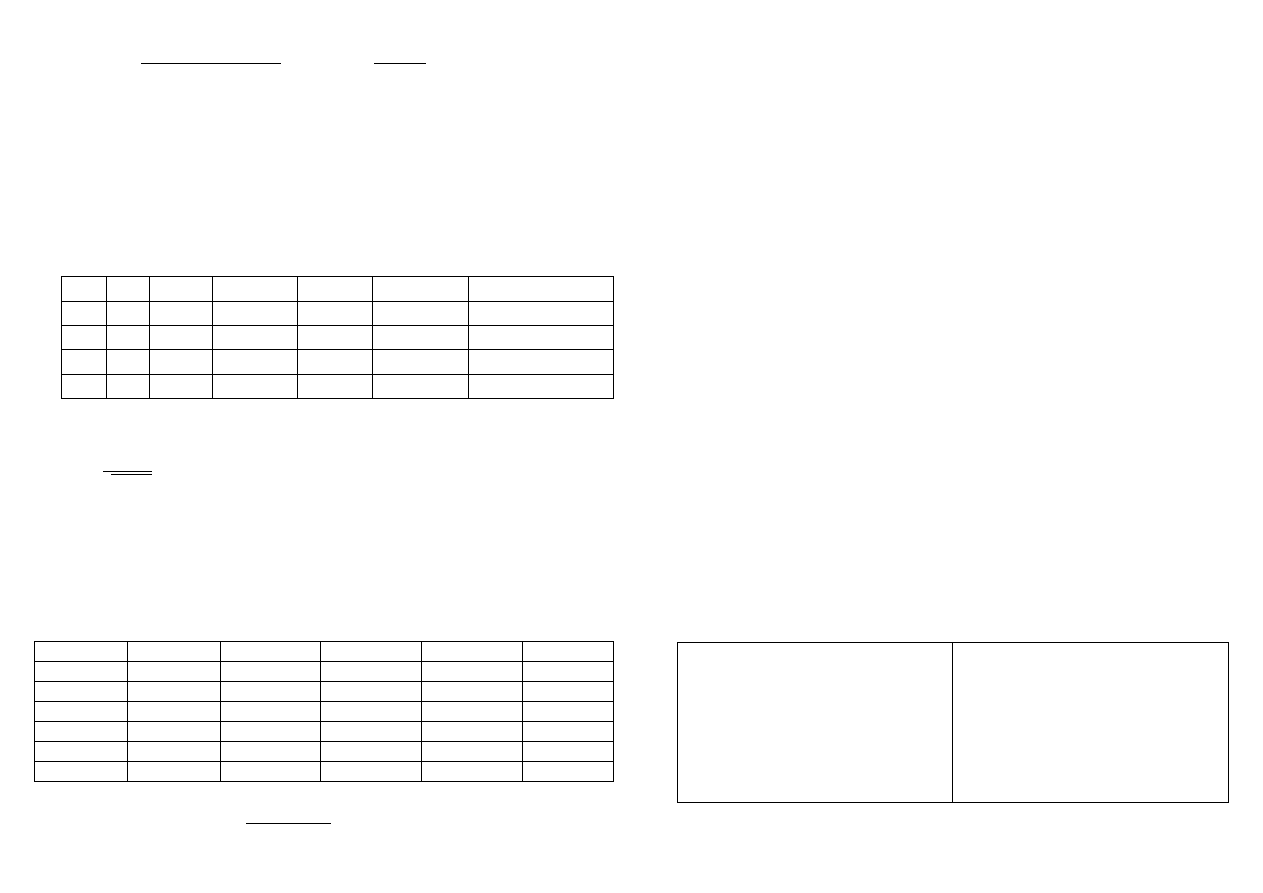
S
2
= 140 864 : 100 = 1 408,64 S = 37,53
Nareszcie mamy wszystkie części składowe do współczynnika:
A
s
= (65,60 – 41,67) : 37,53 = 0,637623… = 0,64
Zad. 12. Staż pracy i premie: (7; 12), (17; 11), (21; 16). Właściwy
współczynnik korelacji wynosi … .
Chodzi tu o współczynnik Pearsona.
X
Y
7
12
-8
64
-1
1
8
17
11
2
4
-2
4
-4
21
16
6
36
3
9
18
104
14
22
r
xy
=
Zad. 13. Tutaj zadanie z oceną obsługi komputera i oceną pracy.
Sprawdzono 5 osób, wyniki następujące (obsługa komputera; poziom
pracy): (;przeciętna), (średnia; dobra), (;przeciętna), (słaba; przeciętna),
(słaba; zła). Współczynnik korelacji Spearmana wynosi …
(Niestety nie pamiętam dokładnie wariantów, ale pamiętam że suma d
i2
wyszła
mi 5).
x
y
ranga x
ranga y
d
i
=d
x
-d
y
d
i2
3
2
1,5
3
-1,5
2,25
3
3
1,5
0,25
2
2
0
1
2
2,25
1
1
0,25
5
5
Zad. 14. W latach 2007-2011 odnotowano następujące zmiany wydatków
na „coś tam”: -11%, -14%, -4%, …. Nakłady w 2010 w stosunku do roku
2008 wzrosły/zmalały o …… %.
Cóż, nie było mnie ani na wykładzie ani na ćwiczeniach kiedy to było
opracowywane więc policzyłam logiczno-matematycznie czyli:
2007 – 0 (rok bazowy)
2008 => -11%
2009 => -14%
2010 => -4%
2011 => ileś tam
Zmiana w roku 2009 w stosunku do 2008 to -14% a więc 0,86x
Zmiana w roku 2010 w stosunku do 2009 to -4% a więc
0,96*0,86x = 0,8256x co nam daje: 82,56%x 100%-82,56=17,44%
Logicznie rzecz ujmując spadek o 17,44% nakładów w roku 2010 w
stosunku do roku 2008.
Zad. 15. Liczba sprzedanych rowerków w roku 2008 zwiększyła się o
102% w stosunku do roku poprzedniego, a cena spadła o 33%. Wartość
sprzedanych rowerków wzrosła/spadła o …… %.
i
w
= i
p
* i
q
nasze i
p
= 1 – 0,33 = 0,67
i
q
= 1 + 1,02 = 2,02 (bo wzrosła o 102% a nie o 2%!)
i
w
= 0,67 * 2,02 = 1,3534 = 1,35 = 135%
Czyli wartość wzrosła o 35%.
(ja niestety napisałam 135% .......)
Tabelka wyników:
1.
2.
3.
4.
5.
6.
7.
8.
9. 90,53
10. 43,57%
11. 0,64
12. 0,58
13. 0,75
14. zmalały o 17,44%
15. wzrosła o 35%