1

12. Model pasmowy ciała stałego. Metale, półprzewodniki i izolatory.

Poszczególnym orbitom elektronów w atomie odpowiadają określone wartości energii, rozumianej

jako suma energii kinetycznej i potencjalnej tych elektronów. Dlatego mając na myśli orbity elektronów
zwykło się mówić o poziomach lub stanach energetycznych. Elektrony w atomie mogą zajmować tylko
ściśle określone dozwolone poziomy energetyczne. Im większy jest promień orbity elektronu, tym
większa jest jego energia, gdyż do przejścia elektronu z pewnej orbity na kolejną, bardziej zewnętrzną,
konieczne jest dostarczenie określonej porcji (kwantu) energii z zewnątrz. Zatem każdy atom
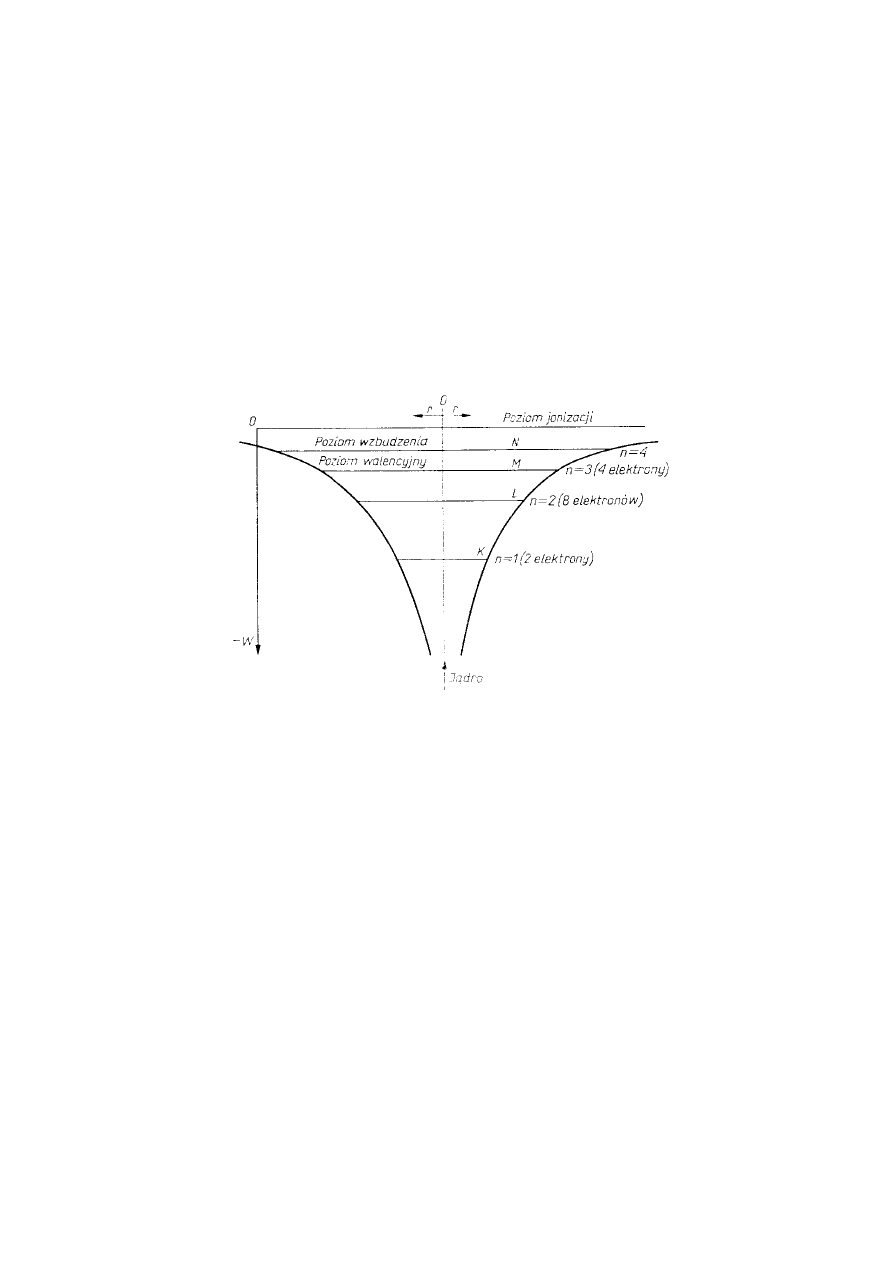
charakteryzuje się pewnym widmem energetycznym. Na rysunku 1.8 przedstawiono przykładowy wykres
dyskretnych poziomów energetycznych w atomie krzemu wraz z dwiema symetrycznymi krzywymi
zależności energii elektronu w funkcji jego odległości od jądra.

Rys. 1.8 Dyskretne poziomy energetyczne elektronów w atomie krzemu.

W tym przypadku dogodnie było przyjąć za bazę odliczania energii poziom energetyczny

elektronu nieskończenie odległego od jądra (chodzi o taką odległość elektronu od jądra, przy której znika
między nimi oddziaływanie elektrostatyczne); ten poziom energetyczny jest nazwany poziomem jonizacji.
Na rysunku l .8 pokazano poziomy energetyczne zajęte przez elektrony wraz z dozwolonymi poziomami
nie zajętymi. Najwyższy poziom zajęty jest nazywany poziomem walencyjnym. a kolejny nie zajęty
poziom o większej energii nosi nazwę poziomu wzbudzenia. Zgodnie z ogólnymi prawami materii
elektrony w atomie dążą do zajęcia jak najniższych poziomów energetycznych (struktura o mniejszej
energii jest bardziej stabilna). Jednakże — jak stwierdzono wcześniej — liczba elektronów na posz-
czególnych poziomach energetycznych (powłokach elektronowych) jest ściśle ograniczona do 2. 8 itd.
Jeżeli wszystkie elektrony w atomie zajmują najniższe z możliwych poziomów energetycznych, to mówi
się. że atom jest w stanie normalnym. Jeżeli pod wpływem jakiegoś bodźca energetycznego elektron lub
kilka elektronów zwiększą swą energię i zajmą poziom wzbudzenia, to atom znajdzie się w stanie
wzbudzenia.

Dla większej jasności dalszych rozważań konieczny jest dodatkowy komentarz do zagadnienia

liczby elektronów zajmujących wspólny poziom energetyczny. Jedno z podstawowych praw fizyki
atomowej — sformułowana w 1925 r. zasada Pauliego — mówi, że w atomie nie ma dwu identycznych
elektronów w sensie identyczności ich stanu energetycznego. Bardziej ściśle to prawo brzmi: w atomie
nie ma dwu elektronów o jednakowych czterech liczbach kwantowych. Pierwsze trzy liczby kwantowe,
oznaczone literami n, l, m, opisują odpowiednio kształt., rozmiary i położenie orbity elektronu w
przestrzeni, a czwarta liczba s, nazywana liczbą spinową, odnosi się do ruchu obrotowego elektronu.

2

Poprzednie zatem stwierdzenie o 2. 8 itd. elektronach na poszczególnych poziomach energetycznych
należy rozumieć w ten sposób, że są to poziomy określone z dokładnością do pierwszej liczby
kwantowej, nie dające pełnej informacji o stanach energetycznych poszczególnych elektronów. Na
przykład 8 elektronów na poziomie odpowiadającym powłoce L to po prostu osiem elektronów o
jednakowej liczbie kwantowej n (w tym przypadku n = 2), których stany energetyczne jednakże różnią
się wzajemnie od siebie kolejnymi liczbami kwantowymi.

Dotychczas omawiano widmo energetyczne pojedynczego atomu. Widma energetyczne atomów

jednego pierwiastka są identyczne. Można by stąd wnioskować, że zbiór atomów jednego pierwiastka
można opisać takim samym modelem energetycznym jak dla pojedynczego atomu, przy zwiększeniu
liczb elektronów na poszczególnych poziomach tyle razy, ile jest atomów w rozpatrywanym zbiorze.
Okazuje się. że takie podejście jest słuszne tylko wówczas, gdy odległości między atomami są na tyle
duże, że można pominąć ich wzajemne oddziaływanie. W przeciwnym przypadku należy rozszerzyć
działanie zasady Pauliego na cały zbiór atomów; wówczas zasadę tę można sformułować w następujący
sposób: w zbiorze wzajemnie oddziałujących na siebie atomów nie ma dwu elektronów o identycznych
stanach energetycznych. Taki przypadek istnieje w krysztale półprzewodnika, gdyż — jak wcześniej już
stwierdzono — każdy atom w sieci krystalicznej jest powiązany z sąsiednimi atomami przez
oddziaływania kowalencyjne. Stąd struktura energetyczna kryształu będzie inna niż dla pojedynczego
atomu, gdyż z poszczególnych pojedynczych poziomów energetycznych odosobnionego atomu utworzy
się tyle różnych poziomów, ile jest atomów w krysztale. W tej sytuacji zwykło się mówić o
rozszczepieniu poziomu energetycznego. Należy zauważyć, że różnice energetyczne między poziomami
powstałymi z rozszczepienia pojedynczego poziomu energetycznego są znikomo małe. Na przykład w
krysztale o objętości l cm

3

jest ok. 10

23

atomów, czyli w strukturze energetycznej tego kryształu każdy

poziom energetyczny pojedynczego atomu zostanie rozszczepiony na 10

23

poziomów. Jeśli przyjmie się,

że odstęp energetyczny między skrajnymi poziomami w paśmie wynosi l eV, to — średnio biorąc —
odstęp między dwoma sąsiednimi poziomami wynosi 10

-23

eV. Jest to tak mała wartość energii, że

można mówić o prawie ciągłym paśmie dozwolonych energii. W ten sposób z modelu dyskretnych
poziomów energetycznych w pojedynczym atomie przechodzimy do energetycznego modelu pasmowego
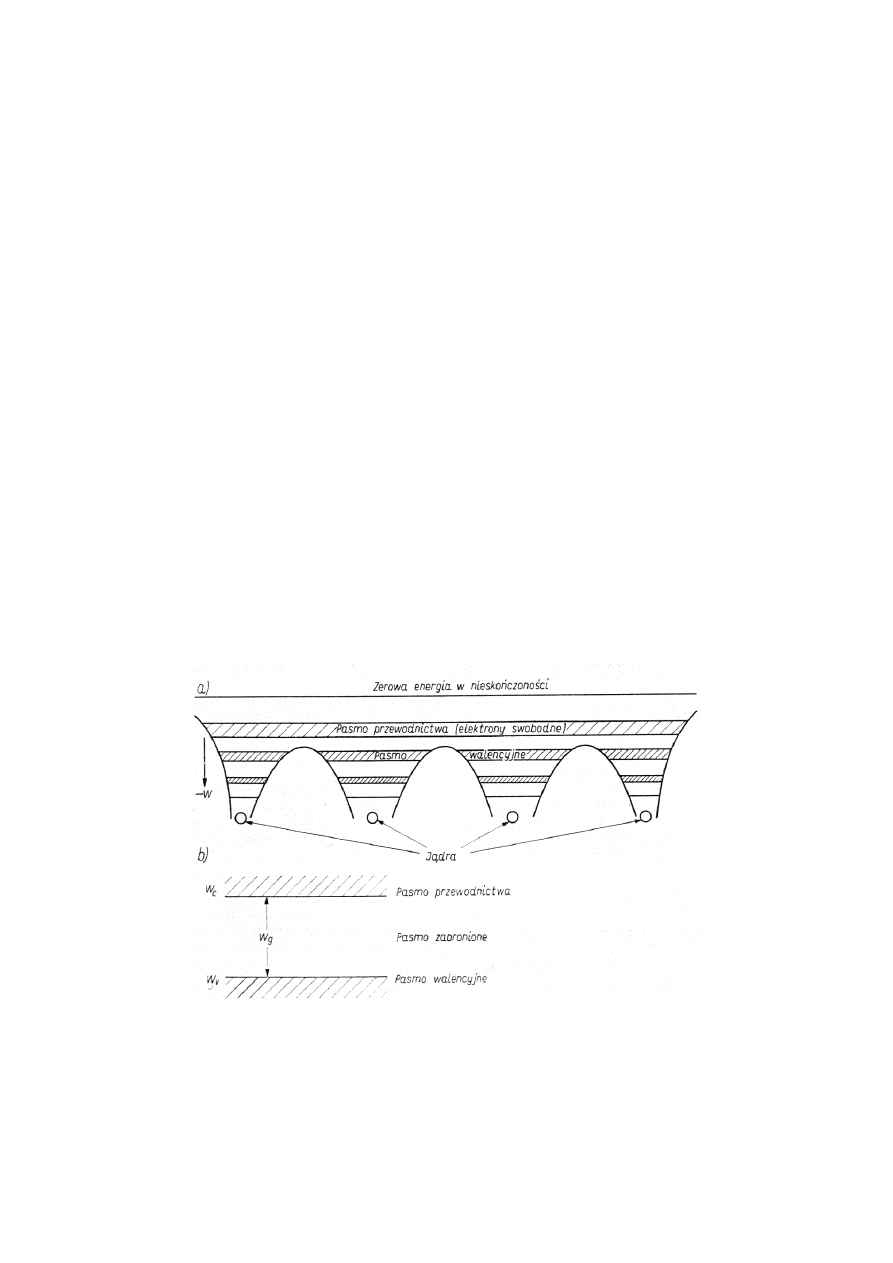
w krysztale. Typowy wykres energetycznego modelu pasmowego ciała stałego przedstawiono na rys.
1.9a.

Rys. 1.9 Energetyczny model pasmowy ciała stałego (a) oraz jego uproszczona ilustracja (b)

Należy zauważyć, że bariera energetyczna między sąsiednimi atomami jest mniejsza niż na

krawędziach kryształu. Obniżenie bariery energetycznej między poszczególnymi atomami jest
jednoznaczne z istnieniem wspólnych elektronów walencyjnych. Ponieważ właściwości elektryczne
półprzewodnika są uwarunkowane zjawiskami zachodzącymi w paśmie walencyjnym i kolejnym
wyższym paśmie dozwolonych energii (w paśmie przewodnictwa), dalej będziemy się posługiwać
bardziej uproszczonym wykresem energetycznego modelu pasmowego, przedstawionym na rys. 1.9b.

3

Odstęp W

g

między wierzchołkiem pasma walencyjnego W

v

a dnem pasma przewodnictwa W

c

jest

nazywany przerwą energetyczną lub pasmem zabronionym. W temperaturze zera bezwzględnego pasmo
walencyjne jest całkowicie zapełnione elektronami, co odpowiada efektywnie ośmioelektronowej
strukturze poziomu walencyjnego w atomie związanym kowalencyjnie z innymi atomami w sieci
krystalicznej. Pasmo przewodnictwa

natomiast jest w tych warunkach całkowicie puste. W miarę wzrostu temperatury część

elektronów z pasma walencyjnego „przeskakuje" do pasma przewodnictwa pozostawiając w paśmie
walencyjnym wolne miejsca nazywane dziurami. Taki proces jest nazywany generacją par elektron-
dziura. Szerokość pasma zabronionego jest wartością energii, jaką trzeba dostarczyć do sieci
krystalicznej dla uwolnienia elektronu z wiązania kowalencyjnego.

Dielektryki różnią się od półprzewodników tylko większą szerokością pasma zabronionego

(W

g

> 2 eV), co oczywiście oznacza, że w tych samych warunkach mniejsze jest prawdopodobieństwo

uwolnienia elektronu z wiązania, mniejsza jest zatem koncentracja nośników swobodnych ładunku.
W energetycznej strukturze metali nie ma w ogóle pasma zabronionego. Może to wynikać
z dwu powodów:

- pasmo walencyjne jest tylko częściowo zapełnione elektronami, nie zapełniona zatem część

pasma walencyjnego, nie rozdzielona przerwą energetyczną od części zapełnionej, spełnia funkcję
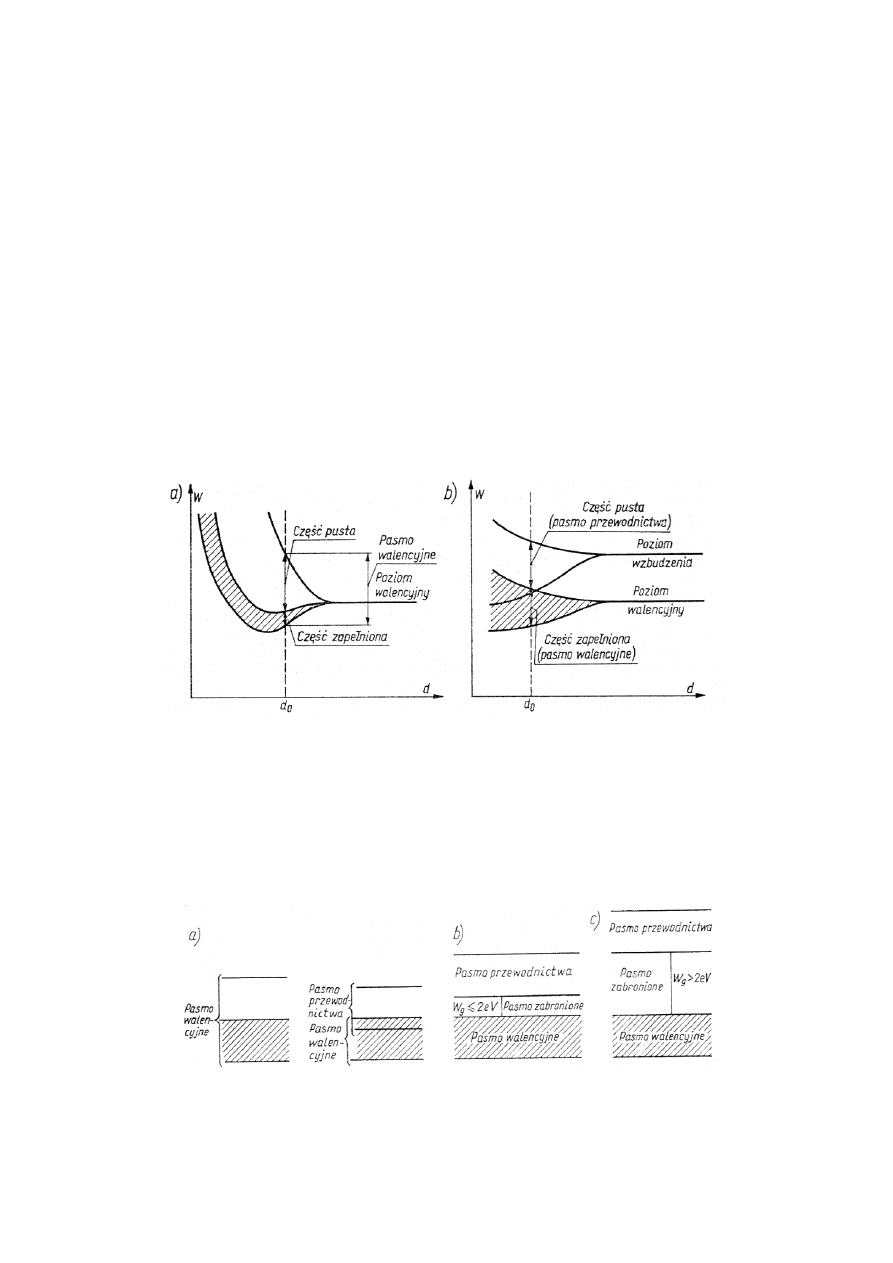
analogiczną do pasma przewodnictwa w półprzewodnikach, co na przykładzie litu przedstawiono na
rys. l.lO a;

Rys. 1.10 Rozszczepienie zewnętrznych poziomów energetycznych atomów

litu (a) i berylu (b) w ciele stałym (d

0

— odległość między atomami w ciele stałym).

- pasmo walencyjne i pasmo przewodnictwa wzajemnie zachodzą na siebie, co na

przykładzie berylu przedstawiono na rys. l.10 b.

Energetyczny model pasmowy dla metalu, półprzewodnika i dielektryka porównano na

rys. 1.11.

Rys. 1.11 - Porównanie energetycznego modelu pasmowego dla

metalu (a), półprzewodnika (b) i dielektryka (c)

4

Nieco szerszego komentarza wymaga pojęcie dziury. Wiadomo już, że dziura jest zerwanym

wiązaniem kowalencyjnym dwu atomów, powstałym wskutek oderwania elektronu z tego wiązania.
W modelu pasmowym dziura jest pustym poziomem energetycznym w paśmie walencyjnym. Istnieje
duże prawdopodobieństwo przejścia elektronu z jednego z sąsiednich wiązań międzyatomowych do
luki utworzonej w zerwanym wiązaniu. Takiemu przejściu elektronu odpowiada przesunięcie dziury
w kierunku przeciwnym. W stanie neutralnym, tj. bez zewnętrznego pola elektrycznego, ruch dziury
jest chaotyczny ze średnią prędkością równą zeru w sensie wektorowym. W przypadku działania pola
elektrycznego następują kolejne przesunięcia elektronów z wiązań kowalencyjnych do sąsiednich luk
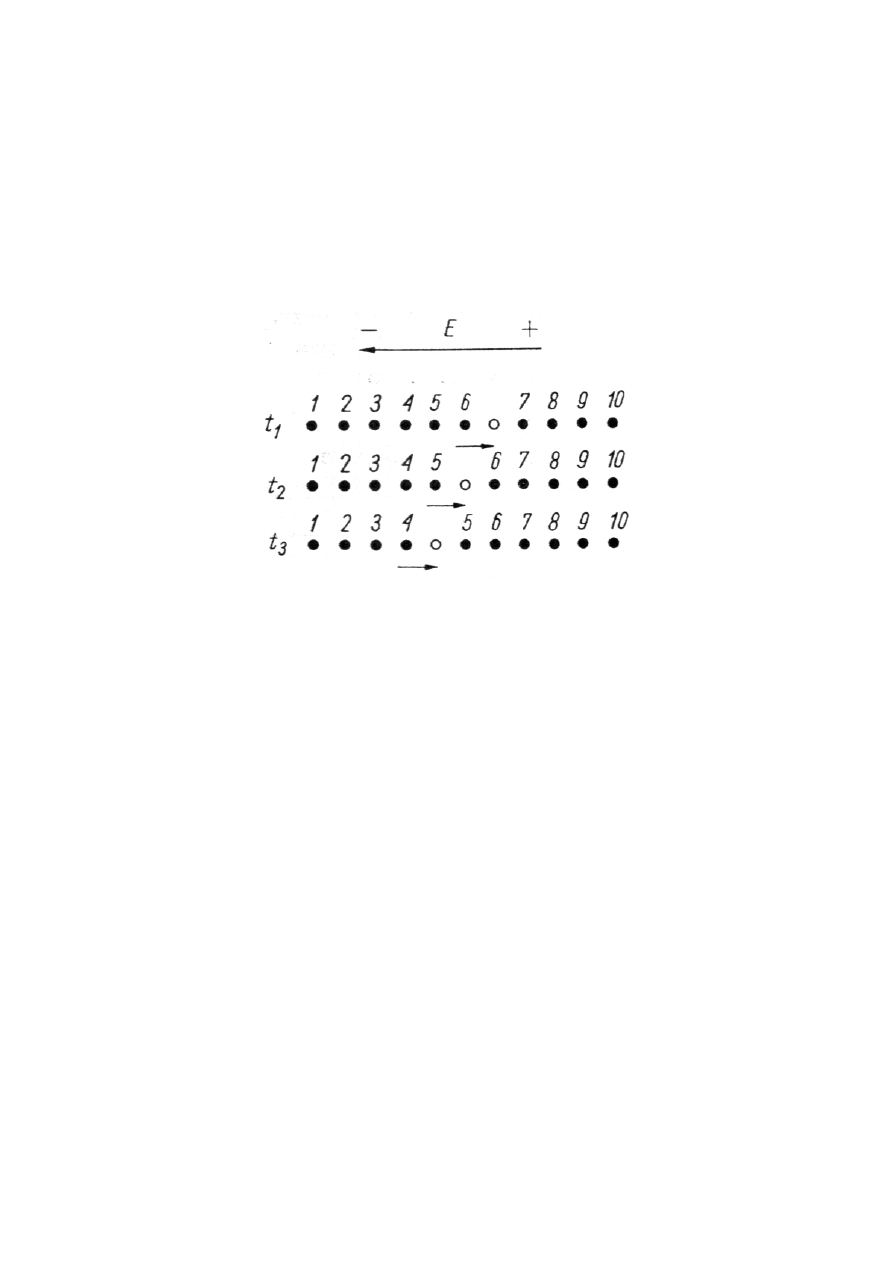
w wiązaniach zerwanych. Kierunek tego jakby „sztafetowego" ruchu elektronów (rys. 1.12) ma
przeważającą składową zgodną z kierunkiem działania pola elektrycznego.

Rys. 1.12. Ilustracja transportu dziury w rezultacie „sztafetowego” ruchu elektronów

(t

1

, t

2

, t

3

– kolejne chwile czasu).

Z uwagi na bardzo duże trudności w opisie takiego „sztafetowego" ruchu wielu elektronów

zajmujących kolejno puste miejsce korzystniej jest opisywać ruch tego jednego pustego miejsca, czyli
dziury. Wówczas dziurze należy przypisać ładunek dodatni, równy co do wartości bezwzględnej
ładunkowi elektronu, oraz określoną masę.

Niekiedy dla zilustrowania istoty pojęcia dziury przytacza się analogię do naczynia napełnionego

wodą, do którego na dnie jest wpuszczony pęcherzyk powietrza. Pęcherzyk powietrza (dziura) porusza się
w kierunku przeciwnym względem działającego pola ciężkości (pola elektrycznego) jako skutek opadania
kolejnych cząstek cieczy (transportu kolejnych elektronów) do pęcherzyka (do dziury) zgodnie z
kierunkiem działania siły ciężkości (pola elektrycznego). Absolutnie nie wolno mylić ruchu dziury z
transportem jonu dodatniego. Ruch dziury jest kolejną jonizacją atomów nieruchomych związanych w
węzłach sieci krystalicznej.







W zasadzie to, to by było na tyle. Ogólnie rzecz biorąc tekst powyżej wyjaśnia model pasmowy i jego
różnice w metalu, półprzewodniku i izolatorze. Poniżej zamieszczę jeszcze kilka definicji o które mogą się
nas pytać.

5

Poziom Fermiego – Energia odpowiadająca poziomowi, który rozgranicza stany obsadzone od
nieobsadzonych w temperaturze 0K nosi nazwę energii Fermiego – E

F

. W temperaturze większej niż 0K

zawsze istnieją elektrony o energiach większych niż E

F

. Fermi jako pierwszy ustalił funkcję opisującą

rozkład elektronów w paśmie energetycznym. Wykazał on, że prawdopodobieństwo, iż dany poziom o
energii E zostanie obsadzony, dane jest wzorem

gdzie f(E) zwana jest funkcją Fermiego. Jeżeli wykreślimy funkcje f(E) dla dwóch różnych

temperatur, to można zauważyć, że w dowolnej skończonej temperaturze, f(E)=1/2 dla E=E

F

; oznacza to,

że poziom Fermiego można również zdefiniować jako poziom, dla którego prawdopodobieństwo
znalezienia elektronu jest równe 1/2.

Sama funkcja Fermiego nie określa ilości elektronów o danej energii, a tylko

prawdopodobieństwo, że dany stan energetyczny jest obsadzony przez pojedynczy elektron.

Poziom akceptorowy – poziom który jest w stanie dostarczyć dziurę do pasma walencyjnego.

Poziom donorowy – poziom który jest w stanie dostarczyć elektron do pasma przewodnictwa.













Nie wiem co jeszcze można tu wymyśleć. Wydaje mi się że nie ma sensu streszczać prawie całego wykładu
z Mikroelektroniki bądź połowy wykładu z Nakwaskiego. Więc jak Komuś mało to niech wyciągnie stare
notatki i sobie poczyta.

D

A

F

Pasmo przewodnictwa

Pasmo walencyjne