1

Konkurencja 2 firm przy IRS

oraz ograniczonym rynku zbytu

 JJ Michalek

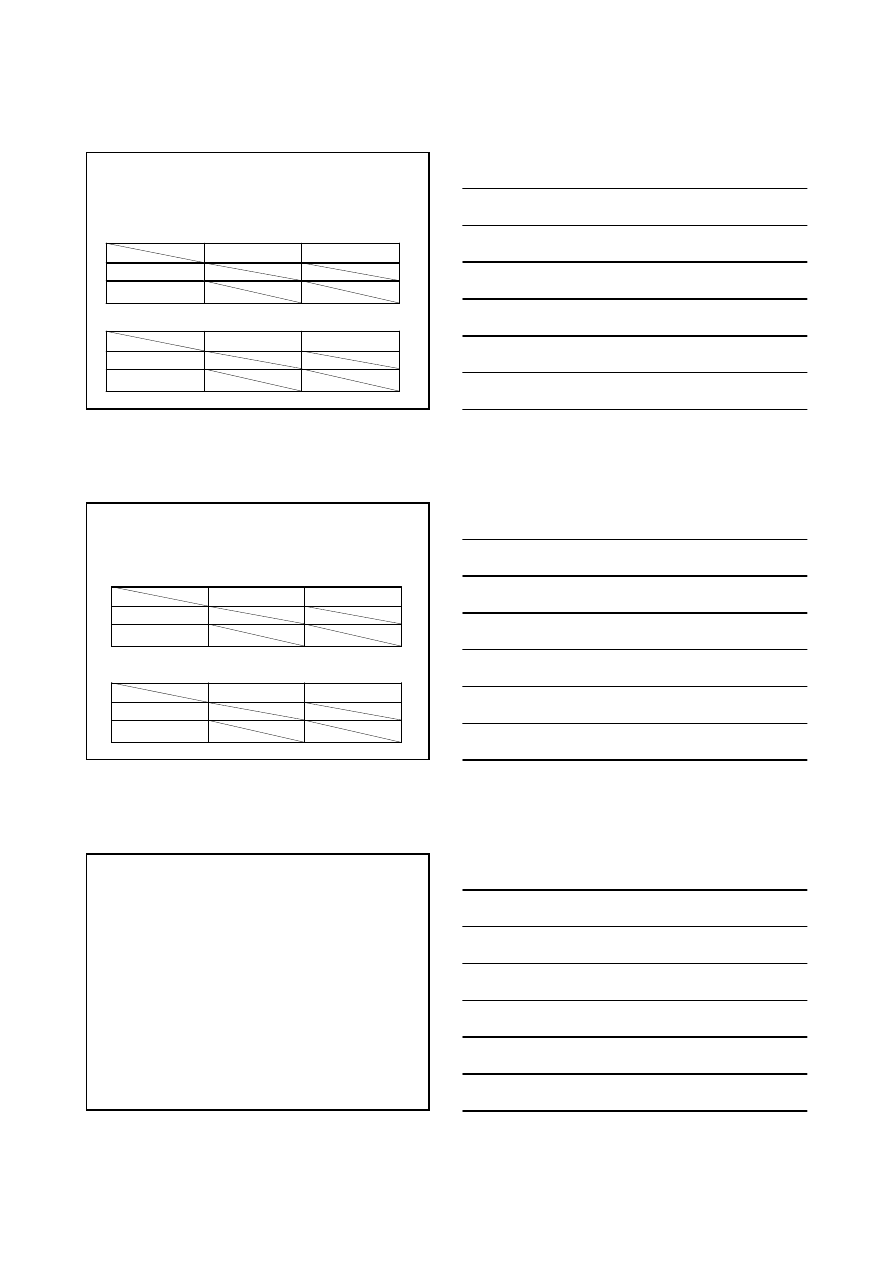
Konkurencja dwóch firm przy korzyściach skali i ograniczonym rynku

Airbus
Boeing

Produkować Nie

produkować

Produkować

-5
-5

0
100

Nie produkować

100
0

0
0

Model Brander-Spencer: subsydium w wysokości 25 dla producenta A:

Airbus
Boeing

Produkować Nie

produkować

Produkować

20
-5

0
100

Nie produkować

125
0

0
0

Przypadek alternatywny: problem

wiedzy na temat kosztów

 JJ Michalek

Konkurencja dwóch firm przy korzyściach skali i ograniczonym rynku

Airbus
Boeing

Produkować Nie

produkować

Produkować

-20
-5

0
125

Nie produkować

100
0

0
0

Model Brander-Spencer: subsydium w wysokości 25 dla producenta A:

Airbus
Boeing

Produkować Nie

produkować

Produkować

5
5

0
125

Nie produkować

125
0

0
0

Î Brak równowagi po zastosowaniu subwencji

Model Jamesa Brandera

i Barbary Spencer:

Export subsidies and international

market share rivalry (1985)

Wersja uproszczona wg.

Marrewijka

© Jan J. Michałek

2

Model B-S: założenia

• -

Analiza sytuacji, w której występują jedynie 2

firmy, wytwarzające identyczny produkt

• -

konkurują ze sobą w ramach modelu równowagi

ilościowej Cournota.

• -

Firmy konkurują na wielu rynkach, ale w krajach ich

pochodzenia nie ma konsumpcji danego dobra,

• -

Æ subsydia mają charakter eksportowy, a nie

produkcyjny.

• -

Występują "rozsądne" rządy, wspierające narodowe

firmy za pomocą subwencji (s).

© Jan J. Michałek

Model B-S: oznaczenia,

funkcja popytu i zysku

- Dwie firmy krajowa: (a) i zagraniczna: b: (*)
- Krajowa wytwarza q a zagraniczna q

*

.

- Produkcja obu firm jest eksportowana do kraju trzeciego o liniowej funkcji popytu:

( )

(

)

*

1

q

q

b

a

p

+

−

=

- c: koszt krańcowy produkcji obu firm;
- s: subsydium (na jednostkę produkcji) przyznawane firmie krajowej;

Æ Funkcje zysku obu firm:

( )

( )

*

*

*

;

2

q

c

q

p

q

s

c

q

p

⋅

−

⋅

=

−

−

⋅

=

π

π

© Jan J. Michałek

Model B-S:

funkcje reakcji obu firm

To wówczas wyliczamy funkcje reakcji (wyliczone z warunku koniecznego I stopnia
maksymalizacji zysku obu firm)
Firma krajowa:

( )

(

)

[

]

(

)

bq

s

c

a

bq

s

c

bq

bq

a

q

sq

cq

bqq

bq

aq

q

s

c

q

q

q

b

a

2

0

2

;

'

2

*

*

*

2

*

−

+

−

=

⇒

=

+

−

−

−

=

∂

∂

+

−

−

−

=

−

−

+

−

=

π

π

Firma zagraniczna:

( )

(

)

[

]

(

)

bq

c

a

bq

c

bq

bq

a

q

cq

bq

bqq

aq

cq

q

q

q

b

a

−

−

=

⇒

=

−

−

−

=

∂

∂

−

−

−

=

−

+

−

=

*

*

*

*

*

2

*

*

*

*

*

*

*

2

0

2

;

"

2

π

π

© Jan J. Michałek

3

Równowaga firm z subsydiami

Maksymalizacja dobrobytu

A więc funkcje reakcji obu form wyglądają następująco:

(3) Firmy krajowej:

;

2

)

(

*

q

b

s

c

a

q

−

+

−

=

firmy

zagranicznej:

(

)

2

2

*

q

b

c

a

q

−

−

=

;

Przecięcie się obu krzywych reakcji wyznacza równowagę produkcyjną między firmami:

( )

;

3

;

3

2

4

*

b

s

c

a

q

b

s

c

a

q

−

−

=

+

−

=

Ustalenie optymalnego poziomu subwencji (maksymalizującej dobrobyt krajowy):

© Jan J. Michałek

Maksymalizacja dobrobytu

Ustalenie optymalnego poziomu subwencji (maksymalizującej dobrobyt krajowy):

Rząd krajowy dąży do maksymalizacji zysku firmy krajowej minus koszt subwencji
(zał.: mikroekonomiczne: że zyski krajowe są tyle samo warte co przychody budżetowe)
tzn.:

( )

q

c

q

p

q

s

⋅

−

⋅

=

⋅

−

π

5

;

Jest to ekwiwalentne z funkcją zysku firmy krajowej (bez subwencji)

Rząd krajowy dąży by zagraniczna krzywa reakcji była styczna do krajowej krzywej jednakowego zysku
bez subwencji.

© Jan J. Michałek

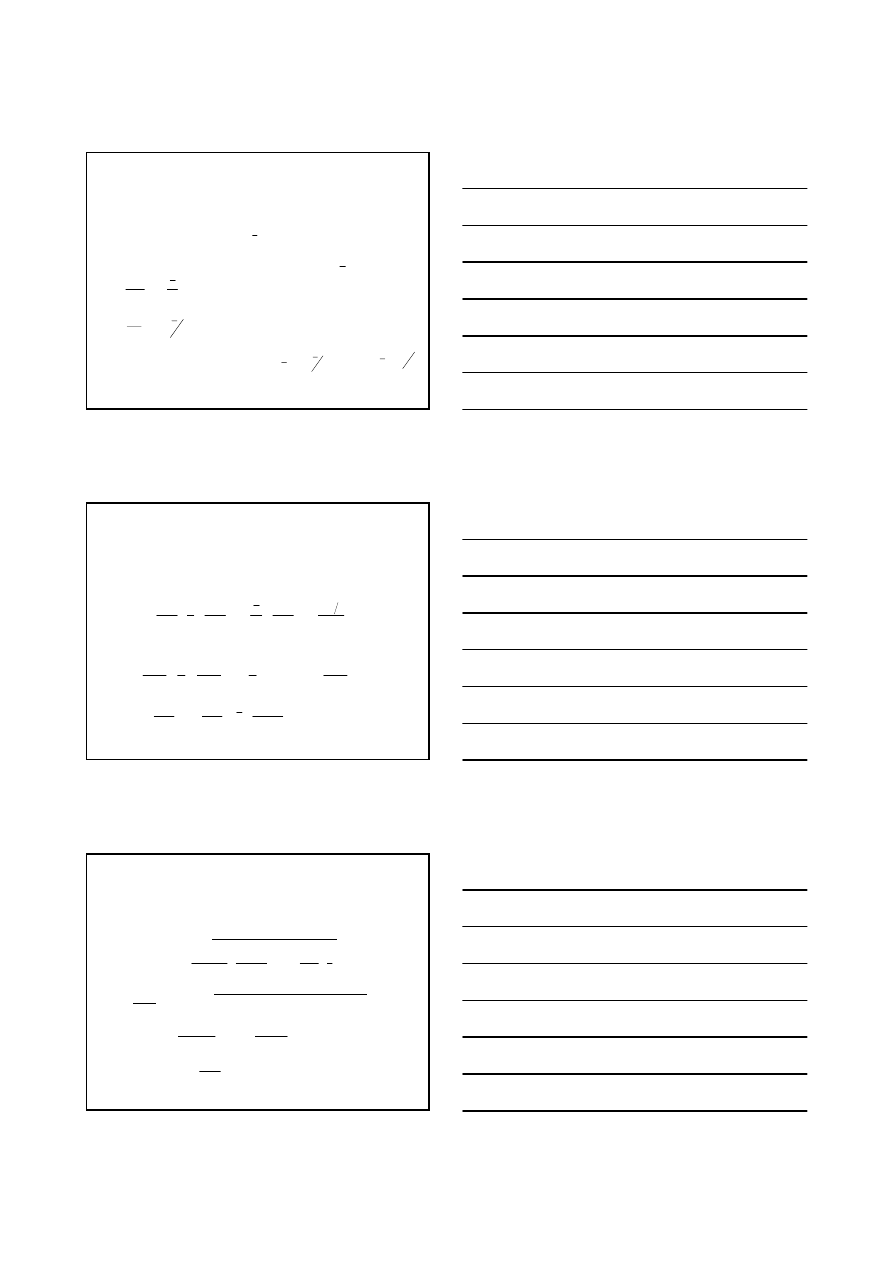
International Trade & the World Economy;

 Charles van Marrewijk

0

1

2

3

4

0

2

4

6

8

output domestic firm

out

put

fo

reign

firm

Domestic firm
reaction curve

Foreign firm
reaction curve

Brander-Spencer

Domestic firm
reaction curve
after subsidy

Cournot

Domestic firm
iso-profit curves

Strategic
trade
policy

4

Wyznaczania równowagi

maksymalizującej krajowy dobrobyt

Dla danego poziomu zysków firmy krajowej (

π ) to krzywa jednakowego zysku firmy krajowej

bez subwencji jest dana przez kombinację produkcji obu firm, tzn.:

( )

(

)

(

)

[

]

(

)

π

=

−

−

−

=

−

+

−

=

−

2

*

*

6

bq

q

bq

c

a

q

c

q

q

b

a

q

c

p

;

Î

bq

q

b

c

a

q

π

−

−

−

=

*

Î nachylenie krzywej jednakowego zysku (pochodna po q) jest zatem równe:

( )

2

*

1

'

6

bq

q

q

π

+

−

=

∂

∂

;

Rząd krajowy dąży by zagraniczna krzywa reakcji (nachylenie =-1/2) była styczna do krajowej

krzywej jednakowego zysku bez subwencji. A więc:

2

1

2

1

bq

π

+

−

=

−

Î

( )

2

"

6

2

bq

=

π

© Jan J. Michałek

Ustalenie równowagi firm

Wstawiając równanie do krajowej krzywej jednakowego zysku (6) równej zagranicznej
krzywej reakcji (3) otrzymujemy:

( )

bq

bq

q

b

c

a

bq

q

b

c

a

q

b

c

a

q

2

2

2

7

2

*

−

−

−

=

−

−

−

=

−

−

=

π

Wyliczając z tego równania najpierw q

( )

b

c

a

q

q

q

b

c

a

q

b

c

a

2

2

2

2

'

7

−

=

⇒

−

−

−

=

−

−

i wstawiając do innych zmiennych otrzymujemy następujące rozwiązania:

( )

(

)

b

c

a

c

a

s

b

c

a

q

8

;

4

;

4

8

2

*

−

=

−

=

−

=

π

© Jan J. Michałek

Zmiany cen pod wpływem

strategicznej polityki handlowej

Wyznaczamy najpierw p’ cena z subwencją (z równania (4)):

( )

3

3

2

3

3

2

'

8

s

c

a

a

b

s

c

a

b

s

c

a

b

a

p

−

−

−

=













−

−

+

+

−

−

=

Następnie wyznaczamy cenę bez subwencji (p) w warunkach wolnego
handlu

W równaniu 4:

( )

;

3

;

3

2

4

*

b

s

c

a

q

b

s

c

a

q

−

−

=

+

−

=

przyjmujemy, że subwencja s=0 Î

*

3

)

'

2

(

q

b

c

a

q

=

−

=

⇒

tzn. symetryczne wielkości dostaw obu firm bez subwencji

© Jan J. Michałek

5

Zaniżenie ceny światowej wskutek

strategicznej polityki handlowej

Cena w warunkach wolnego handlu ( po wstawieniu q i q* do krzywej popytu (1)
otrzymujemy):

( )

(

)

c

a

a

b

c

a

b

a

p

−

−

=

−

⋅

−

=

3

2

3

2

9

a przy stosowaniu subwencji:

( )

(

)

'

3

3

2

'

8

p

p

s

c

a

a

p

>

⇒

−

−

−

=

(dla b,s>0)

=> optymalna subwencja obniża cenę światową w stosunku do wolnego handlu

© Jan J. Michałek

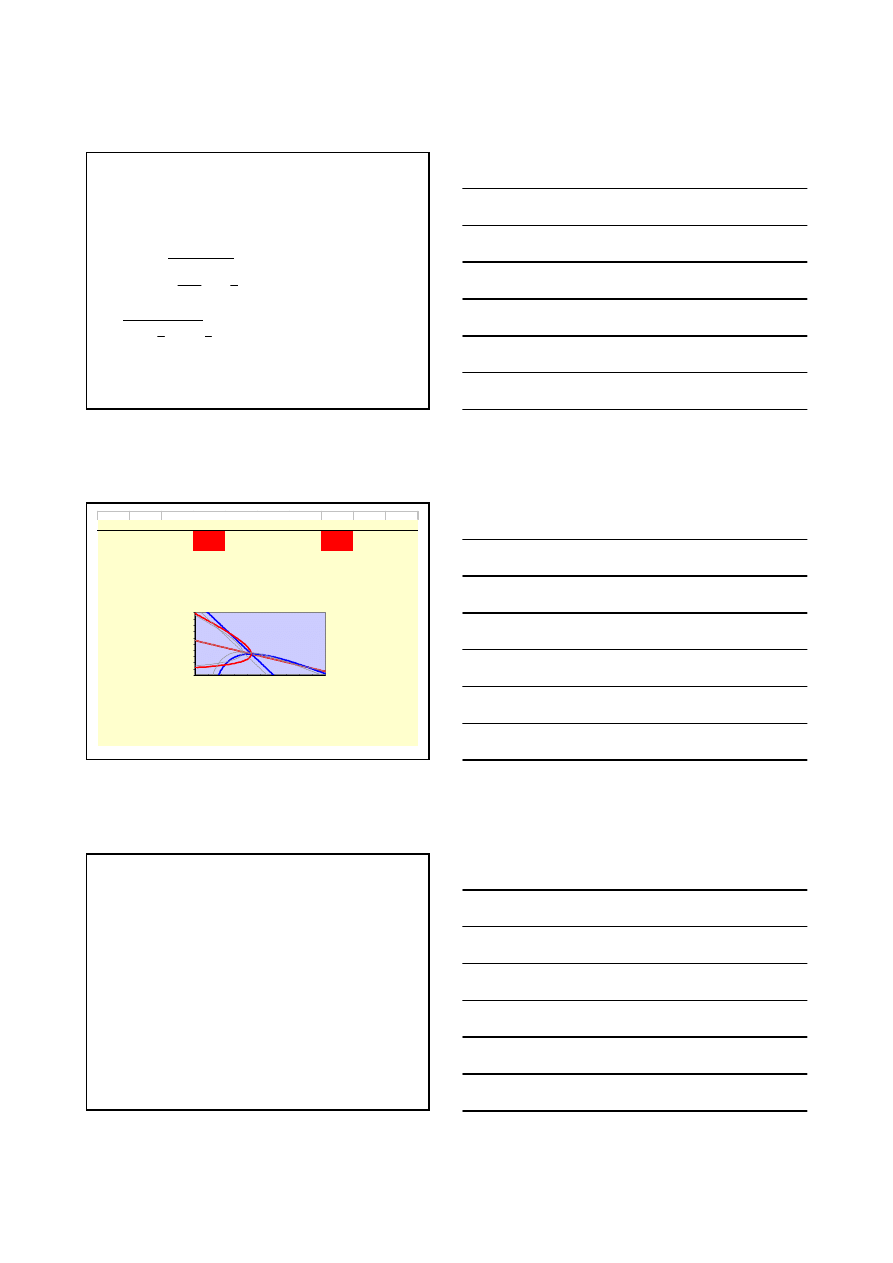
Simulations on strategic trade policy (sim.11-10)

Marginal cost

1

Marginal cost

1

Total output

EC subsidy (per unit)

1

US subsidy (per unit)

0

Price level

Output

4,3

Output

3,3

Profit

18,8

Profit

11,1

Received subsidies

4,3

Received subsidies

0,0

Legend

Reaction and iso-profit curve Airbus

Reaction and iso-profit curve Boeing

Base case reaction and iso-profit curves

Airbus

Boeing

Southeast A

0,00

1,00

2,00

3,00

4,00

5,00

6,00

7,00

8,00

9,00

10,00

0,00

1,00

2,00

3,00

4,00

5,00

6,00

7,00

8,00

9,00

10,00

Output Airbus

Out

p

ut

B

o

e

ing

Wnioski końcowe z modelu B-S

•

W klasycznym już modelu Brandera-Spencer wykazano, że zastosowanie

strategicznych subwencji zmienia charakter konkurencji (firma krajowa staje

się liderem Stackelberga) i powinno zwiększyć dobrobyt krajowy.

•

Jednak analiza ta jest oparta na szeregu rygorystycznych założeń (konkurencja

typu Cournota, duża firma krajowa, doskonała informacja, niekosztowne

transfery od społeczeństwa do firmy).

•

Późniejsze modyfikacje modelu Brandera-Spencera, uchylające niektóre z

powyższych założeń, pokazują, że wnioski nie są już tak jednoznaczne. W

szczególności, konkurencja cenowa typu Bertranda, niedoskonała informacja,

kosztowne transfery i zmienna liczba firm, powodują, że udzielenie subwencji

nie musi prowadzić do podniesienia dobrobytu

•

W krańcowych przypadkach bardziej pożądane może być nawet stosowanie

podatków. Natomiast przy braku informacji na temat sposobu konkurencji

(model Eatona-Grossmana) lub nierzetelnej informacji (Brainard-Martimort)

od firm najlepsza może być polityka nieinterwencji (wolnego handlu).

•

Wnioski te są w dużym stopniu zbieżne z konkluzjami płynącymi z analizy

subwencji w doskonałej konkurencji.

© Jan J. Michałek