EKSPLOATACJA GAZU ZIEMNEGO - PROJEKT
1
OBLICZENIE ZASOBÓW GAZU METODĄ OBJĘTOŚCIOWĄ
Metoda ta opiera się na założeniu, że złoże węglowodorów znajduje się w przestrzeni
porowej posiadającej określoną objętość.
Objętość przestrzeni porowej dostępna dla węglowodorów:
= · ℎ · · (1 − )
gdzie:
A – powierzchnia,
h – miąższość złoża
φ – porowatość złoża
S
w
– nasycenie wodą
Pierwotne zasoby gazu ziemnego w złożu:
=
· · ·(
)
gdzie:
B
gi
– początkowy współczynnik objętościowy gazu ziemnego
Współczynnik objętościowy gazu ziemnego
=
· ·
·
gdzie:
T
z
, p
z
– temperatura i ciśnienie w warunkach złożowych,
T
n
, p
n
– temperatura i ciśnienie w warunkach normalnych,
Z – współczynnik ściśliwości gazu ziemnego w warunkach złożowych.
2
PROGNOZOWANIE WYDOBYCIA GAZU
2.1
WYZNACZANIE PARAMETÓW GAZU
2.1.1
LEPKOŚĆ GAZU
Lepkością gazu ziemnego jest miara jego oporu wewnętrznego przeciw płynięciu. W inżynierii
gazowniczej najczęściej mamy do czynienia z lepkością dynamiczną (µ
g
) wyrażaną w
centypłazach (cp):
1 = 10
"
#$ · %
Lepkość kinematyczna (ν
g
) jest skorelowana z lepkością dynamiczną gęstością gazu (ρ
g
):
& =
µ
'
Lepkość kinematyczna jest rzadko stosowana w przemyśle gazowniczym.
Najbardziej wskazane są oczywiście bezpośrednie pomiary lepkości danego gazu, jednak w
przypadku, kiedy dysponujemy jego składem dość wygodnym sposobem na wyznaczenie
lepkości mieszaniny gazowej jest korelacja Lee, na podstawie, której lepkość może zostać
opisana następującym wzorem:
( = )*+ (, · -
'
...
/
0
) · 10
1
[#$ · %]
gdzie:
) =
(4,67.,.89)( ,: )
;,<
8.47 497 ,:
, = 3,5 +
4:@
,:
+ 0,01A
B = 2,4 − 0,2 ∙ ,
F
G
−
Hę%IJść H$KL [
MH
N
3
]
T – temperatura [K]
M – masa molowa [kg/kmol]
Korelacja ta powstała na podstawie serii doświadczalnych pomiarów lepkości czterech
różnych gazów ziemnych w zakresie temperatur od 100 do 340 [K] i ciśnieniu wahającym się
od 100 do 8000 [psia]. Wzór ten opisuje lepkość z odchyleniem standardowym ±2,7, zaś
maksymalny błąd sięga 9%.
2.1.2
GĘSTOŚĆ GAZU
Znając współczynnik ściśliwości gazu (Z-factor) gęstość gazu, dla zadanych warunków
ciśnienia (p) i temperatury (T), można wyznaczyć w oparciu o równanie stanu gazu
rzeczywistego:
F =
O
2.1.3
WSPÓŁCZYNNIK ŚCIŚLIWOŚCI GAZU (Z-FACTOR)
Najbardziej powszechnym sposobem wyznaczania współczynnika ściśliwości jest korelacja
Standinga-Katza. Wykorzystanie tej korelacji wymaga wprowadzenia parametrów opisujących
mieszaninę. Średnia masa cząsteczkowa (reguła Kay’a) jest pseudo-własnością układu i jest
definiowana, jako:
A
P
= ∑ +
R
A
R
,
gdzie:
M
a
średnia masa cząsteczkowa mieszaniny,
M
i
masa cząsteczkowa i-tego składnika mieszaniny,
x
i
udział molowy i-tego składnika mieszaniny
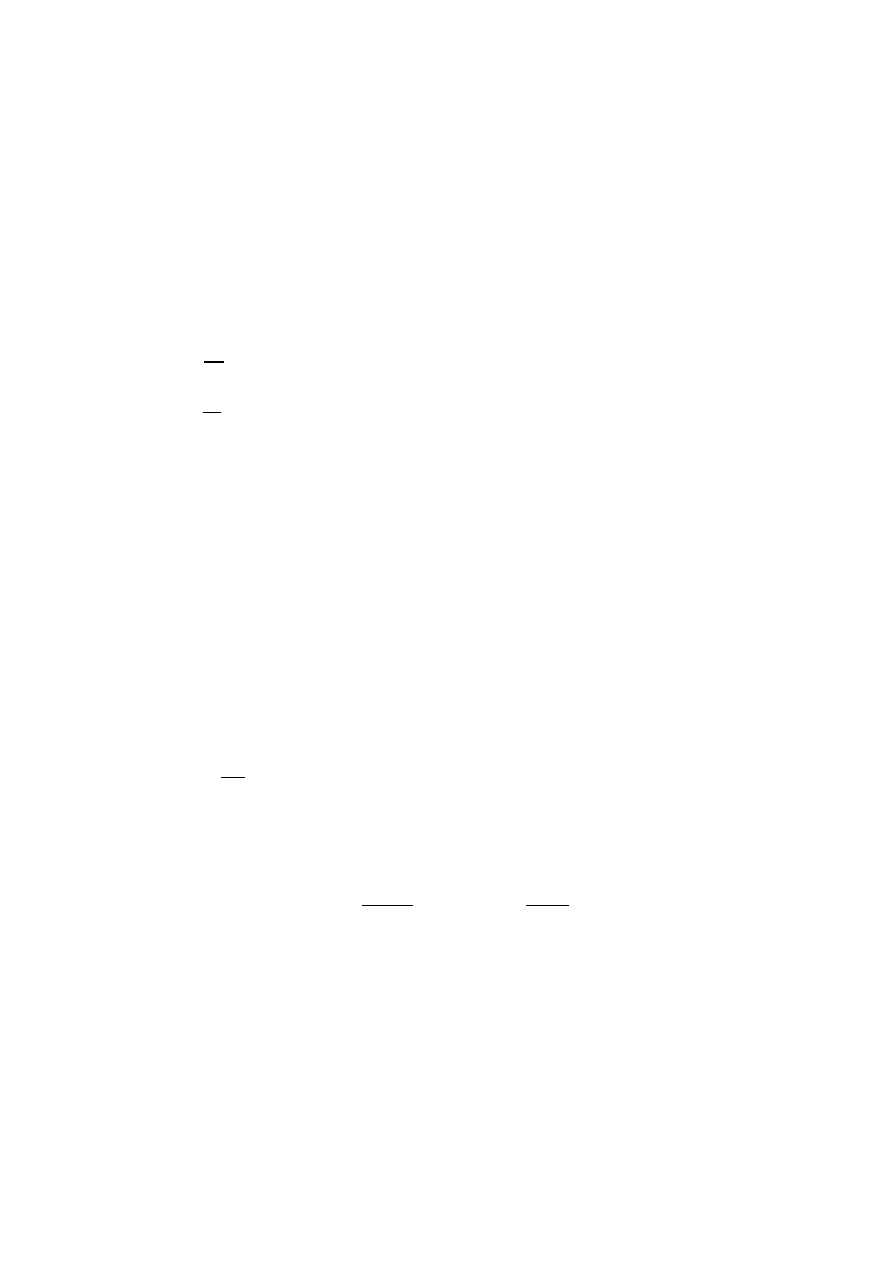
Deklaracje parametrów pseudo-krytycznych (układ wieloskładnikowy - mieszanina), zgodnie
z zasadą Kay’a:
S
= ∑ +
R
·
SR
T
S
= ∑ +
R
· T
SR
gdzie:
p
ci
,T
ci
– ciśnienie i temperatura krytyczne i-tego składnika mieszaniny.
Parametry pseudo-zredukowane:
U
=
VW
T
U
=
VW
Bazując na dwuparametrowym twierdzeniu o stanach wzajemnie odpowiadających oraz
przyjmując, że układ wieloskładnikowy będzie charakteryzowany za pomocą parametrów
pseudo-zredukowanych możemy napisać zależność:
X = YZ
U
, T
U
\
Zależność powyższa została przedstawiona w formie uniwersalnego wykresu przez Standinga
i Katza w 1942 r. Wykres ten może być stosowany do wyznaczania współczynnika ściśliwości
lekkich gazów ziemnych o niewielkiej zawartości węglowodorów cięższych oraz o małej
zawartości składników nieorganicznych. Wykres Standinga-Katza jest jedną z najszerzej
zaakceptowanych korelacji w przemyśle naftowymi gazowniczym.
Innym dość wygodnym sposobem wyznaczania współczynnika ściśliwości jest korelacja
Beggs’a-Brill’a, która może zostać zapisana w postaci:
X = +
]
^
+ _
U
`
gdzie:
= 1,39(T
U
− 0,92)
.,b
− 0,36T
U
− 0,1
= Z0,62 − 0,23T
U
\
U
+ d
.,.@@
Ve
.,:@
− 0,037g
U
8
+
.,"8
Ve
h
.
i
_ = 0,132 − 0,32log (T
U
)
m = 10
n
o = 9(T
U
− 1)
p = 0,3106 − 0,49T
U
+ 0,1824T
U
8
2.2
WYZNACZENIE WYDAJNOŚCI GAZU Z FORMUŁY DWUCZŁONOWEJ
Równanie dopływu płynu do odwiertu (w geometrii radialnej dla stanu ustalonego) z
uwzględnieniem turbulencji przepływu oraz tzw. skin efektu można zapisać jako:
rł
8
−
s
8
=
t∙u∙ ∙ ∙
v∙w∙ ∙
-Gx -
U
y
U
/ − 0.75 + %
{
+ m
|
}/
gdzie:
rł
- średnie ciśnienie złożowe,
s
- ciśnienie denne ruchowe,
( - współczynnik lepkości dynamicznej dla gazu,
} - wydatek przepływu gazu,
M - przepuszczalność złoża,
ℎ - miąższość złoża,
~
]
- promień zasięgu odwiertu,
~ - promień odwiertu,
T - średnia temperatura złożowa,
•
, T
•
- ciśnienie i temperatura normalne,
%
{
– współczynnik mechanicznego uszkodzenia strefy przyodwiertowej,
m
|
- parametr przepływu turbulentnego wyrażający się wzorem:
m
|
=
€' w
8v U u
Gęstość w warunkach normalnych można wyznaczyć na podstawie równania stanu gazu
rzeczywistego. Należy ponadto pamiętać, że współczynnik lepkości dynamicznej (µ
w
)
wyznaczony jest dla warunków ciśnienia dennego.
Analiza równania dopływu wskazuje, że równanie to ma postać kwadratową ze względu na
„q”:
∆
8
=
rł
8
−
s
8
= $} + ‚}
8
gdzie:
[Pa
2
*s/m
3
]
[Pa
2
s
2
/m
6
]
a
µ
i Pn
⋅
zi
⋅
Tsr
⋅
π
k h
⋅
Tn
⋅
ln
re
rw
3
4
−
Sm
+
⋅
:=
b
µ
i Pn
⋅
zi
⋅
Tsr
⋅
π
k
⋅
h
⋅
Tn
⋅
Dt
⋅
:=
[s/m
3
]
Równanie powyższe nosi nazwę formuły dwuczłonowej. Ze względów praktycznych dla
prognozowania zachowania się odwiertów gazowych konieczne jest odpowiednie określenie
współczynników „a” i „b”.
Wyznaczenie wydatku przepływu z formuły dwuczłonowej sprowadza się do rozwiązania
równania kwadratowego, którego jeden z pierwiastków jest rozwiązaniem zaś drugi nie ma
sensu fizycznego:
} =
P7ƒP
„
76…Z
„
†
„
\
8…
WYZNACZENIE CIŚNIENIA ZŁOŻOWEGO
Średnie ciśnienie złożowe można wyznaczyć w oparciu o metodykę p/z (równanie bilansu
masowego). W przypadku braku dopływu wody dla złoża gazu pracującego w warunkach
wolumetrycznych równanie bilansu można zapisać jako:
= -1 −
‡
V
‡
/
Ze względu na fakt, że w równaniu powyższym nieznane są dwie wielkości, ciśnienie oraz
współczynnik z(p), wynik uzyskujemy na drodze iteracji. W pierwszym kroku iteracji
zakładamy Z=1 i dla tej wielkości wyznaczamy wartość ciśnienia złożowego. Następnie dla
tak uzyskanej wartości ciśnienia złożowego wyznaczamy „nowy” współczynnik ściśliwości
gazu będący funkcją właśnie wyznaczonego ciśnienia złożowego. Mając „nową” wartość
współczynnik ściśliwości gazu możemy wyznaczyć bardziej dokładną wartość ciśnienia
złożowego. Cykl takich obliczeń wykonujemy aż do uzyskania zadanej wartości błędu
obliczeń (ε), który możemy zdefiniować np. jako:
|
R7
−
R
| ≤ Š
Dt
β ρ
n
⋅
k
⋅
2
π
⋅
h
⋅
rw
⋅
µ
d1
⋅
:=
2.3.
WYZNACZENIE CIŚNIENIA DENNEGO
Dysponując wielkością średniego ciśnienia złożowego oraz aktualną wydajnością gazu
możemy, korzystając z formuły dwuczłonowej, wyznaczyć aktualne ciśnienia denne:
s
8
= ƒ
rł
8
− $ ∙ } − ‚ ∙ }
8
2.3
WYZNACZENIE CIŚNIENIE GŁOWICOWEGO
2.3.1
WYZNACZENIE WSPÓŁCZYNNIKA OPORÓW HYDRAULICZNYCH
współczynnik oporów hydraulicznych można zapisać w postaci wyrażenia:
λ
= Y(‹*, Š)
gdzie:
Re – liczba Reynoldsa,
ε – chropowatość względna
Liczbę Reynoldsa (jedna z bezwymiarowych liczb podobieństwa stosowanych w mechanice
płynów) może być wyznaczona według wzoru:
‹* =
×`
•
gdzie:
w – prędkość rzeczywista płynu,
ν
– lepkość kinematyczna płynu
Prędkość rzeczywistą można wyznaczyć w następujący sposób:
Ž =
t
e
=
t
••„
‘
=
6t
v`
„
Przy założeniu, że mamy do czynienia z przepływem turbulentnym (większość odwiertów
gazowych) do wyznaczenia współczynnika oporów liniowych możemy posłużyć się korelacją
Jein’a:
√λ
= 1,14 − 2GJH -
“
`
+
8 ,8b
O]
”,•
/
Kryteria stosowalności:
5000<Re<10
8
10
-6
<
“
`
<10
-2
2.3.2
RÓWNANIE PRZEPUSTOWOŚCI ODWIERTU
Dysponując danymi dotyczącymi geometrii odwiertu, własności płynu, który nim przepływa
wielkościami wydatku gazu i ciśnienia dennego jesteśmy w stanie oszacować wielkość
ciśnienie głowicowego. W tym celu posłużymy się równaniem przepustowości odwiertu, które
można zapisać w postaci:
s
8
=
8
*
„ –
—˜ ™
+
:λ
„ „ „
(]
„ –
—˜ ™
)t
„
v
„
`
< „
gdzie:
P
d
– ciśnienie denne dynamiczne,
P
g
– ciśnienie głowicowe,
P
n
, T
n
– ciśnienie i temperatura normalne,
T – temperatura średnia panująca w odwiercie
H – długość (głębokość) odwiertu,
Z – współczynnik ściśliwości gazu,
R – uniwersalna stała gazowa,
λ
- współczynnik oporów hydraulicznych,
D – średnica odwiertu,
g – przyspieszenia ziemskie,
q – wydatek odwiertu.
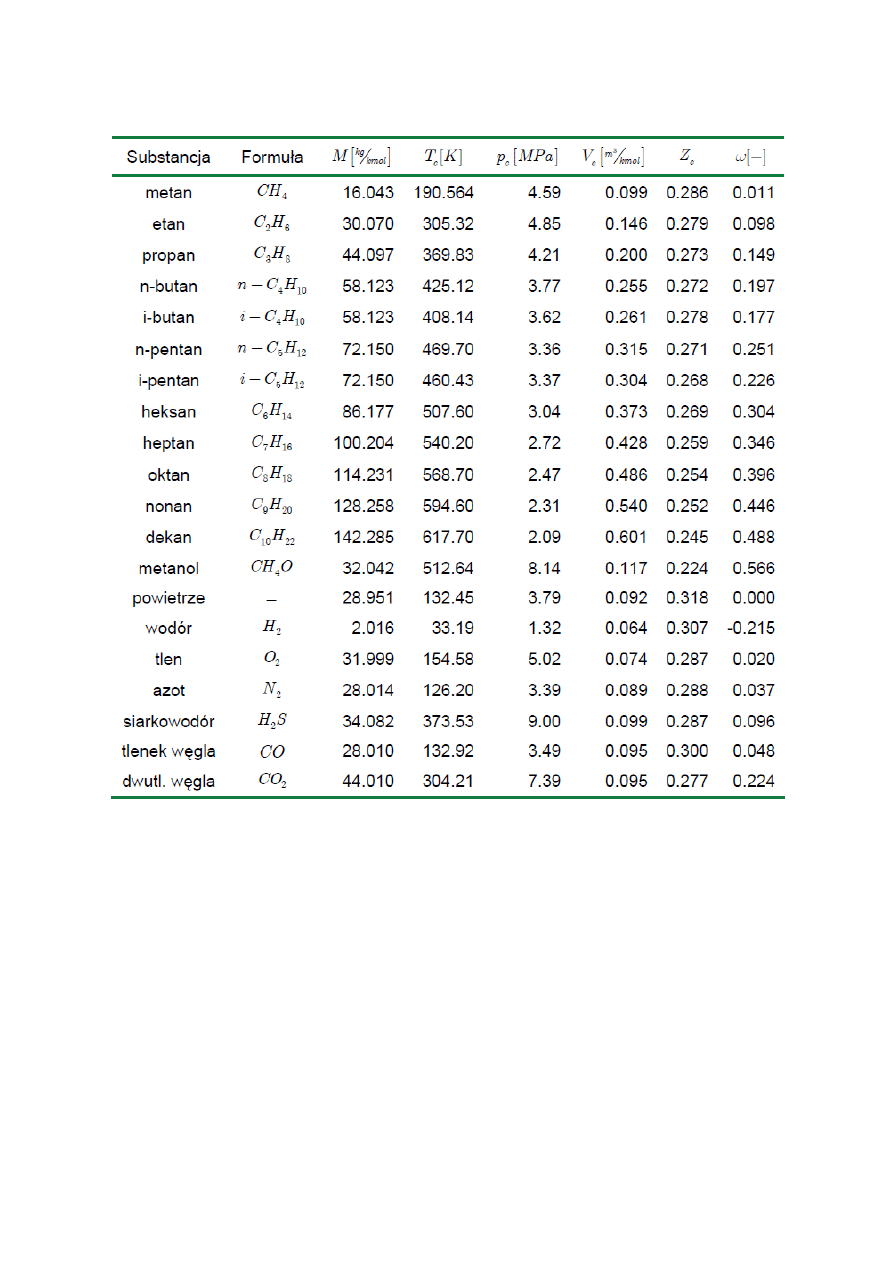
PARAMETRY TERMOFIZYCZNE:
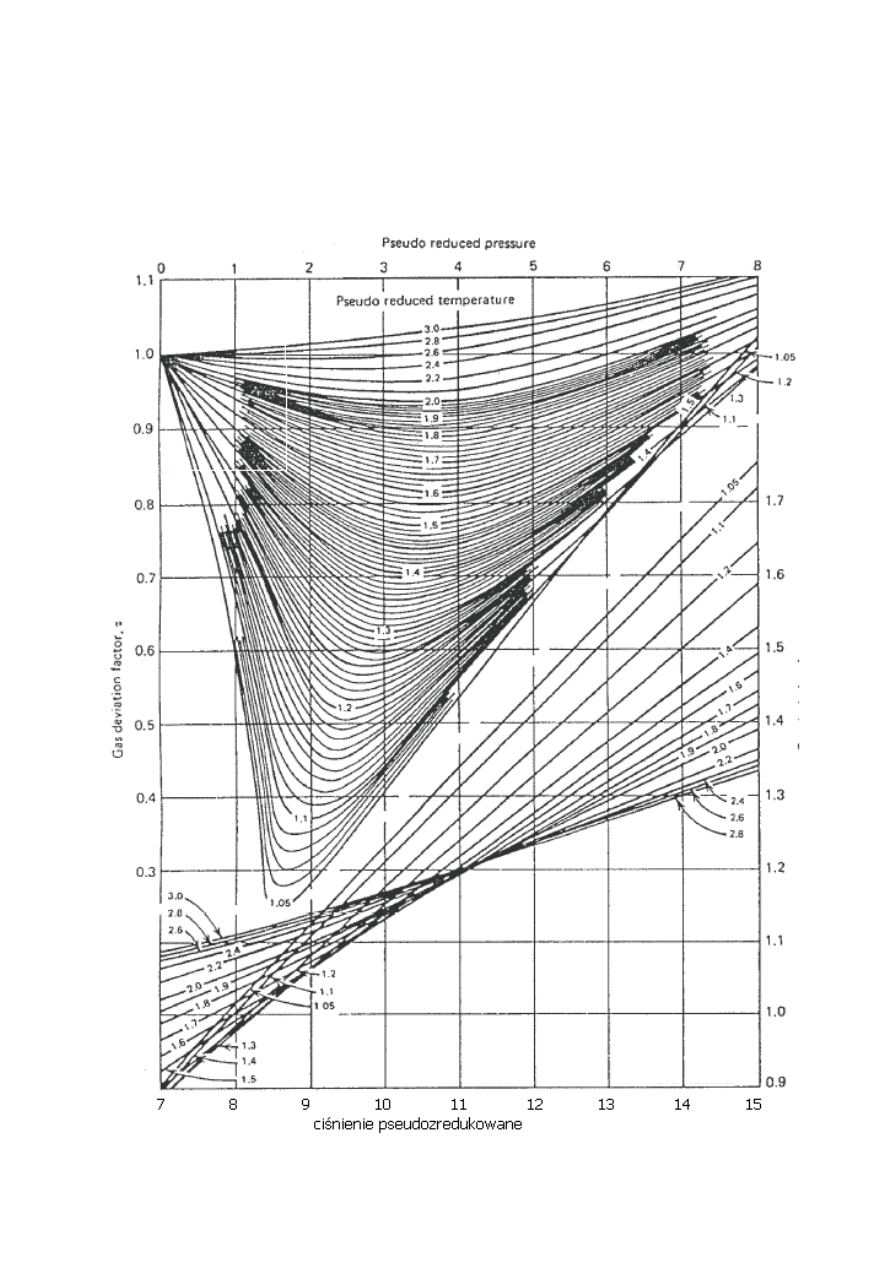
WYKRES STANDINGA-KATZA:
Współczynnik ściśliwości z znajduje się na osi pionowej, odczytuje się go dla parametrów
pseudozredukowanych dla mieszaniny.