Politechnika Śląska

Wydział Elektryczny

Technika Inżynierska II Laboratorium

Sprawozdanie nr 8, temat:

Wyznaczanie pojemności i indukcyjności metodą

techniczną

Grupa II, sekcja 3:

Patryk Kuźma

1

1. Wstęp teoretyczny:

Napięcie elektryczne – skalarna wielkość fizyczna. Praca wykonana przez siły pola elektrycznego
przy przenoszeniu jednostkowego ładunku elektrycznego z jednego punktu pola do drugiego.
Jednostką w układzie SI jest wolt.

Prąd elektryczny – uporządkowany przepływ ładunków elektrycznych wywołany różnicą
potencjałów.

Pojemność elektryczna C (kapacytacja) – wielkość charakteryzująca zdolność przewodnika do
gromadzenia ładunku. Jednostką w układzie SI jest Farad. Pojemność elektryczna przewodnika jest
równa stosunkowi ładunku Q zgromadzonego na przewodniku do potencjału V wywołanego
obecnością tego ładunku:

C=

q

ΔV

=

q

U

=

ε

0

ε

r

s

d

(1)

gdzie:

ΔV – różnica potencjałów [V],
U – napięcie [V],
d – odległość między okładkami kondensatora [m],
ε

0 –

przenikalność elektryczna w próżni,

ε

r –

przenikalność elektryczna względna,

Kondensator elektryczny – układ 2 elektrod rozdzielonych warstwą dielektryka (powietrze, mika,
ceramika, papier, polistyren itp.), służący do gromadzenia ładunku elektrycznego. Jego
podstawowym parametrem jest pojemność elektryczna C. W obwodach prądy stałego stanowi on
przerwę. Symbolem elektrycznym kondensatora jest:

Reaktancja pojemnościowa – jest parametrem odpowiadającym za ograniczenie prądu w danej
gałęzi obwodu. Wyrażana jest wzorem:

X

c

=

1

ωC

=

1

2πfC

(2)

gdzie:

Xc – reaktancja pojemnościowa [

Ω],

ω – pulsacja (prędkość kątowa) [Hz],
f – częstotliwość napięcia zasilania [Hz].

Indukcyjność (współczynnik indukcji) – wielkość charakteryzująca oddziaływania indukcyjne
obwodów z prądem elektrycznym. Oznaczana dużą literą L. Jednostką w układzie SI jest Henr.
Oblicza się ją ze wzoru:

L=

√

Z

2

−

R

2

2πf

(3)

2

gdzie:

Z – impedancja cewki [

Ω],

R – rezystancja cewki [Ω],,
f – częstotliwość napięcia zasilania [Hz].

Cewka w obwodach prądy stałego stanowi pewnego rodzaju opór. Parametrem opisującym ten opór
jest reaktancja indukcyjna wyrażana wzorem:

X

L

=

ωL=2πfL

(4)

gdzie:

X

L –

reaktancja indukcyjna [Ω],

ω – pulsacja (prędkość kątowa) [Hz],
f – częstotliwość napięcia zasilania [Hz].

2. Opis ćwiczenia:

a) Cel ćwiczenia:

Celem ćwiczenia było wyznaczenie pojemności i indukcji badanych elementów przy pomocy
metody technicznej. Metoda ta zalicza się do metod wychyleniowych, które bazują na prawie
Ohma. Korzystając z tego prawa odpowiednio zestawiając wartości mierzonego napięcia i prądu
uzyskuje się wartość reaktancji. Należy pamiętać, że dla cewki i kondensatora zasilanego napięciem
przemiennym impedancja ma cześć rzeczywistą i zespoloną.

b) Przebieg ćwiczenia:

Dla odpowiednich wartości napięcia stałego z zakresu od 1 do 10 V, co 1V odczytano z ekranu
amperomierza wartości prądu przepływającego przez badany element, którym była cewka.
Pozwoliło to na wyznaczenie jej rezystancji. Podobnie postąpiono w przypadku napięcia
zmiennego, mierząc prąd dla napięć z zakresu 1 do 10V co 1V. Pomiary wykonano dla takich
elementów jak cewka z rdzeniem, bez rdzenia, kondensator oraz połączonych kondensatorów w
różnych konfiguracjach.

c) Układ pomiarowy:
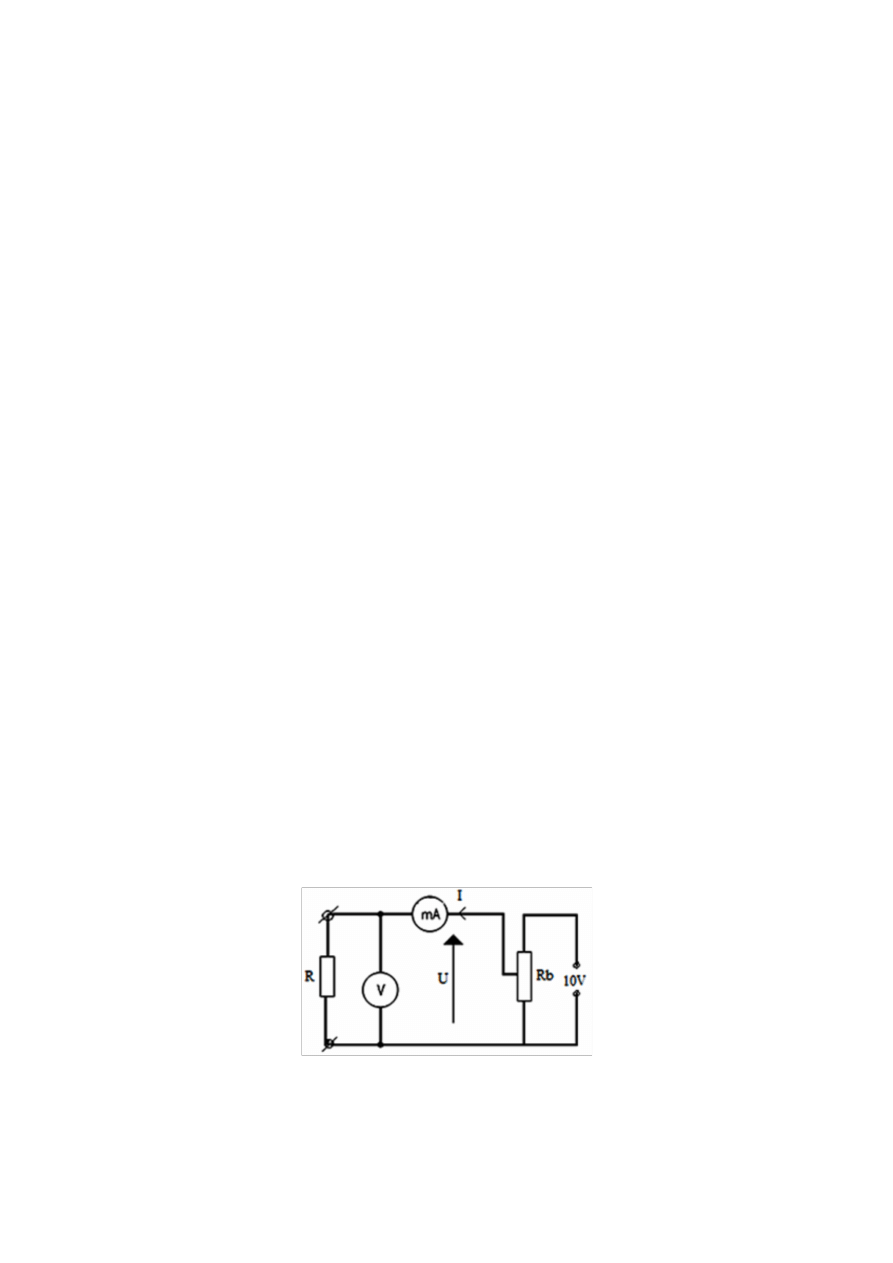
Na rysunkach przedstawionych poniżej (rys.1, rys.2, rys.3) znajdują się schematy pomiarowe do
wyznaczania pojemności i indukcji metodą techniczną.

Rys. 1. Schemat układu do pomiaru rezystancji cewki

3

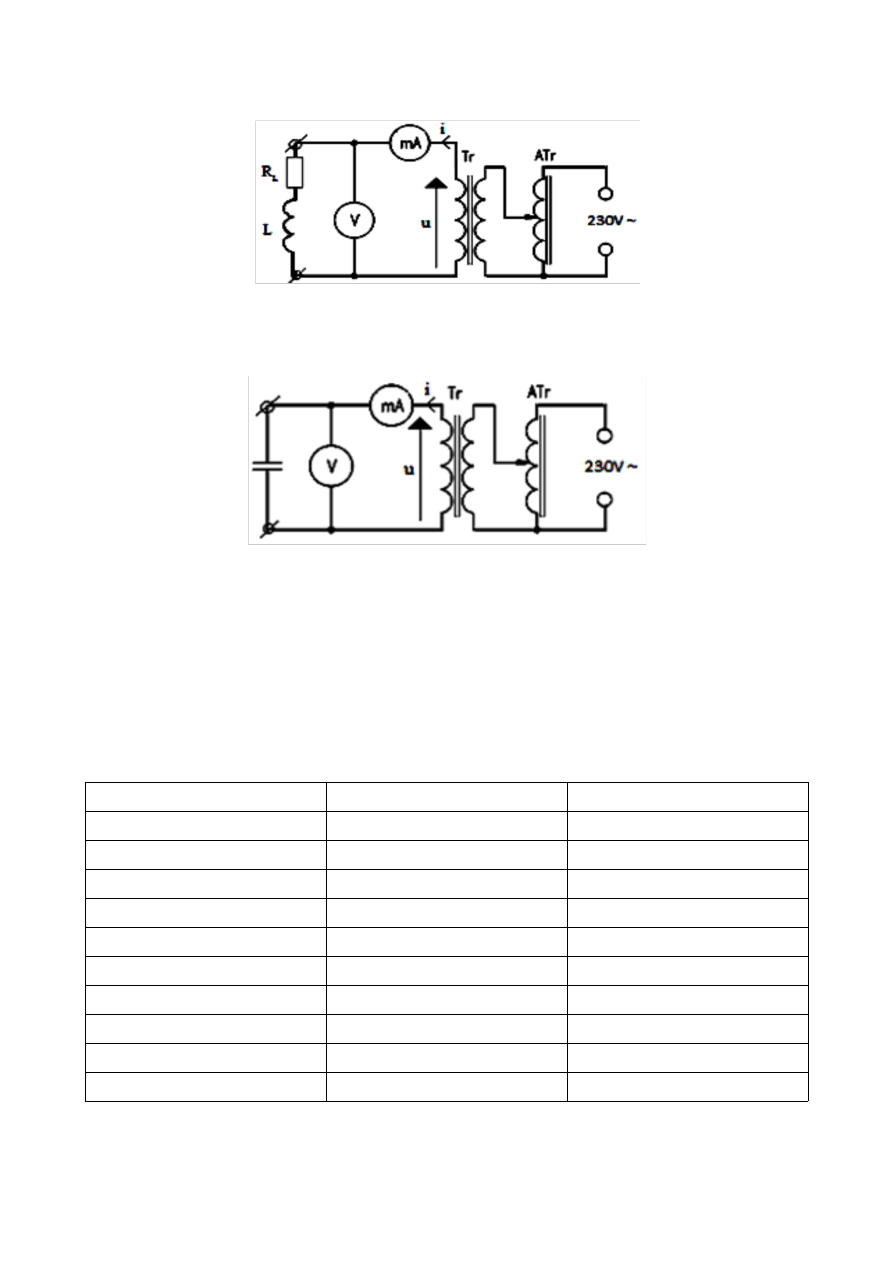
Rys. 2. Schemat układu do pomiaru impedancji cewki

Rys. 3. Schemat układu pomiarowego do pomiaru reaktancji pojemnościowej

3. Opracowanie wyników pomiarów:

a) Tabele i wykresy:

Dla odpowiednich wartości napięcia stałego z zakresu od 1 do 10 V odczytano z ekranu
amperomierza wartości prądu przepływającego przez badaną cewkę. Otrzymane wartości zapisano
w tabeli numer 1.

Tab.1 Wyniki pomiarów cewki przy zasilaniu napięciem stałym.

Lp.

U[V]

I[mA]

1

1,01

16,50

2

2,00

32,50

3

3,00

48,70

4

3,99

64,80

5

5,02

81,60

6

6,00

97,00

7

7,00

113,50

8

8,00

129,70

9

8,98

145,50

10

10,03

162,40

4

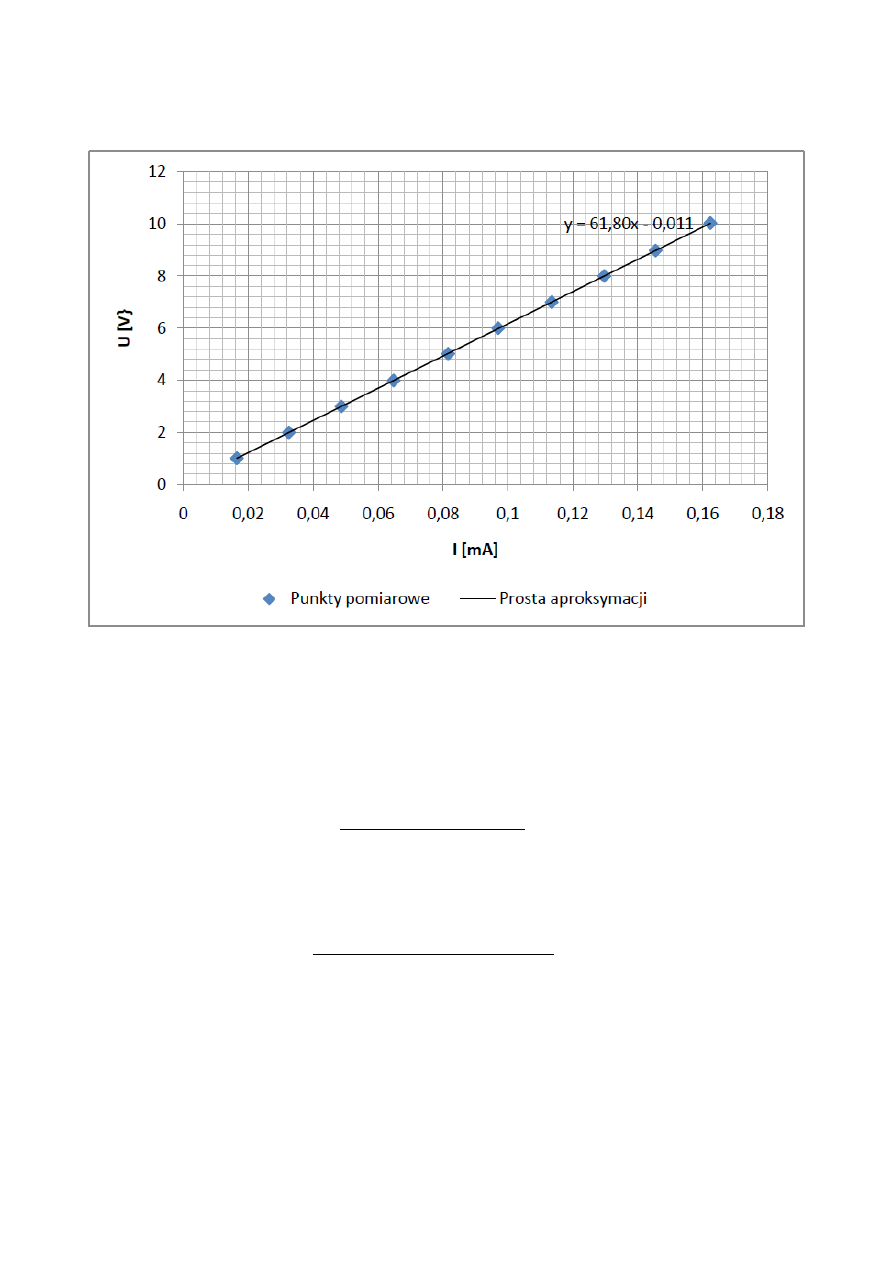
Z danych zawartych w tabeli 1 wykreślono charakterystykę napięciowo – prądową cewki zasilanej
napięciem stałym. 4

Rys. 4. Charakterystyka napieciowo – prądowa cewki zasilanej napięciem stałym wraz z

równaniem prostej i jej parametrami.

Metodą regresji liniowej wyznaczono prostą i jej równanie. Współczynnik kierunkowy a oraz
wyraz wolny b wyznaczono przy użyciu wzorów 5 i 6. Szczegółowe obliczenia znajdują się w
załączniku numer 1.

a=

n

∑

i=1

n

x

i

y

i

−

(

∑

i=1

n

x

i

)

(

∑

i=1

n

y

i

)

n

∑

i=1

n

x

i

2

−(

∑

i =1

n

x

i

)

2

(5)

b=

(

∑

i=1

n

x

i

2

)(

∑

i =1

n

y

i

)

−

(

∑

i =1

n

x

i

)(

∑

i=1

n

x

i

y

i

)

n

∑

i=1

n

x

i

2

−

(

∑

i=1

n

x

i

)

2

(6)

gdzie:

x

i,

y

i

– wartości doświadczalne,

n- liczba dokonanych pomiarów,

5

Błędy wyznaczonego współczynnika kierunkowego a i wyrazu wolnego b wyznaczono ze wzorów:

u (a )=

√

n

n−2

∑

i =1

n

ε

i

2

n

∑

i =1

n

x

i

2

−

(

∑

i=1

n

x

i

)

2

(7)

u (b )=

√

1

n−2

(

∑

i =1

n

x

i

2

)(

∑

i=1

n

ε

i

2

)

n

∑

i=1

n

x

i

2

−

(

∑

i=1

n

x

i

)

2

(8)

gdzie:

ε

i

=

y

i

−

a x

i

−

b

Analogicznie jak w przypadku cewki zasilanej napięciem stałym postępujemy przy badaniu cewki
zasilanej napięciem przemiennym z rdzeniem i bez rdzenia, pojedynczych kondensatorów oraz
połączonych według różnych konfiguracji. W pierwszej kolejności łączymy układ pomiarowy, dla
zadanych wartości napięcia odczytujemy z amperomierza wartości prądu i zapisujemy do tabeli.
Następnie wykreślamy charakterystykę napięciowo – prądową oraz wyznaczamy parametry prostej.

Tab. 2.Wyniki pomiarów drutu cewki przy zasilaniu napięciem przemiennym.

Lp.

U [V]

I [mA]

bez rdzenia

z rdzeniem

1

1,02

12,30

2,40

2

2,00

23,90

4,60

3

3,00

35,90

6,90

4

4,01

48,00

9,30

5

5,01

60,10

11,40

6

5,98

71,80

13,60

7

7,00

84,10

15,80

8

8,02

96,40

18,00

9

9,02

107,80

20,20

10

10,02

121,00

22,30

6

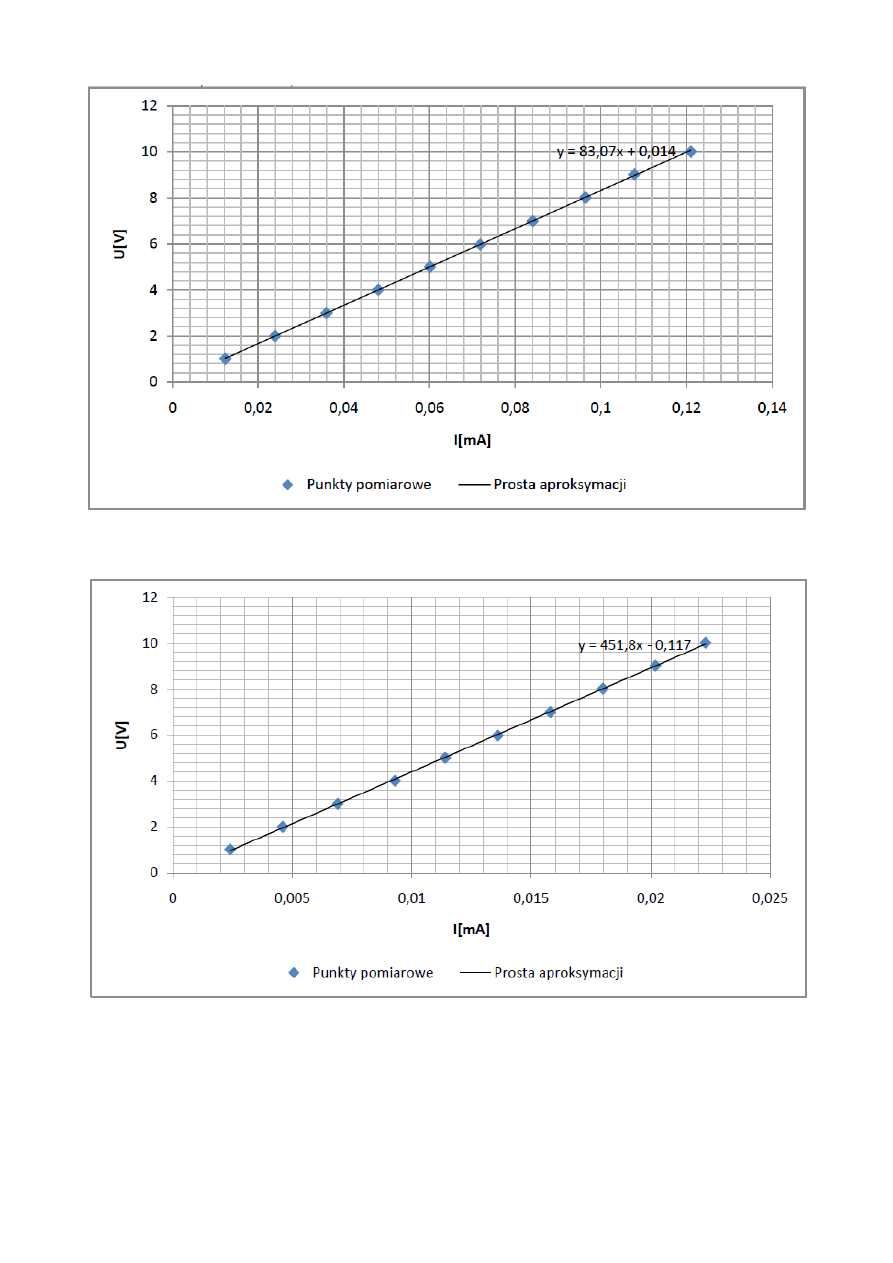
Rys. 5. Charakterystyka napieciowo – prądowa cewki bez rdzenia zasilanej napięciem zmiennym

wraz z równaniem prostej i jej parametrami.

Rys. 6. Charakterystyka napieciowo – prądowa cewki z rdzeniem zasilanej napięciem zmiennym

wraz z równaniem prostej i jej parametrami.

7

Tab. 3.Wyniki pomiarów kondensatorów C

1

, C

2

, C

3

.

Lp.

U [V]

I [mA]

C

1

C

2

C

3

Równolegle

Szeregowo

1

1,01

5,10

5,80

2,30

13,70

2,30

2

2,00

10,40

11,80

4,90

27,40

4,80

3

3,00

15,60

17,70

7,60

41,20

7,30

4

3,98

22,00

22,90

9,90

54,60

9,80

5

5,00

26,00

29,20

12,70

68,80

12,30

6

6,02

30,20

33,90

14,90

82,90

14,80

7

7,01

36,90

41,60

18,20

96,30

17,30

8

7,97

40,00

45,20

19,70

109,70

19,50

9

9,02

47,20

53,30

23,10

124,00

22,30

10

10,02

51,10

57,90

24,80

137,60

24,70

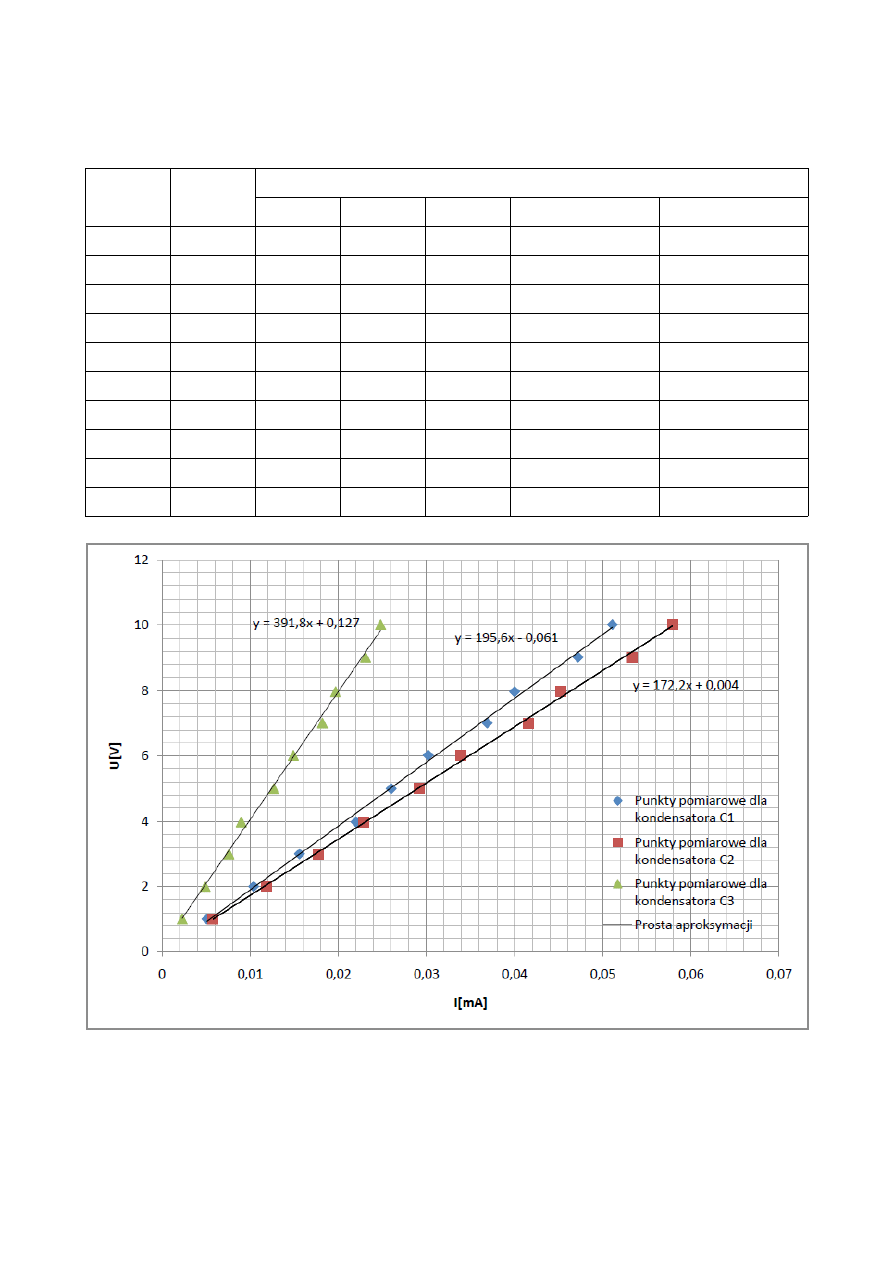
Rys. 7. Charakterystyki napieciowo – prądowe kondensatorów C

1

, C

2

, C

3

zasilanych napięciem

zmiennym wraz z równaniami prostych i ich parametrami.

8

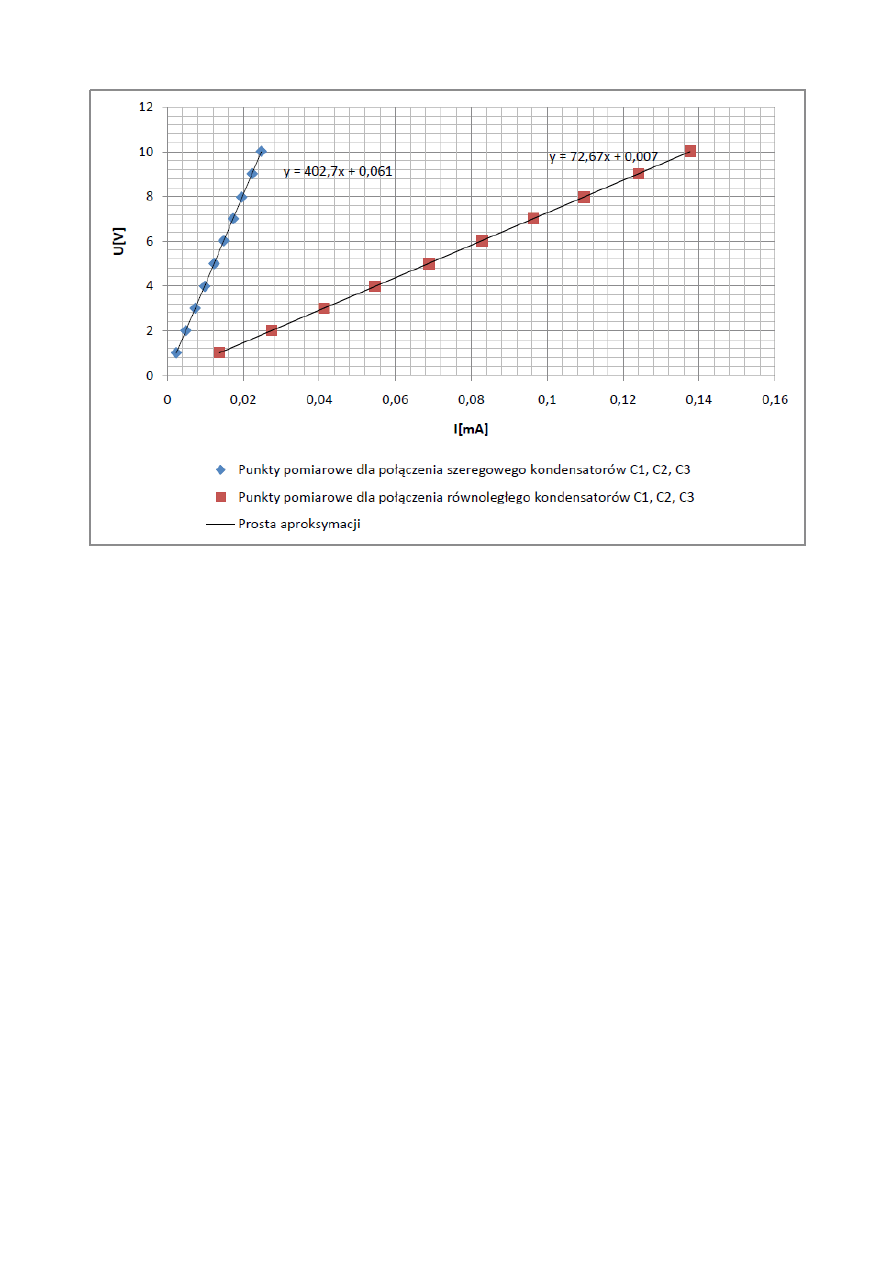
Rys. 8. Charakterystyki napieciowo – prądowe kondensatorów C

1

, C

2

, C

3

połączonych szeregowo

i równolegle zasilanych napięciem zmiennym wraz z równaniami prostych i ich parametrami.

b) Obliczenia:

Rezystancja cewki:

Rezystancję drutu cewki obliczono za pomocą metody regresji liniowej. Dla danych z tabeli 1
obliczono wartość współczynnika kierunkowego a oraz jego niepewność ze wzorów 5, 7.
Szczegółowe obliczenia parametrów prostej zamieszczono w załączniku numer 1. Współczynnik
kierunkowy a prostej jest jednocześnie rezystancją drutu cewki przy zasilaniu napięciem stałym.

Współczynnik a = 61,8

Ω

Błąd współczynnika a = 0,053

Ω

Rezystancja drutu cewki R = (61,8

± 0,053) Ω

Impedancja drutu cewki bez rdzenia:

Dla danych z tabeli 2 obliczono wartość współczynnika kierunkowego a oraz jego niepewność ze
wzorów 5, 7. Współczynnik kierunkowy a prostej jest jednocześnie impedancją drutu cewki bez
rdzenia przy zasilaniu napięciem zmiennym.

Współczynnik a = 83,07

Ω

Błąd współczynnika a = 0,229

Ω

Impedancja drutu cewki bez rdzenia Z = (83,07

± 0,229) Ω

9

Indukcyjność drutu cewki bez rdzenia:

Indukcyjność drutu cewki bez rdzenia obliczono podstawiając wartości rezystancji i impedancji do
wzoru 3.

Indukcyjność drutu cewki bez rdzenia L = 0,177 H

Impedancja drutu cewki z rdzeniem:

Dla danych z tabeli 2 obliczono wartość współczynnika kierunkowego a oraz jego niepewność ze
wzorów 5, 7. Współczynnik kierunkowy a prostej jest jednocześnie impedancją drutu cewki z
rdzeniem przy zasilaniu napięciem zmiennym.

Współczynnik a = 451,85

Ω

Błąd współczynnika a = 2,29

Ω

Impedancja drutu cewki z rdzeniem Z = (451,85 ± 2,29) Ω

Indukcyjność drutu cewki bez rdzenia:

Indukcyjność drutu cewki z rdzeniem obliczono podstawiając wartości rezystancji i impedancji do
wzoru 3.

Indukcyjność drutu cewki z rdzeniem L = 1,425 H

Pojemność kondensatorów:

Reaktancję pojemnościową poszczególnych kondensatorów obliczono za pomocą metody regresji
liniowej. Dla danych z tabeli 2 obliczono wartość współczynnika kierunkowego a oraz jego
niepewność ze wzorów 5, 7. Szczegółowe obliczenia parametrów prostej zamieszczono w
załączniku numer 1. Współczynnik kierunkowy a prostej jest jednocześnie reaktancją
pojemnościową kondensatora. Pojemność kondensatora obliczono ze wzoru 2.

Kondensator

C

1

:

Współczynnik a = 195,6

Ω

Błąd współczynnika a = 3,4

Ω

Reaktancja pojemnościowa kondensatora

C

1

wynosi

Xc

1

=

(195,6 ± 3,4) Ω

Pojemność kondensatora C

1

= 0,164μF

Kondensator

C

2

:

Współczynnik a = 172,2

Ω

Błąd współczynnika a = 2,36

Ω

Reaktancja pojemnościowa kondensatora

C

2

wynosi Xc

2

= (172,2 ± 2,36) Ω

Pojemność kondensatora C

2

= 0,184μF

10

Kondensator

C

3

:

Współczynnik a = 172,2

Ω

Błąd współczynnika a = 2,36

Ω

Reaktancja pojemnościowa kondensatora

C

3

wynosi Xc

3

= (391,79 ± 7,88) Ω

Pojemność kondensatora C

3

= 8,1286μF

Kondensatory C

1

, C

2

, C

3

połączone szeregowo:

Współczynnik a = 402,77

Ω

Błąd współczynnika a = 1,17

Ω

Reaktancja pojemnościowa kondensatorów

C

1

, C

2

, C

3

połączonych szeregowo

Xc

sz

= (402,77 ± 1,17) Ω

Pojemność kondensatorów połączonych szeregowo C

szer

= 7,9μF

Kondensatory C

1

, C

2

, C

3

połączone równolegle:

Współczynnik a = 72,67

Ω

Błąd współczynnika a = 0,066

Ω

Reaktancja pojemnościowa kondensatorów

C

1

, C

2

, C

3

połączonych równolegle

Xc

rów

= (402,77 ± 1,17) Ω

Pojemność kondensatorów połączonych równolegle C

rów

= 0,44μF

4. Analiza niepewności pomiaru:

Niepewność pomiaru indukcji cewki z rdzeniem i bez rdzenia obliczono ze wzoru:

u (L)=

√

(

R

√

Z

2

−

R

2

×

2πf

×

u( R))

2

+

√

(

Z

√

Z

2

−

R

2

×

2πf

×

u(Z ))

2

(9)

Niepewność pomiaru indukcji dla cewki:

•

bez rdzenia 0,00079H,

•

z rdzeniem 0,009H.

Niepewność pomiaru pojemności kondensatorów C

1

, C

2

, C

3

posłużono się wzorem:

u (C)=∣

δC

δX

c

×

u( X

c

)∣

(10)

11

Niepewność pomiaru pojemności dla:

•

kondensatora C

1

0,55nF,

•

kondensatora C

2

0,63nF,

•

kondensatora C

3

0,46nF,

•

kondensatorów C

1

, C

2

, C

3

połączonych szeregowo 0,092nF,

•

kondensatorów C

1

, C

2

, C

3

połączonych równolegle 0,028nF.

5. Zestawienie wyników:

Tab. 5. Końcowe wyniki obliczonej indukcyjności i pojemności

Cewka

L

bez rdzenia

0,177(0,00079)H

L

z rdzeniem

1,425(0,009)H

Kondensatory

C

1

0,164(0,00055)μF

C

2

0,184(0,00063)μF

C

3

8,1286(0,00046)μF

C

połączene szeregowo

0,079(0,000092)μF

C

połączone równolegle

0,44(0,000028)μF

6. Wnioski:

Na podstawie przeprowadzonych pomiarów i obliczeń można zauważyć, że pojemność
kondensatorów połączonych równolegle okazała się większa od największej pojemności
pojedynczych kondensatorów, natomiast przy połączeniu szeregowym mniejsza od najmniejszej
pojemności pojedynczego kondensatora. Sprawdza się tow odniesieniu do teorii. Indukcja cewki

zauważalnie wzrosła po umieszczeniu w niej rdzenia.

12