R O Z D Z I A Ł 13

T E S T Y N I E P A R A M E T R Y C Z N E

I. Wprowadzenie

W poprzednich rozdziałach (za wyjątkiem rozdziału 12) przedstawiliśmy różnorodne
parametryczne testy statystyczne. Ich użycie do opracowywania wyników badań jest
ograniczone określonymi założeniami - zmienne mierzalne, zmienne mające rozkład
normalny, jednorodność zbioru itd. W a r u n k i e m użycia tych testów jest więc sprawdzenie
wyżej wymienionych założeń. W przypadku ich niespełnienia wyciągnięte wnioski nie są
całkowicie poprawne lub tracą swoją wiarygodność. Testy te stają się też bezużyteczne dla
danych jakościowych i danych uporządkowanych. W tych wszystkich przypadkach
stosujemy testy nieparametryczne. Za pomocą testów nieparametrycznych (jak i testów
parametrycznych) m o ż e m y rozstrzygnąć, czy określoną hipotezę m o ż e m y odrzucić, czy też
nie m a m y do tego podstaw. W tym ostatnim przypadku nie oznacza to, że nasza hipoteza

jest całkowicie słuszna, lecz że nie stoi w sprzeczności z otrzymanymi wynikami naszych

badań. Testy nieparametryczne nie zależą od kształtu rozkładu zmiennej oraz od p e w n y c h
parametrów rozkładu populacji. Dla testów nieparametrycznych również wzory służące do
ich obliczenia są proste, a same obliczenia nie zajmują dużo czasu. M o ż e m y je więc
szeroko stosować wszędzie tam, gdzie nie są spełnione założenia w y m a g a n e dla testów
parametrycznych. Stosujemy je również wtedy gdy nasze dane są jakościowe lub m o ż n a je
tylko uporządkować według określonych kryteriów oraz dla grup o małej liczebności. Siła
testów nieparametrycznych (1 minus wielkość błędu drugiego rodzaju) jest j e d n a k niższa
niż siła testów parametrycznych. Stosujemy je więc tylko wówczas, gdy nie m o ż e m y
posłużyć się testem parametrycznym. Niniejszy rozdział jest w całości poświęcony testom
nieparametrycznym.

Testy przez nas przedstawione podzielimy na sześć grup:

1. Testy dla dwóch niezależnych próbek (nieparametryczne odpowiedniki testu

t-Studenta dla zmiennych niepowiązanych)

• Test serii Walda-Wolfowitza
• Test U Manna-Whitneya
• Test Kołmogorowa-Smirnowa

2. Testy dla dwóch zależnych próbek (nieparametryczne odpowiedniki testu

t-Studenta dla zmiennych powiązanych)

• Test z n a k ó w
• Test kolejności par Wilcoxona
• Test M c N e m a r y

3. Testy dla n próbek (nieparametryczne odpowiedniki analizy wariancji)

• Test Kruskala-Wallisa
• Test Friedmana
• Test Q Cochrana

263

Przystępny kurs statystyki

4. Korelacje nieparametryczne

• R Spearmana
• Tau Kendalla
• Test χ

2

5. Testy

zgodności

• Test χ

2

• Test

Kołmogorowa-Smirnowa

Przykład 1
W dwóch grupach chorych na pewną chorobę neurologiczną przeprowadzono badania
stężenia adrenaliny w surowicy krwi. Zebrane wyniki dla 24 pacjentów przedstawia
poniższa tabela:

N u m e r

grupy

Wielkość

stężenia

R a n g a

N u m e r

grupy

Wielkość

stężenia

R a n g a

14,34

14

II

5,33

1

I

20,33

17

II

22,50

19

I

18,79

15

II

11,74

9

I

8,22

4

II

7,39

2

I

31,5

22

II

12,34

12

I

12,08

10

II

13,22

13

I

22

18

II

8,53

5

I

9,22

7

II

22,80

20

I

19,50

16

II

12,70

11

I

78,89

24

II

7,78

3

I

30,48

21

II

9,63

8

I

45,86

23

II

8,90

6

Przyjmując poziom istotności p = 0,05, zweryfikujemy hipotezę, że stężenie adrenaliny
w obu grupach jest jednakowe. Ponieważ zmienna opisująca p o z i o m adrenaliny nie ma
rozkładu normalnego, nie m o ż e m y zastosować testu t-Studenta, p o s ł u ż y m y się więc j e g o
nieparametrycznym odpowiednikiem testem Manna-Whitneya.

Punktem wyjścia w opisywanym teście jest nadanie w y n i k o m obserwacji rang.

Przebiega to następująco:

1. Porządkujemy rosnąco wartości obu prób.

2. Zaczynając od wartości najmniejszej (lub największej) przyporządkowujemy

poszczególnym obserwacjom kolejne liczby naturalne.

3. W przypadku wystąpienia wartości jednakowych, przyporządkowujemy im

tzw. rangi wiązane (średnia arytmetyczna z rang, jakie p o w i n n o im się
przypisać).

Rangi przypisane obserwacjom z analizowanego przykładu podane są w powyższej tabelce.
Wykorzystamy obecnie wspomniany test Manna-Whitneya następującej postaci:

264

Testy nieparametryczne

Po obliczeniu sumy rang w poszczególnych grupach otrzymujemy R

1

= 191 oraz R

2

= 109.

Statystyka U przyjmuje teraz wartość U= 144+(12*13)/2 - 191 = 3 1 . Z tabeli wartości
krytycznych testu U Manna-Whitneya dla p o z i o m u istotności p = 0,05 otrzymujemy
U

p

(n

1

,n

2

) = 37. Ponieważ obliczona wartość statystyki U jest niniejsza (!) od krytycznej,

zatem w o m a w i a n y m przykładzie odrzucamy hipotezę zerową i stwierdzamy, że różnica
między stężeniami adrenaliny z obu grup jest statystycznie istotna.

Przykład 2
Przeprowadzono badania w celu porównania czterech m e t o d leczenia pewnej choroby.
Pobrano pięcioelementowe próby losowe spośród chorych na daną chorobę, których
leczono odpowiednio metodą I, II, III i IV. Wyniki terapii oceniono w specjalnym teście.
Wartości testu (podane w umownej punktacji) wraz z przypisanymi im rangami p o d a n o
w poniższej tablicy:

265

Przystępny kurs statystyki

Metoda I

Rangi

Metoda II Rangi Metoda III Rangi Metoda IV Rangi

57

2

74

20

63

8,5

62

6,5

58

3

66

11,5

68

15

63

8,5

67

13

65

10

59

4,5

66

11,5

50

1

72

19

59

4,5

71

18

62

6,5

68

15

68

15

70

17

25,5

75,5

47,5

61,5

Chcemy zweryfikować hipotezę, że wszystkie metody leczenia dają j e d n a k o w e wyniki
w leczeniu choroby.

T y m razem m u s i m y zastosować test sprawdzający hipotezę, że k niezależnych

próbek pochodzi z tej samej populacji. Najczęściej w tym celu używany jest test sumy rang
Kruskala-Wallisa będący nieparametryczną alternatywą analizy wariancji z klasyfikacją
pojedynczą. Stosujemy go również, gdy założenia analizy wariancji nie są spełnione. Jest
to test słabszy, ale równocześnie w y m a g a słabszych założeń. Test ten ma postać:

Założenia testu:
Danych jest k populacji, w których badana cecha ma rozkłady typu ciągłego i dane m o ż n a
rozpatrywać w skali porządkowej. O z n a c z m y przez Fi( x ), F

2

(x ), F

k

( x ) dystrybuanty

rozpatrywanych populacji.
Z populacji tych wylosowano po n j (i = 1 , ...,k) elementów do prób (n, > 5).

Weryfikacja hipotezy:

H

0

: F,(x) = F

2

(x) =... = F

k

(x)

266

Testy nieparametryczne

Dla naszego przykładu obliczona wartość statystyki H ( u w z g l ę d n i a j ą c poprawkę) wynosi
H= 7,8414, co pozwala odrzucić hipotezę zerową na poziomie istotności 0,05 (wartość

krytyczną χ

20,05:3

= 7,815 znajdujemy w tablicach statystycznych).

Wartość statystyki

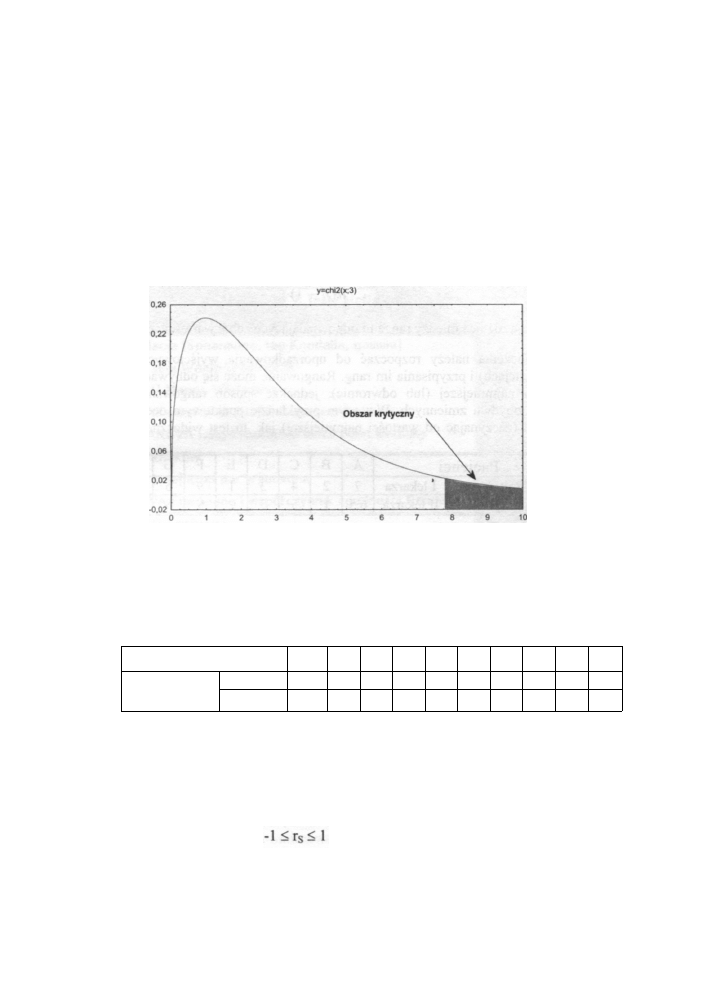
H należy bowiem do obszaru krytycznego, co ilustruje poniższy rysunek:

Rys. 13.1 Obszar krytyczny dla testu Kruskała-Wallisa

Wybór metody leczenia ma zatem istotnie statystyczny wpływ na wynik terapii.

Przykład 3
Chcemy ustalić współzależność między opiniami wydanymi przez dwóch lekarzy
o zdrowiu 10 pacjentów. Opinie te zostały ujęte w punktach:

Pacjenci

A

B

C

D

E

F

G

H

I

J

Punkty

uzyskane od

I lekarza

42

27

36

33

24

47

39

52

43

37

Punkty

uzyskane od II lekarza

39

24

35

29

26

47

4 4

51

39

32

Ponieważ istnieje możliwość uporządkowania opinii lekarzy (wyrażonej w punktach), to

jako miarę korelacji dwóch wyrażonych opinii użyjemy współczynnik korelacji rang

Spearmana. Współczynnik ten służy do opisu siły korelacji cech jakościowych, które
możemy uporządkować. Miarę tę stosujemy również do badania zależności między
cechami ilościowymi w przypadku niewielkiej liczby obserwacji. Podobnie j a k
współczynnik korelacji liniowej Pearsona, współczynnik korelacji rang Spearmana

oraz ma podobną interpretację.

przyjmuje wartości z przedziału

Przystępny kurs statystyki

Współczynnik korelacji rang Spearmana obliczamy według wzoru:

Jak widać, obliczenia należy rozpocząć od uporządkowania wyjściowych informacji
rosnąco (lub malejąco) i przypisania im rang. Rangowanie m o ż e się odbywać od wartości
największej do najmniejszej (lub odwrotnie), j e d n a k ż e sposób rangowania musi być

jednakowy dla obydwu zmiennych. W n a s z y m przykładzie p u n k t o w y m o c e n o m lekarzy

nadajemy rangi (zaczynając od wartości najmniejszej) jak, to jest widoczne w poniższej
tabeli:

Pacjenci

A

B

C

D

E

F

G

H

I

J

Rangi

I lekarza

7

2

4

3

1

9

6

10

8

5

uzyskane od

II lekarza 6,5

1

5

3

2

9

8

10 6,5

4

Wykorzystując powyższy wzór na współczynnik Spearmana otrzymujemy

r

s

= 1 - 63/10(100-1) = 0,936

Otrzymany wynik wskazuje na silną współzależność opinii d w ó c h lekarzy o stanie zdrowia
pacjenta.

Przedstawione powyżej przykłady wskazują obszar zastosowań testów
nieparametrycznych. O m ó w i o n o w nich również testy rozwiązujące postawione tam
problemy bez użycia komputera. Dziś nikt j e d n a k nie prowadzi analizy statystycznej „na
piechotę" (bez użycia techniki komputerowej). Pozostałe testy o m ó w i m y więc w oparciu
o pakiet STATISTICA.

II. A jak to się liczy w programie STATISTICA

W programie STATISTICA testy nieparametryczne tworzą swój własny m o d u ł n a z w a n y
Statystyki nieparametryczne/Rozkłady. Po otwarciu tego m o d u ł u na ekranie pokazuje się
okno przedstawione na poniższym rysunku.

268

Testy nieparametryczne

Rys. 13.2 O k n o m o d u ł u - Statystyki nieparametryczne

Powyższe okno umożliwia dostęp do wszystkich statystyk nieparametrycznych i rozkładów
opisanych w o m a w i a n y m module. Każdy z testów zawartych w t y m oknie zostanie
szczegółowo opisany poniżej w tym rozdziale. Na samej górze okna m a m y opcje
umożliwiające przejście do okna dialogowego realizującego testowanie zgodności rozkładu
danych z dowolnie wybranym rozkładem hipotetycznym.

II. 1 Testy dla dwóch niezależnych próbek

Omówienie testów zawartych w m o d u l e Statystyki Nieparametryczne rozpoczniemy od
opisania grupy testów będących nieparametrycznymi odpowiednikami testu t-Studenta.
Należą do niej testy:

• test serii Walda-Wolfowitza
• test U Manna-Whitneya
• test Kołmogorowa-Smirnowa

Testy te służą do weryfikacji hipotezy, że dwie analizowane próby pochodzą z różnych
populacji. Wymagają one założenia, że analizowane zmienne m o g ą być uporządkowane od
wartości najmniejszej do wartości największej (tzn. są mierzone na skali porządkowej). Ich
interpretacja właściwie jest taka sama, jak w przypadku testu t-Studenta dla zmiennych
niepowiązanych. Dane powinny być podobnie rozmieszczone w dwóch kolumnach (dwie
zmienne). Jedna kolumna zawiera zmienne do przeprowadzenia odpowiedniego

Przystępny kurs statystyki

porównania, a druga zawierająca zmienną grupującą (zmienna niezależna) do

jednoznacznej identyfikacji grup. Sytuację taką widzimy na poniższym rysunku:

Rys. 13.3 Fragment arkusza danych

Po dwukrotnym kliknięciu na nazwie testu otwiera się okno dialogowe umożliwiające
wybór zmiennych do analizy, podania k o d ó w oraz przeprowadzenia interpretacji graficznej
otrzymanych wyników. Okna te dla wszystkich o m a w i a n y c h testów są takie same,
przykładowo więc opiszemy j e d n o związane z testem Walda-Wolfowitza. O k n o to

przedstawione jest na poniższym rysunku.

Rys. 13.4 O k n o testu Walda-Wolfowitza

Do dyspozycji m a m y opcje:

[1] - przycisk Zmienne, powodujący otwarcie okna wyboru zmiennych. O k n o to

umożliwia wybór zmiennych, a także oferuje rozmaite opcje przeglądania zawartości
zbioru danych (więcej informacji na ten temat znajduje się w rozdziale trzecim).

270

Testy nieparametryczne

[2] - pola umożliwiające określenie k o d ó w użytych do identyfikacji grup.

Wartości kodów wpisujemy bezpośrednio w tych polach lub wybieramy z listy otwierającej
się po dwukrotnym kliknięciu na tym polu.

[3] - przyciski tworzące interpretację graficzną otrzymanych w y n i k ó w analizy

statystycznej. M a m y możliwość utworzyć Wykres R a m k o w y charakteryzujący
podstawowe właściwości rozkładu zmiennej. Jest więc on użytecznym narzędziem do
porównywania rozkładu zmiennych w różnych grupach. Drugi typ wykresu to
Skategoryzowany Histogram rozkładu wyselekcjonowanej zmiennej. Wykresy
skategoryzowane są tworzone przez podzielenie danych na podzbiory, a następnie
odwzorowanie wszystkich podzbiorów na oddzielnych m a ł y c h wykresach,
rozmieszczonych na j e d n y m obrazie.

Sposób weryfikacji hipotez przy p o m o c y nieparametrycznych odpowiedników testu
t przedstawimy w oparciu o dane z przykładu 1.

Przykład 1 cd.
Analizę rozpoczniemy od testu Walda-Wolfowitza (test najbardziej konserwatywny). Test
ten oparty jest na rozkładzie liczby serii. Jeśli serii jest mało, będziemy mogli odrzucić
hipotezę zerową, w przeciwnym wypadku niemożliwe jest odrzucenie hipotezy zerowej, że
dwie próby pochodzą z tej samej populacji.

Po wprowadzeniu danych i określeniu k o d ó w klikamy na przycisku OK dla

rozpoczęcia analizy. Wynik zostanie wyświetlony w oknie, którego postać przedstawiona

jest na poniższym rysunku.

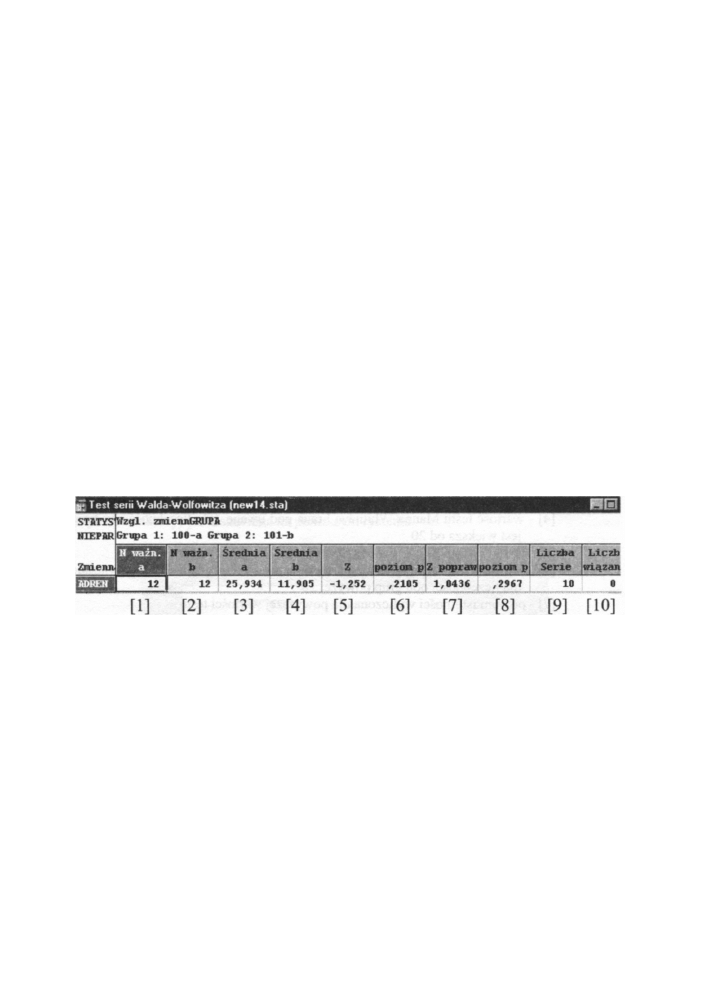
Rys. 13.5 Arkusz w y n i k ó w testu Walda-Wolfowitza

Poszczególne pola w arkuszu wyników oznaczają odpowiednio:

[1] - liczebność grupy oznaczonej symbolem „ a "
[2] - liczebność grupy oznaczonej symbolem „ b "
[3] - średnia wartości grupy oznaczonej k o d e m „ a "
[4] - średnia wartości grupy oznaczonej k o d e m „ b "
[5] - wartość testu Walda-Wolfowitza brana p o d uwagę, gdy liczebność obu

grup jest większa od 20

[6] - poziom istotności wyliczona dla powyższej wartości testu
[7] - wartość testu skorygowanego stosowanego dla małych liczebności (poniżej

20). Tę p o p r a w k ę na ciągłość wprowadził Siegel w 1956 roku

[8] - poziom istotności dla testu poprawionego
[9] - liczba serii - podstawowa wielkość w konstrukcji testu Walda-Wolfowitza.

Hipotezę zerową odrzucamy gdy liczba serii jest zbyt m a ł a

[10] - liczba rang wiązanych

271

Przystępny kurs statystyki

Jak wynika z arkusza w y n i k ó w testu Walda-Wolfowitza dla przykładu pierwszego nie
m a m y podstaw do odrzucenia hipotezy zerowej.

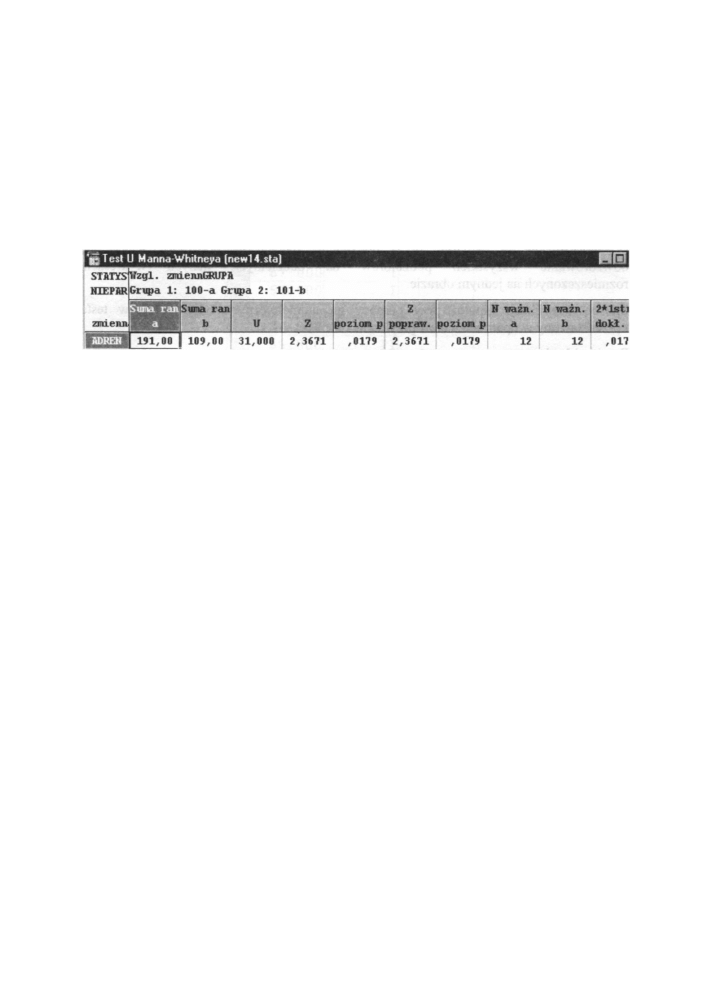
A tak wygląda arkusz w y n i k ó w testu Manna-Whitneya (rysunek poniżej). Test ten został
dokładnie omówiony na początku tego rozdziału. T y m razem, j a k wynika z arkusza
wyników, m o ż e m y n a poziomie istotności p = 0,018 odrzucić hipotezę zerową.

Stwierdzamy więc, że różnica między stężeniami adrenaliny z obu grup jest statystycznie
istotna.

[1] [2] [3] [4] [5] [6] [7] [8] [9]

[10]

Rys. 12.6 Arkusz w y n i k ó w testu Manna-Whitneya

Poszczególne pola w arkuszu w y n i k ó w oznaczają odpowiednio:

[1] - suma rang dla grupy oznaczonej symbolem „ a "
[2] - suma rang dla grupy oznaczonej symbolem „ b " (stanowią one podstawę

podejmowanych decyzji)

[3] - wartość testu Manna-Whitneya stosowanego dla małych liczebności

(poniżej 20)

[4] - wartość testu Manna-Whitneya brana p o d uwagę, gdy liczebność obu grup

jest większa od 20

[5] - poziom istotności wyliczona dla powyższej wartości testu
[6] - wartość testu skorygowanego, stosowanego ze względu na rangi wiązane

dla liczebności obu grup powyżej 20

[7] - poziom istotności wyliczona dla powyższej wartości testu
[8] - liczebność grupy oznaczonej symbolem „ a "
[9] - liczebność grupy oznaczonej symbolem „ b "
[10] - dla prób o małej liczebności obliczana jest wartość 2*p, gdzie p jest równe

1 minus odpowiednia wartość dystrybuanty rozkładu statystyki U.

Stosujemy, gdy nie występują rangi wiązane

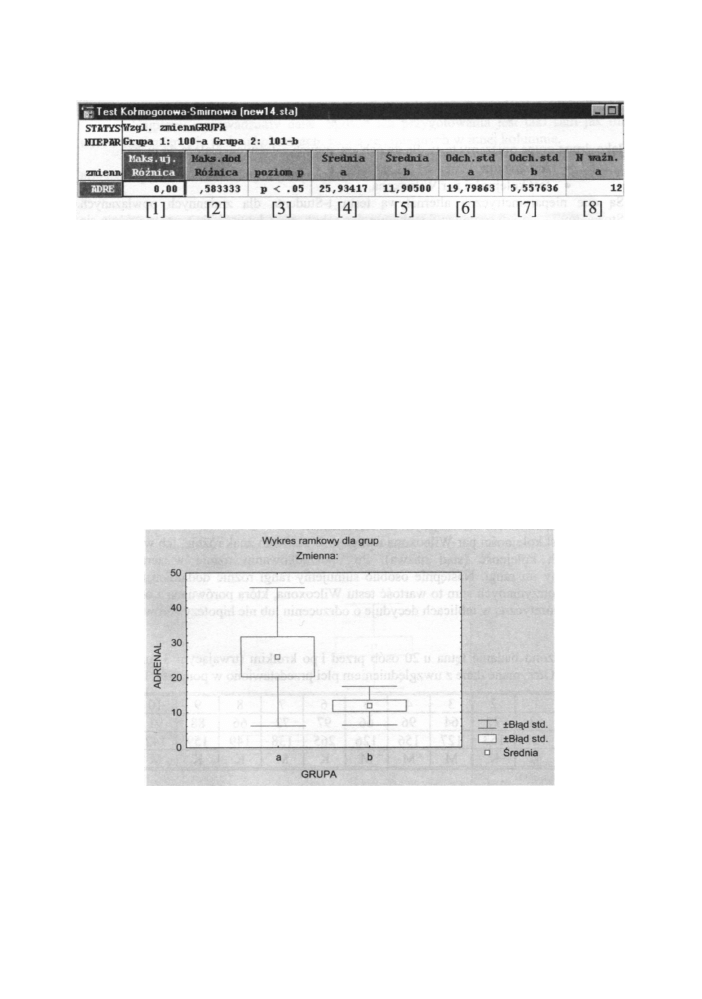
Z kolei arkusz w y n i k ó w testu K o ł m o g o r o w a - S m i r n o w a (dla tych samych danych)
przyjmuje postać widoczną na poniższym rysunku.

272

Testy nieparametryczne

Rys. 13.7 Arkusz wyników testu K o ł m o g o r o w a - S m i r n o w a

Poszczególne pola w arkuszu wyników oznaczają odpowiednio:

[1] - maksymalna wartość ujemnych różnic
[2] - maksymalna wartość dodatnich różnic

M a k s i m u m z bezwzględnych wartości powyższych liczb stanowi podstawę
wnioskowania statystycznego w teście Kołmogorowa-Smirnowa.

[3] - p o z i o m istotności wyliczona dla powyższej wartości testu
[4] - średnia wartości grupy oznaczonej k o d e m „ a "
[5] - średnia wartości grupy oznaczonej k o d e m „ b "
[6] - odchylenie standardowe grupy oznaczonej k o d e m „ a "
[7] - odchylenie standardowe grupy oznaczonej k o d e m „ b "
[8] - liczebność grupy oznaczonej symbolem „ a "
[9] - liczebność grupy oznaczonej symbolem „ b "

Otrzymujemy, jak poprzednio, że różnica między stężeniami adrenaliny z obu grup jest
statystycznie istotna (poziom istotności p< 0,05). Potwierdza to interpretacja graficzna
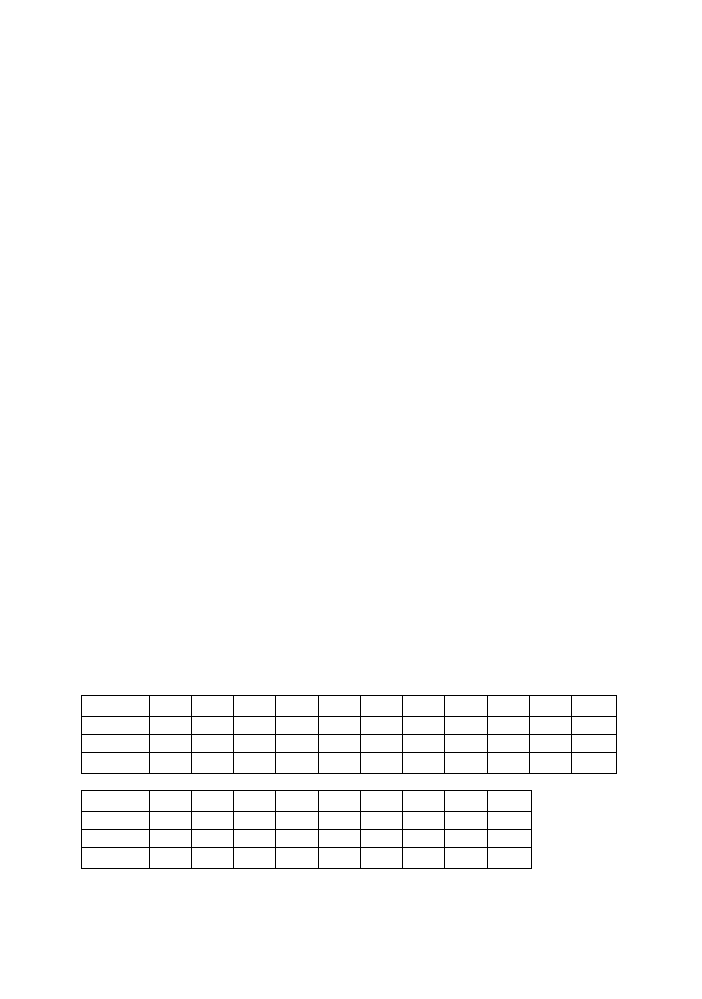
(wykres ramkowy) przedstawiona na poniższym rysunku.

Rys. 13.8 Wykres ramkowy dla danych z przykładu 1

273

Przystępny kurs statystyki

II. 2 Testy dla dwóch zależnych próbek

Jako drugą grupę opiszemy testy dla d w ó c h zmiennych zależnych. Należą do nich:

• test znaków
• test kolejności par Wilcoxona.

Są one nieparametryczną alternatywą testu t-Studenta dla z m i e n n y c h powiązanych.
Stosujemy je, gdy dysponując d w o m a pomiarami c h c e m y dowieść, że pomiary różnią się.
Inaczej mówiąc, testy te przeznaczone są do sprawdzania istotności różnic między d w i e m a

zależnymi próbkami. Te dwie zależne próbki to albo dwie obserwacje u tej samej osoby
(np. przed i po zabiegu) albo też badania p r o w a d z i m y dla par osób o tych samych
właściwościach. Ich hipoteza zerowa mówi, że wyniki obu próbek są j e d n a k o w e . Testy te

stosujemy również wtedy, gdy nie są spełnione założenia testu t dla zmiennych
powiązanych. Za ich p o m o c ą m o ż e m y stwierdzić, czy próbki (zmienne) różnią się między
sobą pod względem pewnych własności. Te łatwe w użyciu testy wymagają jedynie
założenia, że badane zmienne m o ż e m y uporządkować (są mierzalne na skali porządkowej).

Test znaków, jak sama n a z w a wskazuje, oparty jest na znakach różnic między

kolejnymi parami wyników (czy są ujemne, czy dodatnie). Test ten stosujemy więc przede
wszystkim dla cech jakościowych. Wystarczy b o w i e m sprawdzić, że dana jednostka
charakteryzuje się obecnością „ + " lub nieobecnością „-" danego zjawiska. Ogólnie
mówiąc, test znaków, to ustalenie liczby plusów i m i n u s ó w oraz porównanie ich
z wartością teoretyczną podaną w odpowiednich tablicach. Dla danych mierzalnych nie
uwzględniamy wartości różnic, a jedynie ich znaki. Różnice o wartości zero są pomijane.
W teście znaków tracimy więc informację niesioną przez liczbowe wartości różnic. Ta
znacząca informacja jest w pełni wykorzystywana przez test Wilcoxona. Staje się on więc
w tym wypadku testem mocniejszym niż test znaków.

Test kolejności par Wilcoxona uwzględnia zarówno znak różnic, ich wielkość, j a k

również ich kolejność (stąd nazwa). Po uporządkowaniu różnic w szereg rosnący
przypisujemy im rangi. Następnie osobno sumujemy rangi różnic dodatnich i ujemnych.
Mniejsza z otrzymanych sum to wartość testu Wilcoxona, która p o r ó w n a n a z odpowiednią
wartością teoretyczną w tablicach decyduje o odrzuceniu lub nie hipotezy zerowej.

Przykład 4
Przeprowadzono badanie tętna u 20 osób przed i po krótkim (trwającym 3 min) wysiłku
fizycznym. Otrzymane dane z uwzględnieniem płci przedstawiono w poniższej tabeli.

Lp.

1

2

3

4

5

6

7

8

9

10

11

Tętno I

63

77

64

96

66

97

72

66

88

91

68

Tętno II

127

153

127

156

126

265

138

149

159

142

112

Płeć

M

K

M

M

M

K

M

K

K

M

M

Lp.

12

13

14

15

16

17

18

19

20

Tętno I

92

76

80

68

86

70

88

70

65

Tętno II

141

147

137

116

145

121

154

134

142

Płeć

M

K

M

M

K

M

K

K

K

274

Testy nieparametryczne

Czy otrzymane wyniki przeczą hipotezie, że wysiłek w p ł y w a na przyspieszenie tętna?

Najpierw w p r o w a d z a m y dane. Sposób ich przygotowania jest taki s a m j a k dla

testu t. Zapisujemy je w dwu kolumnach, każdą ze z m i e n n y c h w innej kolumnie.

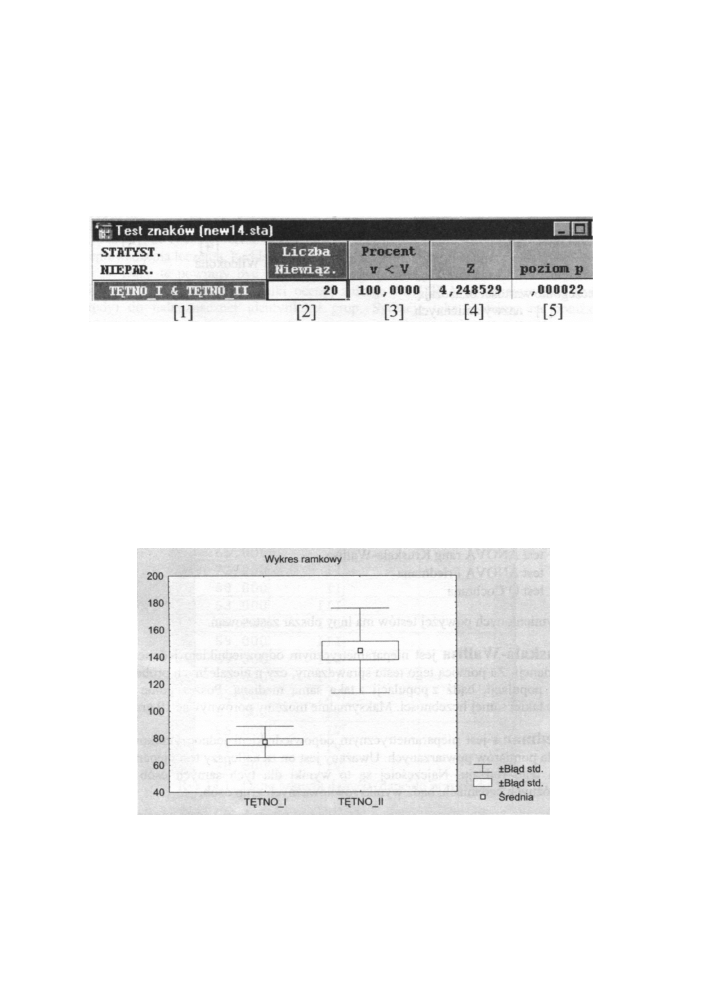
Jako pierwszy zastosujemy test znaków. Po wprowadzeniu danych klikamy OK

uruchamiając analizę. Otrzymujemy arkusz w y n i k ó w przedstawiony na poniższym
rysunku.

Rys 13.9 Arkusz w y n i k ó w testu z n a k ó w

Poszczególne wartości oznaczają:

[1] - nazwy zmiennych
[2] - liczebność grup
[3] - procent liczebności zmiennych, dla których różnica ma wartość ujemną

(znak „-")

[4] - wartość testu z n a k ó w
[5] - p o z i o m istotności dla testu z n a k ó w

M o ż e m y zatem stwierdzić, że z bardzo w y s o k i m p o z i o m e m ufności 1 - 0,000022 =
0,99998 można wykazać wpływ wysiłku fizycznego na przyspieszenie tętna. Potwierdza to
graficznie wykres r a m k o w y przedstawiony na poniższym rysunku.

Rys. 13.10 Wykres r a m k o w y dla danych z przykładu 4

275

Przystępny kurs statystyki

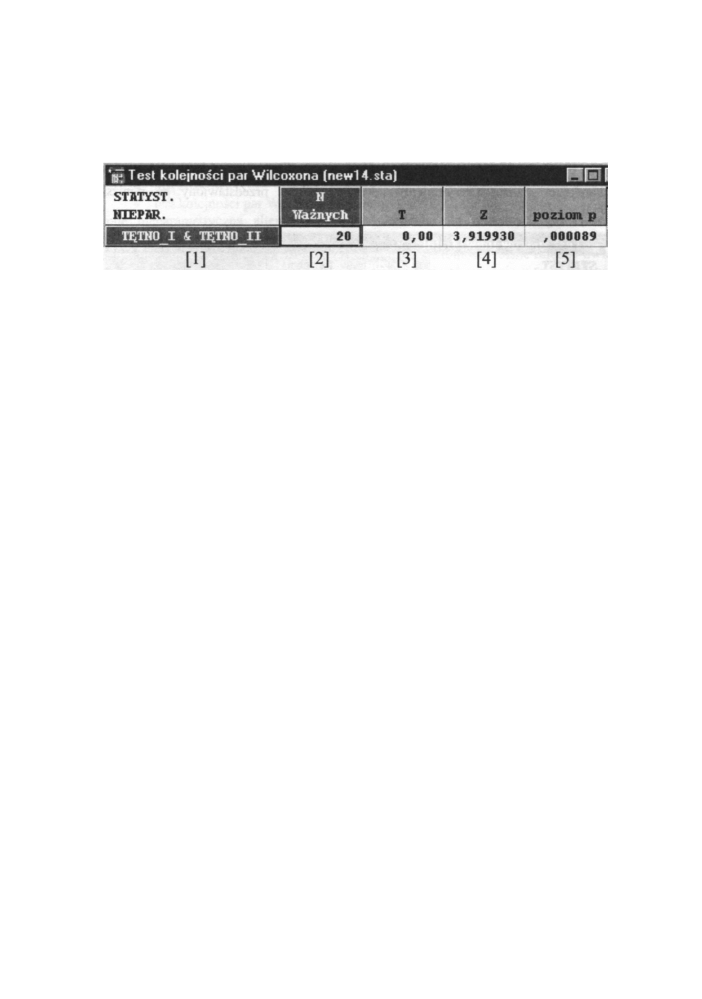
Z kolei zastosowanie testu kolejności par Wilcoxona do danych z przykładu 2 dostarcza
poniższy arkusz wyników.

Rys. 13.11 Arkusz w y n i k ó w dla testu Wilcoxona

Poszczególne wartości oznaczają:

[1] - nazwy zmiennych
[2] - liczebność grup
[3] - wartość testu Wilcoxona dla grup o liczebności n

< lub = 25

[4] - wartość testu Wilcoxona dla grup o liczebności n

> 25

[5] - poziom istotności dla testu Wilcoxona

Otrzymane wyniki dla testu Wilcoxona potwierdzają, że hipotezę o równości rozkładów
zmiennych T E S T I i T E S T I I należy odrzucić i to z p r a w d o p o d o b i e ń s t w e m popełnienia
błędu p = 0,000089.

II 3. Testy dla wielu próbek (nieparametryczne odpowiedniki
analizy wariancji)

Jako trzecią grupę opiszemy testy dla wielu populacji. Należą do nich:

• test A N O V A rang Kruskala-Wallisa
• test A N O V A Friedmana
• test Q Cochrana

Każdy z wymienionych powyżej testów ma inny obszar zastosowań.

Test Kruskala-Wallisa

jest nieparametrycznym odpowiednikiem jednoczynnikowej

analizy wariancji. Za p o m o c ą tego testu sprawdzamy, czy n niezależnych próbek pochodzi
z tej samej populacji, bądź z populacji z taką samą medianą. Poszczególne próbki nie
muszą mieć takiej samej liczebności. Maksymalnie m o ż e m y p o r ó w n y w a ć 10 grup.

Test Friedmana

jest nieparametrycznym odpowiednikiem jednoczynnikowej analizy

wariancji dla pomiarów powtarzanych. U w a ż a n y jest on za najlepszy test nieparametryczny
dla danych tego rodzaju. Najczęściej są to wyniki dla tych samych osób otrzymane
w n (n>2) różnych badaniach, bądź wyniki r ó w n o w a ż n y c h grup osób.

Test Q Cochrana

jest uogólnieniem na więcej niż dwie próby testu M c N e m a r y .

W teście tym m a m y do czynienia z co najmniej trzema z m i e n n y m i zależnymi
i stwierdzamy, czy kolejne liczebności lub proporcje różnią się istotnie między sobą. Test

276

Testy nieparametryczne

wymaga danych dychotomicznych,tzn. przyjmujących wartości zakodowane j a k o 0 i 1 (np.
zdarzenie zaszło lub nie oraz odpowiedź poprawna lub zła). Z m i e n n e mierzalne m u s i m y
więc sztucznie przeskalować na zmienne dychotomiczne (np. powyżej średniej lub
poniżej).

• Jako pierwszy o m ó w i m y przykład zastosowania testu Kruskala-Wallisa.

Przykład 5
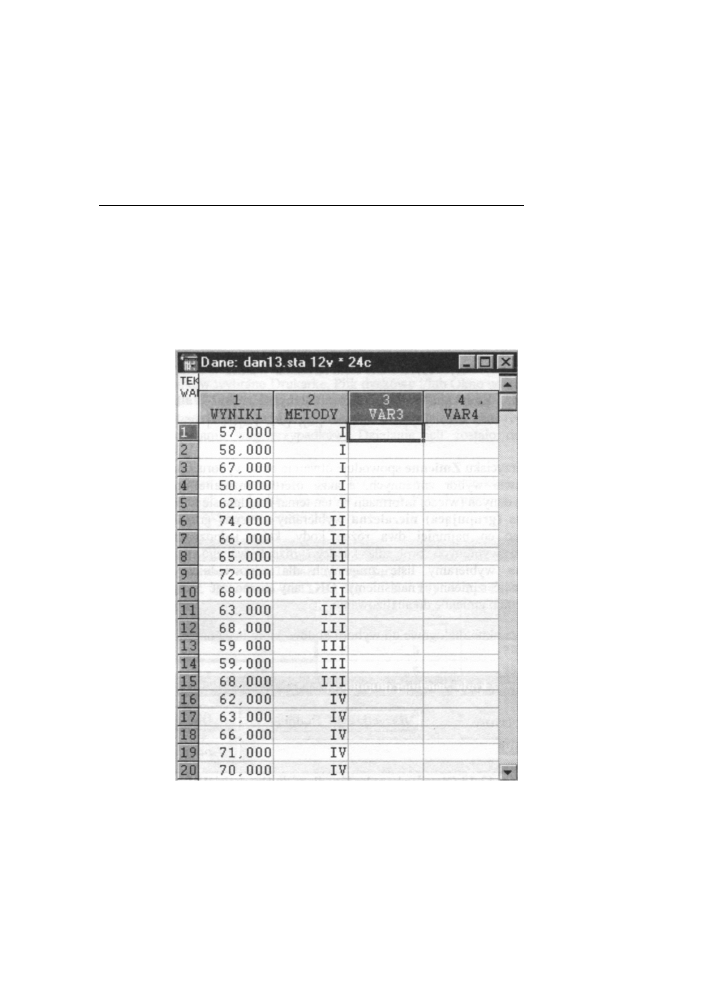
Przypuśćmy, że chcemy ocenić cztery metody terapii dla znalezienia najlepszego sposobu
przeprowadzenia leczenia. Każda metoda terapii oceniana jest w umownej skali punktowej.

Dane te powinny być podobnie rozmieszczone j a k w analizie wariancji. Jedna

zmienna W Y N I K I zawiera wyniki oceny, a druga M E T O D A zawierająca kod (numer
metody) do jednoznacznej identyfikacji grup. Sytuację taką widzimy na poniższym
rysunku:

Rys 13.12 O k n o arkusza danych (dane do przykładu 5)

Po uruchomieniu testu (dwukrotnie klikając na nazwie) otrzymujemy następujące okno
dialogowe:

277

Przystępny kurs statystyki

Rys. 13.13 O k n o testu Kruskala-Wallisa

W oknie A N O V A Kruskala-Wallisa i test mediany (Kruskai-Wallis A N O V A and
Median Test) przyciski o kolejnych numerach [1], [2], [3], [4] realizują następujące
funkcje:

[1] - Kliknięcie przycisku Zmienne spowoduje otwarcie okna wyboru zmiennych.

Okno to umożliwia wybór zmiennych, a także oferuje rozmaite opcje przeglądania
zawartości zbioru danych (więcej informacji na ten temat znajduje się w rozdziale trzecim).
W polu Zmienna (grupująca) niezależna wybieramy zmienną grupującą. Z m i e n n a ta

powinna zawierać co najmniej dwa różne kody, które jednoznacznie identyfikują
przynależność do wybranych prób dla każdego rozpatrywanego przypadku. W polu
zmienna zależna wybieramy listę zmiennych dla odpowiednich porównań. Jeśli
zapomnimy określić zmienne i naciśniemy OK aby rozpocząć statystyczną analizę,
STATISTICA

zapyta o zmienne do analizowania.

[2] - Kody otwiera okno dialogowe do wyboru kodów, które będą używane w grupowaniu

zmiennej.

Rys. 13.14 O k n o wyboru k o d ó w dla testu Kruskala-Wallisa

O k n o to oferuje różnorodne funkcje. Przykładowo przed d o k o n a n i e m wyboru m o ż e m y
przejrzeć wartości pojedynczych zmiennych lub wypełnić pole k o d ó w wartościami dla

jednoznacznej identyfikacji przynależności do interesujących nas grup dla każdego

przypadku. Jeśli nie w p r o w a d z i m y żadnego kodu i naciśniemy OK, program

278

Testy nieparametryczne

automatycznie wypełni pole kodu wszystkimi różnymi wartościami wybranej zmiennej
i zamknie okno dialogu.

[3] - przycisk wywołujący serię okien dialogowych dla utworzenia wykresu Wykres
ramkowy („pudełko z wąsami"). Wykres ten charakteryzujący podstawowe właściwości

rozkładu zmiennej jest użytecznym narzędziem do porównywania rozkładu zmiennych
w różnych grupach.

[4] - Skategoryzowany Histogram - opcja ta umożliwia tworzenie skategoryzowanego

histogramu rozkładu wyselekcjonowanej zmiennej. Wykresy skategoryzowane są tworzone
przez podzielenie danych na podzbiory, a następnie odwzorowanie wszystkich podzbiorów
na oddzielnych małych wykresach, rozmieszczonych na j e d n y m obrazie.

W oknie tym znajduje się również pole wyboru Przetwarzanie wsadowe/drukowanie.
Umożliwia ono automatycznie powtarzanie przez program analizy wraz z drukowaniem
rezultatów dla każdej wybranej zmiennej bez dodatkowych działań ze strony użytkownika.
Opcja ta jest aktywna, jeżeli w oknie dialogowym Strona/Ustawienie wydruku j a k o
docelowe dla wyników wybrano Drukarkę, Plik dyskowy i/lub O k n o wyników.

W oknie A N O V A Kruskala - Wallisa i test mediany m a m y ponadto (podobnie

jak w innych oknach dialogowych opisanych wcześniej) dwa przyciski - do selekcji

przypadków i określania wag przypadków. Działanie ich zostało dokładnie opisane
wcześniej.

Przeanalizujemy teraz w programie STATISTICA dane z przykładu 3. Ustawienie
wszystkich potrzebnych opcji i kliknięcie OK powoduje wykonanie analizy i pojawienie
się (jako pierwszego) okna pokazanego poniżej.

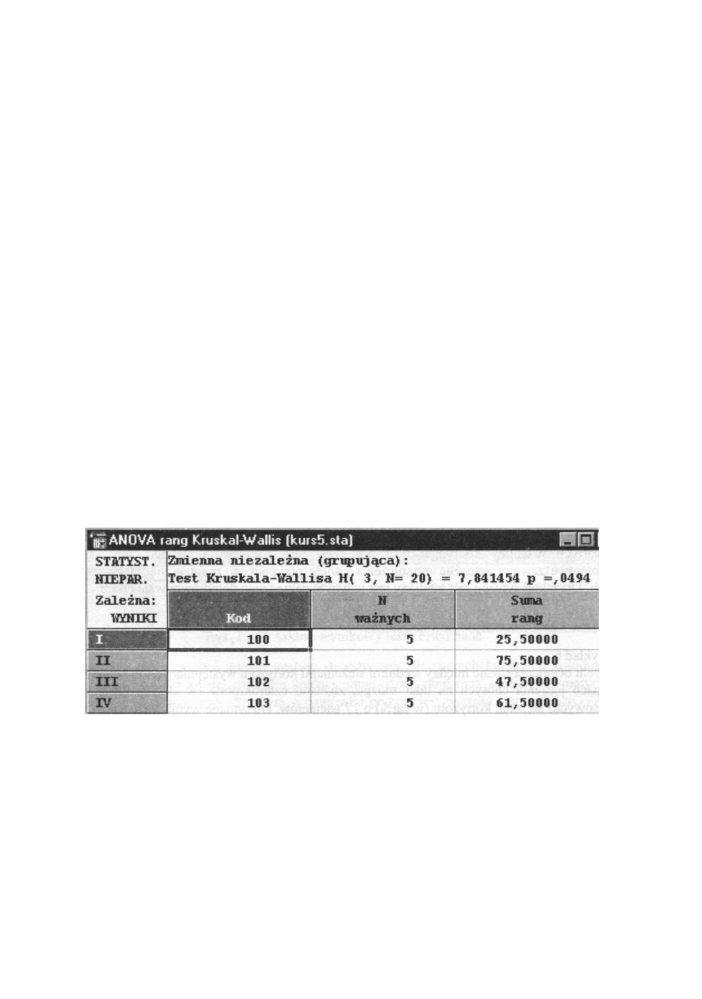
Rys. 13.15 Arkusz wyników testu Kruskala-Wallisa

Powyższe okno zawiera wyniki analizy statystycznej. W trzech kolejnych kolumnach
podane m a m y kod, liczbę przypadków oraz sumę rang. Powyżej w nagłówku podana jest
wartość testu Kruskala-Wallisa H= 7,841454 oraz poziom istotności p= 0,0494, który
pozwala na odrzucenie hipotezy wyjściowej (zerowej). Wyniki analizy pozwalają (na
poziomie istotności p = 0,049) wyciągnąć wniosek, że m e t o d y leczenia mają istotnie
statystyczny wpływ na wynik terapii.

279

Przystępny kurs statystyki

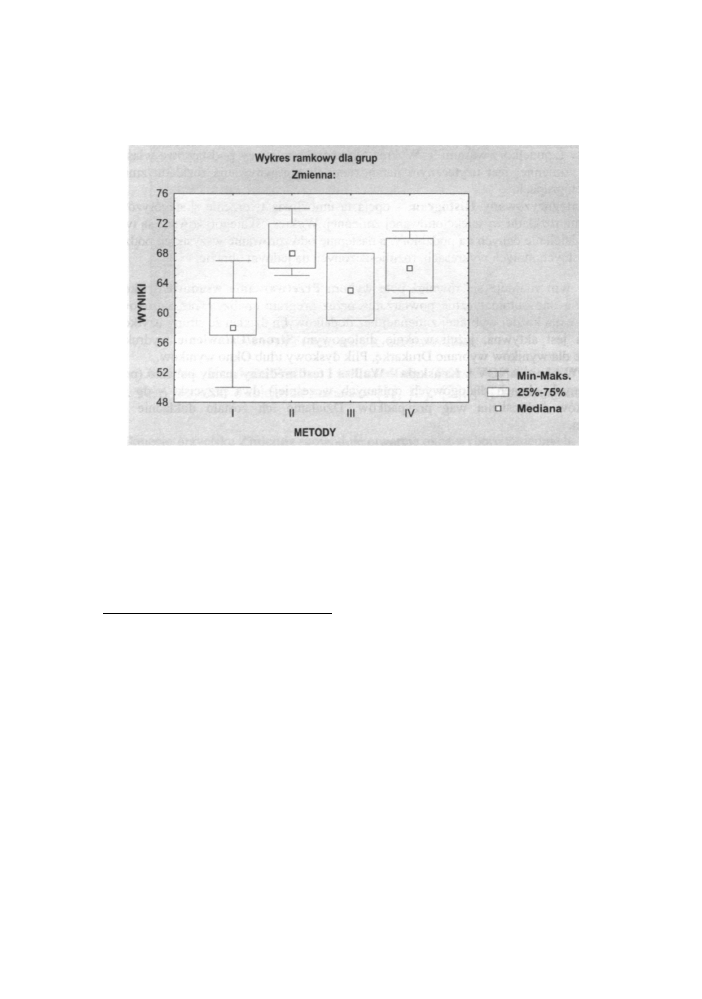
Dla interpretacji graficznej wykorzystamy przyciski Wykres r a m k o w y
i Skategoryzowany histogram w oknie A N O V A Kruskala-Wallisa i test mediany. Po
wybraniu rodzaju „pudelka" i wciśnięciu OK otworzy okno z poniższym rysunkiem.

Rys. 13.16 Wykres r a m k o w y dla danych z przykładu 5

W tym samym polu co test Kruskala-Wallisa, znajduje się jego mniej dokładna wersja, test
mediany. STATISTICA oblicza dla każdej z prób liczbę przypadków, które wypadają
powyżej lub poniżej mediany. Następnie wyliczana jest wartość statystyki dla wyników
zawartych w tablicy kontyngencji 2 x n. Test ten stosujemy w sytuacji, gdy skala
pomiarowa zawiera sztuczne ograniczenia i wiele przypadków znajdzie się na krańcach
skali. Dla takiej sytuacji test mediany jest j e d y n y m narzędziem do porównywania prób.

• Jako koleiny o m ó w i m y test Friedmana

Przykład 6
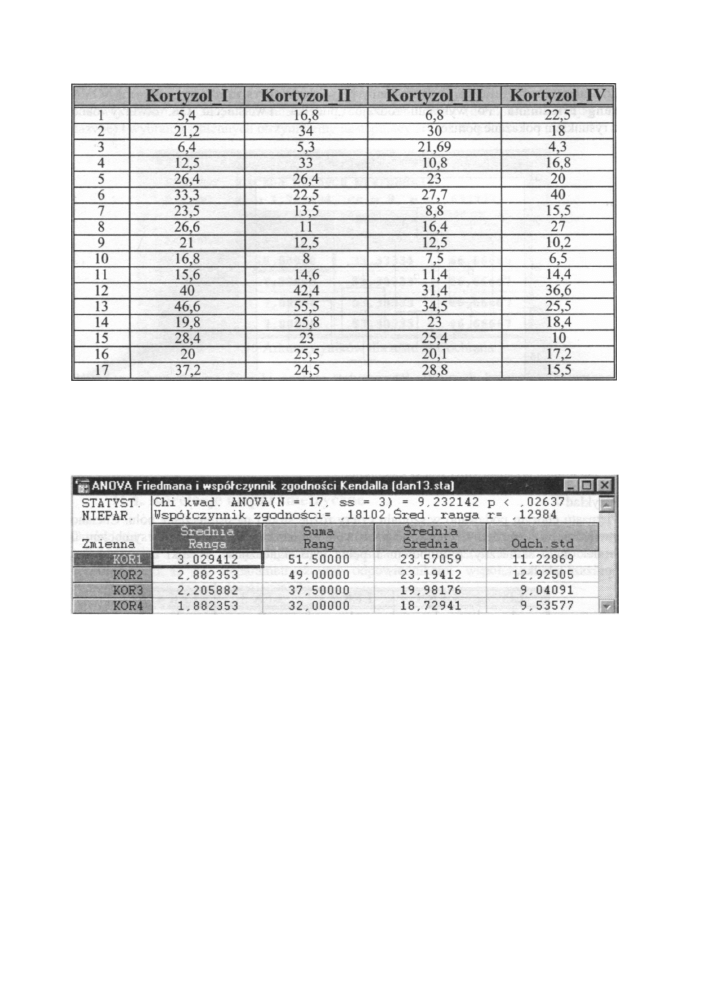
W celu ocenienia różnic między średnimi stężeniami kortyzolu występującymi w kolejnych
etapach leczenia chorych na udar mózgu, zbadano czterokrotnie (w stałych odstępach
czasowych) stężenie kortyzolu (w μg%) u 17 pacjentów. O t r z y m a n e wyniki przedstawione
są w poniższej tabeli. Czy między średnimi stężeniami kortyzolu występują istotne
różnice?

280

Testy nieparametryczne

Hipoteza zerowa, którą chcemy odrzucić, zakłada, że kolumny danych zawierają próby
pobrane z tej samej populacji. D a n e w p r o w a d z a m y kolumnami, tzn. wszystkie wyniki
kolejnych pomiarów zapisane są w nowej kolumnie (nowa zmienna). Po uruchomieniu
testu (dwukrotnie klikając na nazwie) i wybraniu zmiennych otrzymujemy okno dialogowe:

Rys. 13.17 Arkusz wynikowy testu Friedmana

Powyższe okno zawiera wyniki analizy statystycznej. W czterech kolejnych kolumnach
m a m y podane dla każdej zmiennej średnią rangę, s u m ę rang oraz średnią arytmetyczną
i odchylenie standardowe. Powyżej w nagłówku podana jest wartość testu χ

2

A N O V A =

9,232142 oraz p o z i o m

istotności p= 0,02637, który pozwala na odrzucenie hipotezy

wyjściowej (zerowej). Wyniki analizy pozwalają (na poziomie istotności p= 0,026)
wyciągnąć wniosek, że istnieje statystycznie istotna różnica między średnimi stężenia
kortyzolu w kolejnych etapach leczenia. W arkuszu w y n i k o w y m m a m y również obliczony
współczynnik zgodności Kendalla. Statystyka ta opisuje współzależność pomiędzy
n przypadkami skorelowanych prób. Wartość tę wykorzystujemy do oceny zgodności tzw.
niezależnych sędziów.

281

Przystępny kurs statystyki

Dla interpretacji graficznej wykorzystamy przyciski Wykres r a m k o w y w oknie A N O V A
rang Friedmana. Po wybraniu rodzaju „ p u d e ł k a " i wciśnięciu OK otworzy okno
z rysunkiem pokazane poniżej.

Rys. 13.18 Wykres r a m k o w y dla danych z przykładu 6

• Na koniec przedstawimy test Q Cochrana.

Przykład 7
Piętnastu chorym podawano w szpitalu cztery różne środki na uśmierzenie bólu. Chciano
stwierdzić, czy m o ż e m y je uważać za równie skuteczne. Pacjent oceniał symbolem 0
środek mało skuteczny, a symbolem 1 pełną jego skuteczność. Wyniki oceny zawiera
poniższa tabelka.

282

Testy nieparametryczne

Dane wprowadzamy kolumnami tzn. wszystkie wyniki kolejnych p o m i a r ó w zapisane są
w nowej kolumnie (nowa zmienna). Po uruchomieniu testu (dwukrotnie klikając na
nazwie) i wybraniu zmiennych otrzymujemy następujący arkusz wyników:

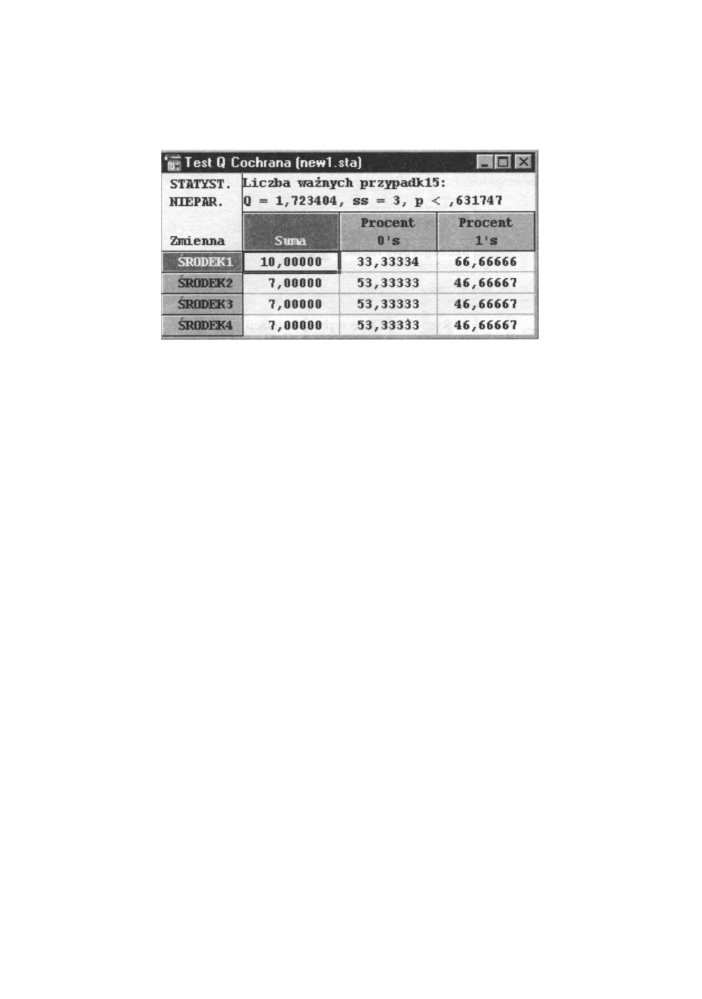
Rys. 13.19 Arkusz wyników dla testu Q Cochrana

Powyższe okno zawiera wyniki analizy statystycznej. W trzech kolejnych k o l u m n a c h
podane m a m y : sumę k o d ó w o wartości 1 procent osób oceniających lek negatywnie (kod 0)
oraz procent osób oceniający dany lek pozytywnie (kod 1). Powyżej w nagłówku p o d a n a

jest wartość Q = 1,723404 oraz poziom istotności p= 0,631747, który nie pozwala na

odrzucenie hipotezy wyjściowej (zerowej) o jednakowej wartości wszystkich leków.
Różnica między średnimi m o ż e wynikać z przyczyn losowych.

II4. Korelacje nieparametryczne

Omówienie testów zawartych w module Statystyki Nieparametryczne kontynuujemy
przedstawiając grupę współczynników opisujących nieparametryczne korelacje.
Współczynniki te są nieparametrycznymi odpowiednikami współczynnika korelacji
Pearsona. Należą do nich współczynniki:

• współczynnik R Spearmana
• Tau Kendalla
• G a m m a

Dla obliczenia tych współczynników dwukrotnie klikamy na opcji Korelacje (Spearmana,
tau Kendalla, g a m m a ) w oknie Statystyki nieparametryczne/Rozkłady
(Nonparametrics and Distribution). Otrzymujemy w ó w c z a s następujące okno dialogowe.

283

Przystępny kurs statystyki

Rys. 13.20 O k n o wyboru korelacji

Do dyspozycji m a m y opcje:

[1] - przycisk Zmienne powodujący otwarcie okna wyboru listy dwu zmiennych. O k n o to

umożliwia wybór zmiennych, a także oferuje rozmaite opcje przeglądania zawartości
zbioru danych (więcej informacji na ten temat znajduje się w rozdziale trzecim).

[2] - lista rozwijalna Korelacja umożliwia wybór współczynnika korelacji, który chcemy

policzyć. Do wyboru m a m y :

• współczynnik korelacji rang S p e a r m a n a - współczynnik ten został obszernie

omówiony na początku tego rozdziału

• współczynnik tau Kendalla (τ-Kendalla) - współczynnik ten opiera się na różnicy

między prawdopodobieństwem tego, że dwie zmienne układają się w tym s a m y m
porządku (dla obserwowanych danych) a prawdopodobieństwem, że ich
uporządkowanie się różni. Z a p r o p o n o w a n y przez Kendalla (1955 r.) wymaga, aby
wartości zmiennych m o ż n a było uporządkować (zmienne muszą być mierzone co
najmniej na skali porządkowej). Współczynnik ten przyjmuje wartości z przedziału <-l,

1>. Wartość 1 oznacza pełną zgodność, wartość 0 brak zgodności uporządkowań,

natomiast wartość -1 całkowitą ich przeciwstawność. Współczynnik Kendalla wskazuje
więc nie tylko siłę, lecz również kierunek zależności. Jest doskonałym narzędziem do
opisu podobieństwa uporządkowań zbioru danych. Dokładniejsze opisanie tego
współczynnika nastąpiło w rozdziale 12.

• statystyka g a m m a - współczynnik ten ma podobną konstrukcję i interpretację j a k

współczynnik R Spearmana lub Τ Kendalla. W y m a g a też p o d o b n y c h założeń. Stosuje
się go w przypadkach, gdy dane zawierają wiele obserwacji powiązanych
(reprezentujących ten sam wariant cechy).

[3] - lista rozwijalna Oblicz

następujące możliwości:

umożliwia wybór sposobu przeprowadzenia obliczeń. M a m y

284

Testy nieparametryczne

• szczegółowy raport - wybór tej opcji powoduje obliczenie nie tylko współczynników

korelacji, ale także dodatkowych informacji o liczbie poprawnych przypadków,
wartości statystyki t i poziomu istotności dla oceny istotności współczynnika korelacji;

• macierz dwóch list - wybranie tej opcji powoduje wyliczenie tylko w s p ó ł c z y n n i k ó w

korelacji pomiędzy wybranymi zmiennymi;

• macierz kwadratowa - wybranie tej opcji powoduje wyliczenie w s p ó ł c z y n n i k ó w

korelacji w postaci macierzy kwadratowej dla wszystkich par wybranych zmiennych.

[4] - przycisk Wykres macierzowy - przycisk ten umożliwia utworzenie m a c i e r z o w e g o

wykresu rozrzutu dla wszystkich wybranych zmiennych. Przykładowy macierzowy wykres
widoczny jest na poniższym rysunku.

Rys. 13.21 Macierzowy wykres rozrzutu

Przykładowe wyliczanie współczynników współzależności przeprowadzimy w oparciu
o dane z przykładu trzeciego. Po wprowadzeniu danych (każda z m i e n n a w osobnej
kolumnie) wybieramy do obliczeń współczynnik korelacji rang Spearmana (z listy
Korelacja). Kliknięcie OK uruchamia obliczenia.

Wyświetlone zostaje okno z wynikami pokazane na rysunku poniżej.

[1] [2] [3] [4] [5]

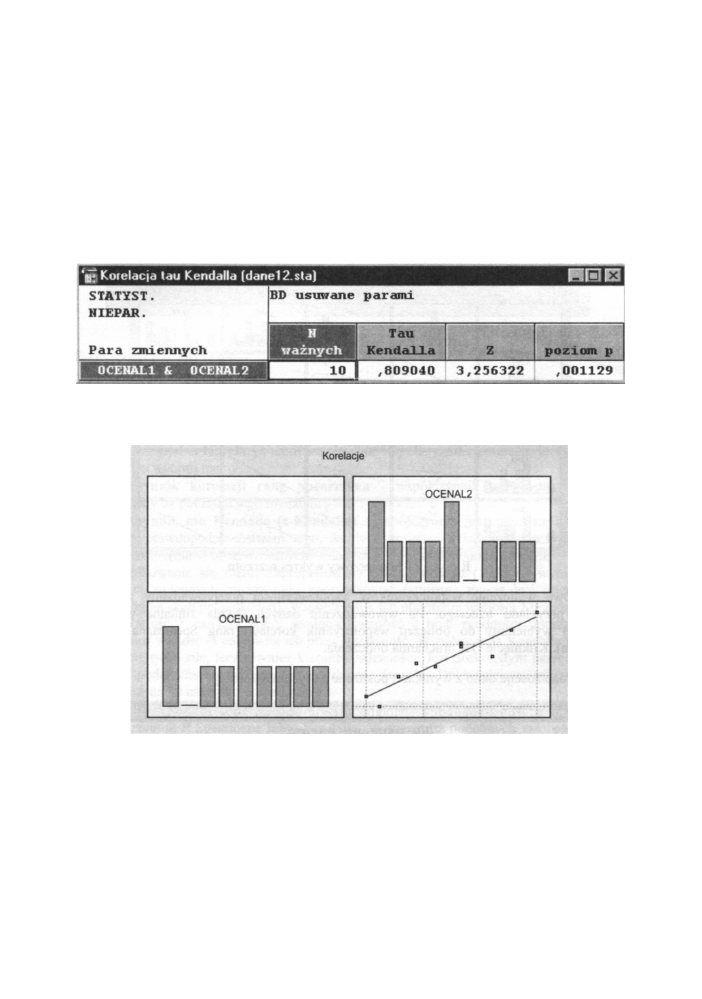
Rys. 13.22 Arkusz w y n i k ó w obliczania współczynnika Spearmana

285

Przystępny kurs statystyki

Poszczególne wartości oznaczają:

[1] - nazwy zmiennych
[2] - liczebność grup
[3] - wartość współczynnika R Spearmana
[4] - wartość statystyki t sprawdzaj istotność współczynnika R Spearmana
[5] - poziom istotności dla powyższej statystyki t

Uzyskany współczynnik R Spearmana R

s

= 0,936175 wskazuje na silną, istotną

współzależność opinii dwóch lekarzy o stanie zdrowia pacjenta. P o d o b n e wyniki
otrzymujemy, wyliczając współczynnik x Kendalla. Widoczne są one w poniższym oknie.

Rys. 13.23 Arkusz wyników obliczania współczynnika tau Kendalla

Nasze obliczenia m o ż e m y zilustrować na koniec wykresem macierzowym.

Rys. 13.24 Wykres macierzowy dla danych z przykładu 3

II. 5. Test χ

2

i miary na nim oparte

Opcja Tablice 2x2 , chi/V/Fi kwadrat, test McNemary,.. .

umożliwia obliczenie statystyki

χ

2

dla tablic 2x2 oraz innych statystyk

związanych z χ

2

(dokładny test Fishera, test

286

Testy nieparametryczne

M c N e m a r y itd.). Test χ

2

został przez nas dokładnie o m ó w i o n y w rozdziale 12.

Przypomnimy tylko najważniejsze fakty.

Dla tabel dwudzielczych 2x2 postaci wartość statystyki χ

2

w y z n a c z a m y

według prostszego,

praktycznego wzoru:

Zgryz prawidłowy Z g r y z nieprawidłowy R a z e m

Chłopcy

80

70

150

Dziewczynki

50

100

150

R a z e m

130

170

300

Stosujemy ją, jeżeli 20 < N < 4 0 i którakolwiek z liczebności oczekiwanych jest niniejsza
od 5. Dokładne omówienie wszystkich poprawek nastąpi poniżej przy omawianiu, jak
analizy tego typu obliczane są w pakiecie STATISTICA.

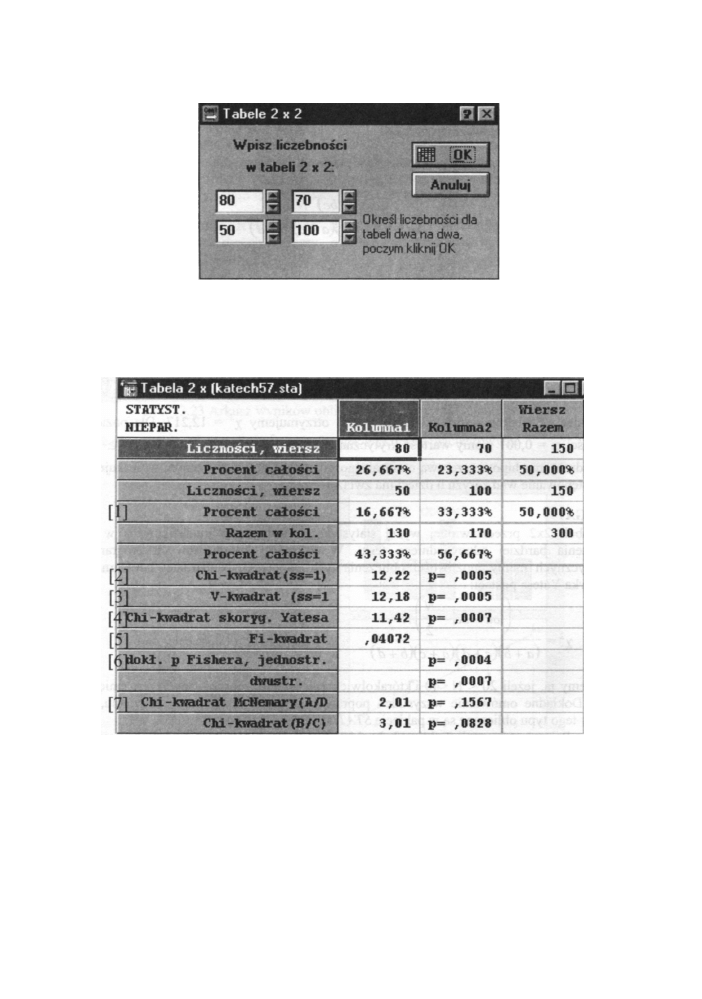
Po wybraniu opcji Tablice 2x2, chi/V/Fi kwadrat, test M c N e m a r y , otwiera się

okno do wprowadzania danych postaci:

287

Przykład 8 (Miller[40])
Zebrano dane na temat wad zgryzu u chłopców i dzieci Przebadano 300 losowo wybranych
dzieci w wieku przedszkolnym. Szczegółowe dane przedstawione są w poniższej tablicy.

gdzie N liczebność całej próby

Obliczając χ

2

według wzoru podanego wyżej otrzymujemy χ

2

= 12,217. D l a p o z i o m u

istotności α = 0,001 m a m y wartość krytyczną równą

2

= 10,827. Ponieważ χ

2

>=

2

więc odrzucamy hipotezę zerową o niezależności zmiennych, a tym s a m y m wnioskujemy,
że występowanie wad zgryzu u dzieci ma związek z płcią.

U W A G A !
Dla tabeli 2x2 przedstawionej wyżej statystyka χ

2

j e s t

często modyfikowana w celu

utworzenia bardziej odpowiedniego testu. W większości k o m p u t e r o w y c h p r o g r a m ó w
statystycznych m a m y możliwości obliczenia tych poprawek. Najbardziej popularna to
poprawka Yatesa postaci:

Przystępny kurs statystyki

Rys. 13.25 O k n o wprowadzania danych dla testu %

Po wprowadzeniu danych (przy p o m o c y klawisza T A B ) j a k na p o w y ż s z y m rysunku,
klikamy OK, uruchamiając proces obliczania statystyki. O t r z y m a m y w ó w c z a s następujące
okno z wynikami:

Rys. 13.26 Arkusz w y n i k o w y dla testu χ

2

Poszczególne pola zaznaczone w oknie z wynikami zawierają:

[1] - powtórzona tabela z d a n y m i wraz z s u m a m i brzegowymi oraz procenty wszystkich

wartości wyliczane w stosunku do całkowitej liczebności grupy.

[2] - wartość testu χ

2

w r a z z p o z i o m e m

istotności.

[3] - wartość testu V-kwadrat wraz z p o z i o m e m istotności

288

Testy nieparametryczne

[4] - χ

2

z

poprawką Yatesa - Jest to poprawka statystyki χ

2

dla

małych tabel o rozmiarach

2x2, wraz z podanym obok p o z i o m e m istotności. Poprawka ta stosowana jest, jeżeli
liczebności w tabeli są m a ł e tak, że w ó w c z a s liczebności oczekiwane są mniejsze od
5. Poprawka ta została dokładniej o m ó w i o n a na początku tego rozdziału.

[5] - Współczynnik Φ-Yula postaci Φ

2

= χ

2

/N

Współczynnik ten jest miarą korelacji pomiędzy dwiema zmiennymi jakościowymi
w tabeli 2x2. Przyjmuje on wartości od 0 (brak powiązania między zmiennymi) do 1
(całkowite powiązanie pomiędzy zmiennymi).

[6] - dokładny test Fishera - ten test jest obliczany tylko dla tabel 2x2. Oblicza on przy

założeniu hipotezy zerowej dokładne prawdopodobieństwo otrzymania tabeli
o liczebnościach obserwowanych. Podawane jest zarówno prawdopodobieństwo

jedno, jak i dwustronne. Dokładny test Fishera stosujemy, jeżeli całkowita liczebność

obserwacji jest mała lub jeśli bardzo małe są liczebności oczekiwane.

[7] - wartości testów M c N e m a r y (A/D) i (B/C) wraz z p o z i o m e m istotności. Dokładne

omówienie tego testu nastąpiło w rozdziale 12.

Aby nie zgubić się w gąszczu tych poprawek, p o d a m y w s k a z ó w k ę - kiedy i jaką poprawkę
zastosować.

Liczebności Rodzaj testu

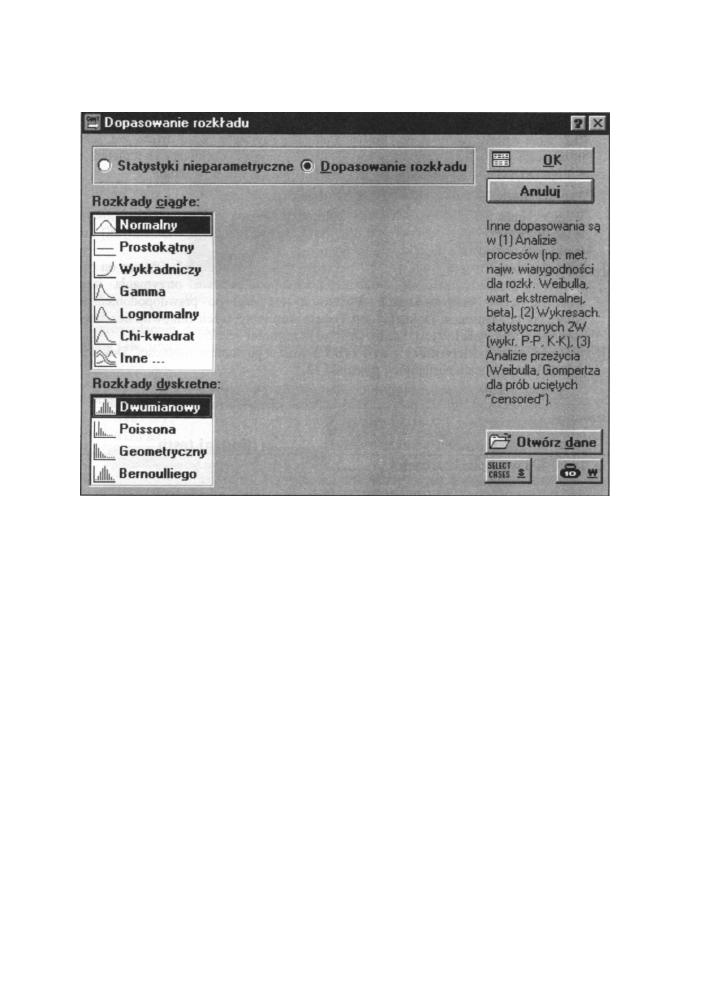
III. Dopasowanie rozkładu

Na samej górze okna Statystyki Nieparametryczne m a m y opcje umożliwiające przejście
do okna dialogowego, realizującego testowanie zgodności rozkładu danych z dowolnie
wybranym rozkładem hipotetycznym. Po jej wybraniu, okno dialogowe zmienia się,
przyjmując postać:

289

Przystępny kurs statystyki

Rys. 13.27 O k n o startowe dopasowywania rozkładów

W

oknie tym istnieje możliwość testowania zgodności rozkładu danych użytkownika

z dowolnym rozkładem.

Do dyspozycji m a m y d w a testy zgodności: test zgodności χ

2

i test

zgodności

Kołmogorowa-Smirnowa. Test zgodności χ

2

m o ż e być użyty tylko wtedy, gdy wszystkie

częstości oczekiwane są zawsze większe niż 5. Jest więc bezużyteczny w stosunku do
próbek o małej liczebności (n<30). W takim w y p a d k u należy zastosować test
Kołmogorowa-Smirnowa. Po wybraniu zmiennej, użytkownik m o ż e d o k o n y w a ć

przełączania dopasowania różnych rozkładów (tego s a m e g o typu, tzn. ciągłych lub
dyskretnych) w oknie opcji Rozkład. Po określeniu zmiennej, obliczane są parametry
dające najlepsze dopasowanie dla każdego z odpowiednich typów rozkładu. Parametry te
są wyświetlane j a k o wartości domyślne. Użytkownik ma także możliwość wprowadzania
własnych wartości.

Najczęstszym zastosowaniem procedur dopasowania jest weryfikacja założenia
o normalności rozkładu. Taki też przykład przeanalizujemy.

290

Testy nieparametryczne

Przykład 9
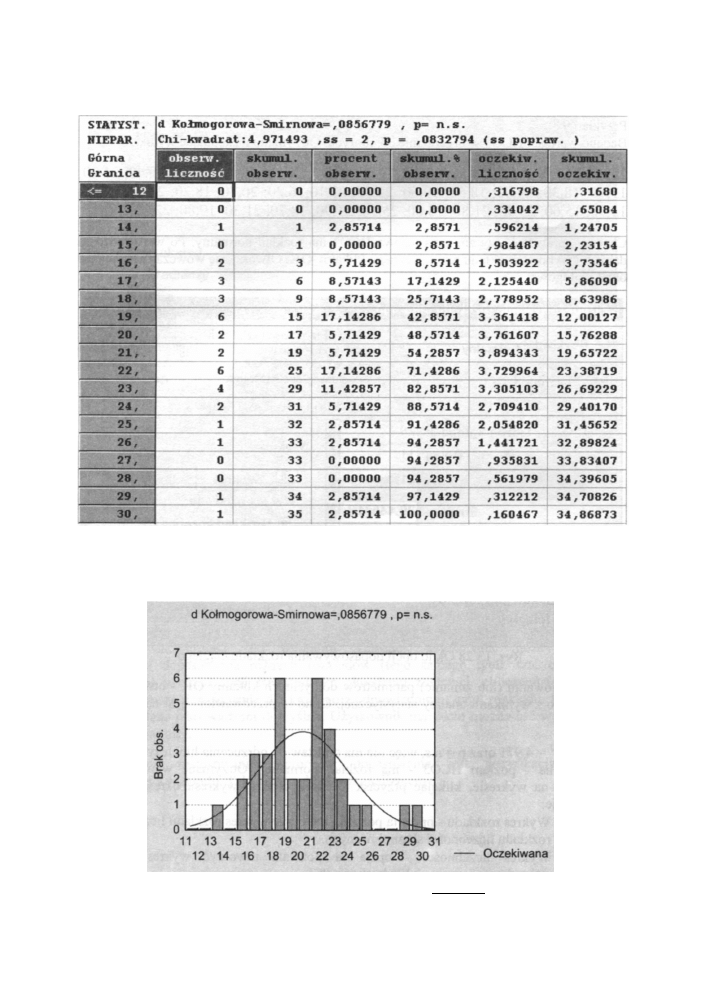
Badano wartości H C 0 3 w organizmie 35 chorych. O t r z y m a n o następujące wyniki:

19,30; 21,60; 16,50; 28,50; 22,80; 13,40; 24,90; 20,20; 18,00; 18,30; 29,40; 21,20;
17,70; 18,30; 24,00; 18,50; 19,60; 21,80; 22,10;16,20; 20,70; 18,20; 23,00; 18,50;
15,90; 15,60; 23,90; 21,80; 18,00; 25,90; 21,90; 18,70; 21,30; 19,80; 22,80.

Chcemy sprawdzić, czy zmienna losowa H C 0 3 ma rozkład normalny. Po wprowadzeniu
danych i wyborze rozkładu hipotetycznego klikamy OK. Otworzy się w ó w c z a s następujące
okno dialogowe:

Rys. 13.28 O k n o opcji dopasowywania rozkładu ciągłego

Po zaakceptowaniu (lub zmianie) parametrów domyślnych klikamy OK - otwierając tym
samym okno z wynikami analizy statystycznej. O k n o to przedstawione jest na poniższym
rysunku.

Ponieważ χ

2

= 4,971 o r a z p = n.s.

więc nie ma podstaw do odrzucenia hipotezy zerowej, że

badana cecha - p o z i o m H C 0 3 - ma rozkład normalny. Otrzymane wynik m o ż e m y
zilustrować na wykresie, klikając przycisk Wykres. Rodzaj wykresu określają poniżej
podane opcje:

• Wykres rozkładu - opcja ta pozwala utworzyć wykres rozkładu liczebności lub

rozkładu liczebności skumulowanych.

• Wykres liczebności - opcja ta pozwala utworzyć wykres w oparciu

o liczebności surowe lub odsetkowe (%)

291

Przystępny kurs statystyki

Rys 13.29 Arkusz wynikowy dopasowywania rozkładów

Poniższy wykres (utworzony przy wyborze opcji Rozkład liczebności) graficznie
interpretuje uzyskane wyniki.

d Kołmogorowa-Smirnowa=,0856779 , p= n.s.

11 13 15 17 19 21 23 25 27 29 31

12 14 16 18 20 22 24 26 28 30 Oczekiwana

Rys. 13.30 Wykres histogram dla danych z przykładu 9

292