Testy

Testy

nieparametryczne

nieparametryczne

Testy nieparametryczne

losowości

zgodności

jednorodności

Testy losowości

Testy losowości

►

Weryfikują hipotezę, że dobór

Weryfikują hipotezę, że dobór

jednostek do próby był jednakowy

jednostek do próby był jednakowy

Test serii Stevensa

Test serii Stevensa

1. Ho: Dobór jednostek do próby jest losowy

1. Ho: Dobór jednostek do próby jest losowy

H1:Dobór jednostek do próby nie jest losowy

H1:Dobór jednostek do próby nie jest losowy

2. Procedura testowa:

2. Procedura testowa:

2a. Wyznaczamy na podstawie uporządkowanych

2a. Wyznaczamy na podstawie uporządkowanych

danych medianę

danych medianę

2b. Danym nieuporządkowanym przyporządkowujemy

2b. Danym nieuporządkowanym przyporządkowujemy

następujące oznaczenia:

następujące oznaczenia:

A gdy x<Me

A gdy x<Me

B gdy x>Me

B gdy x>Me

0 gdy x=Me (zera pomijamy w dalszej analizie)

0 gdy x=Me (zera pomijamy w dalszej analizie)

Statystyką testową jest liczba serii (k)

Statystyką testową jest liczba serii (k)

►

Seria – ciąg identycznych symboli (A

Seria – ciąg identycznych symboli (A

lub B)

lub B)

np.

np.

AAAA

AAAA

B

B

A

A

BB

BB

k=4

k=4

AAA 0 A

AAA 0 A

BBB

BBB

0

0

AA

AA

k=3

k=3

3. Ustalamy poziom istotności

3. Ustalamy poziom istotności

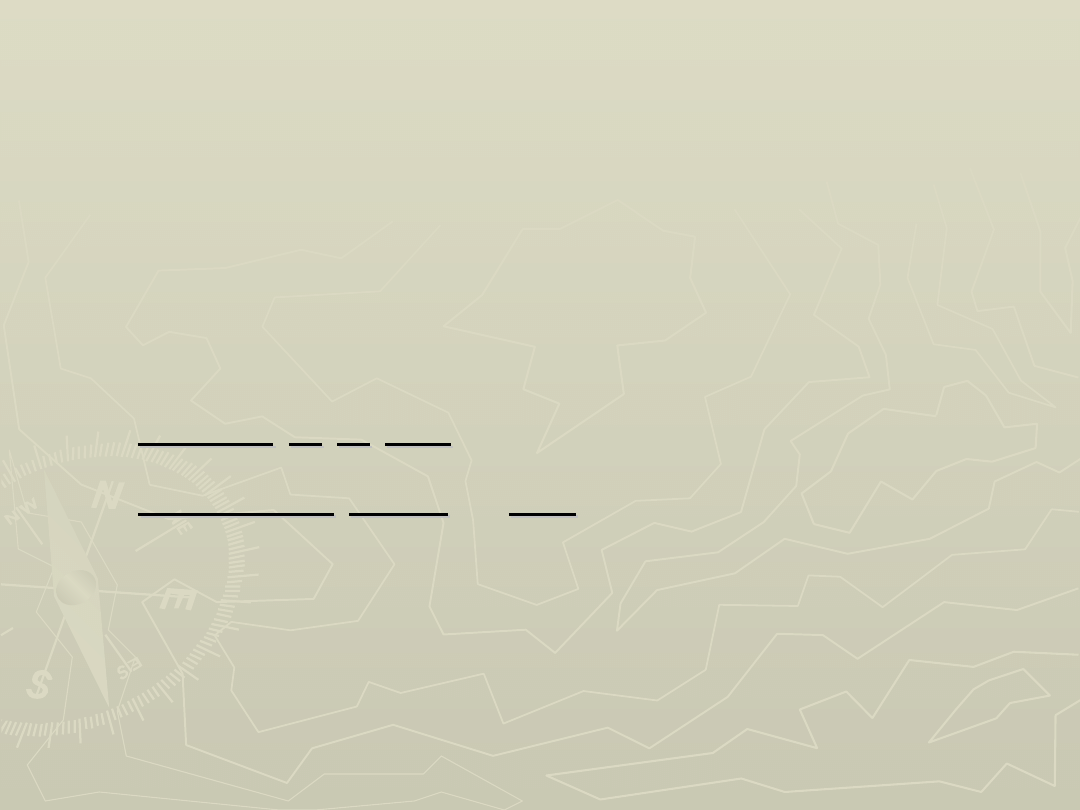
4. Obszar krytyczny testu jest zawsze dwustronny.

4. Obszar krytyczny testu jest zawsze dwustronny.

Odczytujemy z rozkładu liczby serii wartości

Odczytujemy z rozkładu liczby serii wartości

krytyczne

krytyczne

5. Podejmujemy decyzję

5. Podejmujemy decyzję

)

;

;

2

1

(

)

;

;

2

(

2

1

B

A

B

A

n

n

k

n

n

k







Przykład 1:

Przykład 1:

Wylosowano 12 spółek i zbadano cenę ich

Wylosowano 12 spółek i zbadano cenę ich

akcji (w zł). Otrzymano następujące

akcji (w zł). Otrzymano następujące

wyniki:

wyniki:

74,5 191,0 55,5 5,15 36,4 35,0 46,0

74,5 191,0 55,5 5,15 36,4 35,0 46,0

10,9 7,35 6,65 173,5 26,0.

10,9 7,35 6,65 173,5 26,0.

Czy dobór spółek do próby był losowy?

Czy dobór spółek do próby był losowy?

Wysuniętą hipotezę zweryfikuj na poziomie

Wysuniętą hipotezę zweryfikuj na poziomie

istotności 0,05.

istotności 0,05.

Rozwiązanie:

Rozwiązanie:

Ho: dobór jednostek do próby jest losowy

Ho: dobór jednostek do próby jest losowy

H1:Dobór jednostek do próby nie jest losowy

H1:Dobór jednostek do próby nie jest losowy

Wyznaczamy medianę:

Wyznaczamy medianę:

Poz. Me=(n+1)/2=6,5

Poz. Me=(n+1)/2=6,5

Me=35,7

Me=35,7

Danym pierwotnym przypisujemy litery A, B, 0

Danym pierwotnym przypisujemy litery A, B, 0

kolejnym obserwacjom

kolejnym obserwacjom

5,15

6,65

7,35

10,9

26

35

36,4

46

55,5

74,5

173,5

191

74,5

191

55,5

5,15

36,4

35

46

10,9

7,35

6,65

173,5

26

B

B

B

A

B

A

B

A

A

A

B

A

►

Obliczamy liczbę serii:

Obliczamy liczbę serii:

►

k=8

k=8

►

Poziom istotności 0,05

Poziom istotności 0,05

►

Odczytujemy wartości krytyczne:

Odczytujemy wartości krytyczne:

10

)

6

;

6

;

975

,

0

2

1

(

3

)

6

;

6

;

025

,

0

2

(

2

1



















B

A

B

A

n

n

k

n

n

k





►

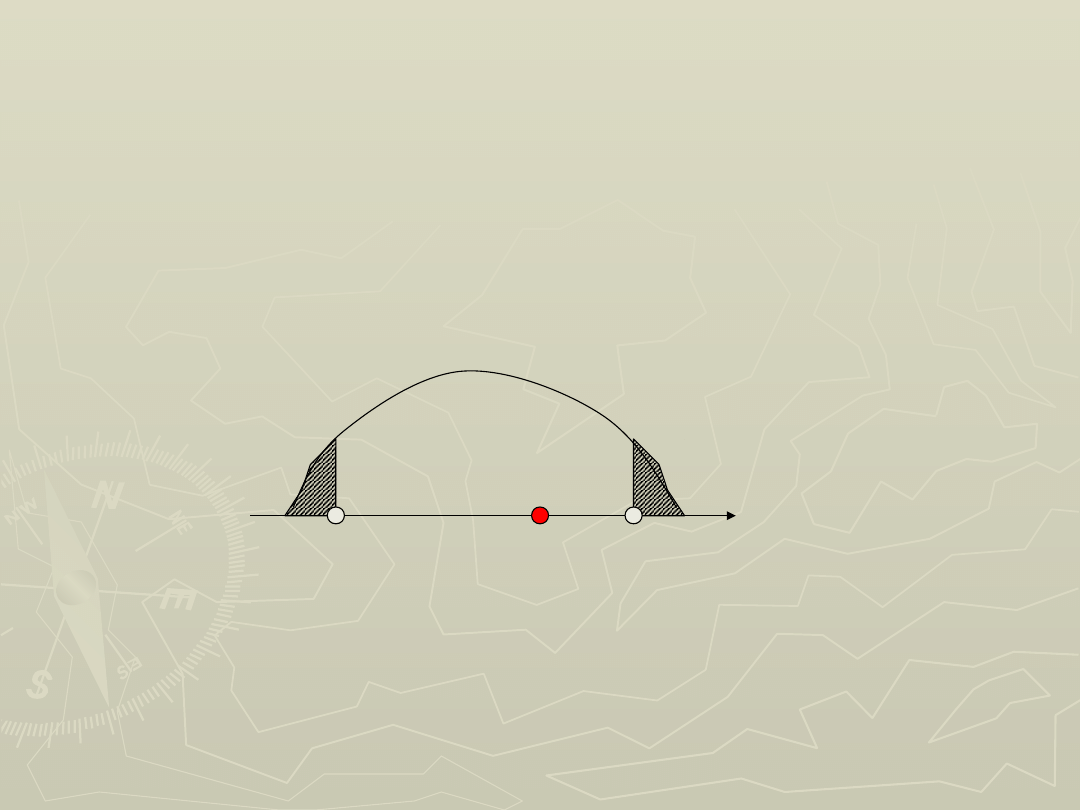
Porównujemy wartość statystyki z próby z

Porównujemy wartość statystyki z próby z

wartościami krytycznymi:

wartościami krytycznymi:

►

Brak podstaw do odrzucenia hipotezy

Brak podstaw do odrzucenia hipotezy

zerowej, która mówi, że dobór jednostek do

zerowej, która mówi, że dobór jednostek do

próby był losowy.

próby był losowy.

3

10

8

Testy zgodności:

Testy zgodności:

►

Weryfikują hipotezę o zgodności rozkładu

Weryfikują hipotezę o zgodności rozkładu

empirycznego (rozkładu z próby losowej) z

empirycznego (rozkładu z próby losowej) z

rozkładem teoretycznym (np. normalnym,

rozkładem teoretycznym (np. normalnym,

dwumianowym itp.) lub inaczej ujmując –

dwumianowym itp.) lub inaczej ujmując –

dotyczą postaci rozkładu badanej cechy w

dotyczą postaci rozkładu badanej cechy w

populacji.

populacji.

)

(

)

(

:

)

(

)

(

:

0

1

0

0

x

F

x

F

H

x

F

x

F

H





Testy zgodności

Testy zgodności

(normalności)

(normalności)

1.

1.

Test Kołmogorowa- Smirnowa (D)

Test Kołmogorowa- Smirnowa (D)

(próby małe n<100, zmienna ciągła)

(próby małe n<100, zmienna ciągła)

2.

2.

Test

Test





- Kołmogorowa

- Kołmogorowa

(próby duże n

(próby duże n





100, zmienna ciągła)

100, zmienna ciągła)

3.

3.

Test

Test





2

2

(wszystkie zmienne, szeregi rozdzielcze o dużych

(wszystkie zmienne, szeregi rozdzielcze o dużych

liczebnościach w przedziałach , próby

liczebnościach w przedziałach , próby

duże)

duże)

8



i

n

Etapy testów zgodności

Etapy testów zgodności

(aproksymacja rozkładu

(aproksymacja rozkładu

normalnego):

normalnego):

1. Ustalamy parametry rozkładu normalnego

1. Ustalamy parametry rozkładu normalnego

2. Standaryzujemy prawe (górne) granice

2. Standaryzujemy prawe (górne) granice

przedziałów (poza ostatnim)

przedziałów (poza ostatnim)

3. Odczytujemy wartości dystrybuant z tablicy

3. Odczytujemy wartości dystrybuant z tablicy

rozkładu normalnego (jako ostatnią dystrybuantę

rozkładu normalnego (jako ostatnią dystrybuantę

przyjmujemy wartość 1)

przyjmujemy wartość 1)

4a. Z dystrybuant obliczamy skumulowane wartości

4a. Z dystrybuant obliczamy skumulowane wartości

teoretyczne (test Chi-kwadrat)

teoretyczne (test Chi-kwadrat)

lub

lub

4b. Obliczamy dystrybuanty empiryczne (test

4b. Obliczamy dystrybuanty empiryczne (test

Kołmogorowa)

Kołmogorowa)

n

z

F

n

i

isk





)

(

ˆ

n

n

z

F

isk

i



)

(

Etapy testów zgodności (c.d.):

Etapy testów zgodności (c.d.):

5. Obliczamy wartość statystyki testowej

5. Obliczamy wartość statystyki testowej

6 a. Odczytujemy wartość krytyczną z

6 a. Odczytujemy wartość krytyczną z

tablic

tablic

Lub

Lub

6 b. Obliczamy prawdopodobieństwo testu

6 b. Obliczamy prawdopodobieństwo testu

7. Podejmujemy decyzję

7. Podejmujemy decyzję

Przykład 1:

Przykład 1:

)

(

)

(

0

x

F

x

F



)

(

)

(

:

)

(

)

(

:

0

1

0

0

x

F

x

F

H

x

F

x

F

H





Wiek w

latach

Liczba

osób

Z

F(Z)

nisk

F(X)

 

15-25

2

-1,38

0,0833

2

0,1176 0,0343

25-35

3

-0,46

0,3224

5

0,2941 0,0283

35-45

6

0,46

0,6776

11

0,6471 0,0305

45-55

5

1,38

0,9167

16

0,9412 0,0245

55-65

1

x

1

17

1,0000 0,0000

 Suma

17

x

x

x

x

 

lat

x 40



lat

s

85

,

10



s

x

x

z

i

i





1

0343

,

0

)

(

)

(

max

0







x

F

x

F

D

05

,

0





206

,

0

)

17

,

05

,

0

(







n

D





0,206

0,0343

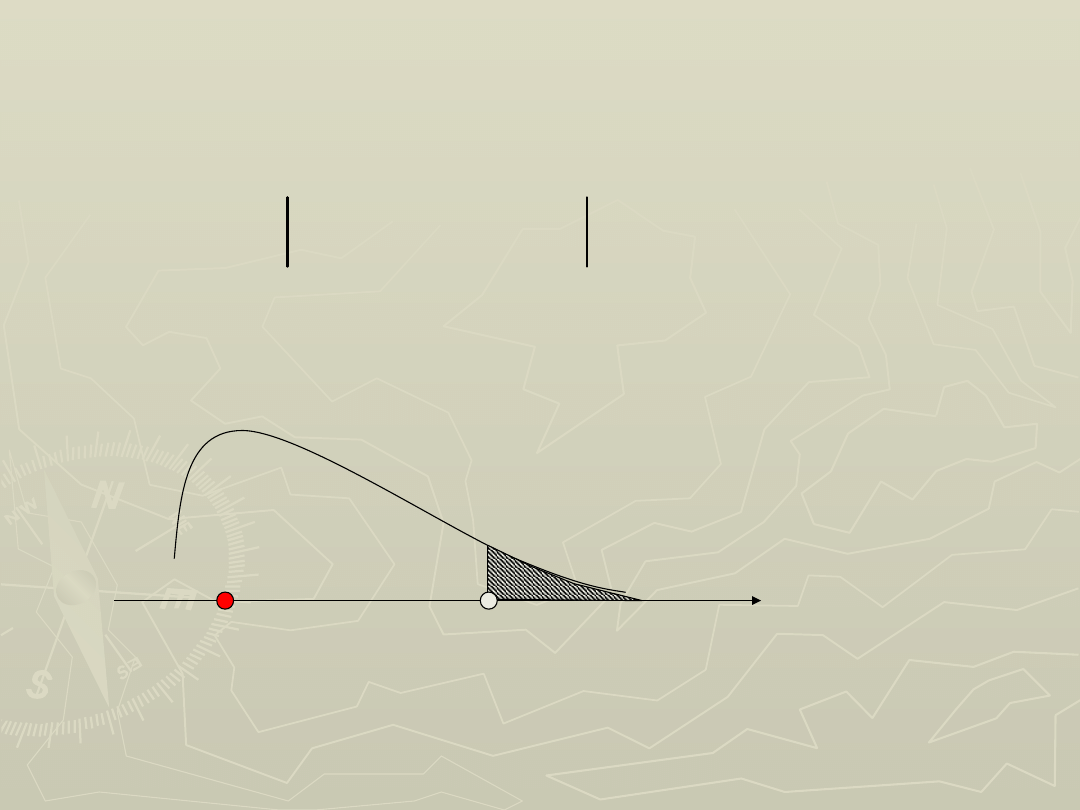
Brak podstaw do odrzucenia hipotezy zerowej o zgodności
rozkładu wieku inwestorów z rozkładem normalnym.

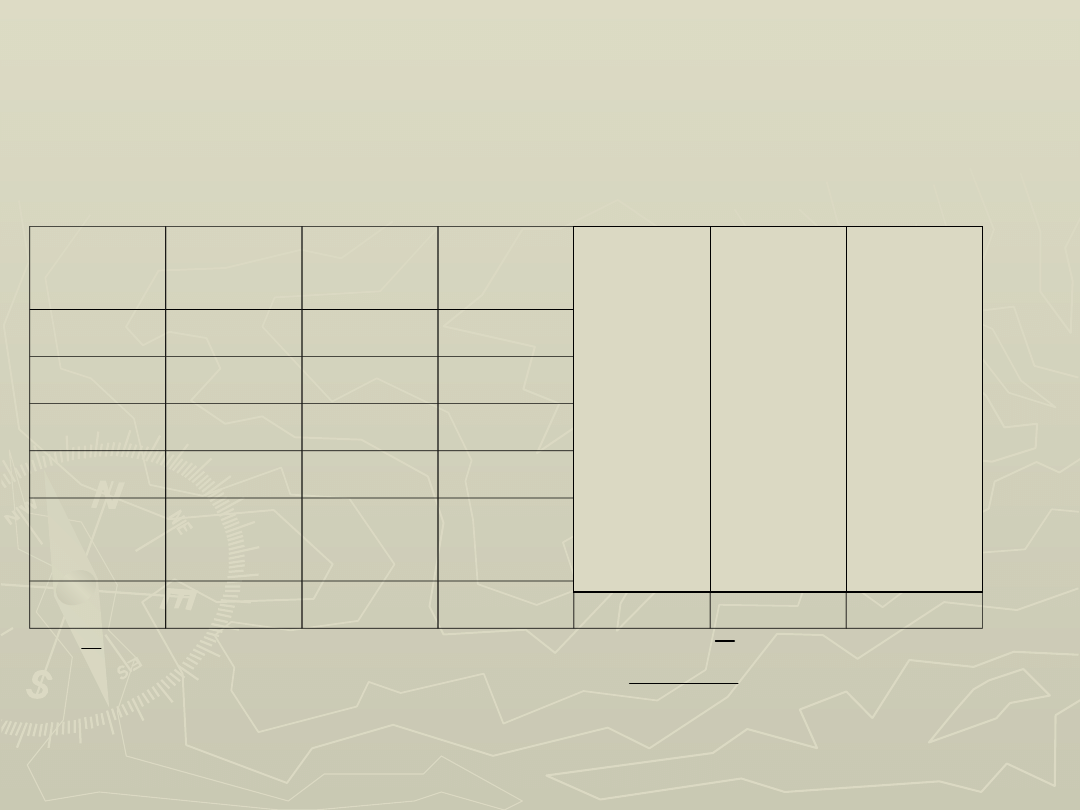
Przykład 2:

Przykład 2:

I sposób (test

I sposób (test





- Kołmogorowa)

- Kołmogorowa)

)

(

)

(

0

x

F

x

F



)

(

)

(

:

)

(

)

(

:

0

1

0

0

x

F

x

F

H

x

F

x

F

H





Wiek w

latach

Liczba

osób

Z

F(Z)

nisk

F(X)

 

15-25

20

-1,38

0,0833

20

0,1176 0,0343

25-35

30

-0,46

0,3224

50

0,2941 0,0283

35-45

60

0,46

0,6776

110

0,6471 0,0305

45-55

50

1,38

0,9167

160

0,9412 0,0245

55 i

więcej

10

x

1

170

1,0000 0,0000

 Suma

170

x

x

x

x

 

lat

x 40



lat

s

85

,

10



s

x

x

z

i

i





1

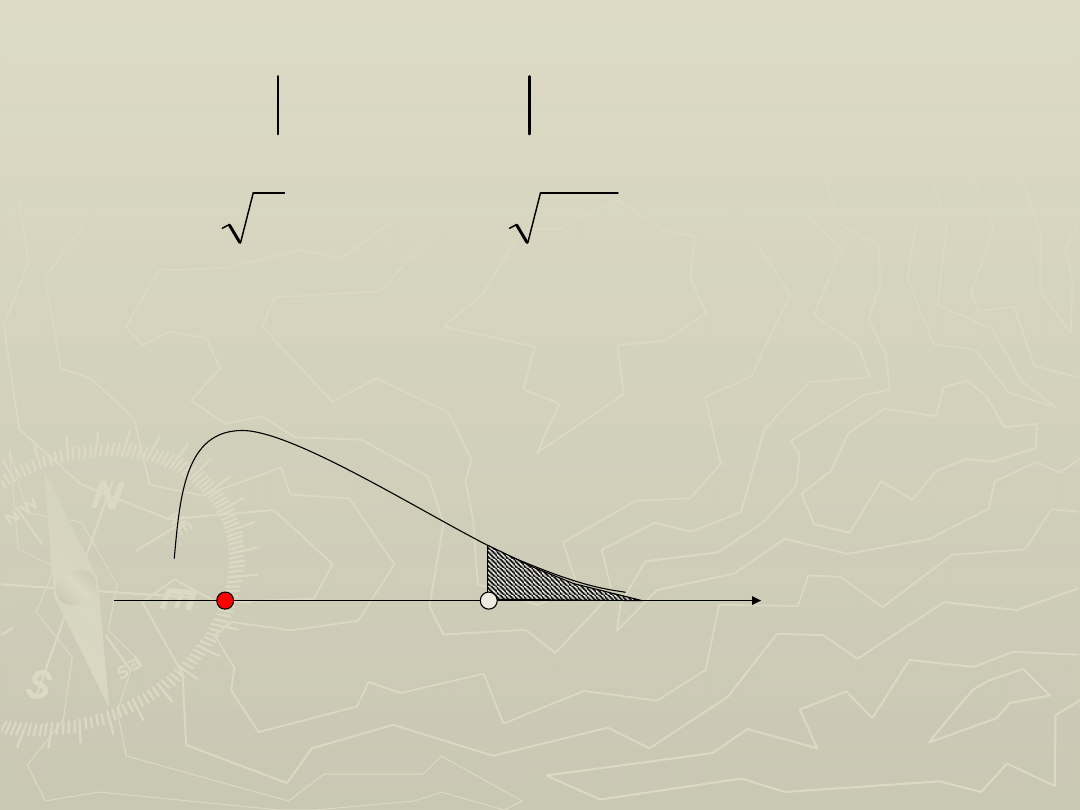
0343

,

0

)

(

)

(

max

0







x

F

x

F

D

05

,

0





36

,

1







1,36

0,447

Brak podstaw do odrzucenia hipotezy zerowej o zgodności
rozkładu wieku inwestorów z rozkładem normalnym.

447

,

0

170

0343

,

0









n

D



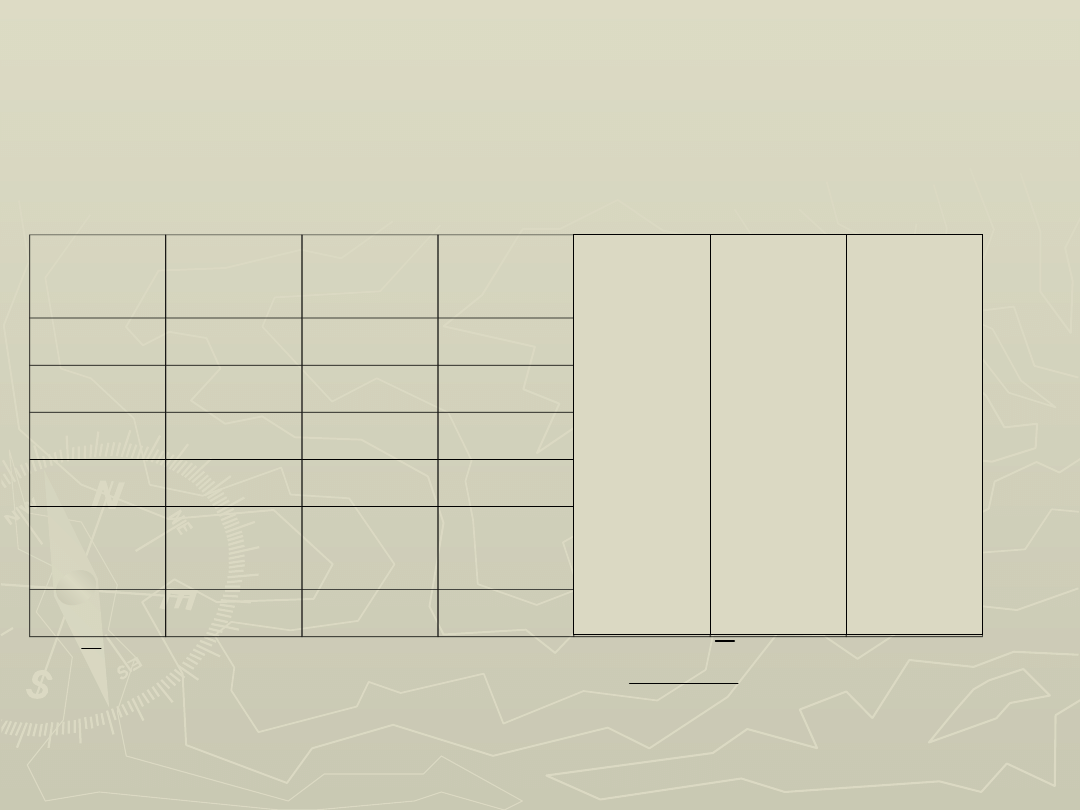
Przykład 2:

Przykład 2:

II sposób (test Chi - kwadrat)

II sposób (test Chi - kwadrat)

isk

nˆ

i

i

n

n

ˆ

2

i

nˆ

)

(

)

(

:

)

(

)

(

:

0

1

0

0

x

F

x

F

H

x

F

x

F

H





Wiek w

latach

Liczba

osób

Z

F(Z)

 

15-25

20

-1,38

0,0833

14,16

14,16

28,25

25-35

30

-0,46

0,3224

54,81

40,65

22,14

35-45

60

0,46

0,6776 115,19

60,38

59,62

45-55

50

1,38

0,9167 155,84

40,65

61,50

55 i

więcej

10

x

1

170

14,16

7,06

 Suma

170

x

x

x

170

178,57 

lat

x 40



lat

s

85

,

10



s

x

x

z

i

i





1

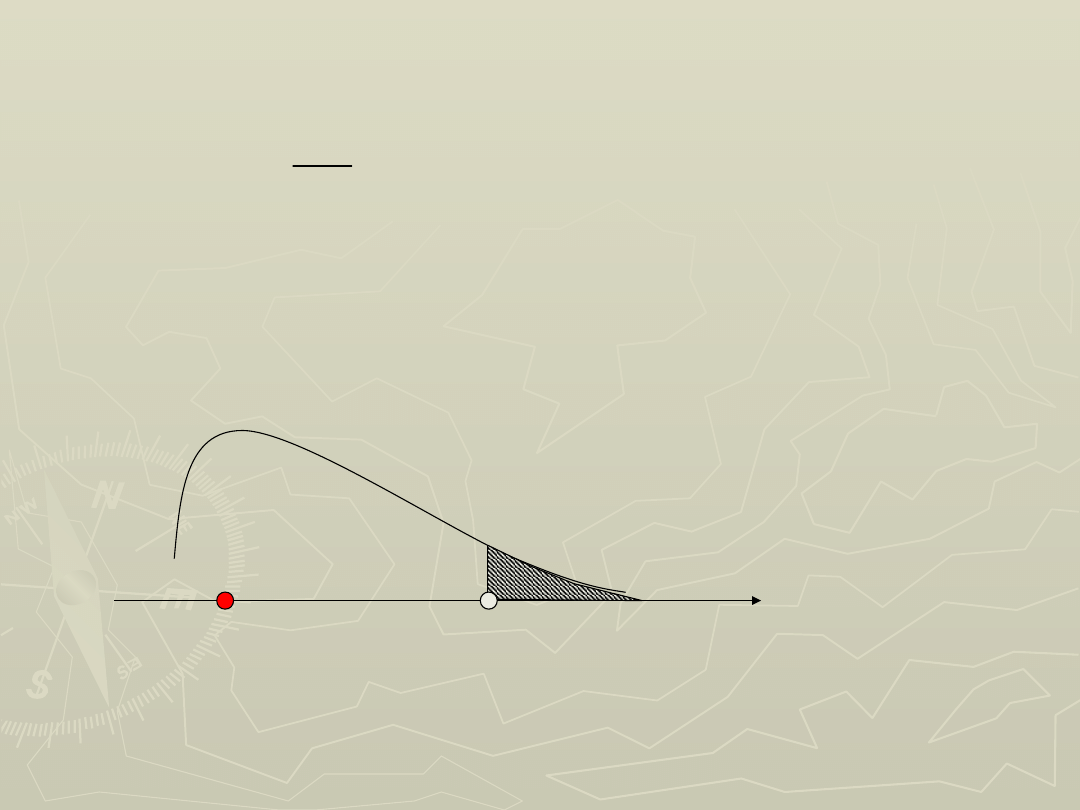
57

,

8

170

57

,

178

ˆ

1

2

2













n

i

i

i

n

n



05

,

0





)

1

,

(

2







r

k

v







1,36

8,57

Brak podstaw do odrzucenia hipotezy zerowej o zgodności
rozkładu wieku inwestorów z rozkładem normalnym.

Testy jednorodności

Testy jednorodności

►

Weryfikują hipotezę o zgodności dwóch

Weryfikują hipotezę o zgodności dwóch

rozkładów empirycznych ze sobą (oba

rozkładów empirycznych ze sobą (oba

rozkłady pochodzą z tej samej populacji)

rozkłady pochodzą z tej samej populacji)

)

(

)

(

:

)

(

)

(

:

2

1

1

2

1

0

x

F

x

F

H

x

F

x

F

H





Testy jednorodności

Testy jednorodności

►

Test serii Walda – Wolfowitza

Test serii Walda – Wolfowitza

(próby niezależne, małe, dane szczegółowe)

(próby niezależne, małe, dane szczegółowe)

►

Test

Test





2

2

(Snedeckora)

(Snedeckora)

(próby niezależne, duże, szeregi rozdzielcze o

(próby niezależne, duże, szeregi rozdzielcze o

licznych przedziałach , wszystkie rodzaje

licznych przedziałach , wszystkie rodzaje

cech)

cech)

►

Test Kołmogorowa - Smirnowa (

Test Kołmogorowa - Smirnowa (





)

)

(próby niezależne, duże, tylko cechy ilościowe

(próby niezależne, duże, tylko cechy ilościowe

ciągłe)

ciągłe)

►

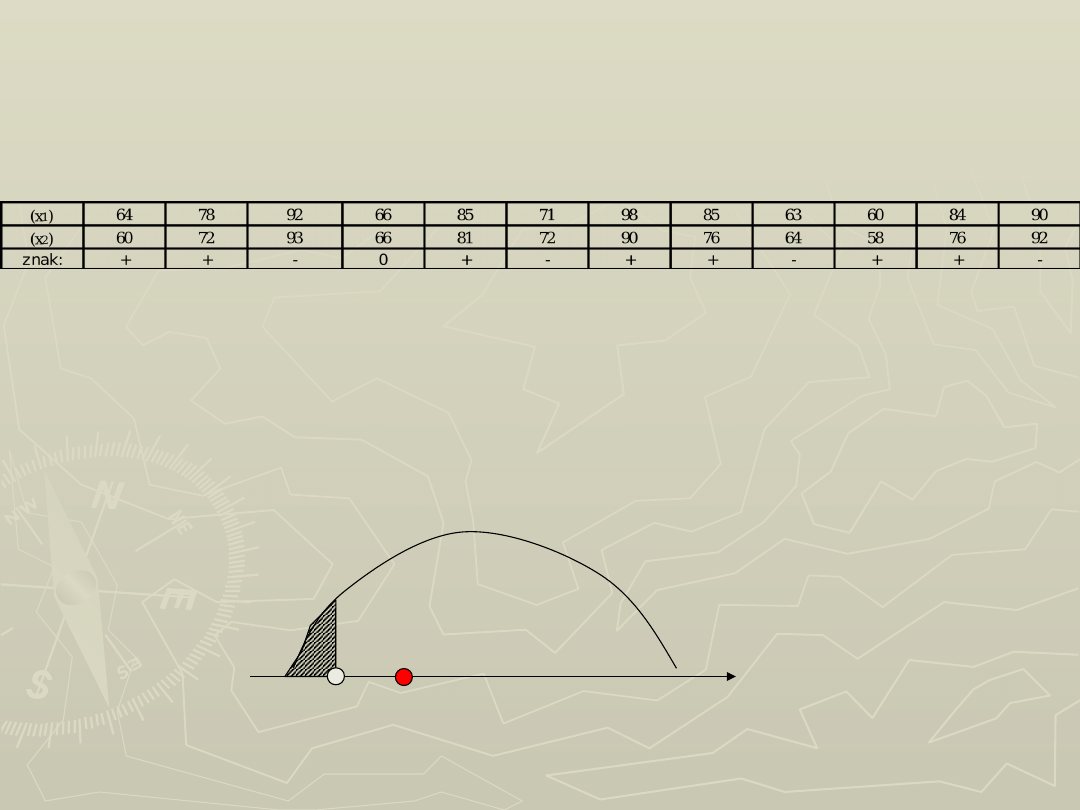
Test znaków (Dixona - Mooda)

Test znaków (Dixona - Mooda)

(próby zależne, małe, dane szczegółowe, cechy

(próby zależne, małe, dane szczegółowe, cechy

ilościowe ciągłe)

ilościowe ciągłe)

Przykład:

Przykład:

Liczba zgonów niemowląt wg wieku w losowo wybranych
próbach w 1989 roku i 1990 roku.

Wiek

Liczba niemowląt
198
9

1990

0 dni

112 73

1-6

132 135

7-13

27

21

14-20

11

17

21-29

8

9

1-2 m-
ce

28

26

3-5

24

37

6-11

24

21

Razem 366 339

Czy rozkłady zgonów
niemowląt według wieku
w obu badanych próbach są
takie same? =0.05

)

(

)

(

:

)

(

)

(

:

2

1

1

2

1

0

x

F

x

F

H

x

F

x

F

H





Test jednorodności chi-kwadrat



























k

i

i

i

i

n

n

n

n

n

n

n

n

n

n

1

2

1

2

1

2

1

2

1

1

1

2

1

2

)

(



Wiek

Liczba niemowląt

 

 

198

9

1990

0 dni

112

73

67,81

06-sty 132

135

65,26

13-lip

27

21

15,19

14-20

11

17

4,32

21-29

8

9

3,76

1-2 m-

ce

28

26

14,52

05-

mar

24

37

9,44

11-cze

24

21

12,80

Razem 366

339

193,1

0

i

i

i

n

n

n

2

1

2

1



017566

,

0

339

366

366

10

,

193

339

366

)

339

366

(

2

2



























018

,

0

2





067

,

14

)

7

1

8

1

;

05

,

0

(

2















k

v







14,067

0,018

Brak podstaw do odrzucenia hipotezy zerowej o
jednorodności rozkładu zgonów niemowląt.

Przykład:

Przykład:

)

(

)

(

:

)

(

)

(

:

2

1

1

2

1

0

x

F

x

F

H

x

F

x

F

H





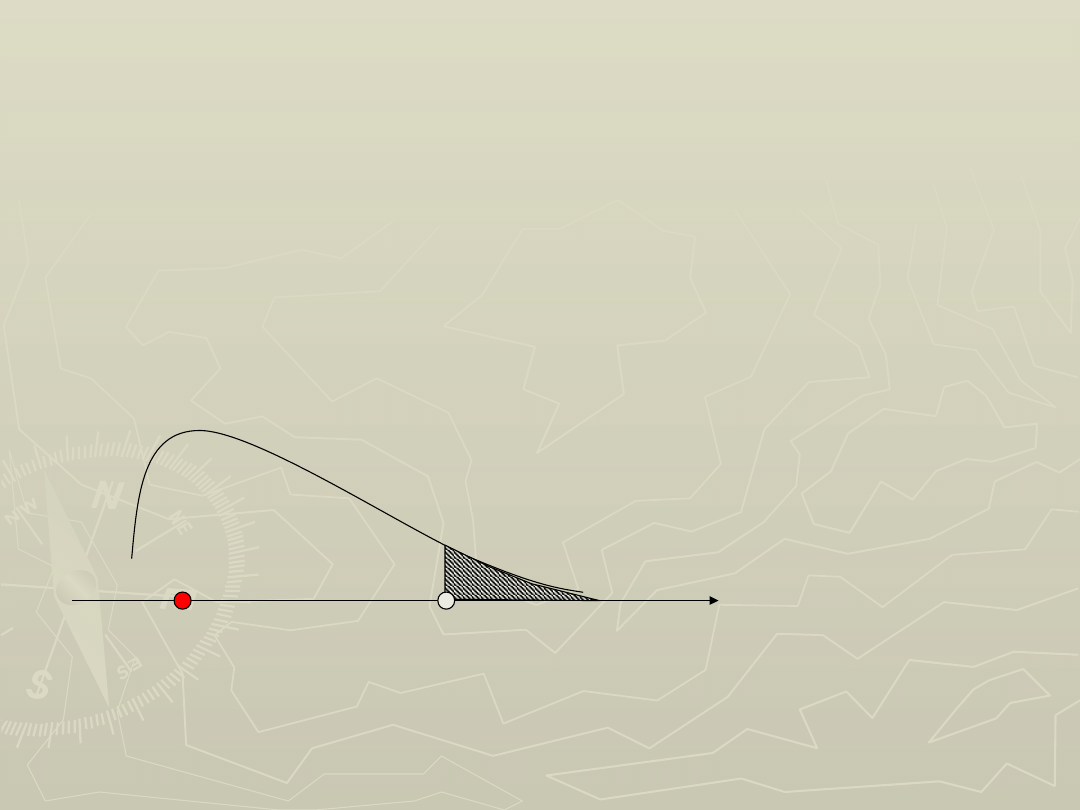
05

,

0





4

)

7

;

4

min(

)

;

min(











r

r

r

2

)

;

05

,

0

(













r

r

n

r





2

4

Brak podstaw do
odrzucenia
hipotezy zerowej o
identyczności
rozkładów wagi
przed i po kuracji.