MECHANIKA TEORETYCZNA
Wykładowca:
Prof. dr hab. inż.
KRZYSZTOF WILDE
Kontakt:
krzysztof.wilde@gmail.com
(dla starostów grup)
Materiały przygotowano z wykorzystaniem prac i materiałów Prof. J. Przewłóckiego (PG, PWSZ
Elbląg), a także materiałów Prof. J. Górskiego i dr. M. Skowronka (PG)
1
Kratownica drewniana
Kratownica żelbetowa
Bixby Bridge in Big Sur, California
Konstrukcji dachu hali „Olivia”
Kratownica stalowa
78,54 m
4,0 m
pas dolny
(2 C 220p)
pas górny
(2 dwuteownik 450)
słupki
stężenia
cięgna
sprężając
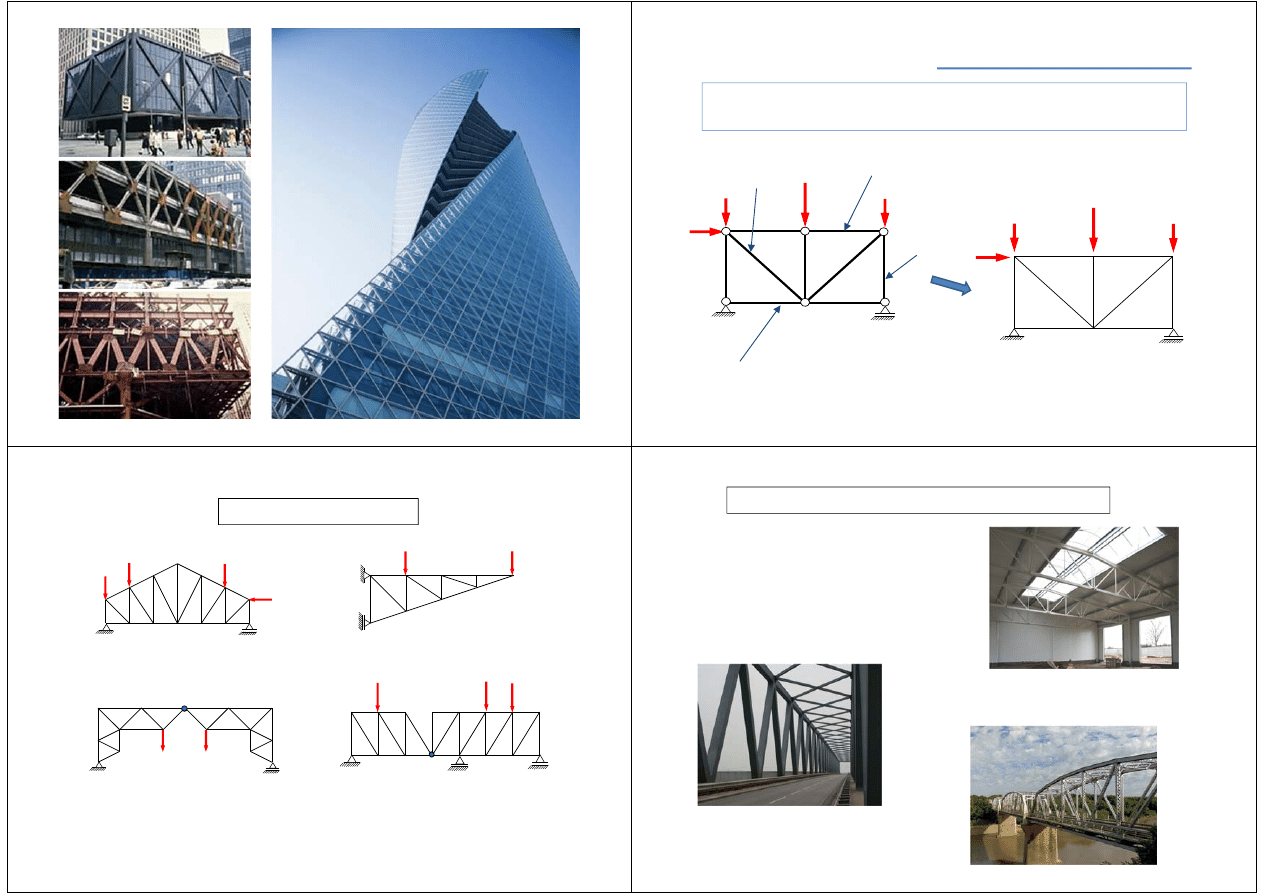
Kratownicą nazywamy konstrukcję złożona z prostoliniowych
prętów połączonych ze sobą za pomocą przegubów.
Dla uproszczenia na rysunkach konstrukcji
kratownic
pomijamy
oznaczanie kółkami
węzłów kratownic
.
KRATOWNICE
pas górny
pas dolny
słupek
krzyżulec
Kratownica wspornikowa
kratownica trójprzegubowa
kratownica swobodnie podparta
kratownica ciągła-przegubowa
TYPY KRATOWNIC
Najczęściej stosowane kształty kratownic
Kratownice trójkątne i trapezowe
znajdują zastosowanie głównie
jako wiązary dachowe.
Kratownice o pasach parabolicznych używane
są głównie jako konstrukcje mostów
Kratownice o pasach równoległych są
najczęściej używane w budownictwie
przemysłowym i mostach.
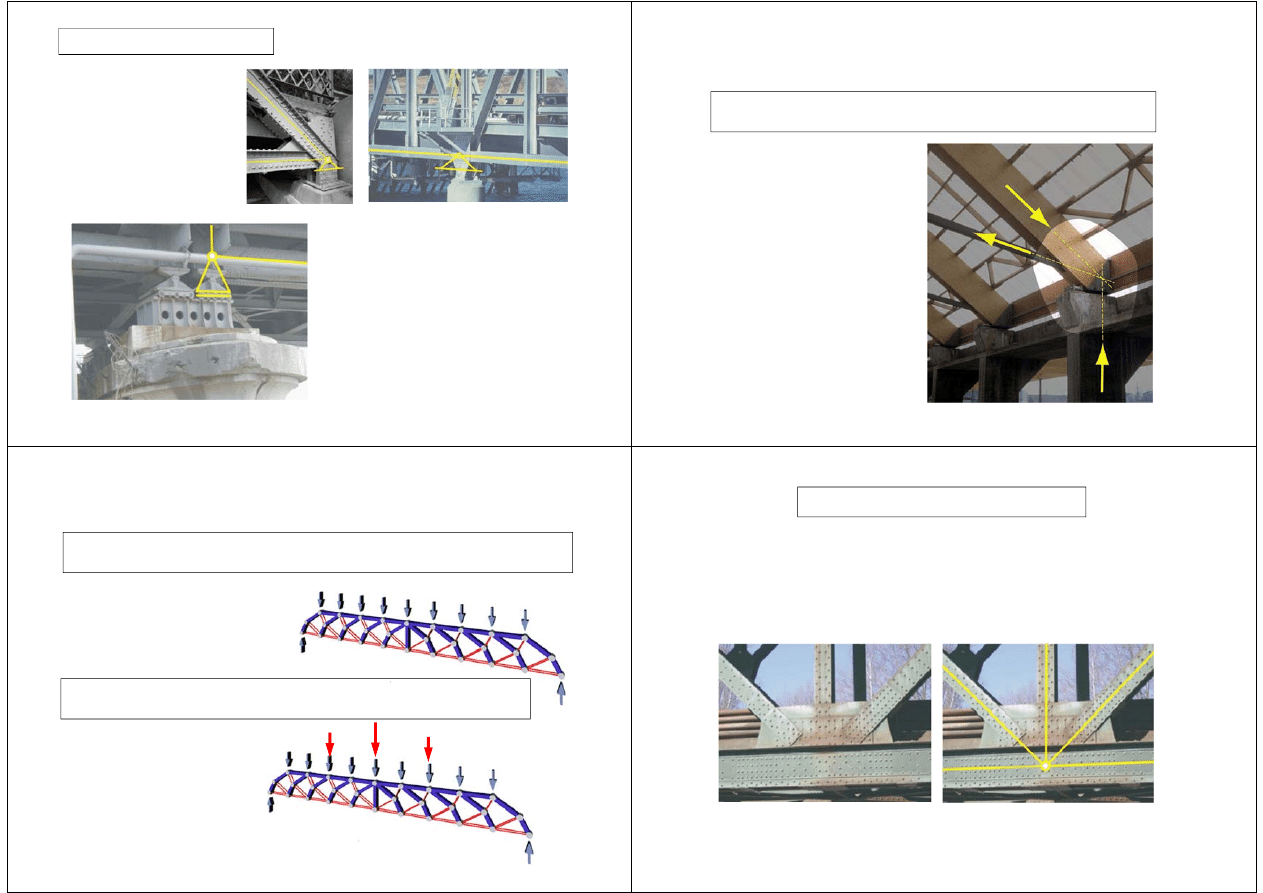
Podpora przegubowo-nieprzesuwna kratownicy
Podpora przegubowo-przesuwna kratownicy
Podpory kratownic
1. Osie prętów kratownicy schodzących się w węźle przecinają się
w jednym punkcie – środku przegubu.
ZAŁOŻENIA do wyznaczania sił wewnętrznych:
2. Ciężar własny konstrukcji, zazwyczaj niewielki w porównaniu z obciążeniem
użytkowym, zastępuje się siłami skupionymi przyłożonymi w węzłach.
ZAŁOŻENIA do wyznaczania sił wewnętrznych:
Ciężar własny
3. Obciążenie zewnętrzne działające na kratownice przykładane jest
wyłącznie w węzłach, w postaci sił skupionych.
Ciężar własny
Obciążenia zewnętrzne
Przeguby kratownicy nie są idealnymi przegubami pozbawionymi tarcia.
W rzeczywistości obroty prętów nie muszą dokonywać się idealnie
względem teoretycznego miejsca przegubu (np. połączenia na gwoździe
lub nity z zastosowaniem blach węzłowych).
Przegub czy połączenie sztywne?
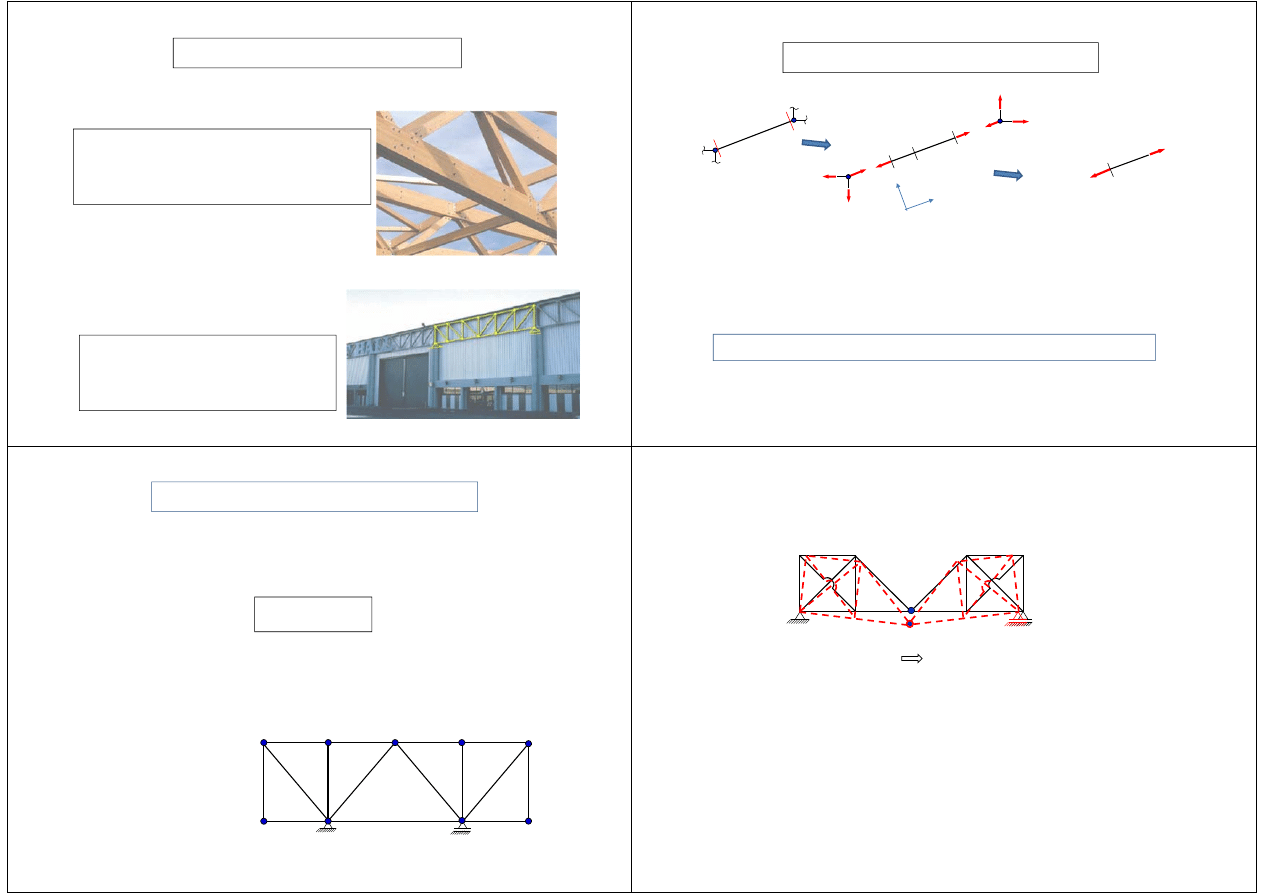
W rzeczywistości nie spełnione są
warunki obciążenia w formie sił
skupionych. Jednak, w większości
przypadków ciężar własny prętów
kratownicy sprowadza sie do jednej siły,
której kierunek przechodzi przez przegub.
Sztywność połączeń węzłowych powoduje powstanie w prętach
dodatkowych sił (tnących i momentów).
Przegub kratownicy drewnianej
Dodatowe siły są
jednak
drugorzędne
i
powodują powstanie niewielkich różnic w
porównaniu z siłami obliczonymi przy
założeniu idealnych przegubów.
Przegub czy połączenie sztywne?
Założenia
dotyczące
obliczania
kratownic
umożliwiają
szybkie
i
wystarczająco dokładne
obliczenie
sił w konstrukcjach kratownicowych.
A
B
S
3
S
1
S
2
A
W
1
W=W
1
B
S
4
W
2
W=W
2
N=W
W
- Momenty zginające w przegubach A i B z definicji są równe zeru.
- Gdyby w przegubach działały siły poprzeczne, to pręt nie byłby w
równowadze. W prętach kratowych siły tnące są równe zeru.
- W pręcie kratowym mogą wystąpić jedynie siły równoległe do osi pręta.
Równowaga pręta kratownicy
P
x
= 0,
P
y
= 0,
M
A
= 0
x
y
Siły rozciągające w prętach określa sie jako dodatnie, siły
ściskające oznaczamy jako ujemne.
W pręcie kratowym występują tylko siły normalne.
W każdym węźle kratownicy występuje zbieżny układ sił, który musi spełniać
warunki równowagi:
P
x
= 0,
P
y
= 0.
2
0
r
p
w
Kratownica jest statycznie wyznaczalna, jeżeli spełniony jest następujący
warunek:
r – składowe reakcji podpór
Niewiadome: r + p
p – liczba prętów kratownicy
Liczba równań: 2w
w – liczba węzłów kratownicy
Statyczna wyznaczalność kratownic
Przykład:
Kratownica trójkątna
(dodajemy 2 pręty+węzeł)
Kratownica
geometrycznie zmienna - mechanizm
r =3, p=16, w=9 s=3+16-2·9=1
Analiza statyczna polega na wyznaczeniu sił normalnych występujących w
prętach. W trakcie obliczania sił normalnych w prętach kratownicy oraz reakcji
podporowych stosuje się założenie o małych odkształceniach (zasadę
zesztywnienia). Ugięcia kratownicy są bardzo małe w porównaniu z jej
długością (rzędu paru procent) i można pominąć ich wpływ na reakcje oraz siły
normalne.
Analiza kinematyczna polega na sprawdzeniu, czy sposób połączenia
prętów kratownicy zapewnia jej geometryczną niezmienność.
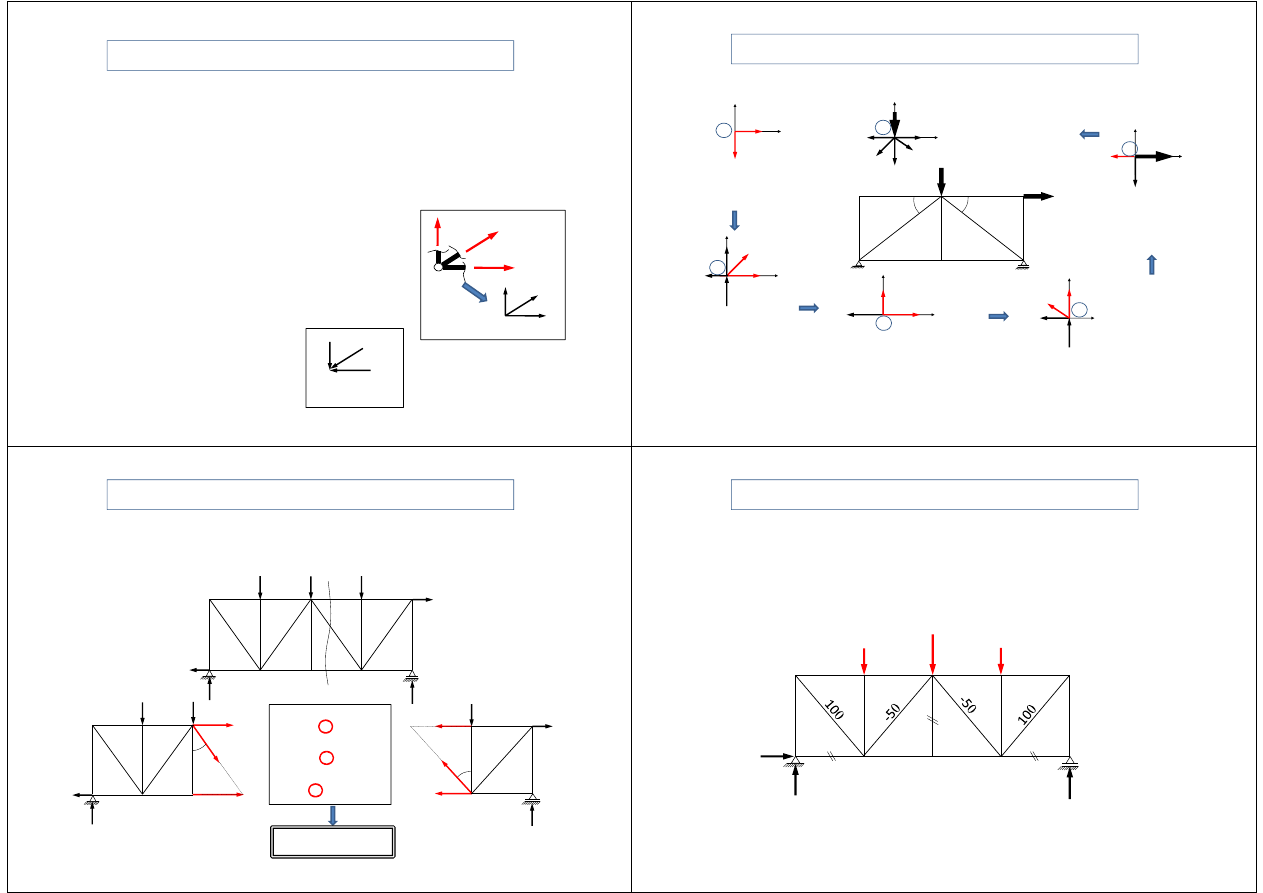
Metody wyznaczania sił w prętach kratownicy
• Przyjmuje się, że nieznane siły są rozciągające
tzn. na rysunkach oznacza się jako wychodzące
z węzłów. Są to siły dodatnie.
• Jeżeli siła obliczona posiada znak ” - ” oznacza
to, że pręt podlega ściskaniu.
Stosowany techniki:
• metoda Cremony
– metoda wykreślna (historyczna)
• metoda równoważenia węzłów – metoda analityczna
• metoda przekrojów Rittera
– metoda analityczna
W pierwszym etapie analizy z reguły wyznacza się składowe reakcji
podporowych z odpowiednich równań równowagi zapisanych dla całej
kratownicy (tak samo jak dla ram lub belek).
D
K
S
Rozciąganie
D
K
S
D
K
S
Ściskanie
Obliczenia rozpoczyna się od węzła, w którym występują co najwyżej dwie
nieznane siły i przechodzi się do kolejnego węzła z dwiema niewiadomymi.
H
A
A
S
1
K
1
D
1
x
y
R
A
B
D
2
K
2
S
3
x
y
R
B
E
G
1
K
1
K
2
G
2
S
2
x
y
F
G
2
S
3
x
y
D
G
1
x
y
S
1
C
D
1
D
2
x
y
S
2
D
E
F
A
C
B
G
1
K
1
K
2
G
2
S
2
S
3
S
1
D
1
D
2
Metoda równoważenia węzłów jest prosta w zastosowaniu, jednak z uwagi na
„przechodzenie” w obliczeniach od węzła do węzła, popełnienie błędu rachunkowego na
początku obliczeń, prowadzi do błędnego rozwiązania całości.
1
1
0 0
0 0
x
y
P
G
P
S
1
1
0
0
y
x
P
K
P
D
2
2
0
0
y
x
P
S
P
D
2
3
0
0
x
y
P
K
P
S
2
0
0
1
x
y
P
G
P
k o n t r o l a
0
2
0
3
x
y
P
P
k ο n t r o l a
k ο n t r o l a
Metoda równoważenia węzłów
Metoda umożliwia niezależne wyznaczenie sił w dowolnych prętach kratownicy.
Stosuje się ją wyłącznie dla przekrojów kratownic zawierających co najwyżej
trzy pręty, których kierunki nie przecinają się w jednym punkcie.
F
G
H
J
K
A
B
D
E
C
R
A
R
B
H
A
G
HJ
K
HE
D
DE
H
J
K
E
B
G
HJ
K
HE
D
DE
R
B
R
A
H
A
G
HJ
K
HE
D
DE
F
G
H
A
C
D
E
Metoda przekrojów (Rittera)
0 ,
0 ,
0
E
H
y
M
M
P
G
HJ
K
HE
D
DE
40 kN
40 kN
80 kN
‐60
‐60
‐60
‐60
‐4
0
‐4
0
‐8
0
‐8
0
90
90
R
A
=80
R
B
=80
H
A
=0
W przypadku kratownic nie ma potrzeby wykonywania wykresów sił
wewnętrznych, gdyż siły (normalne) w każdym pręcie są stałe.
W podsumowaniu można wykonać spis (listę) uzyskanych wyników lub
umieścić wartości sił, jak na rysunku.
Uwaga: Znak „minus” oznacza ściskanie pręta.
Prezentacja wyników
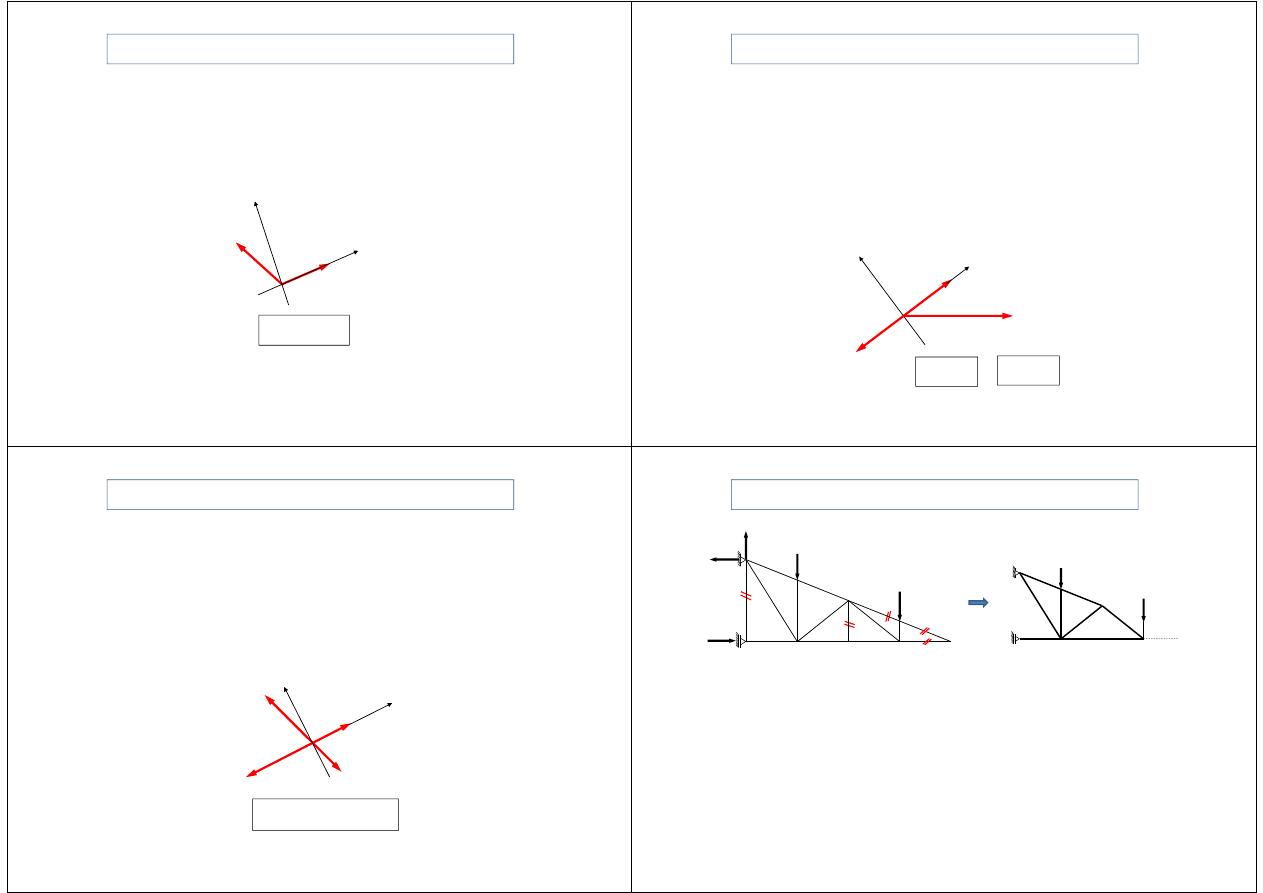
1. Jeżeli nieobciążony węzeł łączy dwa pręty o dowolnych
kierunkach, to nie wystąpią w nich siły
S
1
= S
2
= 0.
x
y
S
1
S
2
S
1
=S
2
=0
Zasady wyznaczania prętów „zerowych”
2. Jeżeli w węźle nieobciążonym zbiegają się trzy pręty, z których
dwa leżą na jednej prostej, to siła w trzecim dochodzącym do
nich pręcie jest równa zeru (S
3
= 0). Ponadto w prętach
leżących na jednej prostej siły będą jednakowe (S
1
= S
2
).
Reguła ta dotyczy także węzła obciążonego, w którym zbiegają
się dwa pręty i jeden z nich leży wzdłuż linii działania siły.
S
1
x
y
S
2
S
3
=0
S
3
Zasady wyznaczania prętów „zerowych”
S
1
=S
2
x
y
S
1
S
2
S
3
S
4
S
1
=S
3
, S
2
=S
4
3. Jeżeli węzeł nieobciążony łączy cztery pręty leżące parami na
dwóch prostych, to wartości sił w każdej parze są sobie równe
(S
1
= S
3
, S
2
= S
4
).
Reguła ta dotyczy także węzła obciążonego, w którym jedną
lub obie pary tworzą pręt i siła leżące na jednej prostej.
Zasady wyznaczania prętów „zerowych”
A
C
E
G
K
B
D
F
H
P
R
B
H
B
H
A
P
Pręty o zerowych wartościach sił, teoretycznie są zbędne.
Na przykład, usunięcie zerowego pręta EF z kratownicy i zastąpienie dwóch
prętów CE i EG jednym prętem CG, nie zmienia rozkładu sił wewnętrznych
kratownicy. Taka zmiana jednak zwiększy podatność pręta CG na
wyboczenie.
Pręty zerowe mogą być także potrzebne dla zapewnienia stateczności
kratownicy w czasie jej konstrukcji lub z uwagi na obciążenia użytkowe.
Które pręty są „zerowe”?
A
C
E
G
K
B
D
F
H
P
P
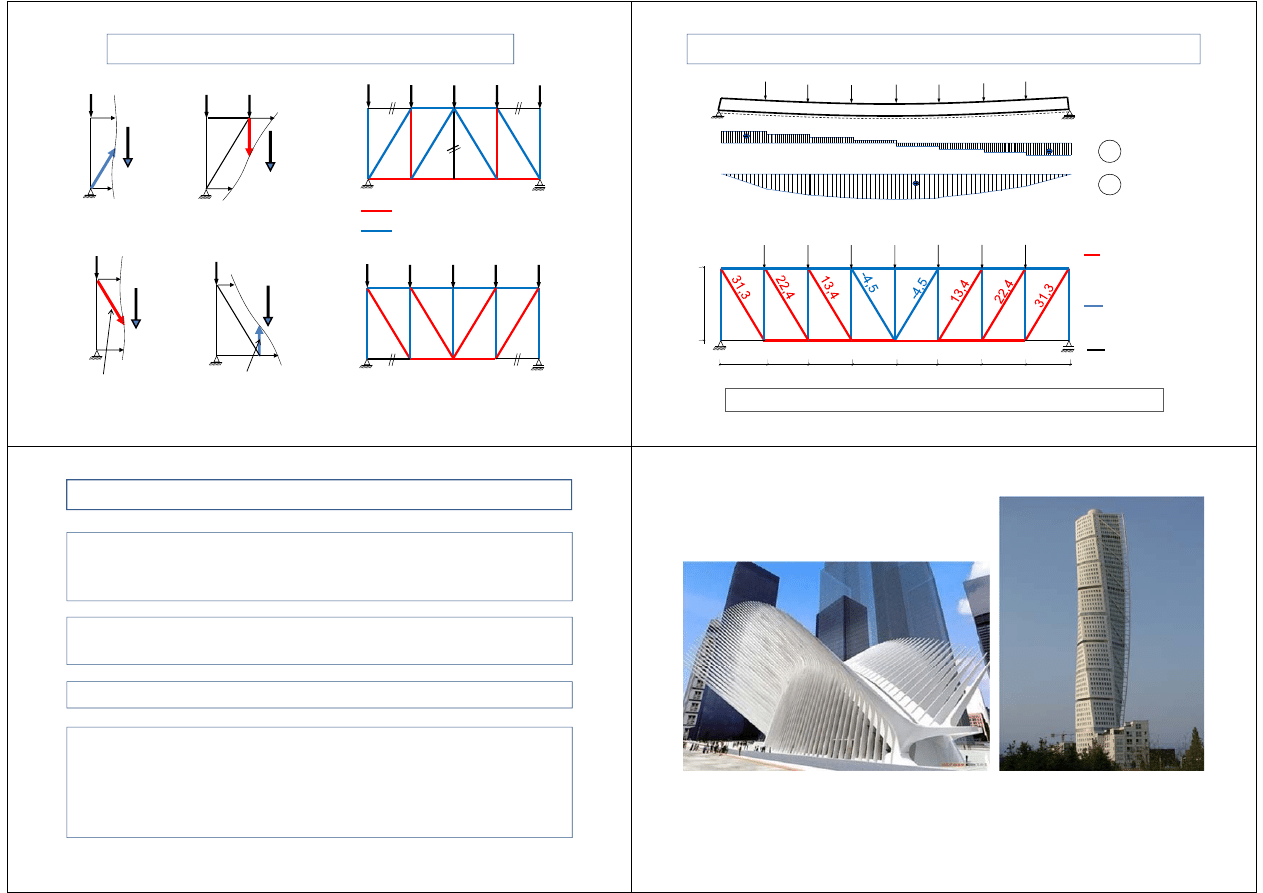
Pręty rozciąganie
Pręty ściskane
T
Krzyżulec
ściskany
T
Krzyżulec
rozciągany
T
Słupek
rozciągany
T
Słupek
ściskany
Analiza pracy prętów kratownicy
8 kN 8 kN 8 kN 8 kN 8 kN 8 kN 8 kN
Pręty
rozciąganie
Pręty
ściskane
Pręty
zerowe
8 kN
8 kN 8 kN
8 kN
8 kN
8 kN 8 kN
4 m
2 m
2 m
2 m
2 m
2 m
2 m
2 m
2 m
30
30
24
24
14
-14
14
-24
-14
-30
-24
-30
-32
-32
-28
-28
-28
-28
-12
-20
-12
-20
-8
Siły w pasach kratownicy maleją wraz ze wzrostem jej wysokości.
120
120
56
M
56
96
96
[kNm]
128
T
28
20
12
20
12
4
4
[kN]
28
Porównanie belka wolnopodparta - kratownica
• Przy kształtowaniu kratownic, najmniejsze siły w prętach
ukośnych występują przy ich nachyleniu do poziomu 45
0
-60
0
.
• Kratownice pozwalają na wykonanie konstrukcji o znacznych
rozpiętościach ponieważ materiał, z którego są wykonane jest
lepiej wykorzystany niż np. w belkach.
• W praktycznych obliczeniach, siły w niektórych prętach
najczęściej wyznacza się metodą równoważenia węzłów a w
innych metodą przekrojów. W wielu przypadkach oblicza się
jedynie siły w wybranych prętach, w których spodziewamy się
wystąpienia wartości ekstremalnych.
• Pręty ściskane powinny być możliwie najkrótsze.
Uwagi ogólne dotyczące kratownic
World Trade Center Transportation Hub,
New York City, USA
Turning Torso, Malmo,
Szwecja
SANTIAGO CALATRAVA
Katastrofy i awarie
Awaria wiaduktu
w ciągu ul. Braci Lewoniewskich
W Gdańsku
10.10.2004r.
10.10.2004r.
Wiaduktu w ciągu ul. Braci Lewoniewskich
W Gdańsku
10.10.2004r.
Wiaduktu w ciągu ul. Braci Lewoniewskich
W Gdańsku
10.10.2004r.
Wiaduktu w ciągu ul. Braci Lewoniewskich
W Gdańsku
10.10.2004r.
Koncepcja remontu wiaduktu w ciągu ul. Braci Lewoniewskich
Obliczanie etapów
pośrednich remontu
Zdjęcie w trakcie prac
remontowych