Wykładowca: Prof. dr hab. inż.

KRZYSZTOF WILDE

Kontakt:

[e-mail]

(dla starostów grup)

Materiały do wykładu przygotowano na bazie prac i materiałów

Prof. Jarosława Przewłóckiego (Politechnika Gdańska, PWSZ Elbląg)

MECHANIKA OGÓLNA

PODSTAWOWE ZAŁOŻENIA TEORII KONSTRUKCJI

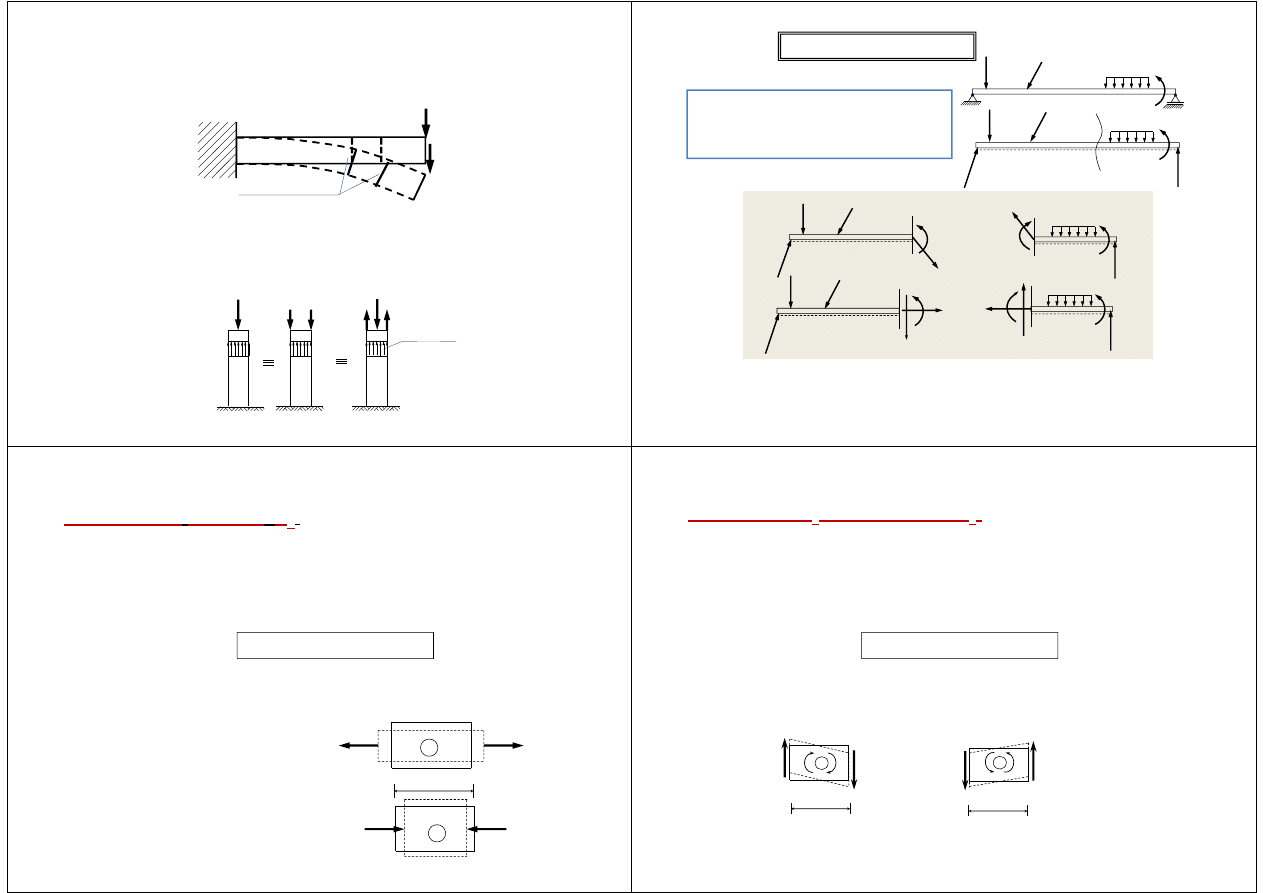
1. Założenie statyczności obciążeń.

Przyjmuje się, że działające na

konstrukcję siły wzrastają od wartości zerowej aż do ich ostatecznej
wartości w sposób ciągły i nieskończenie powolny, co pozwala na
pominięcie sił bezwładności.

P

P

l

l

0

l=l

0



v



2. Założenie o małych odkształceniach (przemieszczeniach)

pozwala rozwiązywać zagadnienia dotyczące równowagi układów

ulegającym odkształceniom.

3. Zasada superpozycji.

Zakłada się, że poszczególne siły działają

niezależnie od siebie. W wyniku tego reakcje podporowe, siły wewnętrzne
lub odkształcenia konstrukcji spowodowane łącznym działaniem układu sił
są równe sumie odpowiednich wielkości, od działania każdej z tych sił z
osobna.

Każdy układ, dla którego zależności między obciążeniem
a siłami wewnętrznymi są liniowe, nazywamy

układem

liniowym

.

P

1

P

2

y





P

1

y







Układ liniowy geometrycznie i fizycznie (prawo Hooke’a)
nazywamy układem liniowym. Liniowość układu jest warunkiem
wystarczającym i koniecznym stosowania zasady superpozycji.

1

2

y

y

y











P

2

y







4.

Założenie ciągłości, jednorodności i izotropii materiału

.

Podstawowe materiały budowlane, takie jak stal i beton,
można uznać za ciągłe, jednorodne i izotropowe.

Założenie ciągłości pozwala do opisu zachowania się materiału
przy użyciu rachunku różniczkowego i całkowego.

Ciągłość

materiału oznacza, że wypełnia on dane ciało w

sposób ciągły. Materiał jest

jednorodny

, jeżeli w każdym

punkcie danego ciała ma takie same właściwości mechaniczne

(wytrzymałość, odkształcalność). Materiał

izotropowy

to taki,

w którym właściwości te są jednakowe we wszystkich
kierunkach; materiał niespełniający tego założenia nazywa się

anizotropowym

(np. drewno).

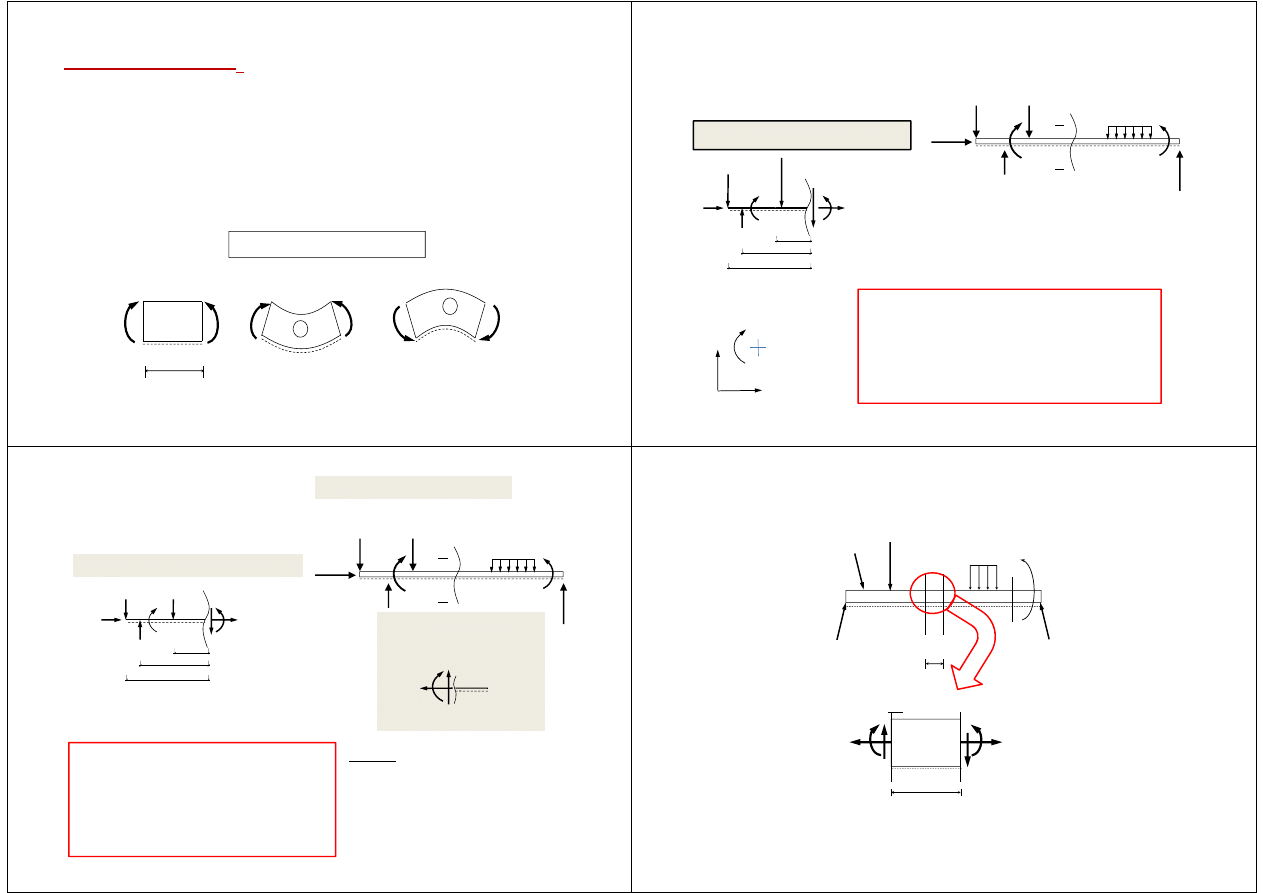
5.

Założenie płaskich przekrojów

(Bernoulliego). Przyjmuje

się, że przekrój płaski, przeprowadzony w sposób myślowy w
ciele nieodkształconym, może zmienić swe położenie po
odkształceniu, ale pozostaje nadal płaski.

6.

Zasada de Saint-Venanta

. Zakłada się, że przyłożona w

danym miejscu siła wpływa tylko w bliskim sąsiedztwie na
rozkład naprężeń (siły wewnętrzne rozłożone na powierzchni

przekroju).

Płaskie przekroje

Naprężenia

P

P/2

P/2

P/2

P/2

2P

A

B





R

B

N



T



M



R

A

R

B





SIŁY WEWNĘTRZNE

N



R

A





T



M



R

A





Część lewa

W



M



Część prawa 





R

B

W



M



M



– moment zginający, T



– siła tnąca, N



– siła podłużna

M



,

T



,

N



-

składowe sił wewnętrznych

Siły wewnętrzne (przekrojowe)
to jedno z najważniejszych pojęć
mechaniki budowli.



x

N



N



+

N



N



-

Siła normalna

(

podłużna

)

N



w dowolnym przekroju

poprzecznym



pręta jest równa sumie rzutów wszystkich sił

działających z lewej (prawej) strony rozważanego przekroju, na
kierunek prostej stycznej do osi pręta, poprowadzonej przez
środek ciężkości przekroju.

Siła podłużna jest dodatnia, jeżeli działa
na przekrój rozciągająco, i ujemna, gdy
działa ściskająco.

Konwencja znaków

Dodatnia

Ujemna

Siła tnąca T



(poprzeczna V



)

w dowolnym przekroju

poprzecznym



pręta jest równa sumie rzutów wszystkich sił

działających z lewej (prawej) strony rozważanego przekroju, na
kierunek prostej prostopadłej do osi pręta, poprowadzonej przez
środek ciężkości przekroju.

T



T





x

+

T



T





x

-

Siła poprzeczna jest dodatnia, gdy na prawą część pręta
działa do góry, a na lewą do dołu.

Dodatnia

Ujemna

Konwencja znaków

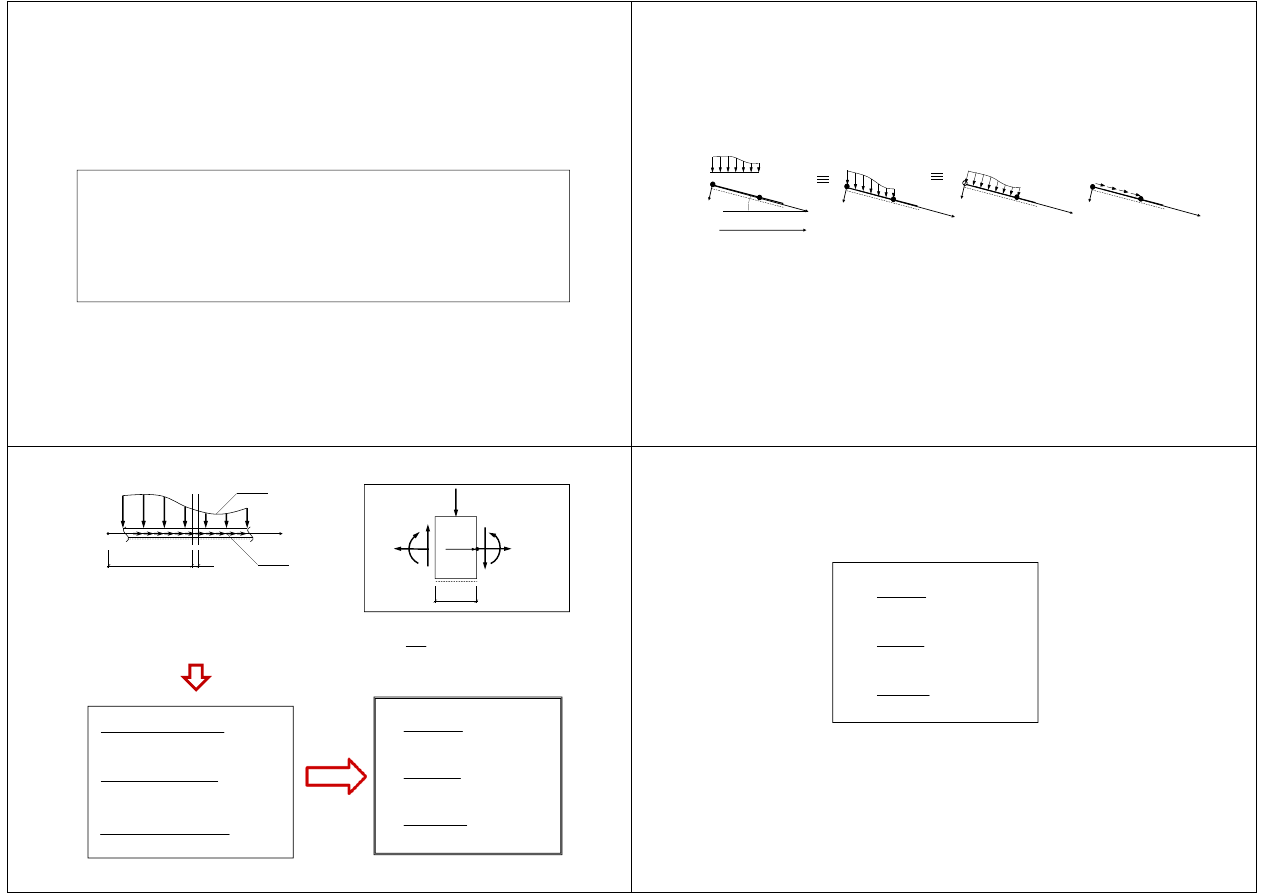
Moment zginający M



w dowolnym przekroju poprzecznym



pręta jest równy sumie momentów statycznych wszystkich sił
działających z lewej (prawej) strony rozważanego przekroju,
liczonych względem środka ciężkości tego przekroju.

Moment ten jest dodatni, gdy rozciągane są włókna spodu pręta.
Moment określamy jako ujemny, jeżeli jego działanie powoduje
ściskanie przyjętych spodów.

M



M



M



M



M



M



spód rozciągany

spód ściskany



x

+

-

Dodatni

Ujemny

Konwencja znaków

Obliczenia sił wewnętrznych można przeprowadzić z

warunków

równowagi

lub „bezpośrednio z

definicji

, dla wyodrębnionych

fragmentów układu.

Z warunków równowagi

1

0

x

P

P

N



 





2

3

4

0

y

P

P

P

P

T



   







 

2

2

3

3

4

4

0

M

P a

P a

M

P a

M





     

  





Przyjęty dodatni kierunek
sumowania momentów

x

y

1

N

P



 

2

2

3

3

4

4

+

M

P a

P a

M

P a



    





2

3

4

T

P

P

P



   

Siły wewnętrzne w przekroju







M

P



P



P



P



M



P



P



P



M

a



a



N



T







P



a



Obliczenia sił wewnętrznych „bezpośrednio z

definicji”

,

(porównując z „wybraną” konwencją znaków)

M



P



P



P



M

a



a



N



T







P



a



Obliczenia

od lewej

strony belki

1

N

P



 

2

2

3

3

4

4

+

M

P a

P a

M

P a



    





2

3

4

T

P

P

P



   

Siły wewnętrzne w przekroju



T



M



N







Konwencja znaków
z

lewej strony

przekroju

Czy siła zewnętrzna jest zgodna z konwencją znaków?

Tak – „+”; Nie – „ –”

Uwaga:
obliczając siły wewnętrzne od
prawej strony belki siły
zewnętrzna trzeba porównywać
z konwencją znaków dla
przekroju z prawej strony





M

P



P



P



P



Siły wewnętrzne występują w każdym przekroju konstrukcji i są
one wypadkowymi wszystkich sił z wybranej części układu.

Sily wewnętrzne - nieskończenie mały element o długości



x



L



L



P



P



x



L



L



P



P



x

N



N



T



T



M



M





L



L

Wartości sił wewnętrznych, obliczone w tym samym punkcie
z obu stron przekroju, muszą być sobie równe.

Można przeprowadzać obliczenia sił wewnętrznych z dowolnej
strony przekroju belki. Zazwyczaj wybiera się tę stronę, z
której wykonanie odpowiednich działań będzie łatwiejsze.

ZWIĄZKI MIĘDZY SIŁAMI WEWNĘTRZNYMI I OBCIĄŻENIEM

x

q(x)

A

B

y

x

p(x)

A

B

y

+

x

n(x)

A

B

y

x

q’(x’)

A

B



y

x’

p

(x) – obciążenie poprzeczne (dodatnie, jeżeli działa ku spodowi

pręta),

n

(x) –obciążenie osiowe (dodatnie, jeżeli ma zwrot zgodny z

osią x).

p(x)



x

x

x

n(x)

O



1



1



2



2

A

B

p(x)



x

M(x+



x)

N(x+



x)

T(x+



x)



x

T(x)

N(x)

M(x)

n(x)



x

C





   

0

x

P

N x

x

N x

n x

x



  



 







 

 

N x

x

N x

n x

x

  

 



 

 

 

 

 

 

d N

x

n x

d x

d T

x

p x

d x

d M

x

T

x

d x

 

 









 

 

0

y

P

T x

x

T x

p x

x



  



 







 

 

 

0

2

C

x

M

M x

x

M x

T x

x

p x

x





  



 









  

 

T x

x

T x

p x

x

  

 







 

 

M x

x

M x

T x

x

  





W niektórych przypadkach obliczenia łatwiej jest przeprowadzić,
przyjmując

oś x skierowaną w stronę przeciwną

i wtedy wyrażenia

znajdujące się po prawej stronie zależności różniczkowych

zmienią znaki na przeciwne

.

Przedstawione zależności różniczkowe spełniają ważną rolę w
analizie układów prętowych i noszą nazwę

równań

różniczkowych równowagi elementu pręta

. Istotne jest

zwłaszcza ostatnie z równań, które może służyć między innymi
do kontrolowania zgodności wykresów sił poprzecznych i
momentów zginających.

 

 

 

 

 

 

dN x

n x

dx

dT x

p x

dx

dM x

T x

dx





 

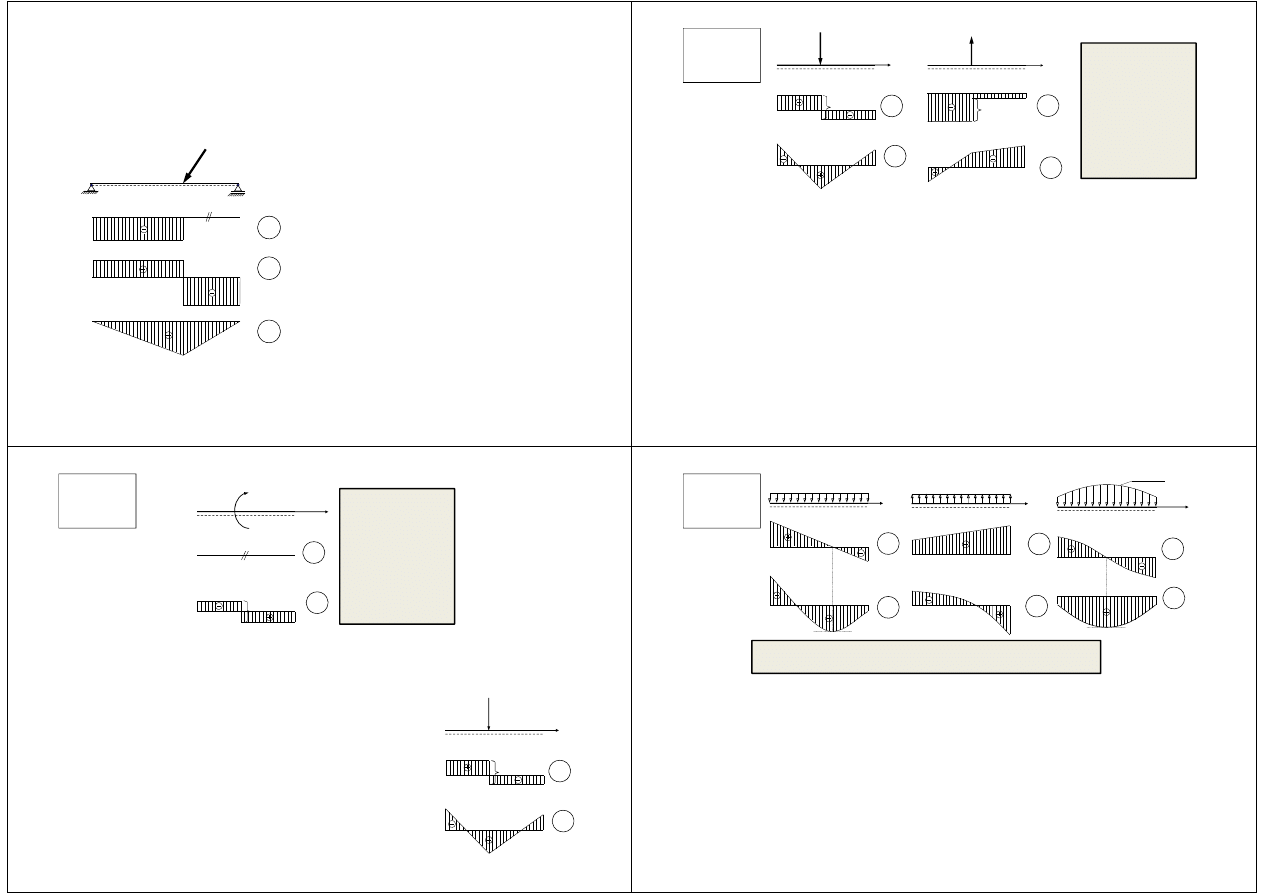
Graficzna prezentacja sił wewnętrznych

Wykresy sporządzamy, odkładając od osi pręta, w obranej skali,
rzędne odpowiednich funkcji.

Rysując wykresy sił
wewnetrznych, przyjmuje się

konwencję

, według której

wartości dodatnie momentów
zginających umieszcza się po
stronie spodu pręta

, a ujemne po

stronie przeciwnej.
Wykresy sił poprzecznych rysuje
się odwrotnie, czyli po stronie
spodu odkłada się wartości
ujemne.
Zerowe siły wewnętrzne oznacza
się dwiema pochyłymi kreskami.

P

N

T

M

M’=T
T’=-q

M=a x+b

T=a

q=0

• Jeżeli wykres sił poprzecznych będzie opisany prostą poziomą,

to wykres momentów zginających jest opisany równaniem
prostej nachylonej.

• Pochodna funkcji rosnącej jest dodatnia, a malejącej – ujemna,

zatem moment zginający rośnie w przedziałach, w których siła
poprzeczna jest dodatnia i maleje w przedziałach, w których jest
ujemna.

• W przypadku działania na układ siły skupionej, w miejscu jej

zaczepienia wystąpi nieciągłość na wykresie sił poprzecznych.

P

P

T

M

x

P

x

P

T

M

x

M

M

T

M

M’=T
T’=-q

M=a

T=0

q=0

• W przypadku działania na układ momentu skupionego, w

miejscu jego zaczepienia wystąpi nieciągłość na wykresie
momentów zginających.

• Wartości maksymalne momentu zginającego

mogą również wystąpić w punktach
przyłożenia sił skupionych, w których siła
poprzeczna jest nieciągła i przecina oś x,
natomiast wykres momentów jest załamany.

P

x

P

T

M

q=const

T

M

x

T

q=const

M

x

M’=T
T’=-q

M=a x

2

+bx+c T=2ax+b

q=-2a

• Jeżeli wykres siły poprzecznej będzie opisany równaniem prostej

o współczynniku kierunkowym różnym od zera, to wykres
momentów zginających jest opisany parabolą.

• Dla znalezienia ekstremum dowolnej funkcji, przyrównuje się jej

pochodną do zera, a więc ekstrema momentu zginającego
znajdują się w miejscach zerowania się siły poprzecznej.

x

q(x)

T

M

Wykres momentów zginających jest zakrzywiony
wypukłością w tę stronę, w którą działa obciążenie ciągłe.

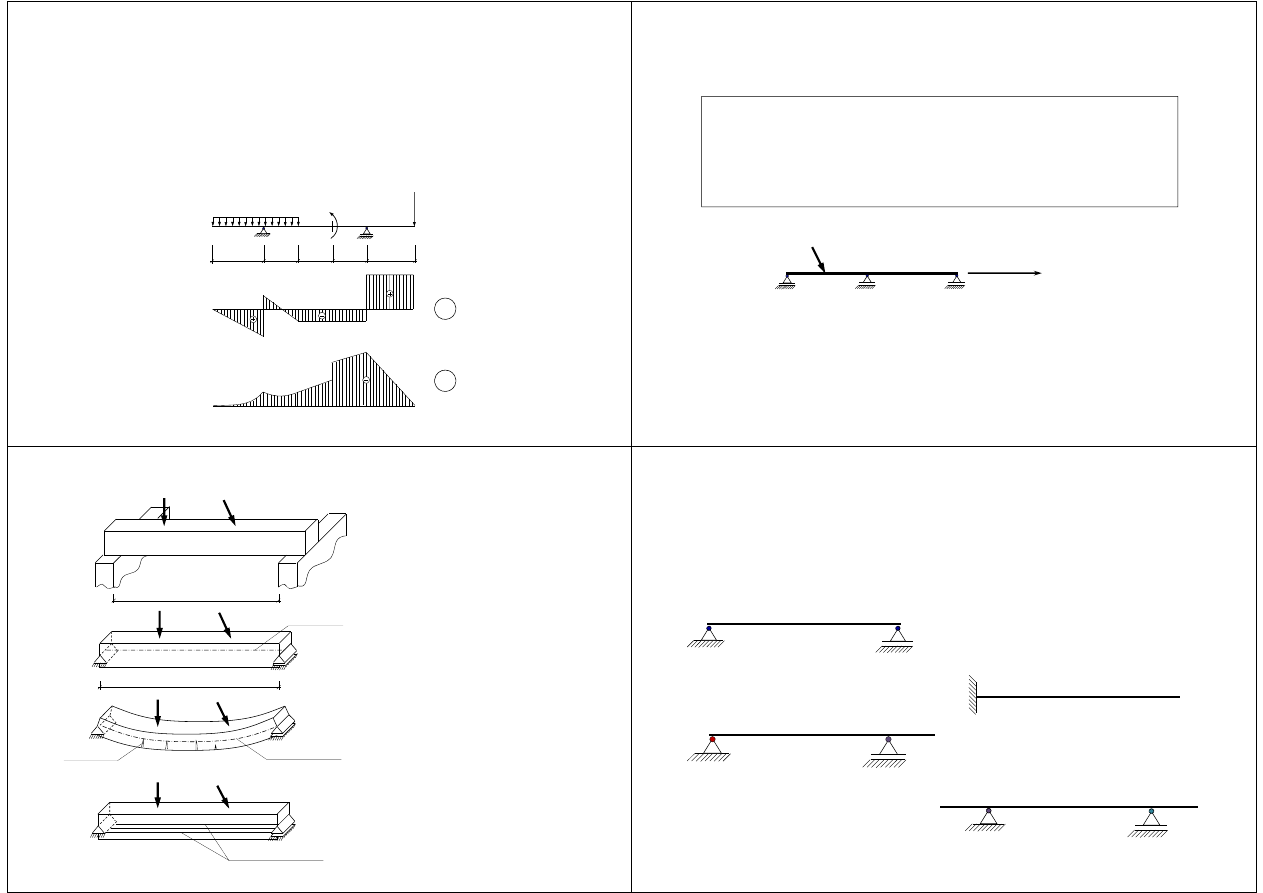
Przyrost siły poprzecznej (podłużnej) między dwoma punktami osi
pręta jest równy minus umownemu polu wykresu obciążenia
ciągłego poprzecznego (osiowego) zawartego między tymi
punktami.
Przyrost momentu zginającego między dwoma punktami osi pręta
jest równy umownemu polu wykresu siły poprzecznej zawartego
między tymi punktami.

T

10

40

10

30

[kN]

M

45

45

65

100

120

[kNm]

q=10 kN/m

M=35 kNm

P=40 kN

3 m

3 m

2 m 2 m 2 m

BELKI PROSTE

Płaski, dowolny układ prętowy określa się jako

statycznie

wyznaczalny

, jeżeli do jego rozwiązania, czyli wyznaczenia

wszystkich reakcji i sił wewnętrznych, wystarczą tylko trzy
równania równowagi. Jednakże jest to tylko warunek
konieczny, ale niewystarczający, statycznej wyznaczalności.

Ruch układu

Mechanizm, układ chwiejny lub geometrycznie zmienny

Linia ugięcia

Ściskanie

Rozciąganie

Spękanie

Pręty zbrojeniowe

Oś belki 

l

0

=1,05l

s

l

0

- rozpiętość obliczeniowa

l

s

l

s

- rozpiętość w świetle ścian

BELKA SWOBODNIE PODPARTA

Jeden z najstarszych
elementów konstrukcyjnych,
i najczęściej występujący w
praktyce budowlanej.

Część belki zawartą
między podporami nazywa
się

przęsłem

. Zamiast

używać pojęcia

długość

belki

, mówi się, że przęsło

ma

rozpiętość

l

.

belka swobodnie podparta ze
wspornikiem

belka swobodnie podparta ze
wspornikami

Pręt odpowiednio podparty i obciążony siłami prostopadłymi
lub ukośnymi do jego osi nazywany jest

belką

.

BELKI SWOBODNIE PODPARTE – SCHEMATY STATYCZNE

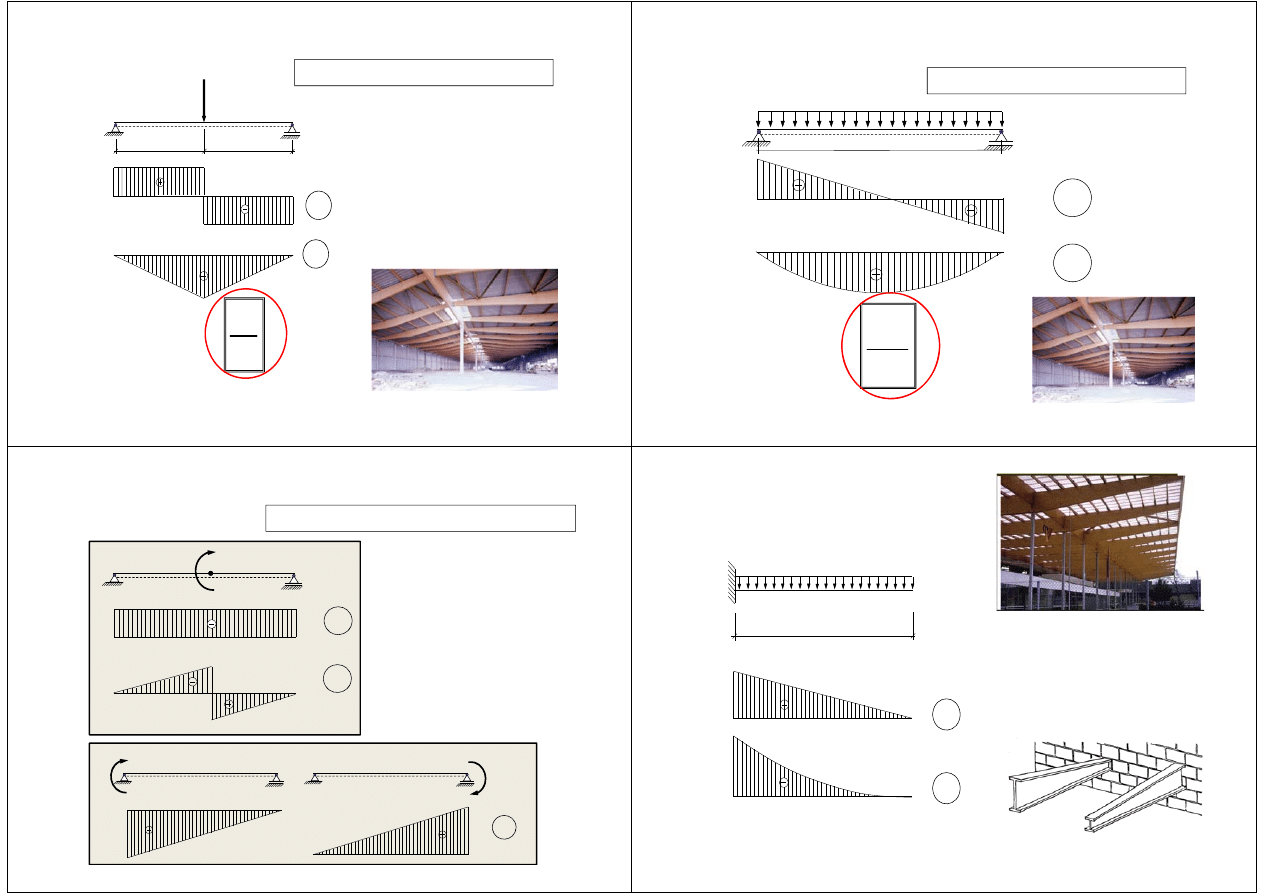
PODSTAWOWE PRZYPADKI

P

l/2

l/2

T

P/2

M

B

A

P/2

4

Pl

Obciążenie – SIŁA SKUPIONA

PODSTAWOWE PRZYPADKI

q

T

M

B

A

ql/2

ql/2

2

8

ql

l

Obciążenie RÓWNOMIERNE

M

M

M

M

M

A

C

B

T

M

M

M

M/l

M/l

PODSTAWOWE PRZYPADKI

Obciążenie – MOMENT SKUPIONY

q

A

l

T

M

ql

2

2

ql

BELKA WSPORNIKOWA

(WSPORNIK)

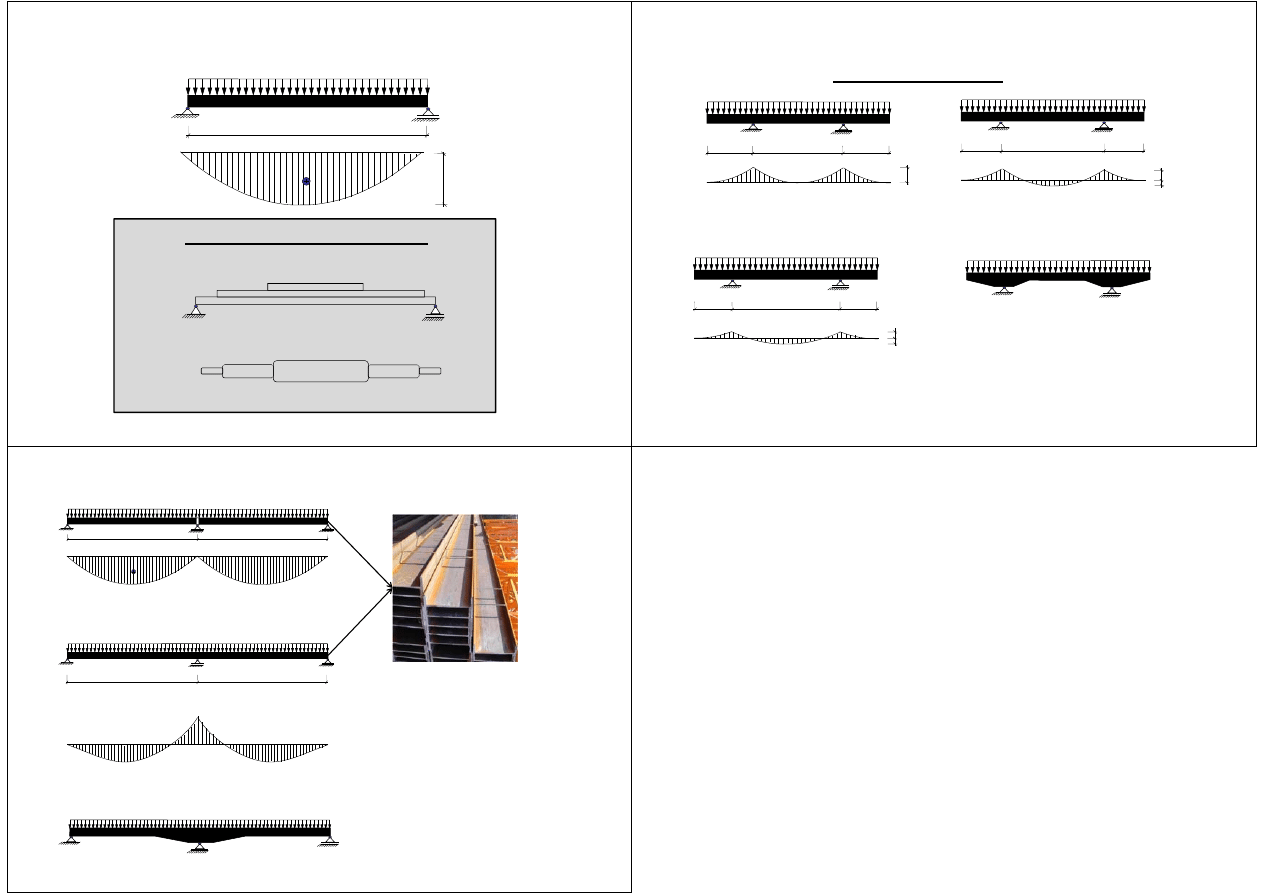
q

l

M

KSZTAŁTOWANIE BELEK

Zmiana szerokości pasów blachownicy

Zmiana grubości pasów blachownicy

Blachownica

Kształtowanie przekroju belki

q

M/4

l/2

l/4

l/4

q

M/5

0,56l

0,22l

0,22l

M/9

q

0,586l

0,207l

0,207l

M/5,8

M/5,8

Belka stalowa o stałej wysokości

Belka żelbetowa

KSZTAŁTOWANIE BELEK

Przesunięcie podpór

Można dać mniej zbrojenia w przęśle

Belka stalowa

M

M

M

0,56M

0,56M

Belka żelbetowa

Jednakowa wysokość
belki ciągłej i swobodnie
podpartych

q

l

q

l

Belki swobodnie podparte

q

l

l

Belka ciągła