Wykładowca: Prof. dr hab. inż.
KRZYSZTOF WILDE
Kontakt:
krzysztof.wilde@gmail.com
(dla starostów grup)
Materiały do wykładu przygotowano na bazie prac i materiałów
Prof. Jarosława Przewłóckiego (Politechnika Gdańska, PWSZ Elbląg)
MECHANIKA OGÓLNA
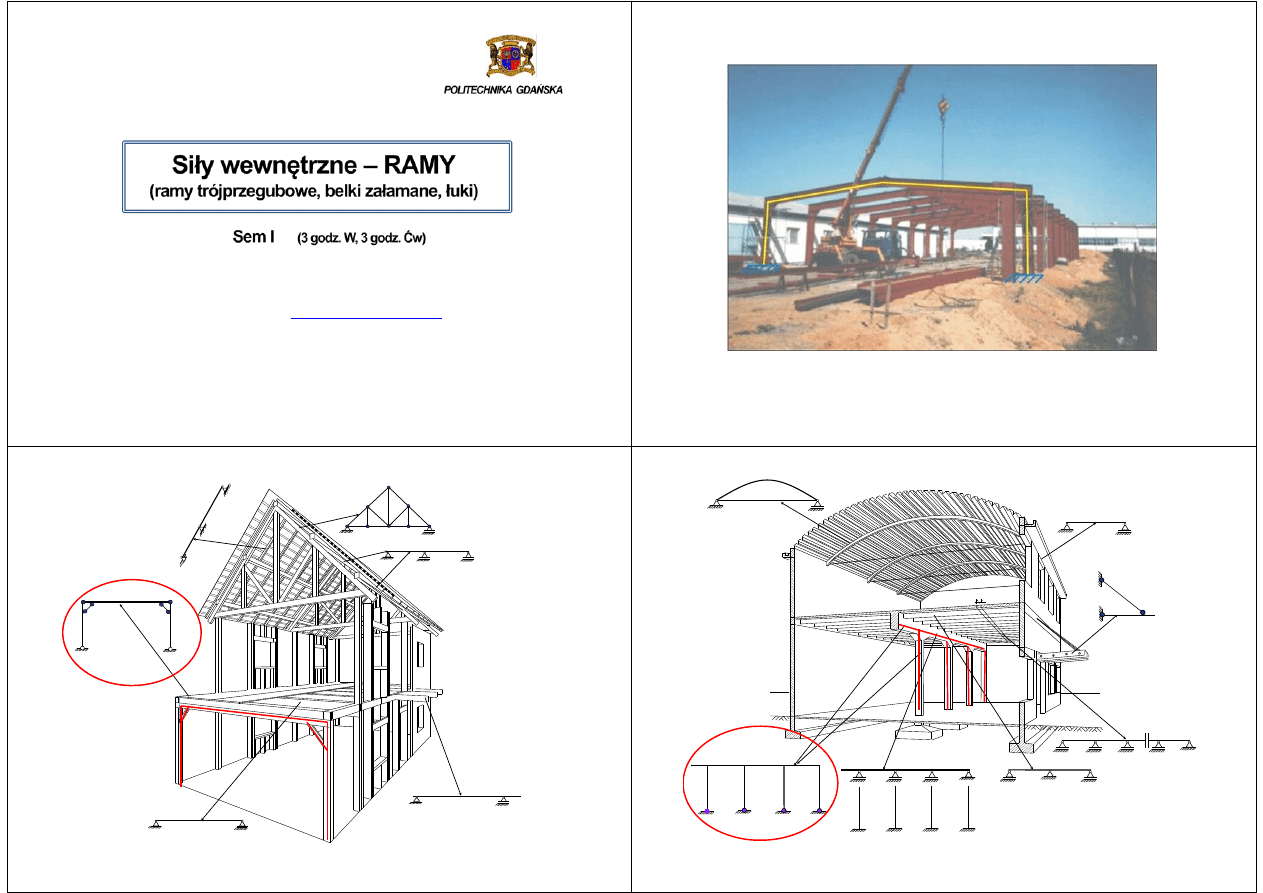
Przykładowa rama płaska ze schematem statycznym
Drewniany dom mieszkalny o konstrukcji szkieletowej
1
Konstrukcja hali żelbetowej z podciągiem opartym na słupach
UKŁADY RAMOWE
Konstrukcje składające się z prętów prostoliniowych,
połączonych ze sobą w węzłach w sposób sztywny lub
przegubowy, nazywają się ramami.
Belka załamana
Rama trójprzegubowa
Sztywność węzła uniemożliwia wzajemny
obrót połączonych w nim prętów.
Połączenia przegubowe umożliwiają
swobodny obrót łączonych prętów.
UKŁADY RAMOWE
A
A
A
B
B
Rozpora (rygiel)
Słupek
Rama wspornikowa
Belkami załamanymi nazywane są układy prętowe podparte na
dwóch podporach, przegubowo-przesuwnej i nieprzesuwnej, o
prostokątnej siatce prętów lub prętach ukośnych.
BELKI ZAŁAMANE
B
A
4 m
C
D
E
4 m
1m
8 kN
2 m
2 kN/m
Umiejętne stosowanie równań równowagi prowadzi do niezależnego
obliczenia kolejnych składowych reakcji belek załamanych.
2 4
0
8 kN
x
B
B
P
H
H
Sprawdzenie
8
2 10 8
0
y
A
B
P
R
R
4
8 1
0
2 kN
B
A
A
M
R
R
4
8 5
0
10 kN
F
B
B
M
R
R
2 kN/m
B
A
C
D
E
R
A
R
B
H
B
F
8 kN
4 m
4 m
1m
2 m
Wyznaczanie reakcji
Przykład
Równania sił wewnętrznych należy
zapisywać oddzielnie dla każdego
elementu konstrukcji. Równania te
będą się zmieniać w węzłach układu
oraz
w
punktach
zmiany
typu
(funkcji) obciążenia.
1
1
0
2 kN
x
P
N
x
2
2
1
( )
1
1
2
0
2
x
M
M
x
x
1
1
1
0
2
y
P
T
x
x
B
A
C
D
E
2 kN/m
8 kN
2 kN
10 kN
8 kN
4 m
4 m
1m
2 m
x
1
Wyznaczanie sił N, T i M
1
:
0
4 m
A C
x
y
1
T
N
M
x
1
A
2 kN
2 kN/m
x
2
M
T
N
A
2 kN
C
y
2
2 kN/m
Wyznaczanie sił N, T i M
2
:
0
4 m
C
D
x
B
A
C
D
E
2 kN/m
8 kN
2 kN
10 kN
8 kN
4 m
2 m
4m
1m
x
2
2
2
0
4 2
8 kN
x
P
N
x
( )
2
2
2
0
2
2 4 2
2
16
M
M
x
x
x
2
2
0
2 kN
y
P
T
x
3
3
0
0
x
P
N
x
( )
3
3
0
8
M
M
x
x
3
3
0
8 kN
y
P
T
x
3
:
0
1 m
E
D
x
E
M
T
N
x
3
y
3
8 kN
B
A
C
D
E
2 kN/m
8 kN
2 kN
10 kN
8 kN
1m
4 m
4 m
2 m
x
3
Wyznaczanie sił N, T i M
4
4
0
10 kN
x
P
N
x
10 kN
8 kN
T
N
M
x
4
y
4
4
:
0
2 m
B
D
x
( )
4
4
0
8
M
M
x
x
4
4
0
8 kN
y
P
T
x
B
A
C
D
E
2 kN/m
8 kN
2 kN
10 kN
8 kN
4 m
2 m
1m
4 m
x
4
Wyznaczanie sił N, T i M
Poprawność rozwiązania należy sprawdzić analizując równowagę wszystkich
składowych sił wewnętrznych, działających na węzeły (np. na węzeł D).
N
2
10
8
Wyznaczanie sił N, T i M ‐ WYKRESY
[kN]
D
24
16
8
0
24 8 16
0
D
M
D
8
8
8
10
2
0
8 8
0
0
10 8 2
0
x
y
P
P
Równowaga sił T i N w węźle D
T
2
8
8
8
[kN]
M
16
16
24
8
D
[kNm]
RAMY TRÓJPRZEGUBOWE
H
B
R
A
R
B
H
A
A
C
B
l
R
A
R
B
H
B
H
A
A
C
B
l
H
A
R
A
R
B
H
B
C
f
A
B
l
Układy prętowe nazywane są trójprzegubowymi, jeżeli obydwie
podpory są wykonane jako przegubowe-nieprzesuwne oraz jeden z
węzłów zaprojektowano jako połączenie przegubowe.
Odległość między podporami A i B
nazywa się rozpiętością ramy
trójprzegubowej l.
RAMY TRÓJPRZEGUBOWE
rozpór
rozpiętość
Cechą charakterystyczną układów trójprzegubowych
jest występowanie na podporach składowych
poziomych reakcji nazwanych rozporem. Reakcje
poziome występują także w przypadku, gdy układów
obciążonych wyłącznie siłami pionowymi.
Wyznaczanie reakcji. W układach trójprzegubowych są cztery
reakcje. Wykorzystujemy trzy równania równowagi (dostępne
dla płaskiego układu sił) oraz dodatkowy warunek zerowania się
momentu zginającego w przegubie (M
C
= 0).
Równanie sumy momentów można zapisać, analizując lewą
lub prawą stronę układu.
Wyznaczenie sił wewnętrznych w przekrojach ram
trójprzegubowych przeprowadza się identycznie jak
dla belek załamanych czy zwykłych ram.
RAMY TRÓJPRZEGUBOWE
W układach ramowych, w których pręty w węzłach łączone są za
pomocą przegubów, istotny jest sposób konstrukcji węzłów.
Węzeł łączący przegubowo trzy pręty
Węzeł łączący przegubowo dwa pręty
RAMY TRÓJPRZEGUBOWE
2 m
20 kN
B
A
C
1m
4 m
I
20 kN
B
A
C
III
H
A
H
B
R
B
R
A
20 kN
B
A
C
II
H
A
H
B
R
A
R
B
25kN
20 kN
H
B
=0
5 kN
H
A
=0
25
N
[kN]
20
5
T [kN]
20
M
[kN
m]
Położenie I
Pręt z lewej strony węzła C może się swobodnie obrócić, a więc układ jest
geometrycznie zmienny. Wyznaczenie reakcji i sił wewnętrznych dla takiego
układu nie jest możliwe.
Położenie II
2
0
0
L
C
A
A
M
H
H
20kN
R
B
=0
10
20
10
M
20
20
[kN
m]
20
T
10
[kN]
Położenie
III
4
0
0
P
C
B
B
M
R
R
N
10
20
[kN]
W obydwu przypadkach, różniących się jedynie położeniem przegubu w
węźle, inne są reakcje i wykresy sił wewnętrznych. Analiza rozwiązania
pozwala stwierdzić, że umieszczając odpowiednio przegub C można
modelować rozkład sił wewnętrznych w układzie.
25kN
20kN
H
B
=0
5 kN
H
A
=0
25
20
5
20
N
M
T
[kN
m]
[kN]
[kN]
Porównanie wykresów
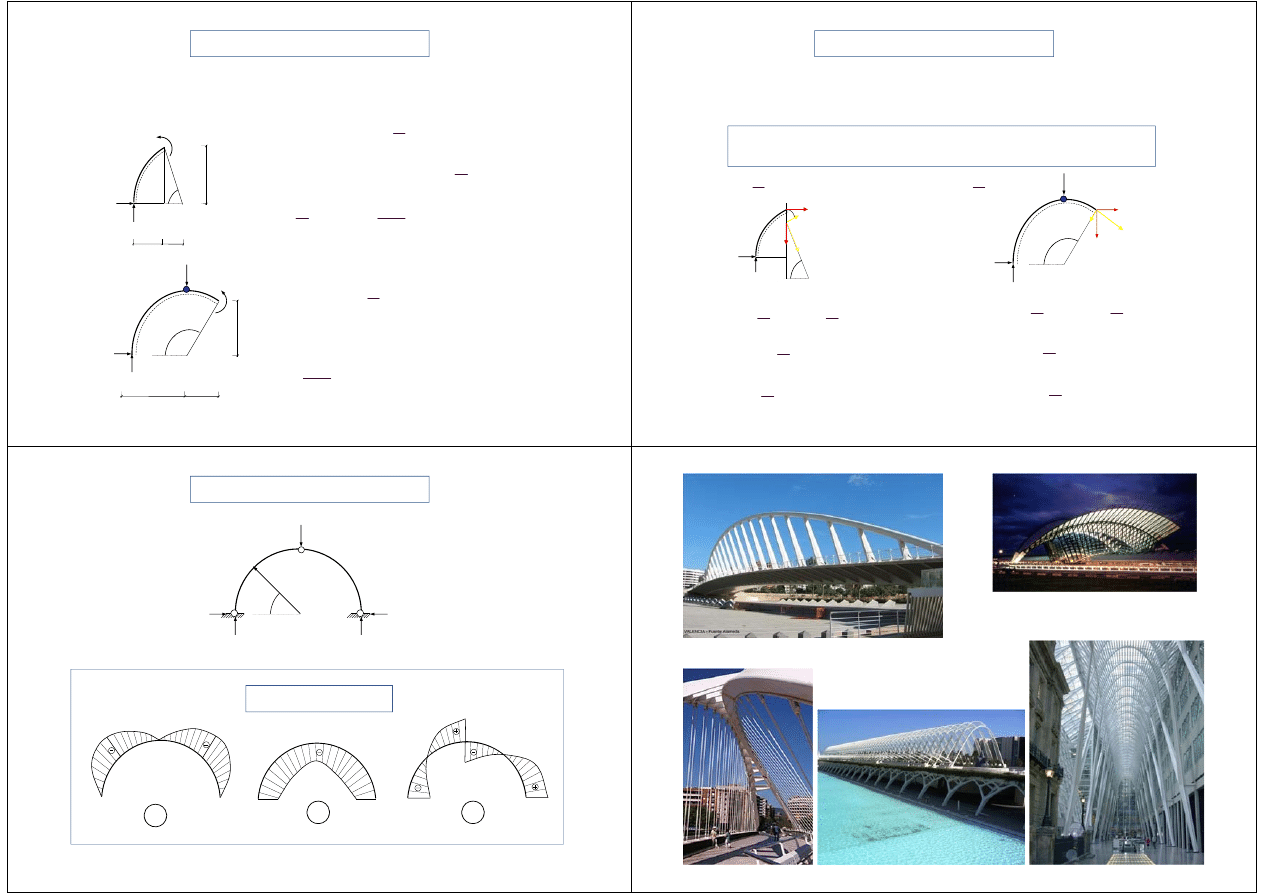
ŁUKI
ŁUKI
ŁUKI
r
Dobrze zaprojektowany i wykonany łuk może być nie tylko konstrukcją o
wyróżniających się walorach estetycznych, ale także układem bardziej
bezpiecznym i ekonomicznym.
Kształtowanie geometrii łuku pozwala zmniejszyć wielkości momentów
zginających i sił poprzecznych, co umożliwia lepsze wykorzystanie materiału.
ŁUKI
Belka o osi zakrzywionej
Łuk trójprzegubowy
paraboliczny
Łuk trójprzegubowy
kołowy
Konstrukcja magazynu i jego schemat statyczny
Współcześnie łuki są stosowane
przede wszystkim w konstrukcjach
o dużych rozpiętościach.
q
P
M
y
y
x
x
A
B
C
f
l/2
l/2
R
A
R
B
P
x
P
y
H
A
q
M
y
x
x
A
B
C
y
H
B
Odległość między podporami l, podobnie jak w belkach lub ramach, nazywa się
rozpiętością łuku, najwyższy punkt – kluczem łuku, a jego wysokość
mierzoną od poziomu podpór – strzałką łuku f.
2
4 f
y
x l
x
l
Kształt łuku można zaprojektować według równań dowolnych krzywych, np.
jako parabole lub wycinki okręgów. Najczęściej stosowane są łuki, których osie
opisane są parabolami
.
ŁUKI
P
x
P
y
N
M
T
H
A
R
A
x
y
y=f(x)
0
0
cos
sin
N
N
T
Momenty zginające oblicza się tak jak dla układów ramowych. Na
wartość M
nie wpływa krzywizna układu, a jedynie położenie
obciążenia względem przekroju
.
Obliczanie sił poprzecznych i podłużnych
0
0
cos
sin
T
T
N
t
T
T
0
N
0
N
W
Kąt nachylenia stycznej
w dowolnym punkcie łuku
2
4
t g
2
dy
f
l
x
dx
l
sin
cos
P=90 kN
H
A
=54
H
B
=54 kN
R
A
=54 kN
R
B
=36 kN
B
C
A
P=90 kN
A
B
C
4 m
5 m
9 m
6 m
l=18 m
f=9 m
D
15
5
6 90
0
54 kN
54 kN
9
9
0
B
A
A
A
L
A
C
A
A
M
R
H
R
H
M
R
H
15
5
9 90
0
36 kN
54 kN
6
4
0
A
B
B
B
P
B
C
B
B
M
R
H
R
H
M
R
H
54 54
0
x
A
B
A
B
P
H
H
H
H
H
54 36 90
0
y
A
B
P
R
R
P
Przykład
Wyznaczenie reakcji podporowych
2
4 9
1
18
18
9
18
y
x
x
x
2
t g
2
9
dy
x
dx
0
0
54 kN
x
P
N
H
54
54
A
M
R x
Hy
x
y
0
54 kN
N
H
54 cos
36sin
36 cos
54 sin
N
T
54
54
90
9
36
54
810
M
x
y
x
x
y
0
0
54 kN
y
A
P
T
R
0
54 90
36 kN
A
T
R
P
H=54 kN
R
A
=54 kN
x
y
N
0
T
0
M
P=90 kN
H=54 kN
R
A
=54 kN
x
y
N
0
T
0
M
54 cos
54 sin
54 cos
54 sin
N
T
Wyznaczenie funkcji sił wewnętrznych
x
[m]
y
[m]
N
[kN]
V
[kN]
M
[kN
m]
0
0
2,000
0,894
0,447
-72,4
-24,1
0
3,0
5,0
1,333
0,800
0,600
-75,6
-10,8
-108
6,0
8,0
0,667
0,555
0,832
-74,9
15,0
-108
9,0
9,0
0,000
0,000
1,000
-54,0
54,0
0
12,0
8,0
-0,667
-0,555
0,832
-64,9
0,0
-54
15,0
5,0
-1,333
-0,800
0,600
-61,2
21,6
0
tg
sin
cos
A
B
C
P=90 kN
N
M
T
24,1
21,6
54
36
121,5
54
[kN]
[kN
m]
[kN]
72,4
61,2
54
Tablica N, T, M
Wykresy N, T, M
q
C
H
A
f
y
H
B
R
B
R
A
A
B
x
l/2
l/2
2
4 f
y
x l
x
l
0
2
2
0
2
2
B
A
A
A
B
B
l
ql
M
R l
ql
R
l
ql
M
R l
ql
R
0
x
A
B
A
B
P
H
H
H
H
H
2
1
0
2
2 4
8
L
C
A
l
l
l
ql
M
R
Hf
q
H
f
Przykład
Wyznaczenie reakcji podporowych
2
2
2
2
1
1
4
( )
0
2
2
2
8
A
ql
ql
f
M
x
R x
qx
Hy
x
qx
x l
x
f l
2
0
0
1
,
,
8
2
ql
N
T
ql
qx
f
2
1
cos
sin
8
2
ql
N
ql
qx
f
Moment zginający jest równy zeru w każdym punkcie łuku.
Siła tnąca jest pochodną momentów zginających, a więc też w każdym
punkcie łuku jest równa zeru T
(x)=0.
q
A
B
N
T
M
2
2
16
8
ql l
f
f
2
8
ql
f
2
2
8
A
ql
R
ql
H
f
q
H
y
R
A
A
x
T
0
N
0
M
Wyznaczenie sił wewnętrznych łuku
Wykresy N, T, M
Konstrukcja, w której występują jedynie ściskające siły normalne, jest w
pewnym sensie konstrukcją idealną. W takim przypadku każdy punkt
przekroju poprzecznego pręta jest jedynie ściskany, co pozwala na bardziej
ekonomiczne wykorzystanie materiału. Tę cechę wykorzystywano już w
starożytności, wykonując łuki z klińców kamiennych.
Rzeczywiste konstrukcje obciążone są jednak w bardziej skomplikowany
sposób niż obciążenie równomierne (np. obciążenie wiatrem). Powoduje to
powstawanie momentów zginających i siły tnących. Jednakże, optymalna
konstrukcja kształtu łuku prowadzi do zerowania się momentu zginającego
od obciążenia ciężarem własnym, które zazwyczaj stanowi główne
obciążenie konstrukcji o dużej rozpiętości.
ŁUKI
r
R
A
R
B
H
A
H
B
A
B
C
P
O
2
0
2
A
B
B
P
M
R
r
P r
R
2
0
2
B
A
A
P
M
R
r
P r
R
0
2
2
L
C
A
A
B
P
P
M
r
H
r
H
H
Przykład
Wyznaczenie reakcji podporowych
Kołowy łuk trójprzegubowy
cos
2
sin
1 cos
sin
2
2
A
A
P
M
R
x
H
y
r
r
P
P r
r
1 cos
sin
cos
2
A
A
M
R
x
H
y
P
x
r
P r
P r
0
2
2
W przypadku łuków kołowych wyrażenia określające siły wewnętrzne
wygodniej jest zapisać w funkcji kąta
.
y
x r-x
O
M
r
H
A
=P/2
R
A
=P/2
O
M
r
P
H
A
=P/2
R
A
=P/2
r
x-r
y
Kołowy łuk trójprzegubowy
0
2
Wzory na siły tnące i normalne dla łuku kołowego różnią się od analogicznych
wyrażeń dla łuku parabolicznego z uwagi na inna definicje kąta
.
P/2
P/2
O
T
N
0
T
0
N
r
P/2
P/2
O
T
N
r
P
T
0
N
0
0
0
,
2
2
P
P
N
T
0
0
,
2
2
P
P
N
T
2
sin
cos
2
sin
cos
2
P
N
P
T
sin
cos
2
sin
cos
2
P
N
P
T
0
0
sin
cos
N
N
T
0
0
cos
sin
T
N
T
Kołowy łuk trójprzegubowy
3
3 1
4
P
3 1
4
P
2
P
2
P
2
P
2
P
2
P
2
P
2
P
M
T
N
3
3 1
4
P
3 1
4
P
r
P/2
A
B
C
P
O
P/2
P/2
P/2
Kołowy łuk trójprzegubowy
Wykresy N, T, M
[kN
m]
[kN]
[kN]
SANTIAGO
CALATRAVA
[
( )]
0
M x
M x
H y
Moment zginający dla linii ciśnień jest w każdym punkcie układu równy zeru:
Dla znalezienia linii ciśnienia dla danego obciążenia, potrzebna jest znajomość
momentu zginającego [M(x)] wyznaczonego dla odpowiedniej belki swobodnie
podpartej.
Aby rozwiązanie było jednoznaczne należy znać położenie jeszcze jednego
punktu układu (oprócz danego położenia podpór).
Przyjmując przykładowo, że wysokość łuku w środku rozpiętości wynosi f,
otrzymuje się następujący dodatkowy warunek:
( 2)
y l
f
( 2)
H
M l
f
LINIA CIŚNIENIA
( )
y
M x
H
Równanie linii ciśnienia
Projektując układ konstrukcyjny według linii ciśnienia zakłada się, że
znane jest obciążenie zewnętrzne i należy wyznaczyć równanie osi
układu w taki sposób, aby występowały w nim tylko siły normalne.
LINIA CIŚNIENIA
q
[H]=0
[R
B
]
[R
A
]
A
B
l/2
l/2
q
y
C
H
f
y
H
R
B
R
A
A
B
x
x
[
]
2
A
x
M
R x
qx
Hy
M
H y
[
]
0
C
C
M
M
H f
[
]
2
A
x
M
R x
qx
2
8
C
M
ql
H
f
f
Rozpór jest tym
większy im
mniejsza jest
strzałka łuku f.
Przykład
3
1
1
( )
6
6
q
M x
qlx
x
l
2
2
16
M l
ql
3
3
( )
8
8
3
3
M x
f
f
y x
x
x
H
l
l
M
l
q [kN/m]
q
[kN/m]
l/2
l/2
f
B
C
A
2
1
( 2)
16
ql
H
M l
f
f
Przykład
Linia ciśnień
/ 2
4
Pl
M l
f
l/2
l/2
P
B
A
C
( 2)
4
Pl
H
M l
f
f
M
P
l/2
l/2
Pl/4
( )
2
P
M x
x
A-C
C-B
( )
2
P
M x
l
x
( )
2
2
4
P
x
M x
f
y x
x
Pl
H
l
f
A-C
2 f
y x
l
x
l
C-B
Przykład
Linia ciśnień
Wyszukiwarka
Podobne podstrony:
MechTeor wyk 8 kratownice bw
MechTeor wyk 6a belki ciagle bw Nieznany
MechTeor wyk 4 oddziływania na konstrukcję biale tlo
MechTeor wyk 6 sily wewnetrzne Nieznany
MechTeor wyk 4 oddziływania na konstrukcję biale tlo
bw wyk Archeologia starożytnego Bliskiego Wschodu Notatka z wykładu, dr hab Dorota Ławec, dr hab pro
EDI wyk
Wyk ad 5 6(1)
zaaw wyk ad5a 11 12
Wyk 02 Pneumatyczne elementy
Automatyka (wyk 3i4) Przel zawory reg
Wyk ECiUL#1 2013
wyk II
Wyk 07 Osprz t Koparki
więcej podobnych podstron