Mechanika ogólna
Mechanika ogólna
1
1
Wykład nr 7
Wykład nr 7
Obliczanie sił wewnętrznych
Obliczanie sił wewnętrznych w
w
ramach.
ramach.
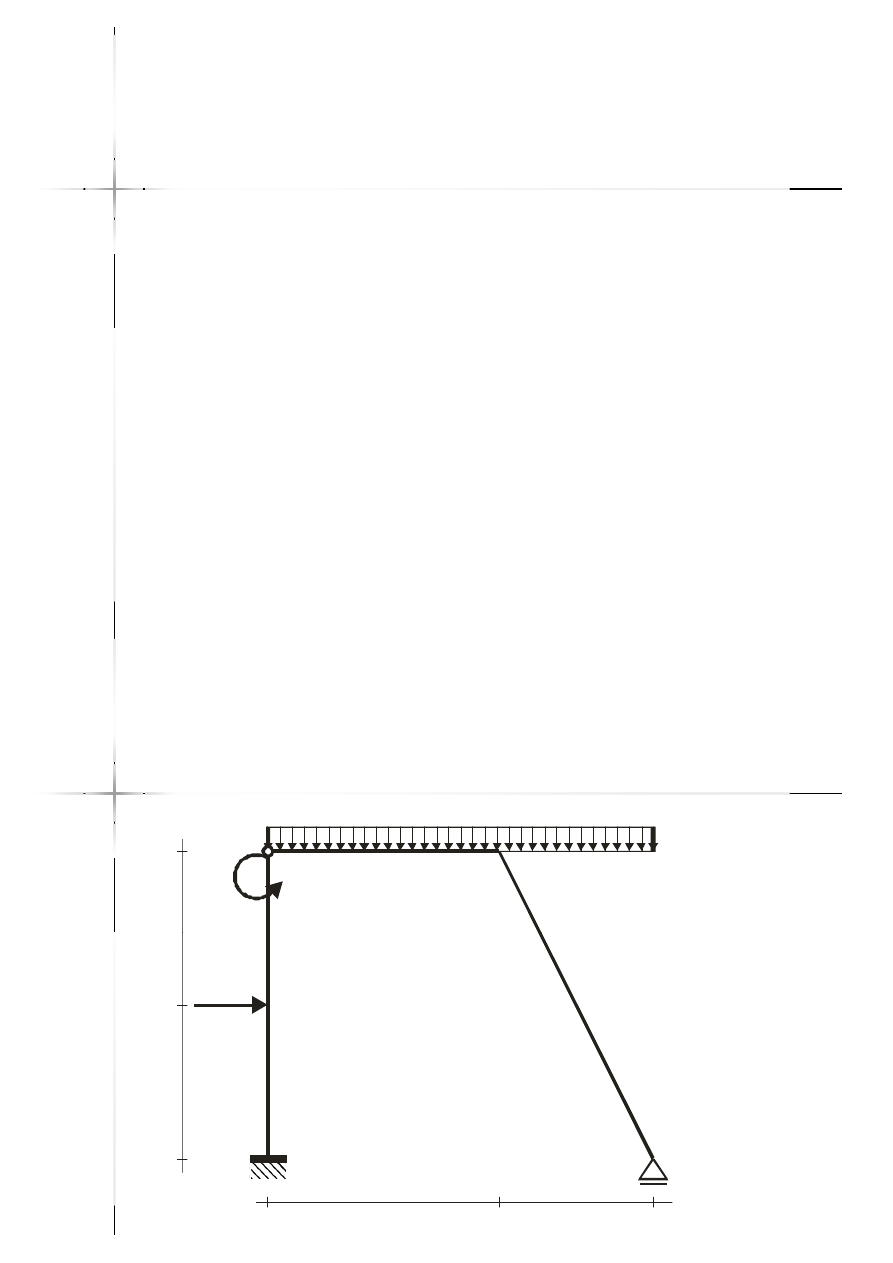
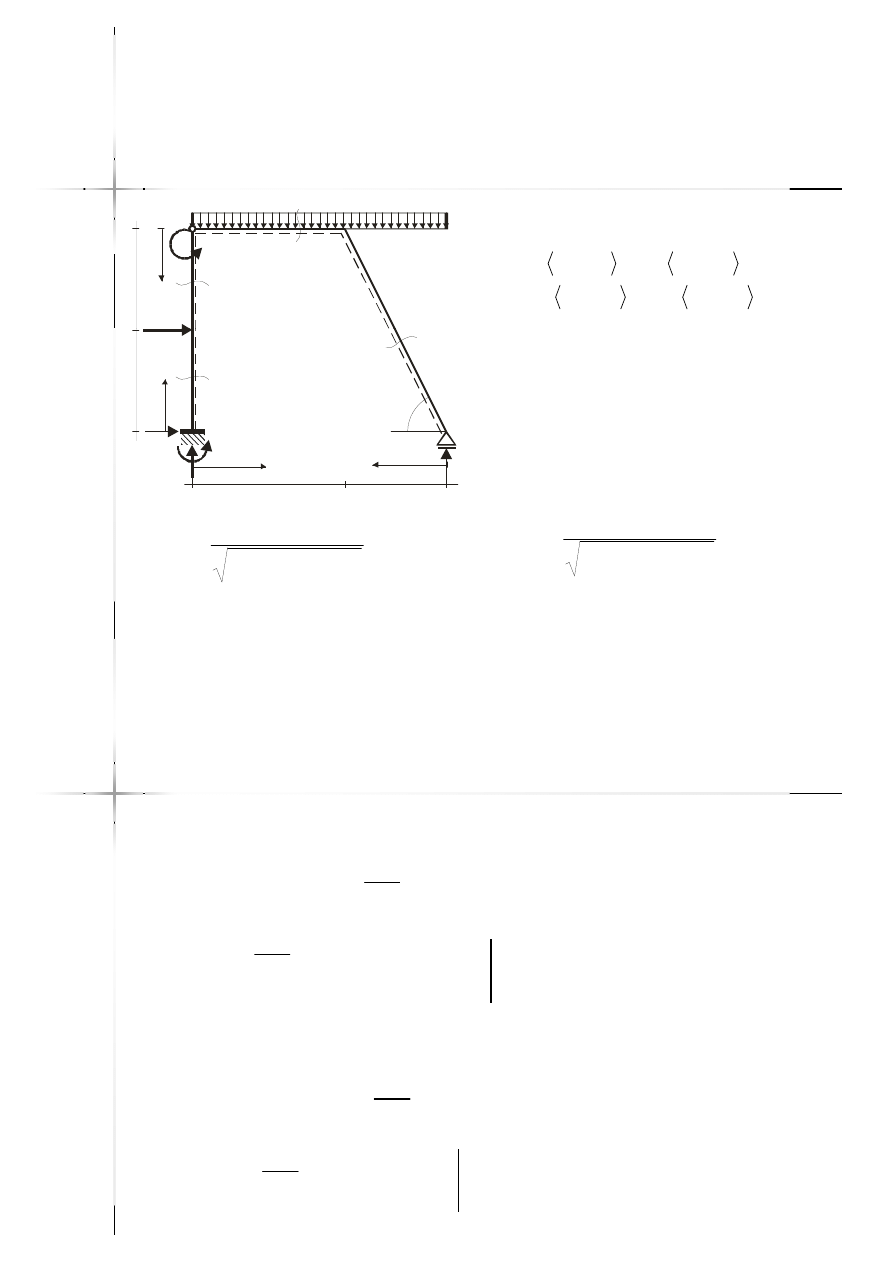
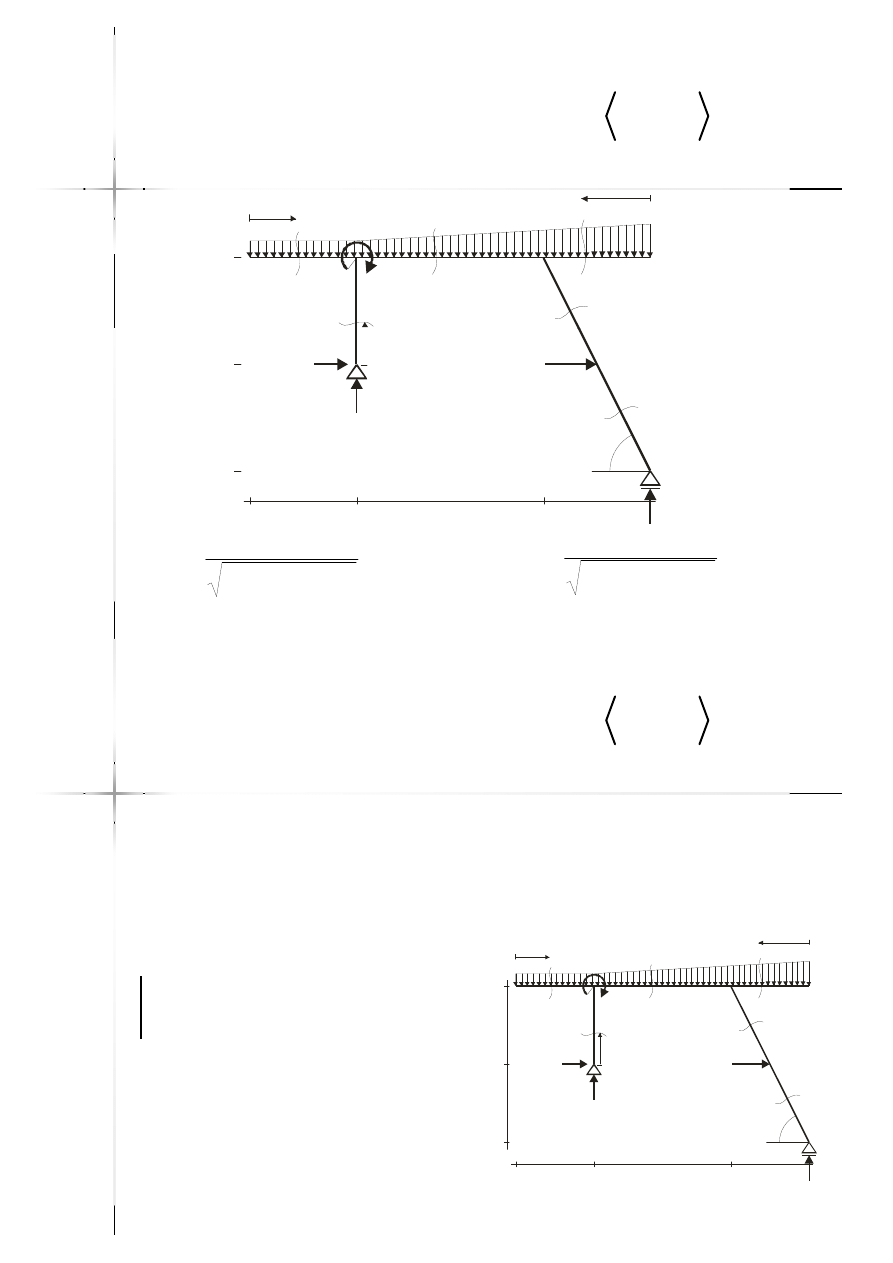
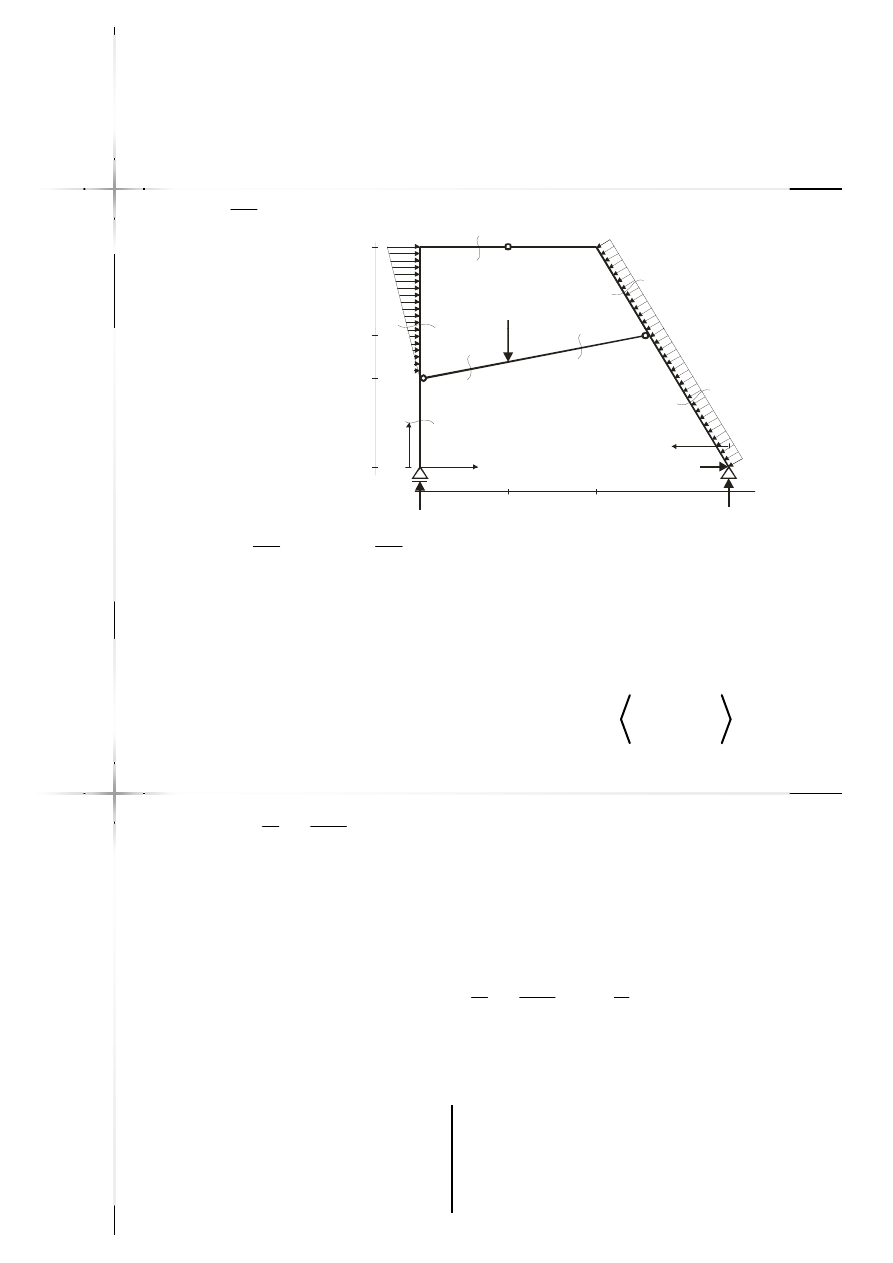
Przykład
Przykład –
– rama
rama
10kNm
15kN/m
2
m
2
2
3m
2
m
20kN
2m
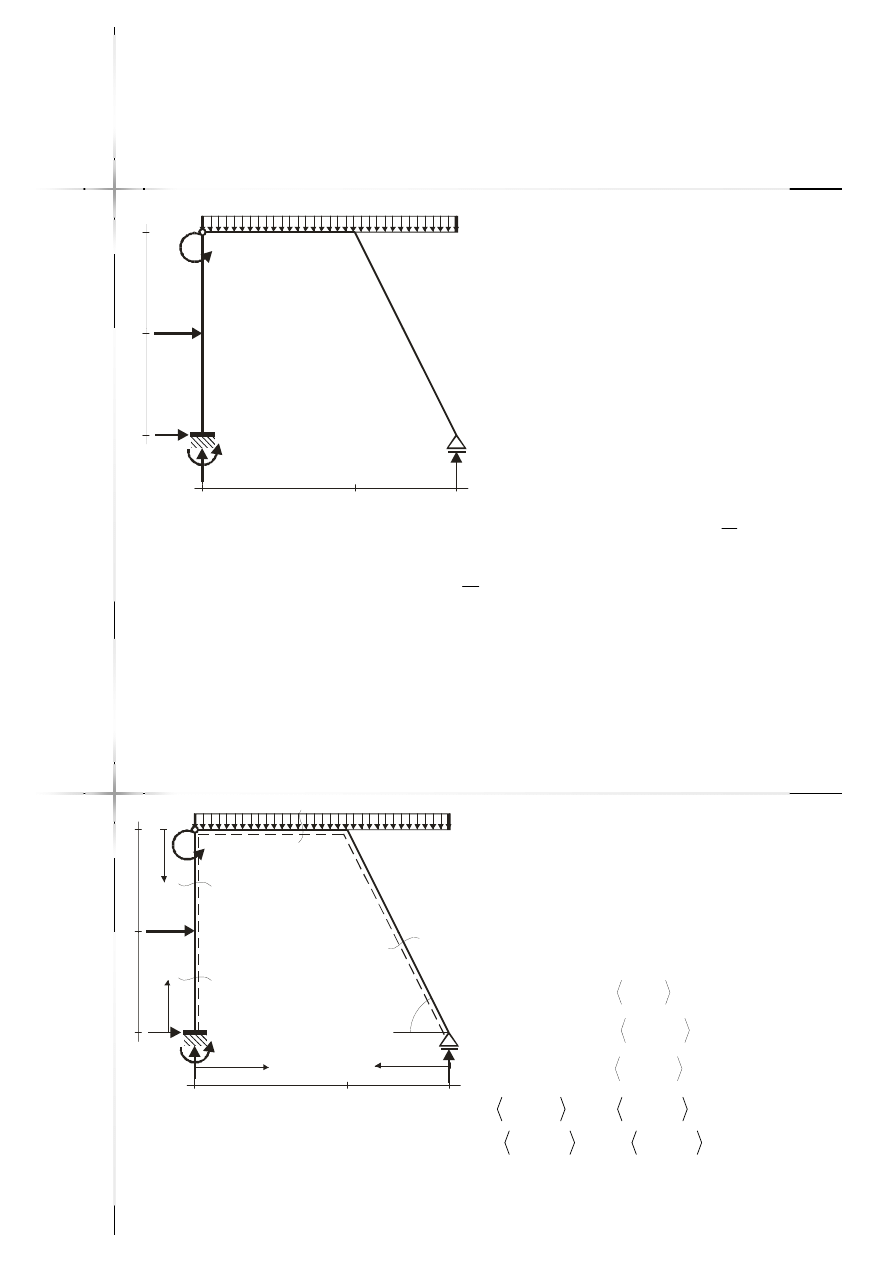
Reakcje
Reakcje
10kNm
15kN/m
2
m
20kN
C
3
3
0
20
:
kN
H
X
A
0
5
15
:
m
kN
R
V
Y
B
A
0
5
2
1
5
/
15
2
20
10
5
:
m
m
m
kN
m
kN
kNm
m
R
M
M
B
A
A
1
:
5
15
/
5
5
0
2
p
C
B
M
R
m
kN m
m
m
3m
2
m
20kN
2m
R
B
V
A
M
A
H
A
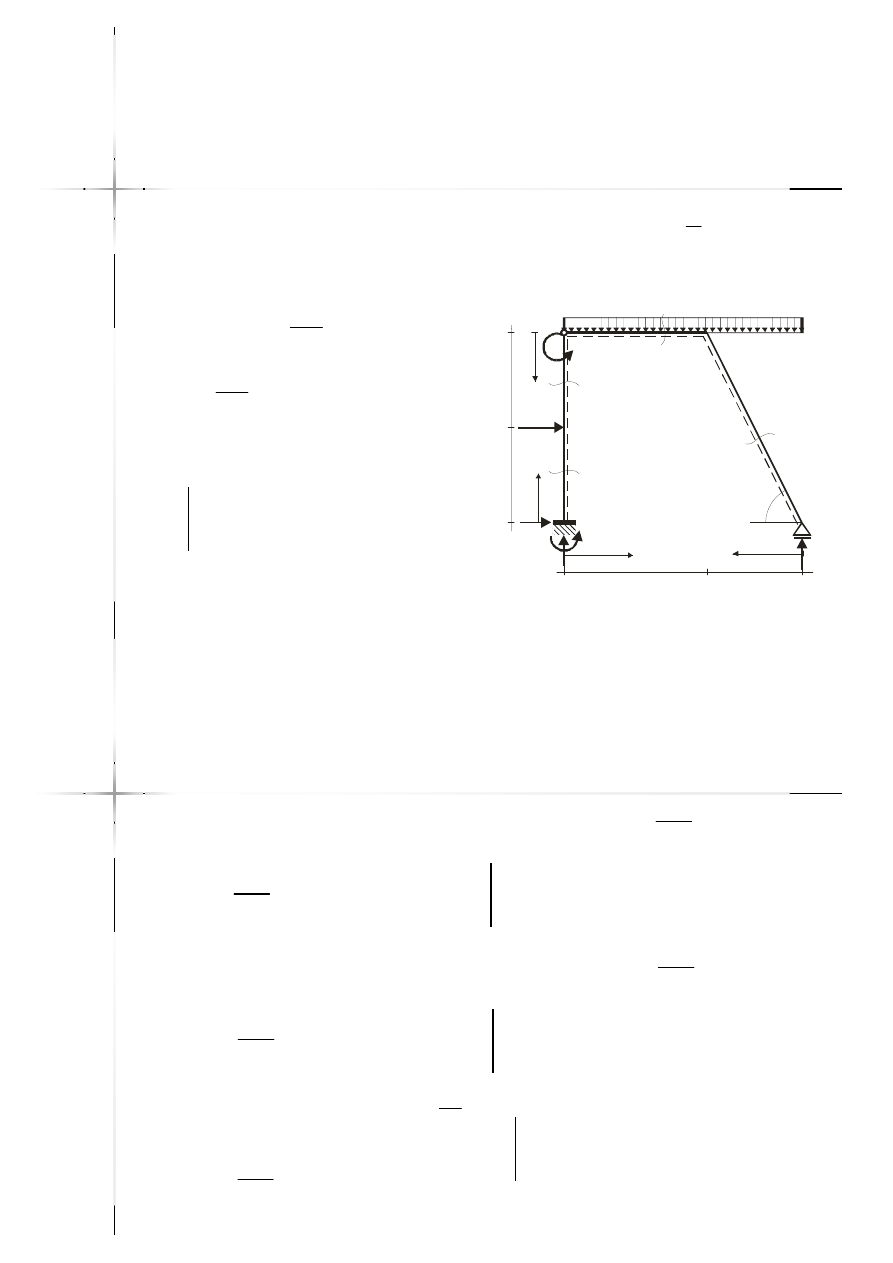
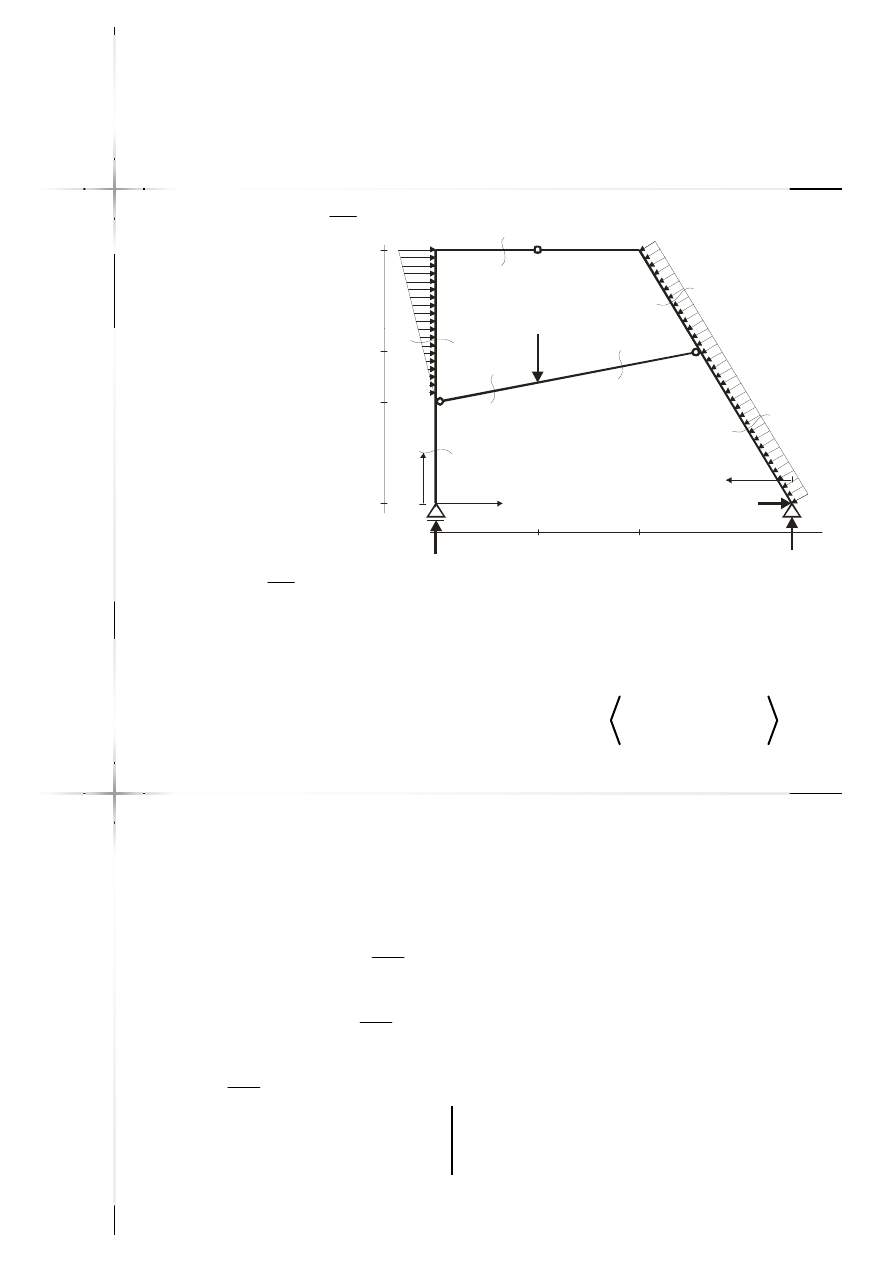
Przyjęcie przekrojów,
Przyjęcie przekrojów,
przedziały
przedziały
kN
H
A
20
kNm
M
30
kN
V
A
5
,
37
kN
R
B
5
,
37
10kNm
15kN/m
2
m
20kN
3
4
2
y’
D
C
4
4
kNm
M
A
30
m
y
2
;
0
1
1
m
m
y
4
;
2
2
2
m
m
x
3
;
0
3
3
4
4
3 ;5
0 ; 4
0 ; 2
0 ; 4
3 ,
4 ,
2 ,
0
5 ,
0,
0,
4
x
m m
y
m m
x
m m
y
m m
punkt D
x
m
y
m
x
m
y
punkt B
x
m
y
x
y
m
3m
2
m
2m
R
B
V
A
M
A
H
A
4
1
x
x’
y
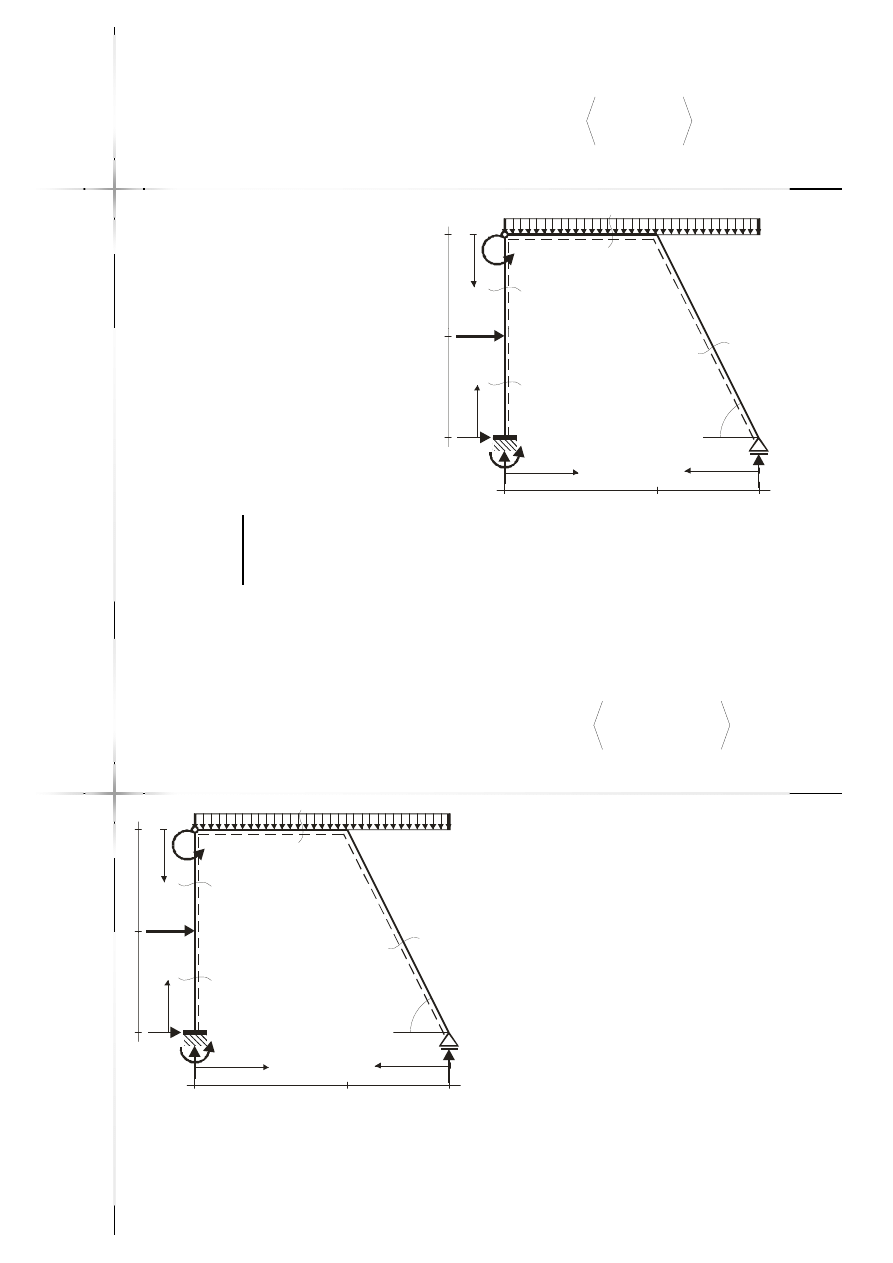
Przekrój
Przekrój
m
y
2
;
0
1
1
kN
V
N
A
5
,
37
1
10kNm
15kN/m
2
m
20kN
3
2
y’
5
5
kN
H
T
A
20
1
kNm
y
kN
y
H
M
M
A
A
30
20
1
kNm
M
m
y
kNm
M
y
10
2
30
0
1
1
3m
2
m
20kN
2m
R
B
V
A
M
A
H
A
4
1
x
x’
y
Przekrój
Przekrój
m
m
y
4
;
2
2
2
10kNm
15kN/m
2
m
20kN
3
4
2
y’
6
6
kN
N
5
,
37
2
0
20
2
kN
H
T
A
2
20
30
20
2
10
M
kN y
kNm
kN
y
m
kNm
3m
2
m
2m
R
B
V
A
M
A
H
A
4
1
x
x’
y
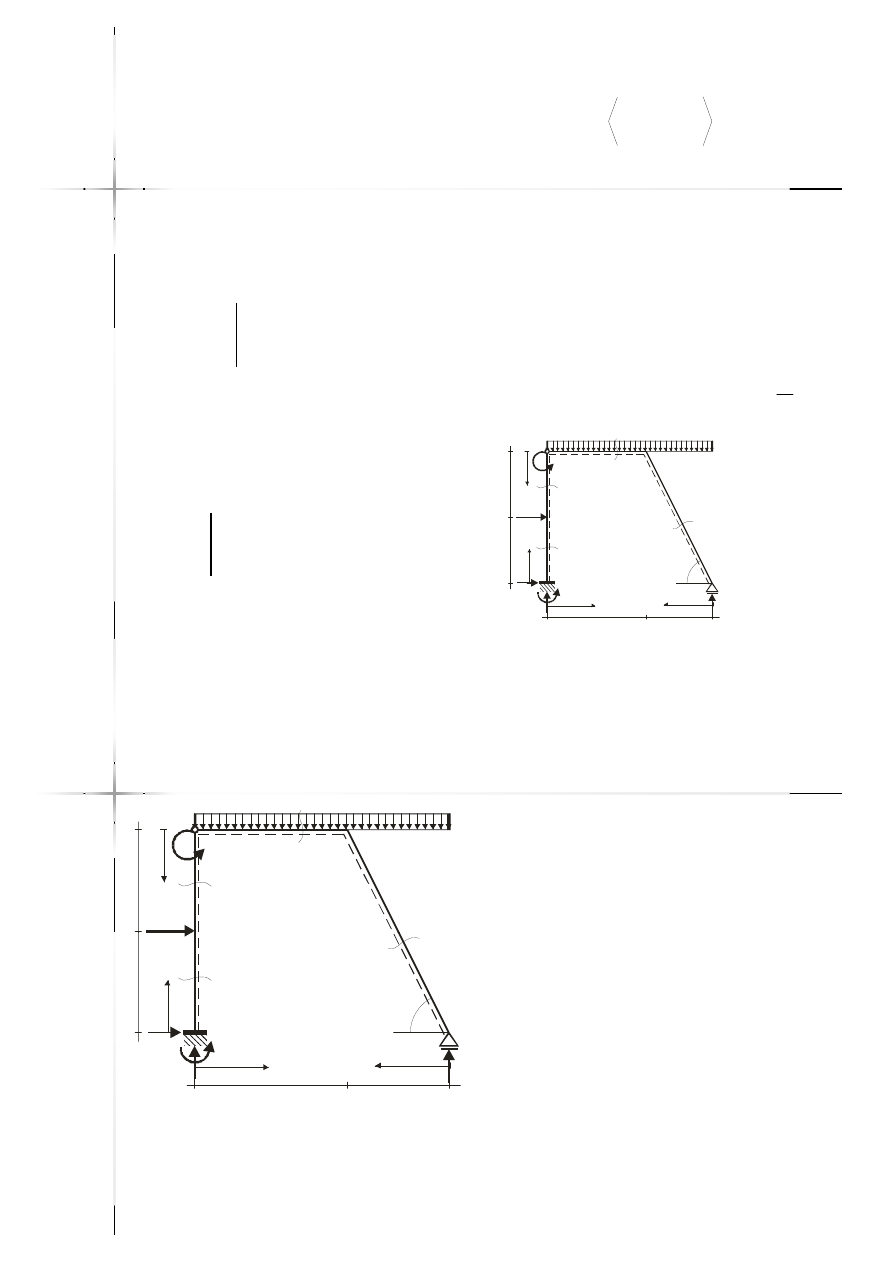
Przekrój
Przekrój
m
x
3
;
0
3
3
0
20
20
20
3
kN
kN
kN
H
N
A
x
m
kN
kN
x
m
kN
V
T
A
/
15
5
,
37
/
15
3
kN
T
m
x
5
,
37
0
3
7
7
3
2
4
20
2
10
15
/
2
7, 5
/
37, 5
A
A
A
x
M
V
x
H
m M
kN
m
kNm
kN m x
kN m x
kN x
kNm
M
m
x
M
m
x
45
3
0
0
3
3
kN
T
m
x
5
,
7
3
3
10kNm
15kN/m
3m
2
m
2
m
20kN
2m
R
B
V
A
M
A
H
A
3
4
1
2
x
x’
y
y’
Ekstremum
Ekstremum
3
37, 5
15
/
0
T
kN
kN m x
2, 5
x
m
10kNm
15kN/m
2
m
20kN
3
4
2
y’
8
8
2
3
7, 5
/
37, 5
M
kN m x
kN x
2, 5
x
m
3
2, 5
46,875
M
m
kNm
3m
2
m
2m
R
B
V
A
M
A
H
A
4
1
x
x’
y
Przekrój
Przekrój
4
4
4
4
3 ;5
0 ; 4
0 ; 2
0 ; 4
3 ,
4 ,
2 ,
0
x
m m
y
m m
x
m m
y
m m
punkt D
x
m
y
m
x
m
y
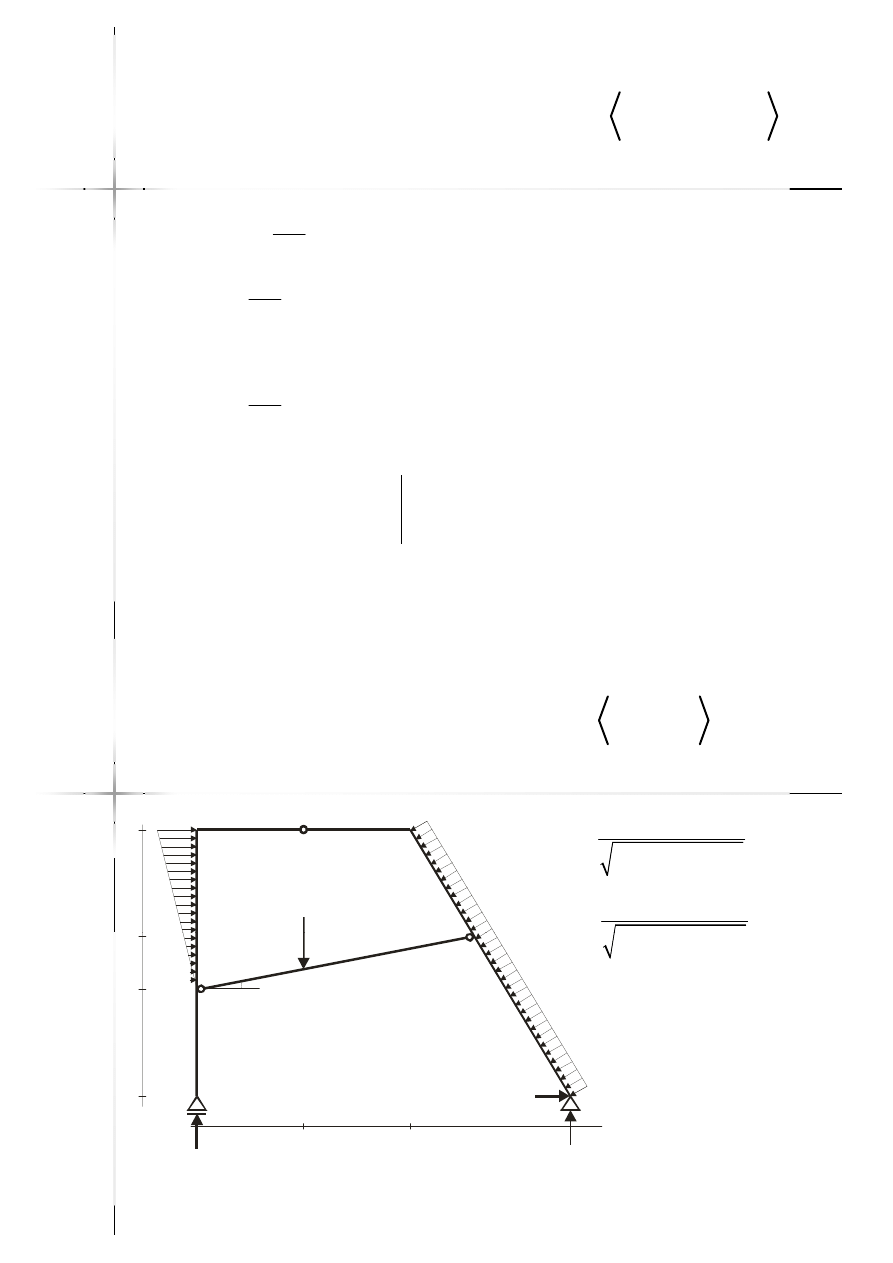
10kNm
15kN/m
2
m
20kN
3
4
2
y’
9
9
3 ,
4 ,
2 ,
0
5 ,
0,
0,
4
punkt D
x
m
y
m
x
m
y
punkt B
x
m
y
x
y
m
894
,
0
2
4
4
sin
2
2
m
m
m
447
,
0
2
4
2
cos
2
2
m
m
m
3m
2
m
2m
R
B
V
A
M
A
H
A
4
1
x
x’
y
Przekrój
Przekrój
(z lewej strony)
(z lewej strony)
4
4
kN
x
m
kN
kN
x
q
V
kN
H
N
A
A
sin
15
sin
5
,
37
sin
sin
cos
20
cos
4
kN
N
m
x
705
,
6
3
10
10
kN
x
m
kN
525
,
33
41
,
13
kN
N
m
x
kN
N
m
x
525
,
33
5
705
,
6
3
4
4
4
sin
20
sin
cos
cos
37, 5
cos
15
cos
6, 705
16, 763
A
A
T
H
kN
V
q x
kN
kN
x
m
kN
x
kN
m
kN
N
m
x
kN
N
m
x
762
,
16
5
352
,
3
3
4
4
4
2
20
2
15
/
10
2
37, 5
20
20
40
30
7, 5
10
A
A
A
x
M
V
x
H
y
kN
y
m
M
kN m x
kNm
kN x
kN y
kN y
kNm
kN
kNm
x
kNm
Przekrój
Przekrój
(z lewej strony)
(z lewej strony)
4
4
15kN/m
3
11
11
2
30
7, 5
10
7, 5
37, 5
kNm
x
kNm
m
kN
x
kN x
m
0
5
45
3
4
4
M
m
x
kNm
M
m
x
10kNm
3m
2
m
2
m
20kN
2m
R
B
V
A
M
A
H
A
4
1
2
x
x’
y
y’
Przekrój
Przekrój
(z prawej strony)
(z prawej strony)
4
4
4
sin
sin
37, 5
sin
15
sin
13, 41
33, 525
B
kN
N
R
q x
kN
x
m
kN
x
kN
m
kN
N
m
x
kN
N
x
705
,
6
2
525
,
33
0
4
4
12
12
4
cos
cos
37, 5
cos
15
cos
6, 705
16, 763
B
kN
T
R
q x
kN
x
m
kN
x
kN
m
kN
N
m
x
kN
N
x
353
,
3
2
763
,
16
0
4
4
x
kN
x
m
kN
x
x
m
kN
x
R
M
B
5
,
37
5
,
7
2
/
15
2
4
kNm
M
m
x
M
x
45
2
0
0
4
4
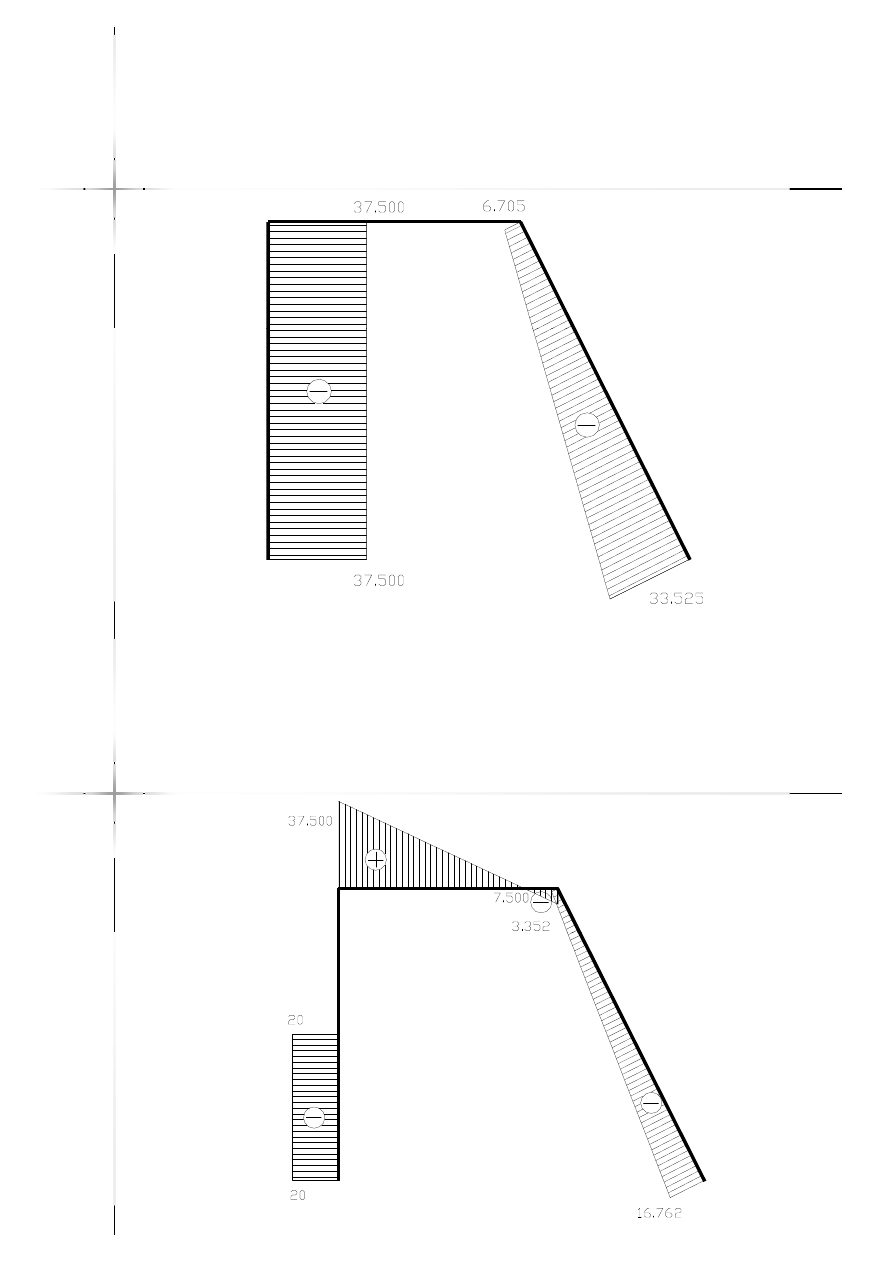
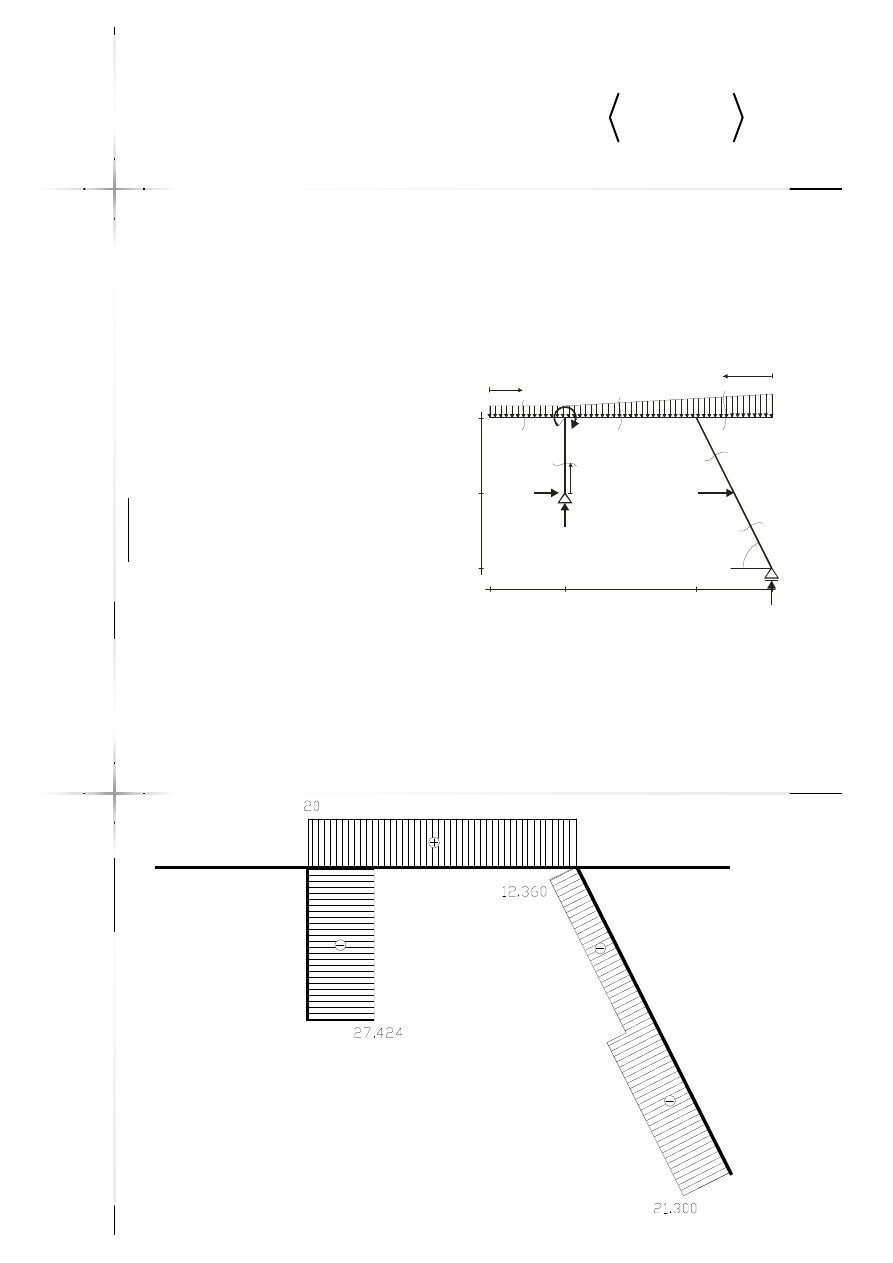
Wykres sił normalnych
Wykres sił normalnych
13
13
N [kN]
Wykres sił tnących
Wykres sił tnących
14
14
T [kN]
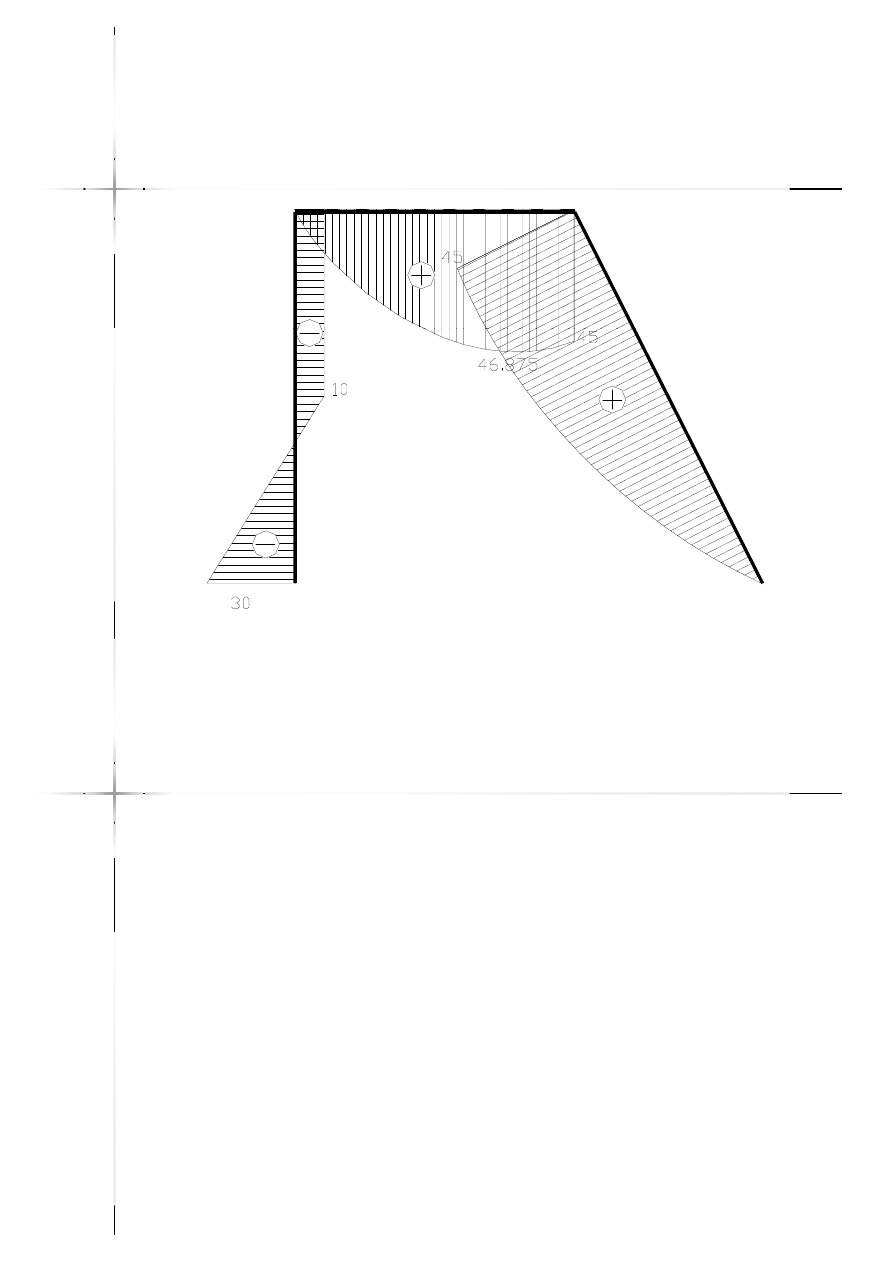
Wykres momentów
Wykres momentów
zginających
zginających
15
15
M [kNm]
Kontrola wyników
Kontrola wyników
Sprawdzenie równowagi ogólnej
Sprawdzenie równowagi ogólnej
–– Suma rzutów sił na nową oś,
Suma rzutów sił na nową oś,
nierównoległą do wcześniej
nierównoległą do wcześniej
16
16
nierównoległą do wcześniej
nierównoległą do wcześniej
wykorzystywanych.
wykorzystywanych.
–– Suma momentów względem dowolnego
Suma momentów względem dowolnego
punktu na płaszczyźnie. Punkt powinien
punktu na płaszczyźnie. Punkt powinien
być dobrany tak, aby jak najwięcej reakcji
być dobrany tak, aby jak najwięcej reakcji
znalazło się w równaniu.
znalazło się w równaniu.
Sprawdzenie równowagi w węzłach:
Sprawdzenie równowagi w węzłach:
Kontrola wyników
Kontrola wyników
T
A-B
N
A-B
P
:
0
A B
A C
A D
X T
N
T
P
17
17
T
A-C
T
A-D
N
A-C
N
A-D
P
M
A-C
M
A-B
M
A-D
M
:
0
A B
A C
A D
Y N
T
N
:
0
A
A B
A C
A D
M
M
M
M
M
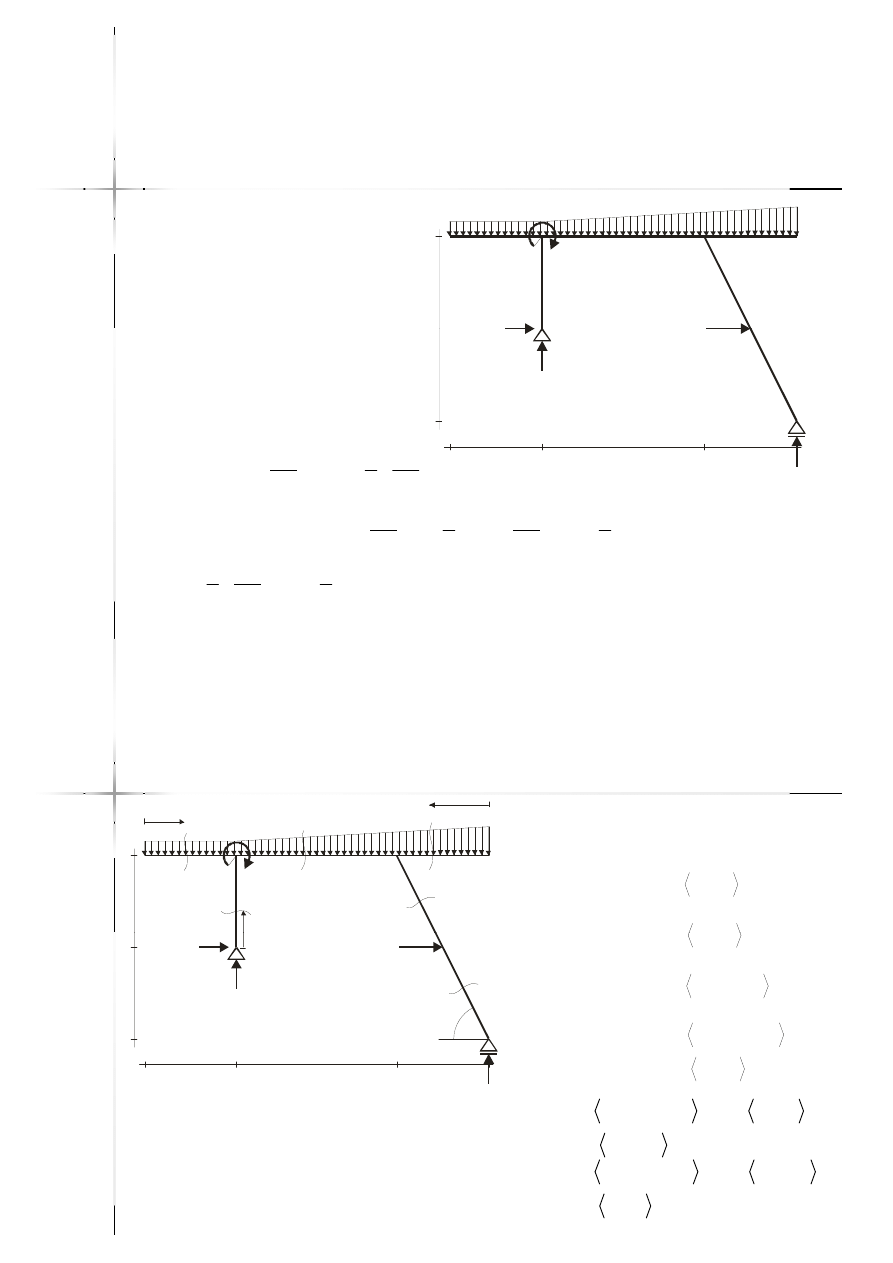
Przykład
Przykład –
– rama
rama
15kNm
5kN/m
2
m
10kN/m
18
18
3,5m
2
m
2
20kN
2m
2m
Reakcje
Reakcje
15kNm
5kN/m
2
m
20kN
10kN/m
H
A
19
19
0
20
:
kN
H
X
A
0
5
,
5
5
2
1
5
,
7
5
:
m
m
kN
m
m
kN
R
V
Y
B
A
0
5
,
5
3
2
5
,
5
5
2
1
5
,
5
2
1
5
,
5
5
2
2
1
2
5
15
5
,
5
:
m
m
m
kN
m
m
m
kN
m
m
m
kN
kNm
m
R
M
B
A
3,5m
2
m
2m
2m
R
B
V
A
Przyjęcie przekrojów,
Przyjęcie przekrojów,
przedziały
przedziały
m
y
2
;
0
1
1
m
x
2
;
0
15kNm
5kN/m
2
m
10kN/m
H
5
1
2
3
4
y
x
x’
20
20
kN
H
A
20
kN
V
A
424
,
27
kN
R
B
826
,
23
m
x
2
;
0
2
2
m
m
x
5
,
5
;
2
3
3
m
x
m
m
x
2
;
0
5
,
7
;
5
,
5
4
4
5
5
5, 5 ; 6, 5
0; 2
1 ; 2
x
m
m
y
m
x
m m
6
6
6, 5 ; 7,5
2 ; 0
0;1
x
m
m
y
m
x
m
3,5m
2
m
20kN
2m
2m
R
B
V
A
H
A
6
y
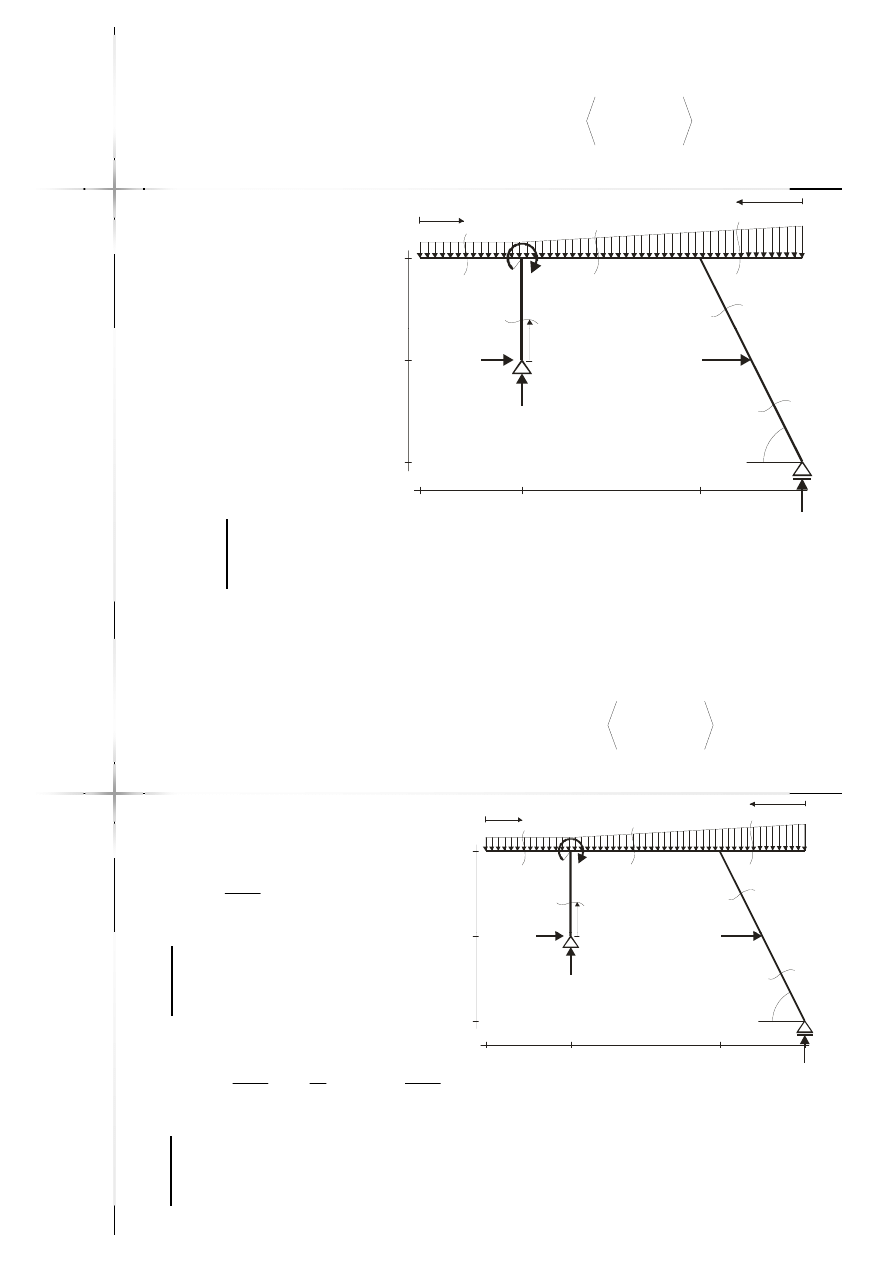
Przekrój
Przekrój
m
y
2
;
0
1
1
kN
V
N
A
424
,
27
1
15kNm
5kN/m
2
m
10kN/m
5
1
2
3
4
x
x’
21
21
kN
H
T
A
20
1
y
kN
y
H
M
A
20
1
kNm
M
m
y
M
y
40
2
0
0
1
1
3,5m
2
m
20kN
2m
2m
R
B
V
A
H
A
6
y
Przekrój
Przekrój
m
x
2
;
0
2
2
0
2
N
x
m
kN
T
5
2
15kNm
5kN/m
2
m
20kN
10kN/m
H
A
5
1
2
3
4
y
x
x’
22
22
2
2
5
,
2
2
5
x
m
kN
x
x
m
kN
M
kN
T
m
x
T
x
10
2
0
0
2
2
kNm
M
m
x
M
x
10
2
0
0
2
2
3,5m
2
m
20kN
2m
2m
R
B
V
A
H
A
6

Przekrój
Przekrój
m
m
x
5
,
5
;
2
3
3
kN
H
N
A
20
3
5
5,5
2
kN
m
m
q
x
m
2
2
0,909
2
0, 909
1,818
kN
kN
kN
q
x
m
x
m
m
m
23
23
3
2
2
2
1
5
2
2
1
27, 424
5
0, 909
1,818
2
2
0, 455
3,182
25, 606
A
kN
T
V
x
q x
m
m
kN
kN
kN
kN
x
x
x
m
m
m
m
kN
kN
x
x
kN
m
m
kN
T
m
x
kN
T
m
x
659
,
5
5
,
5
422
,
17
2
3
3
2
q
x
m
m
m
m
Przekrój
Przekrój
m
m
x
5
,
5
;
2
3
3
3
2
2
5
2
1
1
2
2
15
2
3
A
A
kN
x
M
V
x
m
H
m
x
m
q
x
m
x
m
kNm
kN
24
24
2
2
2
3
2
2
27, 424
2
20
2
2, 5
1
0, 909
1,818
2
15
6
0,156
1, 591
25, 606
1, 364
kN
kN
x
m
kN
m
x
m
kN
kN
x
x
m
kNm
m
m
kN
kN
x
x
kN x
kNm
m
m
kNm
M
m
x
kNm
M
m
x
115
,
68
5
,
5
964
,
44
2
3
3
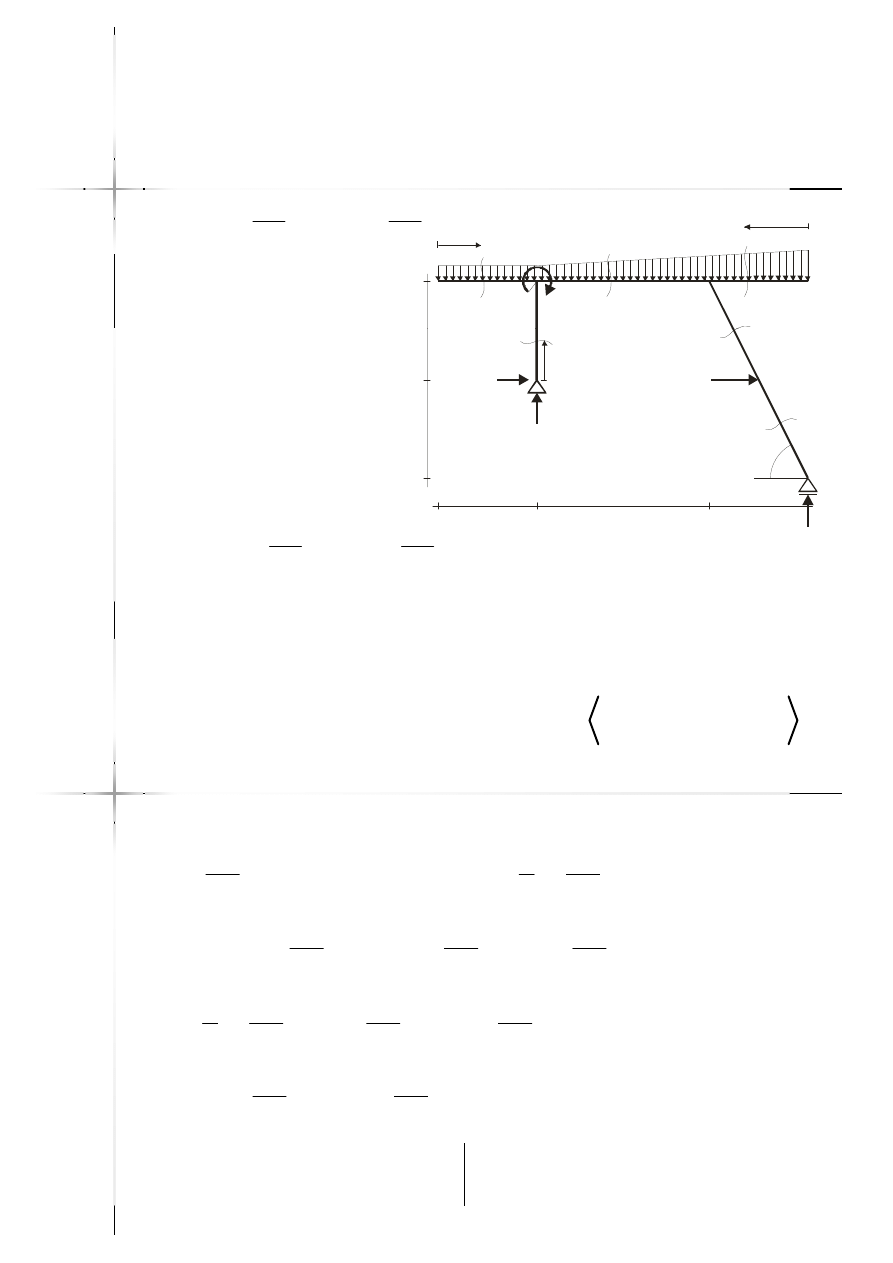
Ekstremum
Ekstremum
2
3
2
0, 455
3,182
25, 606
0
kN
kN
T
x
x
kN
m
m
4, 78
x
m
15kNm
5kN/m
2
m
10kN/m
5
2
3
4
x
x’
25
25
3
2
3
2
0,156
1, 591
25, 606
1, 364
kN
kN
M
x
x
kN x
kNm
m
m
3
4.78
70, 371
M
m
kNm
3,5m
2
m
20kN
2m
2m
R
B
V
A
H
A
1
6
y
Przekrój
Przekrój
4
4
5, 5 ; 7, 5
x
m
m
0
4
N
x
m
kN
x
kN
x
kN
kN
x
m
q
m
kN
x
m
q
x
m
m
kN
T
5
,
7
818
,
1
909
,
0
5
5
,
37
5
,
7
5
2
1
5
,
7
5
,
7
5
4
26
26
kN
x
m
kN
x
m
kN
x
m
m
kN
x
m
kN
m
kN
x
m
m
kN
x
m
kN
x
m
kN
kN
433
,
49
182
,
3
454
,
0
5
,
7
808
.
1
909
,
0
5
2
1
5
,
7
818
,
1
909
,
0
5
5
,
37
2
2
2
2
0
031
,
0
5
,
7
199
,
18
5
,
5
4
4
kN
T
m
x
kN
T
m
x
Przekrój
Przekrój
4
4
5, 5 ; 7, 5
x
m
m
4
1
1
5
7, 5
7, 5
7, 5
7, 5
2
2
1
2
5
7, 5
7, 5
2
3
1
1
kN
M
m
x
m
x
q
m
x
m
x
m
kN
q
m
x
m
x
m
kN
kN
kN
27
27
2
2
2
2
2
3
2
2
1
1
5
7, 5
0, 909
1,818
7, 5
2
2
1
2
5
0, 909
1,818
7, 5
2
3
0,152
1, 591
49,
kN
kN
kN
m
x
m
x
m
m
m
kN
kN
kN
m
x
m
m
m
kN
kN
x
x
m
m
433
217, 331
kN x
kNm
4
4
5, 5
18,886
7, 5
0, 202
0
x
m
M
kNm
x
m
M
kNm
Przekrój
Przekrój
4
4
Zwiększenie dokładności przy
Zwiększenie dokładności przy
xx
w
w
najwyższej potędze (większa liczba
najwyższej potędze (większa liczba
cyfr znaczących):
cyfr znaczących):
28
28
2
4
2
0, 4545
3,182
49, 433
kN
kN
T
x
x
kN
m
m
cyfr znaczących):
cyfr znaczących):
3
2
4
2
0,1515
1, 591
49, 433
217, 331
kN
kN
M
x
x
kN x
kNm
m
m
4
4
4
4
5, 5
18.183
18, 783
7, 5
0, 002
0
0, 009
x
m
T
kN
M
kNm
x
m
T
kN
M
kNm
Przekrój
Przekrój
6
6
0;1
x
m
15kNm
5kN/m
2
m
10kN/m
5
1
2
3
4
x
x’
29
29
894
,
0
2
4
4
sin
2
2
m
m
m
447
,
0
2
4
2
cos
2
2
m
m
m
3,5m
2
m
20kN
2m
2m
R
B
V
A
H
A
6
y
Przekrój
Przekrój
6
6
0;1
x
m
6
sin
23,826
0,894
21, 300
B
N
R
kN
kN
6
cos
23,826
0, 447
10, 650
B
T
R
kN
kN
23,826
M
R
x
kN x
30
30
6
23,826
B
M
R
x
kN x
6
6
0
0
1
23,826
x
M
x
m
M
kNm
15kNm
5kN/m
3,5m
2
m
2
m
20kN
2m
2m
10kN/m
R
B
V
A
H
A
5
1
2
3
4
6
y
x
x’
Przekrój
Przekrój
5
5
1 ; 2
x
m m
5
sin
20 cos
23,826
0,894 20
0, 447
12, 360
B
N
R
kN
kN
kN
5
cos
20 sin
23,826
0, 447 20
0,894
28, 530
B
T
R
kN
kN
kN
31
31
23,826
0, 447 20
0,894
28, 530
kN
kN
kN
5
20
23,826
20
B
M
R
x
y
kN x
kN y
5
5
1
0
23,826
2
2
87, 652
x
m
y
M
kNm
x
m
y
m
M
kNm
15kNm
5kN/m
3,5m
2
m
2
m
20kN
2m
2m
10kN/m
R
B
V
A
H
A
5
1
2
3
4
6
y
x
x’
Wykres sił normalnych
Wykres sił normalnych
32
32
N [kN]
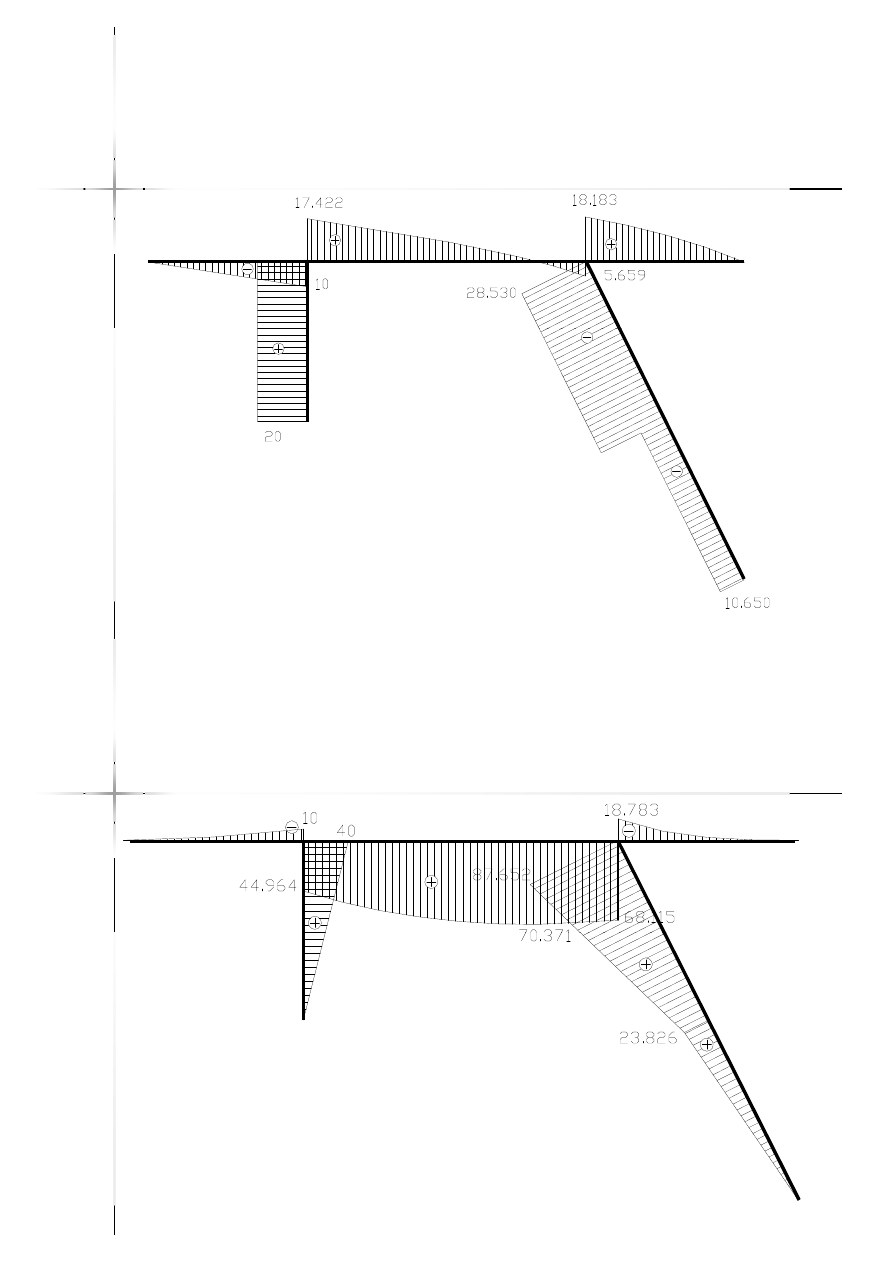
Wykres sił tnących
Wykres sił tnących
33
33
T [kN]
Wykres momentów
Wykres momentów
zginających
zginających
34
34
M [kNm]
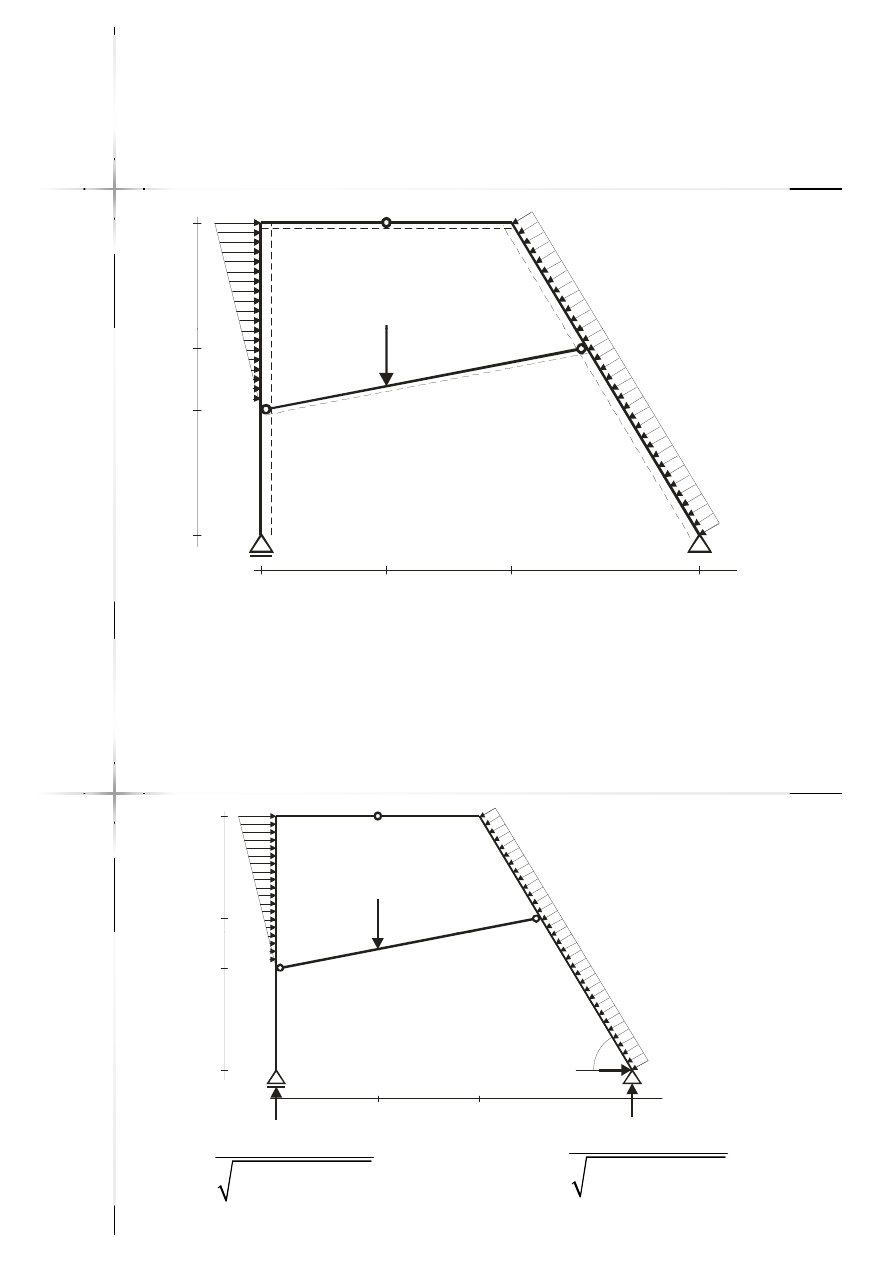
Przykład
Przykład –
– rama ze ściągiem
rama ze ściągiem
2
m
10kN/m
5kN/m
35
35
2
m
2m
2m
3m
1
m
5kN/m
10kN
Reakcje podporowe
Reakcje podporowe
2
m
10kN/m
5kN/m
10kN
36
36
2
2
5
sin
0,857
3
5
m
m
m
2
2
3
cos
0, 514
3
5
m
m
m
2
m
2m
2m
3m
1
m
5kN/m
R
A
V
B
H
B
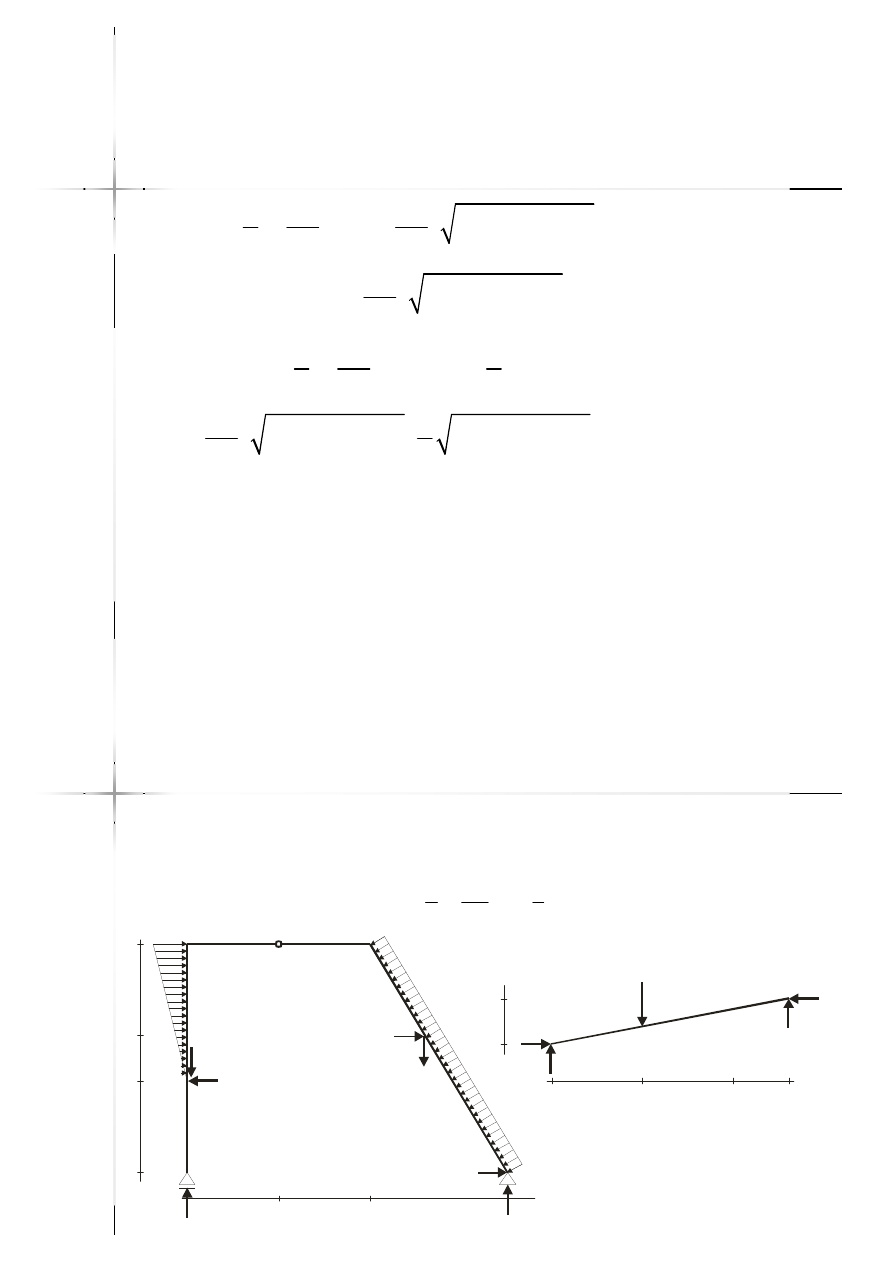
Reakcje podporowe
Reakcje podporowe
2
2
1
:
10
3
5
3
5
sin
0
2
B
kN
kN
X H
m
m
m
m
m
2
2
:
10
5
3
5
cos
0
A
B
kN
Y R
V
kN
m
m
m
37
37
2
2
2
2
1
2
:
7
10
3
2
3
10
5
2
3
1
5
3
5
3
5
0
2
B
A
kN
M
R
m
m
m
m
kN
m
m
kN
m
m
m
m
m
9, 986
B
H
kN
10, 714
A
R
kN
14, 272
B
V
kN
Reakcje w przegubach
Reakcje w przegubach
ściągu
ściągu
:
0
D
E
X H
H
:
10
0
D
E
Y V
V
kN
:
5, 2
1
10
2
0
D
E
E
M
V
m
H
m
kN
m
1
1
:
2
2
3
10
3
3
0
2
3
l
C
A
D
D
kN
M
R
m V
m
H
m
m
m
m
2, 247
D
H
kN
2, 247
E
H
kN
6,586
D
V
kN
3, 414
V
kN
10kN/m
C
38
38
3, 414
E
V
kN
2m
2m
1,2m
1
m
10kN
V
D
V
E
H
D
H
E
2
m
2
m
2m
2m
3m
1
m
10kN/m
5kN/m
5kN/m
R
A
V
B
H
B
V
D
H
D
H
E
V
E
C
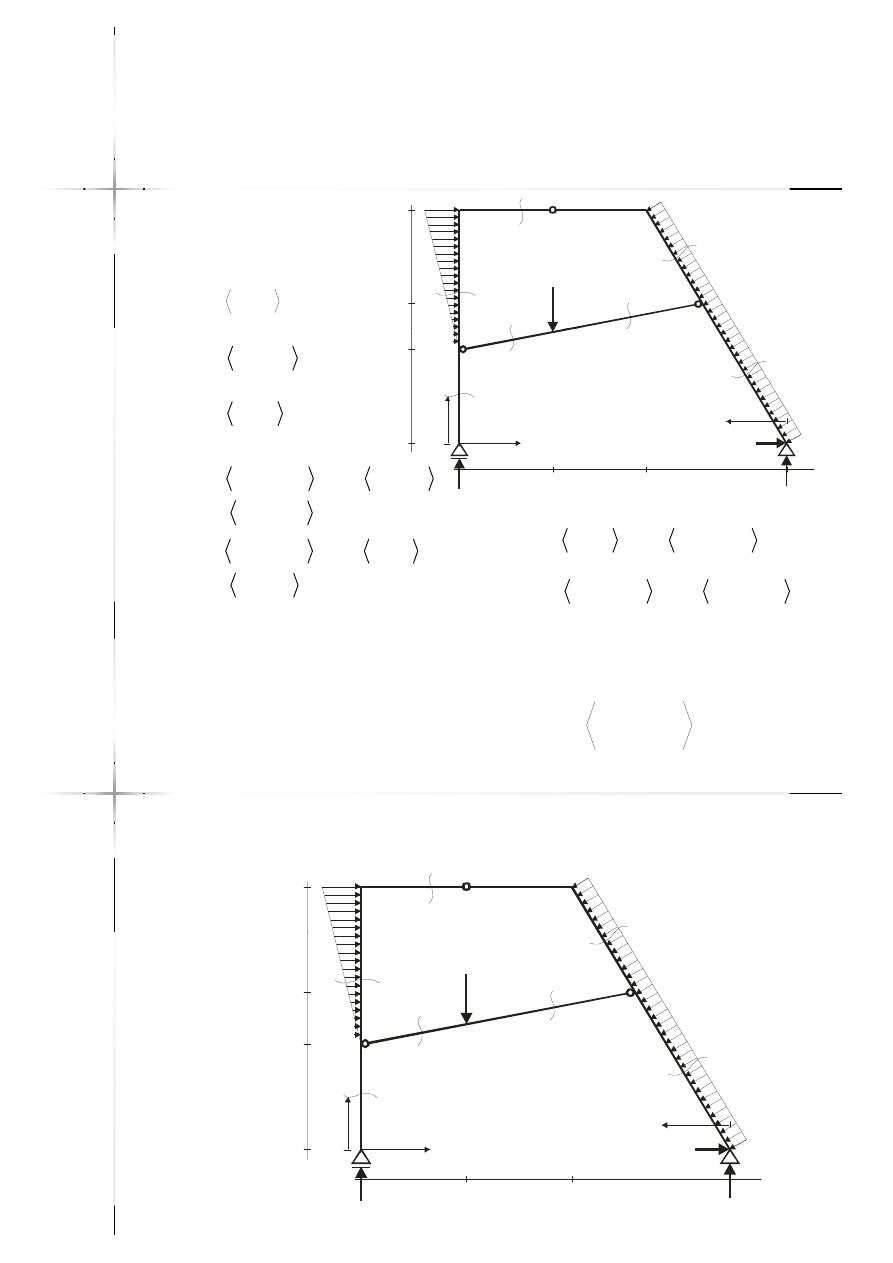
Przyjęcie przekrojów,
Przyjęcie przekrojów,
przedziały
przedziały
m
y
2
;
0
1
1
2
m
m
10kN/m
5kN/m
10kN
2
3
6
7
4
39
39
2
2
2 ;5
y
m m
3
3
0; 4
x
m
4
4
4 ;5, 2
3 ;5
1,8 ;3
x
m
m
y
m m
x
m m
5
5
5, 2 ; 7
0;3
0;1,8
x
m m
y
m
x
m
6
6
0; 2
2 ; 2, 6
x
m
y
m
m
7
7
2 ;5, 2
2, 6 ;3
x
m
m
y
m m
2
m
2m
2m
3m
1
m
5kN/m
R
A
V
B
H
B
1
5
y
x
x’
Przekrój
Przekrój
m
y
2
;
0
1
1
1
10, 714
A
N
R
kN
1
0
T
2
m
10kN/m
5kN/m
3
4
40
40
1
0
M
2
m
2m
2m
3m
1
m
5kN/m
10kN
R
A
V
B
H
B
1
2
6
7
5
y
x
x’
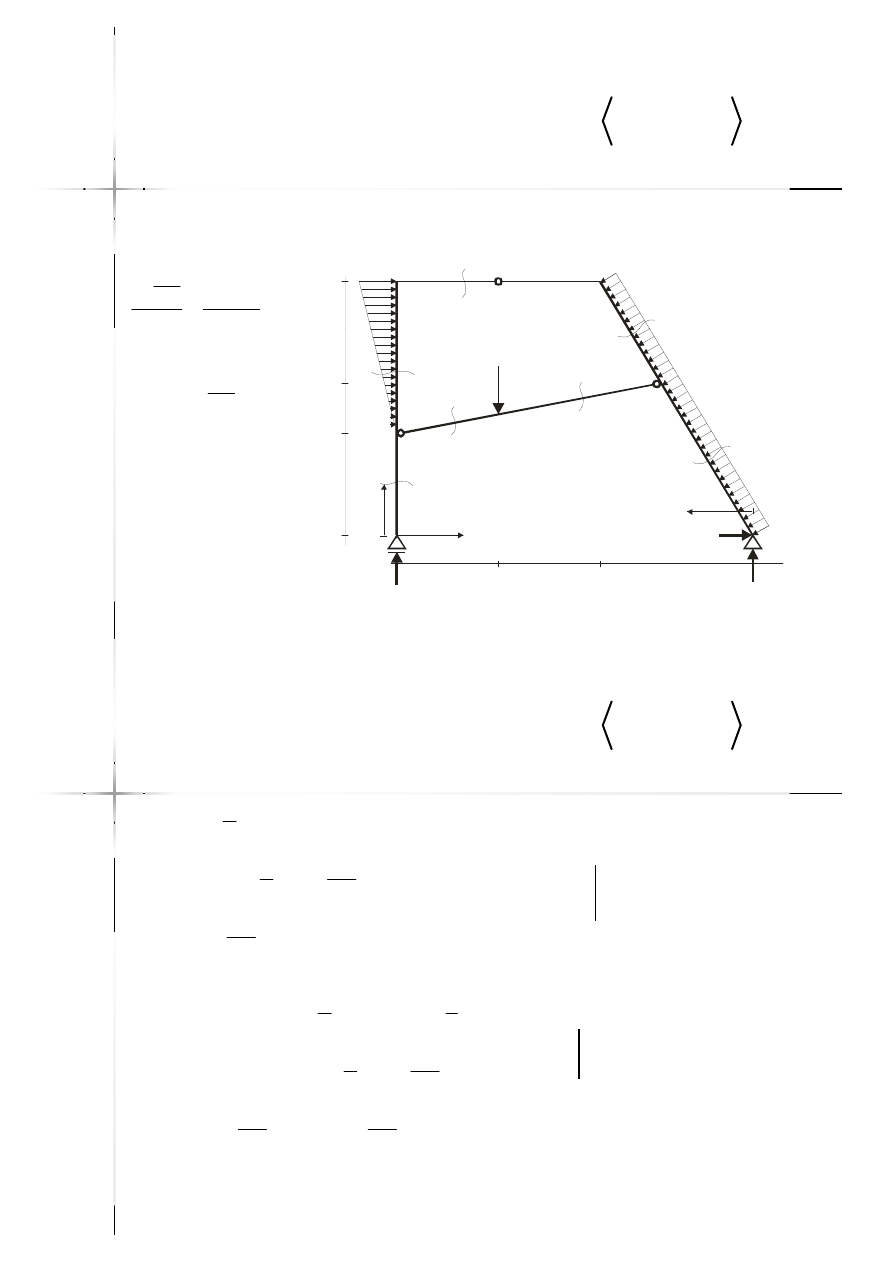
Przekrój
Przekrój
2
2
2 ;5
y
m m
2
10, 714
6, 586
4,128
A
D
N
R
V
kN
kN
kN
10
3
2
kN
m
m
q
y
m
2
m
10kN/m
5kN/m
3
4
41
41
2
q
y
m
2
3, 333
2
kN
q
y
m
m
2
m
2m
2m
3m
1
m
5kN/m
10kN
R
A
V
B
H
B
1
2
6
7
5
y
x
x’
Przekrój
Przekrój
2
2
2 ;5
y
m m
2
2
2
2
1
2
2
1
2, 247
3, 333
2
2
1, 667
6, 666
4.419
D
T
H
q
y
m
kN
kN
y
m
m
kN
y
kN y
kN
2
2
2
2, 245
5
12, 764
y
m T
kN
y
m T
kN
42
42
2
3
2
3
2
2
1
1
2
2
2
2
3
1
2, 247
2
3, 333
2
6
0, 5555
3, 333
4, 419
0, 050
D
M
H
y
m
q
y
m
y
m
kN
kN
y
m
y
m
m
kN
kN
y
y
kN y
kNm
m
m
2
2
2
0
5
8, 258
y
m
M
y
m
M
kNm
2
2
1, 667
6, 666
4.419
kN
y
kN y
kN
m
Ekstremum
Ekstremum
2
2
2
1, 667
6, 666
4.419
0
kN
T
y
kN y
kN
m
3.16
y
m
2
m
10kN/m
5kN/m
10kN
2
3
7
4
43
43
3
2
2
2
0,5555
3, 333
4, 419
0, 050
kN
kN
M
y
y
kN y
kNm
m
m
2
3,16
1.739
M
m
kNm
2
m
2m
2m
3m
1
m
5kN/m
10kN
R
A
V
B
H
B
1
6
7
5
y
x
x’
Przekrój
Przekrój
3
3
0; 4
x
m
3
1
10
3
2
2, 247
15
12, 753
D
kN
N
H
m
m
kN
kN
kN
10, 714
6, 586
4,128
T
R
V
kN
kN
kN
44
44
3
10, 714
6, 586
4,128
A
D
T
R
V
kN
kN
kN
3
3
3
0
8, 259
2
0, 003
0
4
8, 253
x
m
M
kNm
x
m
M
kNm
x
m
M
kNm
3
1
1
3
10
3
3
2
3
10, 714
6, 586
2, 247
3
15
4,128
8, 259
A
D
D
kN
M
R
x V
x
H
m
m
m
m
kN x
kN x
kN
m
kNm
kN x
kNm
Przekrój
Przekrój
5
5
0 ;1,8
x
m
m
5
cos
sin
9, 986
0,514 14, 272
0,857
7, 098
B
B
N
H
V
kN
kN
kN
2
2
sin
cos
5
kN
T
H
V
x
y
45
45
2
2
5
2
2
2
2
sin
cos
5
9, 986
0,857 14, 272
0, 514 5
15,894
5
15,894
9, 720
B
B
T
H
V
x
y
m
kN
kN
kN
x
y
m
kN
kN
x
y
m
kN
kN
x
m
5
5
0
15,894
1,8
1, 602
x
m T
kN
x
m T
kN
2
2
2
2
5
2
2
1
5
2
14, 272
9,986
2, 5
B
B
kN
M
V
x
H
y
x
y
x
y
m
kN
kN x
kN y
x
y
m
Przekrój
Przekrój
5
5
0 ;1,8
x
m
m
46
46
5
5
0
0
1,8
25, 046
x
M
x
m
M
kNm
2
2
2
14, 272
9, 986
1, 667
2, 5
1, 667
9, 447
30, 919
m
kN
kN x
kN
x
x
x
m
kN
x
kN x
m
Ekstremum
Ekstremum
5
15,894
9, 720
0
kN
T
kN
x
m
1.635
x
m
2
m
10kN/m
5kN/m
3
4
47
47
2
5
9, 447
30,919
kN
M
x
kN x
m
5
1.635
25.299
M
m
kNm
2
m
2m
2m
3m
1
m
5kN/m
10kN
R
A
V
B
H
B
1
2
6
7
5
y
x
x’
Przekrój
Przekrój
4
4
1,8 ; 3
x
m
m
4
7, 098
cos
sin
7, 098
2, 247
0, 514 3, 414
0,857
3, 008
E
E
N
kN
H
V
kN
kN
kN
kN
kN
48
48
4
15,894
9, 720
sin
cos
15,894
9, 720
2, 247
0,857 3, 414
0, 514
9, 720
16, 065
E
E
kN
T
kN
x
H
V
m
kN
kN
x
kN
kN
m
kN
x
kN
m
4
4
0
1, 431
1,8
13, 095
x
T
kN
x
m T
kN
Przekrój
Przekrój
2
4
2
9, 447
30, 919
3
1,8
9, 447
30, 919
2, 247
1, 667
3
E
E
kN
M
x
kN x
H
y
m
V
x
m
m
kN
x
kN x
kN
x
m
m
4
4
1,8 ; 3
x
m
m
49
49
4
4
1,8
25, 048
3
8,134
x
m
M
kNm
x
m
M
kNm
2
3, 414
1,8
9, 447
31, 251
0, 596
m
kN
x
m
kN
x
kN x
kNm
m
Przekrój
Przekrój
6
6
0; 2
x
m
2
2
1
sin
0,189
1
5, 2
m
m
m
2
2
5, 2
cos
0, 982
1
5, 2
m
m
m
2
m
10kN/m
5kN/m
10kN
50
50
2
2
1
5, 2
m
m
2
m
2m
2m
3m
1
m
5kN/m
10kN
R
A
V
B
H
B
Przekrój
Przekrój
6
6
0; 2
x
m
6
cos
sin
2, 247
0, 982 6, 586
0,189
3, 451
D
D
N
H
V
kN
kN
kN
2m
2m
1,2m
1
m
10kN
V
D
V
E
H
D
H
E
6
7
51
51
6
6
0
0
2
12, 308
x
m
M
x
m
M
kNm
6
2
2, 247
2
2
6, 586
5, 2
0, 432
6, 586
6,154
D
D
M
H
y
m
V
x
x
kN
m
m
kN x
x
x
x
2, 247
0, 982 6, 586
0,189
3, 451
kN
kN
kN
6
sin
cos
2, 247
0,189 6, 586
0, 982
6, 043
D
D
T
H
V
kN
kN
kN
Przekrój
Przekrój
7
7
2 ;5, 2
x
m
m
7
3, 451
10
sin
3, 451
10
0,189
1, 561
N
kN
kN
kN
kN
kN
7
6, 043
10
cos
T
kN
kN
52
52
7
6, 043
10
cos
6, 043
10
0, 982
3, 777
T
kN
kN
kN
kN
kN
7
6,154
10
2
3,846
20
M
x
kN
x
m
x
kNm
7
7
2
12, 308
5, 2
0, 001
0
x
m
M
kNm
x
m
M
kNm
2m
2m
1,2m
1
m
10kN
V
D
V
E
H
D
H
E
6
7
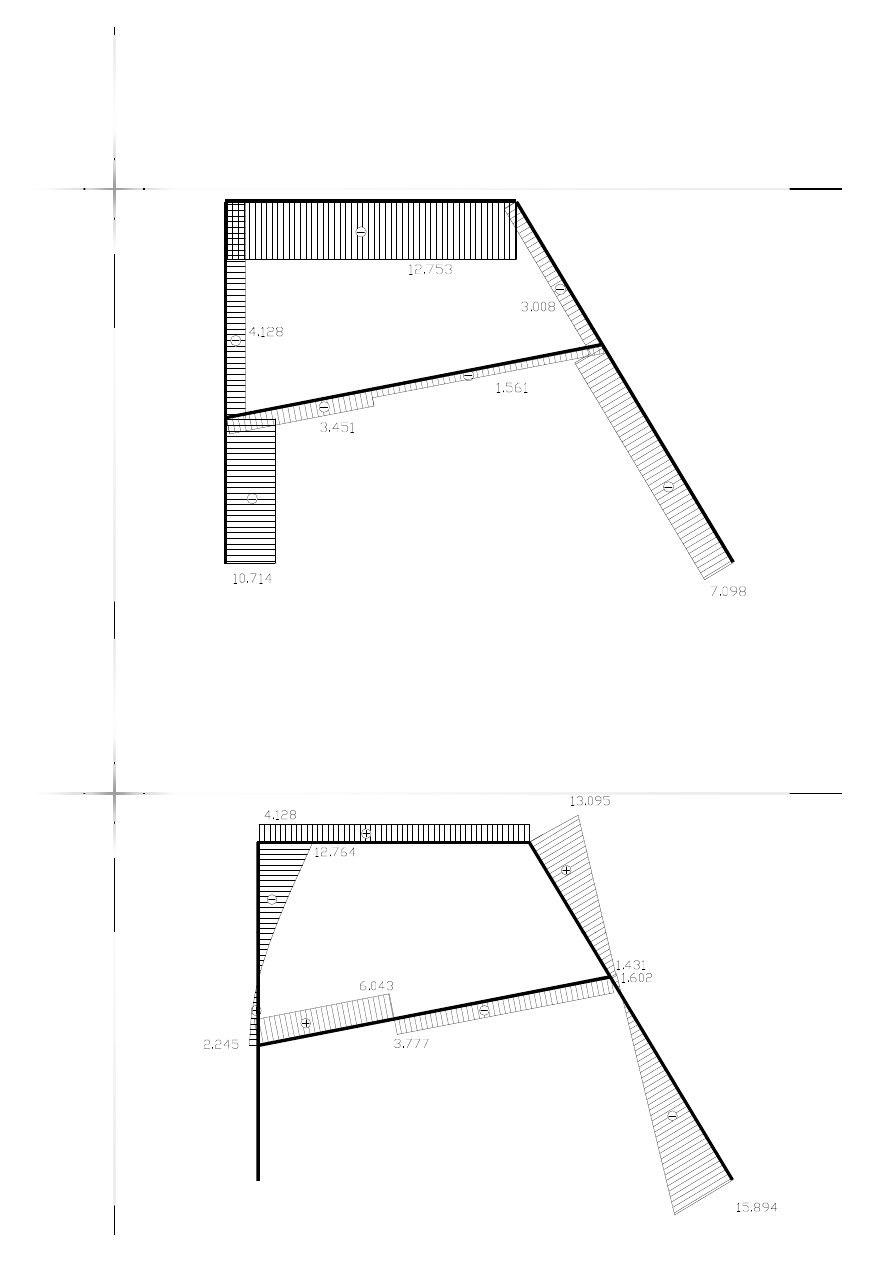
Wykres sił normalnych
Wykres sił normalnych
53
53
N [kN]
Wykres sił tnących
Wykres sił tnących
54
54
T [kN]
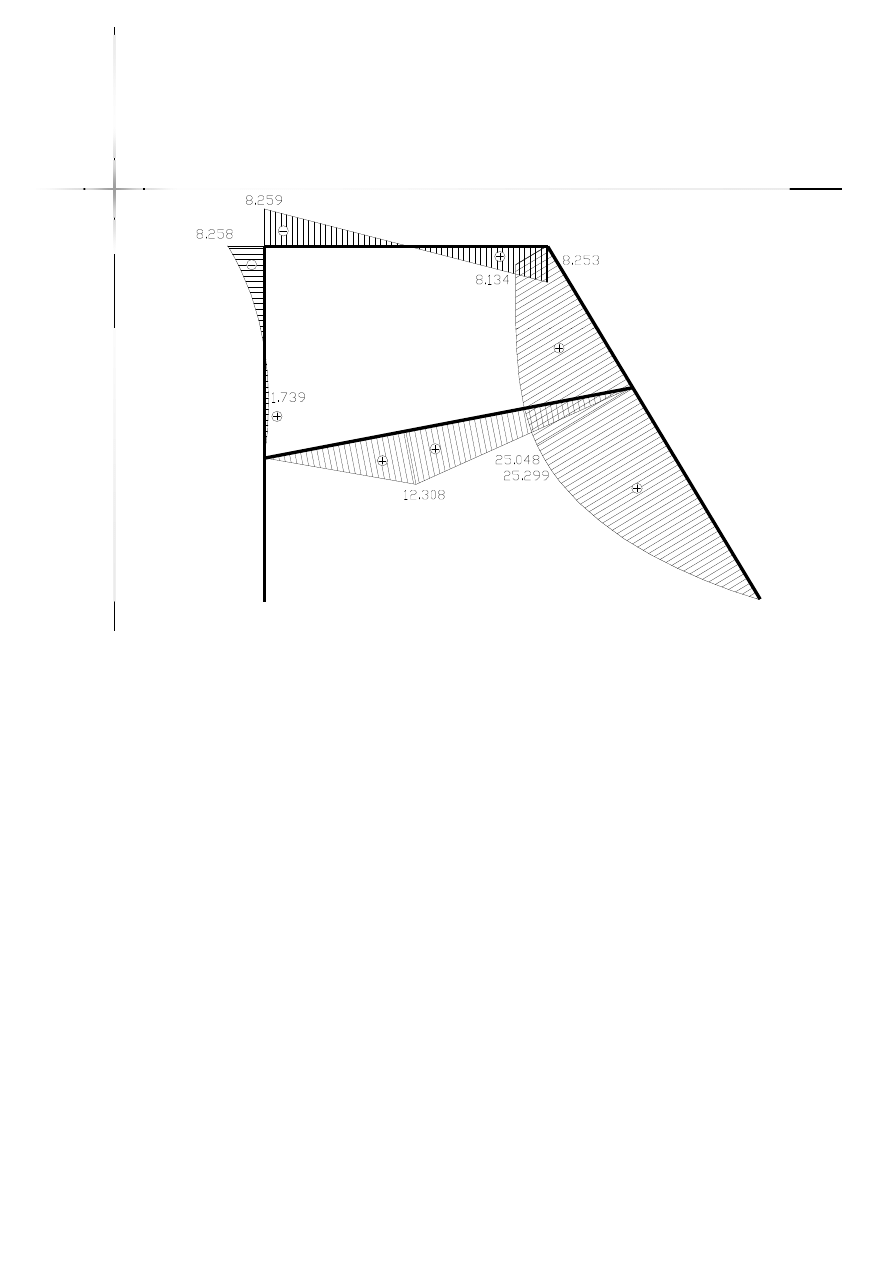
Wykres momentów
Wykres momentów
zginających
zginających
55
55
M [kNm]
Wyszukiwarka
Podobne podstrony:
Belki proste Siły wewnętrzne 3
Belki proste Siły wewnętrzne
Druzga, wytrzymałość materiałów Ć,SIŁY WEWNĘTRZNE
MechTeor wyk 6 sily wewnetrzne Nieznany
notatek pl sily wewnetrzne i odksztalcenia w stanie granicznym
Siły wewnętrzne w ustrojach statycznie wyznaczalnych, Energetyka Politechnika Krakowska Wydział Mech
siły wewnetrzne
Arch 2011 W4 Warunki równowagi Siły wewnętrzne
Druzga, wytrzymałość materiałów Ć, siły wewnętrzne zadania
5 Statyczna wyznaczalność układu Siły wewnętrzne
SILY WEWNETRZNE, Studia, Budownictwo Ladowe i Wodne, Semestr II, Mechanika ogolna
Siły wewnętrzne
Belki proste Siły wewnętrzne 2
Belki proste Siły wewnętrzne 3
Siły wewnętrzne
Belki proste Siły wewnętrzne 2
Sily wewnętrzne 1
więcej podobnych podstron