Mechanika ogólna

Mechanika ogólna

1

1

Wykład

Wykład nr 5

nr 5

Statyczna

Statyczna wyznaczalność układu.

wyznaczalność układu.

Siły wewnętrzne.

Siły wewnętrzne.

Stopień statycznej

Stopień statycznej

wyznaczalności

wyznaczalności





Stopień zewnętrznej statycznej

Stopień zewnętrznej statycznej

wyznaczalności n:

wyznaczalności n:

–– Belka:

Belka: n=r

n=r--gg--rs

rs;;

–– Rama: n=r+3o

Rama: n=r+3o--gg--rs;

rs;

2

2

–– Rama: n=r+3o

Rama: n=r+3o--gg--rs;

rs;

–– Kratownica:

Kratownica: n=r

n=r--rs

rs lub n=p

lub n=p--2w.

2w.





Oznaczenia:

Oznaczenia:

–– rr –– liczba reakcji;

liczba reakcji;

–– g

g –– liczba przegubów pojedynczych;

liczba przegubów pojedynczych;

–– o

o –– liczba pól zamkniętych;

liczba pól zamkniętych;

–– rs=3

rs=3 –– liczba równań statyki;

liczba równań statyki;

–– p

p –– liczba prętów;

liczba prętów;

–– w

w –– liczba węzłów.

liczba węzłów.

Stopień statycznej

Stopień statycznej

wyznaczalności

wyznaczalności





Określenie stopnia statycznej

Określenie stopnia statycznej

wyznaczalności odnośnie do reakcji:

wyznaczalności odnośnie do reakcji:

–– Układ jest

Układ jest statycznie wyznaczalny

statycznie wyznaczalny,

,

3

3

–– Układ jest

Układ jest statycznie wyznaczalny

statycznie wyznaczalny,

,

jeżeli współczynnik n = 0;

jeżeli współczynnik n = 0;

–– Układ jest

Układ jest statycznie niewyznaczalny

statycznie niewyznaczalny,

,

jeżeli współczynnik n

jeżeli współczynnik n > 0;

> 0;

–– Układ jest

Układ jest geometrycznie zmienny

geometrycznie zmienny,

,

jeżeli współczynnik n

jeżeli współczynnik n < 0.

< 0.

Sposób podparcia a

Sposób podparcia a

statyczna wyznaczalność

statyczna wyznaczalność





Nie zawsze stopień statycznej

Nie zawsze stopień statycznej

wyznaczalności n=0 gwarantuje statyczną

wyznaczalności n=0 gwarantuje statyczną

wyznaczalność.

wyznaczalność.
Niewłaściwe rozmieszczenie podpór może

Niewłaściwe rozmieszczenie podpór może

4

4





Niewłaściwe rozmieszczenie podpór może

Niewłaściwe rozmieszczenie podpór może

powodować, że układ będzie geometrycznie

powodować, że układ będzie geometrycznie

zmienny (np. reakcje równoległe

zmienny (np. reakcje równoległe ––

płaszczyzna przesuwu) lub chwilowo

płaszczyzna przesuwu) lub chwilowo

geometrycznie zmienny (reakcje

geometrycznie zmienny (reakcje

przecinające się w jednym punkcie

przecinające się w jednym punkcie ––

chwilowy środek obrotu).

chwilowy środek obrotu).

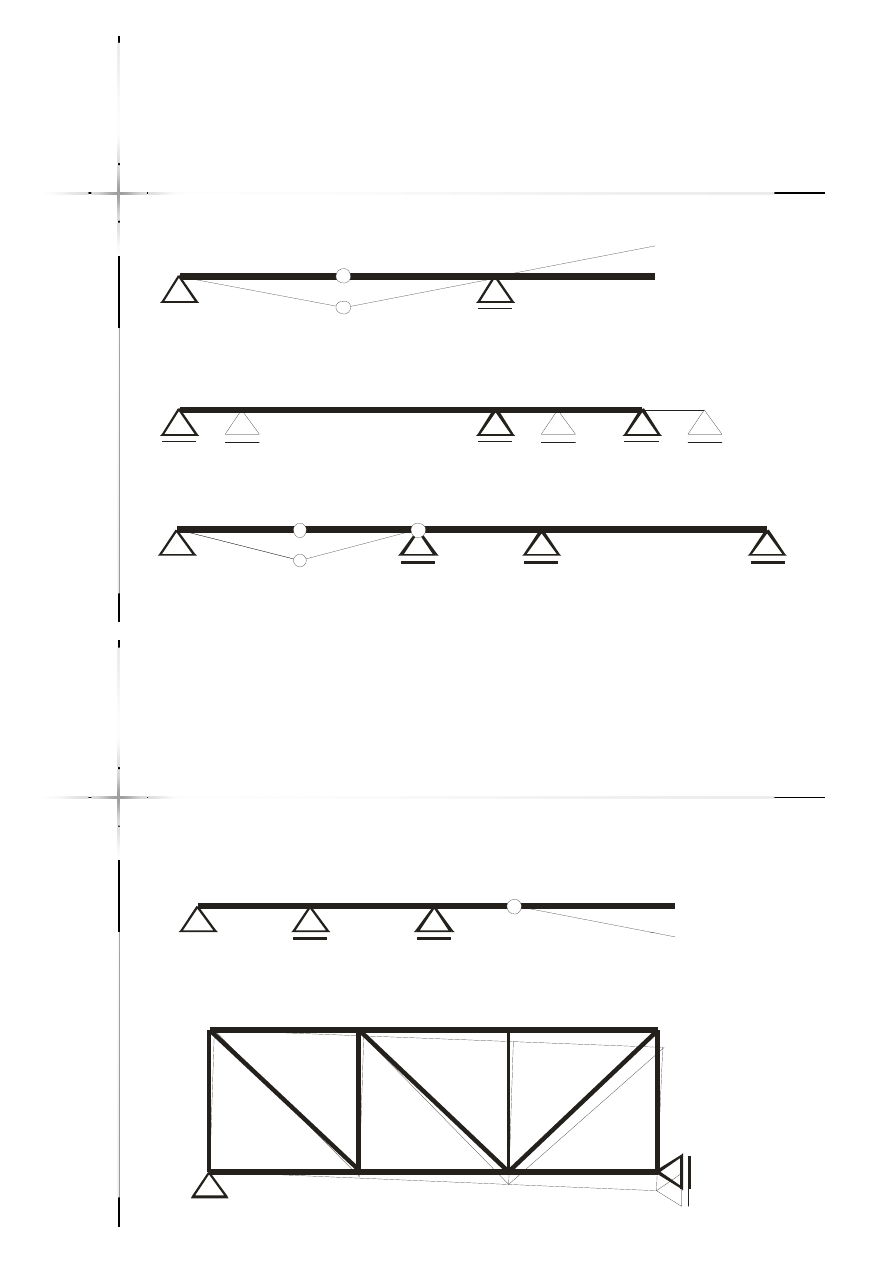
Układy geometrycznie

Układy geometrycznie

zmienne (przykłady)

zmienne (przykłady)

(1)

(1)





Niedostateczna liczba podpór.

Niedostateczna liczba podpór.





Belka na trzech podporach

Belka na trzech podporach

5

5





Belka na trzech podporach

Belka na trzech podporach

przesuwnych.

przesuwnych.





Trzy niepodparte przeguby obok siebie.

Trzy niepodparte przeguby obok siebie.

Układy geometrycznie

Układy geometrycznie

zmienne (przykłady)

zmienne (przykłady)

(2)

(2)





Belka z niepodpartym przęsłem

Belka z niepodpartym przęsłem

przegubowym.

przegubowym.

6

6





Trzy reakcje kratownicy przecinające się

Trzy reakcje kratownicy przecinające się

w jednym punkcie.

w jednym punkcie.

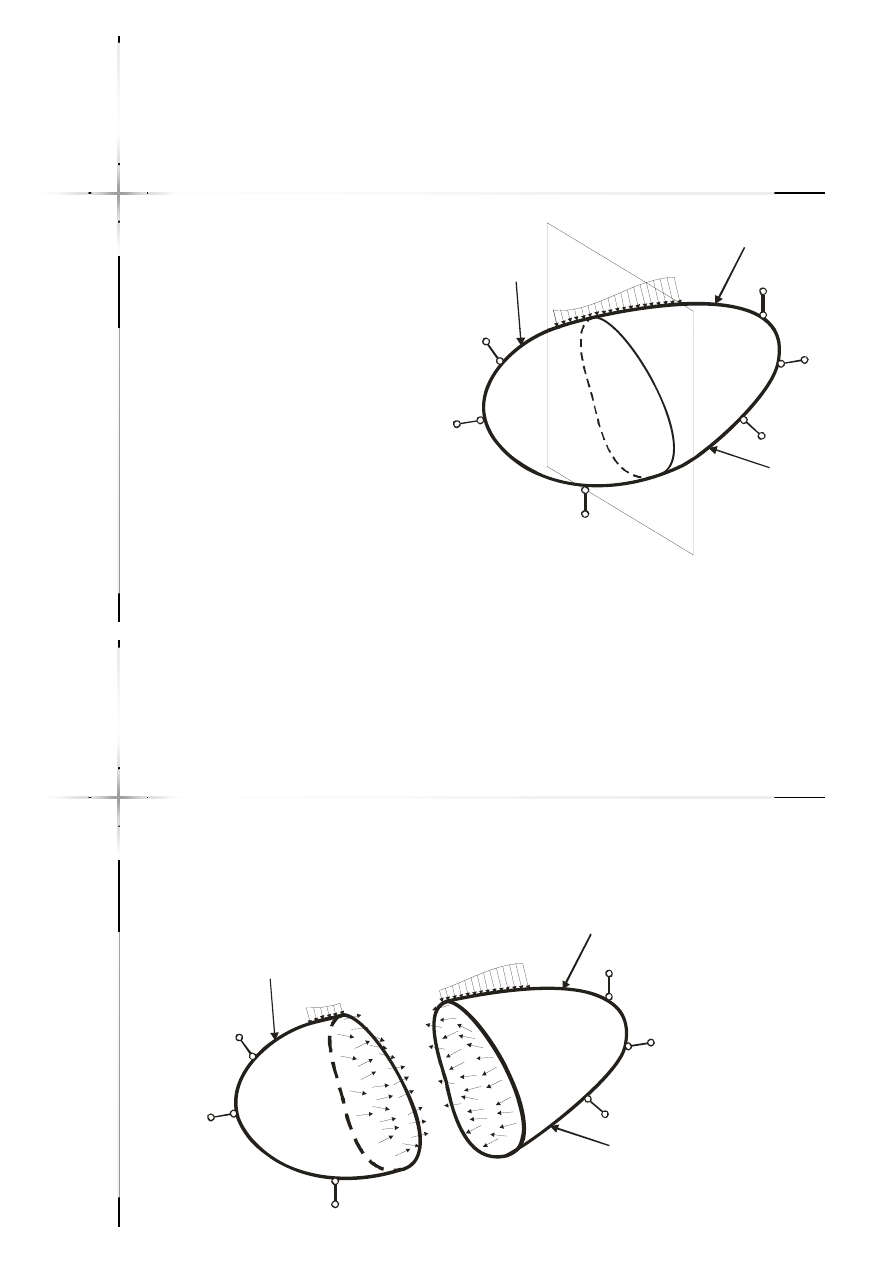
Siły wewnętrzne

Siły wewnętrzne

(1)

(1)





Mamy bryłę materialną

Mamy bryłę materialną

obciążoną układem sił

obciążoną układem sił

(siły zewnętrzne,

(siły zewnętrzne,

reakcje), będących w

reakcje), będących w

P

P

q



7

7

reakcje), będących w

reakcje), będących w

równowadze.

równowadze.

Rozetniemy myślowo

Rozetniemy myślowo

tę bryłę na dwie części

tę bryłę na dwie części

przekrojem

przekrojem



--

 ..

P



Siły wewnętrzne

Siły wewnętrzne

(2)

(2)





Aby fragment bryły był w równowadze

Aby fragment bryły był w równowadze

musimy zastąpić wzajemne oddziaływanie

musimy zastąpić wzajemne oddziaływanie

fragmentów brył przez przyłożenie w sposób

fragmentów brył przez przyłożenie w sposób

ciągły do płaszczyzny

ciągły do płaszczyzny



--

 układu sił.

układu sił.

8

8

P

P

P

q

q

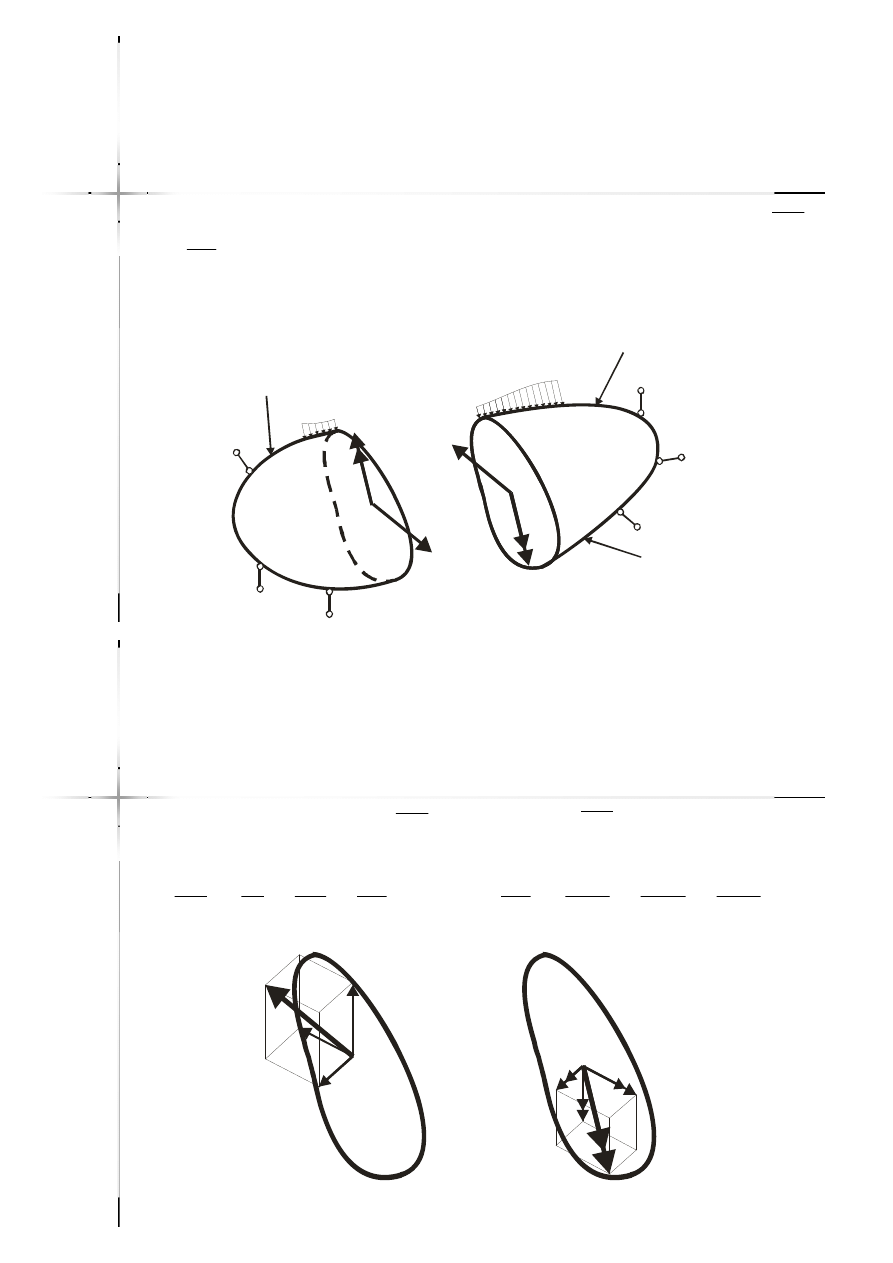
Siły wewnętrzne

Siły wewnętrzne

(3)

(3)





Siły te można zastąpić przez ich wypadkowe

Siły te można zastąpić przez ich wypadkowe

i , przyłożone w dowolnym punkcie

i , przyłożone w dowolnym punkcie

przekroju

przekroju



--

. W przypadku naszych rozważań

. W przypadku naszych rozważań

punktem tym będzie środek przekroju.

punktem tym będzie środek przekroju.

M

W

9

9

punktem tym będzie środek przekroju.

punktem tym będzie środek przekroju.

P

P

P

q

q

M

W

W

M

Siły przekrojowe

Siły przekrojowe





Wypadkową siłę i moment można

Wypadkową siłę i moment można

wyrazić przez ich składowe:

wyrazić przez ich składowe:

M

W

z

y

T

T

N

W







z

y

x

M

M

M

M







10

10

z

y

z

y

x

M

W.

N

T

z

T

y

M

x

M

y

M

z

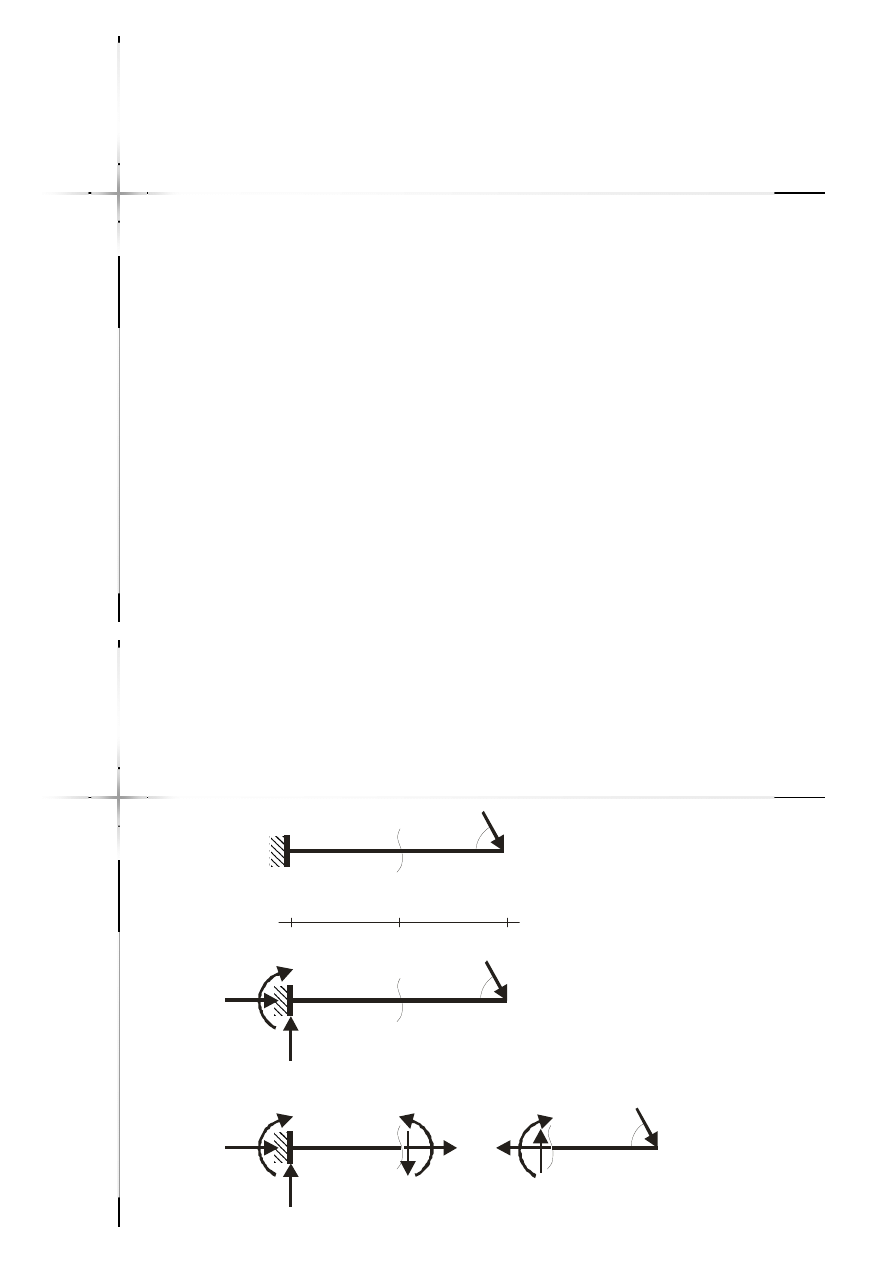
Nazwy sił przekrojowych

Nazwy sił przekrojowych





Wielkości te nazwano:

Wielkości te nazwano:

–– N

N –– siła podłużna (normalne)

siła podłużna (normalne) –– wywołuje

wywołuje

rozciąganie lub ściskanie;

rozciąganie lub ściskanie;

–– TT , T

, T (lub Q

(lub Q , Q

, Q )

) –– siły poprzeczne

siły poprzeczne

11

11

–– TT

yy

, T

, T

zz

(lub Q

(lub Q

yy

, Q

, Q

zz

)

) –– siły poprzeczne

siły poprzeczne

(tnące)

(tnące) –– wywołują ścinanie;

wywołują ścinanie;

–– M

M

xx

–– moment skręcający

moment skręcający –– wywołuje

wywołuje

skręcanie;

skręcanie;

–– M

M

yy

, M

, M

zz

–– momenty zginające

momenty zginające –– wywołują

wywołują

zginanie.

zginanie.

Przykład

Przykład

l / 2

l / 2

P





12

12

V

A

H

A

M

A



V

A

H

A

M

A





N



N



T



T



M



M



P



P



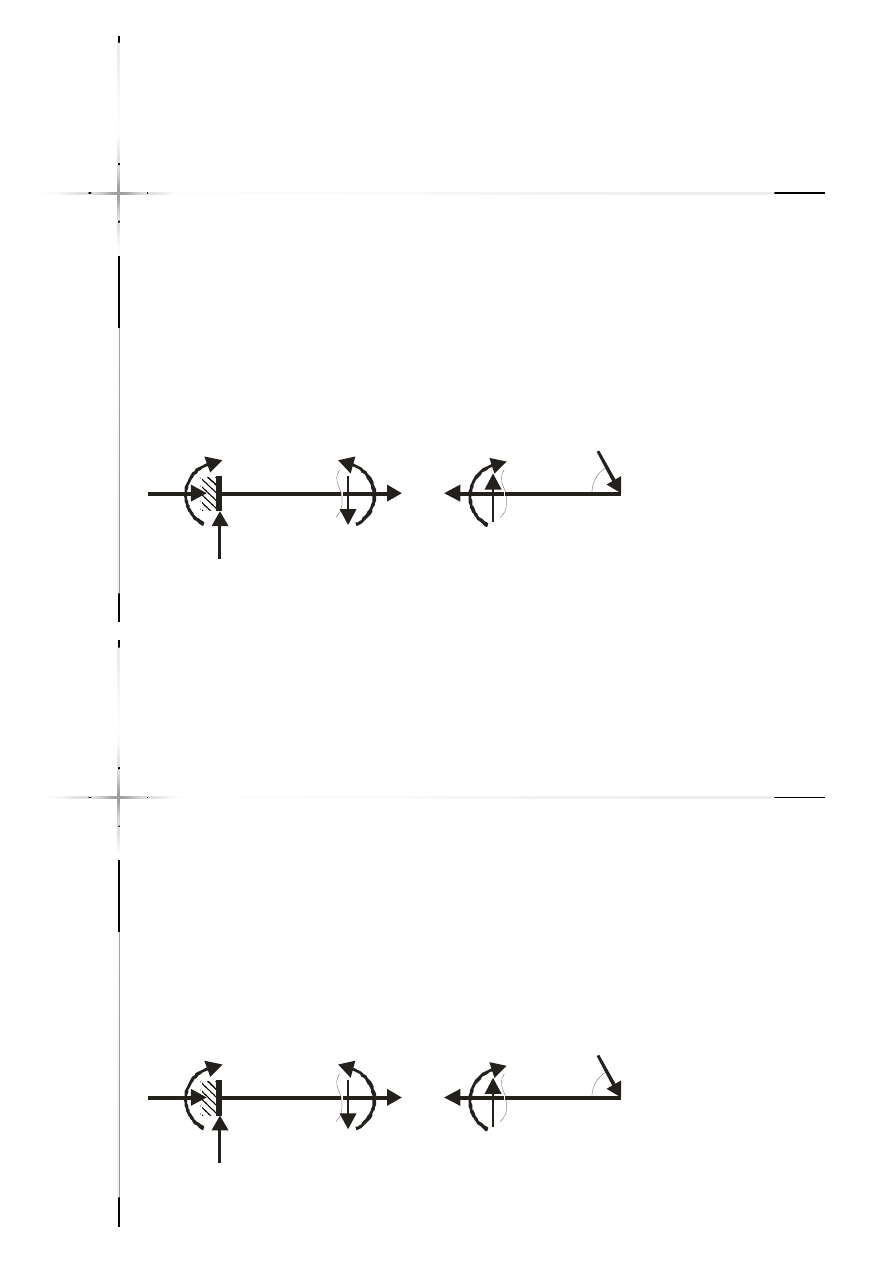
Siły wewnętrzne w układach

Siły wewnętrzne w układach

płaskich

płaskich –

– definicje

definicje

(1)

(1)





Siła normalna (osiowa, podłużna)

Siła normalna (osiowa, podłużna) ––

wzajemne oddziaływanie części

wzajemne oddziaływanie części

konstrukcji przeciwdziałające ich

konstrukcji przeciwdziałające ich

13

13

konstrukcji przeciwdziałające ich

konstrukcji przeciwdziałające ich

przesunięciu się wzdłuż osi pręta w

przesunięciu się wzdłuż osi pręta w

rozważanym punkcie.

rozważanym punkcie.

V

A

H

A

M

A





N



N



T



T



M



M



P







cos

P

N



Siły wewnętrzne w układach

Siły wewnętrzne w układach

płaskich

płaskich –

– definicje

definicje

(2)

(2)





Siła poprzeczna (tnąca)

Siła poprzeczna (tnąca) –– wzajemne

wzajemne

oddziaływanie części konstrukcji

oddziaływanie części konstrukcji

przeciwdziałające ich przesunięciu się

przeciwdziałające ich przesunięciu się

14

14

przeciwdziałające ich przesunięciu się

przeciwdziałające ich przesunięciu się

poprzecznie do osi pręta w

poprzecznie do osi pręta w

rozważanym punkcie.

rozważanym punkcie.

V

A

H

A

M

A





N



N



T



T



M



M



P







sin

P

T



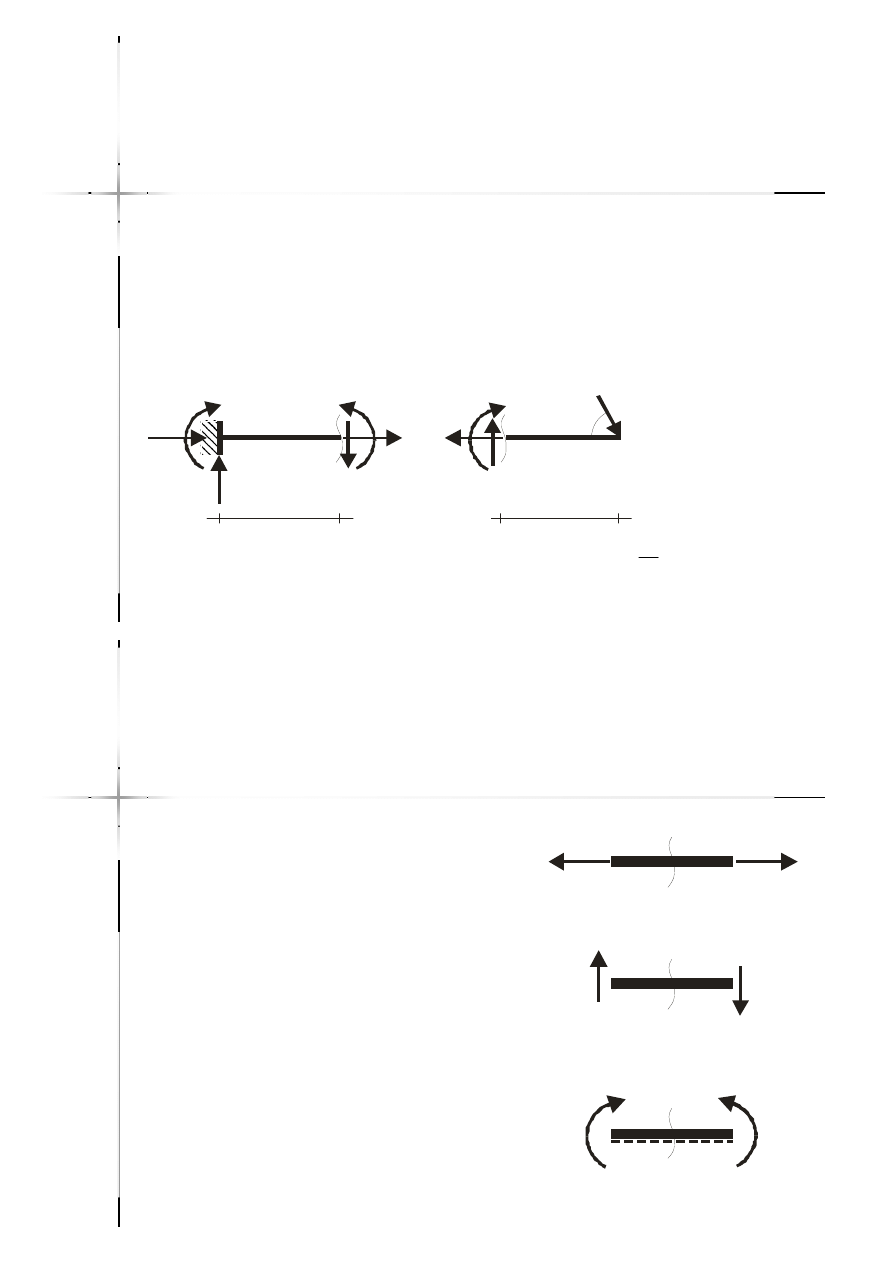
Siły wewnętrzne w układach

Siły wewnętrzne w układach

płaskich

płaskich –

– definicje

definicje

(3)

(3)





Moment zginający

Moment zginający –– wzajemne

wzajemne

oddziaływanie części konstrukcji

oddziaływanie części konstrukcji

przeciwdziałające ich wzajemnemu

przeciwdziałające ich wzajemnemu

15

15

przeciwdziałające ich wzajemnemu

przeciwdziałające ich wzajemnemu

obrotowi w rozważanym punkcie.

obrotowi w rozważanym punkcie.

V

A

H

A

M

A





N



N



T



T



M



M



P



l / 2

l / 2





sin

2

l

P

M





Siły wewnętrzne

Siły wewnętrzne –

–

konwencja znaków

konwencja znaków





Siła normalna rozciągająca

Siła normalna rozciągająca

pręt jest dodatnia.

pręt jest dodatnia.





Siła poprzeczna

Siła poprzeczna

powodowana przez

powodowana przez



N



N



16

16

powodowana przez

powodowana przez

obciążenie działające po

obciążenie działające po

lewej stronie przekroju do

lewej stronie przekroju do

góry lub po prawej stronie

góry lub po prawej stronie

do dołu jest dodatnia.

do dołu jest dodatnia.





Moment rozciągający

Moment rozciągający

włókna dolne jest dodatni.

włókna dolne jest dodatni.



T



T





M



M



spody (włókna dolne)

Siły wewnętrzne

Siły wewnętrzne –

–

wykresy

wykresy

(1)

(1)





Kreskowanie (rzędne wykresu) należy

Kreskowanie (rzędne wykresu) należy

zaznaczać prostopadle do osi pręta.

zaznaczać prostopadle do osi pręta.





Rzędne dodatnie wykresów sił

Rzędne dodatnie wykresów sił

17

17





Rzędne dodatnie wykresów sił

Rzędne dodatnie wykresów sił

normalnych i tnących odkłada się

normalnych i tnących odkłada się

zazwyczaj u góry.

zazwyczaj u góry.





Wykresy sił podłużnych i poprzecznych

Wykresy sił podłużnych i poprzecznych

rysujemy ze znakiem.

rysujemy ze znakiem.

Siły wewnętrzne

Siły wewnętrzne –

–

wykresy

wykresy

(2)

(2)





Wykresy momentów nie muszą być

Wykresy momentów nie muszą być

znakowane, ale należy zwracać uwagę, aby

znakowane, ale należy zwracać uwagę, aby

rzędne momentu odkładać po stronie

rzędne momentu odkładać po stronie

włókien rozciąganych.

włókien rozciąganych.

18

18

włókien rozciąganych.

włókien rozciąganych.





Rzędne dodatnie wykresu momentów

Rzędne dodatnie wykresu momentów

zginających odkłada się u dołu (moment

zginających odkłada się u dołu (moment

dodatni, gdy rozciągane są włókna dolne).

dodatni, gdy rozciągane są włókna dolne).





Wykres momentu wskazuje jak odkształci

Wykres momentu wskazuje jak odkształci

się pręt i gdzie, w poszczególnych

się pręt i gdzie, w poszczególnych

elementach, włókna są rozciągane.

elementach, włókna są rozciągane.

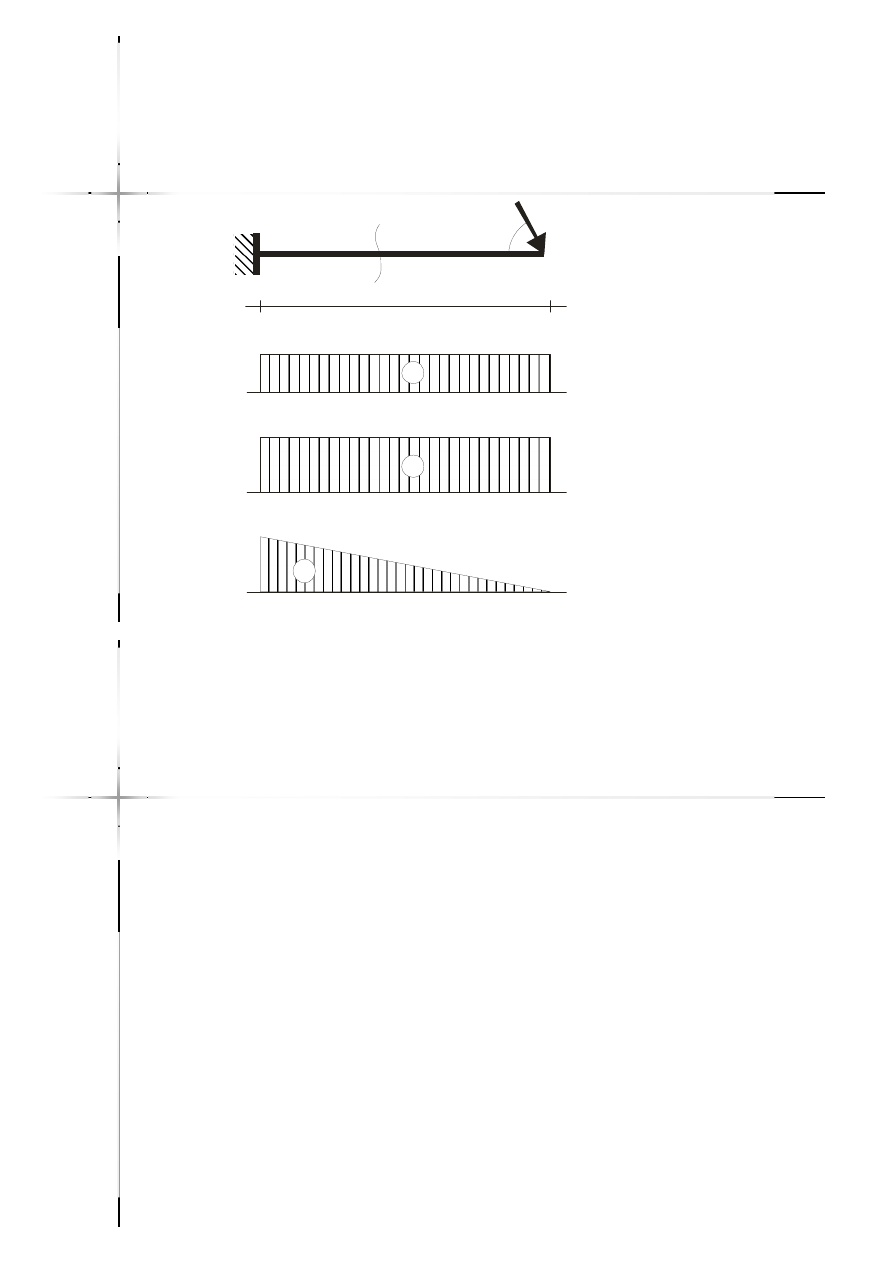
Wykresy sił

Wykresy sił

wewnętrznych

wewnętrznych

l



P



P

cos



19

19

N



[kN]

+

T



[kN]

-

M



m

[kN ]

P

cos



P

sin



Pl

sin



+

Punkty charakterystyczne,

Punkty charakterystyczne,

przekroje

przekroje





Ze względu na konieczność

Ze względu na konieczność

modyfikacji równań sił wewnętrznych:

modyfikacji równań sił wewnętrznych:

–– w belkach i ramach

w belkach i ramach –– końce prętów,

końce prętów,

20

20

–– w belkach i ramach

w belkach i ramach –– końce prętów,

końce prętów,

punkty przyłożenia sił:

punkty przyłożenia sił:

–– czynnych: siła skupiona, moment skupiony,

czynnych: siła skupiona, moment skupiony,

początek lub koniec obciążenia ciągłego;

początek lub koniec obciążenia ciągłego;

–– biernych: punkty podporowe;

biernych: punkty podporowe;

–– w ramach

w ramach –– dodatkowo węzły (połączenia

dodatkowo węzły (połączenia

prętów o różnej krzywiźnie).

prętów o różnej krzywiźnie).

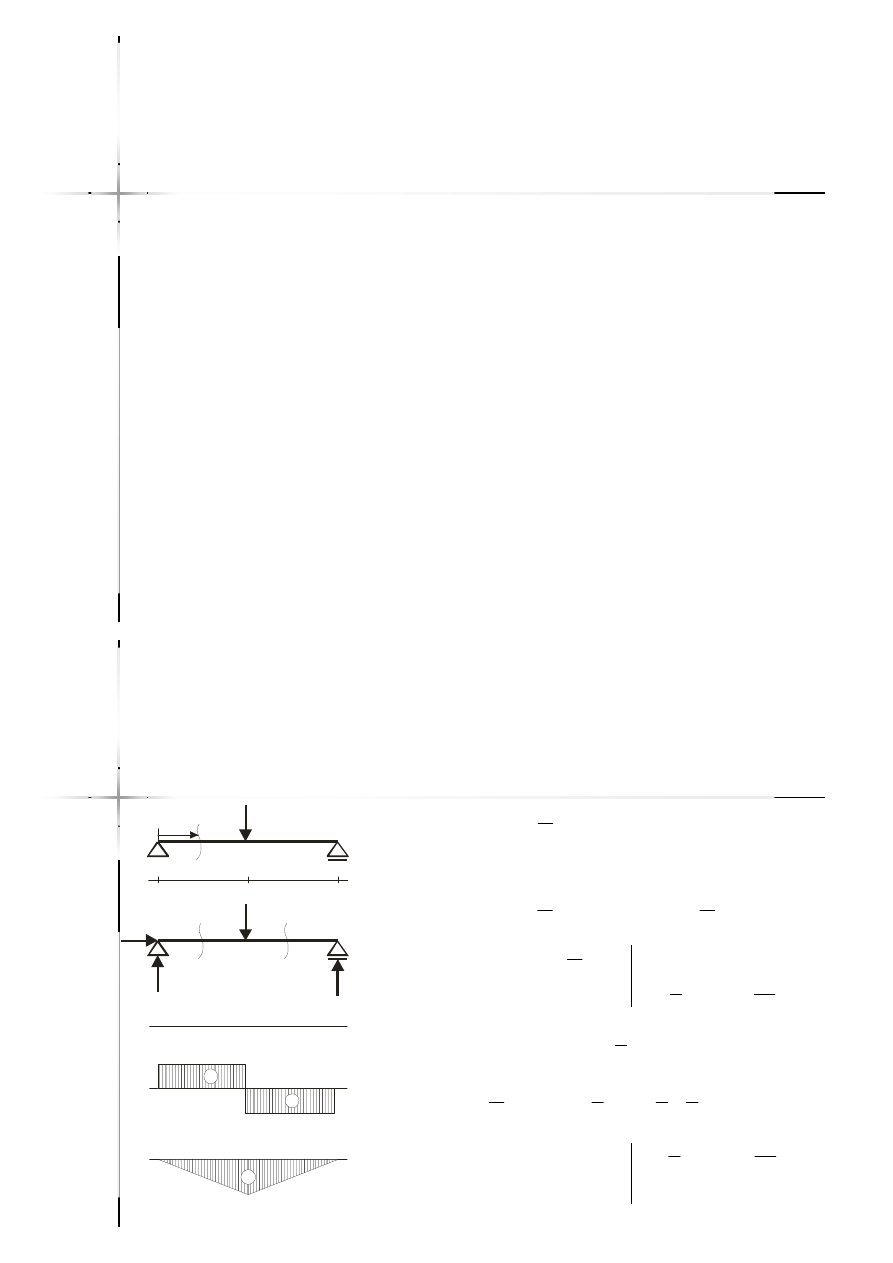
Przegub

Przegub





Przegub jest jedynie punktem

Przegub jest jedynie punktem

kontrolnym (moment równy jest 0).

kontrolnym (moment równy jest 0).

Nie powoduje on konieczności

Nie powoduje on konieczności

21

21

Nie powoduje on konieczności

Nie powoduje on konieczności

wprowadzenia dodatkowego

wprowadzenia dodatkowego

przekroju.

przekroju.

Siła skupiona

Siła skupiona

l / 2

P

l / 2

P

H

A



x



1



2

0

2







A

B

A

H

P

R

V

0

0

2

1









N

N

2

2

2

1

P

P

V

T

P

V

T

A

A

















22

22

V

A

H

A

R

B

N



[kN]

+

T



[kN]

M



m

[kN ]

P/ 2

0

-

+

P/ 2

Pl / 4

2

2

x

P

x

V

M

A









2

1













 













 



















 







2

2

2

2

2

2

x

l

P

l

x

P

x

P

l

x

P

x

V

M

A



4

2

0

0

1

1

Pl

M

l

x

M

x













0

4

2

2

2













M

l

x

Pl

M

l

x

Moment skupiony

Moment skupiony

l

/2

V

A

H

A

R

B

M

l

/2



1



2

x

0









A

B

A

H

l

M

R

l

M

V

0

0

2

1









N

N

l

M

T

l

M

V

T

A











2

1





23

23

l

/2

l

/2

N



[kN]

T



[kN]

M



m

[kN ]

0

-

+

M/ l

-

M/ 2

M/ 2

l

l

x

l

M

x

V

M

A











1













 











l

x

M

M

x

V

M

A

1

2



2

2

0

0

1

1

M

M

l

x

M

x















0

2

2

2

2













M

l

x

M

M

l

x

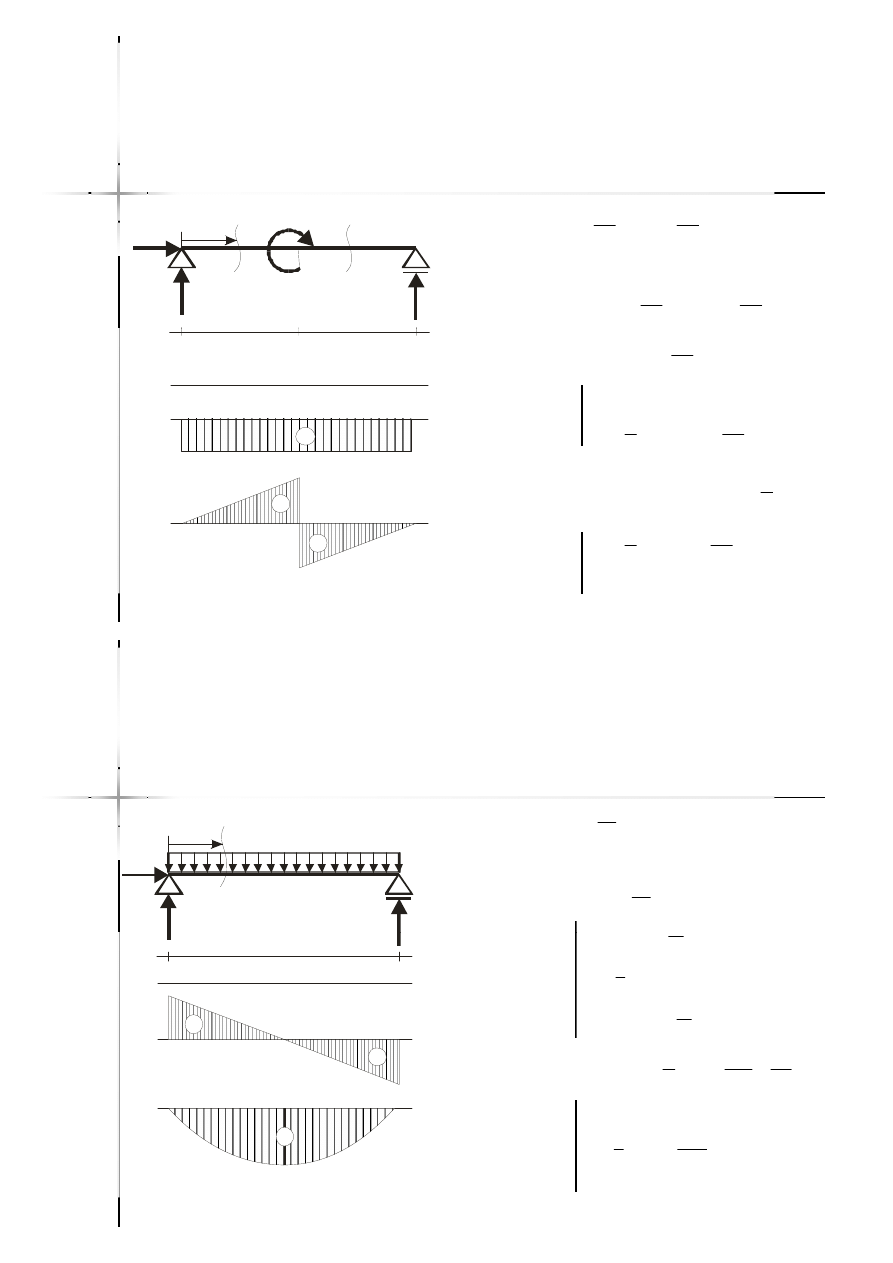
Obciążenie ciągłe

Obciążenie ciągłe

równomierne

równomierne

0

2







A

B

A

H

ql

R

V

0





N

qx

ql

qx

V

T

A









2



0

ql

T

x





V

A

H

A

R

B

q



x

24

24































2

2

2

2

x

x

l

q

x

x

q

x

V

M

A



2

0

2

2

0

ql

T

l

x

T

l

x

ql

T

x





















0

8

2

0

0

2





















M

l

x

l

q

M

l

x

M

x

l

V

A

R

B

N



[kN]

T



[kN]

M



m

[kN ]

0

-

+

+

ql / 2

ql / 2

ql

2

/ 8

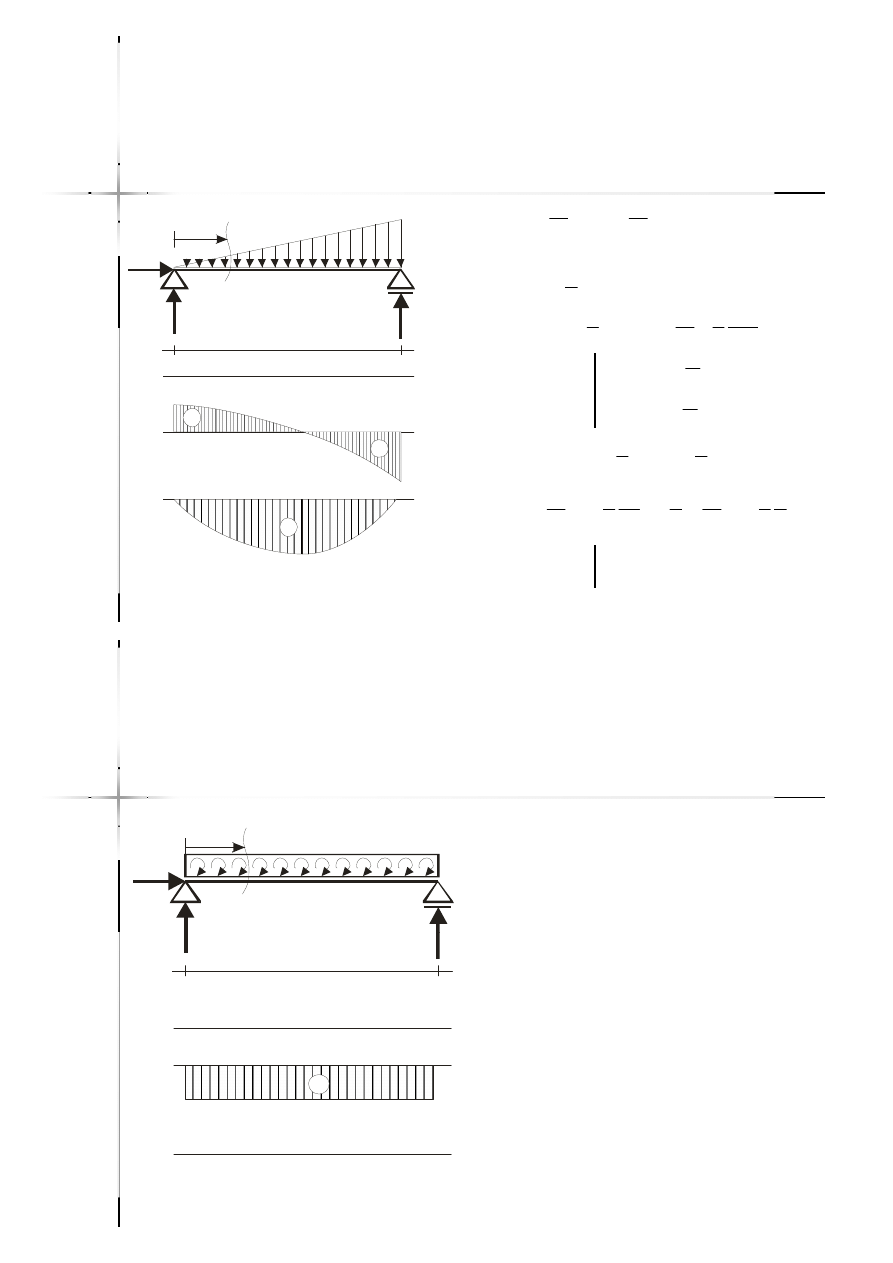
Obciążenie ciągłe liniowo

Obciążenie ciągłe liniowo

zmienne

zmienne

0

3

6







A

B

A

H

ql

R

ql

V

0





N

qx

ql

x

x

q

V

T

A

2

1

)

(

1













x

l

q

x

q





)

(

l

V

A

H

A

R

B

q



x

q

25

25

l

x

x

q

V

T

A

2

6

)

(

2













3

6

1

6

3

2

1

6

3

)

(

2

1

x

l

q

x

ql

x

x

l

qx

x

ql

x

x

x

q

x

V

M

A































3

6

0

ql

T

l

x

ql

T

x













0

0

0













M

l

x

M

x

l

A

R

B

N



[kN]

T



[kN]

M



m

[kN ]

0

-

+

+

ql / 6

ql / 3

Obciążenie ciągłe

Obciążenie ciągłe

momentem

momentem

0









A

B

A

H

m

V

m

V

0





N

m

V

T

A









V

H

A

R

m



x

26

26

0

















mx

mx

x

m

x

V

M

A



l

V

A

R

B

N



[kN]

T



[kN]

M



m

[kN ]

0

-

m

0

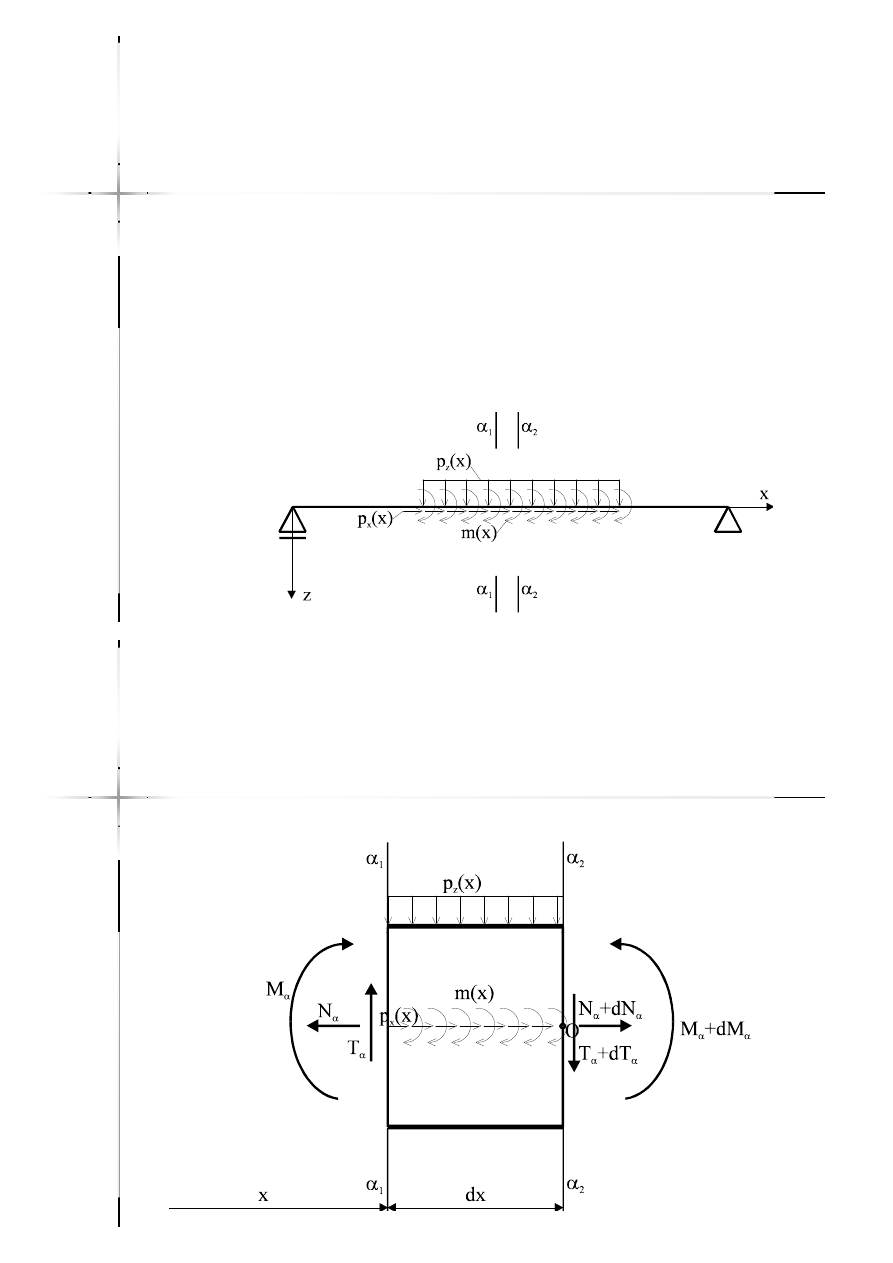
Warunki różniczkowe

Warunki różniczkowe

(1)

(1)





Zależności różniczkowe

Zależności różniczkowe między M

między M





, T

, T





,

,

N

N





i p

i p

zz

(x), p

(x), p

xx

(x), m(x).

(x), m(x).





Aby wyznaczyć te zależności rozważymy

Aby wyznaczyć te zależności rozważymy

belkę swobodnie podpartą, obciążoną

belkę swobodnie podpartą, obciążoną

27

27

belkę swobodnie podpartą, obciążoną

belkę swobodnie podpartą, obciążoną

obciążeniami ciągłymi i ciągłym momentem

obciążeniami ciągłymi i ciągłym momentem

na fragmencie belki.

na fragmencie belki.

Warunki różniczkowe

Warunki różniczkowe

(2)

(2)

Z tej belki wycinamy fragment przedstawiony na

Z tej belki wycinamy fragment przedstawiony na

rysunku.

rysunku.

28

28

Warunki różniczkowe

Warunki różniczkowe

(3)

(3)





Suma rzutów wszystkich sił na oś poziomą

Suma rzutów wszystkich sił na oś poziomą

x

x

::





Suma rzutów wszystkich sił na oś pionową

Suma rzutów wszystkich sił na oś pionową

z

z

::

X





0











N

p

x dx

N

dN

x







( )

(

)

0

29

29





Suma rzutów wszystkich sił na oś pionową

Suma rzutów wszystkich sił na oś pionową

z

z

::





Suma momentów wszystkich sił względem punktu O :

Suma momentów wszystkich sił względem punktu O :

Z





0











T

p

x dx

T

dT

z







( )

(

)

0

M

o





0

M

T dx

m

x dx

p

x dx

dx

M

dM

x

z





















( )

( )

(

)

2

0

Warunki różniczkowe

Warunki różniczkowe

(4)

(4)





Po odrzuceniu wielkości małej w

Po odrzuceniu wielkości małej w

porównaniu z pozostałymi ,

porównaniu z pozostałymi ,

otrzymujemy:

otrzymujemy:

2

dx

(x)dx

p

z

30

30

otrzymujemy:

otrzymujemy:





Z powyższych równań wynika, że:

Z powyższych równań wynika, że:

dN

dx

p

x

x



  ( )

dT

dx

p

x

z



  ( )

dM

dx

T

m x







 ( )

)

(

2

2

x

p

dx

dT

dx

M

d

z











Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(1)

(1)





Jeżeli w przedziale nie ma obciążenia

Jeżeli w przedziale nie ma obciążenia

ciągłego poprzecznego to wykres sił

ciągłego poprzecznego to wykres sił

tnących jest stały, równoległy do osi

tnących jest stały, równoległy do osi

31

31

tnących jest stały, równoległy do osi

tnących jest stały, równoległy do osi

pręta.

pręta.

0

)

(







x

p

dx

dT



 

const

C

x

T





1



P

+

T



[kN]

P/ 2

-

P/ 2

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(2)

(2)





Jeżeli w przedziale nie ma obciążenia

Jeżeli w przedziale nie ma obciążenia

ciągłego poprzecznego i nie występuje

ciągłego poprzecznego i nie występuje

obciążenie ciągłe momentem to

obciążenie ciągłe momentem to

32

32

obciążenie ciągłe momentem to

obciążenie ciągłe momentem to

wykres momentu jest linią prostą

wykres momentu jest linią prostą

nachyloną do pręta.

nachyloną do pręta.

 

1

C

x

T

dx

dM









 

2

1

C

x

C

x

M









P

M



m

[kN ]

+

Pl / 4

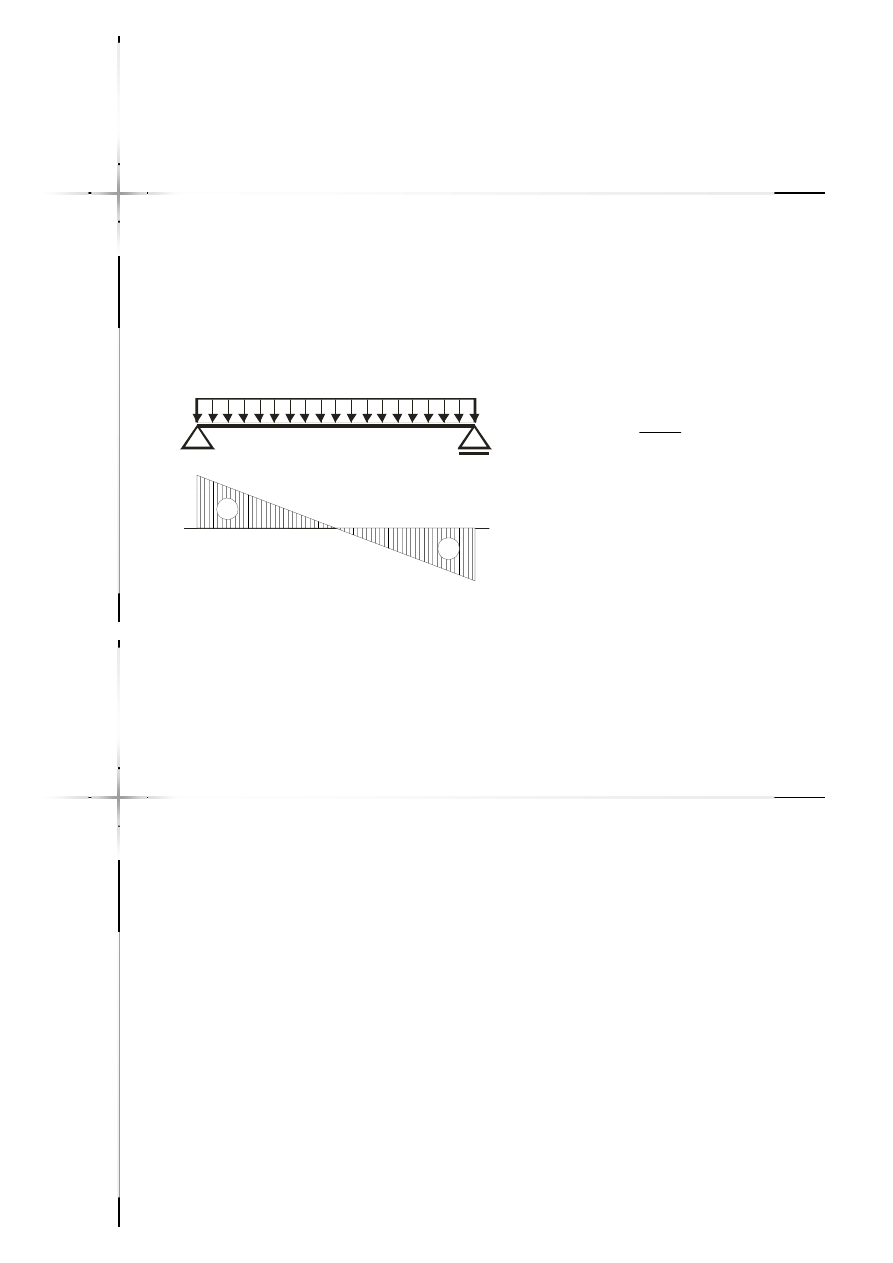
Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(3)

(3)





Jeżeli w przedziale działa stałe

Jeżeli w przedziale działa stałe

obciążenie ciągłe to wykres sił

obciążenie ciągłe to wykres sił

tnących jest nachylony do pręta,

tnących jest nachylony do pręta,

rzędne maleją wraz ze wzrostem x.

rzędne maleją wraz ze wzrostem x.

33

33

rzędne maleją wraz ze wzrostem x.

rzędne maleją wraz ze wzrostem x.

q

dx

dT







1

C

qx

T









q

T



[kN]

-

+

ql / 2

ql / 2

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(4)

(4)





Jeżeli w przedziale działa stałe

Jeżeli w przedziale działa stałe

obciążenie ciągłe i nie ma

obciążenie ciągłe i nie ma

obciążenia ciągłego momentem, to

obciążenia ciągłego momentem, to

34

34

obciążenia ciągłego momentem, to

obciążenia ciągłego momentem, to

wykres momentów zginających

wykres momentów zginających

jest parabolą drugiego stopnia.

jest parabolą drugiego stopnia.





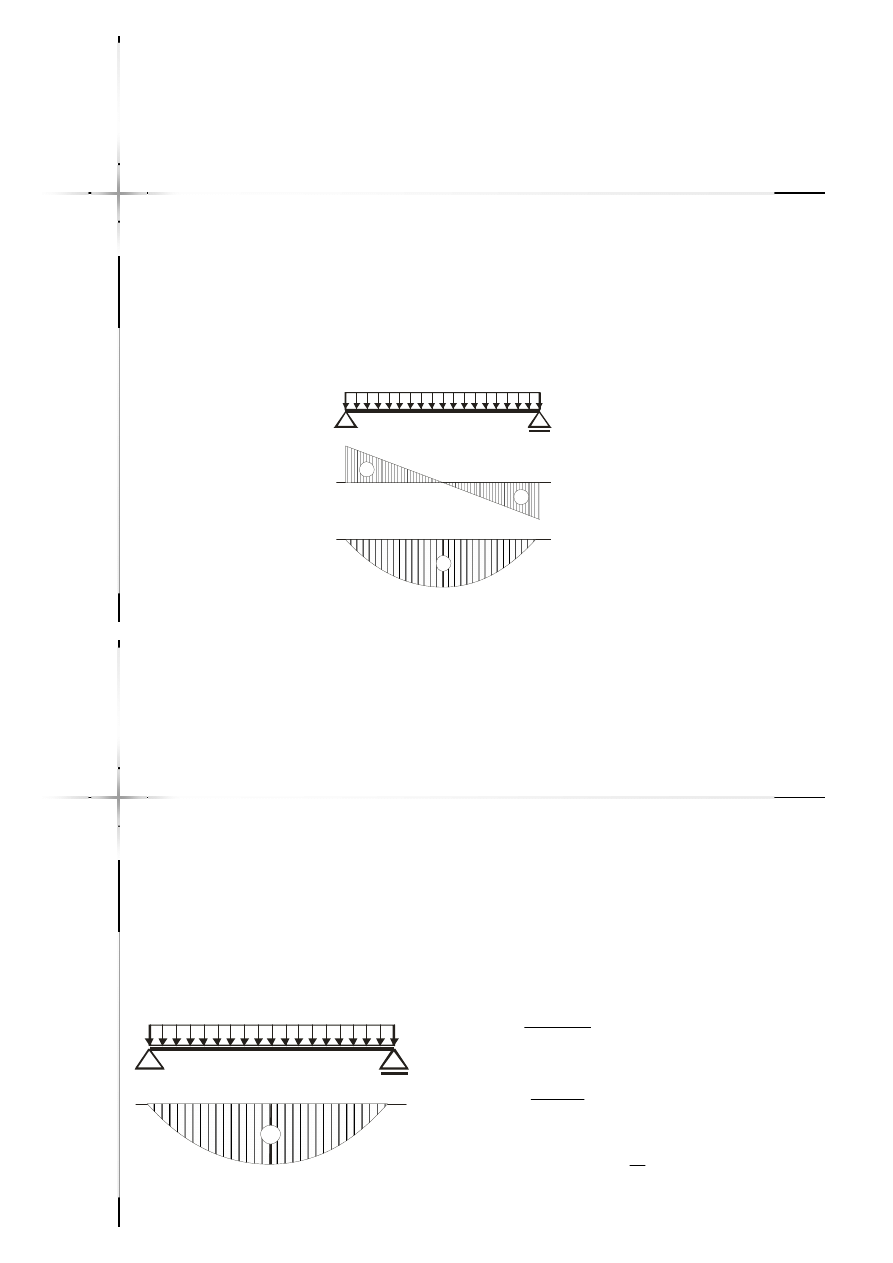
Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(5)

(5)





Jeżeli w przedziale zeruje się

Jeżeli w przedziale zeruje się

równanie siły tnącej to wykres

równanie siły tnącej to wykres

momentów osiąga ekstremum w

momentów osiąga ekstremum w

35

35

momentów osiąga ekstremum w

momentów osiąga ekstremum w

tym punkcie.

tym punkcie.





q

T



[kN]

-

+

ql / 2

ql / 2

M



m

[kN ]

+

ql / 8

2





Jeżeli obciążenie ciągłe jest

Jeżeli obciążenie ciągłe jest

skierowane do dołu, to wypukłość

skierowane do dołu, to wypukłość

wykresu jest skierowana w dół i

wykresu jest skierowana w dół i

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(6)

(6)

36

36

wykresu jest skierowana w dół i

wykresu jest skierowana w dół i

odwrotnie.

odwrotnie.

q

M



m

[kN

]

+

ql / 8

2

 

q

x

p

dx

M

d









2

2



 

2

1

2

2

1

C

x

C

qx

x

M









1

C

qx

dx

dM













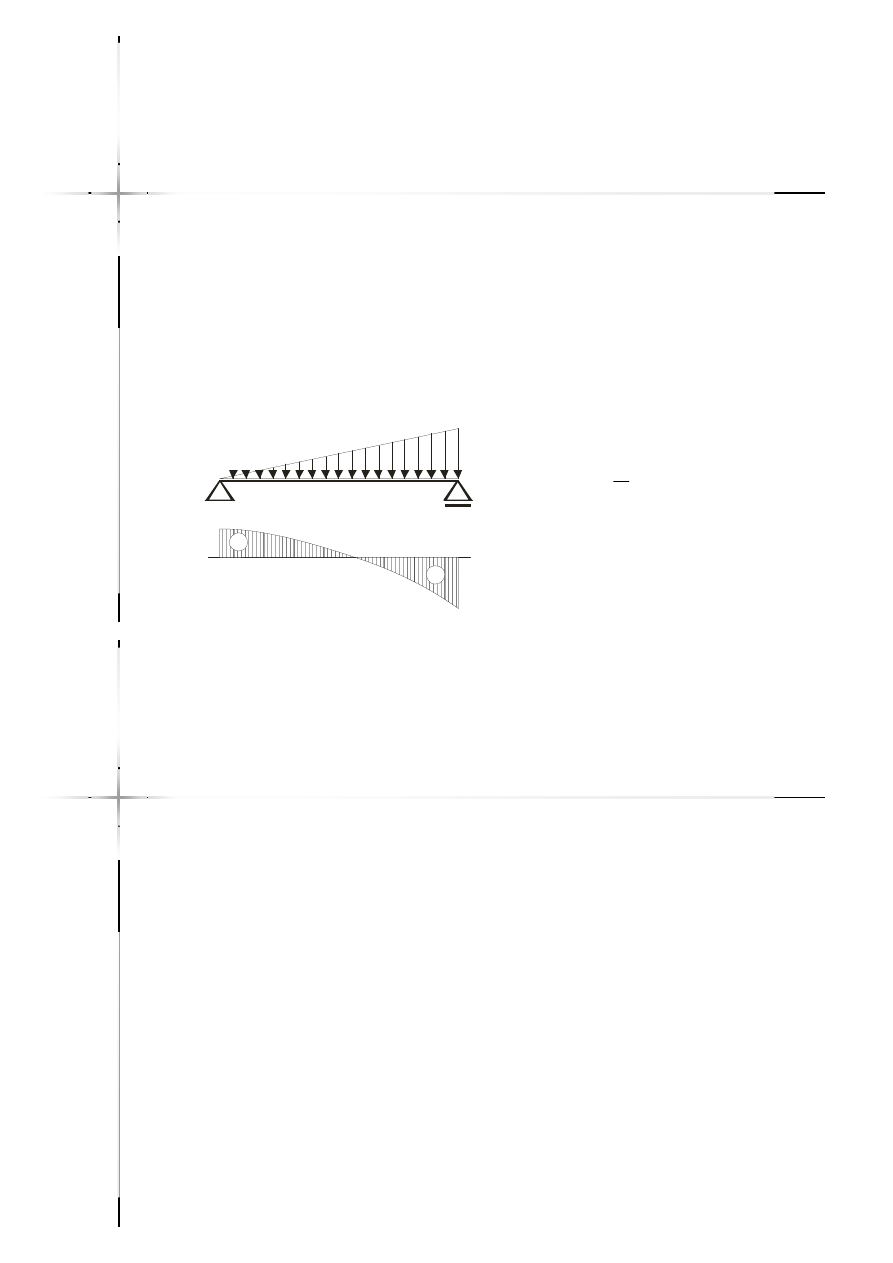
Jeżeli w przedziale działa obciążenie ciągłe

Jeżeli w przedziale działa obciążenie ciągłe

liniowo zmienne i nie ma obciążenia ciągłego

liniowo zmienne i nie ma obciążenia ciągłego

momentem to wykres sił poprzecznych jest

momentem to wykres sił poprzecznych jest

parabolą drugiego stopnia. W punkcie, gdzie

parabolą drugiego stopnia. W punkcie, gdzie

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(7)

(7)

37

37

parabolą drugiego stopnia. W punkcie, gdzie

parabolą drugiego stopnia. W punkcie, gdzie

obciążenie ciągłe się zeruje parabola jest

obciążenie ciągłe się zeruje parabola jest

styczna do osi do pręta.

styczna do osi do pręta.

T



[kN]

-

+

ql / 6

ql / 3

q

 

2

1

C

x

C

x

p





 

3

2

2

1

2

1

C

x

C

x

C

x

T













Jeżeli w przedziale działa obciążenie

Jeżeli w przedziale działa obciążenie

ciągłe liniowe to wykres momentów

ciągłe liniowe to wykres momentów

zginających jest parabolą trzeciego

zginających jest parabolą trzeciego

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(8)

(8)

38

38

zginających jest parabolą trzeciego

zginających jest parabolą trzeciego

stopnia.

stopnia.





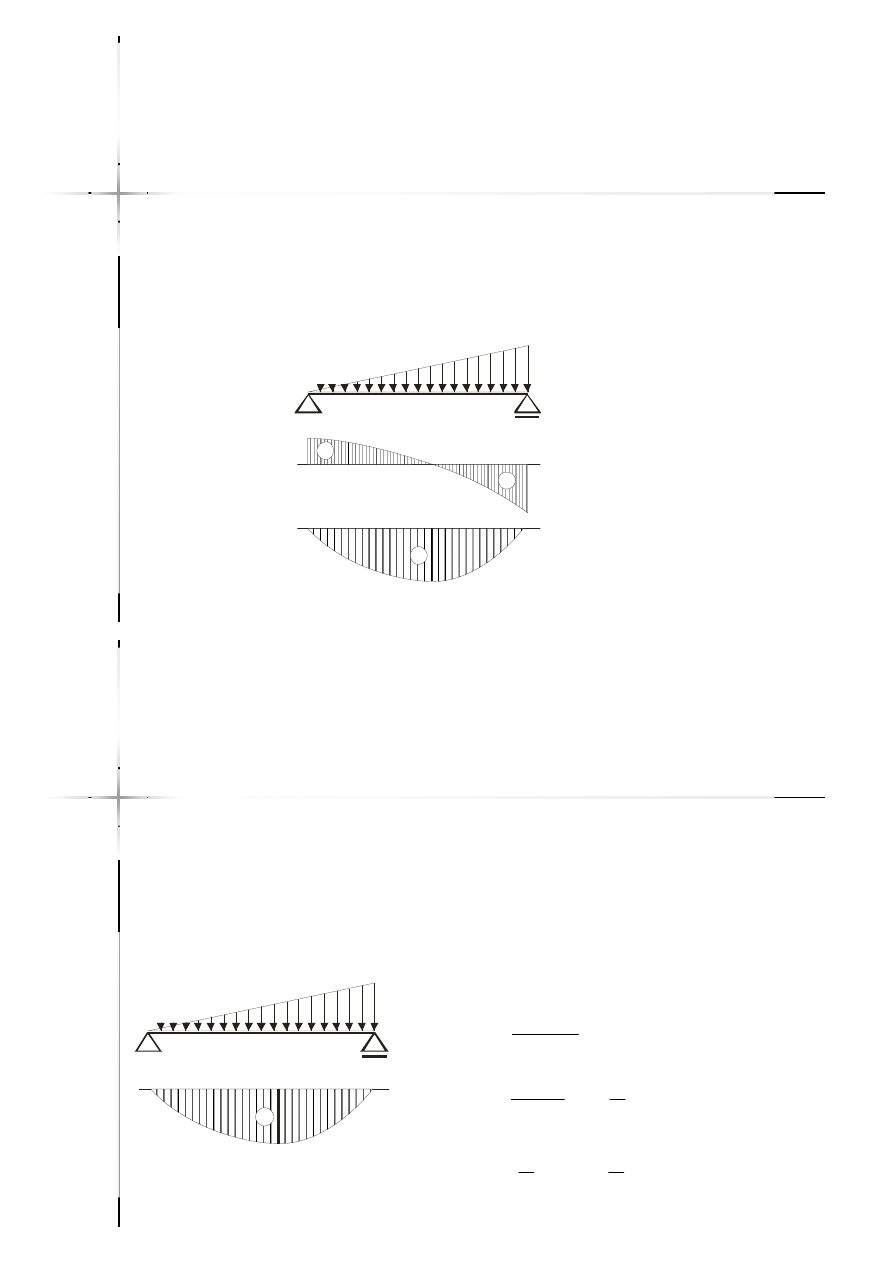
Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(9)

(9)





Jeżeli równanie sił tnących zeruje się

Jeżeli równanie sił tnących zeruje się

w przedziale, to wykres momentów

w przedziale, to wykres momentów

osiąga ekstremum w tym punkcie.

osiąga ekstremum w tym punkcie. 



39

39

osiąga ekstremum w tym punkcie.

osiąga ekstremum w tym punkcie. 



T



[kN]

-

+

ql / 6

ql / 3

q

M



m

[kN ]

+

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(10)

(10)





Jeżeli obciążenie ciągłe jest

Jeżeli obciążenie ciągłe jest

skierowane do dołu, to wypukłość

skierowane do dołu, to wypukłość

wykresu jest skierowana w dół i

wykresu jest skierowana w dół i

odwrotnie.

odwrotnie.

40

40

odwrotnie.

odwrotnie.

q

M



m

[kN

]

+

 

2

1

C

x

C

x

p





 

2

1

2

2

C

x

C

x

p

dx

M

d













 

4

3

2

2

3

1

2

1

6

1

C

x

C

x

C

x

C

x

M











3

2

2

1

2

1

C

x

C

x

C

dx

dM















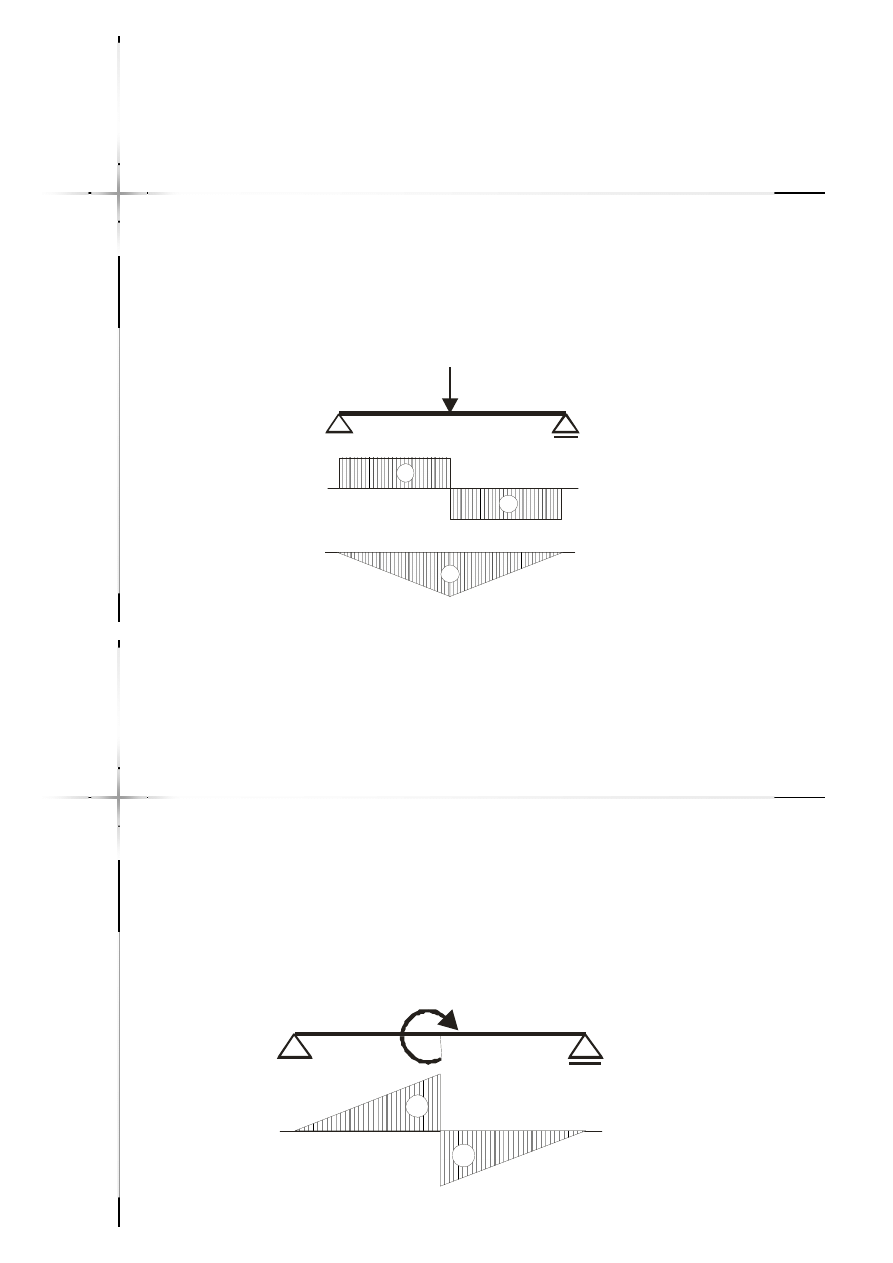
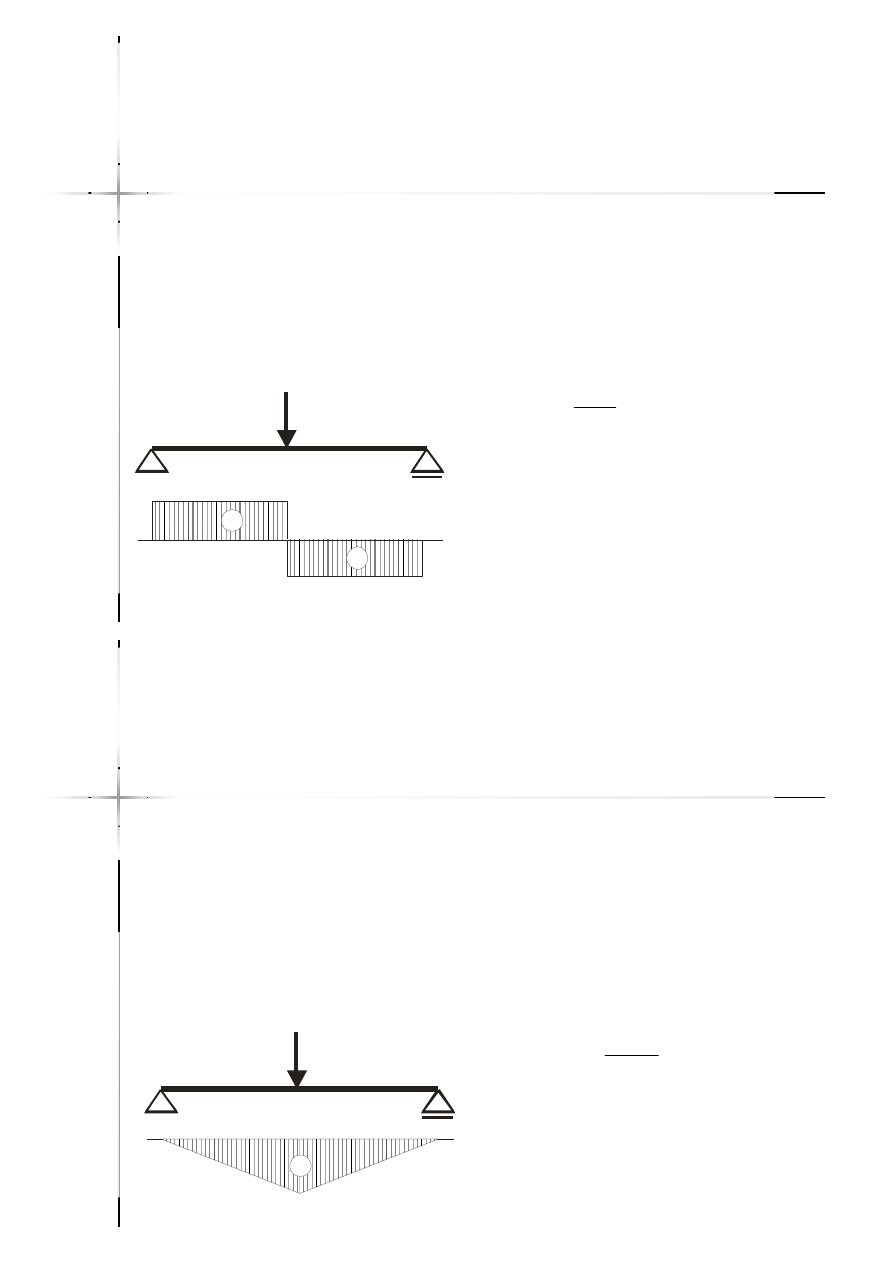
Jeżeli na pręcie występuje siła skupiona,

Jeżeli na pręcie występuje siła skupiona,

to na wykresie sił poprzecznych wystąpi

to na wykresie sił poprzecznych wystąpi

„skok” o tą wartość, a na wykresie

„skok” o tą wartość, a na wykresie

momentów zginających wystąpi

momentów zginających wystąpi

„załamanie” wykresu.

„załamanie” wykresu.

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(11)

(11)

41

41

„załamanie” wykresu.

„załamanie” wykresu.

M



m

[kN ]

P

+

T



[kN]

P/ 2

-

P/ 2

+

Pl / 4





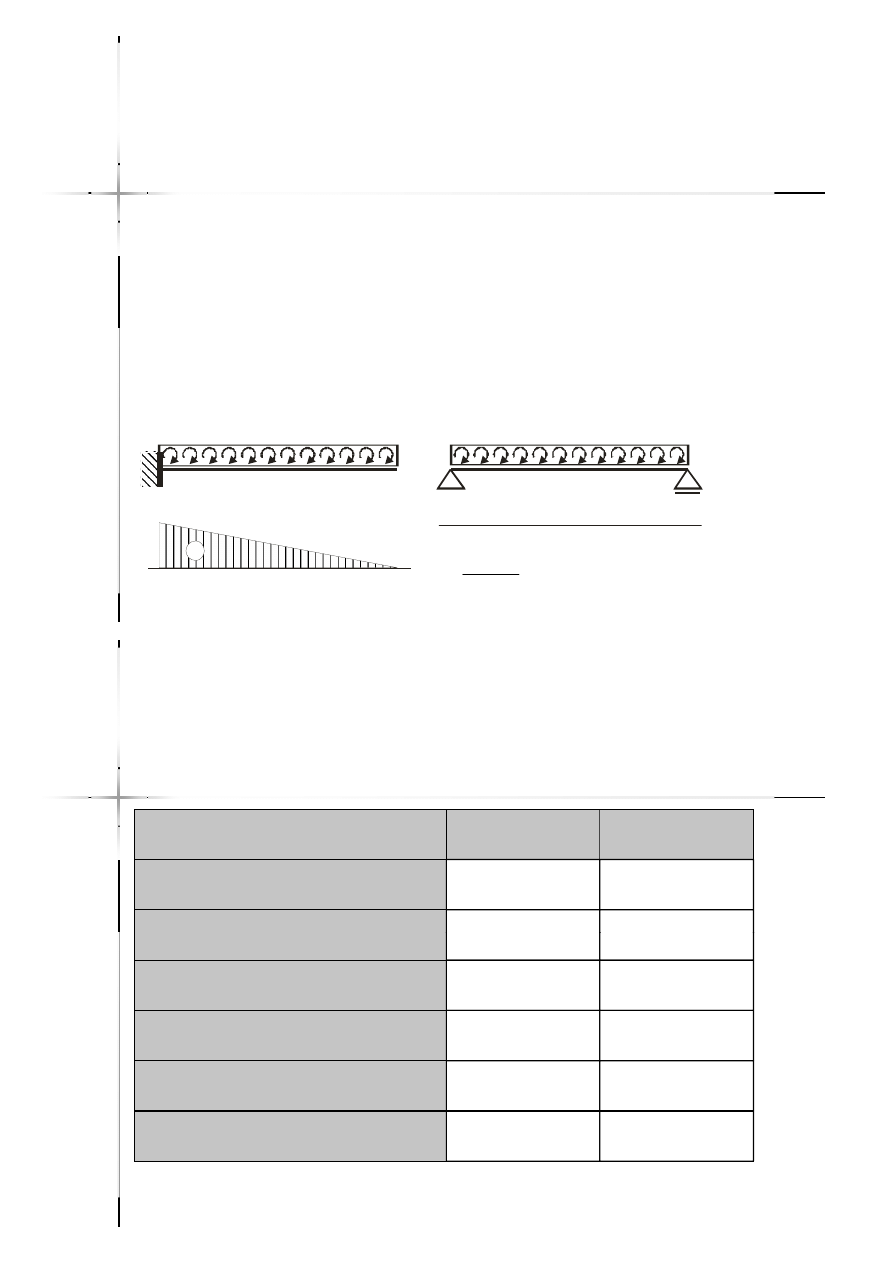
Jeżeli na pręcie występuje moment

Jeżeli na pręcie występuje moment

skupiony, to na wykresie momentów

skupiony, to na wykresie momentów

zginających wystąpi „skok” o wartość

zginających wystąpi „skok” o wartość

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(12)

(12)

42

42

zginających wystąpi „skok” o wartość

zginających wystąpi „skok” o wartość

tego momentu.

tego momentu.

M

M



m

[kN ]

+

-

M/ 2

M/ 2

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

i i

m

m

(13)

(13)





Jeżeli w przedziale działa obciążenie

Jeżeli w przedziale działa obciążenie

ciągłe momentem to wykres

ciągłe momentem to wykres

momentów zginających jest liniowy

momentów zginających jest liniowy

43

43

momentów zginających jest liniowy

momentów zginających jest liniowy

(liniowo zmienny lub w szczególnym

(liniowo zmienny lub w szczególnym

przypadku stały, gdy T

przypadku stały, gdy T





=

=--m).

m).

m

-

ml

M



m

[kN

]

0

m

dM

dx

T

m x







 ( )

Zależności między

Zależności między

M

M



,

,

TT



oraz

oraz

q

q

(14)

(14)

Obciążenie

Wykres T Wykres M

Brak obc. ciągłego

stały

prosta

Obc. ciągłe stałe

prosta

parabola 2

o

44

44

Obc. ciągłe stałe

prosta

parabola 2

o

Obc. ciągłe trójkątne

parabola 2

o

parabola 3

o

Siła skupiona

skok

załamanie

Moment skupiony

–

skok

Obc. ciągłe momentem

–

prosta