E. Żak
Teoria sterowania, P. A. – wykład
PIERWSZA METODA LAPUNOWA
Weźmy pod uwagę układ nieliniowy autonomiczny, opisany
wektorowym równaniem różniczkowym o postaci :
F(x)
x
(1)
przy czym: x – n wymiarowy wektor stanu; F – funkcja wektorowa
nieliniowa, różniczkowalna względem x.
Niech punkt x=0 będzie punktem równowagi tego układu, czyli
0
F(0)
Przybliżenie liniowe równania nieliniowego (1) ma postać
Ax
x
(2)
przy czym macierz kwadratowa A jest określona zależnością
0
x
x
F
A
(3)
Pierwsza metoda Lapunowa formułuje warunki stabilności
lokalnej w punkcie równowagi x = 0 układu nieliniowego, opisanego
równaniem (1), w oparciu o przybliżenie liniowe (2).
Układ nieliniowy jest stabilny lokalnie asymptotycznie w
punkcie równowagi x=0, jeżeli przybliżenie liniowe jest stabilne
asymptotycznie, tzn. gdy wszystkie pierwiastki równania
charakterystycznego
det [sI – A] = s
n
+a
n-1
s
n-1
+…+a
1
s+a
0
= 0
(4)
leżą w lewej półpłaszczyźnie płaszczyzny zmiennej zespolonej s.
Jeżeli przybliżenie liniowe (2) jest niestabilne, to układ
nieliniowy jest niestabilny. Jeżeli przybliżenie liniowe jest stabilne,
ale nieasymptotyczne, to o zachowaniu układu nieliniowego nic nie
można powiedzieć na podstawie przybliżenia liniowego (2).
W przypadku, gdy przybliżenie liniowe (2) jest stabilne
asymptotycznie lub niestabilne, część nieliniowa rozwinięcia w szereg
Taylora R(x) funkcji F(x) nie ma wpływu na stabilność w punkcie
równowagi układu nieliniowego. W przypadku natomiast, gdy
przybliżenie liniowe (2) jest stabilne, ale nieasymptotycznie, to o
stabilności układu nieliniowego decyduje część nieliniowa
rozwinięcia w szereg Taylora R(x).
E. Żak
Teoria sterowania, P. A. – wykład
Przykład 1.
Określić, dla jakich wartości współczynnika a układ nieliniowy opisany
równaniem różniczkowym
0
dt
dx
b
x
dt
dx
a
dt
x
d
2
2
2
(5)
jest stabilny lokalnie w punkcie równowagi x = 0,
0
dt
dx
.
Przybliżenie liniowe równania nieliniowego (5) ma postać
0
x
dt
dx
a
dt
x
d
2
2
(6)
Z kryterium Hurwitza wynika, że równanie charakterystyczne przybliżenia
liniowego
s
2
+as+1 = 0
(7)
ma oba pierwiastki w lewej płaszczyźnie dla a > 0.
Układ nieliniowy, opisany równaniem (5), jest więc stabilny lokalnie w
punkcie równowagi dla a > 0.
E. Żak
Teoria sterowania, P. A. – wykład
DRUGA METODA LAPUNOWA
Druga metoda Lapunowa, zwana również metodą bezpośrednią,
formułuje tylko warunki dostateczne stabilności zwykłej i
asymptotycznej w obszarze ograniczonym i nieograniczonym. Przy
sformułowaniu tej metody korzysta się z pojęcia funkcji dodatnio i
ujemnie określonej oraz funkcji dodatnio półokreślonej i ujemnie
półokreślonej.
Funkcję V(x) wektora stanu x nazywamy dodatnio (ujemnie)
określoną w obszarze D, zawierającym początek układu
współrzędnych przestrzeni stanu, jeżeli funkcja ta w każdym punkcie
tego obszaru D, różnym od początku układu współrzędnych x
0,
przyjmuje wartość dodatnią (ujemną) i wartość równą zeru tylko w
punkcie x = 0.
Funkcję V(x) wektora stanu x nazywamy dodatnio (ujemnie)
półokreśloną lub nieujemnie (niedodatnio) określoną w obszarze D,
zawierającym początek układu współrzędnych przestrzeni stanu, jeżeli
funkcja ta w dowolnym punkcie tego obszaru D przyjmuje wartość
nieujemną (niedodatnią).
Np. funkcja
2
2
2
1
x
x
V
(jest nieujemnie określoną) – w
przestrzeni trójwymiarowej x
1
, x
2
, x
3
, gdyż funkcja ta przyjmuje
wartość równą zeru dla x
1
= 0, x
2
= 0 i dowolnego x
3
.
Jednoznaczną funkcję V(x) ciągłą wraz z pierwszymi
pochodnymi względem zmiennych stanu x
1
, x
2
, …, x
n
(składowych
wektora stanu x) nazywać będziemy funkcją Lapunowa w
obszarze D, jeżeli:
1)
V(x) jest dodatnio określona w obszarze D, tzn. V(x) > 0 dla
x
0 i V(0) = 0;
2)
pochodna względem czasu t funkcji V(x) jest ujemnie
określona w obszarze D, tzn. V(x) < 0 dla x
0 i V(x) = 0
tylko dla x = 0;
3)
V(x)
dla
n
n
2
2
2
1
2
x
...
x
x
x
.
E. Żak
Teoria sterowania, P. A. – wykład
Korzystając z pojęcia gradientu funkcji V(x), określonego
zależnością
n
1
dx
V(x)
x
V(x)
V(x)
grad
(8)
oraz równania (1) można pochodną funkcji V(x) względem czasu t
wyrazić za pomocą wzoru
T
n
n
1
1
dt
dx
dt
dx
x
V(x)
...
dt
dx
x
V(x)
(x)
V
grad V(x) =
[F(x)]
T
grad V(x)
(9)
przy czym T oznacza działanie transpozycji.
Z zależności (9) wynika, że w pochodnej po czasie funkcji
Lapunowa zawarta jest dynamika układu.
Druga metoda Lapunowa
Układ nieliniowy opisany równaniem (1) jest stabilny
asymptotycznie w obszarze D, zawierającym początek układu
współrzędnych, jeżeli można dobrać funkcję Lapunowa V(x),
dodatnio określoną w obszarze D, której pochodna względem czasu
(x)
V
wzdłuż trajektorii fazowej jest funkcją ujemną określoną w
tym obszarze. Jeżeli pochodna
(x)
V
jest funkcją ujemnie
półokreśloną (niedodatnio określoną) w obszarze D, to układ
nieliniowy jest stabilny w tym obszarze D, ale niekoniecznie
asymptotycznie.
E. Żak
Teoria sterowania, P. A. – wykład
Poniżej naszkicowano geometryczną ideę dowodu powyższego twierdzenia. Jako
funkcję Lapunowa weźmy funkcję dodatnio określoną postaci
n
1
k
2
k
2
k
x
a
V(x)
(10)
przy czym:
x
1
, x
2
, …, x
n
są zmiennymi stanu (składowymi wektora stanu x), natomiast a
1
, a
2
,
…, a
n
są liczbami rzeczywistymi różnymi
od zera.
Niech funkcja (10) przyjmuje kolejno rosnące wartości, równe 0, C
1
, C
2
, … (0 < C
1
< C
2
<…). Otrzymamy wówczas
n
1
k
2
k
2
k
0
x
a
(
11)
1
n
1
k
2
k
2
k
C
x
a
(
12)
2
n
1
k
2
k
2
k
C
x
a
(
13)
W przestrzeni stanów wyrażeniu (11) odpowiada początek układu współrzędnych
x = 0, a wyrażeniom (12), (13), …,n-wymiarowe hiperelipsoidy, przy czym hiperelipsoida
określana wyrażeniem (13) obejmuje hiperelipsoidę określoną wyrażeniem (12) (rys. 1).
Jeżeli pochodna
(x)
V
jest funkcją ujemnie określoną, to punkt opisujący na
trajektorii przesuwa się w czasie w kierunku malenia funkcji V, czyli w kierunku
początku układu współrzędnych. Oznacza to, że zmienne stanu x
1
,x
2
, …,
x
n
maleją w
czasie do zera, a rozpatrywany układ jest układem stabilnym asymptotycznie.
Jeżeli pochodna
(x)
V
jest funkcją ujemnie półokreśloną to można dobrać taką
hiperelipsoidę, że punkt opisujący dla dowolnej chwili t > 0 będzie się znajdował
wewnątrz tej hiperelipsoidy. Oznacza to, że zmienne stanu x
1
, x
2
, …, x
n
są ograniczone, a
układ rozpatrywany jest układem stabilnym, ale nieasymptotycznie.
Rys. 1. Ilustracja geometryczna idei dowodu
drugiej metody Lapunowa w
przestrzeni trójwymiarowej.
E. Żak
Teoria sterowania, P. A. – wykład
Wybór funkcji Lapunowa
Jako funkcję Lapunowa V(x) wybiera się najczęściej formę
kwadratową dodatnio określoną lub sumę formy kwadratowej
dodatnio określonej i całki charakterystyki członu nieliniowego.
Bx
x
x
x
b
V(x)
T
n
1
j
i,
j
i
ij
(14)
przy czym B jest macierzą symetryczną (b
ij
= b
ji
) o postaci
nn
n2
n1
2n
22
21
1n
12
11
b
...
b
b
...
...
...
...
b
...
b
b
b
...
b
b
B
(15)
a x wektorem o składowych x
1
, x
2
, …, x
n
.
Forma kwadratowa (14) jest dodatnio określona wtedy i tylko
wtedy, gdy wszystkie podwyznaczniki główne oraz sam wyznacznik
macierzy B są dodatnie czyli
;
b
0
11
1
;
b
b
b
b
0
22
21
12
11
2
…;
0
b
....
b
b
....
....
....
....
b
....
b
b
b
....
b
b
Δ
nn
n2
n1
2n
22
21
1n
12
11
n
(
16)
Weźmy pod uwagę układ autonomiczny liniowy stacjonarny,
opisany równaniem jednorodnym
Ax
x
(17)
przy czym x – n-wymiarowy wektor stanu, A – macierz kwadratowa
n
n o stałych niezależnych od czasu elementach.
Jako funkcję Lapunowa V(x) dla tego układu weźmy formę
kwadratową (14)
V(x) = x
T
Bx
(
18)
Pochodna względem czasu funkcji Lapunowa (18) jest równa
x
B
x
Bx
x
(x)
V
T
T
(
19)
E. Żak
Teoria sterowania, P. A. – wykład
Po podstawieniu zależności (17) do (19) otrzymujemy
Wx
x
x
BA)
B
(A
x
(x)
V
T
T
T
20
przy czym
-W = A
T
B + BA
21
Macierz W dobieramy tak, aby pochodna względem czasu funkcji
Lapunowa (20) była funkcją ujemnie określoną. Dla danych macierzy A i W
rozwiązując równanie macierzowe (21) wyznaczamy macierz B. Jeżeli elementy
tej macierzy spełniają warunki (16), to funkcja Lapunowa (18) jest dodatnio
określona. Z powyższych rozważań wynika następujący wniosek.
Układ autonomiczny liniowy stacjonarny, opisany równaniem
(17), jest stabilny asymptotycznie w punkcie x = 0 wtedy i tylko
wtedy, gdy dla dowolnej symetrycznej dodatnio macierzy W istnieje
symetryczna dodatnio określona macierz B, będąca jedynym
rozwiązaniem równania (21), a funkcja (18) jest funkcją Lapunowa.
Często jako macierz dodatnio określoną W przyjmuje się macierz jednostkową,
W = I. W tym przypadku równanie (21) przyjmuje postać
A
T
B + BA = -I
(22)
Przykład 1. Jest dany układ autonomiczny liniowy stacjonarny, opisany
równaniem
2
1
x
x
4
0
7
3
x
x
23
W tym przypadku
4
0
7
3
A
;
21
12
12
11
b
b
b
b
B
24
a równanie (22) ma postać
1
0
0
1
4
0
7
3
b
b
b
b
b
b
b
b
4
7
0
3
22
12
12
11
22
12
12
11
25
Wykonując wskazane mnożenie macierzy i porównując odpowiednie elementy
macierzy otrzymamy układ trzech równań o postaci
-6 b
11
= -1
-7 b
12
– 7 b
11
= 0
26
E. Żak
Teoria sterowania, P. A. – wykład
-14 b
12
– 8 b
22
= -1
Rozwiązując ten układ równań otrzymamy b
11
=
6
1
, b
12
= -
6
1
, b
22
=
12
5
Macierz B ma zatem postać
B =
5
2
2
2
12
1
27
Warunki (16) dla macierzy (27) mają postać
0
6
1
11
1
b
;
0
24
1
12
5
6
1
6
1
6
1
22
12
12
11
2
b
b
b
b
Funkcja Lapunowa (18)
V(x) = [x
1
x
2
]
)
5x
x
4x
(2x
12
1
x
x
5
2
2
2
12
1
2
2
2
1
2
2
1
27’
jest więc dodatnio określona, a układ opisany równaniem (23) jest stabilny
asymptotycznie.
Przykład 2. Jako funkcję Lapunowa dla układu nieliniowego, opisanego
równaniem (5), przyjmuje formę kwadratową dodatnio określoną w całej
płaszczyźnie x
1
, x
2
o postaci
V(x) =
2
2
2
1
x
x
2
1
28
Wprowadzając zmienne stanu x
1
= x, x
2
= x, możemy równanie (5) napisać w
postaci
2
1
x
x
29
3
2
2
1
2
bx
ax
x
x
Wobec tego
)
bx
ax
(
)
bx
ax
x
(
x
x
x
x
x
)
x
(
V
x
x
)
x
(
V
)
x
(
V
4
2
2
2
3
2
2
1
2
2
1
2
2
1
1
30
Pochodna
(x)
V
jest ujemnie określona w całej płaszczyźnie dla
a >0 i b > 0. Układ nieliniowy jest zatem stabilny asymptotycznie globalnie dla
a > 0 i b > 0.
Z zależności (30) wynika, że dla a > 0 i b < 0 pochodna (x)
V
jest ujemnie
określona dla
b
a
x
0
2
2
31
E. Żak
Teoria sterowania, P. A. – wykład
W tym przypadku układ nieliniowy jest stabilny asymptotycznie w
obszarze ograniczonym, określonym nierównością
j
K
1
Δarg
= n
-(n-2k)
= 2k
Weźmy pod uwagę układ autonomiczny nieliniowy, opisany równaniem
(1), którego punktem równowagi jest punkt x = 0. Jako funkcję Lapunowa dla
tego układu A. Krakowski proponuje formę kwadratową o postaci
V(x) = [F(x)]
T
BF(x)
32
przy czym:
F(x) – wektor n-wymiarowy będący prawą stroną równania (1) o
składowych f
1
(x)
,
f
2
(x), …,f
n
(x);
B – macierz symetryczna dodatnio określona o stałych, niezależnych od
czasu elementach.
Biorąc pod uwagę, że
AF(x)
x
x
F(x)
(x)
F
33
gdzie
n
n
1
n
1
1
1
1
x
(x)
f
......
x
(x)
f
.
..........
......
.
..........
n
(x)
f
......
x
(x)
f
x
F(x)
A
34
możemy napisać następujące wyrażenie na pochodną względem czasu funkcji
(31):
(x)
V
[
F
(x)]
T
BF(x) + [F(x)]
T
F
B
(x) =
35
=[F(x)]
T
[A
T
B + BA]F(x) = - [F(x)]
T
WF(x)
przy czym
A
T
B + BA = -W
36
Aby pochodna
(x)
V
była funkcją ujemnie określoną, macierz W musi być
dodatnio określona.
Często jako macierz B przyjmuje się macierz jednostkową I. W tym
przypadku szczególnym po podstawieniu B = I zależności (32) i (36) przyjmują
postać
V(x) = [F(x)]
T
F(x)
37
oraz
A
T
+ A = -W
38
E. Żak
Teoria sterowania, P. A. – wykład
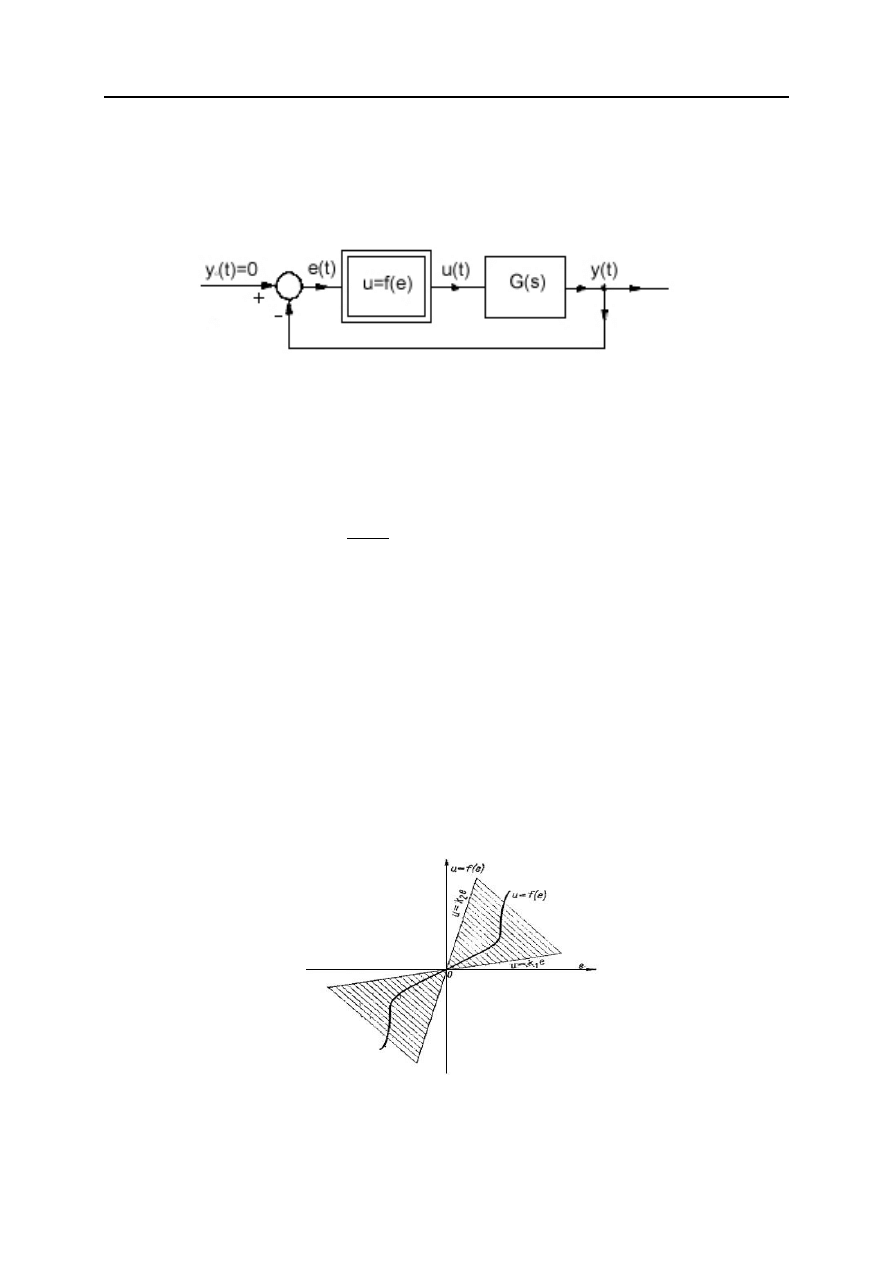
Weźmy pod uwagę układ nieliniowy z ujemnym sprzężeniem
zwrotnym (rys. 3), który składa się z członu nieliniowego o
charakterystyce u = f(e) oraz z członu liniowego o transmitancji
operatorowej G(s).
Rys. 3.
Schemat blokowy układu nieliniowego z ujemnym
sprzężeniem zwrotnym.
Niech charakterystyka u = f(e) członu nieliniowego spełnia warunek
2
1
k
e
f(e)
k
,
f(0) = 0
47
przy czym: k
1
i k
2
są dowolnymi nieujemnymi liczbami
rzeczywistymi.
Warunek (47) oznacza, że charakterystyka u = f(e) leży między
prostymi u = k
1
e oraz u = k
2
e, przechodzącymi przez początek układu
współrzędnych (rys. 4). W przypadku szczególnym może być k
1
= 0, a
k
2
=
.
Załóżmy, że część liniowa rozpatrywanego układu nieliniowego
jest członem stabilnym, tzn. że wszystkie bieguny transmitancji
operatorowej G(s), leżą w lewej półpłaszczyźnie zmiennej zespolonej
s.
Rys. 4.
Przykładowy przebieg charakterystyki u = f(e), spełniający
warunek (47).
E. Żak
Teoria sterowania, P. A. – wykład
Dla tej klasy układów nieliniowych w wielu przypadkach jako funkcję
Lapunowa wygodnie jest przyjąć sumę formy kwadratowej dodatnio
określonej L(x) i całki charakterystyki członu nieliniowego f(e), czyli
przyjąć funkcję Lapunowa o postaci
V(x) = L(x) +
ε
0
d
)
(
f
48
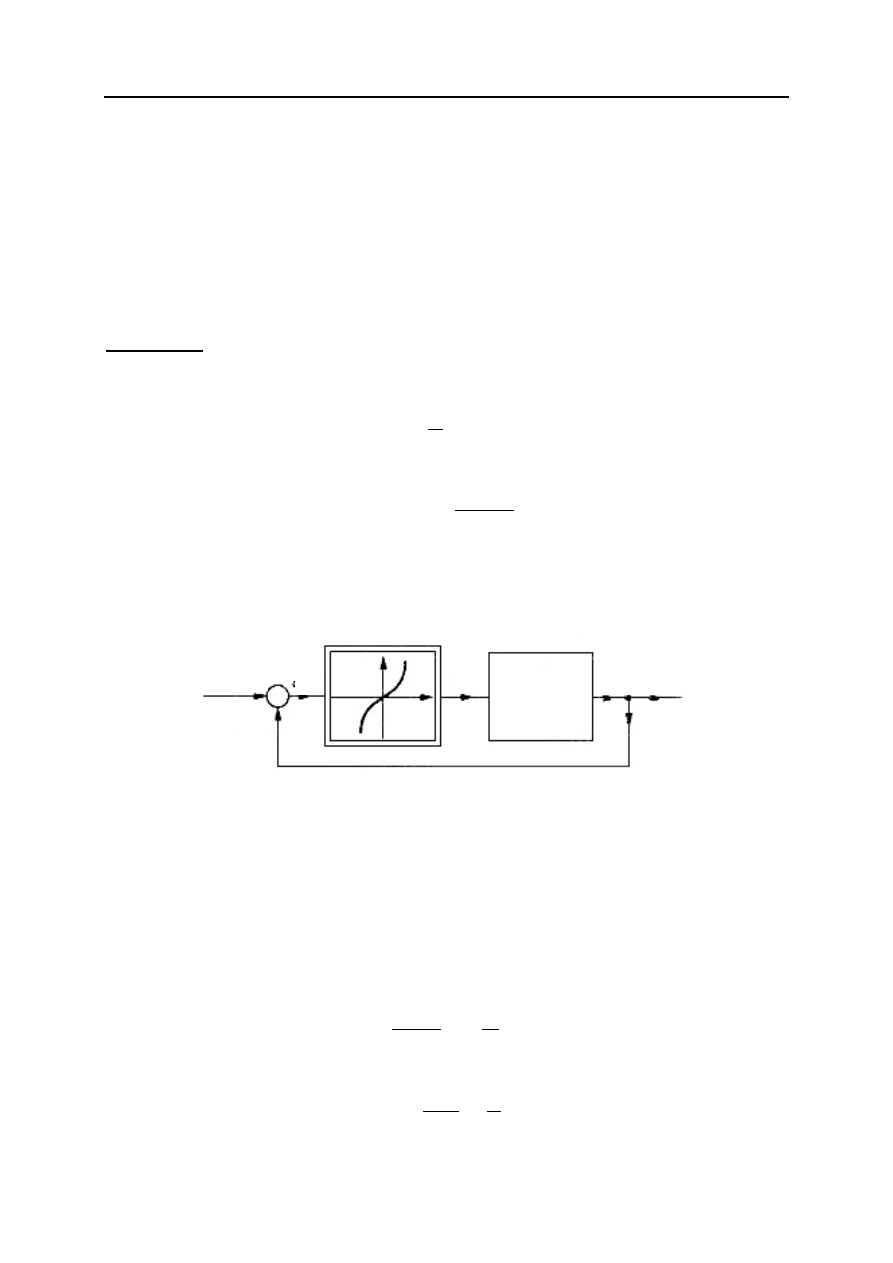
Przykład 3.
Jest dany układ nieliniowy z dodatnim sprzężeniem zwrotnym (rys. 2), który
składa się z członu nieliniowego o charakterystyce
3
e
e
2
1
u
39
oraz z członu liniowego o transmitancji
sT
1
k
G(s)
40
przy czym współczynnik k i stała czasowa T są dodatnie.
Należy wyznaczyć wartości początkowe wielkości regulowanej y(t) = y,
dla których układ ten jest stabilny asymptotycznie.
Rys. 2.
Schemat blokowy układu nieliniowego z dodatnim
sprzężeniem zwrotnym.
Człon liniowy jest opisany równaniem
ku
y
y
T
41
Podstawiając zależność (39) do równania (41) po uwzględnieniu, że w
tym przypadku e = y(y
0
(t) = 0), otrzymamy
2
2
2
y
T
k
y
T
k
y
42
Jako funkcję Lapunowa przyjmujemy funkcję o postaci
V(y) =
2
3
y
T
k
y
T
2
2
k
43
Wobec tego
y(t)
y
0
(t)=0
u
G(s)
e(t)
E. Żak
Teoria sterowania, P. A. – wykład
2
2
3
3
2
2
2
2
2
y
T
k
T
k
y
T
k
y
T
k
y
y
)
y
(
V
)
y
(
V
44
Pochodna względem czasu funkcji Lapunowa będzie zatem ujemnie
określona, gdy
0
y
T
k
3
T
2
2
k
2
45
czyli rozpatrywany układ nieliniowy jest stabilny asymptotycznie dla wartości
początkowych wielkości regulowanej y, spełniających warunek (46).
k
k
y
6
2
2
46
Przykład 4.
Korzystając z drugiej metody Lapunowa należy wykazać, że układ nieliniowy
złożony z członu nieliniowego o charakterystyce u = f(e) spełniającej warunek
(47) oraz członu liniowego o transmitancji (40) jest stabilny asymptotycznie w
obszarze nieograniczonym.
Przebieg uchybu regulacji e = e(t) w tym układzie jest opisane równaniem
)
e
(
f
T
k
T
e
e
49
Jako funkcję Lapunowa przyjmujemy funkcję o postaci (48).
e
d
)
(
f
e
)
e
(
V
0
2
2
1
50
Dla charakterystyk u = f(e) spełniający warunek (47) funkcja (50), jest
funkcją dodatnio określoną dla dowolnej wartości uchybu regulacji e oraz
przyjmuje wartość nieskończenie wielką dla e dążącego do nieskończoności.
Pochodna względem czasu funkcji (50) jest równa
x
)
e
(
f
e
e
)
e
(
f
e
e
de
dV
)
e
(
V
)
e
(
ef
T
k
)
e
(
f
T
k
T
e
)
e
(
f
T
k
T
e
1
2
2
51
Z założenia k > 0 i T > 0. Pochodna
)
e
(
V
jest więc funkcją ujemnie określoną
dla każdej charakterystyki u = f(e) spełniającej warunek ef(e)
0, czyli warunek
(47). Rozpatrywany układ nieliniowy jest zatem stabilny asymptotycznie w
przedziale nieograniczonym tzn. dla dowolnych warunków początkowych.
Powyższe rozważania dotyczące drugiej metody Lapunowa można
uogólnić na przypadek układów impulsowych.